1 引言
无线信息与能量协同传输(Simultaneous Wireless Information and Power Transfer, SWIPT)是解决能量受限网络中能量稀缺问题的无线传输技术。不同于传统的依靠外界电源供能的网络,SWIPT网络节点从接收的射频信号中收集能量,并将其用于后续信息的发送,克服了能量收集技术对外界电源的依赖。同时,无线节点不便配置可靠电源的缺陷也得到了弥补[1-3]。SWIPT中继通过缓存队列机制,中继配备能量和信息两种存储器,可利用能量存储器中的能量转发信息存储器缓存队列中的信息,拥有更多的自由度。
在半双工(Half-duplex,HD)中继中加入缓存队列(缓存队列长度有限或无限),中继可以在一个时隙实现收和发,与没有缓存队列的半双工中继相比拥有更高的频谱效率[4- 6]。文献[7]研究基于能效优先的缓存队列机制SWIPT最佳接收/转发中继节点选择方案,在保证能量收集约束和信息传输频带利用率约束下,综合考虑缓存队列的状态,选出一对HD中继,在同一个时隙分别进行收发,实现虚拟全双工(Full-duplex,FD),所提方法使系统的中断概率性能得到了提升。
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)因为其对频率选择性衰落信道的鲁棒性以及具有较高的频谱利用率而成为当前无线通信系统中的一种高效多载波调制。在OFDM系统中,合理的资源(子载波、功率、比特)分配与调度对于充分利用系统资源至关重要[8]。当前,网络资源分配技术指标主要包括频带利用率、能量有效性(Energy Efficiency,EE)、用户服务质量、公平性、干扰限制等[9]。目前SWIPT的资源分配大多以频带利用率为优化目标。文献[10]研究了单中继两跳SWIPT的资源分配问题,在发送端功率受限的条件下,通过对源到中继和中继到目的节点子载波功率的分配,最大化端到端的可达速率。文献[11]在文献[10]的基础上考虑了电路功耗,结合遗传算法和非线性规划算法,得到了频带利用率的最优值。
论文以缓存队列机制SWIPT网络为研究背景,以最大化SWIPT转发中继到目的端的能效[12]为目标,在满足能量、信息传输速率、最佳接收中继干扰等多个约束条件下,通过构造与求解优化问题,在选择SWIPT最佳转发中继的同时得到OFDM子载波与能量联合分配的最优解。仿真结果表明,与文献[10]最大化端到端可达速率为目标的SWIPT资源分配算法相比,所提方案考虑了SWIPT网络中继间干扰。且当源端发送功率较大时,所提方案可获得较高的能效。
该文结构安排如下:第2部分详细阐述SWIPT网络缓存队列中继能量分配模型,第3部分对优化问题进行建模,第4部分通过对优化问题进行求解,第5部分为数值仿真分析,最后为全文总结。
2 系统建模与假设
在图1所给出的保障能效的SWIPT缓存队列中继选择场景图中,SWIPT网络包括源节点S、目的节点D以及包含K个SWPIT中继节点{R1,R2,...,RK}的节点簇。其中, Ri(1≤i≤K)表示第i个SWIPT中继节点,采用基于功率分割的SWIPT中继接收机结构,每个中继处均配备功率分割器、信息收发机和能量收集器。信息收发机用于接收S发送的数据并对其进行解码,配备有长度为L的缓存队列。存储在中继Ri的数据包数量用参数Li表示。能量收集器用于收集能量,存储在Ri的能量用参数Ei表示。在每一时隙选出一对最佳接收中继
和最佳转发中继
接收S发送的数据,解码后将其存放在缓存队列中;
利用其能量收集器中的能量将缓存队列中的数据转发至D。
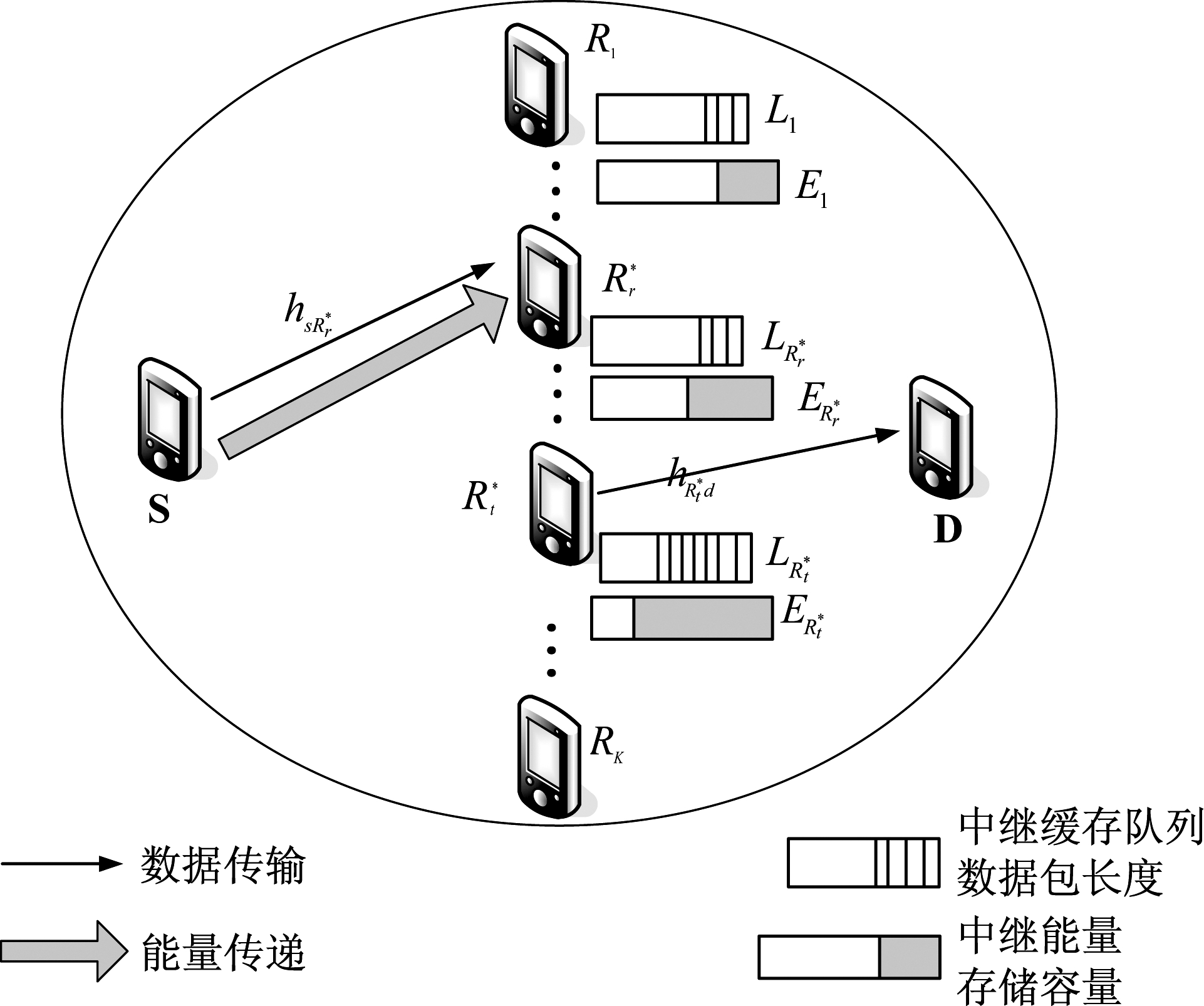
图1 SWIPT网络缓存队列中继选择场景
Fig.1 Buffer-aided SWIPT relay selection scenario
不失一般性,在某一时隙,论文首先根据文献[6]中的方法选出了一对最佳接收中继和最佳转发中继
其中,最佳转发中继的频带被分为N个正交子载波,将缓存队列中的信息通过OFDM技术转发到目的端D,hD, j(1≤j≤N)表示第j个子载波到目的端D的信道系数,
表示第j个子载波到的信道系数。假设T为完成一次传输的总时间,最佳接收中继和最佳转发中继根据如表1所示能量收集与信息传输协议进行收发。
表1 能量收集与信息传输协议
Tab.1 Energy harvesting and information transmission protocol
第一阶段T/2R∗r从S收集能量lR∗rPs;S向R∗r传输信息(1-lR∗r)Ps;第二阶段T/2R∗t为每个子载波分配能量,子载波以功率PR∗t, j将信息转发到D。
在文献[7]的基础上考虑最佳转发中继多个子载波的情况,最佳接收中继接收到的信号包括来自源端的信号以及最佳转发中继对它的干扰
(1)
其中,S发送功率为PS,xs表示源端归一化发送信号,
表示源到最佳接收节点的信道系数,
为当前时隙的功率分割因子,
表示最佳转发中继为第j个子载波分配的功率,
表示最佳转发中继每个子载波的归一化发送信号,由于两个中继在同一中继簇内,不考虑他们之间的距离,S与最佳接收中继之间距离为
为路径衰耗指数,噪声服从均值为零、方差为σ2的高斯分布。
最佳接收中继收集到的能量为
(2)
目的节点D接收到的信号为
(3)
其中,最佳转发中继到目的节点的距离为
最佳转发中继当前要转发信息的可用能量为其在接收当前要发送的信息时收集的能量表示为
(4)
其中,能量转换效率
表示接收该信息时的功率分割因子,
表示转发中继在接收当前要发送的信息时的信道状态,
表示源到最佳转发中继的距离。
最佳转发中继的可用功率可以表示为
(5)
源节点S-最佳接收中继
最佳发送中继
目的节点D间的频带利用率分别表示为
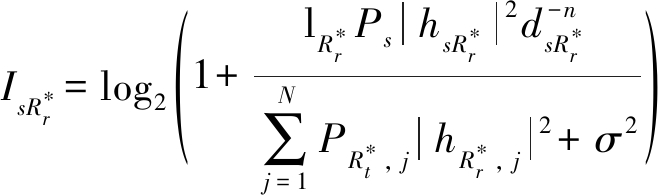
(6)
为了不失一般性,在具体描述能量分配算法之前,做出如下假设:
(1)中继节点的信息收发机和能量收集器的存储空间足够大。因此,数据与能量溢出问题无需考虑。
(2)在完成一次传输所需时间T内,一个中继节点只能接收或转发一个数据包,且接收某数据包时收集的能量只能用于转发该数据包。
(3)系统中所有信道都服从瑞利平坦衰落,且信道状态在一个传输时隙内保持不变,信道系数相互独立。
(4)当最佳转发中继对最佳接收中继的干扰小于某个门限Ith时,最佳接收中继可以忽略其干扰的影响。
3 优化问题建模
考虑最佳转发中继多个子载波的情况,最佳转发中继的信息速率可以表示为
(7)
其中,
能量效率通常被定义为单位能量消耗所达到的信息速率,参考文献[13]中能效的表达式,并考虑功率放大系数为1的情况,最佳转发中继到目的端的能效可以表示为
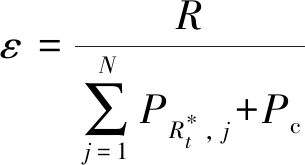
(8)
其中,ε表示最佳转发中继到目的端的能效,单位为
表示分配给子载波用于转发的功率,Pc表示最佳转发中继的电路消耗。
论文建立了最佳接收中继子载波功率分配最大化能效的优化问题1,如式(9)所示。
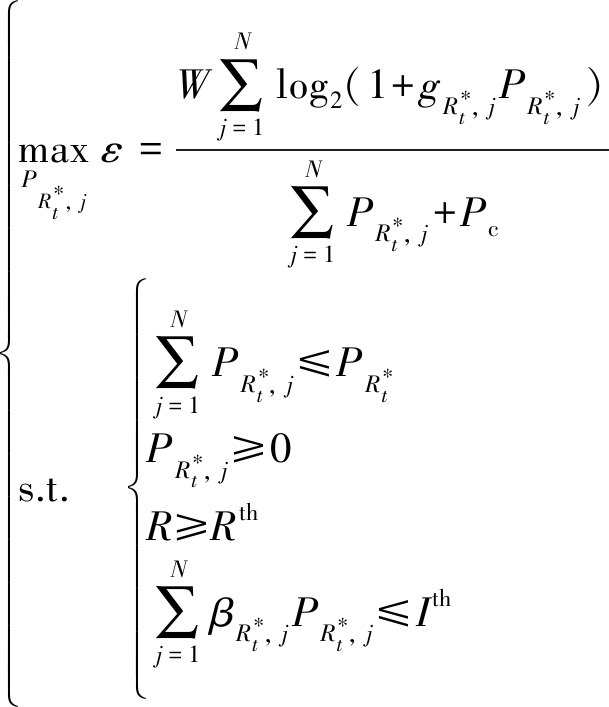
(9)
其中,约束1表示转发该信息所消耗的能量要小于接收该信息时收集的能量。约束2表示每次分配的功率要为非负值,约束3表示目的端达到的信息速率要超过目的端信息速率要求,约束4表示最佳转发中继对最佳接收中继的干扰小于门限
目标函数是关于的非凸函数,所以目标问题是一个非凸优化的问题,不能利用卡罗需库恩塔克(Karush-Kuhn-Tucker, KKT)条件进行直接求解,参考注水因子辅助的策略,论文将在下一小节对优化问题进行求解。
4 优化问题求解
由于约束条件
和
是关于
的凸函数,论文考虑建立如下子优化问题
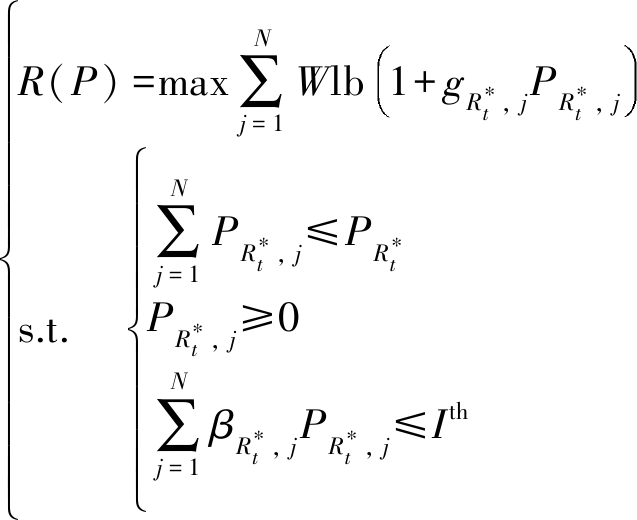
(10)
其中,
表示最佳转发中继实际的总发送功率,介于
之间,在不考虑干扰限制的情况下,对于所有的P≥0,R(P)都有不同的值。
根据文献[14],原优化问题1可以转化为优化问题2,如式(11)所示。
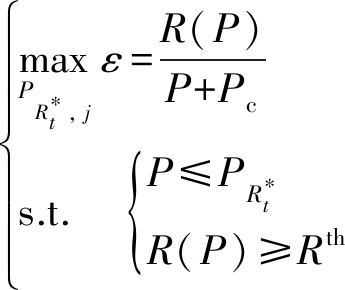
(11)
关于R(P)的子优化问题是一个凸优化问题,利用KKT条件,结合拉格朗日乘子法,可以求得最佳转发中继为第j个子载波分配的功率的优化解
(12)
其中,u和ν分别表示发射功率限制和干扰功率限制的拉格朗日乘子,考虑子载波功率分配后可以出现负值的情况,功率分配的优化解还需满足
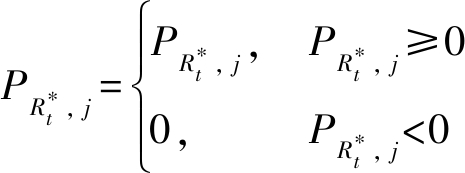
(13)
以8个子载波为例,最佳转发中继的子载波功率联合分配可以由图2表示。首先将u和ν代入求出注水水面,然后根据每个子载波的信道状态为其分配功率。
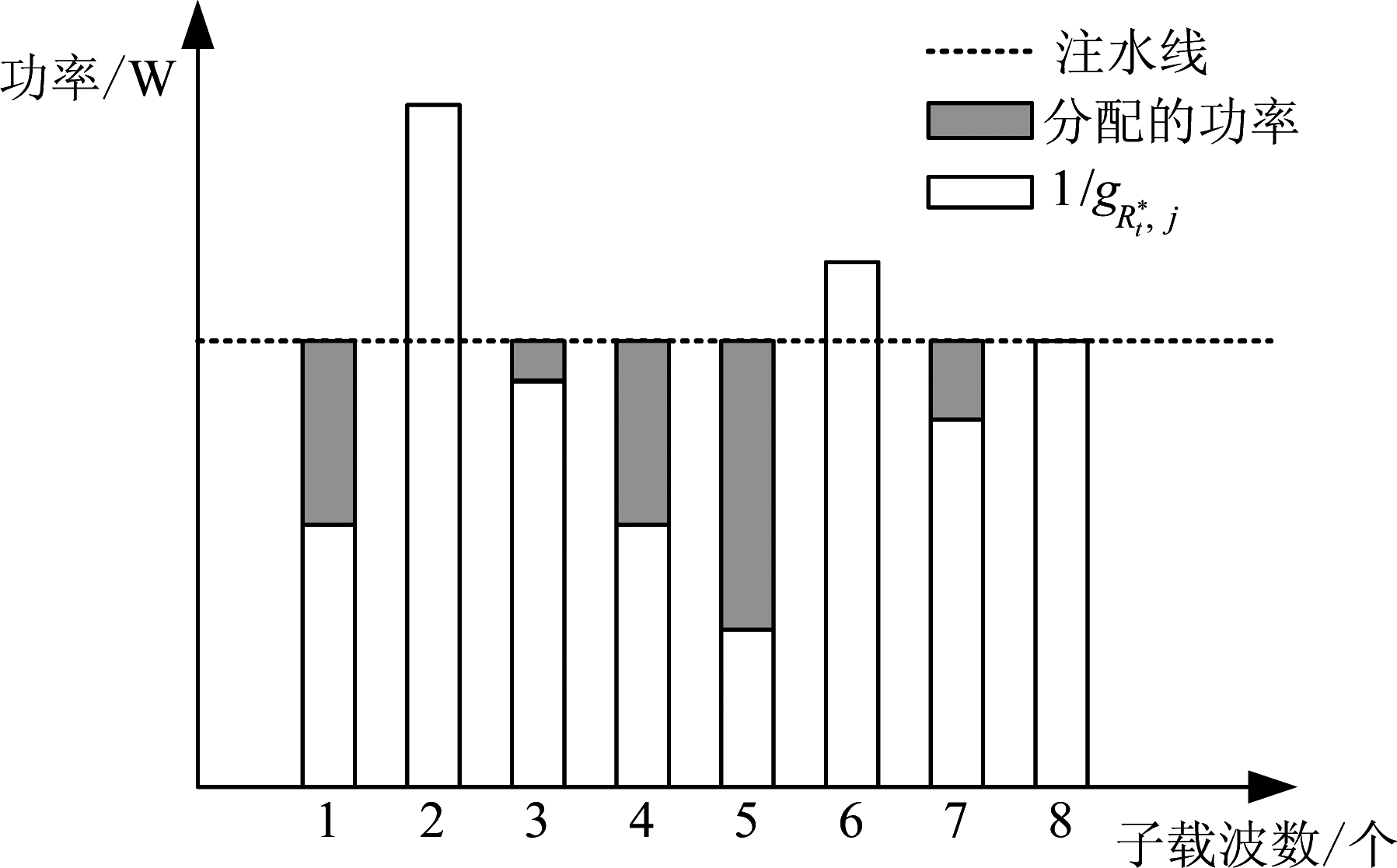
图2 最佳转发中继子载波功率分配场景
Fig.2 Subcarrier power joint allocation scenario for the best SWIPT forward relay
R(P)是关于P严格单调递增的函数,由于干扰约束的存在,当P达到一定值以后,R(P)不再递增,而是保持恒定,此时分配的功率保持恒定。因此,可以求得使R(P)到达最大值的最小P值,即为最佳转发中继的最小发送功率,其对应的子载波功率分配即为最优子载波功率分配。所提出的子载波功率分配方案,在达到最大速率的同时消耗的能量最少,因此具有最大的能效,故所提方案也是优化问题2的最优方案。
假设
为使得R(P)可以达到最大值得最小P值,可以通过一对一映射将
的值映射到
范围。使用P(u)来表示这个映射关系,则P(u)是关于u严格单调递增函数。由于P的值同样可以影响ν值的变化,可以把ν也看作关于u的函数,利用ν(u)来表示
范围内的函数关系。再通过拉格朗日对偶问题在范围内求解R(P),可以得到使功率分配最优的最小ν值。
功率分配算法首先使用二分查找方法,然后利用了u和ν两个拉格朗日乘子进行对子载波通过注水法分配功率,求出优化的功率分配结果
和
可求出对应的R
和ε。
最佳转发中继子载波功率联合分配算法流程图与最佳转发中继信息速率求解流程图分别如图3和图4所示。其中,各变量初始值设置如下
分别由式(12)和优化问题式(10)给出。最佳转发中继对最佳接收中继的干扰功率
表示收敛精度。
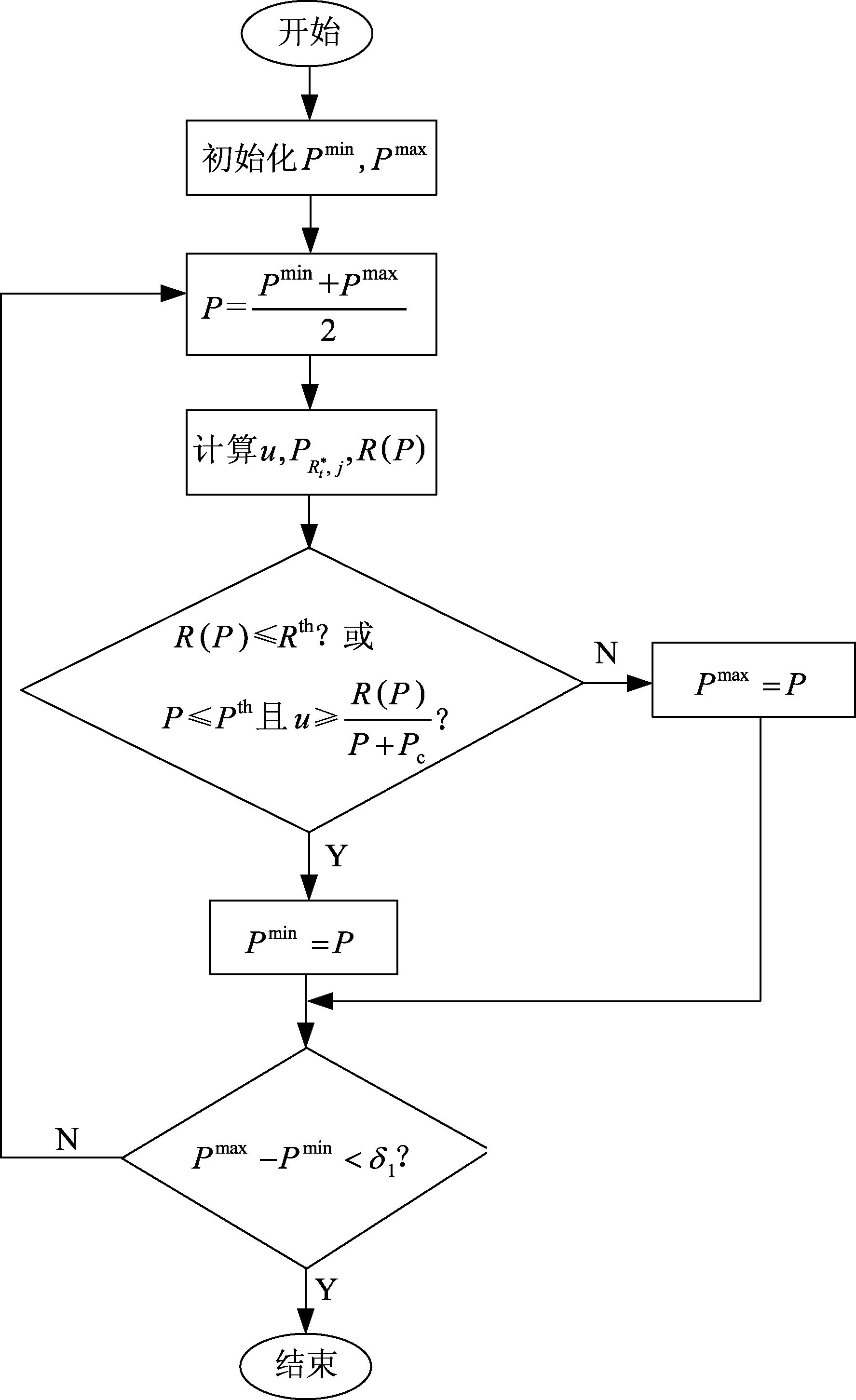
图3 最佳转发中继子载波功率联合分配算法流程图
Fig.3 Subcarrier power joint allocation algorithm flowchart for the best SWIPT forward relay
5 仿真性能分析
本节通过Matlab数值仿真分析最佳转发中继子载波功率分配算法的性能。仿真参数作如下设置[15]。
假设最佳转发中继到接收端的信道带宽被分为多个正交子载波,单个子载波固定带宽为W=15 kHz,最佳转发中继对最佳接收中继的干扰功率阈值Ith=0.2N0,接收端最低信息传输速率阈值Rth=20 kb/s。归一化距离
归一化后的系统总噪声功率为
服从均值为1的指数随机分布,
取(0.04,0.1,0.2,0.4,0.4,0.2,0.1,0.04,0.04,0.1,0.2,0.4,0.2,0.1,0.04…)的前|Χm|个数,|Χm|表示子载波的数目。收敛精度δ1=10-3,δ2=10-5。
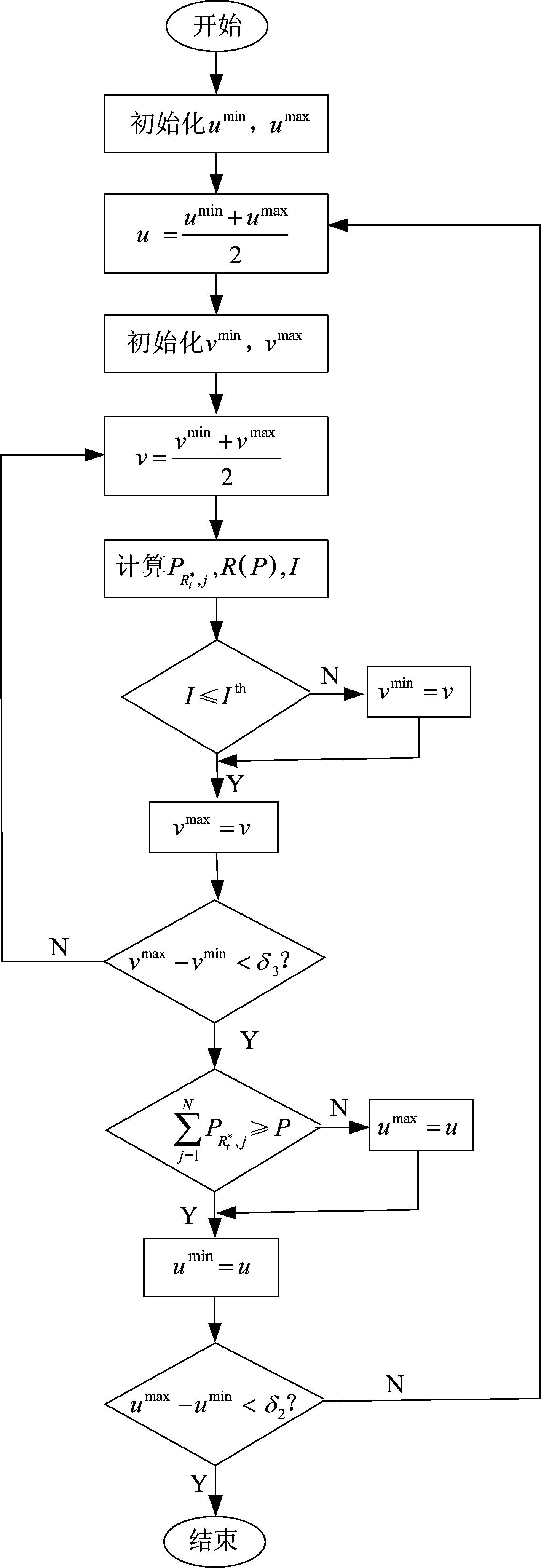
图4 最佳转发中继信息速率求解流程图
Fig.4 Information rate solution flowchart for the best SWIPT forward relay
5.1 源发送功率Ps对能效的影响
图5给出了源发送功率对系统能效的影响。在仿真中设置能量转换效率η为0.5,功率分割因子
为0.3。从图中可以看出,随着源发送功率的增大,中继端的能效逐渐上升,逐渐到达最优值,并保持最优值不变。这是由于,随着源发送功率增大,最佳转发中继可用于分配能量变多,系统能效逐渐上升,但是在可用于分配的能量到达一定数量时,功率分配算法已经获得了最优能效。最佳接收中继子载波数越多,最终优化得到的能效越大。
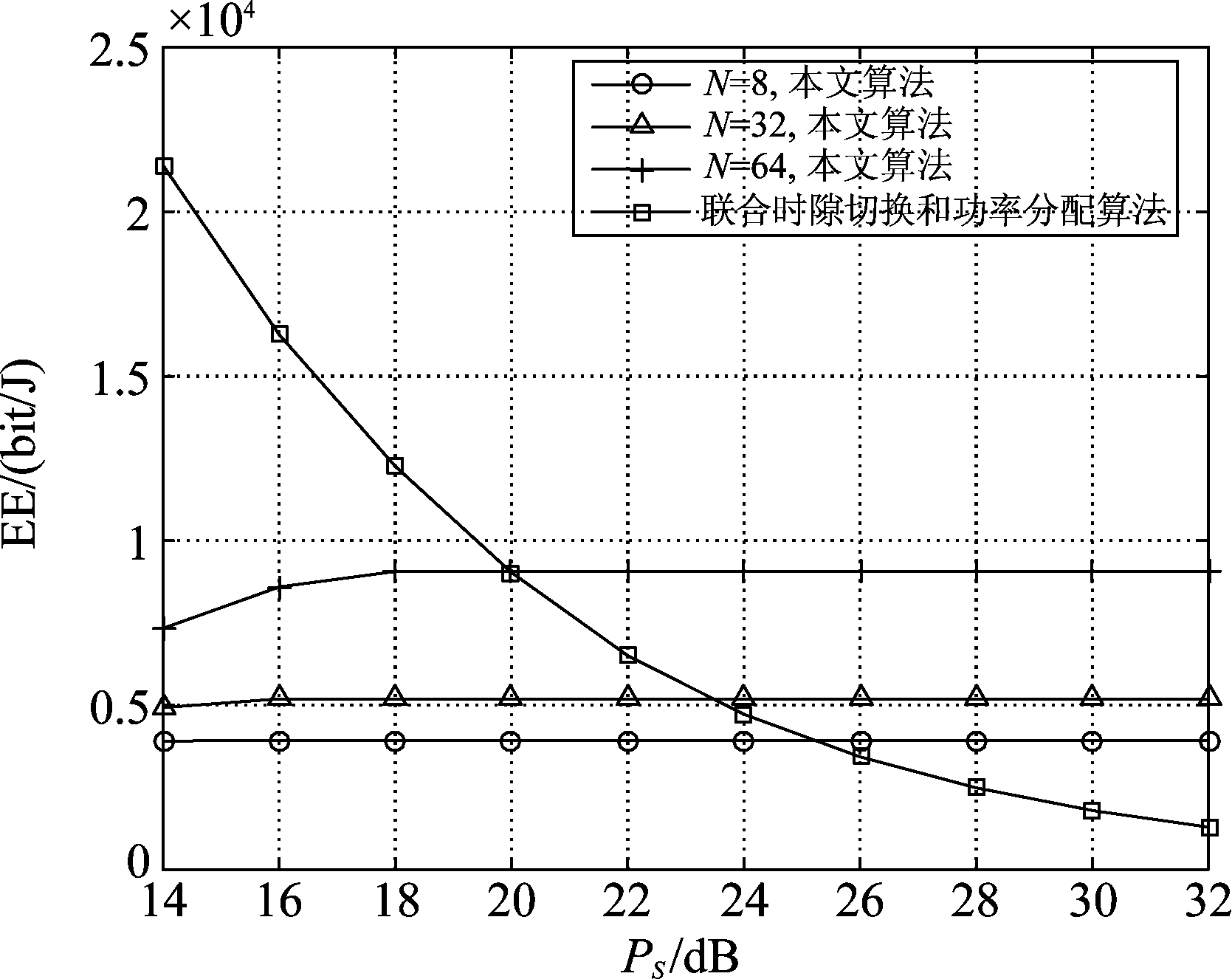
图5 源端发送功率对系统能效的影响
Fig.5 Effect of source-relay power on EE
同时可以看到,当源发送功率大于20 dB(100 W)、子载波数为64时,本文算法能效优于对比文献[10]中的联合时隙切换和功率分配算法。这是因为,随着源发送功率的增大,联合时隙切换和功率分配算法的频谱利用率增大,但其能效逐渐降低。
5.2 功率分割因子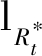对能效的影响
图6给出了功率分割因子对系统能效的影响,在仿真中设置能量转换效率η为0.5,源发送功率为12 dB(15.85 W)。从图中可以看出,随着功率分割因子的增大,SWIPT最佳转发中继的能效逐渐上升,逐渐到达最优值,并保持最优值不变。究其原因,随着功率分割因子的增大,SWIPT最佳转发中继中可用于分配的能量增加,系统能效逐渐上升,但是当可用于分配的能量到达一定值时,功率分配算法已经获得了最优能效。最佳接收中继的子载波数越多,最终优化得到的能效值越大。这与图5的性能一致。
5.3 能效和谱效的关系
图7给出了SWIPT网络中能效与谱效的关系。由图可知,随着源发送功率的增大,SWIPT最佳转发中继可分配的能量逐渐变大,谱效和能效均相应增加。由于干扰约束的存在,当中继可分配能量达到一定值时,目的端频谱利用率和消耗的能量保持不变,谱效和能效不再增加。最终优化得到的谱效和能效均随着子载波数的增加而增大。此外,对SWIPT最佳接收中继的干扰抑制是以牺牲能效和谱效为代价的。
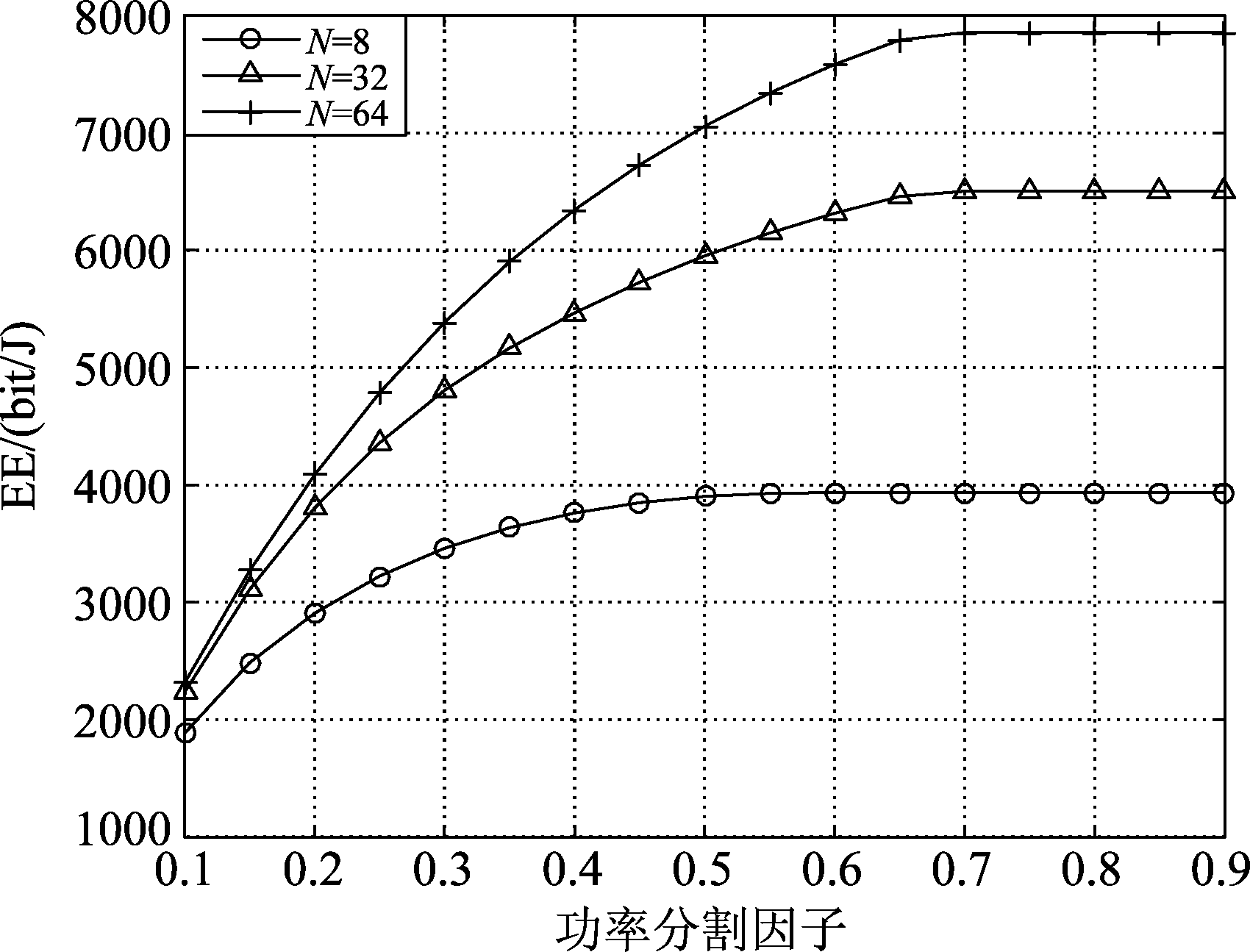
图6 功率分割因子对系统能效的影响
Fig.6 Effect of power split factor on EE
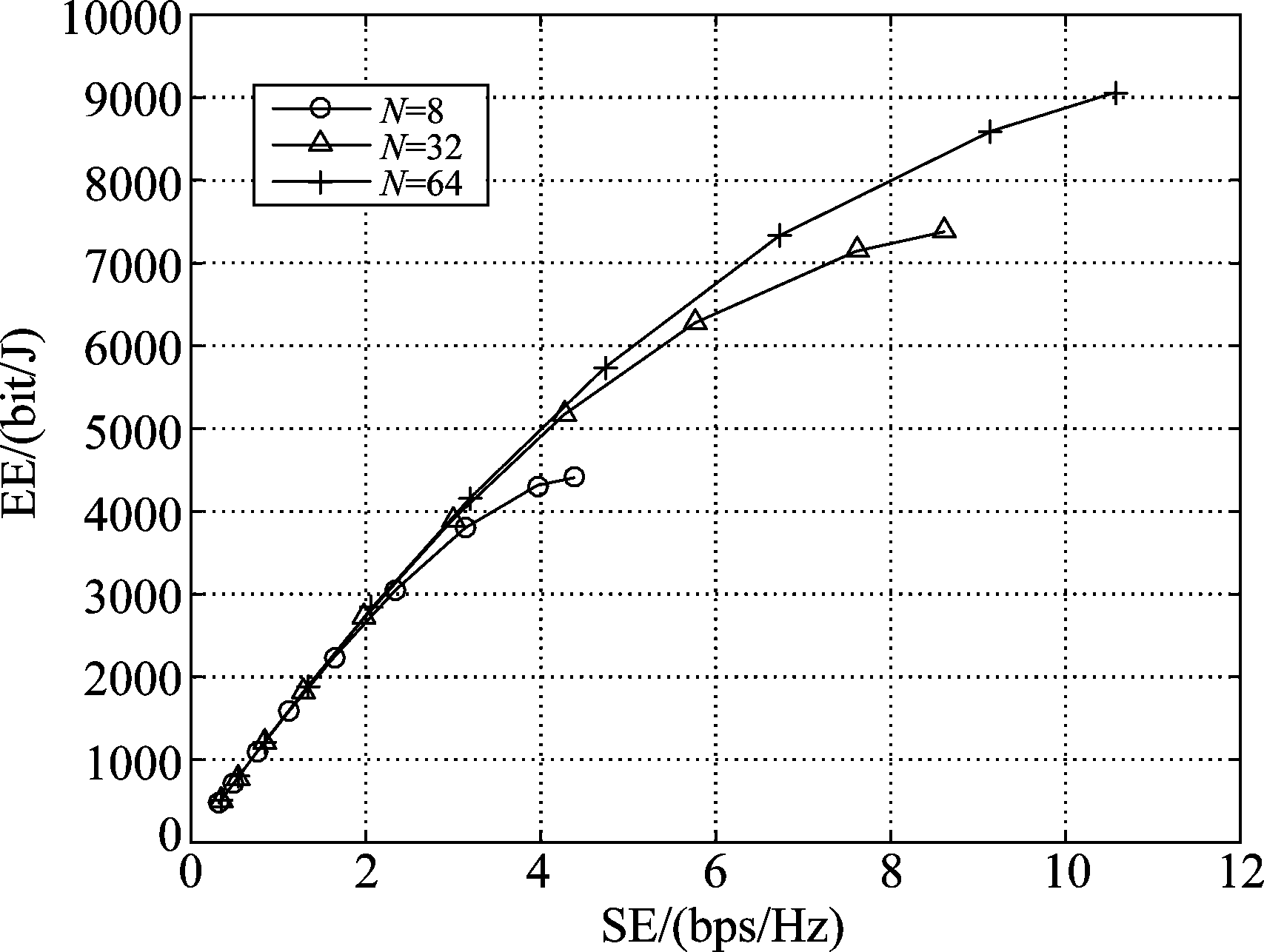
图7 SWIPT网络中能效与谱效的关系
Fig.7 Relationship between EE and SE in SWIPT network
6 结论
论文研究了缓存队列SWIPT网络中保障能效的最佳转发中继选择与子载波能量联合分配方案。首先建立了缓存队列中继能量分配模型,然后以最佳转发中继的能效为优化目标,在满足能量约束,对最佳发送中继干扰约束和目的端速率约束等条件下,构建优化问题并求解,得到最优转发中继选择方案与子载波能量的联合分配方案。仿真结果表明,所提方案在满足对转发中继干扰约束的情况下,随着源端发送功率和功率分割因子的增大,可以得到最优能效。所提方案考虑了SWIPT网络中继间干扰,且当源端发送功率较大时可获得较高的能效。
[1] Bi S Z, Ho C K, Zhang R. Wireless powered communication: opportunities and challenges[J]. IEEE Communications Magazine, 2015, 53(4): 117-125.
[2] 张海洋. 无线携能通信网络系统中新型传输方案的研究[D]. 南京: 东南大学, 2017.
Zhang Haiyang. Effective transmission schemes for simultaneous wireless information and power transfer systems[D]. Nanjing: Southeast University, 2017.(in Chinese)
[3] Moon J, Lee H, Song C, et al. Secrecy performance optimization for wireless powered communication networks with an energy harvesting jammer[J]. IEEE Transactions on Communications, 2017, 65(2): 764-774.
[4] Xia B, Fan Y, Thompaon J, et al. Buffering in a three-node relay network[J]. IEEE Transactions on Wireless Communications, 2008, 7(11): 4492- 4496.
[5] Zlatanov N, Schober R, Popovski P. Throughput and diversity gain of buffer-aided relaying[C]∥2011 IEEE Global Telecommunications Conference(GLOBECOM), Houston, TX, USA, 2011: 1- 6.
[6] Zlatanov N, Schober R, Popovski P. Buffer-aided relaying with adaptive link selection[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(8): 1530-1542.
[7] 洪鑫龙, 许晓荣, 石振波. 无线携能网络中一种基于时隙切换的中继辅助信能同传协议[J]. 信号处理, 2018, 34(12): 1467-1473.
Hong Xinlong, Xu Xiaorong, Shi Zhenbo. A relay-aided information and power transfer protocol based on time switching structure in SWIPT[J]. Journal of Signal Processing, 2018, 34(12): 1467-1473.(in Chinese)
[8] 吴佳颖. 基于OFDM资源分配的无线携能通信技术研究[D]. 杭州: 浙江工业大学, 2017.
Wu Jiaying. Researches on simultaneous wireless information and power transfer based on resource allocation in OFDM systems[D]. Hangzhou: Zhejiang University of Technology, 2017.(in Chinese)
[9] 李婷. 认知无线电系统中资源分配算法研究[D]. 宁波: 宁波大学, 2017.
Li Ting. Resource allocation algorithm for cognitive radio systems[D]. Ningbo: Ningbo University, 2017.(in Chinese)
[10] Huang G, Zhang Q, Qin J. Joint time switching and power allocation for multicarrier decode-and-forward relay networks with SWIPT[J]. IEEE Signal Processing Letters, 2015, 22(12): 2284-2288.
[11] 柳颖. 无线中继网络中基于携能通信技术的联合资源分配算法[D]. 邯郸: 河北工程大学, 2017.
Liu Ying. Joint resource allocation for simultaneous wireless information and energy transfer in wireless relay networks[D]. Handan: Hebei University of Engineering, 2017.(in Chinese)
[12] Li G Y, Xu Z, Xiong C, et al. Energy-efficient wireless communications: tutorial, survey, and open issues[J]. IEEE Wireless Communications, 2011, 18(6): 28-35.
[13] Xiong C, Li G Y, Zhang S, et al. Energy-and spectral-efficiency tradeoff in downlink OFDMA networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(11): 3874-3886.
[14] Mao J, Xie G, Gao J, et al. Energy efficiency optimization for OFDM-based cognitive radio systems: a water-filling factor aided search method[J]. IEEE Transactions on Wireless Communication, 2013, 12(5): 2366-2375.
[15] 伍伟伟, 许晓荣, 王云川, 等. 采用注水因子辅助搜索的能效优先子载波功率联合优化算法[J]. 西安交通大学学报, 2017, 51(8):59- 64.
Wu Weiwei, Xu Xiaorong, Wang Yunchuan, et al. Joint optimization algorithm for subcarrier and power with priority of energy efficiency based on water-filling factor aided search[J]. Journal of Xi’an Jiaotong University, 2017, 51(8):59- 64.(in Chinese)
