1 引言
随着无线通信的发展,具有上下行不对等特性的数据业务逐渐成为无线通信业务的主导。时分双工(TDD)技术作为LTE标准中的一个重要制式,成为无线通信中的一个研究热点[1]。TDD不需要对等的上下行带宽即可灵活部署,在业务自适应方面增加了很大的灵活性。TDD可以通过小区的灵活配置,满足不同小区上下行业务的不同需要,既能够满足用户需要也能够节省频谱资源。
近年来,蜂窝网络的组成正由早期的单层结构向多层结构发展,基站的部署也根据业务分布呈现出一定程度的随机特性。因此,传统的格型网络不仅不适用于如今单层蜂窝网络的建模,更不适用于随机化且多元化的多层异构蜂窝网络[2]。最近,一种基于随机几何理论的新型建模方法被广泛用于蜂窝网络建模,它不仅能够体现网络节点的随机分布特性,而且可以给出易于处理的结果[3]。文献[4]首次采用泊松点过程(Poison Point Process,PPP)对宏基站蜂窝网络进行建模,并对下行覆盖概率和传输速率这两个网络性能指标进行了分析。文献[5]对上行蜂窝网络进行随机几何建模,并分析了闭环功率控制因子对网络覆盖和传输性能的影响。以上是针对宏基站网络建模的研究,而对于异构网络的建模分析,都是在此基础上,釆用相互独立的PPP对异构网络的各类基站分布进行建模[6-7],并未充分体现不同类型基站在概率分布、传输特性等方面的差异。与适用于宏基站分布的二维模型不同,文献[8]首次提出了更适合小基站网络的3-D PPP模型,并基于此模型分析了小基站网络的下行覆盖概率,推导了一定条件下覆盖概率的闭合表达式。然而,以上文献都是基于FDD场景下的蜂窝网络建模。文献[9]采用PPP模型对TDD制式下的蜂窝网络进行建模,假设所有的小区采用相同的帧结构,即在同一时隙所有小区都同时处于上行或下行工作状态,这样就不会产生上下行交叉干扰,也不会体现出TDD制式在业务自适应方面的优势。文献[10-11]分别对TDD场景下毫米波蜂窝网络和D2D网络上下行交叉干扰进行了建模,分析了网络覆盖概率和传输速率。文献[12]分析了小基站蜂窝网络在静态TDD和动态TDD场景下的网络性能,并未考虑基站的随机分布。
本文借助三维随机几何理论对动态TDD小基站蜂窝网络进行建模,并对网络的覆盖概率,频谱效率进行分析。通过仿真分析,得到的理论结果与动态TDD小基站网络的仿真结果基本一致说明本文模型的准确性。除此之外,本文还讨论了网络中下行小区占比和功率控制因子对网络性能的影响。结果表明,下行小区占比和功率控制因子的增大都将导致网络频谱效率的下降。
本文结构组织如下,第2节对小基站网络系统模型进行描述;第3节给出了利用三维随机几何理论推导TDD场景下小基站蜂窝网络上下行覆盖概率及频谱效率;第4节是仿真分析;最后是结束语。
2 系统模型
2.1 网络模型
本文考虑单层小基站蜂窝网络,分析网络中随机选取的某个点的SINR。对于上行而言,这个点是随机选取的某个小基站;反之,对于下行,这个点就是随机选取的某个用户。网络中的小基站和移动台位置的分布服从
上强度分别为λc和λu的3-D PPP Φc和Φu。由于TD-LTE场景中采用正交频分复用多址接入(Orthogonal Frequency Division Multiple Access,简记为OFDMA)[1],网络中仅存在小区间干扰而没有小区内干扰。假设小基站的最大接入用户数为N(即,每个小基站最多提供N个正交子载波),则在基站满负荷情况下,小基站密度λc与占用相同子载波的用户密度λ相同,即,λ=λc=λu/N。
在一个传输时间间隔内,任意小区的数据传输方向是不变的,即某小区只能处于上行或下行工作状态中的一种,不存在上下行同时传输的状态。假定不同小区的传输方向是相互独立的。用随机变量Dir表示小区的传输方向,Dir服从区间[0,1]上的均匀分布,记作Dir～U(0,1),则小区的传输方向为
(1)
其中ξ∈[0,1]是控制网络内上下行小区占比的参数。例如,ξ=0.3则表示网络内处于上行传输状态的小区占整个小区数量的30%。图1表示了TDD制式下小基站网络上下行交叉干扰系统模型,其中小区0为目标小区,其他小区为干扰小区。实线表示有用信号而虚线表示干扰信号。
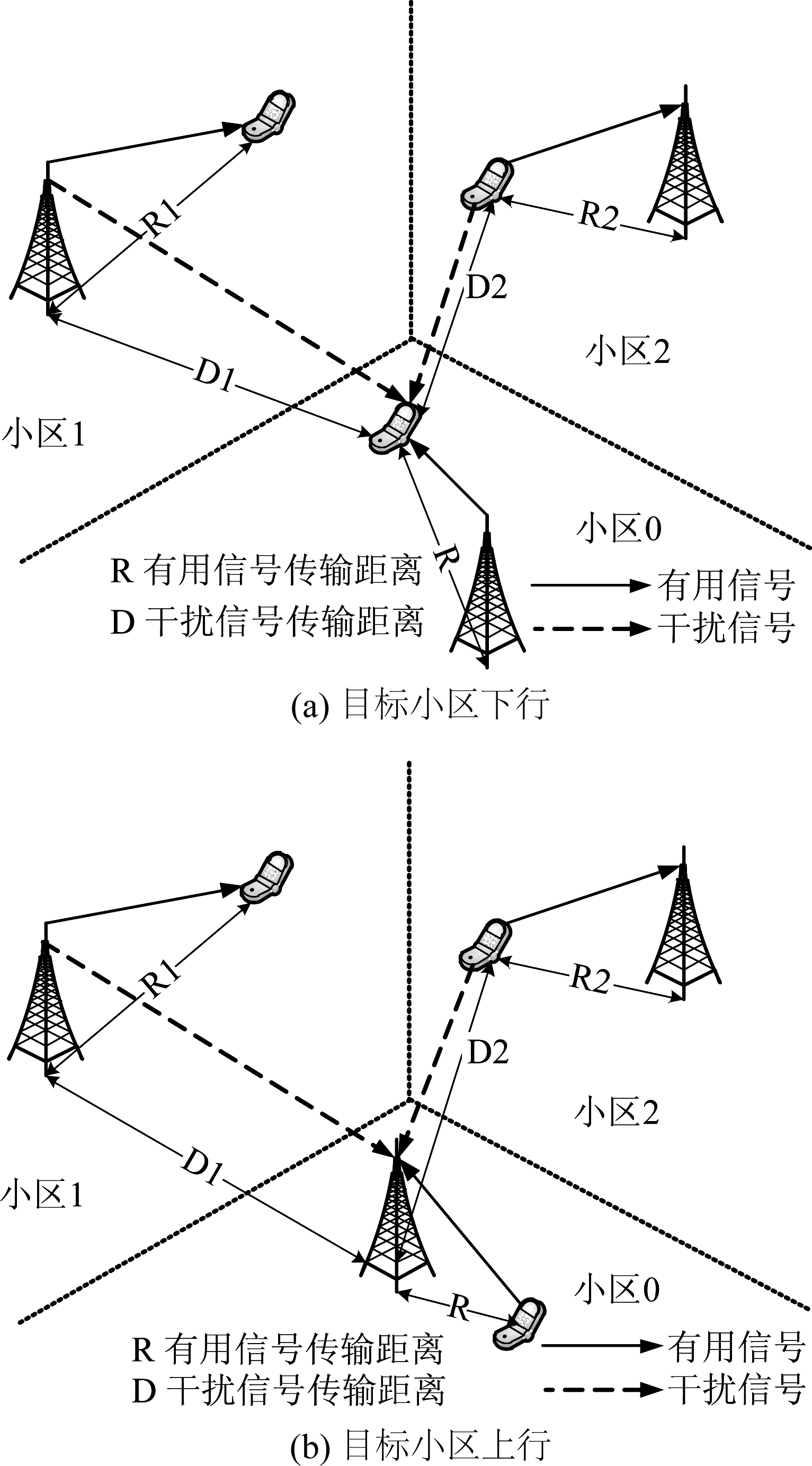
图1 TDD制式下小基站系统模型图
Fig.1 Small cell system model in TDD scenario
假设每个移动台都选择距其最近的基站作为通信基站,根据3-D PPP理论,任一移动台到其通信基站之间的距离r服从分布:
其概率密度函数为
(2)
2.2 信号衰落与功率控制模型
由于小基站通常分布在写字楼、商贸区等城市密集区域,因此采用适用于室内传输的Devasirvatham室内路径损耗模型[13]。为了简化问题,假设发送天线和接收天线增益均为1,无线信号频率为2.4 GHz。路径损耗以dB为单位可表示为
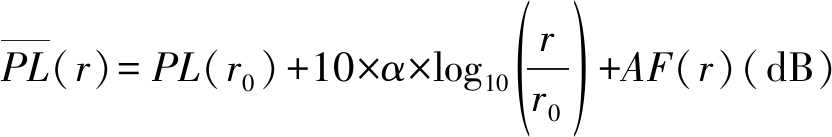
(3)
其中,r以m为单位,PL(r0)(第一米损耗)在信号频率2.4 GHz时为40 dB,AF(r)为墙壁楼层损耗因子,以dB为单位的表达式为AF(r)=10log10(μr)(dB)[14],参数μ是单位路径长度衰减常数。一般而言,路径损耗因子α∈(2,5), μ取0.5 dB/m。因此,路径损耗的数值表达式为Lr-(α+1),其中L为常数,
无线传输信道中除了路径损耗外,还存在阴影效应。本文采用瑞利衰落信道将用来建模移动台与基站间的阴影效应[4]。为了表述方便,定义
和
分别为小基站和移动台发射功率。因此,对于上下行链路而言,目标基站和用户接收到与其距离为r的移动台和基站的信号功率分别为guLr-(α+1)和gcLr-(α+1),其中gu和gc为综合考虑瑞利衰落和发射功率的随机变量,分别服从参数为和的指数分布,gu～exp(μu),gc～exp(μc)。假设所有的移动台都采用与距离成正比的分数功率控制模型(L-1rα+1)ε以补偿路径损耗和墙壁的穿透损耗,其功率控制因子ε∈[0,1][15]。由于小基站的发射功率较小,本文不考虑下行功率控制。
综合以上系统模型,在小基站蜂窝网络中,目标小区的下行SINR和上行SINR分别为
(4)
(5)
其中,Iz为目标用户或者目标基站接收的总干扰功率,由来自相邻小区基站的干扰Izc和用户的干扰Izu累加组成,
且Izc和Izu相互独立,Ri表示第i个干扰基站到目标小区的距离,Dj表示第j个干扰用户到其通信基站的距离,与r具有相同的概率分布(其pdf由公式(2)确定),Rj则表示第j个干扰用户到目标小区的距离,σ2为加性噪声功率。当ε=1时,意味着通过功率控制将路径损耗和墙壁的穿透损耗完全抵消,当ε=0时,意味着不做任何功率控制,所有移动台以相同的功率发射信号[15]。
3 覆盖概率与频谱效率
本节首先推导TDD制式下基于3-D PPP模型的小基站蜂窝网络上下行覆盖概率的数学表达式,然后进一步讨论频谱效率。
覆盖概率定义为pc
P{SINR>T},即目标用户的下行SINR或目标基站的上行SINR大于信干噪比门限T的概率。
定理1 TDD制式下三维小基站网络上下行覆盖概率为:
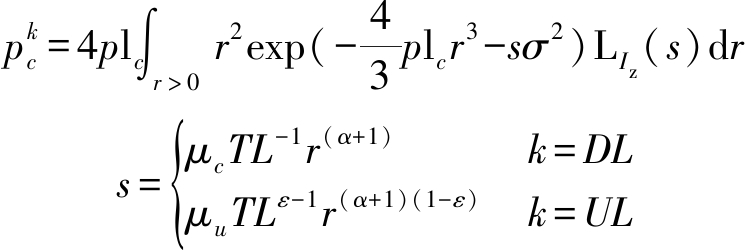
(6)
其中,
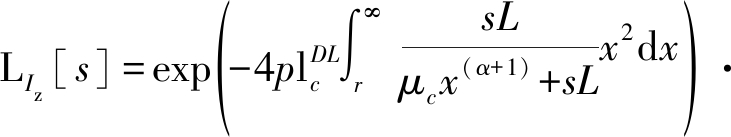
(7)
(8)
(9)
证明 根据覆盖概率的定义,3-D PPP分布特性以及瑞利衰落特性,可得下行覆盖概率
(10)
(11)
(12)
LIz(μcTK-1r(α+1))dr
(13)
其中,步骤(*)依据gc～exp(μc)以及拉氏变换的定义LIz[s]=EIz[e-sIz]。接下来LIz[s]可以进一步表示为
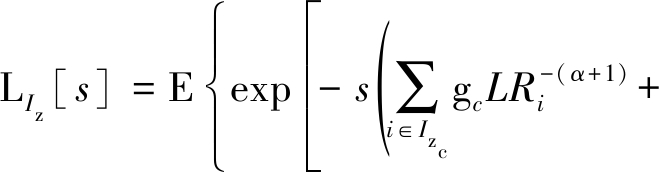
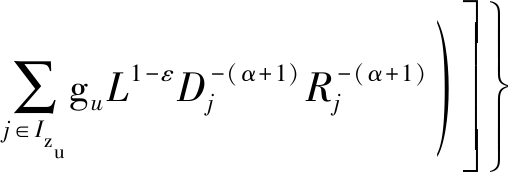
(14)
根据Izc、Izu、gc和gu的独立性,公式(14)可以改写为
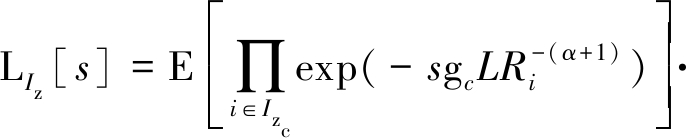
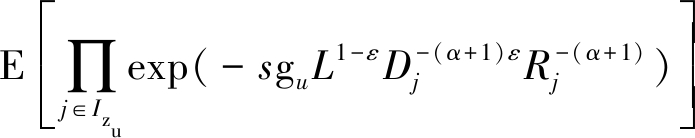
(15)
结合gu～exp(μu)以及gc～exp(μc),公式(15)可以表示为
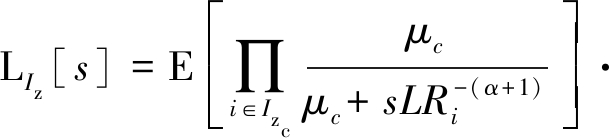
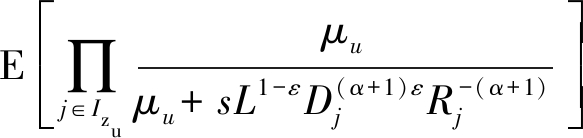
(16)
根据PPP的概率生成函数(probability generating functional,简记为PGFL)[16],拉氏变换LIz[s]可进一步表示为
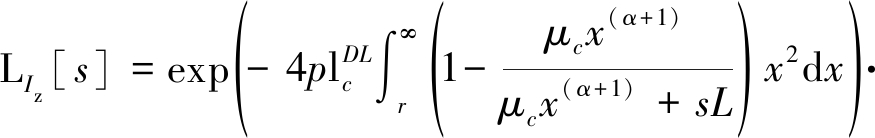
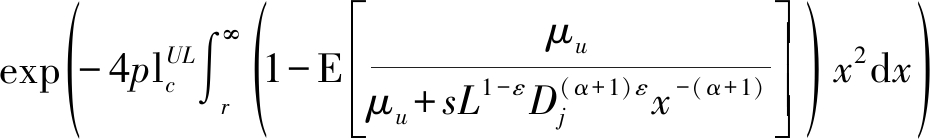
(17)
由于Dj和r为独立同分布随机变量,且具有相同的分布特性(由公式(2)给出),因此,公式(17)中的期望表达式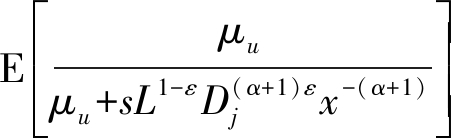
可化简为
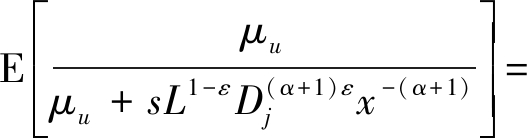
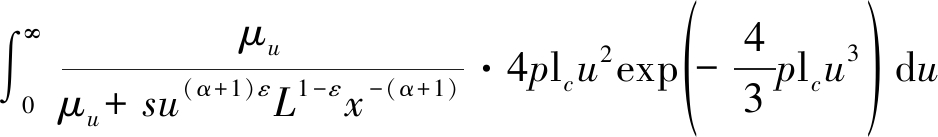
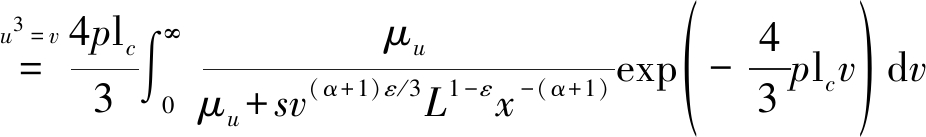
(18)
将公式(18)代入(17),并对(17)中的常数1进行合并整理,可得
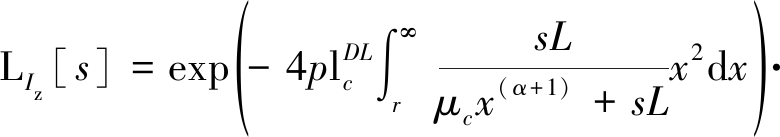
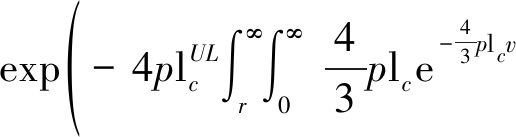
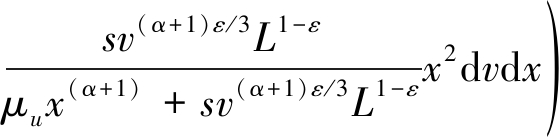
(19)
与下行类似,上行覆盖概率
(20)
根据gu～exp(μu),则,
P{gu>TLε-1r(α+1)(1-ε)(Iz+σ2)}=e-sσ2LIz(s)
(21)
其中,s=μuTLε-1r(α+1)(1-ε)。
对干扰拉式变换LIz(s)的推导与下行一致,不再赘述。考虑到上下行小区的占比有
将公式(21)代入(20)并结合公式(13)、(19)即可得到式(6)。
证毕。
定理2 TDD制式下三维小基站网络上下行频谱效率为:
(22)
其中,干扰的拉式变换LIz(s)与定理1相同。
证明 根据香农定理,可得下行频谱效率
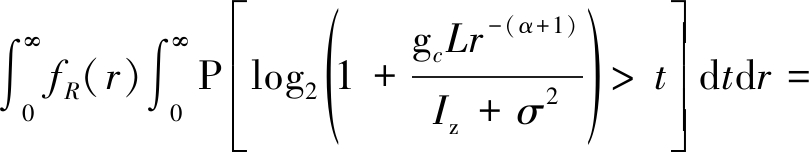
fR(r)P[gc>L-1r(α+1)(2t-1)(Iz+σ2)]dtdr
(23)
根据gu～exp(μu),并记s=μcL-1(2t-1)r(α+1),将式(2)代入,则
(24)
类似,可得上行频谱效率
=
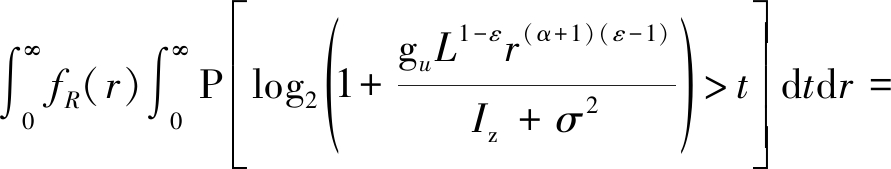
(25)
其中s=μcL-1(2t-1)r(α+1)。将(24)和(25)合并整理即可得到(22)。
证毕。
考虑到频率全复用蜂窝网络中干扰对网络性能的影响要远大于噪声[6],我们在后续的数值结算和仿真中都将忽略噪声功率。
4 仿真结果及分析
首先用仿真的手段验证上一节推导的覆盖概率的正确性,然后利用推导结果并结合仿真对TDD制式下三维小基站网络的频谱效率进行讨论。
4.1 仿真环境
考虑一个分布有大量小基站的城市中心球形区域,其半径R=100 m。根据移动运营商提供的数据,小基站密度设置为5×10-4/m3,则在基站满负荷情况下占用相同子载波的用户密度也为5×10-4/m3,小基站和移动台在该球形区域内服从3-D PPP分布。其他仿真参数设置如下:路径损耗指数α=4,功率控制因子ε=0.8,小基站发射功率30 dBm,用户发射功率范围15～23 dBm。
4.2 覆盖概率
图2给出了TDD制式下小基站蜂窝网络中目标小区的上下行覆盖概率,对区域内上下行小区不同占比情况下的理论值(根据定理1计算)和仿真值进行了比较。从该图中可以看出,本文提出的3-D PPP模型能够很好地匹配实际基站分布环境下的仿真值。除此之外,我们还发现,无论目标小区处于上行还是下行工作状态,同一SINR门限下的覆盖概率都随着区域内下行小区占比的增加而减小;对于上行而言,这一变化更加明显。其原因在于,基站的发射功率要明显大于移动台,随着区域内下行小区的增多,干扰会急剧增大,这必然导致SINR的下降,从而造成覆盖概率的降低。一般而言,蜂窝网络的上行接收功率要明显小于下行,因此,当目标小区上行时,干扰的增加对SINR的影响明显大于下行。由于上述仿真结果已经验证了本文3-D PPP模型的准确性,接下来的仿真我们不再将3-D PPP模型与实际环境下的仿真值做比较。
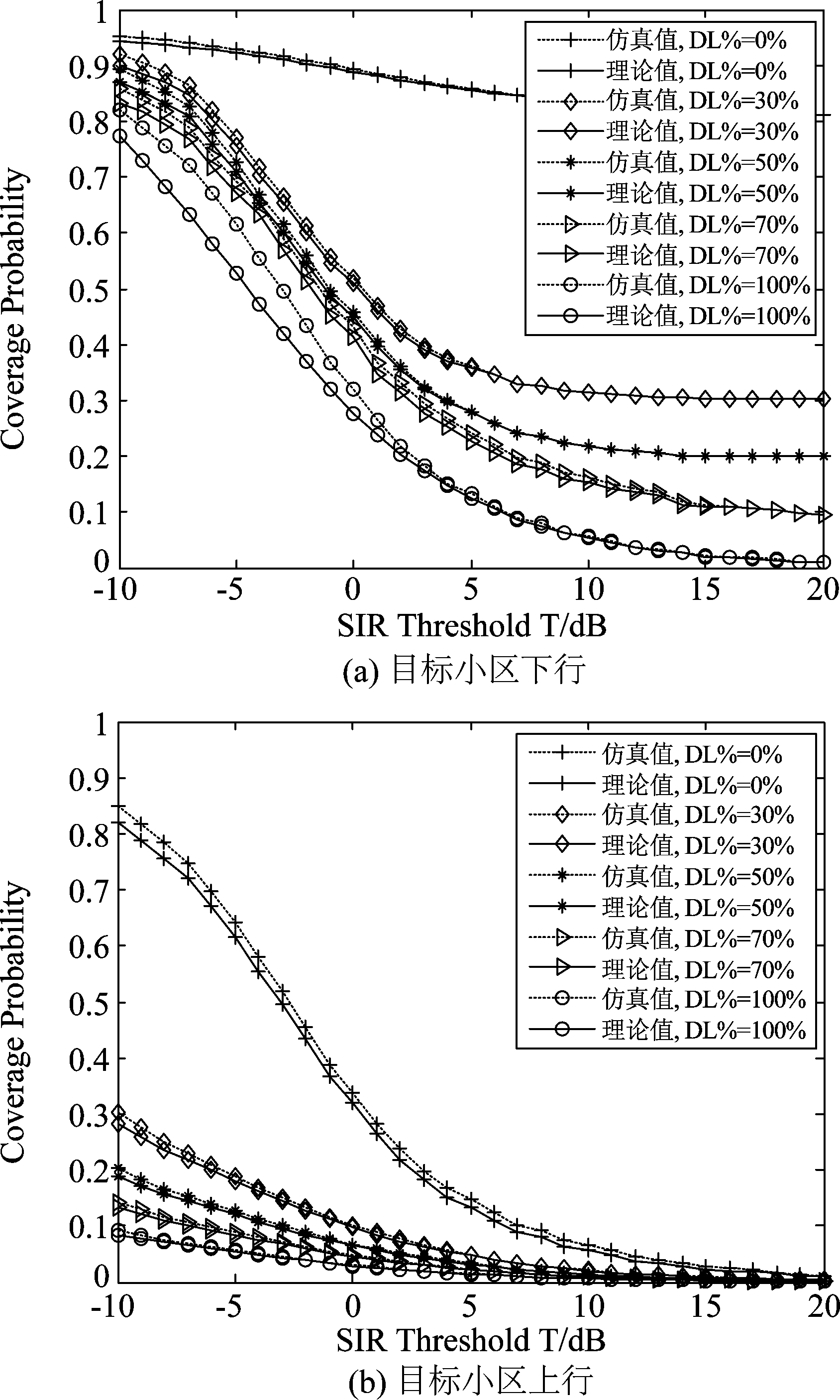
图2 目标小区上、下行覆盖概率
Fig.2 Downlink and uplink coverage probability of target cell
图3展示了TDD场景不同室内环境下小基站蜂窝网络中目标小区的上下行覆盖概率,对区域内无室内布置和室内布置杂乱情况下的仿真结果进行了比较。从该图中可以看出,无论目标小区处于上行还是下行工作状态,室内布置杂乱场景下的覆盖概率均低于无室内布置场景下的覆盖概率值。其原因在于,在室内布置杂乱的场景下,无线电波除了要经历墙壁和楼层损耗外,还要经历室内物品的损耗,这必然导致目标小区接收SINR的下降。当SIR门限较低时,室内物品产生的损耗对SIR的影响更为明显。其原因是低SIR门限时,室内物品产生的损耗导致SIR值下降,因此室内杂乱场景下的覆盖概率低于无室内布置场景下的覆盖概率,这一差距将随着SIR门限的提升而缩小,当SIR门限在20 dB及以上时,无论有无室内物品损耗,覆盖概率都是零,因此覆盖概率曲线上看不出两者的差别。
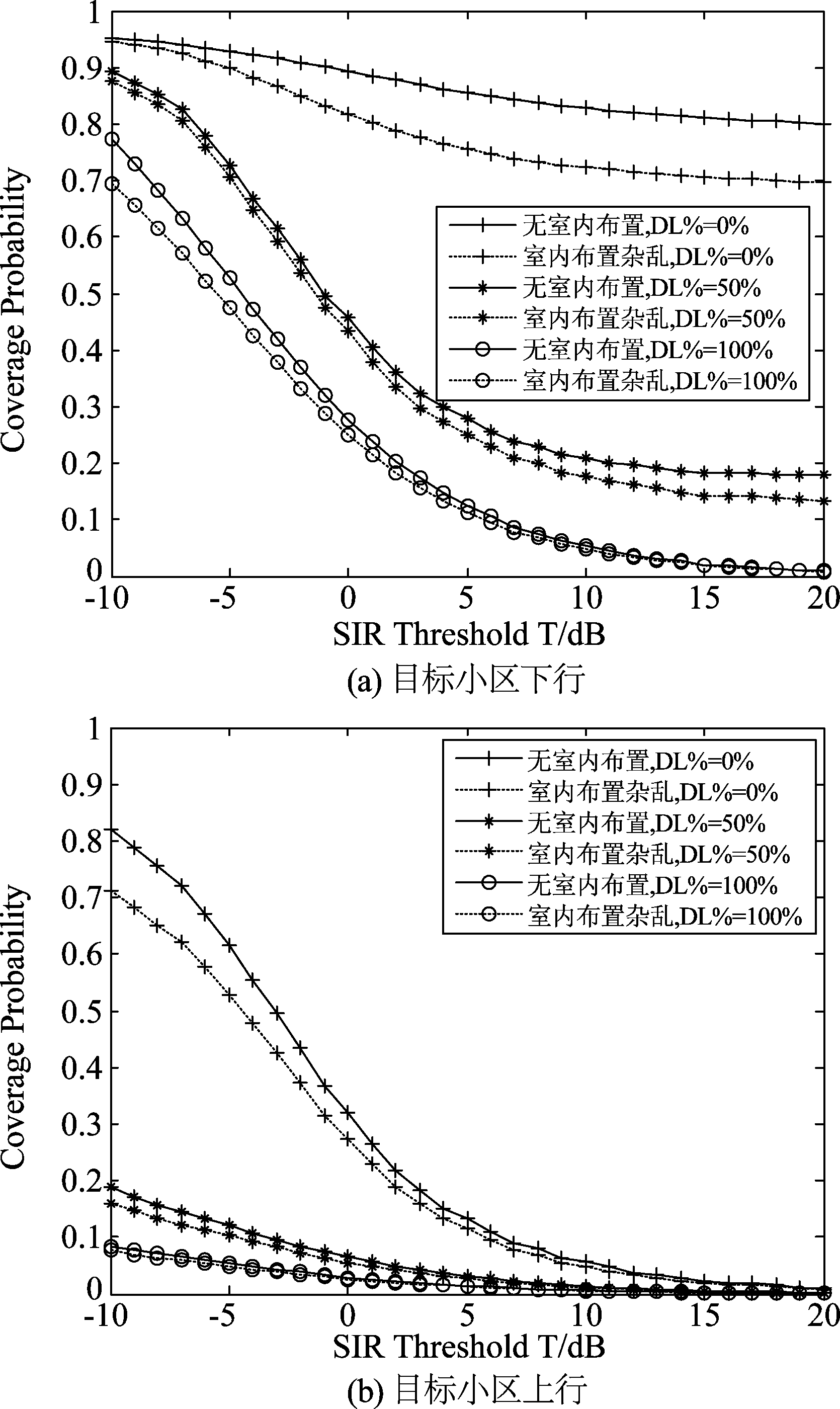
图3 不同室内环境下目标小区上、下行覆盖概率
Fig.3 Downlink and uplink coverage probability of target cell in different indoor environment
4.3 频谱效率
图4分别展示了不同上下行小区占比情况下,小基站网络上下行频谱效率与功率控制因子的关系。从图中可以看出,随着功率控制因子ε的增大,网络的上下行频谱效率都呈现下降趋势。其原因在于,功率控制因子ε越大,对路径损耗的补偿越充分,干扰也就随之增大,因此SINR和频谱效率自然会随之减小。在同一ε下,随着下行小区占比的增大,网络频谱效率也都呈现下降趋势。其原因和4.2节相同,即随着下行小区占比的增大,无论是上行还是下行小区的接收SINR都会降低,从而造成频谱效率的下降。除此之外,我们还可以发现,当下行小区占比增大时,ε对频谱效率的影响趋于平缓。在区域内所有小区都处于下行状态这一极端情况时,ε对下行频谱效率的影响为一横线,即没有任何影响。这是由于本文只考虑移动台端的上行功率控制而未考虑基站端的下行功率控制,当下行小区比例增大时,功率控制因子对频谱效率的影响自然会减小。
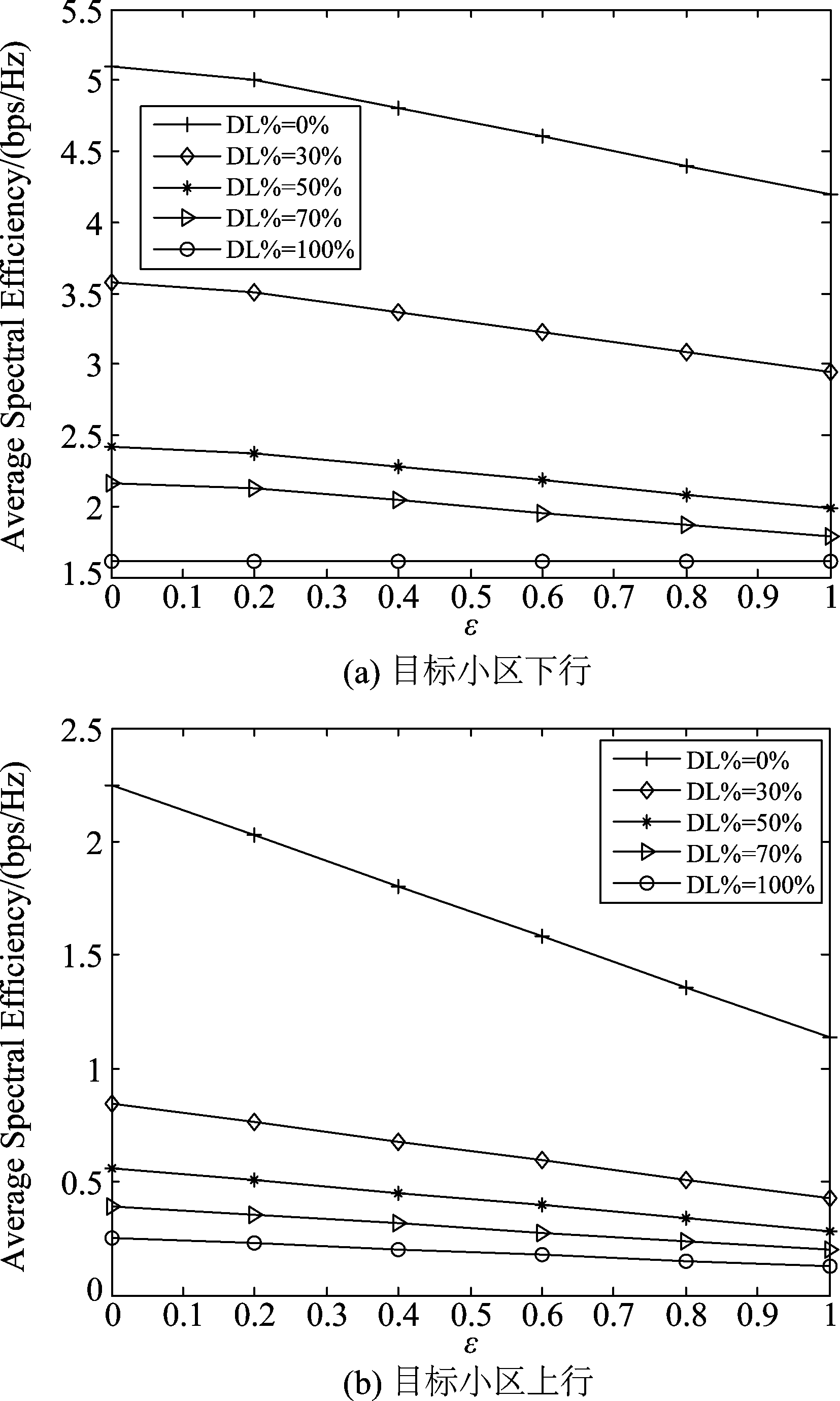
图4 目标小区上、下行频谱效率
Fig.4 Downlink and uplink spectrum efficiency of target cell
图5为不同室内布局下,小基站蜂窝网络中目标小区的上下行频谱效率比较。结论和原因均与图3一致。即室内布置杂乱场景下的频谱效率要低于无室内布置场景下的值,而其原因就在于,室内布置杂乱的场景下的路径损耗要大于无室内布置场景下的。
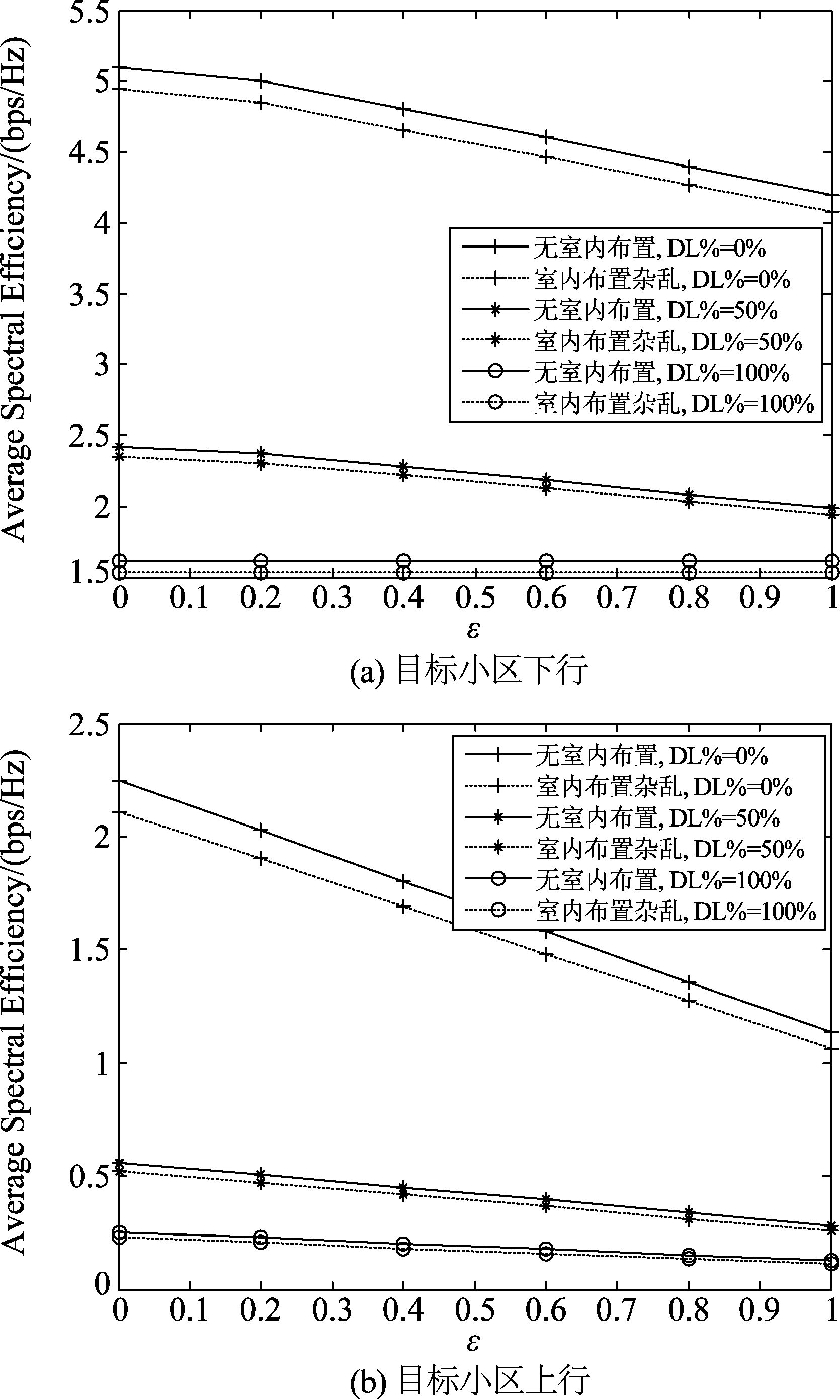
图5 不同室内环境下目标小区上、下行频谱效率
Fig.5 Downlink and uplink spectrum efficiency of target cell in different indoor environment
4.4 蛇形曲线行走实验
在前面的几个仿真实验中,都是将整个空间区域中心位置的小区选为目标小区,其依据为PPP的Plam特性[4]。本小节将通过一个蛇形曲线行走的实验来验证其合理性,其行走轨迹如下图6所示。对于下行链路,假设目标用户在区域内按此轨迹行走;对于上行链路,则按此路径行走的假设为目标小基站。
图6 蛇形行走轨迹
Fig.6 Serpentine walking trajectory
在图6蛇形行走轨迹下,目标小区的上下行覆盖概率如图7所示。横坐标表示行走轨迹,纵坐标为覆盖概率,上、下行SINR分别为0 dB、10 dB。从该图中可以看出,无论目标小区处于上行还是下行工作状态,覆盖概率基本不随行走位置的变化而变化,这即验证了PPP的Plam特性,也验证了“以中心位置小区的网络性能指标代表整个区域网络性能指标”这一假设的合理性。然而,从该图中可以发现,覆盖概率随行走位置的变化存在微小的变化。其原因在于,仿真实验中的区域是有限的,而理论推导时的区域是无限的,在有限的区域内,当目标小区位于区域的边缘时,其相邻小区的数量要低于目标小区位于区域中心位置的值,干扰也自然会减小,因此覆盖概率会略有增大,但这一变化很不明显,在系统仿真时可以忽略不计。
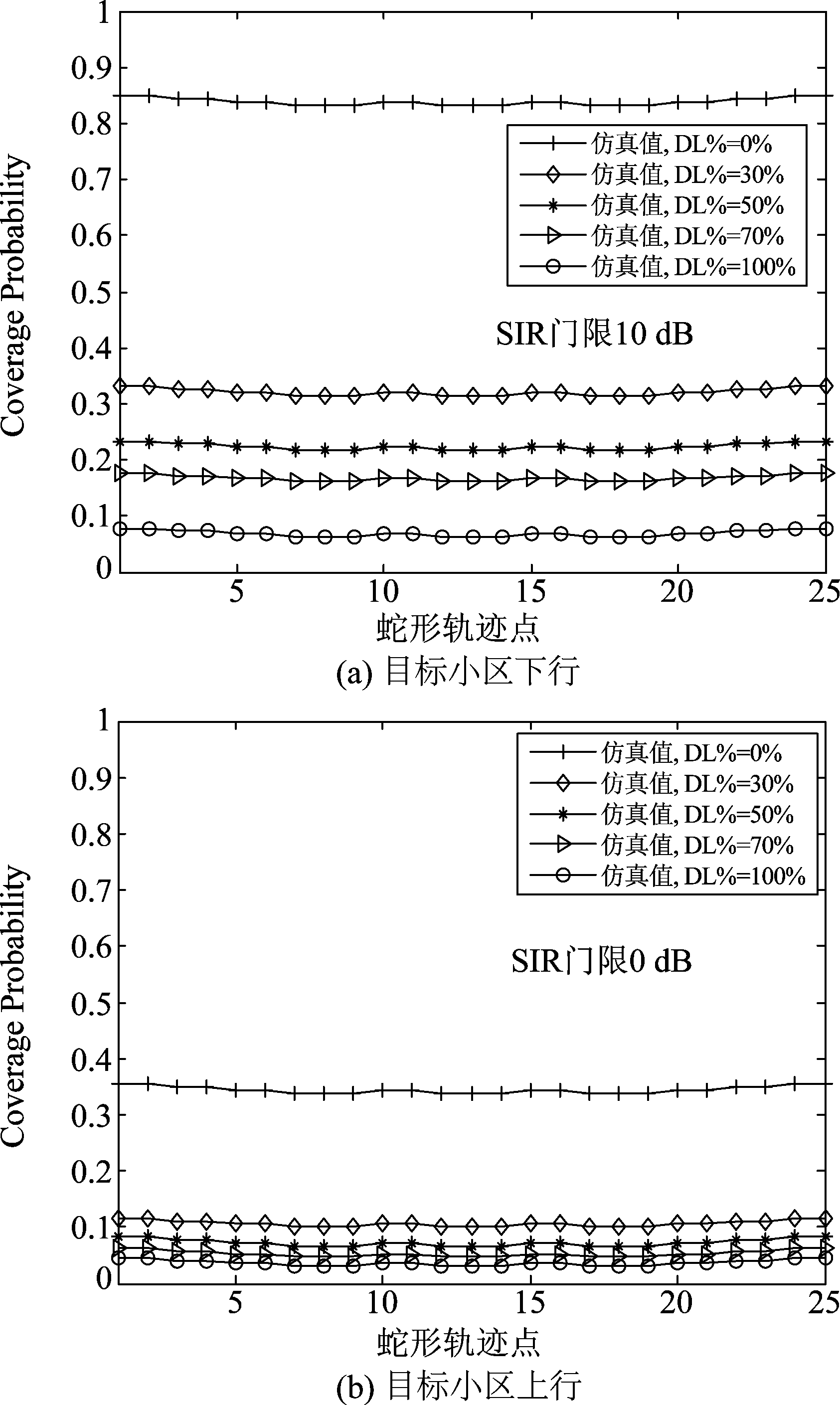
图7 蛇形行走轨迹下目标小区的上、下行覆盖概率
Fig.7 Downlink and uplink coverage probability of target cell in serpentine walking
5 结论
本文提出了一种TDD制式下小基站上下行交叉干扰网络模型,将一定区域内基站和用户的分布建模为3-D PPP,利用点过程理论和随机几何方法推导了网络上下行覆盖概率和频谱效率表达式。仿真结果一方面验证了本文模型在干扰建模方面的合理性,另一方面表明下行小区占比和功率控制因子的增大都将导致网络频谱效率的下降。
[1] TS 36.201 v10.0.0, LTE physical layer; General description[S]. 3GPP, 2010-12.
[2] Turgut E, Gursoy M C. Coverage in Heterogeneous Downlink Millimeter Wave Cellular Networks[J]. IEEE Transactions on Communications, 2017, 65(10): 4463- 4477.
[3] Deng Y, Member S, IEEE, et al. Physical Layer Security in Three-Tier Wireless Sensor Networks: A Stochastic Geometry Approach[J]. IEEE Transactions on Information Forensics and Security, 2017, 11(6): 1128-1138.
[4] Andrews J G, Baccelli F, Ganti R K. A Tractable Approach to Coverage and Rate in Cellular Networks[J]. IEEE Transactions on Communications, 2011, 59(11): 3122-3134.
[5] Novlan T D, Dhillon H S, Andrews J G. Analytical Modeling of Uplink Cellular Networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2669-2679.
[6] Madhusudhanan P, Restrepo J G, Liu Y, et al. Analysis of Downlink Connectivity Models in a Heterogeneous Cellular Network via Stochastic Geometry[J]. IEEE Transactions on Wireless Communications, 2016, 15(6): 3895-3907.
[7] Xu Chao, Sheng Min, Varma V, et al. Wireless Service Provider Selection and Bandwidth Resource Allocation in Multi-tier HCNs[J]. IEEE Transactions on Communications, 2016, 64(12): 5108-5124.
[8] Pan Ziyu, Zhu Qi. Modeling and Analysis of Coverage in 3-D Cellular Networks[J]. IEEE Communications Letters, 2015, 19(5): 831- 834.
[9] Yu B, Mukherjee S, Ishii H, et al. Dynamic TDD support in the LTE-B enhanced Local Area architecture[C]∥Workshops Proceedings of the Global Communications Conference. California, 2012: 585-591.
[10] Kulkarni M N, Andrews J G, Ghosh A. Performance of Dynamic and Static TDD in Self-backhauled Millimeter Wave Cellular Networks[J]. IEEE Transactions on Wireless Communications, 2017, 16(10): 6460- 6478.
[11] Sun Hongguang, Wildemeersch M, Sheng Min, et al. D2D Enhanced Heterogeneous Cellular Networks with Dynamic TDD[J]. IEEE Transactions on Wireless Communications, 2015, 14(8): 4204- 4218.
[12] Yang H H, Geraci G, Zhong Y, et al. Packet Throughput Analysis of Static and Dynamic TDD in Small Cell Networks[J]. IEEE Wireless Communications Letters, 2017, 6(6): 742-745.
[13] Omri A, Hasna M O. Modelling and performance analysis of 3-D heterogeneous cellular networks[C]∥IEEE International Conference on Communications. Kuala Lumpur, 2016: 1-5.
[14] Ma Yue, Wang Xin, Wang Haihong, et al. A Joint Feedback Bit and Power Allocation Strategy for Multi-cell Systems over Composite Fading Channels[J]. Chinese Journal of Electronics, 2016, 25(3): 541-550.
[15] Hu Han, Wang Hong, Zhu Qi, et al. Uplink performance analysis in multi-tier heterogeneous celluar networks with power control and biased user association[J]. China Communications, 2016,13(12): 25-36.
[16] Sung N C, Dietrich S, Wilfrid S K, et al. Stochastic Geometry and Its Applications (3rd Edition)[M]. New York: John Wiley & Sons Inc., 2013.
