1 引言
最小均方算法因其在实时数据处理中的简便性和鲁棒性而被广泛应用,其收敛速度是由输入信号相关矩阵的最大特征值与最小特征值之比(特征值扩散度)所决定的,然而在实际情况中这个比值往往会很大从而导致很慢的自适应过程,这在实时信号处理中是不可接受的。Narayan最早提出使用变换域的方法对高度相关的输入信号进行预白化处理以减小特征值扩散度[1]。近期以来,研究人员使用了包括离散傅里叶变换(DFT)、离散余弦变换(DCT)、离散小波(DWT)和离散哈特利变换(DHT)等正交变换对LMS算法进行变换域处理[2-5],并取得了良好的效果。
同时域算法相似,TDLMS算法的步长因子决定了算法的收敛速度和稳态均方误差(mean-squared error, MSE)。但由于快速收敛对大步长的要求与低稳态失调对于小步长的要求相矛盾,固定步长的方法不能保证算法良好的性能。因此,研究人员在TDLMS算法的基础上应用了各种变步长方案在收敛性和稳态性之间寻找恰当的平衡。文献[6]提出一种VSS-TDLMS算法,应用瞬时误差的平方调整步长因子;文献[7]提出了一种SVS-TDLMS算法,其变步长形式是基于Sigmoid函数的,误差的自相关控制步长因子的更新;文献[8]提出了一种GVS-TDLMS算法,根据误差的Griffths梯度控制步长;文献[9]在提出了一种SNC-TDLMS算法,其基于自动阈值选择在自适应初期使用最大步长而在自适应的末期使用有噪声约束的变步长,但该算法必须获得加性噪声的先验知识,因此本文中没有针对这类问题予以讨论。在特定的情形下,上述算法均被证明可以在较小稳态失调的前提下有效地提高收敛速度。
但是,作者注意到上述基于变换域变步长方案的理论与仿真分析大多是基于广义平稳假定的,很少有针对非平稳信号的论证分析。因此本文在平稳和非平稳状态下,提出了一种改进的变步长TDLMS算法(modified variable step size-transform domain LMS, MVSS-TDLMS),以误差自相关时间平均估计的平方控制其步长因子的更新,进而消除了输入信号中不相关的观测噪声的影响。文章结构组织如下:第2节介绍了变换域的方法,提出一种新的变步长方案;第3节对所提出的算法收敛和稳态性能进行了近似的分析,并给出了算法参数选择的最优解。第4节分别在平稳和非平稳状态下对算法性能进行仿真,与文献中的算法进行比较,并验证了第3节中的参数设置;第5节给出了结论。
2 改进的变步长TDLMS算法
2.1 变换域的方法在自适应滤波上的应用
设自适应滤波器的输入信号矢量为X(n)=[x(n),x(n-1),…,x(n-N+1)]T,使用一个N×N维的正交变换矩阵T对其进行预白化处理,得到近似正交的信号V(n)=TX(n)=[ν1(n),ν2(n),…,νN(n)]T。本文中假设输入信号X(n)是实信号且正交变换矩阵T为实矩阵,则滤波器输出的误差信号可表示为
e(n)=d(n)-VT(n)W(n)
(1)
其中d(n)为期望信号,W(n)=[w1(n),w2(n),…,wN(n)]T为自适应滤波器的权向量。TDLMS算法权向量的调整是基于使式(1)中的均方误差最小的原则,利用功率估计的归一化方程对权向量进行更新
(2)
μ为权矢量梯度下降的步长因子,Pi为正交信号功率
的估计,定义为
其中的δ是一个很小的正常数,其目的是为了防止某些信号功率的估计值接近于零从而导致TDLMS算法的不稳定。通常使用指数加权法对
的值进行估计
期望信号的表达式为
d(n)=VT(n)Wopt(n)+ξ(n)
(3)
其中ξ(n)定义为独立于V(n)的零均值不相关的观测噪声,Wopt(n)为变换域自适应滤波器维纳最佳权向量,定义权向量偏差向量C(n)=W(n)-Wopt(n)。为便于计算,对V(n)和C(n)进行等价的归一化处理
(4)
将式(4)带入式(2)即可得到经过归一化的权偏差向量表达式为
(5)
2.2 改进的变步长方案
与时域LMS算法类似,TDLMS算法中式(2)步长因子μ的选择同样至关重要,若选择过小则会导致自适应过程很慢的收敛,若选择过大则会导致滤波器无法收敛到最佳的权值。因此,TDLMS算法同样需要寻找一个时变步长μ(n)的方案,使得步长因子的值在自适应的初期的值较大以获得较快的收敛速度,在收敛的末期则取较小的步长因子以获得较小的稳态失调。文献[6]提出的变步长方案的步长更新公式为
μ(n+1)=α μ(n)+βe2(n)
(6)
其中0<α<1, β>0, μ(n)的上下限分别为μmax和μmin, μmax在算法稳定的情况下确保了最大的收敛速度,而μmin则确保前提设定的算法稳态失调和跟踪能力。其中,参数β控制着算法的收敛速度和稳态失调。然而,在存在观测噪声的情况下,选择瞬时误差作为测量手段并不能达到预期的效果。将式(1)和式(3)代入式(6)可得
μ(n+1)=α μ(n)+βCT(n)V(n)VT(n)C(n)+
β ξ2(n)-2β ξ2(n)CT(n)V(n)
(7)
归一化的正交输入向量
的自相关矩阵可表示为
对其进行特征值分解可得
其中
为自适应滤波器的阶数,
为相关矩阵的特征值,
为对应的特征向量。根据文献[12]的定义,式(4)中输入向量和权偏差向量经Givens旋转可定义为
对式(7)求期望可得
E[μ(n+1)]=αE[μ(n)]+βE[ξ2(n)]+
(8)
可见,式(8)中的
描述了自适应权值与维纳最佳权值的接近程度,同时控制着步长因子μ(n)的迭代。但由于观测噪声的期望E[ξ2(n)]的存在,步长因子的更新并不能准确地反映收敛前后自适应系统的状态从而严重影响算法性能。并且,权值越接近收敛时,步长因子不能变得足够小从而导致较大的稳态误差。本文提出一种新的变步长方案,使用e(n)与其延时e(n-1)的自相关的时间平均的估计来控制步长因子的更新,在广义平稳状态下其估计为
p(n)=χp(n-1)+(1-χ)e(n)e(n-1)
(9)
借助p(n)用于步长的更新是基于以下两点考虑:1)误差的自相关的时间平均是一种很好的自适应权值与最佳权值接近程度的量度;2)消除了不相关观测噪声序列对步长更新的影响。在自适应的初期,p2(n)较大对应步长因子μ(n)也较大;而接近收敛时,p2(n)也趋向于零对应较小的步长因子μ(n)。因此在观测噪声存在的情况下初始较大的μ(n)能确保算法的快收敛,而且末期较小的μ(n)也能确保算法较小的稳态误差,本文算法步长因子更新公式为
μ(n+1)=α μ(n)+βp2(n)
(10)
其中α, β的设置同文献[6], χ同样也是一个指数加权的权重控制着自相关估计的精度。在广义平稳状态下,p(n)当前时刻的状态(滤波器权值与最佳权值的接近程度)包含过去样本的信息,此时设置χ≈1,(0<χ<1)从而获得较准确的E[e(n)e(n-1)]的估计值。而在广义非平稳状态下,取时间平均的窗口应足够小[10]以使p(n)更好地反映当前时刻的状态,因此,式(10)可重新写为
μ(n+1)=α μ(n)+β[E{CT(n)V(n)VT(n)C(n)}]2
(11)
为提升非平稳状态下算法的跟踪能力,实际上在算法实现过程中步长更新公式同样选择式(9)和式(10),且设置较小的χ以获得准确的时变统计量。
此外,由式(9)和式(10)可知本文算法每次步长因子更新过程仅比TDLMS算法多需要6次乘法和2次加法,因此具有较低的计算复杂度。
特别需要注意的是,本文所做推导是基于不相关的观测噪声序列的假定下的。但在一些应用场合中观测噪声序列具有一定相关性,例如回声抵消[11],或未知系统响应的欠建模引起的误差[12]。在这种情况下,E[ξ(n)ξ(n-1)]在步长更新公式(9)、(10)、(11)中就不能视作零。但如果已知噪声样本间的相关性随时间差而减小的先决条件,则步长更新公式可修正为对e(n)e(n-D),D≪N的估计。
3 算法收敛及稳态性能分析
3.1 稳态均方误差分析
本文对于非平稳状态下系统脉冲响应的假设采用文献[13]中的通用时变模型
Wopt(n)=Wopt(n-1)+φ(n-1)
(12)
其中φ(n-1)为零均值相关矩阵
的平稳过程噪声。对于平稳过程,则有
以及Wopt(n)=Wopt。文献[14]给出TDLMS算法的最小均方误差可表示为
(13)
其中εmin=E[ξ2(n)]定义为额外最小均方误差,
为
的自相关矩阵可表示为
因此,算法的MSE与
的对角线元素直接相关。式(5)可写为
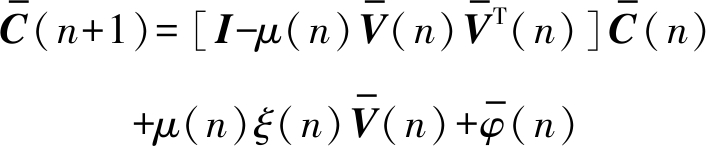
(14)
对式(14)两边同乘
并取期望可得
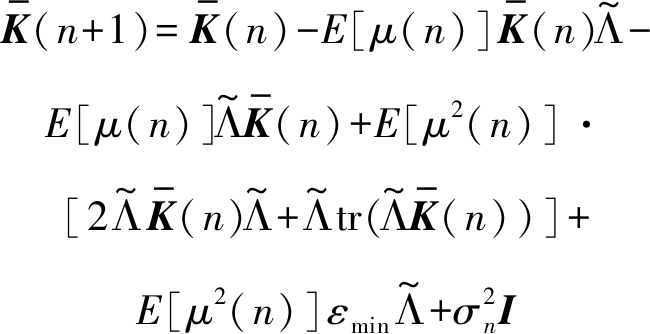
(15)
由式(9)递归形式得到p(n)的表达式
(16)
e(n-j)e(n-j-1)
(17)
下面的分析中,本文对算法的稳态性能进行研究。假定此时的算法已收敛,误差e(n)的样点间互不相关,即E[e(n-i)e(n-j)]=0, ∀i≠j。将式(16)和式(17)代入式(10)中得到算法收敛后步长因子及其平方的均值
E[e2(n-i)]E[e2(n-i-1)]
(18)
E[μ2(n+1)]≈α2E[μ2(n)]+2α β(1-χ)2E[μ(n)]·
(19)
综上,结合式(13)、(15)、(18)及式(19)可得到本文算法的稳态最小均方误差。
3.2 收敛性及稳态失调分析
为了描述算法收敛后的稳态性能,稳态失调在文献[15]中被定义为
(20)
一般而言εex(
)≪εmin,由式(18)和式(19),设定一个新参数q
(21)
由于0<α<1, β>0,0<χ<1,则有
文献[14]中证明了TDLMS算法均方误差收敛的充分条件与标准LMS算法在形式上是相同的,即
因此本文算法收敛条件为
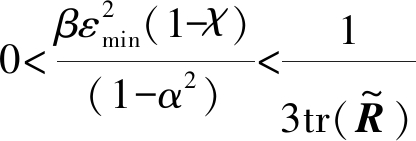
(22)
将式(21)带入式(20)可得本文算法的稳态失调
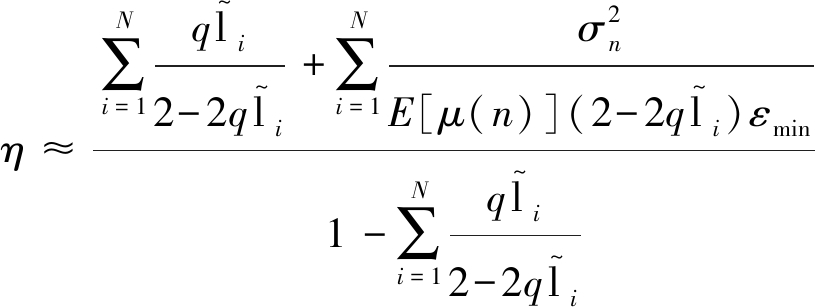
(23)
由于额外稳态均方误差εex()较小,有
因此有
(24)
其中E[μ(n)]的表达式同式(18)。在平稳状态下有
则本文算法稳态失调可写为
(25)
可以发现在平稳状态下式(25)在形式上与固定步长的TDLMS是算法一致的[14],即
因此为获得较小的稳态失调,选择合适算法参数α, β, χ使得q较小,但同时这些参数的选择必须建立在式(22)收敛条件的前提下。由于在式(24)中第一项与β成正比,而在第二项与β成反比,因此为获得最小的稳态失调在给定α, χ的情况下,步长更新公式中最佳的参数β*
(26)
其中t=2α(1-χ)2/(1-α2)(1-α)(1+ χ)2。此外,由于本节推导中存在很多简化和近似的操作,因此不能严格地预测算法的收敛和稳态性能,但对于自适应算法的参数设置具有重要的参考价值。
4 仿真实验分析
为验证提出算法的性能,本文以一个未知失真的三阶线性色散信道的自适应均衡问题为研究对象[15],假设所有的数据均为实数,图1表示仿真实验的系统框图。随机噪声产生器1产生用来探测信道的测试信号u(n),同时通过一定延迟提供用作训练序列的期望响应;随机噪声产生器2产生干扰信道输出的加性噪声ν(n);自适应均衡器用于纠正信道畸变。{u(n)}由伯努利序列组成,且具有零均值和单位方差;ν(n)表示零均值,方差为
的高斯白噪声;FIR横向滤波器长度为11。信道的脉冲响应采用升余弦表示为
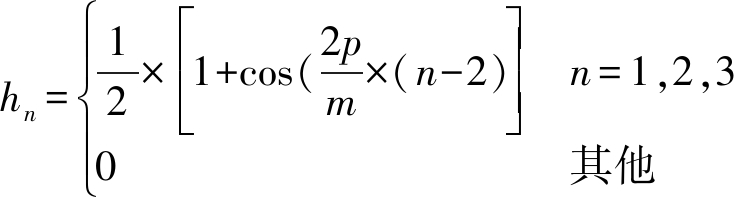
(27)
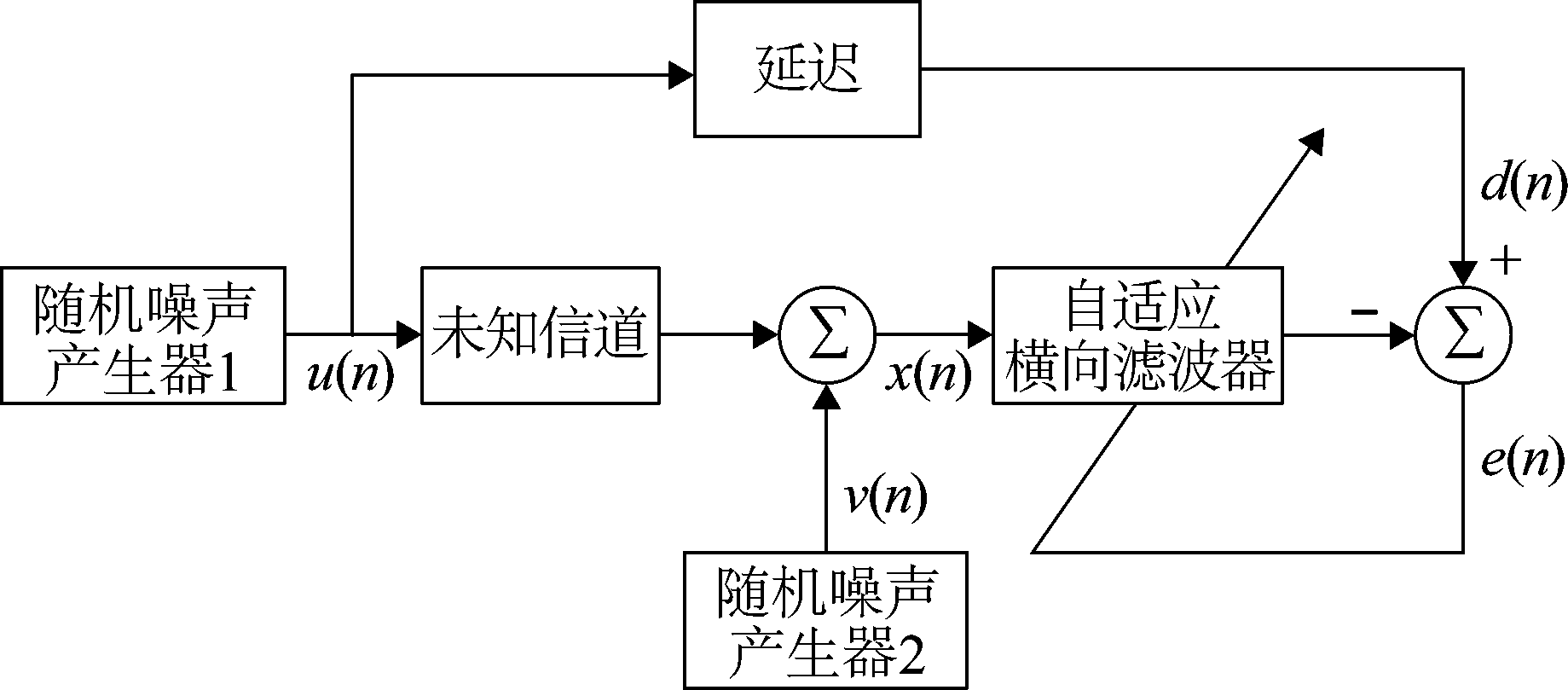
图1 自适应均衡实验框图
Fig.1 Adaptive Equalization experimental block diagram
由于在很多信号模型中DCT被证明是最佳的正交变换形式,因此如无特殊说明,本文仿真中的正交变换均采用DCT。
4.1 平稳信号仿真分析
本节针对平稳信号进行仿真,信噪比定义为SNR=10log10{E[y2(n)]/E[ν2(n)]},设置高低两种信噪比条件30 dB和10 dB,分别对应
和
采样1×104个点,并设置信道脉冲响应参数m=3.3,对应
本文MVSS-TDLMS算法与文献[1]、[6-8]中的TDLMS、VSS-TDLMS、SVS-TDLMS、GVS-TDLMS算法进行比较,所有仿真结果均通过100次蒙特卡罗实验得到。经过实验发现当算法参数设定为α=0.97, χ=0.99可以获得较好的稳态性能,若设定稳态MSE为-25 dB(SNR=30 dB)/-8 dB(SNR=10 dB),则由式(26)可得两种信噪比下的最佳β*≈8.7×10-4/ 0.23,为更好地体现稳态性能的差异,所有算法μmax=8×10-3, μmin=1×10-4,稳态MSE统一设定为-25 dB/-8 dB。由此,表1中给出仿真实验各算法参数取值。
为研究算法的自适应能力,在仿真时给予信道脉冲响应施加一个突变[16](在算法迭代到5×103点时响应系数为初始值的相反数)。图2给出了两种不同信噪比下各算法的学习曲线,可见固定步长的TDLMS算法收敛速度最慢(约在2600点处收敛),且突变点后达到收敛状态的速度明显变慢(约在8200点处收敛),说明其应对突变信道响应能力较差;在各种变步长的TDLMS算法中,本文算法在相同稳态失调水平下最快达到收敛状态(约在1300点处收敛),且对突变信道的跟踪能力较强(约在6500点处收敛)。图3为本文算法的步长因子在算法初始时刻和信道突变前后随迭代次数的变化曲线,其受到误差自相关的控制,可见在自适应初期其值较大保证了算法的快速收敛,而在末期的值较小保证了算法小的稳态失调。
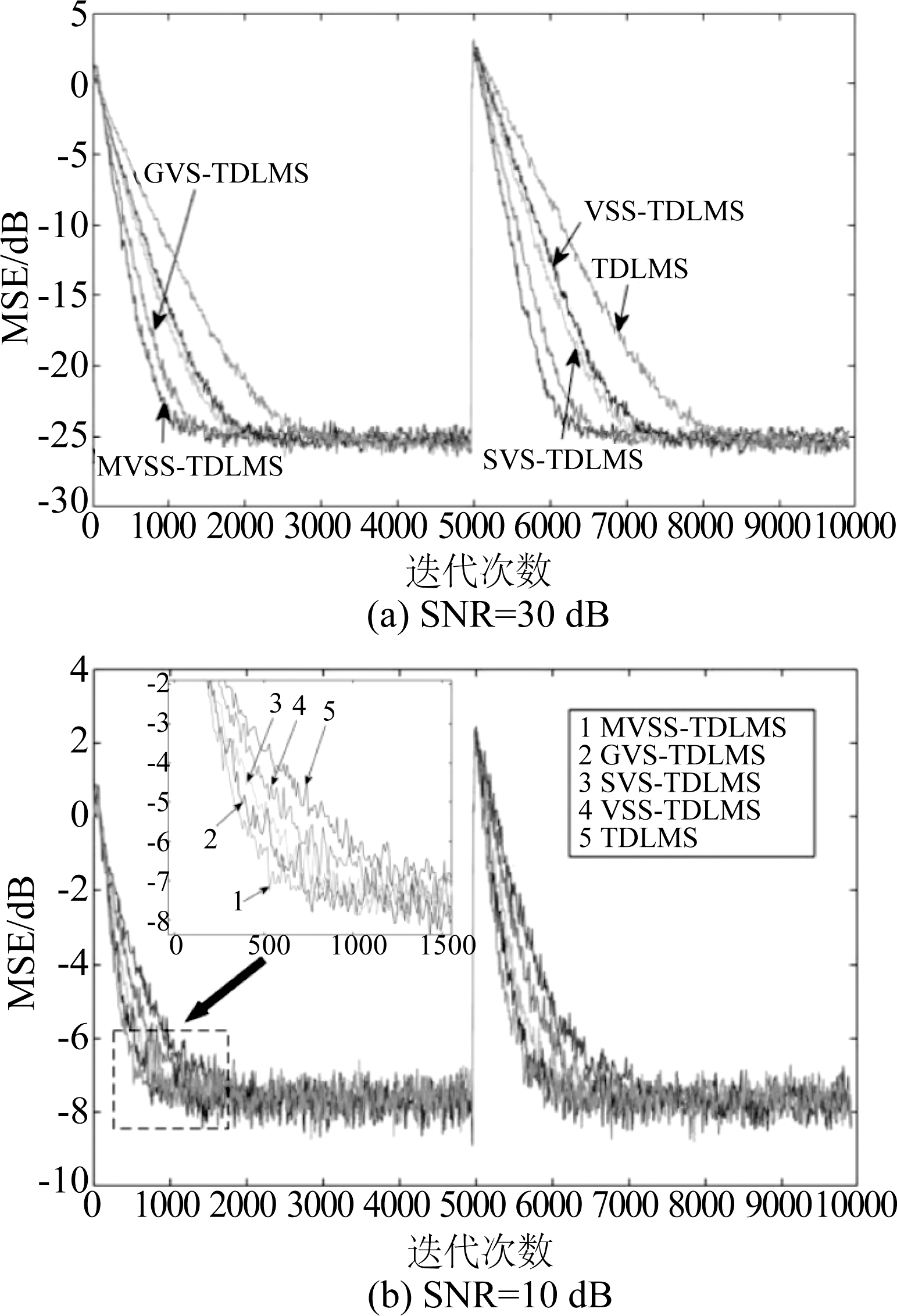
图2 平稳状态高低两种信噪比各种算法学习曲线
Fig.2 Learning curves of various algorithms for high and low SNR under the stationary state
表1 算法参数设置
Tab.1 Algorithm parameter Settings
算法类型步长因子更新公式SNR=30 dBSNR=10 dBTDLMSμ(n)=μFixedμFixed=5×10-3μFixed=5×10-3VSS-TDLMSμ(n+1)=αμ(n)+βe2(n)α=0.97, β=0.011α=0.97, β=0.056SVS-TDLMSμ(n)=α[1-exp(-βe(n)e(n-1))]α=30, β=0.08α=20, β=0.2GVS-TDLMSφ(n)=αφ(n-1)+e∗(n-1)ν～(n-1)μ(n)=μ(n-1)+βR[e(n)ν～H(n)φ(n)]α=0.95β=0.95α=0.95β=0.95本文MVSS-TDLMSp(n)=χp(n-1)+(1-χ)e(n)e(n-1)μ(n+1)=αμ(n)+βp2(n)χ=0.99α=0.97, β=8.7×10-3χ=0.99α=0.97, β=0.23
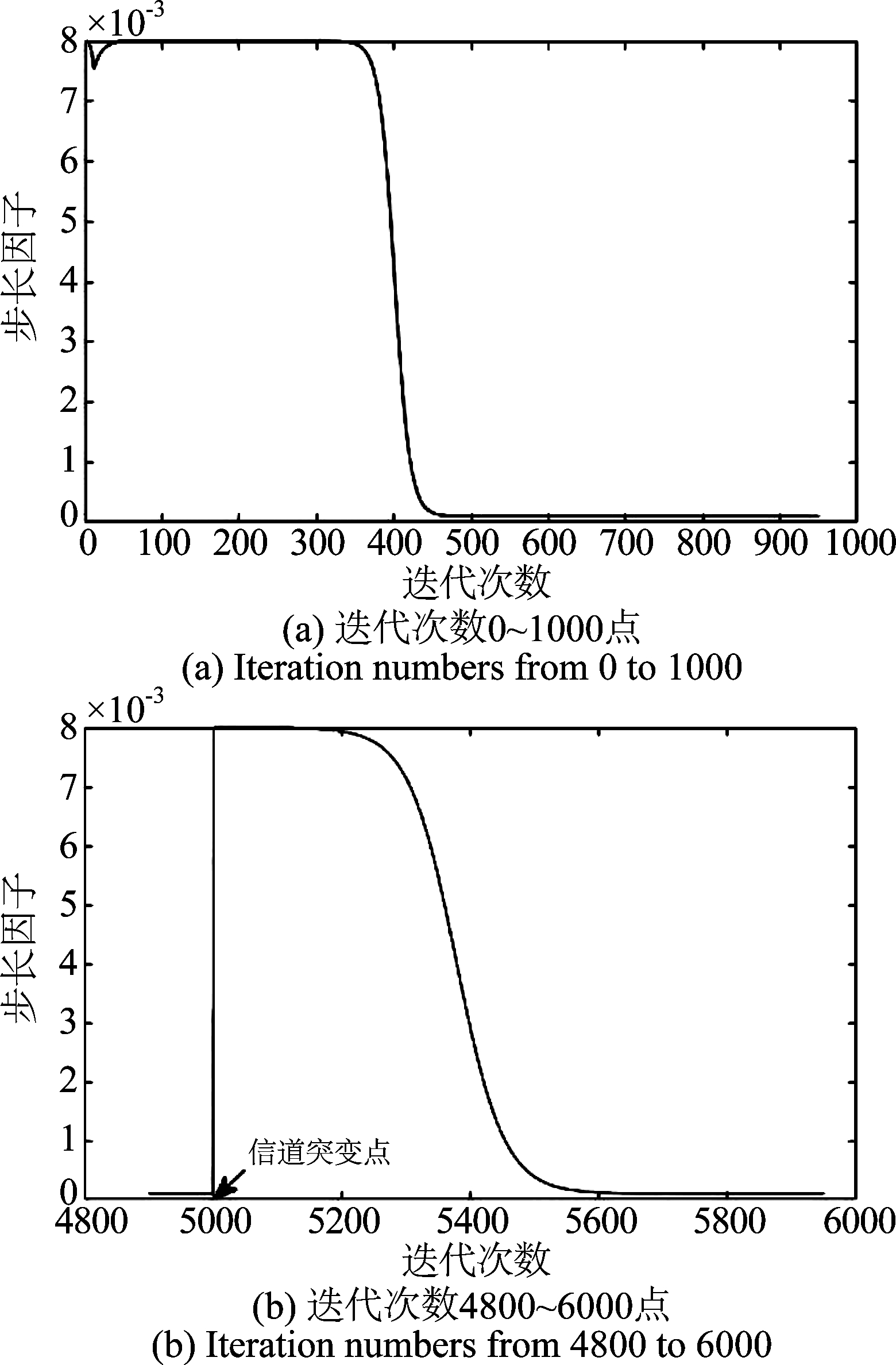
图3 平稳状态本文算法步长因子变化曲线
Fig.3 Variation curves of step size factor of the proposed algorithm under the stationary state
4.2 非平稳信号仿真分析
在本节仿真中系统脉冲响应是非平稳的,仿真条件与4.1节中的设置大致相同,不同之处在于滤波器最佳权向量Wopt是时变的,其迭代更新模型参见3.1节中的式(12)。
同样通过3.2节中的收敛和稳态分析可确定算法最佳变步长参数,α=0.97, χ=0.6, β*=3.8×10-3。图4给出
时各算法学习曲线,可见固定步长的算法约在1800点处收敛,而本文算法约在400点处收敛,说明本文算法在非平稳条件下依旧能够快速收敛,相比其他算法展示出良好的跟踪能力;另外选取β1=1×10-4, β2=9.7×10-3存在关系β1< β*< β2,图5中可见选择β1和β2时学习曲线基本上是重叠的,而通过式(26)计算得到最佳的算法参数绘制的学习曲线有最快的收敛速度和最小的稳态失调。
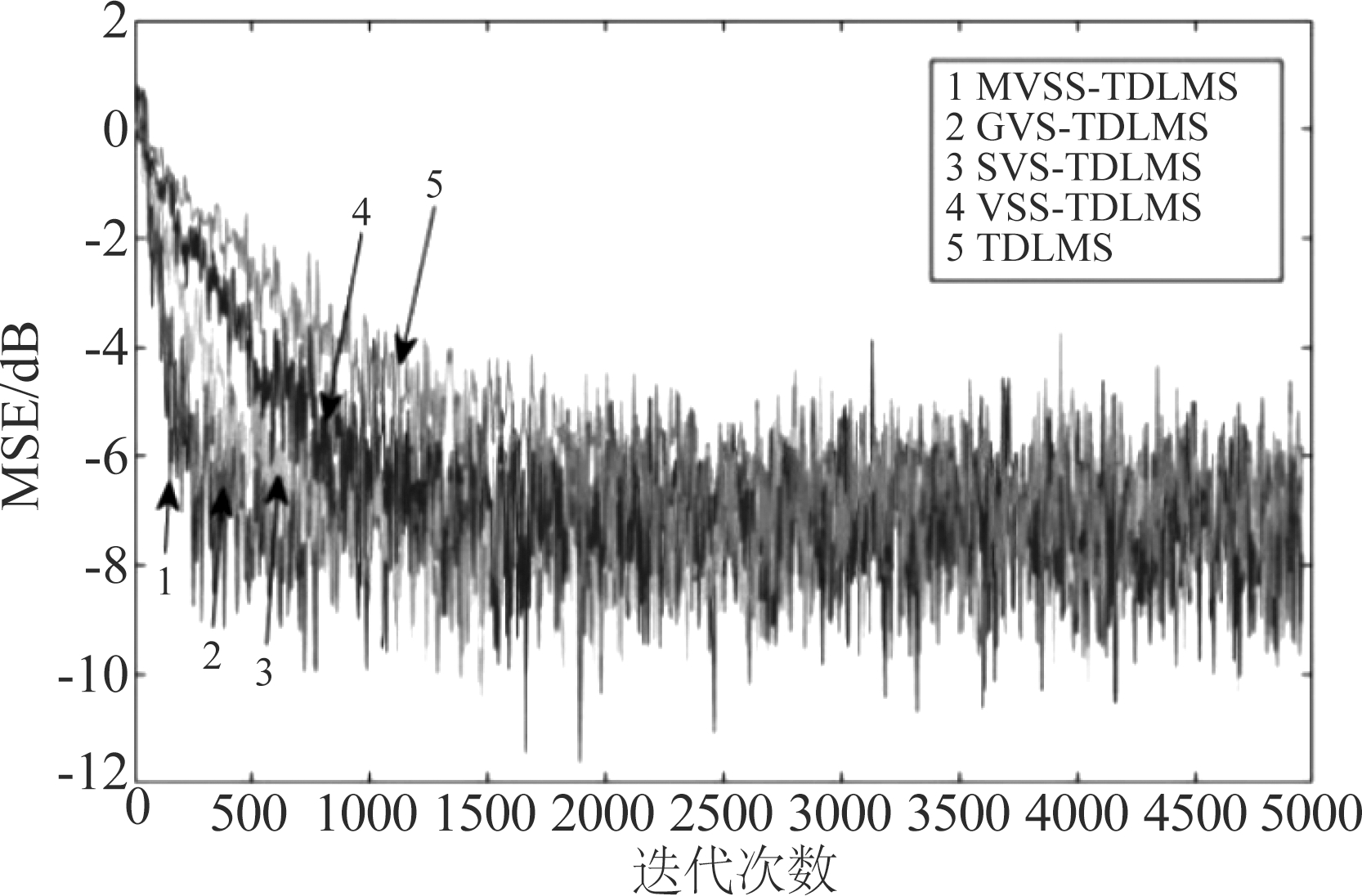
图4 非平稳状态各种算法学习曲线
Fig.4 Learning curves of various algorithms under the non-stationary state (SNR=30 dB, 
图5 非平稳状态不同β值本文算法学习曲线
Fig.5 Learning curves of the proposed algorithm for different values of β under the non-stationary state
5 结论
本文提出了一种在广义的平稳状态和非平稳状态下具有适应性的改进的变步长变换域最小均方算法,算法根据误差自相关时间平均的估计的平方控制步长因子的更新,消除了不相关观测噪声的影响,特别是参数χ的引入增强了算法对非平稳系统的跟踪能力。文中针对算法的收敛和稳态性能进行了理论分析,并推导了最优化算法参数χ选择的原则。仿真实验以自适应均衡问题为研究对象,与文献[1]、[6-8]中算法性能进行了对比,结果表明本文算法在小的稳态失调的前提下可以实现较快的收敛,特别是在非平稳状态下对于系统脉冲响应的变化有着良好的跟踪性能。此外,本文算法每次步长因子更新过程仅比固定步长的TDLMS算法多需要6次乘法和2次加法,具有计算复杂度低,易于工程实现的优势,在自适应滤波技术领域有着广泛的应用前景。
[1] Narayan S, Peterson A, Narasimha M. Transform domain LMS algorithm[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1983, 31(3): 609- 615.
[2] Schneider M, Kellermann W. The generalized frequency-domain adaptive filtering algorithm as an approximation of the block recursive least-squares algorithm[J]. EURASIP Journal on Advances in Signal Processing, 2016, 2016(1): 125-134.
[3] Chergui L, Bouguezel S. A new pre-whitening transform domain LMS algorithm and its application to speech denoising[J]. Signal Processing, 2016, 130(7): 118-128.
[4] Abadi M S E, Mesgarani H, Khademiyan S M. The wavelet transform-domain LMS adaptive filter employing dynamic selection of subband-coefficients[J]. Digital Signal Processing, 2017, 69: S1051200417301124.
[5] 柯熙政, 雷妍, 张颖. Hartley变换OFDM调制的可见光通信研究[J]. 信号处理, 2019, 35(2): 266-274.
Ke X Z, Lei Y, Zhang Y. Research on OFDM System Based on Hartley Transform in Visible Light Communication[J]. Journal of Signal Processing, 2019, 35(2): 266-274.(in Chinese)
[6] Zhao S, Man Z, Khoo S. A New Variable Step-Size Transform Domain LMS Algorithm with System Identification[C]∥Control and Automation, 2007. ICCA 2007. IEEE International Conference on. IEEE, 2007.
[7] 缑新科, 陈卓, 李冬冬. 基于DCT变换的变步长LMS自适应噪声抵消算法[J]. 兰州理工大学学报, 2014, 40(2): 93-97.
Hou X K, Chen Z, Li D D. A variable step LMS adaptive noise cancellation algorithm based on DCT transform[J]. Journal of Lanzhou University of Technology, 2014, 40(2): 93-97.(in Chinese)
[8] Roopa S, Narasimhan S V. Transform domain Variable Step-size Griffiths Least Mean Square adaptive algorithm and its applications[J]. Computers & Electrical Engineering, 2014, 40(4): 1028-1041.
[9] Chan S C, Chu Y J. A New Variable-Regularized Transform-Domain NLMS Algorithm with Automatic Step-Size Selection for Adaptive System Identification and Filtering[J]. Journal of Signal Processing Systems, 2016, 84(2): 181-196.
[10] Wang Y, Gu L, Liu F, et al. An adaptive algorithm for nonstationary active sound-profiling[J]. Applied Acoustics, 2018, 137(3): 51- 61.
[11] Gänsler T, Benesty J. Stereophonic acoustic echo cancellation and two-channel adaptive filtering: an overview[J]. International Journal of Adaptive Control & Signal Processing, 2015, 14(6): 565-586.
[12] Yi Y, Zhao H, Lu L. Steady-state behavior of the improved normalized subband adaptive filter algorithm and its improvement in under-modeling[J]. Signal Image & Video Processing, 2017, 12(4): 1- 8.
[13] Kuhn E V, Kolodziej J E, Seara R. Analysis of the TDLMS algorithm operating in a nonstationary environment[M]. Academic Press, Inc. 2015.
[14] Zhao S, Man Z,Khoo S, et al. Stability and Convergence Analysis of Transform-Domain LMS Adaptive Filters With Second-Order Autoregressive Process[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 119-130.
[15] Haykin S. Adaptive Filter Theory, 5th ed[M]. Englewood Cliffs, New York: Prentice Hall, 2010.
[16] 邹亚州, 向新, 张婧怡. 全双工射频自干扰改进时变步长NLMS对消算法[J]. 信号处理, 2017,33(10): 1360-1367.
Zou Y Z, Xiang X, Zhang J Y. Improved Time-Varying Step-Size NLMS Algorithm for RF Self-Interference Cancellation in Full-Duplex[J]. Journal of Signal Processing, 2017, 33(10):1360-1367.(in Chinese)
