1 引言
在航空气象学领域内,把出现在高度600 m以下风向、风速突然发生变化的大气现象称为低空风切变[1],这一高度正好处于飞机起飞和降落阶段,若此时飞机遭遇低空风切变,将缺乏足够的空间应对风切变的威胁,极易引起严重的坠机事故。目前,常用的风切变雷达包括激光多普勒雷达、微波多普勒雷达等[2]。文献[3]介绍了兰州机场使用激光多普勒雷达进行风切变探测的试验,试验结果表明,利用激光多普勒雷达在很大程度上可以确定机场上空有无风切变的存在,此外,激光多普勒雷达对弱小目标有较强的检测能力,但其对湿的风切变探测性能较弱,且受天气和大气影响大,在恶劣天气条件下作用距离显著减小。微波多普勒雷达受天气和大气影响小,在恶劣天气环境下仍有较好的目标检测能力,但对于干性风切变探测能力较弱。
机载气象雷达可以用来观测飞机前方的地形和发现航线上的障碍物,极大地保障了飞机飞行安全,可以称得上是飞机的“双眼”。目前,机载气象雷达系统的工作方式为脉冲体制,与之相比,LFMCW体制雷达要求的发射峰值功率低,其信号处理系统结构更为简单,同时还存在体积小、重量轻的优势[4]。将LFMCW技术与机载气象雷达完美地兼容,能够促进机载气象雷达朝着小型化的方向发展。小型化雷达系统可以减少载机负荷、节省机上空间,从而提高了载机的灵活性、机动性和续航能力。此外,小型化气象雷达能够装在直升机或小型飞机上,拓宽了机载气象雷达的使用范围。
近年来,国内外围绕LFMCW技术与合成孔径雷达、风廓线雷达、毫米波雷达等相结合的研究报道很多,并在各个领域中取得了一定的成果。文献[5]提出了将LFMCW技术与机载合成孔径雷达(Synthetic Aperture Radar, SAR)相结合的方法,并实现了精确的SAR成像;文献[6]提出了毫米波LFMCW雷达运用于汽车防撞系统中的设计思想,并通过理论分析论述了其具体的实现方法;文献[7]给出了LFMCW技术在地基气象雷达中的应用,并实现了对气象目标云雨的探测。除了理论的深入研究外,许多国家还相继研制出了试验样机。2013年中国航天科工二院23所成功地将连续波体制应用到风廓线雷达上,并顺利完成了实验测试,2015年荷兰成功研制出了机载多波束全极化FMCW合成孔径雷达,并于2016年以Cessna-208民用飞机为搭载平台进行了飞行试验[8]。然而,关于LFMCW技术与机载气象雷达相结合的理论尚未得到充分研究。
在低空风切变检测方面,机载雷达下视工作时会受到严重的地杂波干扰。雷达探测到的地杂波回波信号不仅分布范围广、强度大,而且由于载机平台运动,不同方向的地杂波相对载机的速度也是不相同的,使杂波谱出现扩展现象,导致风切变信号淹没于地杂波中而无法被雷达检测出来,因此,如何有效地抑制地杂波是低空风切变检测过程中需要解决的关键问题。当前空时自适应处理技术的理论研究已经相当成熟,被广泛的应用于机载雷达的杂波抑制处理,其充分利用了空域和时域信息,能够达到较好的杂波抑制效果。机载多通道LFMCW雷达系统通过采用多通道技术增加了系统的空间自由度,使利用空时域联合处理成为可能。如今STAP方法在多通道LFMCW体制雷达上已有应用[9-10],但其处理的对象大多数是点目标,无法将其直接用于低空风切变这类分布式气象目标的检测与估计。
本文提出了基于多通道LFMCW雷达的低空风切变风速估计方法,该方法首先建立了雷达的回波数据模型;其次结合风切变目标的复杂空间分布式特性,设计了一种能够用于检测风场目标信号的空-时自适应处理器结构,实现了地杂波滤除以及风切变信号匹配;最后使用D-PRF解速度模糊算法来修正模糊速度,进而完成对低空风切变场风速的有效估计。
2 信号模型
机载前视多通道LFMCW雷达的示意图如图1所示。载机以恒定速度V水平飞行,距地面高度为H,雷达天线沿航向垂直方向放置,采用独立的发射天线和接收天线,发射天线为定向单天线,接收天线为N个阵元构成的均匀线阵,阵元间距为d=0.5λ,λ为雷达工作波长。θ和φ分别为地面杂波散射单元的方位角和俯仰角,θ0和φl分别为风切变场信号的方位角和俯仰角,ψ为波束指向的空间锥角。
图1 机载前视多通道LFMCW雷达示意图
Fig.1 Geometry of the airborne forward-looking multi-channel LFMCW radar
不失一般性,假设在一个相干处理时间(Coherent Processing Interval, CPI)内,雷达连续发射K个周期LFMCW信号,发射信号的调频带宽为B,调频周期为Tr,占空比为100%,则雷达在第k(k=1,2,…,K)个周期内的发射信号表达式如下[11]:
(1)
其中,α0为发射信号的振幅, f0为载频, μ=B/Tr为调频斜率。
对于低空风切变信号模型的建立而言,为了分析清晰起见,我们首先考虑风场中的一个散射点。机载LFMCW雷达在其探测范围内有L个距离单元,从中选取位于第l(l=1,2,…,L)个距离单元风场中心的散射点进行讨论,设其水平方位角为θ0、俯仰角为φl,则第k个周期的发射信号经该散射点反射后被第n(n=1,2,…,N)个接收阵元接收的回波信号可以表示为:
(2)
式(2)中,αl表示该风场散射点回波信号的幅度,Rl表示该散射点与雷达发射天线的径向距离,τnk,l表示该散射点回波信号的时延[12],且有
(3)
式中,c表示光速,ν表示该风场散射点与载机的相对速度。在LFMCW雷达接收机中,各接收阵元接收到的目标回波信号都单独与发射信号进行混频,从而实现去调频的目的。通过将第n个阵元的回波信号xr,l(n,k,t)与发射信号x0(k,t)进行混频和低通滤波处理后可得该散射点的差拍信号[13]为:
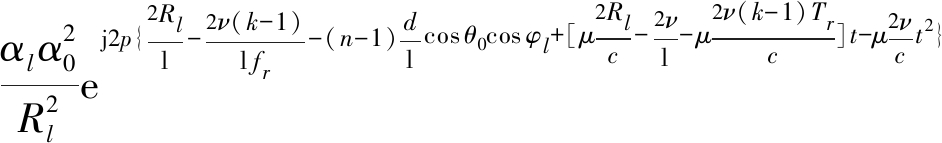
τmax≤t<Tr n=1,2,…,N
(4)
其中, fr=1/Tr,τmax=2Rmax/c,Rmax为LFMCW雷达的最大探测距离。由ν≪c可知,该散射点差拍信号的调频斜率
远远小于发射信号的调频斜率μ,故式中调频斜率项
可忽略不计。进一步,上式可化简为:
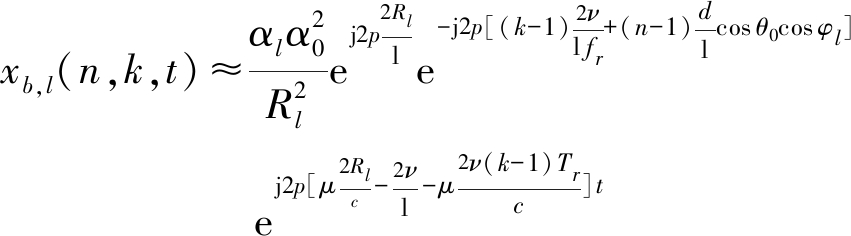
(5)
在LFMCW雷达系统中,通过对差拍信号的傅里叶分析,能够实现目标检测以及参数估计[14]。对式(5)中的快时间t做傅里叶变换,可以得到该散射点的差拍信号频谱如下式所示:
(6)
其中,Te=Tr-τmax,sinc(β)=sin(β)/β,从上式可以看出该散射点差拍信号的频谱χb,l(n,k, f )是一个尖峰很窄的sinc函数,其中心频率为:
(7)
式中,第二项
表示该风场散射点的多普勒频率,第三项
是由于雷达连续照射产生的频移。将f=fb,lk代入式(6)中,便可以得到雷达的第n个接收阵元在第k个周期接收到的第l个距离单元内该风场散射点的回波数据:
n=1,2,…,N k=1,2,…,K
(8)
式中,
为FFT处理后的该风场散射点回波信号复幅度, fd=2ν/λfr为归一化多普勒频率,cos ψ0=cos θ0cos φl,则阵元的第k个周期在第l个距离单元的回波矢量可以表示为:
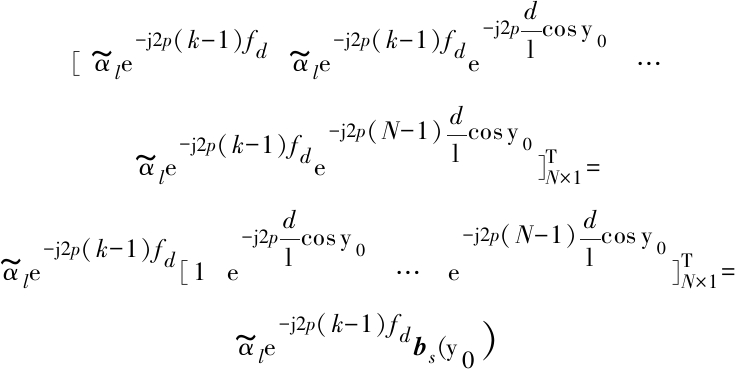
(9)
式中,
表示该距离单元风场中心上的散射点的空间导向矢量。将hl(k)(k=1,2,…,K)排成一个NK×1维的列矢量hl,即:
(10)
式中,⊗表示Kronecker积,
表示第l个距离单元内多普勒中心频率为fd的风场散射点的时间导向矢量。
由于低空风切变属于分布式目标,其存在角度扩展和频谱扩展,所以其回波数据模型已经不能用传统点目标的空时导向矢量来准确描述,但是可以通过对已有的点目标的时间导向矢量和空间导向矢量进行扩展,得到分布式目标的时间导向矢量Bt( fd)和空间导向矢量Bs(ψ0):
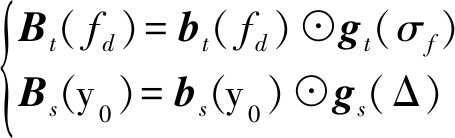
(11)
式中,
表示高斯频率扩展函数,σf表示多普勒谱宽,gs(Δ)=[1,e-1/2(1.2πd/λ)2Δ,…,e-1/2((N-1).2πd/λ)2Δ]T表示空域扩展函数,Δ表示角度扩展[15]。则风切变场的空时二维导向矢量可表示为:
Bl( fd,ψ0)=Bt( fd)⊗Bs(ψ0)
(12)
故第l个距离单元的风切变信号接收数据模型为:
(13)
进而第l个距离单元的雷达回波数据可以表示为:
zl=sl+cl+nl
(14)
其中,cl表示第l个距离单元的地杂波,nl表示第l个距离单元的高斯白噪声。
3 基于最优STAP的风速估计方法
基于最优STAP的风速估计方法首先利用空时最优自适应处理器,完成对地杂波的有效抑制并实现对低空风切变信号的匹配,然后获得风切变目标的多普勒中心频率,进而得到了全距离单元的风速估计值,最后再使用D-PRF解速度模糊算法来订正模糊速度,获得真实的风场速度。
3.1 低空风切变风速估计
根据LCMV准则,可以将空时自适应处理器描述为如下的数学优化问题[16]:
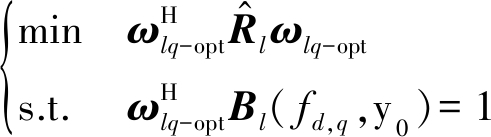
(15)
式中,
为第l个待检测距离单元的杂波协方差矩阵,其中,yj=Tl, jzj为第j个参考距离单元矫正后的数据[15],zj为该参考单元的雷达回波数据,Tl, j为基于配准补偿(registration based compensation, RBC)法的补偿矩阵。Bl( fd,q,ψ0)为该距离单元内风场目标的空时导向矢量,其中, fd,q为第q个多普勒通道的风场目标信号的归一化多普勒频率。求解上述数学优化问题,可以得到最优权矢量ωlq-opt为:
(16)
其中,拉格朗日算子
为归一化常数。利用得到最优权矢量对待检测单元数据zl进行自适应滤波处理,则处理后的结果可以表示为:
(17)
更新求解权矢量设置的多普勒中心频率fd,q( fd,q取值范围为[-1,1]),获得不同多普勒频率下的权矢量,并分别求解最优滤波器输出的信号功率,接着进行峰值搜索,当输出功率最大时,它所对应的多普勒频率值便是该距离单元中风场目标的多普勒频率估计值
(18)
最终得到第l个距离单元的风场速度估计值为:
(19)
依上述方法先计算单个距离单元的风速估计值,再扩展到所有距离单元,进而完成了整个风切变场的风速估计。
3.2 D-PRF解速度模糊
本文同时考虑了实际情况下机载雷达的最大探测距离与LFMCW雷达中τmax<Tr/2的约束条件[9],采用了低脉冲重复频率的LFMCW雷达进行风切变场风速估计。然而低PRF的选取势必会产生速度模糊现象,严重影响了真实风场速度的获取,因此必须进行速度模糊修正处理。
假设所发射的LFMCW信号的调频周期分别为T1和T2(T1<T2),T1
T2=MN,且M与N互质。此时调频周期T1对应的最大不模糊速度νmax1=λ/4T1,测速范围为(-νmax1,νmax1)。T2对应的最大不模糊速度νmax2=λ/4T2,测速范围为(-νmax2,νmax2),经过D-PRF解速度模糊后的最大不模糊速度νmax=λ/4(T2-T1),测速范围为(-νmax,νmax)。
因速度估计结果可能存在模糊问题,所以真实值νz和估计值有如下关系:
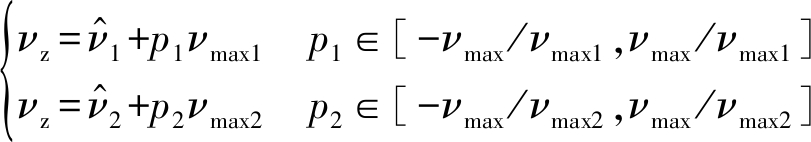
(20)
其中,
和
分别为调频周期T1、T2下的风场速度估计值,p1和p2为模糊次数(或折叠次数)且为整数。考虑到真实速度值并不会受重复频率的影响[17],故一定存在一组确定的值(p1,p2),使通过式(20)中两式求得的速度结果一致,故求解模糊次数p1和p2的过程可以转换为如下数学优化问题:
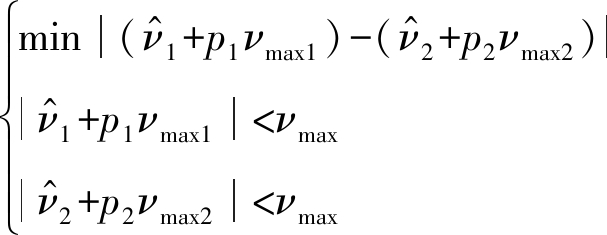
(21)
最终真实速度值可以表示为:
(22)
4 算法流程
图2为本文提出的基于多通道LFMCW雷达低空风切变风速估计方法的流程图。具体实现步骤如下:
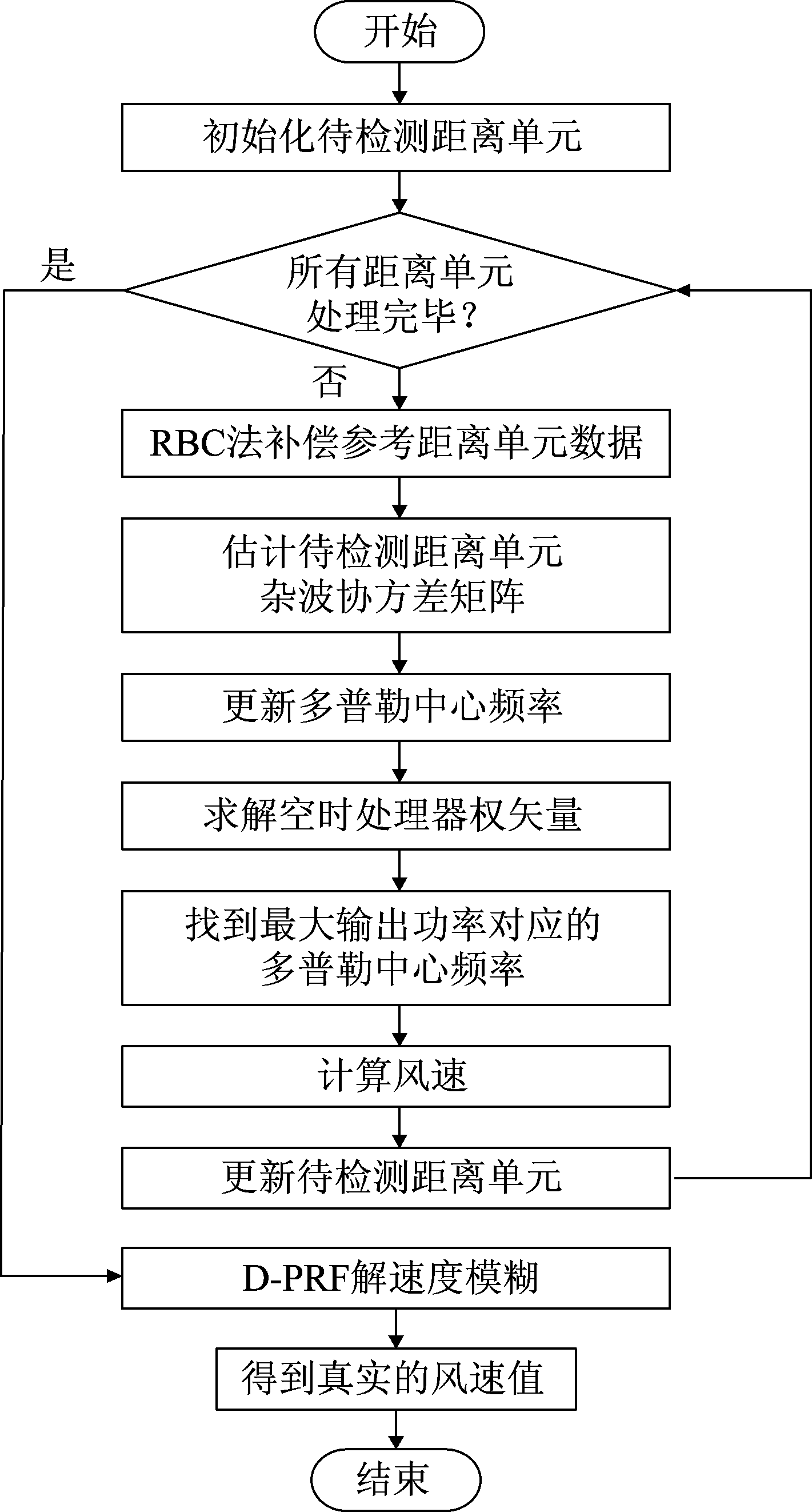
图2 基于多通道LFMCW雷达的低空风切变风速估计方法流程图
Fig.2 Flow chart of low-altitude wind shear speed estimation method based on multi-channel LFMCW radar
步骤1 选取待检测距离单元,采用RBC法对参考距离单元杂波谱进行补偿,使变换后的参考距离单元具有与待检测距离单元相同的杂波空-时二维分布,从而消除了杂波谱对距离的依赖性。再根据补偿后的参考距离单元数据,估计得到待检测距离单元的杂波协方差矩阵;
步骤2 设计适用于低空风切变检测的空时最优自适应处理器,并更新处理器中所设置的多普勒中心频率,进而获得不同多普勒频率下的自适应权矢量,它可以在杂波脊处自适应地形成凹口并在目标信号处进行相干积累;
步骤3 利用得到最优权矢量对待检测单元数据进行自适应滤波处理,输出不同多普勒频率下的信号功率,寻找最大输出功率所对应的多普勒中心频率,并计算该距离单元的风速值;
步骤4 更新待检测距离单元,重复步骤1到步骤3,直到雷达波束范围内所有距离单元的回波数据处理完毕,得到全距离单元风速估计结果;
步骤5 使用D-PRF解速度模糊算法对全距离单元风速估计结果进行处理,获得风切变场的真实风速值。
5 仿真结果及分析
5.1 仿真条件
为了验证本文所建风切变信号模型的正确性以及所提风速估计方法的有效性,进行了相关的仿真实验,仿真过程中所需的主要参数设置如表1所示。
表1 载机与雷达仿真参数
Tab.1 Aircraft and radar simulation parameters
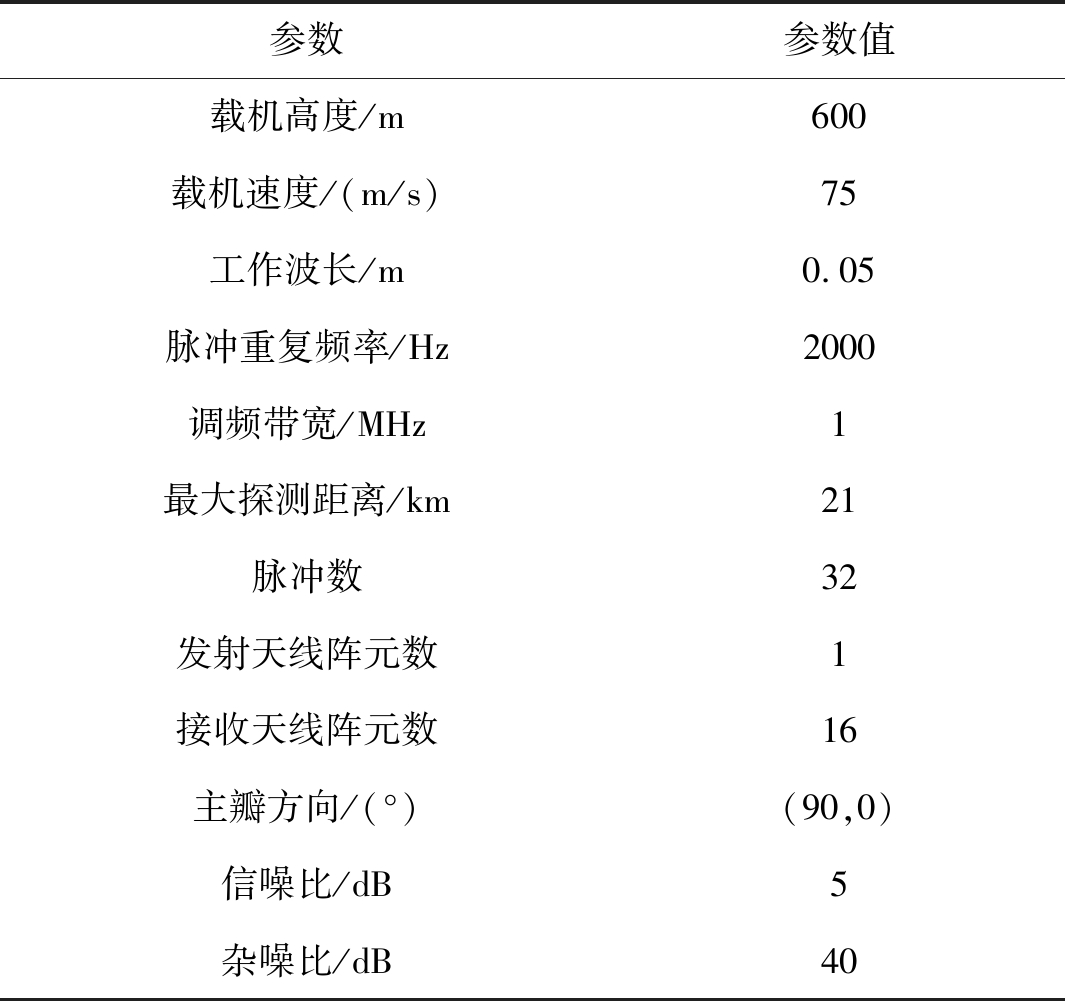
参数参数值载机高度/m600载机速度/(m/s)75工作波长/m0.05脉冲重复频率/Hz2000调频带宽/MHz1最大探测距离/km21脉冲数32发射天线阵元数1接收天线阵元数16主瓣方向/(°)(90,0)信噪比/dB5杂噪比/dB40
5.2 仿真结果分析
图3仿真了机载多通道LFMCW雷达回波信号的功率谱。经观察可以发现,当机载多通道LFMCW雷达工作于前视模式时,地杂波的功率谱呈椭圆形并在空时二维平面上出现了折叠现象,风切变回波信号的空时二维谱是一条沿多普勒域正负连续分布的窄带,而且地杂波的回波功率远远大于风切变场的回波功率,这将导致风切变信号淹没于杂波之中,更加难以被检测出来。
图3 雷达回波信号的功率谱
Fig.3 The spectrum of radar echo signal
图4(a)和图4(b)分别仿真了PRF=2000 Hz和PRF=3000 Hz情况下机载多通道LFMCW雷达地杂波功率谱。从图中可见,旁瓣杂波在空时二维平面上均出现了折叠现象,且杂波功率谱在多普勒域上的展宽都比较严重,这将导致空-时自适应处理器无法形成窄而深的凹口去抑制地杂波,从而不能有效地检测目标。
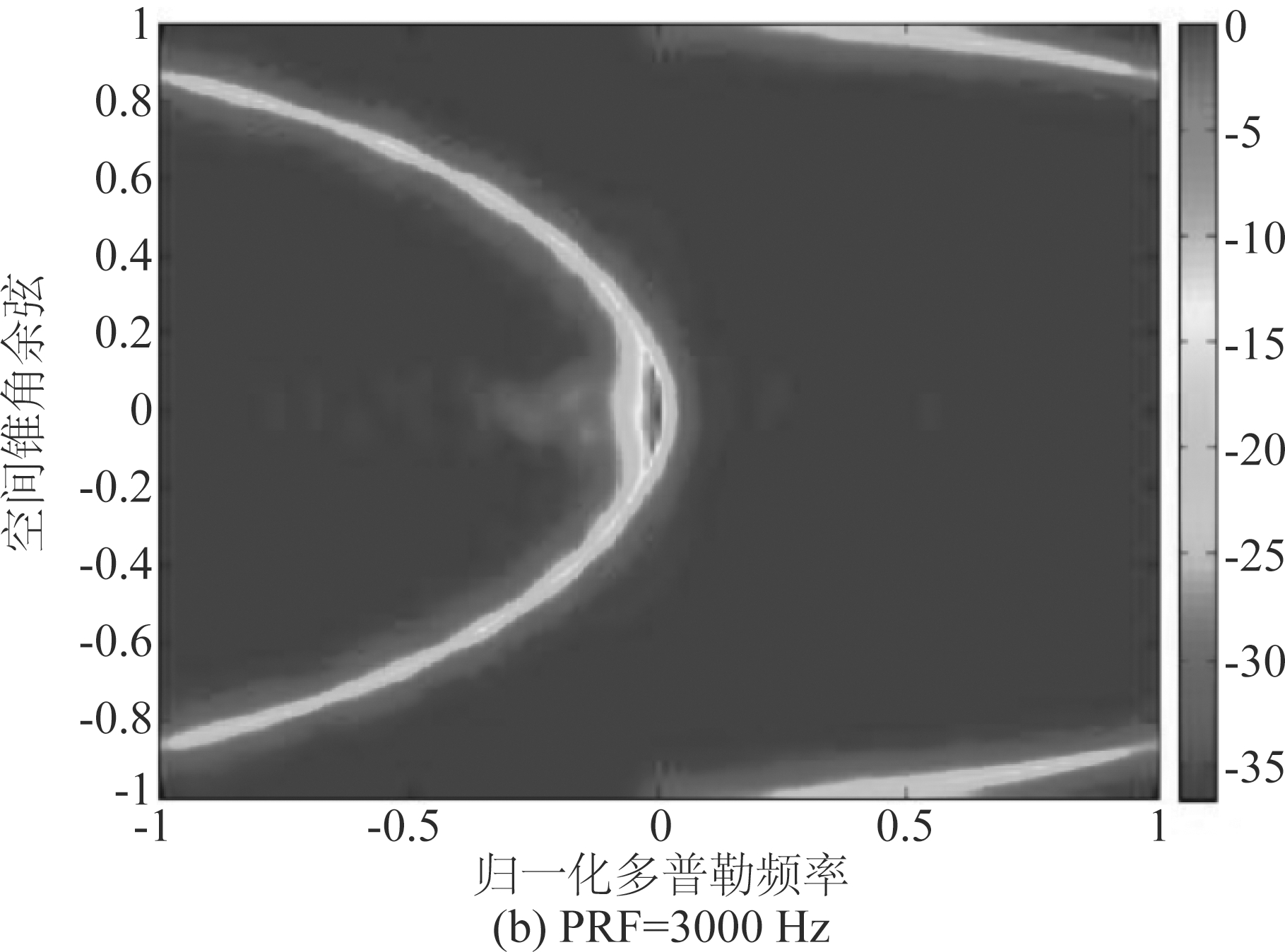
图4 不同PRF条件下的地杂波功率谱
Fig.4 Power spectrum of ground clutter under different PRF conditions
本文选择脉冲重复频率比为3∶ 2(3000 Hz∶ 2000 Hz)的模式进行解模糊处理,当PRF=3000 Hz时,最大不模糊速度νmax1为37.5 m/s,当PRF=2000 Hz时,最大不模糊速度νmax2为25 m/s,经过D-PRF解速度模糊处理后,最大不模糊速度νmax为75 m/s,测速范围比采用单一脉冲重复频率分别扩大了2倍和3倍,可以保证风场速度都能够落在最大不模糊速度范围内。图5给出了解模糊前和解模糊后的风场速度对比图。图5(a)为RPF=2000 Hz时的风速估计结果图,从图中可以看出,抑制地杂波后估计得到的风场速度在速度超过±25 m/s时,速度值发生了正负跳变,即出现了速度模糊现象,此时图5(a)已不能反映真实的风场速度。图5(b)中显示的是PRF=3000 Hz时的风速估计结果,当风场速度在速度大于±37.5 m/s时有正负跳变,同样也无法反映风场的真实情况。而进行解模糊处理后,图5(c)中显示的风场速度与原始风场速度非常贴近,且风场速度随距离呈现反“S”形分布,经计算,风速估计的均方根误差为2.6016 m/s,由此可以说明本文所提方法可以在低信噪比、高杂噪比的环境下有效地估计风场速度。
为进一步验证所提方法的有效性,本文选取杂噪比分别为35 dB和45 dB,脉冲重复频率之比仍选为3∶2(3000 Hz∶2000 Hz),再次采用本文所提方法并进行解模糊处理,图6、图7分别为CNR=35 dB和CNR=45 dB时得到的雷达回波信号功率谱以及估计风场速度与原始风场速度对比图。由图可知估计风场速度与原始风场速度基本吻合,经计算,杂噪比为35 dB时,风速估计的均方根误差为2.5274 m/s,杂噪比为45 dB时,均方根误差为2.6107 m/s,说明改变杂噪比后仍然可以得到良好的风速估计结果。
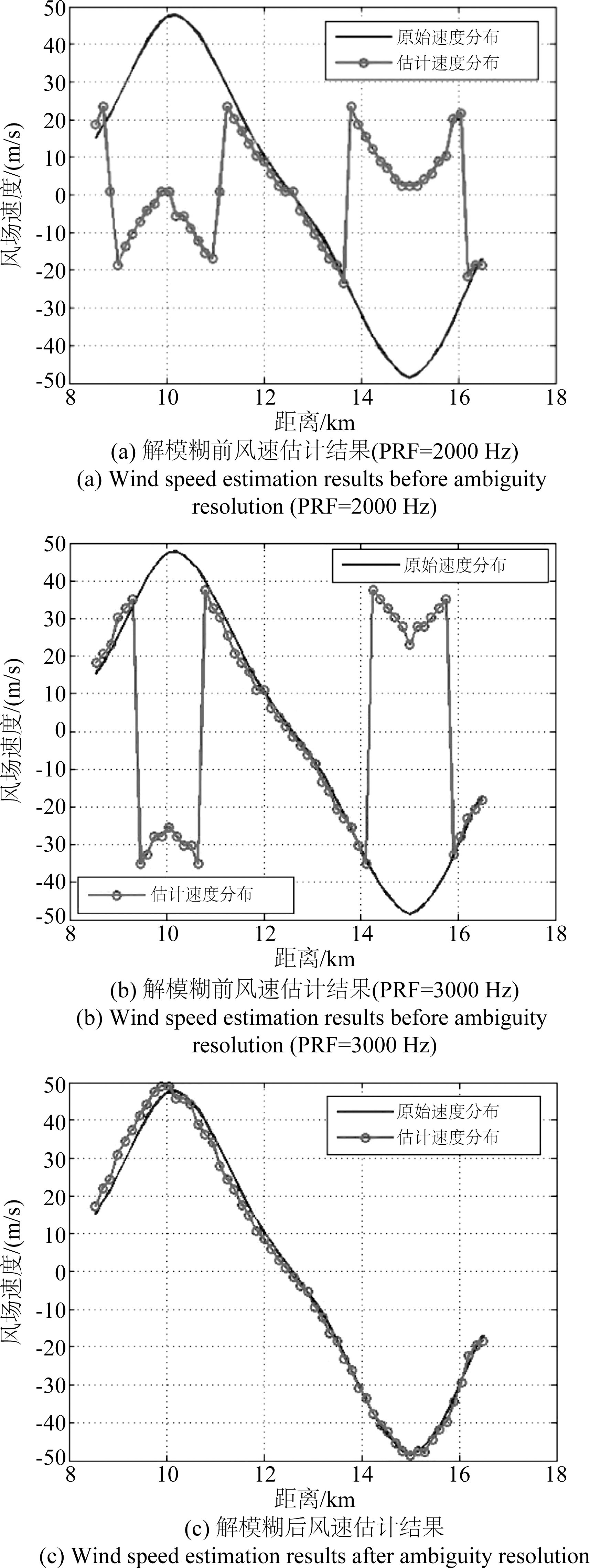
图5 解模糊前后风速估计结果比较
Fig.5 The comparison between wind speed estimation results before and after ambiguity resolution
图6 雷达回波信号功率谱及解模糊前后风速估计结果比较(CNR=35 dB)
Fig.6 The spectrum of radar echo signal and the comparison between wind speed estimation results before and after ambiguity resolution(CNR=35 dB)
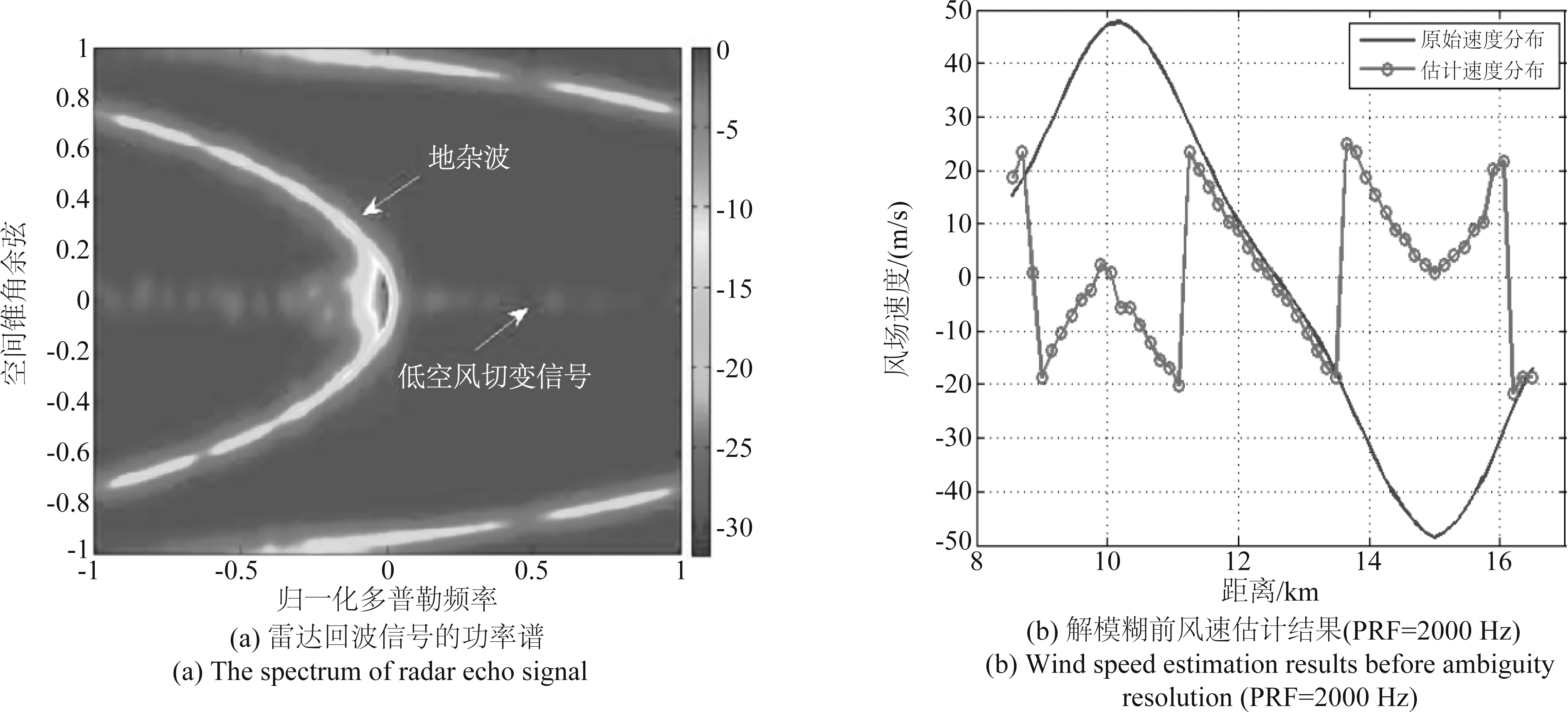
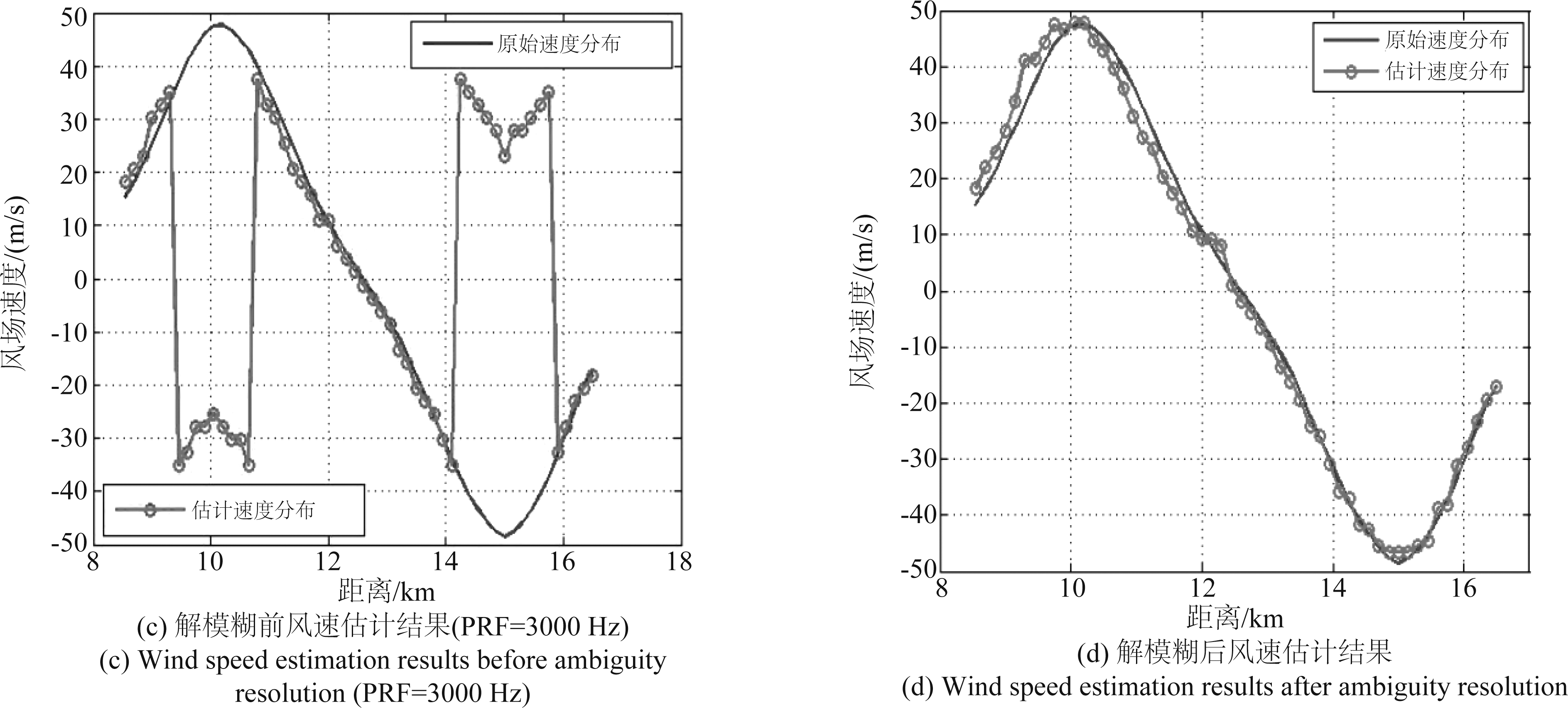
图7 雷达回波信号功率谱及解模糊前后风速估计结果比较(CNR=45 dB)
Fig.7 The spectrum of radar echo signal and the comparison between wind speed estimation results before and after ambiguity resolution(CNR=45 dB)
6 结论
针对传统脉冲雷达在低空风切变检测中存在结构复杂,成本高,体积大,发射功率高等的局限性,本文提出了一种基于多通道LFMCW雷达的低空风切变风速估计方法。该方法首先在LFMCW雷达的理论基础上,建立了机载多通道LFMCW雷达的低空风切变信号模型,然后设计了适用于分布式目标的空-时最优处理器,并通过对每个多普勒通道进行自适应滤波处理,得到了整个风场的速度估计结果,最后进一步采用D-PRF解速度模糊算法进行速度解模糊,以获得真实的风场速度。仿真结果证明了本文所提方法能够有效、准确地估计出风场速度。
[1] Li Hai, Zhou Meng, Guo Qinghua, et al. Compressive sensing-based wind speed estimation for low-altitude wind-shear with airborne phased array radar[J]. Multidimensional Systems and Signal Processing, 2016, 29(7): 1-14.
[2] 赵文治, 付国, 栗中华, 等. 风切变雷达原理与应用[J].中国民航学院学报,2004, 22(4): 115-116.
Zhao Wenzhi, Fu Guo, Li Zhonghua, et al. Principle and Application of Wind Shear Radar[J]. Journal of Civil Aviation University of China, 2004, 22(4): 115-116.(in Chinese)
[3] 孙伟中. 三部激光雷达对兰州机场风场探测的效能统计分析及低空风切变分级预警的探讨[J]. 中国民用航空, 2017, 24(3): 41- 47.
Sun Weizhong. Statistical Analysis of the Effectiveness of Three Laser Radars in Wind Detection of Lanzhou Airport and Discussion on Classified Early Warning of Low Altitude Wind Shear[J]. China Civil Aviation, 2017, 24(3): 41- 47.(in Chinese)
[4] 朱文涛, 苏涛, 杨涛, 等. 线性调频连续波信号检测与参数估计算法[J]. 电子与信息学报, 2014, 36(3): 552-558.
Zhu Wentao, Su Tao, Yang Tao, et al. Detection and Parameter Estimation of Linear Frequency Modulation Continuous Wave Signal[J]. Journal of Electronics & Information Technology, 2014, 36(3): 552-558.(in Chinese)
[5] 王金伟, 周峰, 吴玉峰, 等. FMCW-SAR体制下快速运动目标检测与成像方法[J]. 电子与信息学报, 2014, 36(11): 2684-2690.
Wang Jinwei, Zhou Feng, Wu Yufeng, et al. Approach for Fast-moving Target Detection and Imaging in FMCW SAR[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2684-2690.(in Chinese)
[6] Zhao Shuang, Chen Lei. Research on Target Recognition of the Millimeter Wave Car Collision Avoidance Radar Based on the LFMCW[J]. Advanced Materials Research, 2014, 1056: 244-247.
[7] Co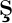
kun S, Çelik M, Yilmaz A Ö, et al. Doppler capable FMCW cloud detection radar[C]∥Spie Remote Sensing. International Society for Optics and Photonics, 2015:96400A-1-96400A-10.
[8] 张昊宇. 机载多波段全极化FMCW合成孔径雷达最新实测成果[J]. 中国水运, 2017, 38(6): 30-31.
Zhang Haoyu. The latest measured results of airborne multi-beam fully polarimetric FMCW synthetic aperture radar[J]. China Water Transport, 2017, 38(6): 30-31.(in Chinese)
[9] Górski T, Kawalec A, Czarnecki W, et al. Application of STAP Technique to FMCW Systems[C]∥2007 European Radar Conference. IEEE, 2007:63- 66.
[10] 金威, 吕晓德, 向茂盛. STAP技术在多通道FMCW SAR上的应用[C]∥全国军事微波会议. 微波学报, 2010:623- 626.
Jin Wei, Lv Xiaode, Xiang Maosheng. Application of STAP Technique for Multi-channel FMCW SAR[C]∥National Military Microwave Technology Conference. Journal of Microwaves, 2010:623- 626.(in Chinese)
[11] Wang Bin, Hu Zhiyou, Guan Wenshuo, et al. Study on the echo signal model and R-D imaging algorithm for FMCW SAR[C]∥International Radar Conference. IET, 2016:1- 6.
[12] Hu Chenxin, Liu Yimin, Meng Huadong, et al. Randomized Switched Antenna Array FMCW Radar for Automotive Applications[J]. IEEE Transactions on Vehicular Technology, 2014, 63(8): 3624-3641.
[13] Wang Peng, Meng Huadong, Wei Yimin. FMCW Radar Imaging with Multi-channel Antenna Array via Sparse Recovery Technique[C]∥International Conference on Electrical & Control Engineering. IEEE Computer Society, 2010: 1018-1021.
[14] Lu Jianbin, Xi Zemin, Zhang Mingmin, et al. Multicycle signal processing based on Keystone transform in LFMCW radar[C]∥International Conference on Signal Processing Systems. IEEE, 2010: 280-284.
[15] 李海, 周盟, 陈筱浅, 等. 基于多通道联合自适应处理的微下击暴流中心风速估计方法[J]. 电子与信息学报, 2017, 39(7): 1619-1625.
Li Hai, Zhou Meng, Chen Xiaqian, et al. Multiple Doppler Channels Joint Adaptive Processing Based Central Wind Speed Estimation for Microburst[J]. Journal of Electronics & Information Technology, 2017, 39(7):1619-1625.(in Chinese)
[16] Wang Xiaye, Yang Zhaocheng, Huang Huiping, et al. Space-Time Adaptive Processing for Airborne Radars with Space-Time Coprime Sampling Structure[J]. IEEE Access, 2018, 6(1): 20031-20046.
[17] 夏梦颖, 苏卫民, 顾红,等. 基于多重频脉冲串信号解速度模糊的研究[J]. 电子与信息学报, 2017, 39(12): 70-75.
Xia Mengying, Su Weimin, Gu Hong, et al. Research on Velocity Ambiguity Resolution for Multiple PRF Radar[J]. Journal of Electronics & Information Technology, 2017, 39(12):70-75.(in Chinese)
