1 引言
随着人工智能、图像分析技术的快速发展,人脸识别技术在许多领域得到广泛应用[1-2]。然而,非约束环境下采集的人脸图像,受光照、遮挡、表情等多种因素混合干扰,人脸识别准确度大大降低。同时,原始图像以高维数据存在,导致人脸识别速度也受影响。因此,数据降维成为非约束人脸识别的关键步骤,它不仅可以降低高维数据的冗余度,加快算法执行速度,还能提高分类模型的准确度。
具有代表性的经典降维方法有主成分分析(Principle Components Analysis, PCA)[3]和线性鉴别分析(Linear Discriminant Analysis, LDA)[4],它们都建立在满足高斯分布的前提下,并取得了一定的成功。然而人脸图像在低维子空间中呈现非线性流形分布,以PCA和LDA为代表的线性降维方法并不理想。这使得人们相继提出适用于非线性结构的流形学习算法,如局部线性嵌入[5]和拉普拉斯特征映射[6],但是这类算法使样本数据从高维空间映射到低维空间属于隐式映射,对于处理新的测试数据效果不佳。为了解决这个问题,He等和Zhang等分别提出了近邻保持嵌入(Neighborhood Preserving Embedding, NPE)[7]算法和线性局部切空间排列算法[8],通过显示的变换矩阵来构建目标函数,将人脸数据投影到本质的流形结构上,上述方法属于无监督学习,没有考虑到样本的类别信息,因此Wang等和Gao等又分别提出了边界费舍分析(Margin Fisher Analysis,MFA)[9]和局部敏感判别分析(Local Discriminant Embedding and Its Variants,LSDA)[10],通过赋予样本类别信息,增强低维子空间鉴别结构。
分析上述降维算法可知,它们的实现原理与Yan等人提出的图形嵌入框架一致[11],这类方法需要用κ近邻和ε邻域等常用方法来构建样本的邻域几何结构,算法的识别效果受参数κ和ε影响较大,普适性差。2009年,Wright等提出的基于稀疏表示的分类器(Sparse Representation Based Classifier, SRC)[12],其基本思想是通过最小化L1范数来求解待测样本在整个训练样本中的稀疏表示系数,然后通过稀疏系统重构测试样本同时求其残差,根据残差值进行分类,因为具有优越的编码能力和重构特性,所以被广泛的运用到人脸图像识别领域。受此启发,Qiao等提出了稀疏保持投影算法(Sparsity Preserving Projections, SPP)[13],采用稀疏表示自适应构建邻域图,这很大程度上降低了图参数选择的问题。近年来,大量学者在此领域进行深入研究。
Liu等提出了一种结合流形学习和鉴别分析的稀疏保持嵌入(Sparsity Preserving Embedding with Manifold Learning and Discriminant Analysis,SPE)[14]的特征提取算法,通过将判别分析和流形学习与稀疏表示技术相结合,对得到的最稀疏重构结果进行子流形空间上类内散度和类间散度的判别分析进行特征降维。然而SPP和SPE在稀疏重构时忽略了样本的类别信息,这会导致分类时鉴别力不足。针对该问题,Zang和Zhang[15]将标签信息和L1图相结合,自适应地构造了数据的内在图,并提出了监督维数算法。Gui等也提出了判别稀疏邻域保持嵌入(Discriminant Sparsity neighborhood Preserving Embedding,DSNPE)[16]算法,该算法添加样本类别信息,分别计算样本的类内散度和类间散度,通过最大化类间离散度和类内离散度之差来寻找最佳投影方向实现降维投影。
另一方面,一些学者针对投影和分类无关联的问题进行改进。例如文献[17]提出了一种基于稀疏表示分类器引导鉴别投影的维数约简算法,该方法利用稀疏表示技术,使其在投影空间实现最佳性能,在减少维数的同时,实现与分类器的最佳匹配。然而,SRC-DP算法在求解投影矩阵时没有同时考虑分类器和特征提取,针对这个问题,Gao和Zheng等分别提出了一种基于稀疏表示与Fisher准则相结合的降维(Dimensionality Reduction by Integrating Sparse Representation and Fisher Criterion and Its Applications,SRC-FDC)[18]算法和基于自适应权值学习的迭代重约束组稀疏人脸识别(Iteratively Re-Constrained Group Sparse Classi cation,IRGSC)[19]算法。SRC-FDC算法使用Fisher判别准则(Fisher Discriminant Criterion,FDC)来提取判别结构,并采用稀疏表示来保证提取的特征满足SRC,经过验证,该算法有一定的效果。而IRGSC算法不仅在分类器上进行了改进,而且在提取过程中将自适应权重学习与组稀疏表示分类进行了联合优化,使分类识别结果得到了很大的提高。
cation,IRGSC)[19]算法。SRC-FDC算法使用Fisher判别准则(Fisher Discriminant Criterion,FDC)来提取判别结构,并采用稀疏表示来保证提取的特征满足SRC,经过验证,该算法有一定的效果。而IRGSC算法不仅在分类器上进行了改进,而且在提取过程中将自适应权重学习与组稀疏表示分类进行了联合优化,使分类识别结果得到了很大的提高。
另外,用L2范数的平方表征数据的几何结构,这对噪声和异常值处理还存在一些缺陷,因此基于L1范数的降维技术得到了广泛的研究。例如Liu和Wen等分别提出了基于L1范数的非贪婪线性判别 (A Non-Greedy Algorithm for L1-Norm LDA,NGL1-LDA)[20]算法和鲁棒稀疏线性判别分析(Robust Sparse Linear Discriminant Analysis,RSLDA)[21]算法。NGL1-LDA算法用非贪婪迭代算法代替贪婪迭代算法来解决基于L1范数的线性判别分析,使目标函数具有局部收敛性。而RSLDA算法不仅通过引入L1范数自适应地选择用于判别分析的特征,还引入正交矩阵和稀疏矩阵以保证提取的特征能够保持原始数据的主要能量,因此它们都取得了比较好的性能。
受上述研究工作启发,本文提出了一种基于加权鉴别保持投影降维(Weighted Discriminant Sparse Preserving Projection, WDSPP)的非约束人脸识别算法,用于克服SPP在处理非约束人脸图像时判别力不足而且效率低下的问题。首先,对待测样本进行稀疏重构时,给整个训练集加上类标签,并用同类样本的平均重构稀疏系数来加强待测样本的重构关系;其次,用logistic函数作为距离权值函数来约束同类样本间稀疏重构系数,剔除在复杂环境下同类样本中对稀疏重构产生的影响的奇异样本。最后,求投影矩阵时通过添加全局约束因子,保留样本的全局信息,来得到最佳变换矩阵实现投影降维,提高识别性能。在经典的AR库和Extended Yale B库上,使用LDA、NPE、SPP、DSNPE、SRC-FDC、NGL1-LDA和RSLDA与本文所提出的WDSPP算法进行对比,而在LFW和Pubfig人脸库上,使用SRC、加权稀疏表示(Weight Sparse Representation Classifier, WSRC)[22]、加权组稀疏表示(Weighted Group Sparse Classifier,WGSC)[23]、LDA、NPE、SPP和DSNPE与WDSPP进行比较,大量的实验结果证明,本文提出的WDSPP算法在处理非约束人脸图像时相比其他同类算法识别性能最好。
2 稀疏表示与稀疏保留投影
假设![]() 是共c类的n个训练样本,其中
是共c类的n个训练样本,其中![]() 是第i类数据的训练样本子集,每类样本有ni个训练样本,满足
是第i类数据的训练样本子集,每类样本有ni个训练样本,满足![]() 为训练样本总数。
为训练样本总数。
2.1 稀疏表示分类
稀疏表示(SRC)的主要思想是将训练样本的稀疏线性组合来表示测试样本。它假定来自每一类的训练样本确实位于子空间上,给定一个过完备的训练集,即所有训练样本,则测试样本y可以表示为训练样本X的线性组合如式(1)。
y=X1φ1+X2φ2+…+Xcφc=Xφ
(1)
式(1)中,![]() 是与整个训练集X对应的系数向量,除了与第i类相关的系数外,其他元素为0。根据这个假设,系数向量φ应该是稀疏的。因此,通过最小化重构误差以及l1范数标准化求解,即如式(2)。
是与整个训练集X对应的系数向量,除了与第i类相关的系数外,其他元素为0。根据这个假设,系数向量φ应该是稀疏的。因此,通过最小化重构误差以及l1范数标准化求解,即如式(2)。
(2)
式(2)中, 参数λ是用来约束重构残差和稀疏系数值的平衡常数因子。通过式子求得稀疏系数φ后, 计算测试样本和所有类的重构样本的残差值, 并根据所求的最小残差值将训练样本y归类为所属的类别,如式(3)。
(3)
式(3)中,δi(φ)是一个选择算子, 表示选择φ中与第i类相关的元素,将第i类外元素设为0值。
2.2 稀疏保留投影
由稀疏表示研究启发而来,稀疏保留投影(Sparse Preserving Projection,SPP)算法,其主要思想是保持原始高维空间中样本的重构关系,通过求解 l1 范数最小化可以得到最优稀疏表示系数,以此来构建l1邻接图[24],其稀疏表示系数计算形式如(4)。
s.t.‖xi-Xiθi‖<ε
(4)
式(4)中,Xi为除xi以外的其余样本组成的字典矩阵,即![]() 就是求解出的最优稀疏表示系数,即
就是求解出的最优稀疏表示系数,即![]() 其值越大,表示该样本与重构表示的样本之间越相似,ε为残差约束值。
其值越大,表示该样本与重构表示的样本之间越相似,ε为残差约束值。
通过计算每个训练样本的最优稀疏重构表示系数,得到重构稀疏表示矩阵![]() 然后把数据投影到低维空间中,根据最小化重构误差准则定义目标函数实现低维投影。它的数学模型如式(5)。
然后把数据投影到低维空间中,根据最小化重构误差准则定义目标函数实现低维投影。它的数学模型如式(5)。
(5)
这里X为全体训练样本构成的矩阵字典,![]() 为投影矩阵。为求式(5)的解可以转化为求解式(6)广义特征值问题得
为投影矩阵。为求式(5)的解可以转化为求解式(6)广义特征值问题得
X(θ+θT-θTθ)XTp=λ XXTp
(6)
对式(6)中求得的广义特征值和特征向量,根据特征值的大小排列,选取其中前d个特征值所对应的特征向量pi构成SPP投影矩阵P=[p1,p2,…,pd]。然后将训练集在投影矩阵P上进行投影映射,得到一个d×n维子空间,同样也对测试集进行降维映射也得到d×n维子空间。最后用SRC进行分类。因为稀疏表示技术表现出很好的稳定性和普适性,所以SPP在分类识别中取得了比较好的性能。
3 加权鉴别稀疏保留投影
稀疏保留投影(SPP)在用和待测样本所有剩余样本进行稀疏重构时,没有考虑到类内的局部结构,本文受DSNPE的启发,在SPP的基础上作出了改进,提出加权鉴别稀疏保留投影(WDSPP)算法。该算法首先引入类内标签和类内紧致项,然后用距离权值约束类内重构系数,最后在投影时增加全局约束因子,因此使得WDSPP具有更多的鉴别信息。
3.1 WDSPP算法描述
在式(4)中SPP算法主要以全体训练样本来计算重构稀疏矩阵,无法获得样本的局部信息,本节以SPP为基础构建加权鉴别稀疏保留投影方法(WDSPP)的数学模型如式(7)。通过增加类内、类间约束和类内样本距离约束,使算法具有更好的鉴别能力。
(7)
式(7)中,Xl(xi)为与xi类别相同的剩余训练样本组成的集合。θi为重构表示系数。Zhang等表明[25],在人脸识别中,用l1范数进行稀疏约束求解起到的作用不大,在本节数学模型中用l2范数替代l1范数对稀疏系数进行约束。式(7)中,第一部分![]() 是类内样本重构误差,第二部分
是类内样本重构误差,第二部分![]() 是进行距离加权的稀疏系数θi的l2范数正则项,Di表示测试样本与同类其他样本距离约束矩阵,即Di=[di1;di2;…;di×(ni-1)]。第三部分
是进行距离加权的稀疏系数θi的l2范数正则项,Di表示测试样本与同类其他样本距离约束矩阵,即Di=[di1;di2;…;di×(ni-1)]。第三部分![]() 是基于SPP基础上添加的类内样本紧致项,Γl(xi)是与xi同类别的所有训练样本稀疏系数的平均表示,通过求
是基于SPP基础上添加的类内样本紧致项,Γl(xi)是与xi同类别的所有训练样本稀疏系数的平均表示,通过求![]() 的最小值,使各类样本的重构系数更加接近于相应类别的重构平均系数,让类内散度最小。λ1为约束系数稀疏性,λ2为约束类内样本紧凑性,它们分别是l2范数正则项和类内紧凑性约束项的平衡因子。
的最小值,使各类样本的重构系数更加接近于相应类别的重构平均系数,让类内散度最小。λ1为约束系数稀疏性,λ2为约束类内样本紧凑性,它们分别是l2范数正则项和类内紧凑性约束项的平衡因子。
对于式(7)中,Γl(xi)的计算形式如式(8)。
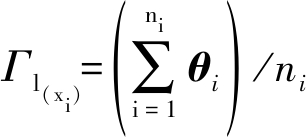
(8)
其中为了简化对θi的求解,令![]() 则式(8)可以转化为式(9)。
则式(8)可以转化为式(9)。
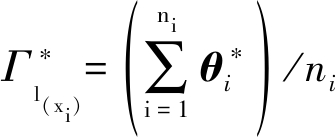
(9)
接下来利用最小二乘法求解稀疏重构系数θi,对式(7)进行化简可得式(10)。
tr[(xi-Xl(xi)θi)T(xi-Xl(xi)θi)]+λ1tr[(Diθi)T(Diθi)]+
(10)
式(10)中对θi求偏导,并令偏导式右边等于0,整理可得到最优θi如式(11)。
(11)
由计算得到的表示系数![]() 构建表征样本关系的重构权值矩阵
构建表征样本关系的重构权值矩阵![]() 其中wi=θi。
其中wi=θi。
求得重构权值矩阵来进行投影降维,它的数学模型如下:
(12)
式(12)中,第一项表示重构误差,使原始空间的样本重构关系在降维前后尽可能保持不变,其中![]() 为投影矩阵;后两项保留样本的全局信息,其中,Bt=[X1-M1,…,Xi-Mi,…,Xc-Mc],Bb=[M1-M,…,Mi-M,…,Mc-M],Xi表示第i类样本集合,Mi表示Xi的样本平均,M表示所有样本的平均。
为投影矩阵;后两项保留样本的全局信息,其中,Bt=[X1-M1,…,Xi-Mi,…,Xc-Mc],Bb=[M1-M,…,Mi-M,…,Mc-M],Xi表示第i类样本集合,Mi表示Xi的样本平均,M表示所有样本的平均。
对式(12)进行变形化简如式(13)。
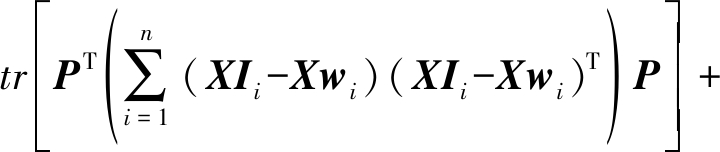
tr[PTX(I-W-WT+WTW)XTP]+
(13)
最终投影降维的数学模型转化成如式(14)。
s.t. tr(PTXXTP)=I
(14)
式(15)中,Wβ=W+WT-WTW,W是重构权值矩阵,由拉格朗日乘子法,设:
λ(PTXXTP-I)
(15)
对式(15)求偏导,即令![]() 得式(16)。
得式(16)。
(16)
对式(16)中求得的广义特征值和特征向量,根据特征值的大小排列,选取其中前d个特征值所对应的特征向量pi构成WDSPP投影矩阵P=[p1,p2,…,pd]。然后对训练集和测试集进行投影映射,分别得到d×n维矩阵,最后进行分类识别。
3.2 距离权值函数
对于测试样本与训练样本用欧氏距离定义它们的相似程度,即ei=‖xi-xj‖2,i≠j,当测试样本与训练样本相似度较高时,欧式距离ei越低,距离权值di越小,反之,当测试样本与训练样本越不相似,欧氏距离ei越高,距离权值函数di越高,因此距离权值函数di的选择有较丰富的形式。当di=ei时,距离权值呈线性函数逼近分布;当![]() 时距离权值呈指数函数逼近分布;当
时距离权值呈指数函数逼近分布;当![]() 时,距离权值呈logistic函数逼近分布[26]。上述三种距离权值函数分布如图1所示。
时,距离权值呈logistic函数逼近分布[26]。上述三种距离权值函数分布如图1所示。
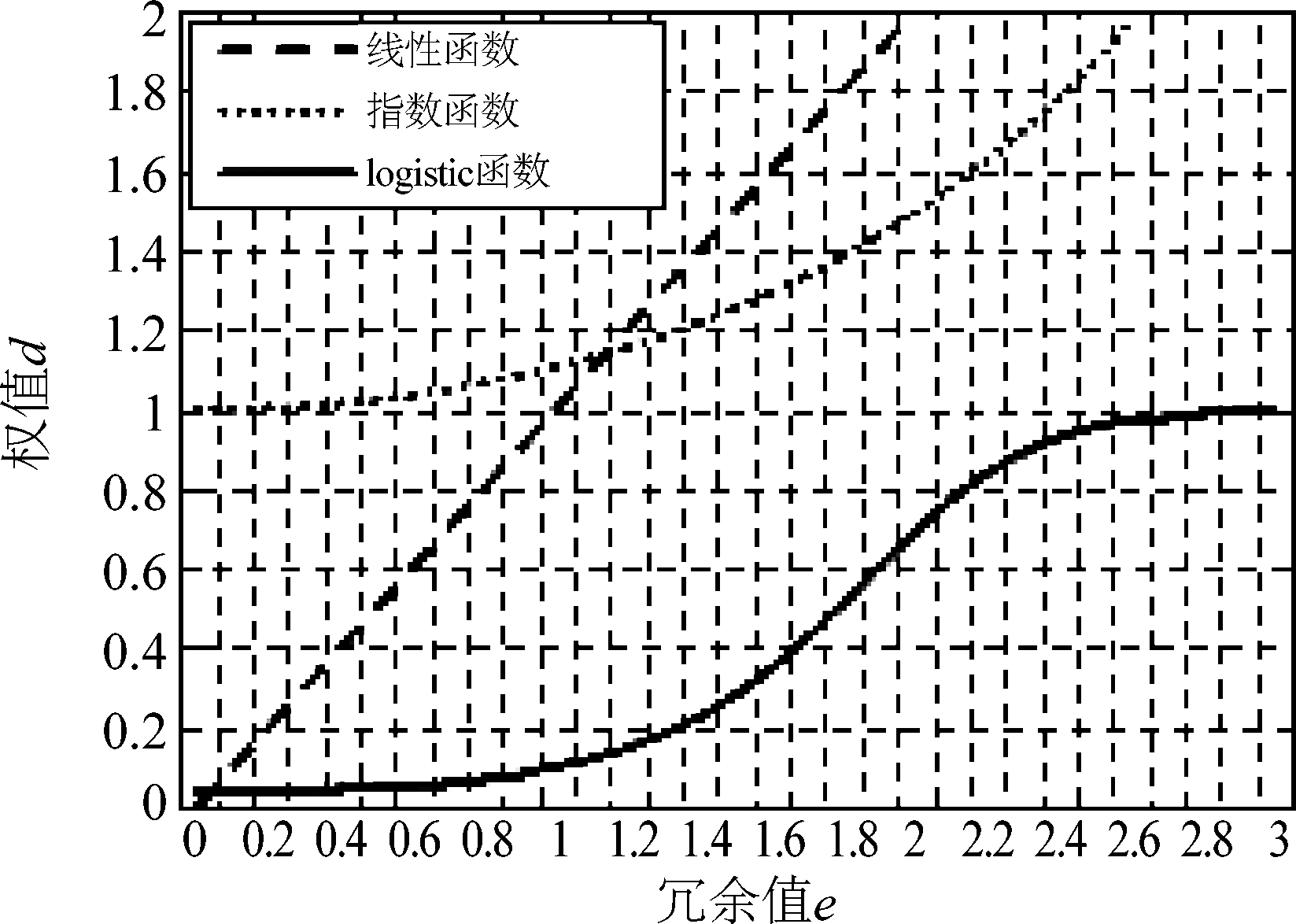
图1 三种距离权值函数的分布
Fig.1 The distribution of three distance weight functions
由图1可知,当线性分布函数和指数逼近分布函数的距离越大时,权值也越大,前期线性分布函数增长较快,后期指数分布函数增长较快,而且两种分布函数值均无上界,这使算法的稳定性比较差;而logistic逼近分布函数的取值范围为[0,1],距离权值有界,使算法具有稳定性,所以本文用logistic分布函数来约束稀疏重构系数。

4 实验结果
为验证所提算法的有效性,本节使用经典的AR库、Extended Yale B库、LFW库和PubFig库4个不同人脸数据库进行仿真实验,算法的主要参数设置为PCARatio=0.98~0.999,λ1=0.08,λ2=1,σ=0.01~0.3, μ=10/σ。实验环境为:win 10 64位操作系统,内存8GB,MATLAB R2017a。
4.1 AR数据库
AR人脸数据库包含4000多张人脸图像,由126类人的组成,其中包含56位女性和70位男性。每类人脸图像都具有不同面部表情,光照和真实遮挡(墨镜和围脖)。与文献[18]和文献[22]中设置一样,本实验选取其子集120类人作为数据库,其中包含65名男性和55名女性,照片分两次拍摄,每个时期包含7张无遮挡图像,6张人脸图像(3张墨镜遮挡,3张围脖遮挡),其中一类人的展示如图2所示。对于每张图像统一裁剪成50×40大小。

图2 AR库中某一类人的人脸图像
Fig.2 Samples of images of one person in the AR database
4.1.1 无遮挡实验
本实验主要针对光照及表情变化,实验环境设置与SRC-FDC算法相同,选取图2中无遮挡图片(a)~(g)作为训练样本,无遮挡图片(n)~(t)作为测试样本。图3分别展示了LDA、SPP、NPE、DSNPE、SRC-FDC和WDSPP在不同维度下的识别率。从图3中我们可以看出当样本维数大于40时,WDSPP算法识别性能优于其他传统算法, SRC-FDC次之,NPE最差。可见,WDSPP性能不受投影维度影响,在处理光照和表情干扰时是具有一定优势。
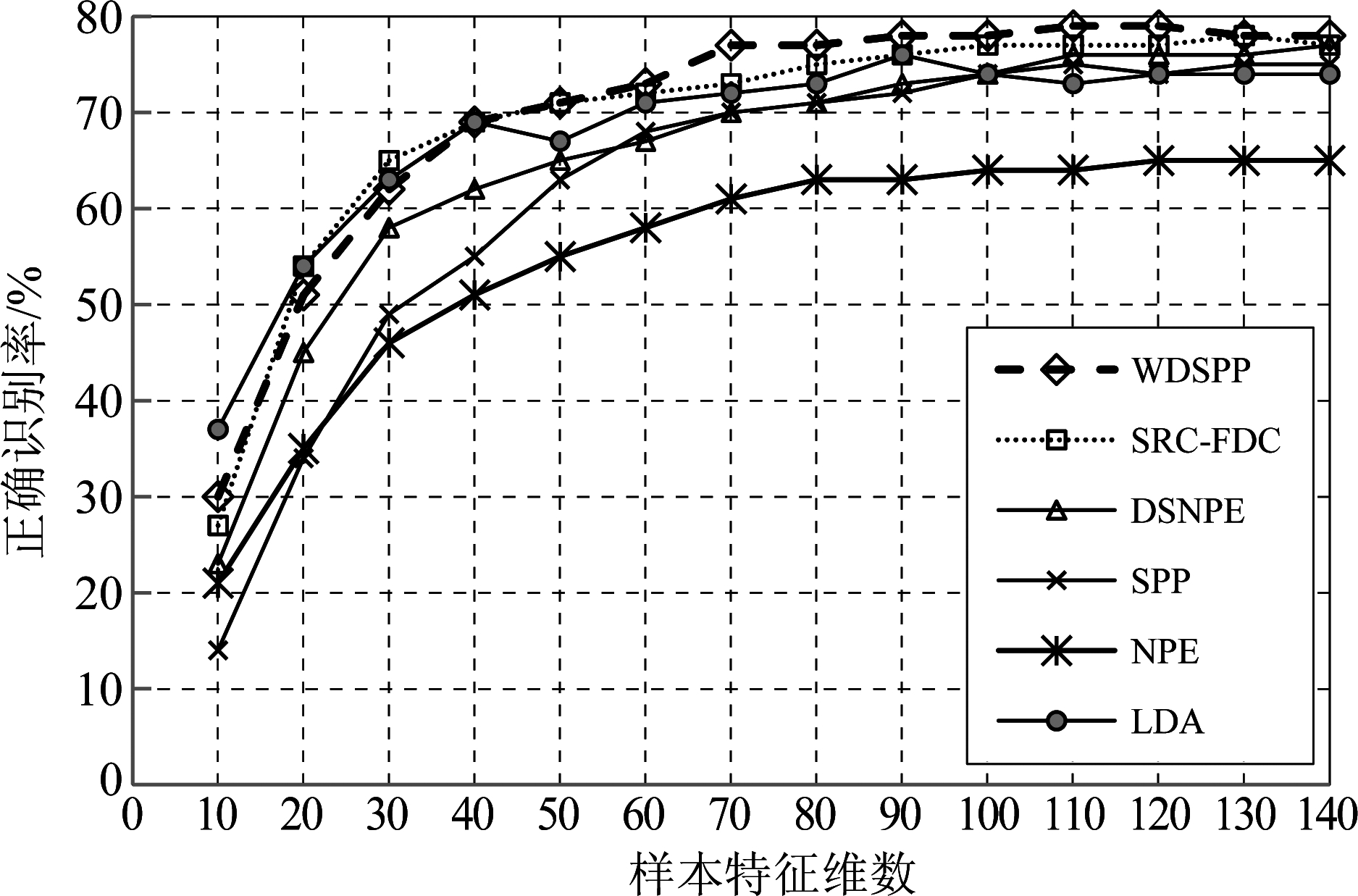
图3 AR库中不同维度下的正确识别率
Fig.3 Recognition rate in different feature dimensions in AR dataset
4.1.2 遮挡实验
实验1 主要考虑以太阳镜为遮挡,选取图2中(a)~(h)8张图像作训练集,另外7张无遮挡图像和带有墨镜的5张图像作为测试样本,即训练样本有960张图片,测试样本有1440张图片。
实验2 主要考虑以围巾为遮挡,选取图2中(a)~(g)和(k)8张图像作为训练集,另外7张无遮挡图像和带有5张围巾的图像作为测试样本,即训练样本有960张,测试样本有1440张。
实验3 考虑太阳镜和围巾的混合遮挡,选取图2中没有遮挡的(a)~(g),有遮挡的(h)和(k)作为训练样本,剩余图像作为测试样本。
三个实验的识别率如表1所示,从表中可以看出,无论是在太阳镜、围巾还是两者混合遮挡情况下,WDSPP都有更好的性能,而SPP等算法的识别率比WDSPP、SRC-FDC和DSNPE都低,这是因为它没有很好的考虑到样本的局部结构。而DSNPE和SRC-FDC因为考虑到了样本的全局与局部的鉴别结构,因此分类识别效果比SPP等算法好。WDSPP不仅添加样本的类别信息和全局约束因子,还用样本距离权值约束稀疏重构系数,减少同类奇异样本的影响,所以对比其他方法,在处理遮挡问题时,具有更好的遮挡鲁棒性。
表1 AR数据库中遮挡实验的正确识别率(%)
Tab.1 Recognition rate (%) comparison in AR occluded dataset
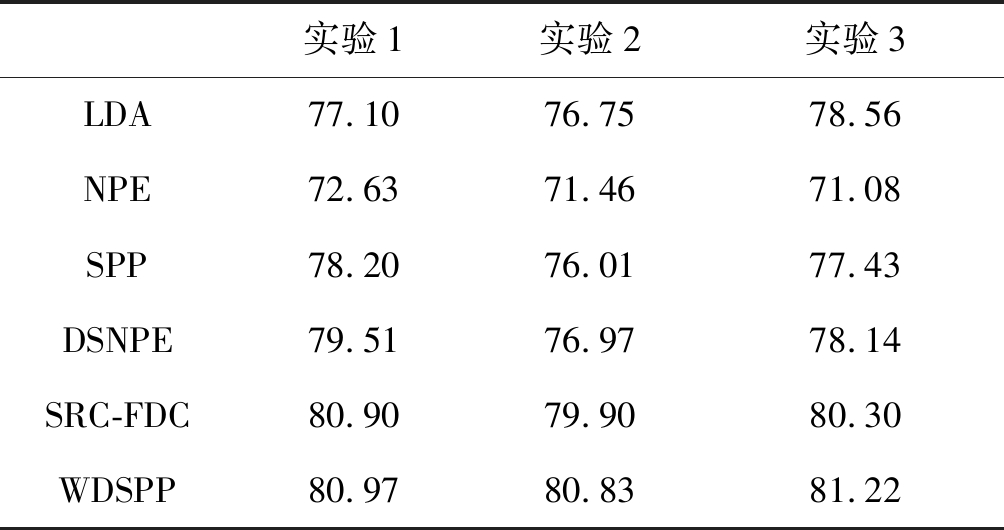
实验1实验2实验3LDA77.1076.7578.56NPE72.6371.4671.08SPP78.2076.0177.43DSNPE79.5176.9778.14SRC-FDC80.9079.9080.30WDSPP80.9780.8381.22
4.1.3 混合实验
本次实验结合光照、表情和遮挡条件来综合说明本文所提算法的性能。实验环境与NGL1-LDA算法相同,随机选取每类人中13张图片作为训练集,剩余图片作为测试集,对实验过程进行10次交叉验证,表2分别展示了在1NN和SVM分类器下各个算法的平均识别率、方差和最佳维数。从表中可以看出,在1NN分类器下,本文提出的WDSPP较传统算法LDA和NPE分别提升了3.67%和5.28%的平均识别率,较SPP和DSNPE算法分别提升了2.77%和1.07%,较最新算法NGL1-LDA也提升了0.77%。同样,在SVM分类器下,WDSPP也分别提升了4.09%、3.43%、1.81%、1.03%和0.08%。可见,WDSPP算法不受分类器影响,无论是采用1NN分类器还是SVM分类器,本文所提的WDSPP算法在处理光照、表情和遮挡等混合干扰因素时,都具有最佳效果。
为了进一步说明本文算法的先进性,分别选取AR数据库中每类人中4、6、8和12张人脸作为训练样本,剩余图像作为测试样本,与RSLDA等算法进行比较,实验结果如表3所示。从表中可以看出,当每类人选4张样本时,WDSPP识别率分别比RSLDA、DSNPE、SPP、NPE和LDA高1.68%、2.92%、8.03%、9.28%和7.27%,当每类人选12张样本时,WDSPP识别率分别提升了0.28%、1.25%、3.45%、6.84%和5.35%。可见无论训练样本为多少,WDSPP算法都保持优越性。
4.2 Extended Yale B数据库
Extended Yale B人脸数据库由38个具有不同光照条件下正面人脸图像组成。每类人约有64张图片,共计2414张图片。在本实验中,实验环境设置与NGL1-LDA算法一样,每幅图像统一裁剪为32×32大小,随机选择每类人的14张图像,使用具有随机分布的黑色和白色噪声对其进行噪声化。噪声的位置是随机的,并且噪声像素与图像像素数的比率在0.05到0.15之间,部分图片如图4所示。
表2 AR数据库中分别使用1NN和SVM分类器下混合实验的正确识别率(%)和维数
Tab.2 Recognition rate (%) and dimension of mixed experiment in AR database using 1NN and SVM as classifiers

LDANPESPPDSNPENGL1-LDAWDSPP识别率(1NN)94.78±0.5493.17±0.9395.68±0.8697.38±0.9597.68±0.4098.45±0.27维数(d)11916020211267169识别率(SVM)94.58±0.4895.24±0.5996.86±0.8397.64±0.6398.59±0.5398.67±0.24维数(d)11949020217268169
表3 AR数据库中不同训练样本下实验的正确识别率(%)
Tab.3 Recognition rate (%) and dimension of different train samples in AR database

SamplesLDANPESPPDSNPERSLDAWDSPP484.8182.8084.0589.1690.4092.08687.5086.0490.2593.4694.5795.67889.9089.0790.2895.5596.2497.311293.1091.6195.0097.2098.1798.45

图4 Extended Yale B数据库中部分样本
Fig.4 Some samples in the Extended Yale B database
4.2.1 无遮挡实验
本次实验考虑光照变化问题,不考虑噪声情况每类人中随机选取32张图片作为训练样本,剩余图片作为测试样本。因为与NGL1-LDA算法相同的实验环境,所以用算法NGL1-LDA参与对比。对实验过程进行10次交叉验证,分类器分别使用1NN和SVM,LDA、SPP、NPE、DSNPE、NGL1-LDA和WDSPP算法平均实验结果、方差和最佳维数如表4所示,NGL1-LDA方法在1NN分类器上平均识别率比LDA低11.12%,比WDSPP低13.36%,在SVM上比LDA低9.91%,比WDSPP低11.88%,可以看出,虽然NGL1-LDA方法在求解目标函数时用非贪婪算法进行了优化,但在处理光照变化问题时效果远不如传统算法LDA,而WDSPP相比其他算法效果是最好的,在两个分类器上平均识别率分别达到98.33%和98.05%,因为WDSPP算法的实现不仅考虑了不同类的类别信息也通过距离权值函数加强了同类样本的离散度,在降维过程中更充分地保持了便于分类的内在结构信息,使算法的判别力得到了提高。
4.2.2 遮挡实验
本次实验主要验证本文算法在处理遮挡人脸时的有效性,做两个实验:实验1: 每类人随机选取32张图像,其中包含14张噪声图像作为训练,剩余图像作为测试。实验2:每类人随机选取32张图像,其中包含7张噪声图像作为训练,剩余图像作为测试。对实验过程进行10次交叉验证。平均实验结果和方差如表5和表6所示。在1NN分类器下,WDSPP的平均识别率较LDA、NPE、SPP、DSNPE和NGL1-LDA分别提升了1.52%、10.79%、4.31%、3.34%和10.78%。在SVM分类器下,WDSPP则分别提升了1.17%、0.78%、3.23%、1.91%和8.93%。可以看出无论是遮挡图片的数量(每类14张或者7张遮挡图像)选择,还是分类器(1NN分类器或SVM分类器)的选择,WDSPP正确识别率都比其他算法好,说明本文所提算法通过整合局部和全局结构信息使其在处理奇异人脸时具有很好的鲁棒性。而NGL1-LDA识别性能依然是最差的,说明其在处理遮挡时效果不理想。
表4 Extended Yale B数据库中分别使用1NN和SVM分类器下无遮挡实验的平均正确识别率(%)和维数
Tab.4 Recognition rate (%) and dimension of unocclusion experiment in Extended Yale B database using 1NN and SVM as classifiers

LDANPESPPDSNPENGL1-LDAWDSPP识别率(1NN)96.09±0.5791.00±1.0794.37±1.1094.82±0.7684.97±0.9798.33±0.67维数(d)322981736670258识别率(SVM)96.08±0.6696.43±0.9895.79±1.0493.35±1.8986.17±0.7698.05±0.78维数(d)3229817310670258
表5 Extended Yale B数据库中分别使用1NN和SVM分类器下实验1的平均正确识别率(%)和维数
Tab.5 Recognition rate (%) and dimension of experiment 1 in Extended Yale B database using 1NN and SVM as classifiers

实验1LDANPESPPDSNPENGL1-LDAWDSPP识别率(1NN)95.01±0.7385.48±1.5891.62±0.4592.49±1.1785.13±0.7696.26±0.99维数(d)3217022412470111识别率(SVM)95.01±0.7395.21±0.9592.27±1.4793.54±1.1486.91±1.0795.94±0.72维数(d)3220032421469191
表6 Extended Yale B数据库中分别使用1NN和SVM分类器下实验2的平均正确识别率(%)和维数
Tab.6 Recognition rate (%) and dimension of experiment 2 in Extended Yale B database using 1NN and SVM as classifiers

实验2LDANPESPPDSNPENGL1-LDAWDSPP识别率(1NN)95.69±0.8086.68±2.2293.50±0.4194.57±0.9287.05±1.0397.47±0.36维数(d)3131126412670130识别率(SVM)95.64±0.8596.23±0.6094.27±0.7295.63±0.6988.23±0.9197.05±0.53维数(d)3128432422670140
表7 Extended Yale B数据库中不同训练样本下实验的正确识别率(%)
Tab.7 Recognition rate (%) and dimension of different train samples in Extended Yale B database

SamplesLDANPESPPDSNPERSLDAWDSPP1082.0189.3382.1583.0987.4691.101587.5791.4986.7787.0491.4394.142090.2492.0891.3593.6593.2696.912591.9493.1692.2193.6494.5398.16
4.2.3 算法的先进性
本次实验旨在说明本文算法的先进性,分别选取Extended Yale B库中每类人10、15、20和25张人脸作为训练样本,剩余图像作为测试样本。实验结果如表7所示。从表中可以看出,当每类人分别选10、15、20和25张样本时WDSPP的识别率分别为91.10%、94.14%、96.16%和98.16%,较最新算法RSLDA和其他传统算法相比性能是最好的,说明训练样本数的选取不影响WDSPP算法识别性能。
4.3 LFW和PubFig数据库
LFW和PubFig人脸数据库中人脸面部是在不受环境约束和不准确对齐的情况下获得的,这对于人脸识别来说,具有很大的挑战性,部分图像分别如图5和图6所示。本实验环境的设置为:在LFW人脸数据库中,选取158类人作为数据库,每类人不少于10张图像。图像统一裁剪为32×32大小。对于每类人,随机选择5个样本进行训练,另外5个样本进行测试。在PubFig人脸数据库中,选取100类人作为数据库,每类人20张图像。图像统一裁剪为64×64大小。对于每类人,随机选择10个样本进行训练,剩余样本作为测试。LDA、SPP、NPE、DSNPE和WDSPP算法都是使用SRC进行分类。

图5 LFW库中一类人中的部分样本
Fig.5 Some samples of one person in the LFW database

图6 PubFig库中一类人中的部分样本
Fig.6 Some samples of one person in the PubFig database
表8展示了SRC、WSRC、WGSC、LDA、SPP、NPE、DSNPE和WDSPP算法在LFW和PubFig人脸数据库上的实验结果。从表中可以看出,在LFW库上,WDSPP性能均优于其他算法,识别率达到了48.73%。同样的,在PubFig数据库上,WDSPP识别率达到了38.00%,比SRC、WSRC 和WGSC提升了3.60%、1.30%和0.5%,比LDA、NPE、SPP和DSNPE提高了12.9%、13.30%、9.8%和4.0%,所以,通过不断改进的分类器算法可以使识别率不断提高,但跟WDSPP比依然存在差距,因为结合稀疏投影的特征降维和SRC使得WDSPP在处理真实环境中的人脸时具有更好的性能,而且WDSPP算法在进行投影降维时通过类标签和权值函数加强了样本的局部结构同时整合了样本间全局信息,使得WDSPP较传统特征降维方法具有更高的鉴别力。值得强调的是,改进分类器可以使算法具有更高的识别率,但本次实验中WDSPP算法使用的分类器为SRC,所以跟改进分类器的IRGSC算法比依然存在差距。
表8 LFW和PubFig数据中实验的正确识别率(%)
Tab.8 Recognition rates (%) in LFW and PubFig database

SRCWSRCWGSCLDANPESPPDSNPEWDSPPLFW32.0341.247.620.3831.0129.7540.7648.73PubFig34.3036.737.525.1024.7028.2034.0038.00
5 结论
本文提出了一种加权鉴别稀疏保留投影算法(WDSPP),该算法针对稀疏保留投影算法(SPP)存在的不足,引入样本类别标签,增加类内紧凑度约束项,然后通过添加距离权值对稀疏重构系数进行约束,降低同类奇异样本的影响,使得求解出的稀疏重构系数更为准确;最后在低维投影阶段,通过添加全局约束因子,保留样本的全局信息,来得到最佳变换矩阵实现投影降维,使WDSPP具有更多的鉴别信息,使得降维后的数据具有更高的识别率。在权值约束时,通过logistic函数进行权值约束,使算法的运行带来更多的稳定性。本文在理想实验环境采集的人脸库(AR库和Extended Yale B库)和真实环境采集的人脸库(LFW库和PubFig库)上均进行了大量实验仿真,实验结果表明无论是进行光照表情识别还是处理遮挡图像,WDSPP识别效果明显高于其他降维算法,同时在处理复杂环境下的人脸时,WDSPP也具有一定的鲁棒性,较传统的模式分类和降维方法而言识别性能也是最好的。
需要注意的是,WDSPP算法在进行类内权值约束求投影矩阵时,降维识别效果不错,但没有引用类间权值约束来更有效的保留样本的全局信息,因此在加强样本局部结构的基础上,通过增加类间权值约束来进一步提高样本的全局结构是下一步工作之一,WDSPP在进行分类时主要使用传统的SRC分类,在处理复杂环境下的人脸时识别性能有待提高,所以对分类器进行改进也是下一步的研究工作。
[1] Sneha, Sanjay Sharma. Face recognition techniques: a survey[J]. International Journal of Scientific Research in Computer Science, Engineering and Information Technology, 2018, 4(1): 221-226.
[2] Handa A, Agarwal R, Kohli N. A survey of face recognition techniques and comparative study of various bi-modal and multi-modal techniques[C]∥International Conference on Industrial & Information Systems. IEEE, 2018: 274-279.
[3] Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433- 459.
[4] Izenman A J. Linear discriminant analysis[M]. Modern multivariate statistical techniques. Springer New York, 2013: 237-280.
[5] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.
[6] Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396.
[7] He X, Cai D, Yan S, et al. Neighborhood preserving embedding[J]. Tenth IEEE International Conference on Computer Vision. Vis, 2005, 2(23): 1208-1213.
[8] Zhang T, Yang J, Zhao D, et al. Linear local tangent space alignment and application to face recognition[J]. Neurocomputing, 2007, 70(7): 1547-1553.
[9] Wang Q, Ma L, Gao Q, et al. Adaptive maximum margin analysis for image recognition[J]. Pattern Recognition, 2017, 61(1): 339-347.
[10]Gao Q, Liu J, Cui K, et al. Stable locality sensitive discriminant analysis for image recognition[J]. Neural Networks, 2014, 54(6): 49-56.
[11]Yan S C, Xu D, Zhang B Y, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(1): 40-51.
[12]Wright J, Yang A Y, Ganesh, et al. Robust face recognition via sparse representation[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.
[13]Qiao L S, Chen S C, Tan X Y. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1): 331-341.
[14]Liu Q, Lan C, Jing X Y, et al. Sparsity preserving embedding with manifold learning and discriminant analysis[J]. IEICE Transactions on Information and Systems, 2012, 95(1): 271-274.
[15]Zang F, Zhang J. Discriminative learning by sparse representation for classification[J]. Neurocomputing, 2011, 74(12): 2176-2183.
[16]Lu G F, Jin Z, Zou J. Face recognition using discriminant sparsity neighborhood preserving embedding[J]. Knowledge-Based Systems, 2012, 31(7): 119-127.
[17]Yang J, Chu D, Xu Y. Sparse representation classifier steered discriminative projection with applications to face recognition[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(7): 1023-1035.
[18]Gao Q X, Wang Y Q, Huang Y F, et al. Dimensionality reduction by integrating sparse representation and fisher criterion and its applications[J]. IEEE Transactions on Image Processing, 2015, 24(12): 5684-5695.
[19]Zheng J W, Yang P, Chen S Y, et al. Iterative re-constrained group sparse face recognition with adaptive weights learning[J]. IEEE Transactions on Image Processing, 2017, 26(5): 2408-2423.
[20]Liu Y, Gao Q X, Miao S, et al. A non-Greedy algorithm for L1-Norm LDA[J]. IEEE Transactions on Image Processing, 2017, 26(2): 684- 695.
[21]Wen J, Fang X, Cui J, et al. Robust Sparse Linear Discriminant Analysis[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2018, 29(2): 390- 403.
[22]Fan Z, Ni M, Zhu Q. Weight sparse representation for face recognition[J]. Neurocomputing, 2015, 151(1): 304-309.
[23]Tang X, Feng G, Cai J. Weighted group sparse representation for undersampled face recognition[J]. Neurocomputing, 2014, 145(18): 402- 415.
[24]Yang Y, Wang Z, Yang J, et al. Data clustering by laplacian regularized L1-Graph[C]∥Twent-Eighth AAAI Conference on Artificial Intelligence, 2014: 3148-3149.
[25]Zhang L, Yang M, Feng X. Sparse representation or collaborative representation: Which helps face recognition?[C]∥2011 International Conference on Computer Vision. IEEE, 2011: 471- 478.
[26]郑建炜, 黄琼芳, 杨平, 等. 特征加权组稀疏判别投影分析算法[J]. 自动化学报, 2016, 42(5): 746-759.
Zheng Jianwei, Huang Qiongfang, Yang Ping, et al. Feature weighted group sparse discriminative projection algorithm[J]. Acta Automatica Sinica, 2016, 42(5): 746-759.(in Chinese)



