1 引言
事件相机[1]是受人类的视网膜系统启发的视觉传感器。与传统的CMOS(Complementary Metal Oxide Semiconductor)相机输出实际的像素强度不同,事件相机,如动态视觉传感器(DVS Dynamic Vision Sensor)[2]能够高速感知到场景中亮度的变化,并输出具有像素位置、事件、及极性信息的事件流。当单个像素强度的绝对变化超过某个阈值时,该像素位置产生独立的事件。因此,DVS相机输出的是空间稀疏的异步事件序列,而不是固定频率的帧序列。与标准光学相机每秒传输的百兆数据相比,DVS以事件流输出形式在很大程度上减少了传输带宽。DVS具有非常快的响应速度(微秒级),以及高动态范围,它可以克服传统光学相机的一些局限性,例如强烈的光照变化、高速运动。这类特性为高速机器人应用的新性能提供了巨大的潜力。因此,基于事件相机的相关应用研究受到了广泛关注[5-8]。
DVS输出的事件序列在时间上分布是连续的,在短时间间隔内,事件在像素平面上的分布近似于场景中物体的边缘结构。DVS对环境中的亮度变化非常敏感,由相机本身构造和环境因素的影响,在该相机捕获场景信息的同时,输出的时空事件序列会受到噪声的干扰,事件点的位置发生波动偏移,直观地解释为沿着时间方向由相同场景触发的事件聚合形成的边缘结构不清晰。在基于事件相机的应用中,噪声会影响后续基于事件的跟踪或检测的准确性,因此事件流去噪是在进行后续应用之前非常重要的预处理。针对这一问题,本文设计了一种有效的方法,可以直接在事件序列上进行降噪处理,为后续的应用提供有效的数据。
由于事件流与标准光学相机的输出本质上不同,基于帧的传统视觉算法不能直接用于事件数据中。针对目前研究的不足,本文设计了新的事件数据的去噪算法。事件流是在时空中分散的点集,它们的分布遵循一个基本的结构,事件点在时间分布上具有一定的连续性并且在空间上揭示了物体的边缘结构。边缘通常具有一定的平滑或规律性。这种平滑先验将在本文中用于事件流去噪。
本文假设事件序列是光滑流形的离散采样,该流形可以通过从事件点构建图来近似。事实上,如果一个图是由流形中采样点构成的,那么这个图的几何结构与流形的几何结构是相似的。现有的基于流形的理论算法已被提出应用于传统图像处理领域,例如SAR图像分类[3- 4]。而本文工作针对事件数据的分布结构,首次将图模型引入事件流的去噪问题中。首先,本文解释如何从事件时空点集中构造一个图模型,然后提出流形正则项作为去噪先验信息,该正则项能够有效保持嵌入事件流中的基本流形结构,最后,事件去噪问题表示为基于流形正则项几何约束的最优化问题,并使用凸优化方法求解。去噪算法可以保持事件流的异步特性,因为它是在每个事件的基础上构建的,不需要像现有的基于事件相机的相关技术估计中间变量,例如图像强度或光流。实验结果证明了本文提出的事件去噪算法的有效性。
2 基于事件相机去噪的相关工作
与传统光学相机相比,事件相机低延迟和稀疏输出的特性使得其在高速移动机器人应用中具有广阔的前景。因此,一些经典的计算机视觉问题被重新定义到这个新的领域进行研究,例如光流估计[5- 6],以及运动估计[7- 8,12]。
目前对于事件流去噪的研究很少,这是由于研究主要由标准光学相机主导,事件相机去噪的研究目前还处于开发阶段。已有基于事件相机的去噪工作是将事件流离散化,在固定的时间间隔内累积事件生成灰度图像或事件帧,然后将传统的视觉算法应用到这类图像中。例如文献[9]提出一个基于事件帧的去噪框架,文中提到在事件流转换成图像之前捕捉到的噪声事件很难去除,所以该方法通过累计20 ms内的事件流将事件转换成二值图像,采用K-SVD算法对图像进行去噪。文献[9]将该方法扩展到DVS视频去噪的应用中[10],使用重叠的时间窗口将连续事件流切割成事件帧,并使用K-SVD算法训练事件图像的共享词典,用于DVS视频去噪,这些方法没有充分地利用事件相机的异步数据流和高时间分辨率的特性。文献[11]提出了利用事件点间相邻时间戳诱导的流形来进行事件相机的灰度图像重构,基于变分模型从累积的事件灰度图像中恢复出高质量的灰度图像,该方法是在重建事件灰度图像中考虑相机的噪声对亮度的影响。
目前的大多数针对事件相机的去噪算法是通过固定的时间窗口,或者累积固定数量的事件,将事件流转换为图像帧进行去噪处理。本文工作与已有的基于重构图像的去噪不同,本文提出的算法是直接对事件流进行去噪,不同于上述算法将事件转换成图像帧以考虑图像的去噪问题。在本文工作中,首次提出了使用图来捕获事件的底层结构,利用图的平滑约束处理含有噪声的事件流。
3 事件相机去噪问题定义
DVS相机捕捉场景中亮度超过阈值的变化,在时空域中以稀疏事件的形式异步输出(图1(b))。给定在短时间内的一个事件时空序列
每个事件可以表示为ei=(xi,yi,ti,pi),其中(xi,yi)表示事件点的像素坐标,ti表示事件时间戳,pi∈{1,-1}表示事件极性,描述了强度的变化。事件去噪实例如图1所示,图1(a)作为场景视觉参考的光学图像,图1(b)显示了短时间间隔内的事件流,图中每个点表示在该时空坐标上所产生的事件,红色和黑色标记分别表示事件的正极性和负极性。图1(c)表示事件序列沿着时间轴方向投影到像素平面上的效果,图中事件存在一些噪点,更关键的是由于噪声的影响,由同一物体边缘触发的事件偏离了原来的位置,如图1(c)所示事件形成的边缘参差不齐。本文提出的算法能够有效地抑制噪声,图1(d)为去噪算法得到的降噪事件投影到像素平面上的结果,图中观察到事件形成的边缘更加清晰光滑。
定义一组事件时空坐标集合
其中νi=(xi,yi,ti)表示事件的时空坐标。则带有噪声的事件流可以表示为:
Vq=Pq+Eq
(1)
其中P∈RN×3表示事件序列未知的真实位置,E为噪声项,q∈{x,y,t}是(x,y,t)坐标的索引。本文考虑事件点集在时间上的分布不变,只处理x, y方向的噪声干扰。在本文算法中,事件流是二维流形在时空域中的离散采样,根据上述定义,去除事件序列的噪声意味着在空间上移动事件使其接近流形,即事件点映射到流形上,误差是该点到流形上的点的最短距离。为了恢复真实位置P,本文构建低维流形[14]来表示事件在时空域上的几何结构,并且提出了在流形正则项下的事件去噪模型。本文去噪算法的流程如图2所示:图中展示了短时间内由场景中直线触发的事件流的去噪过程,可以观察到由于噪声的影响,事件在时间方向上的平面凹凸不平,十字标记点表示离群事件点,经过4.1节中的粗略滤波被剔除,空心标记点则被本文提出的流形约束校正,使得去噪后的事件在时间方向上形成光滑的平面,完成了对事件流的去噪。
图1 本文的事件去噪实例
Fig.1 An sample of the proposed algorithm
图2 本文的事件去噪算法框架
Fig.2 The framework for denoising events in our algorithm
3.1 低维流形表示
本文从事件流中构造一个图模型来近似低维流形。定义一个加权无向图G=(ν,ξ,W),其中ν={ν1,...,νN}为有限节点集合,边集ξ表示节点之间的权重,在图的节点上定义图信号f:ν→R,该信号可以表示为N维向量f=(f(ν1),..., f(νN)),在图模型上定义邻接矩阵W={wij},其中wij表示节点νi和节点νj连接边的权重。
本文的目的是对事件序列去噪。考虑事件序列的时空结构信息,本文首先将事件的时空坐标与图的节点联系起来,即图中的节点为ν={ν1,...,νN}T,νi=(xi,yi,ti),其中每个节点是事件点的时空坐标。然后计算节点之间的权重以表示节点间的相似性,节点之间的权值计算如下式所示:
(2)
其中,权重是由阈值高斯核计算得到的。像素坐标与时间跨度单位不同,因此时间距离需要加上权重γ。本文是在事件序列的时空域上进行去噪,因此图信号被定义为事件坐标: f=V。本文将事件序列的时空坐标与图的节点相关联从而构造的图能够获得数据内部的几何结构信息。根据上述定义,由事件流构造的图模型G可以被视为低维流形的有噪声的离散近似。
3.2 流形正则项
本文算法假设低维流形可以用来表征嵌入在事件时空点集中的底层内部结构。基于此假设,利用上述定义构建图,并计算图拉普拉斯矩阵[15]以获得流形结构,进一步用于事件序列的去噪。
根据上述定义的边的权重W,图模型的拉普拉斯矩阵L可以表示为:
(3)
其中,D是对角度矩阵,Dii是与节点νi连接边的权重总和。
假设输入的时空点集P={p1,...,pN}T∈RN×3是从流形上采样得到,利用拉普拉斯矩阵L推导出如下所示的流形正则项:
(4)
上述的流形正则项充分利用了输入数据的几何结构。以此为基础,本文将事件流的去噪问题表示为图信号处理问题。
4 基于流形正则项的事件相机去噪算法
本文使用上述方法在事件时空域上构造图作为流形的近似,因此,图G上事件时空信号的平滑性与事件点到流形的距离相关,图的平滑度可以用来度量事件时空点集的平滑度。
4.1 离群点去除
事件相机在记录场景变化时,会捕捉到大量的噪声。在实际操作中,第一步是去除距离流形上真实位置非常远的事件点,即离群点,保留下来的事件点即为内点集合,用于后续基于流型正则项的去噪。本文在构造图的过程中首先计算节点之间的欧氏距离,然后每个节点通过加权边与其k个最近邻点相连,节点之间邻接边权重根据式(2)计算得到。根据定义,离群点与内点距离较远,因此离群点的所有邻接边的权重之和明显低于内点。本文计算图中每个顶点的邻接边的权重之和,并将其视为该点是否是离群点的度量。本文通过删除度量低于阈值τ的节点(以及相应的事件点)来剔除离群点,这里的阈值遵循以下原则:删除离群点的数量不超过事件总数的10%。注意去除离群点只是本文事件去噪的预处理部分,为下一步提供粗略滤波的事件点集,文章的重点是后续基于图的流形约束的事件去噪方法的贡献。
4.2 事件流去噪
在事件去噪算法流程中,第一阶段是去除事件点集中的离群点,并在剩余的事件序列上构建图G。第二阶段是利用流行正则项的约束校正剩余事件点的空间位置,完成对事件流的去噪。注意在该阶段中,节点不被删除,但是其位置被修正,使得去噪后的事件信号在图上平滑。
综上所述,事件序列去噪问题可以表示为在保持事件点与其原始位置接近的同时最小化已定义的流形正则项。考虑到事件流在时间上的分布是恒定的,本文对事件序列空间x, y方向施加平滑约束。那么图信号的去噪问题可以写成如下所示的最小化问题:
(5)
其中
为去除异常值后剩余事件的时空坐标,P为去噪后事件的位置,Px,Py分别为矢量化后的x,y坐标。目标函数的第一个能量项将事件保持在其原始位置附近,第二个平滑项则在不改变时间分布的情况下修正事件在像素平面上的位置。根据前面讨论的图构造方法计算图拉普拉斯矩阵L,则x,y方向均由如下所示的线性系统决定:
(λdL+Id)Pd=Vd
(6)
其中d∈{x,y}是事件序列的像素平面(x,y)坐标的索引,Id是一个与拉普拉斯矩阵L相同大小的单位矩阵。在本文的方法中,事件序列的时空坐标用于构造图,同时作为图信号进行滤波处理。因此,在修正事件的位置后,图的结构也需要进行更新,去噪后的事件序列对应的图与原始序列对应的图具有不同的节点和边。通过计算去噪过程输出的事件序列的图结构并再次运行去噪过程,可以对去噪问题(5)进行迭代求解。实验发现一次迭代已经能够取得良好的去噪结果。考虑到性能和计算时间之间的平衡,去噪算法一次迭代后的结果在原则上是可接受的。
表1 本文提出的算法
Tab.1 The proposed algorithm
输入:原始事件的时空坐标{νi}Ni=1,参数k,呅,′1,′2;输出:去噪后事件序列的时空坐标{pi}Mi=1;1.对于每个事件点,选择k个近邻点;2.根据式(2)计算邻接边权重之和并删除离群点;3.由上一步的去除外点后的事件序列{νi}Mi=1构造图G,并使用(3)计算矩阵L;4.使用最小二乘方法解决流形约束下的去噪问题(5);5.输出:去噪后事件序列的时空坐标{pi}Mi=1。
5 实验与分析
5.1 实验数据
为了验证和分析事件流去噪性能,本文分别在仿真数据和真实事件数据上测试去噪算法。本文首先通过仿真事件数据进行算法验证和参数分析实验。本实验仿真了四组不同场景的数据,包含像素位置和时间信息,无噪声的事件时空位置作为本实验的真实值。图3展示了四组无噪声的10 ms的时空事件流在二维图像平面上的投影,图3(a)和(b)分别表示静止的条件下矩形和字母G所触发的事件,(c)和(d)分别表示快速移动条件下矩形和字母G触发的事件数据,观察到短时间间隔内的事件流投影到二维平面出现了严重的拖尾现象。
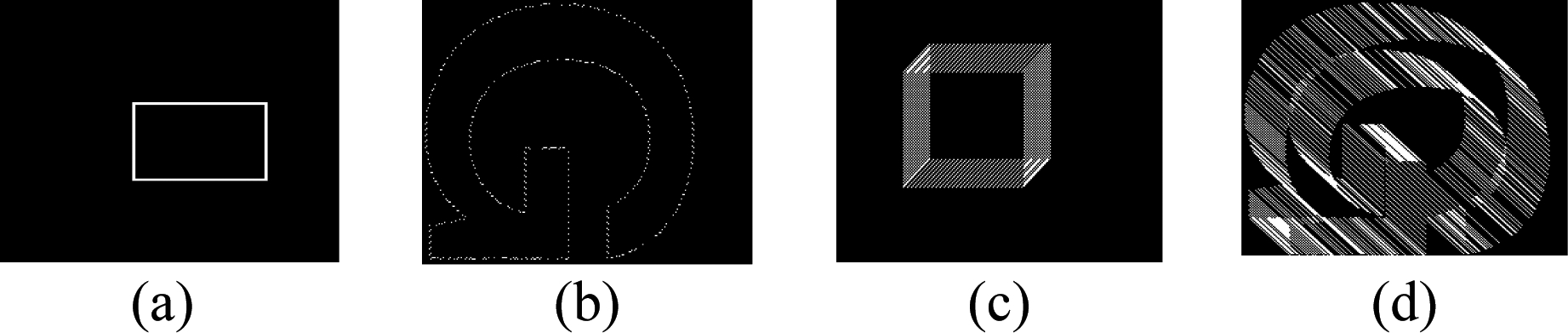
图3 仿真事件数据
Fig.3 The simulated event dataset
除了仿真的实验数据,本文在实际拍摄的事件相机数据集上[13]测试算法的去噪性能。公开的事件数据集由DAVIS传感器[2]记录,它的空间分辨率为240×180像素。该相机具有微秒的时间分辨率和高动态范围(130 dB),并且可以同时记录事件流和光学图像。事件数据集[13]记录了在各种环境和运动条件下的场景的信息,图4为实验测试的七种场景的光学参考图像,其中图4(e)、(f)、(g)是一些具有挑战性的场景,图4(e)、(f)表示两个不同时间段的测试例子,均记录了室外以恒定速度滑雪的场景信息,图4(g)是在高速旋转的运动条件下记录的。本文提出的算法不需要图像信息,只对原始的事件流进行处理,图4中的灰度图像仅作为场景的视觉参考。
图4 事件数据集中测试场景的参考图像
Fig.4 Samples of reference images in the event dataset
5.2 算法参数分析
本实验在Intel(R) Core(TM)i5-7500@3.40 GHz和16 GB内存电脑上使用Matlab R2016b实现本文事件流去噪,并使用GSPBox[16]进行本文算法中的图信号处理。
本文主要在仿真数据上进行算法的参数研究,主要研究的参数有最近邻点个数k值,正则项权重λ以及时间距离权重γ。为了定量分析,对于无噪声的事件数据流,本实验对其像素坐标添加高斯噪声,以模拟事件流受到的噪声干扰,注意本次实验并没有去除离群点处理操作,因为文章的重点是流形约束对事件去噪方法的贡献,所以实验只是对无噪声事件流的像素坐标添加噪声,模拟出事件坐标的波动,来验证本文算法的性能。因此,可以通过计算去噪后事件点P={p1,...,pN}T与事件真实坐标
的平均距离作为事件流去噪的误差度量,如下式所示:
(7)
本实验设置高斯噪声方差var=2.5,在四组仿真数据上统计误差与参数选取结果,用于分析参数对去噪性能的影响,本实验对4.2小节提出的去噪过程执行一次迭代的实验结果进行评估。图5为误差与k值选取结果,本文算法中的k值用于建图中最近邻点个数的选择,若k值较小,对于输入的事件点只有邻近的事件点对去噪起作用,算法的估计误差增大,在k值过大的情况下,与事件点较远的事件对其影响增加,导致图模型变得复杂,算法的性能下降。图6是去噪误差与正则项权重选取的结果,参数λ是被设置用来控制事件流在像素平面上的平滑程度,该参数控制流型正则项的权重,权重过小,流形平滑约束对事件去噪的作用减小,权重过大, 会导致平滑程度过高。图7展示了去噪误差与时间距离权重之间的关系,由于事件相机的时间分辨率是微秒级别,像素和时间的跨度不同,因此进行距离计算时需要在时间距离上添加权重γ。从图7观察到,当时间距离权重过大时,本文算法的去噪性能急剧下降。在其他参数条件相同的情况下,若时间距离权重过大,时间方向上的事件点之间的权重明显降低,图模型获得的事件流内部结构信息不再准确,导致去噪后的事件形成的边缘结构被破坏,事件流去噪的性能下降。 根据实验结果,本文算法的参数设置为k=10,λx=λy=2.6,γ=1e4。
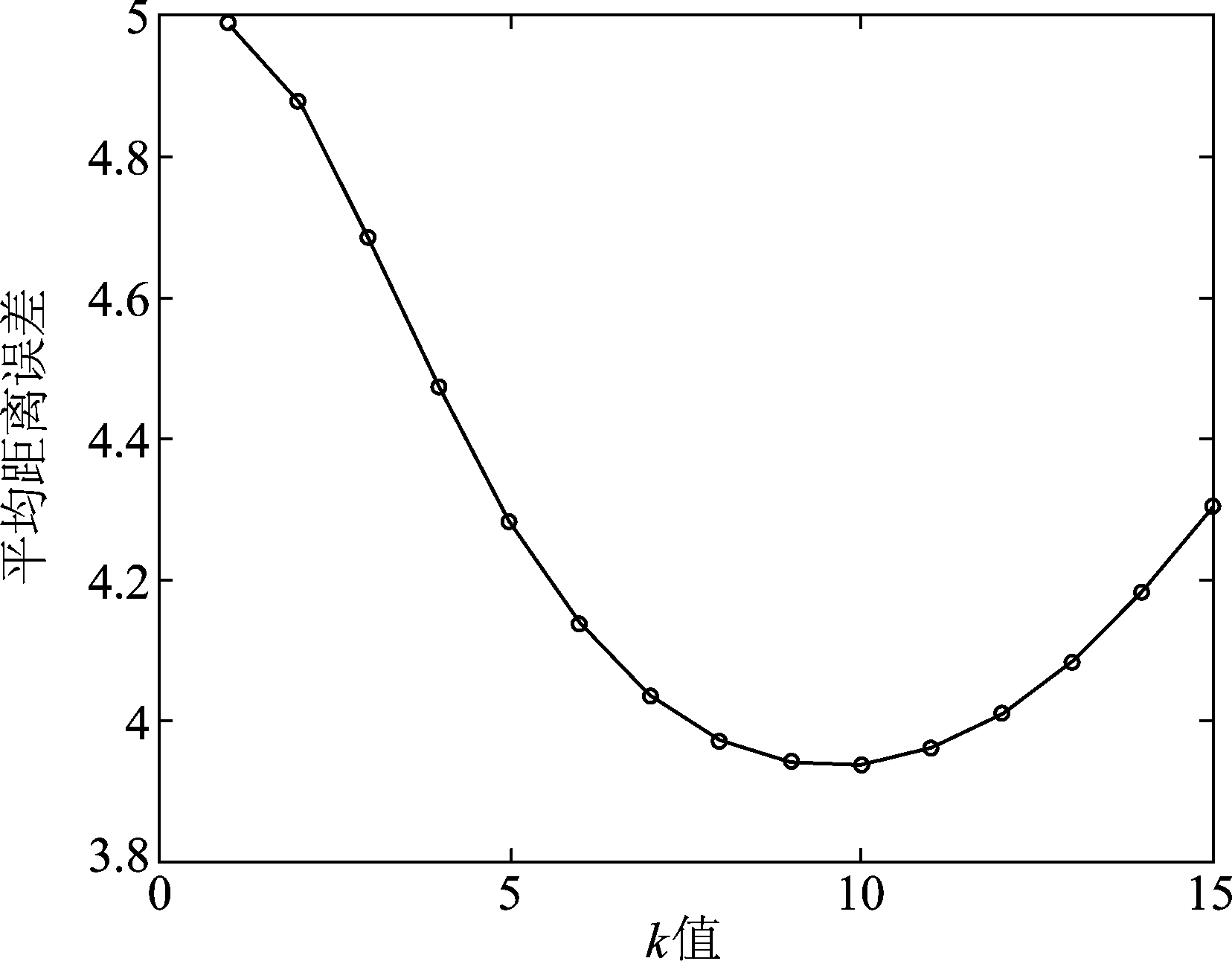
图5 去噪误差与k值的变化关系
Fig.5 The relation between denoising error and k value
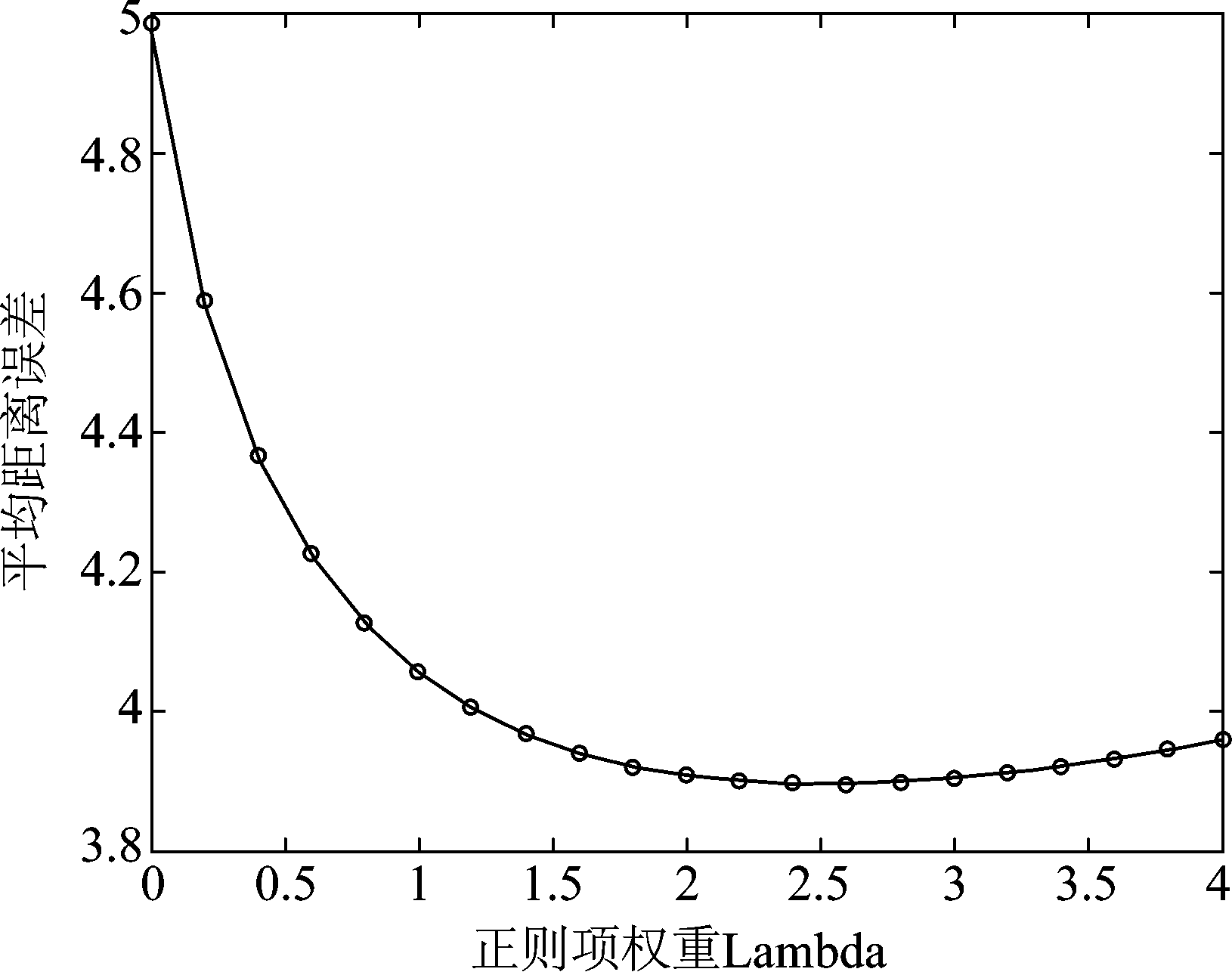
图6 去噪误差与正则项权重的变化关系
Fig.6 The relation between denoising error and regularization weight
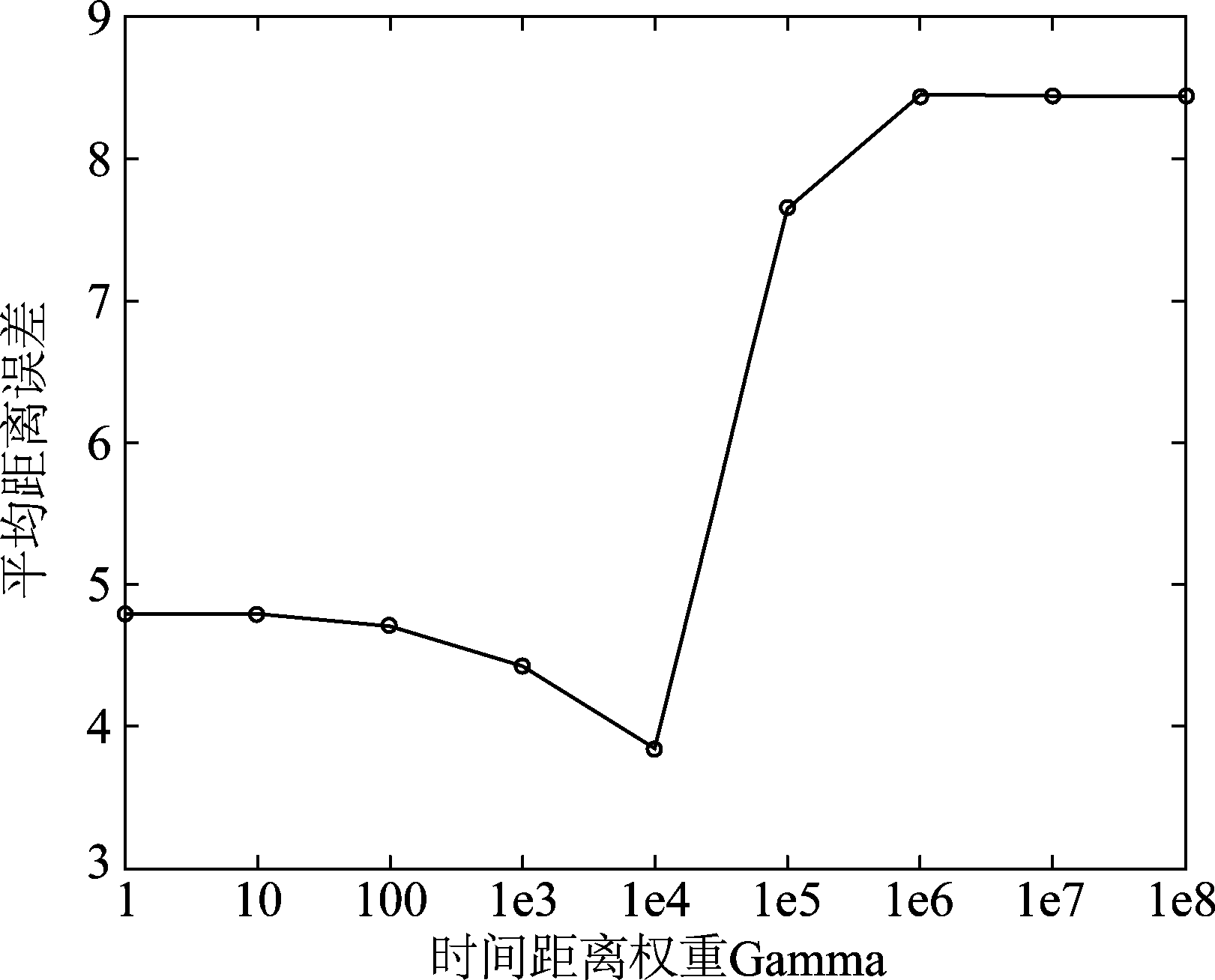
图7 去噪误差与时间距离权重的变化关系
Fig.7 The relation between denoising error and time distance weight
5.3 数据集实验结果与分析
为了评估本文算法在事件流上的去噪性能,实验选择能够直接应用于事件流的传统方法进行对比分析:统计学方法,k-NN[17]。 k-NN算法使用空间分割技术(例如kD-tree)搜索输入数据的k个近邻点,然后计算所有点的最近邻距离的平均值α和标准偏差β,并去除落在α±
·β以外的点[17]。实验将本文算法和k-NN直接应用于相同的事件流进行对比,本算法的实验设置如仿真实验中所述,k-NN算法实验选取的是最优k值,阈值设置=0.2,时间的权重同样设为γ=1e4。
为了定性对比事件流的去噪结果,本文将去噪前后的短时间间隔内的事件流投影在二维像素平面上显示。图8展示了部分测试事件流的去噪对比结果。由上文可知,事件流在像素平面上的分布近似于场景中物体的边缘结构。图8结果显示k-NN算法有效地滤除了事件点集中显著的离群点,但是对于物体边缘附近触发的事件序列的噪声处理效果较差,本文算法去噪后的事件流形成的场景边缘更加尖锐清晰。k-NN算法对事件流的去噪只进行了剔除事件点的操作,并没有处理边缘由噪声引起的偏移,因为该算法只是统计了事件流的时空分布,并没有充分利用嵌入在数据内部的结构信息。对比k-NN算法,本文提出的算法不仅去除了离群点,而且有效地减少了场景边缘触发的事件由于噪声导致的位置波动,在保留场景结构细节同时抑制噪声。
图8 事件流去噪实验对比结果
Fig.8 Comparison result of event denoising
本文是利用图的约束解决事件流的去噪问题,文献[11]使用真实光学图像作为Ground-Truth计算FSIM以评价重构图像的质量,由于事件流没有Ground-Truth,类似于FSIM的图像域评价指标不能直接用于评判本文的事件去噪性能。为了定量分析事件去噪性能,本文将去噪前后的短时间间隔内的事件流投影到二维平面,存在事件点的相应像素位置标记为1,没有事件标记为0,并统计二维平面上1的总个数,即二维平面上存在事件的位置总个数Num作为本文去噪评价指标,该指标在一定程度上反映了事件流构成的边缘的清晰程度。如图9所示,事件流由于噪声的影响边缘参差不平,投影到平面上的点数较多,而去噪后事件流沿着时间方向形成光滑的平面,事件在边缘附近的聚集程度越大,投影到二维平面形成的边缘点数较少。Num越小,表明边缘越清晰,事件流的去噪效果越好。
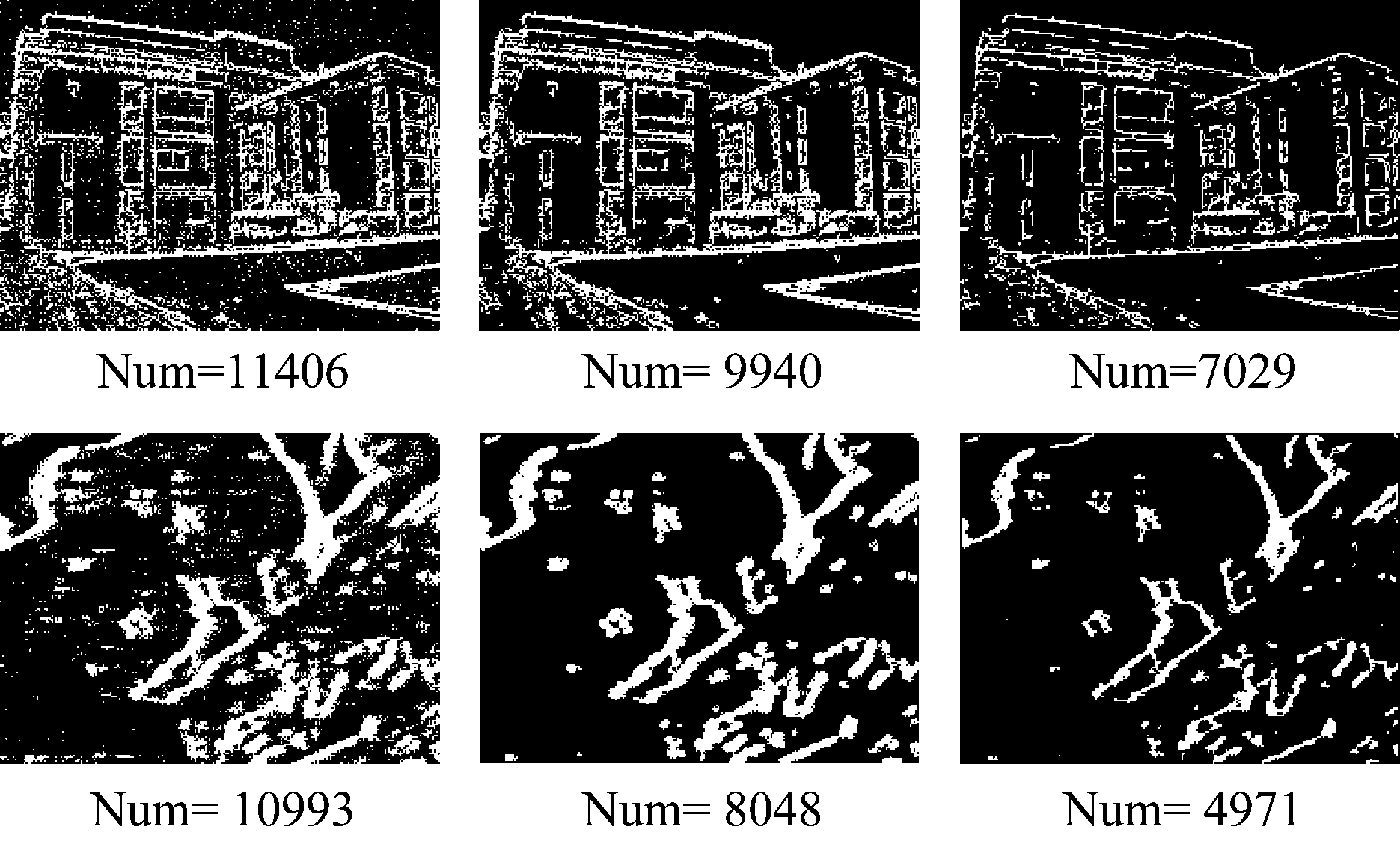
图9 事件流去噪对比结果,从左至右依次是 原始事件流,k-NN结果,本文算法结果
Fig.9 Comparison result of event denoising. From left to right are the original event stream, the k-NN result and the proposed algorithm
表2展示了七组测试事件流的对比实验结果,结果表明本文算法在不同场景事件流中均能取得较好的去噪效果,因为本文加入了事件序列在时空域上底层结构约束,所以有效地抑制位于场景边缘的事件噪声以保持去噪后的边缘更加清晰尖锐。虽然测试实例(e),(f)没有像普通场景具有丰富的几何信息,但是本文低维流形的假设在这类场景中仍然有效。不同场景的实验结果证明了本文事件流去噪算法的鲁棒性。
表2 事件流去噪评价指标对比
Tab.2 Denoising evaluation comparisons
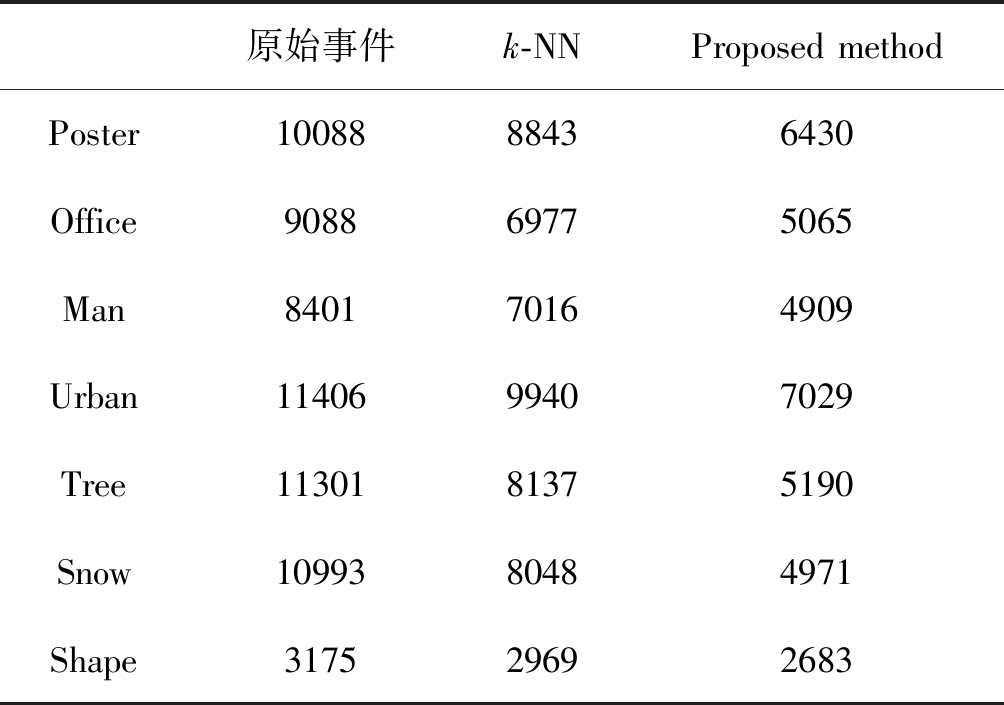
原始事件k-NNProposed methodPoster1008888436430Office908869775065Man840170164909Urban1140699407029Tree1130181375190Snow1099380484971Shape317529692683
正如上文所述,本文提出的算法相对其他算法的主要优势就在于它可以有效地处理事件流中物体边缘结构附近的噪声,上述一系列实验结果表明,本文算法提出的流形正则项约束在事件流去噪方面表现良好,去噪效果较为突出。下面本文将对比分析提出的算法与k-NN算法的运行时间。
表3中展示了在处理的事件点数不同的情况下本文算法与k-NN算法的测试时间,表中记录是本文对4.2小节提出的去噪过程一次迭代的运行时间。从表中看出,随着事件数目的增加,两种算法的运行时间均成倍的增长,本文算法消耗时间较长,运行时间主要消耗在建图过程中。由于k-NN算法只需要查询最近邻点并计算距离,而本文的算法则需要构建图模型以表征事件数据的结构分布,因此所耗时间较长。关于建图和优化求解的快速算法的改进将在未来工作中继续研究。
表3 运行时间对比
Tab.3 Comparisons of running time
事件数目k-NN/sProposed method/s构建图优化求解总和50000.10840.11160.01080.1224100000.12130.12430.02710.1514150000.14080.14620.04980.1960
6 结论
本文提出一种新的事件去噪算法。根据DVS相机输出的事件序列分布的特性,本文利用图模型作为低维流形的近似表达以获得嵌入在事件时空序列中的内部结构,并将去噪问题表示为基于流形正则项的优化问题。文中通过仿真和真实数据实验验证了事件去噪算法的有效性,数据集的结果说明了在不同的事件实例中,本文提出的基于图的流形约束的事件去噪性能优于传统的去噪方法。然而本文算法在运行时间方面有所不足,这将在未来的工作中不断研究改进。
[1] Lichtsteiner P, Posch C, Delbruck T. A 128×128 120 dB 15 μs Latency Asynchronous Temporal Contrast Vision Sensor[J]. IEEE Journal of Solid-State Circuits, 2008, 43(2): 566-576.
[2] Brandli C, Berner R, Yang M, et al. A 240×180 130 dB 3 μs latency global shutter spatio-temporal vision sensor[J]. IEEE Journal of Solid-State Circuits, 2014, 49(10): 2333-2341.
[3] 周乐意, 余文涛, 陈嘉宇, 等. SAR图像球流形局部嵌入建模及其分类方法[J]. 信号处理, 2013, 29(9): 1163-1168.
Zhou L Y, Yu W T, Chen J Y, et al. SAR image spherical local embedding modeling and classification method[J]. Journal of Signal Processing, 2013, 29(9): 1163-1168.(in Chinese)
[4] 刘璐, 靳少辉, 焦李成, 等. 采用流形近邻传播聚类的极化SAR图像分类[J]. 信号处理, 2016, 32(2): 135-141.
Liu L, Jin S H, Jiao L C, et al. Manifold Affinity Propagation Clustering for PolSAR Image Classification[J]. Journal of Signal Processing, 2016, 32(2): 135-141.(in Chinese)
[5] Benosman R, Clercq C, Lagorce X, et al. Event-based visual flow[J]. IEEE Transactions on Neural Networks & Learning Systems, 2014, 25(2): 407- 417.
[6] Bardow P, Davison A J, Leutenegger S. Simultaneous optical flow and intensity estimation from an event camera[C]∥IEEE Conference on Computer Vision and Pattern Recognition, 2016: 884- 892.
[7] Mueggler E, Gallego G, Rebecq H, et al. Continuous-Time Visual-Inertial Odometry for Event Cameras[J]. IEEE Transactions on Robotics, 2018, 34(6): 1425-1440.
[8] Rebecq H, Horstschaefer T, Scaramuzza D. Real-time Visual-Inertial Odometry for Event Cameras using Keyframe-based Nonlinear Optimization[C]∥British Machine Vision Conference, 2017, 3.
[9] Xie X, Du J, Shi G, et al. DVS image noise removal using k-SVD method[C]∥International Conference on Graphic and Image Processing, 2018, 10615: 106153U.
[10]Xie X, Du J, Shi G, et al. An improved approach for visualizing dynamic vision sensor and its video denoising[C]∥Proceedings of the International Conference on Video and Image Processing. ACM, 2017: 176-180.
[11]Munda G, Reinbacher C, Pock T. Real-time intensity-image reconstruction for event cameras using manifold regularisation[J]. International Journal of Computer Vision, 2018, 126(12): 1381-1393.
[12]Gallego G, Scaramuzza D. Accurate Angular Velocity Estimation with an Event Camera[J]. IEEE Robotics and Automation Letters, 2017, 2(2): 632- 639.
[13]Mueggler E, Rebecq H, Gallego G, et al. The event-camera dataset and simulator: Event-based data for pose estimation, visual odometry, and SLAM[J]. The International Journal of Robotics Research, 2017, 36(2): 142-149.
[14]Osher S, Shi Z, Zhu W. Low dimensional manifold model for image processing[J]. SIAM Journal on Imaging Sciences, 2017, 10(4): 1669-1690.
[15]Shuman D I, Narang S K, Frossard P, et al. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains[J]. IEEE Signal Processing Magazine, 2013, 30(3): 83-98.
[16]Perraudin N, Paratte J, Shuman D, et al. GSPBOX: A toolbox for signal processing on graphs[J]. arXiv preprint arXiv: 1408.5781, 2014.
[17]Rusu R B, Marton Z C, Blodow N, et al. Towards 3D Point cloud based object maps for household environments[J]. Robotics and Autonomous Systems, 2008, 56(11): 927-941.
