1 引言
设计和实现高速数据传输并有效抑制无线多径效应所导致的符号间干扰(Inter-Symbol Interference,ISI),一直是宽带无线通信中具有挑战性的研究。具有频域均衡的单载波传输(Single Carrier Frequency Domain Equalization,SC-FDE)与正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)是实现高速率数据传输的两种主要技术,SC-FDE系统将数据调制到单载波上进行传输,通过FFT运算在频域上进行均衡处理,具有比OFDM更低的峰均功率比和更低的载波频率误差灵敏度[1-2], 但复杂度和性能与OFDM系统相似[3- 4]。众多优点使SC-FDE成为一种具有竞争力的物理层传输技术并被IEEE802.11ad和IEEE802.11ay标准采纳为其中的物理层传输方案。单载波频域均衡的关键技术是频域均衡器的设计。
在单载波频域均衡系统中,传统的频域均衡采用迫零(Zero-Forcing,ZF)或最小均方误差(Minimum Mean Square Error,MMSE)[5]准则的线性均衡(Frequency Domain Linear Equalization,FD-LE)算法,虽然复杂度低但对噪声和符号间干扰的抑制能力有限。因此考虑采用具有反馈和迭代机制的非线性均衡算法[6]。在文献[7]中,D.Falconer在时域判决反馈均衡的基础上提出了一种基于最小均方误差准则的混合结构的时-频域判决反馈均衡器(Hybrid Decision Feedback Equalization,H-DFE)[7],具有更好的性能,由于前馈部分处于频域,计算复杂度有一定降低,但反馈部分仍在时域实现且涉及矩阵求逆处理,复杂度依旧偏高。N.Benvenuto在文献[8]提出了一种频域非线性均衡算法,迭代块判决反馈均衡[8](Iterative Block DFE,IBDFE),引入迭代与反馈修正机制消除码间串扰,前馈和反馈滤波器系数根据最小均方误差准则设计均在频域实现。计算复杂度低于TD-DFE或H-DFE,相比于H-DFE前向分量的误差也能被很好地消除,获得更好的性能增益。
同样的,IBDFE也存在不足,IBDFE在每次迭代中必须计算检测到的符号与发送的符号之间的互相关函数;并且需要估计信噪比。当迭代次数很少时IBDFE复杂度低,然而当迭代次数增加时复杂度将快速增高。为此Zhang Chao等在传统IBDFE算法的基础上,通过采用预定义的SER值和近似SNR值,简化了滤波器系数的计算,提出了一种低复杂度的IBDFE算法LC-IBDFE[9]。文献[10]中将迭代判决信号近似为发送信号利用MMSE准则推导出一种新的简化方法[10],误比特率性能有所下降,但有效减少了计算量。文献[11]用WL-MMSE均衡并假设发送与判决信号完美相关进行简化[11],得到与IBDFE类似的性能。文献[12]用发送信号的与线性因子相乘来替代判决信号进行MMSE推导[12],得出降低复杂度的IBDFE算法,在通信系统中性能均优于LC-IBDFE与IBDFE。
本文研究了迭代块判决反馈频域均衡IBDFE算法,根据传统IBDFE所推导出的前馈反馈滤波器系数,用频域迭代判决信号的线性假设简化了传统IBDFE前馈反馈滤波器系数的设计,提出一种基于线性因子化简相关系数的迭代块判决反馈均衡算法(correlation coefficient Simplified IBDFE,CCS-IBDFE)。该算法前馈系数不需要每次迭代都估计统计量。仿真结果表明,在性能收敛情况下算法复杂度低于IBDFE,稍高于LC-IBDFE,误比特率性能均优于IBDFE和LC-IBDFE。
2 系统模型
本文采用的单载波频域均衡基带等效模型如图1所示,发射端产生的二进制数据经数字调制后,将数据按长度M分块,并在每个数据块
后添加长度为N的已知特殊字UW序列
用来抵消相邻数据块间的干扰,同时还可辅助实现接收端的同步和信道估计,长度为P=M+N数据块
可表示为:
s=[s0,s1,…,sP-1]=[d0,…,dM-1,c0,…,cN-1]
(1)
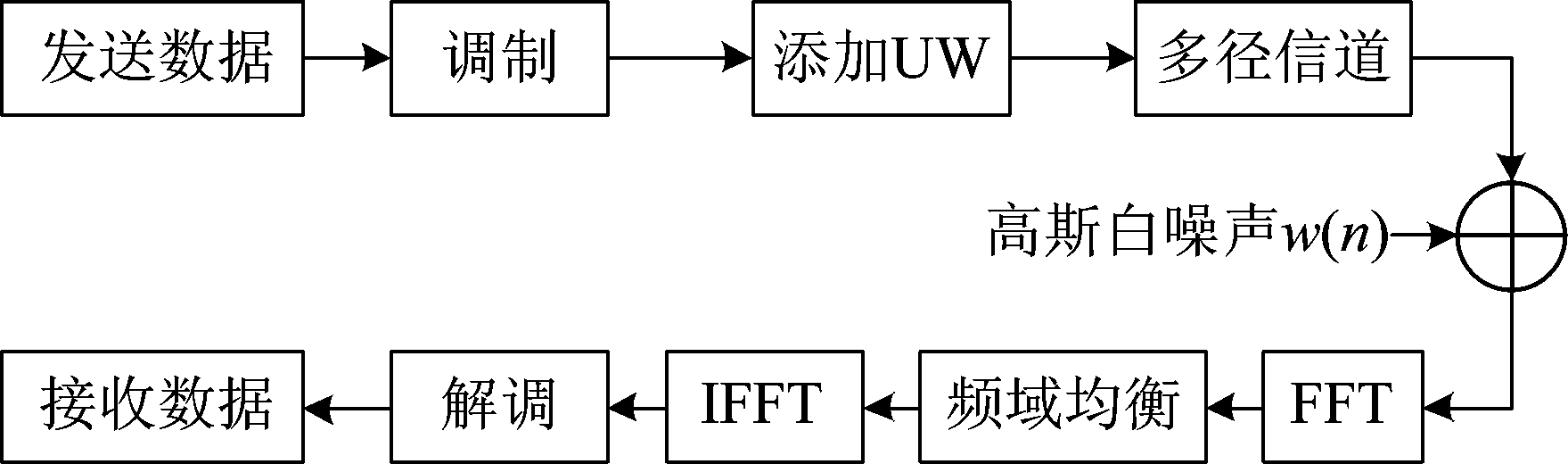
图1 SC-FDE系统模型
Fig.1 SC-FDE system model
设信道最大多径时延为L,且UW序列的长度大于信道冲激响应的最大时延。则数据经过信道后可表示为r(n)=s(n)
h(n)+w(n),其中h(n)为信道冲激响应,w(n)表示高斯白噪声,代表圆周卷积。设Rp、Sp、Wp、Hp(p=0,1,…,P-1)分别为接收信号,发送信号、高斯噪声和信道冲激响应的P点离散傅里叶变换,接收信号Rp经FFT变换到频域可表示为:
Rp=HpSp+Wp
(2)
分块的数据在频域进行均衡后再通过IFFT变换到时域进行解调。
3 迭代判决反馈均衡算法
3.1 频域迭代判决反馈均衡IBDFE
频域迭代判决反馈均衡前馈和反馈均在频域进行,通过多次迭代来增加判决信号的准确性。文献[8]在单载波频域均衡的基础上提出了IBDFE结构,迭代判决反馈均衡的结构如图2所示。
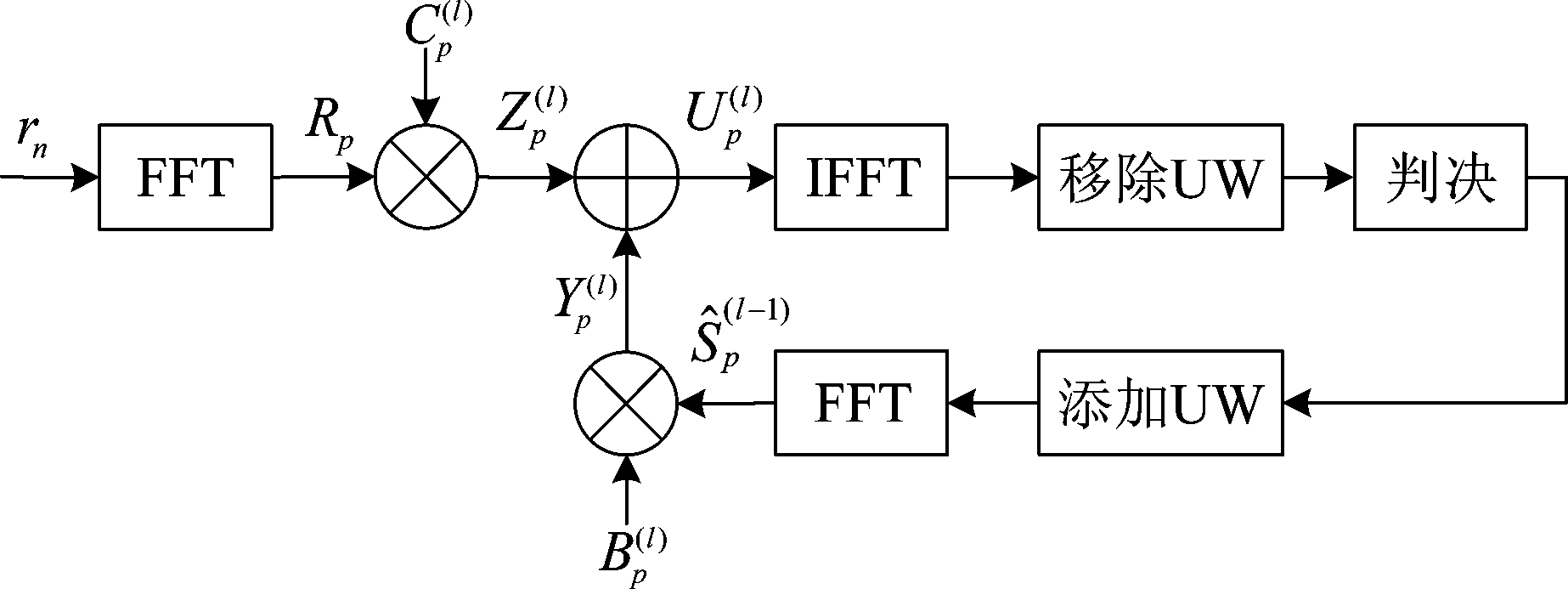
图2 IBDFE结构
Fig.2 IBDFE structure
IBDFE结构主要由两部分构成,分别是前馈和反馈部分,图中
和
分别表示第l次迭代的前馈和反馈滤波器的抽头系数,其中p=1,…,P-1,P表示FFT的长度。在第l次迭代的过程中,时域接收信号rn首先通过FFT转换为频域信号Rp,接收信号Rp经过前馈滤波器得到
信号。由和
相加得到
即:
(3)
其中,频域信号
的产生过程如图2所示,由第l-1次迭代中的
经过IFFT、移除UW产生信号
经判决、添加UW、FFT处理得到检测信号
再经反馈滤波器
滤波得到
信号,在第一次迭代中
为0。其中
是包含UW序列的判决数据。
由公式(3)使用MMSE准则推导,得到第l次迭代的前馈和反馈滤波系数
和
分别可表示成(4)、(5)。
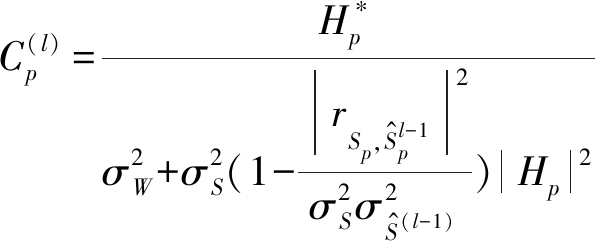
(4)
(5)
其中,
为发射信号功率,
为第l-1次迭代中的判决数据的功率,E{·}代表数学期望,{·}*代表复数取共轭。
为信道噪声在频域的功率。
是相关系数,可表示为:
(6)
由式(4)～(6)可以看出,传统IBDFE每一次迭代均要估算迭代判决信号功率和Sp与
的相关系数,并更新前馈反馈滤波器系数与Bp,计算量大。此外,相关系数计算需要通过训练序列获取或使用均衡后的数据Rp/Hp来近似Sp以计算相关系数,前者降低了系统频带利用率,后者计算复杂度高,同时忽略了信号噪声估算值与实际有偏差,如果小于实际,则反馈滤波器消除ISI效果不明显,迭代均衡收敛慢;如果估值大于实际,反馈滤波器将引入更多ISI,也影响均衡性能。
3.2 低复杂度IBDFE算法LC-IBDFE
传统IBDFE相比H-DFE,前馈反馈滤波器均在频域运算,不需要矩阵求逆,一定程度上降低了复杂度,但每次迭代都需要更新
并计算统计量。针对IBDFE迭代系数计算量大的不足,为降低IBDFE的复杂度,文献[9]首先设定
其中
是第l次迭代判决
相对于发送信号的迭代误差。在此基础上采用MMSE准则计算前馈与反馈滤波器系数。通过每次迭代后的误符号率相同且数值很小,提出一种简化的IBDFE设计方案LC-IBDFE。简化的前馈滤波器系数和反馈滤波器系数Bp为:
(7)
(8)
其中γ与Φ如下:
(9)
(10)
其中β为相邻码元间的欧式距离,SNRPre为预设的信噪比,PS,Pre为预设的误符号率。该算法通过简化将每次迭代的误符号率预设为定值PS,Pre,用预设的信噪比门限SNRPre估计噪声功率
使反馈前馈系数上需要单独计算的参数只有信道频率响应HP,且前馈和反馈系数只需计算一次而不用每次迭代都更新,简化了计算复杂度。但随着迭代次数增加,误差被消除,误符号率PS会不断变小,预设为定值会对性能造成影响。
3.3 提出的简化算法CCS-IBDFE
由公式(4)和(5)可知,传统IBDFE运算复杂度高主要因为每次迭代均要计算发射信号和判决信号的相关系数以及迭代判决信号
的功率
而LC-IBDFE虽然简化了复杂度,但性能受预设的符号率影响大。针对以上问题,本文将每一次迭代中Sp和假设为线性关系,并使用单调递减函数近似误符号率而非使用定值,达到简化前馈和反馈滤波器系数的目的。
第一次迭代时还未产生判决信号
相关系数为0,无反馈信号,反馈滤波器系数Bp也为0,此时的前馈滤波Cp器系数如下式,即第一次迭代前馈滤波器就是基于MMSE的线性均衡器。
(11)
接收信号经过第一次迭代线性MMSE均衡后,信号非线性失真减少,可将近似假设成Sp和线性因子相乘的形式即:
(12)
即每l次迭代的判决信号与发射信号Sp看成是线性的。发射信号Sp是大小为P的块状数据,则每一次迭代的判决数据看成是块状数据Sp的所有数据点乘相同线性因子m(l-1),该假定可简化前馈和反馈滤波器的设计,主要是简化相关系数
所定义的线性因子m(l-1)是随迭代次数l增加而降低的函数,每一次迭代中线性因子是一个的定值,后面将对其进行推导。将式(12)代入相关系数定义(6)可以得到以下相关系数的两种等效表达式:
(13)
由公式(13)计算得到相关系数绝对值平方与第l-1次判决信号功率
发射信号功率
的商为
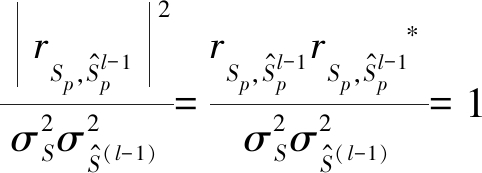
(14)
文献[9]中将前馈反馈系数简化为如下中间过程:
(15)
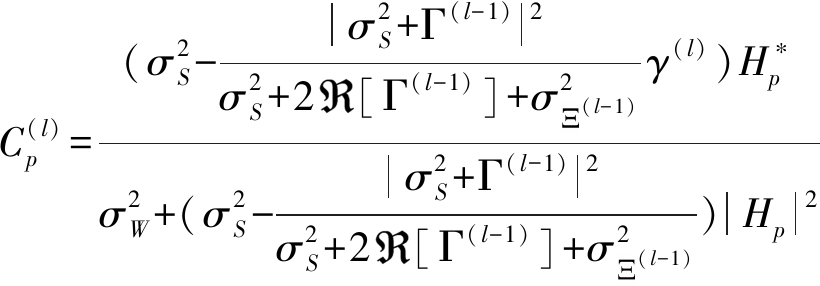
(16)
(17)
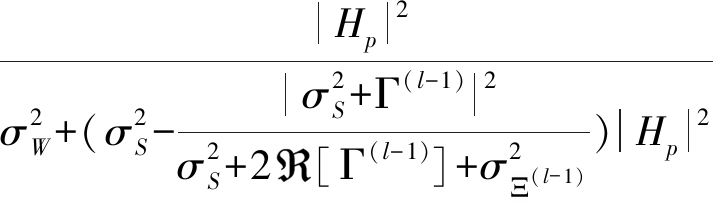
(18)
其中,Γ(l-1)为发射信号和第l-1次频域判决误差
的相关系数,
是频域判决误差的功率。根据
与相关系数
的定义可得:
(19)
(20)
由式(19)、(20)可得前馈系数可表示为:
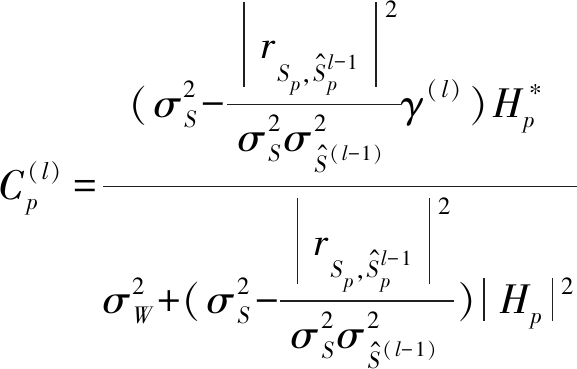
(21)
将式(14)代入式(21),前馈反馈系数最终可简化为:
(22)
同理,联合(13)、(19)、(20)可将(15)、(17)、(18)分别化简为:
(23)
(24)
(25)
采用线性因子计算相关系数,前馈与反馈滤波器系数均得到了简化。反馈滤波器用来消除前向和反向残余码间干扰。由于假设Sp与
呈线性关系会给前馈Φ(l)与γ(l)引入误差,因此给反馈系数添加修正因子μ,其最优值与实际场景相关。
下面推导线性因子m(l-1),假设发送数据独立同分布且调制码元集中的元素等概[13],即
结合(13) 
可将线性因子表示为:
m(l-1)=ejn(l-1)
(26)
式中n(l-1)为迭代次数l的函数,根据式(12),LC-IBDFE中第l-1次迭代后
与Sp间频域迭代误差与Sp也成线性关系即
(27)
其中,的定义为:
(28)
其中,
为第l-1次迭代时域判决残余误差,假设码元只可能在相邻码元出错,则不同调制方式下的时域判决误差功率为
其中
为第l-1次迭代后得到的误符号率,β为星座图上相邻码元间的欧式距离。可得到频域迭代判决误差功率为:
(29)
考虑到
的值随着迭代进行逐渐减小,且大多数情况下迭代判决器输出的信号误符号率一般小于0.1,于是将近似为:
(30)
随着迭代次数l增大而减小,同时引入参数λ修正不同场景下第l-1次迭代后误符号率的估计值,λ与迭代后误符号率下降速度与均衡中存在的ISI和每次迭代消除的ISI有关。将式(26)、(27)、(30)分别代入式(29),用欧拉公式化简得到下式:
(31)
再由式(26)与(31)得到线性因子m(l-1)表达式为:
(32)
至此推导出相关因子m(l-1),可代回式(23)求出反馈系数
综上,改进的IBDFE算法初始迭代相当于对接收信号做线性MMSE均衡,均衡后输出为
由公式(11)得到。第2次迭代开始均衡输出为
其中
与根据式(22)、(23)更新。只用计算一次,每次迭代只用更新线性因子m(l-1),相比传统IBDFE,尤其对于多次迭代,计算复杂度得到降低。
3.4 复杂度分析
IBDFE、LC-IBDFE和CCS-IBDFE采用的频域均衡结构是相同的,频域均衡运算复杂度不同在于滤波器系数取值过程中复乘和复加运算的次数。而复杂度主要来自于前馈反馈系数中复乘和复加运算的次数,而影响总体计算想的主要部分是复乘,假设不同算法在FFT处理上复杂度一致,此处用前馈反馈系数所需复乘次数来评估复杂度。算法迭代次数设为K(K>1)次,P为FFT的长度,观察式(22)～(25),CCS-IBDFE不需要每次迭代均计算统计信息
计算|Hp|2需要P次复乘,每次迭代中计算
需要P次复乘,因此CCS-IBDFE需要复乘为KP+2P,三种算法的复杂度如表1所示。
表1 滤波器设计所需复乘次数
Tab.1 Complex multiplication required for filter design
算法复乘次数IBDFE3KP+PLC-IBDFE3PCCS-IBDFEKP+2P
由表1可以看出在迭代K=4,FFT点数为512条件下,LC-IBDFE与CCS-IBDFE算法复杂度低于IBDFE。CCS-IBDFE的计算复杂度相比IBDFE有约53.9%的减少,且迭代次数K或FFT长度P越大,LC-IBDFE与CCS-IBDFE相对于IBDFE降低的复杂度也越大。
4 算法性能仿真
为验证文中提出的基于相关系数简化的IBDFE算法性能,选择两种多径信道进行仿真,相对时延与功率衰减如表2、表3所示。仿真中假设信道为块衰落,信道同步和信道估计是理想的。对应的系统参数如表4所示。对改进算法进行仿真和对比,分析仿真结果。根据前面提出的修正因子,我们使用λ=8, μ=1.25,LC-IBDFE的预设参数为SNRpre=10, Ps,pre=0.1进行仿真,每个信噪比使用超过20000个信道实现来进行性能统计。
表2 A信道参数
Tab.2 Parameter of channel A
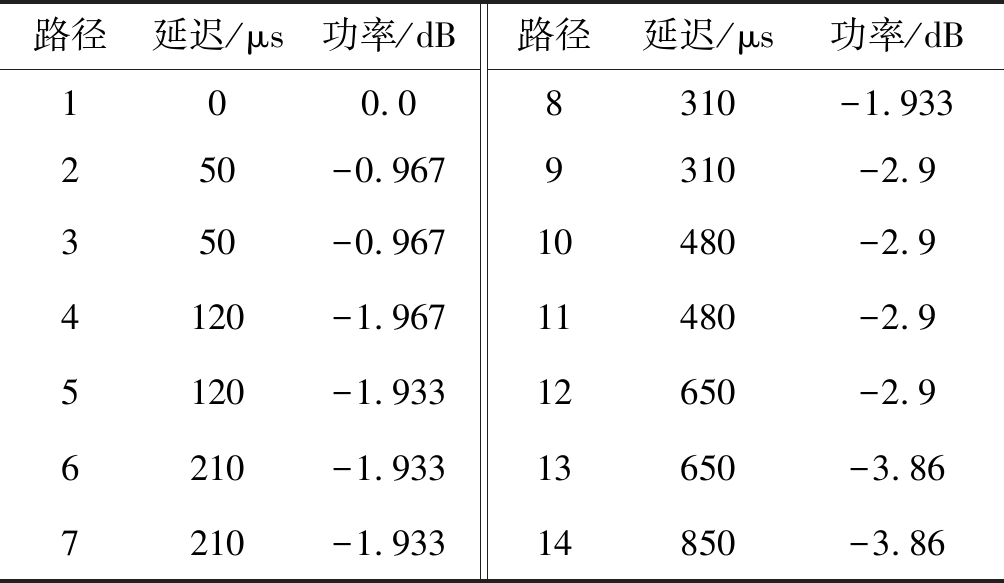
路径延迟/μs功率/dB路径延迟/μs功率/dB100.08310-1.933250-0.9679310-2.93450120-0.967-1.9671011480480-2.9-2.95120-1.93312650-2.96210-1.93313650-3.867210-1.93314850-3.86
表3 ITU-EVA信道参数
Tab.3 Parameters of channel ITU-EVA
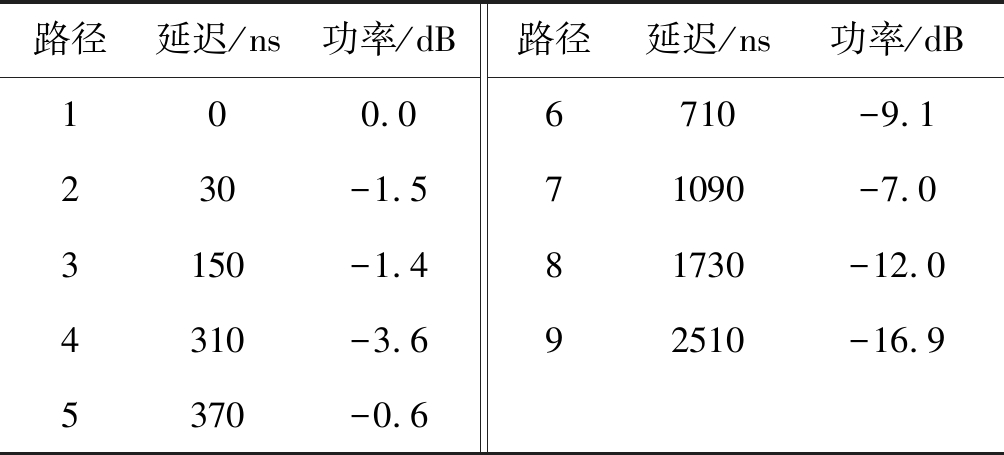
路径延迟/ns功率/dB路径延迟/ns功率/dB100.06710-9.1230-1.571090-7.03150-1.481730-12.04310-3.692510-16.95370-0.6
表4 SC-FDE系统IBDFE频域均衡仿真参数
Tab.4 Simulation parameters of SC-FDE system
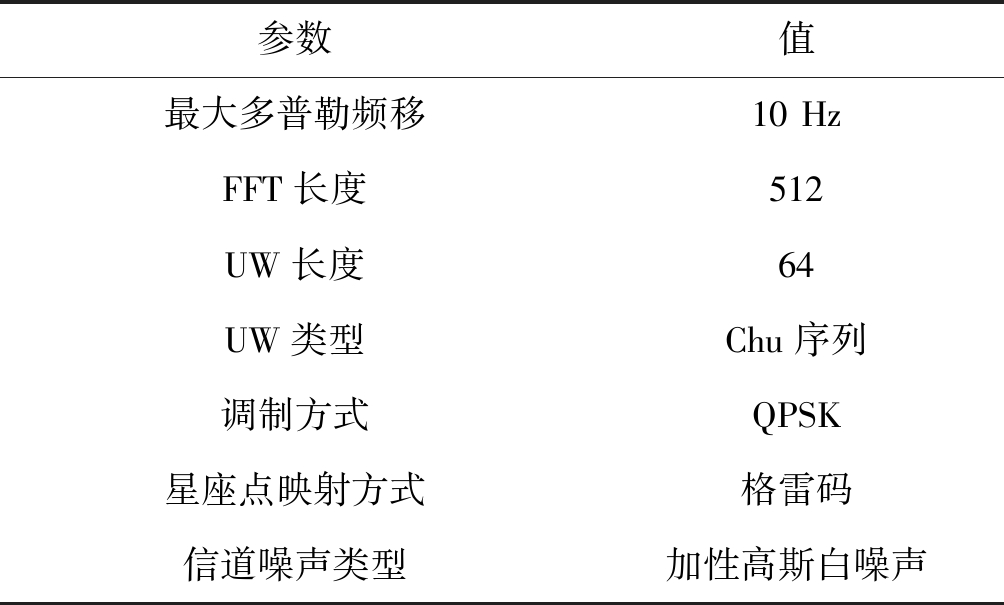
参数值最大多普勒频移10 HzFFT长度512UW长度64UW类型Chu序列调制方式QPSK星座点映射方式格雷码信道噪声类型加性高斯白噪声
图3为λ=8, μ=1.25的改进算法CCS-IBDFE和IBDFE两种算法在所设A信道下迭代1～5次性能比较。CCS-IBDFE第1次迭代与线性MMSE的性能相同,第2次迭代产生了显著的性能增益。第4次迭代相比第3次迭代只有0.1 dB的性能增益,第5次迭代几乎不增加增益,故4次迭代可使算法收敛。与IBDFE相比,在6～9 dB CCS-IBDFE性能上稍微差于IBDFE,而在10～15 dB比IBDFE好,在误比特率为10-5时,CCS-IBDFE性能比IBDFE的性能好约0.12 dB。
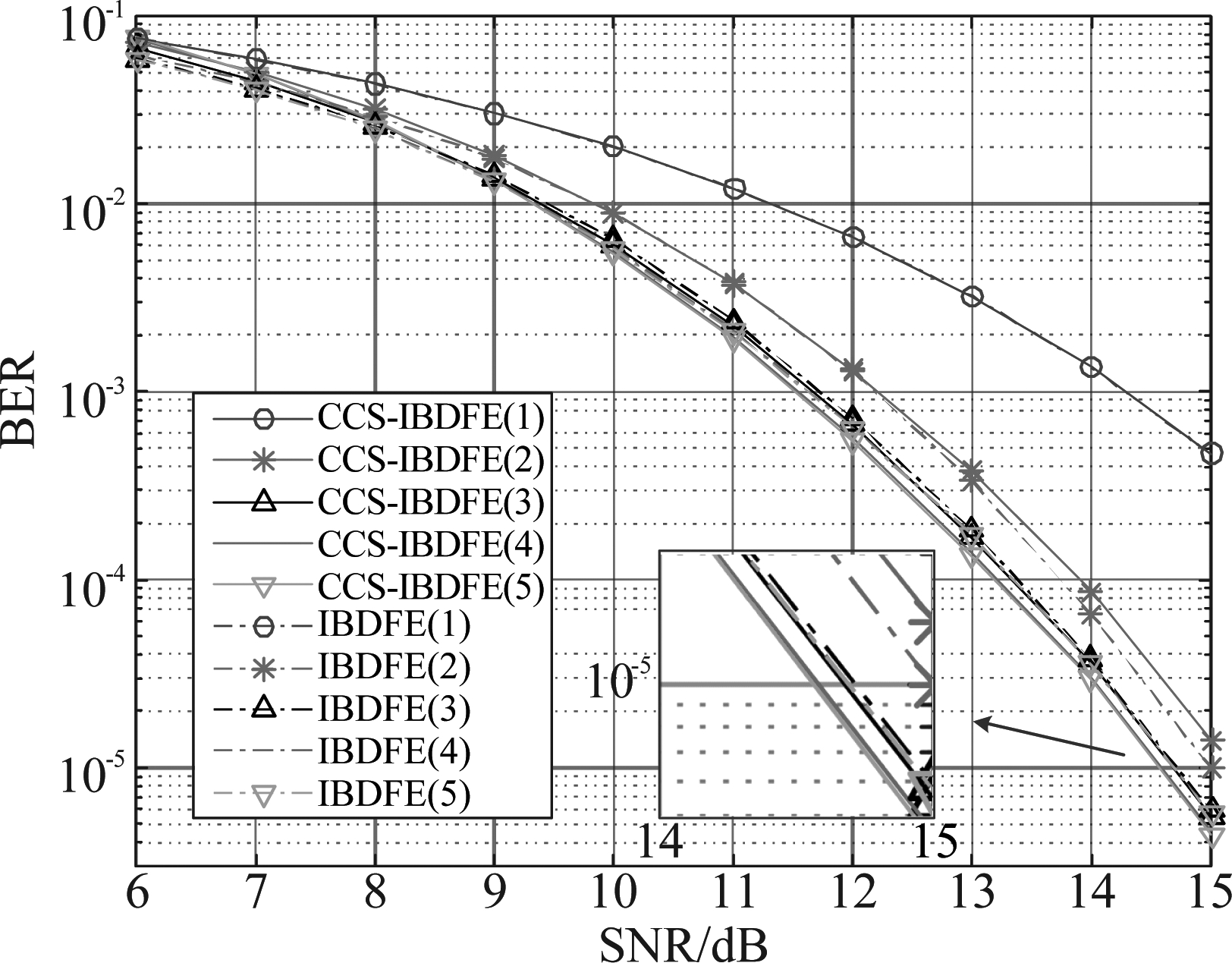
图3 CCS-IBDFE(λ=8, μ=1.25)与传统 IBDFE误比特率性能对比
Fig.3 Comparison of BER between CCS-IBDFE (λ=8, μ=1.25) and traditional IBDFE
图4 CCS-IBDFE与LC-IBDFE(SNRpre=10, Ps,pre=0.1) 误比特率性能对比
Fig.4 Comparison of BER between CCS-IBDFE and LC-IBDFE (SNRpre=10, Ps, pre=0.1)
图4为SNRpre=10, Ps,pre=0.1的LC-IBDFE算法与λ=8, μ=1.25的CCS-IBDFE算法的性能对比,当迭代次数为2且误比特率为10-4时,LC-IBDFE的性能比CCS-IBDFE提升约0.25 dB的增益,迭代3次以上达到收敛后,两者性能基本一致。观察迭代次数为4的曲线,由于LC-IBDFE固定了信噪比和迭代判决误符号率,引入了更多误码,所以CCS-IBDFE在高信噪比的情况下性能优于LC-IBDFE,误比特率下降速率比LC-IBDFE快。当误比特率为10-5时,CCS-IBDFE性能比LC-IBDFE提升了约0.1 dB。
图5比较了的CCS-IBDFE与LC-IBDFE和传统IBDFE三种算法在A信道和ITU-EVA信道下的误比特率性能。由于3次以上算法已基本收敛,为便于对比,仅记录第4次迭代的BER性能。对于channel A衰落信道,所提出的改进算法在第4次迭代与LC-IBDFE和IBDFE相比提高了约0.1 dB的性能增益。同时,在高信噪比条件下,CCS-IBDFE收敛更快,在ITU-EVA信道下,BER为10-5时,CCS-IBDFE性能比LC-IBDFE提高0.25 dB。
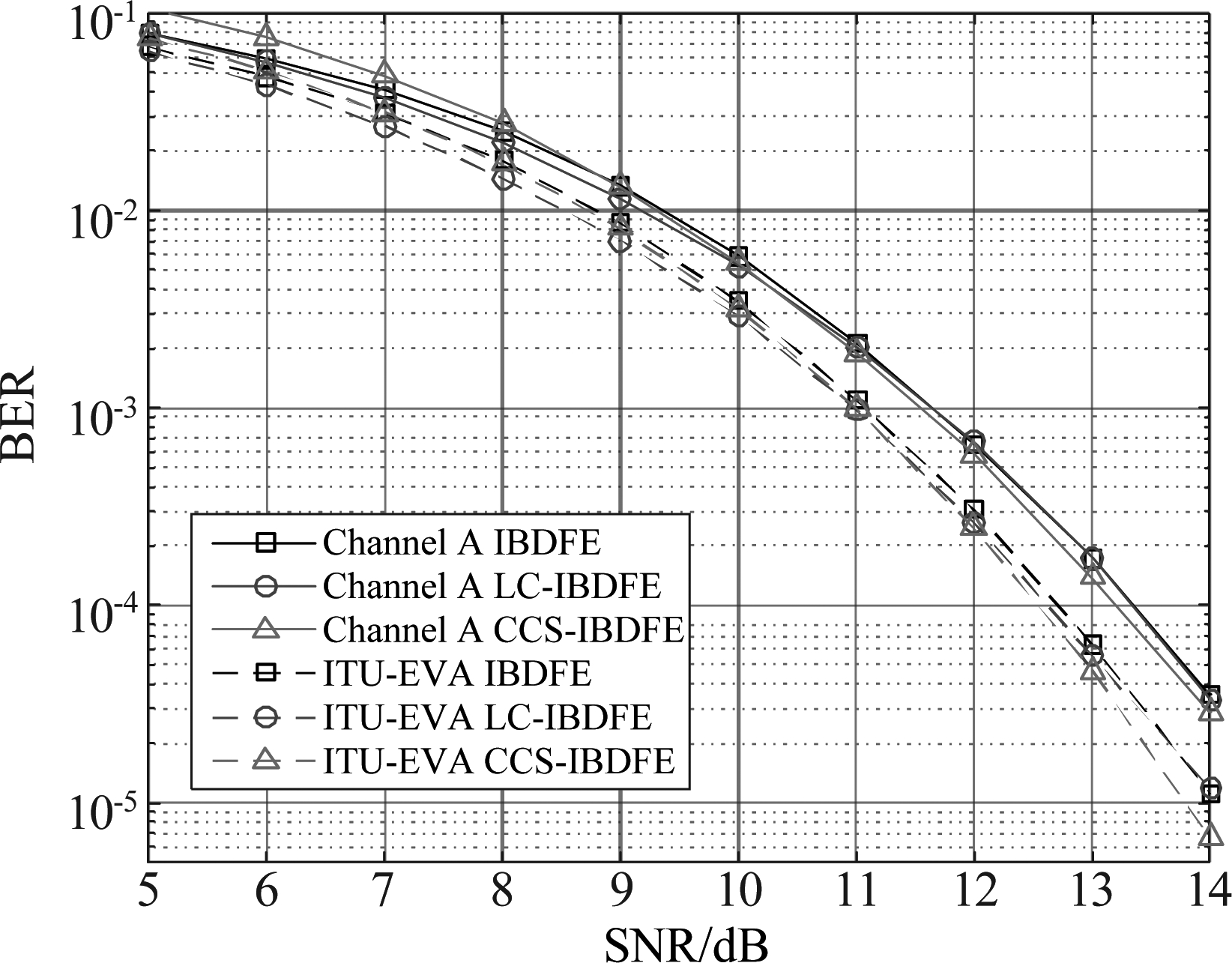
图5 CCS-IBDFE、LC-IBDFE和传统IBDFE 在两个信道下误比特率性能对比
Fig.5 Comparison of BER of CCS-IBDFE、 LC-IBDFE and IBDFE in two channel
改进算法的前馈反馈系数在第2次迭代开始受修正因子λ, μ影响,为验证算法稳健性,进行如下仿真。图6是在信道A和ITU-EVA两条信道下, μ固定为1.25,λ=6,8,10和12时分别得到的第4次迭代的BER性能。图7是两条信道下固定λ为8, μ=1.23,1.24,1.25,1.26下第4次迭代的BER性能。仿真结果表明,CCS-IBDFE在μ微调下模型性能偏差不大,CCS-IBDFE对λ值的选择也不敏感,所以CCS-IBDFE算法具备稳健性,可根据性能要求对λ, μ灵活取值。
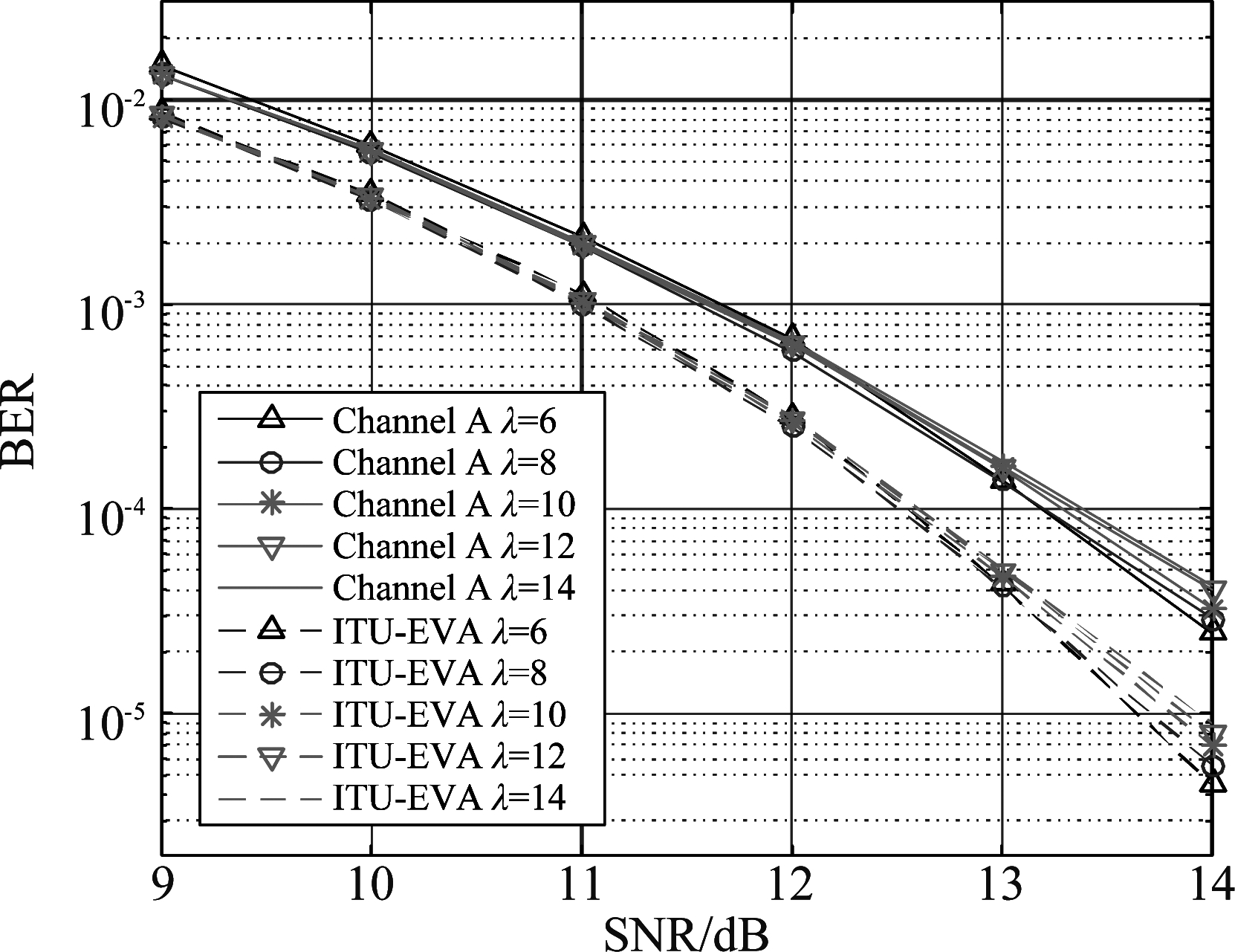
图6 λ=6,8,10 CCS-IBDFE的BER性能
Fig.6 λ=6,8,10 BER performance of CCS-IBDFE
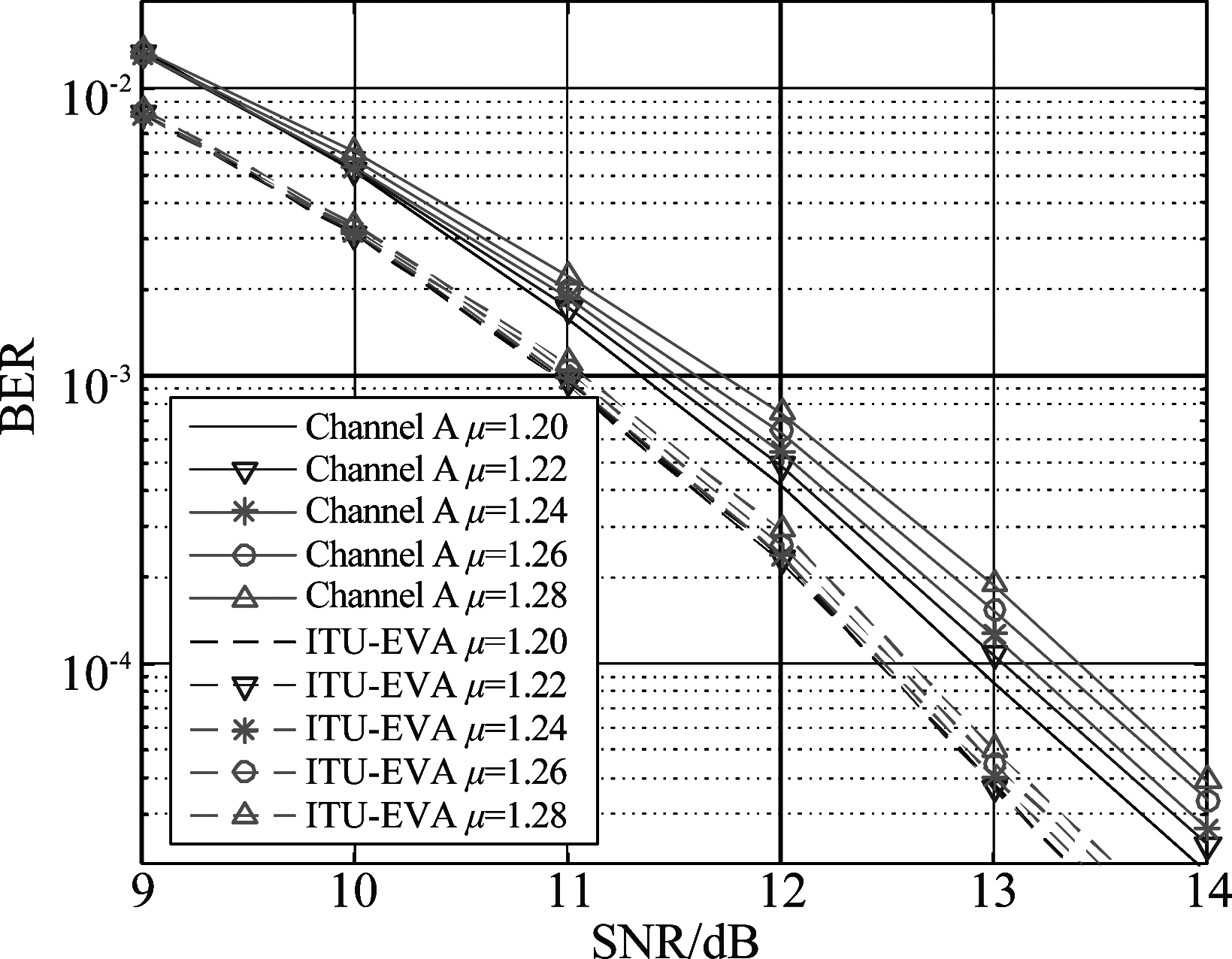
图7 CCS-IBDFE μ=1.23～1.25 的BER性能
Fig.7 BER performance of CCS-IBDFE μ=1.23～1.25
5 结论
本文对SC-FDE系统中的IBDFE算法进行研究,针对传统IBDFE算法每次迭代均需要更新前馈反馈滤波器系数,计算复杂度高的缺点,通过线性假设简化前馈反馈滤波器系数中的相关系数,提出了一种简化算法CCS-IBDFE,并对其计算复杂度和性能进行了分析,CCS-IBDFE在每一次迭代中不需要更新前馈滤波器系数,所需计算复杂度将比IBDFE低2KP,稍高于LC-IBDFE。仿真结果表明,所提出算法性能与传统IBDFE算法相比复杂度降低且在误比特率为10-5时有0.12 dB的性能增益,与简化算法LC-IBDFE相比有0.1 dB的性能增益。针对简化设计所提出的修正因子λ与μ的稳健性也得到了证实。CCS-IBDFE算法为迭代块判决反馈均衡提供了一种有效的简化方案。
[1] Hasegawa F, Okazaki A, Kubo H, et al. A novel PAPR reduction scheme for SC-OFDM with frequency domain multiplexed pilots[J]. IEEE Communications Letters, 2012, 16(9): 1345-1348.
[2] Louveaux J, Vandendorpe L, Sartenaer T. Cyclic prefixed single carrier and multicarrier transmission: bit rate comparison[J]. IEEE Communications Letters, 2003, 7(4): 180-182.
[3] Falconer D, Ariyavisitakul S L, Benyamin-Seeyar A, et al. Frequency domain equalization for single-carrier broadband wireless systems[J]. IEEE Communications Magazine, 2002, 40(4): 58- 66.
[4] Khan U, Baig S, Mughal M J. Performance comparison of Single Carrier Modulation with frequency domain equalization an OFDM for wireless communications[C]∥2009 International Conference on Emerging Technologies. IEEE, 2009: 297-300.
[5] Sari H, Karam G, Jeanclaude I. Transmission techniques for digital terrestrial TV broadcasting[J]. IEEE Communications Magazine, 1995, 33(2): 100-109.
[6] Benvenuto N, Falconer D, Dinis R, et al. Single carrier modulation with nonlinear frequency domain equalization: An idea whose time has come—Again[J]. Proceedings of the IEEE, 2010, 98: 69-96.
[7] Benvenuto N, Tomasin S. On the comparison between OFDM and single carrier modulation with a DFE using a frequency-domain feedforward filter[J]. IEEE Transactions on Communications, 2002, 50(6): 947-955.
[8] Benvenuto N, Tomasin S. Iterative design and detection of a DFE in the frequency domain[J]. IEEE Transactions on Communications, 2005, 53(11): 1867-1875.
[9] Zhang C, Wang Z, Pan C, et al. Low-Complexity Iterative Frequency Domain Decision Feedback Equalization[J]. IEEE Transactions on Vehicular Technology, 2011, 60(3): 1295-1301.
[10]顾晨阳, 杨瑞, 盛文钦, 等. 单载波频域均衡系统中一种简化的IBDFE算法[J]. 电子学报, 2014, 42(9): 1699-1704.
Gu Chenyang, Yang Rui, Sheng Wenqin, et al. A Simplification of IBDFE Algorithm in Single Carrier Frequency Domain Equalization System[J]. Acta Electronica Sinica, 2014, 42(9): 1699-1704.(in Chinese)
[11]Chang B S, Del Monego H I, Munaretto A, et al. A simplified widely linear iterative equalizer for sc-fde systems[C]∥2017 Wireless Days. IEEE, 2017: 159-162.
[12]曾娟, 王颖, 李晓娜, 等. 基于频域迭代判决反馈均衡的低复杂度FTN接收机[J]. 通信学报, 2017, 38(4): 190-198.
Zeng Juan, Wang Ying, Li Xiaona, et al. Low Complexity FTN Receiver Based on Frequency Domain Iterative Decision Feedback Equalization[J]. Chinese Journal of Communications, 2017, 38(4): 190-198.(in Chinese)
[13]Zeng J, Wang Y, Zhang X, et al. Reduced-complexity IBDFE for faster-than-Nyquist communication systems[C]∥MILCOM 2016-2016 IEEE Military Communications Conference. IEEE, 2016: 654- 659.
