1 引言
窗函数法是优化设计滤波器的有效方式,使用窗函数对理想滤波器截短时,会造成Gibbs效应,主要表现为期望得到的频率分量泄露、期望滤除的频率分量引入及边界处理的模糊[1-3]。为了降低通带及阻带内的波动和过渡带的宽度,对窗函数的基本要求是其主瓣能量大且宽度窄,此外,窗函数还应满足下列要求[4- 6]:(1)窗函数是非负的实偶函数;(2)各点幅值从原点处递减;(3)窗函数频谱均值为1。衡量窗函数优劣有三个常用性能参数:(1)3 dB带宽B(Δω);(2)最大旁瓣峰值A(dB);(3)旁瓣衰减速度D(dB/oct)。性能较好的窗函数应是B窄,A低和D高。基于此标准,研究者提出了多种设计窗函数的方法如基于Extended Kalman Filter的算法[7],边带衰减算法[8],Legendre 多项式算法[9]等。在文献[7]中,作者在FIR滤波器中使用一种新型的窗函数以改善FIR滤波器性能。该窗函数是具有等波纹的形状,当阶数较高时,过渡带宽度逼近汉明窗且旁瓣衰减低于汉明窗5~12 dB左右。文献[8]中,通过两个γ函数的乘积获得参数可控的窗函数,通过调节连续参量α可以控制过渡带宽度和旁瓣衰减,并且精确地给出旁瓣衰减相对于α的函数,而汉宁窗是α=2的特殊情形。在文献[9]中,提出了一种基于Legendre多项式的窗函数设计方法,并且证明了过渡带宽度与旁瓣衰减受控于多项式的两个参量。这些算法在三项指标中部分或者全部有所改善,但是由于这些基于FIR设计思想的窗函数改善仍然是从时域上来进行逼近抽样点,因此对频率尤其是边界频率不易控制。此外,窗函数设计与滤波器相关,不同类型的滤波器,其窗函数设计方法也应不同。
全相位数字滤波器是一种时频特性良好的滤波器,按照窗的数量分成无窗、单窗和双窗系统且与全相位等效的FIR结构中卷积窗为双窗卷积[10]。数据窗在FIR滤波器窗函数设计中起着重要作用,它的性能好坏直接影响着滤波器的过渡带宽度和衰减大小。通过改善基窗函数,可以进一步改善全相位滤波器性能。
2 全相位卷积窗
全相位数字滤波器结构[11]如图1所示。
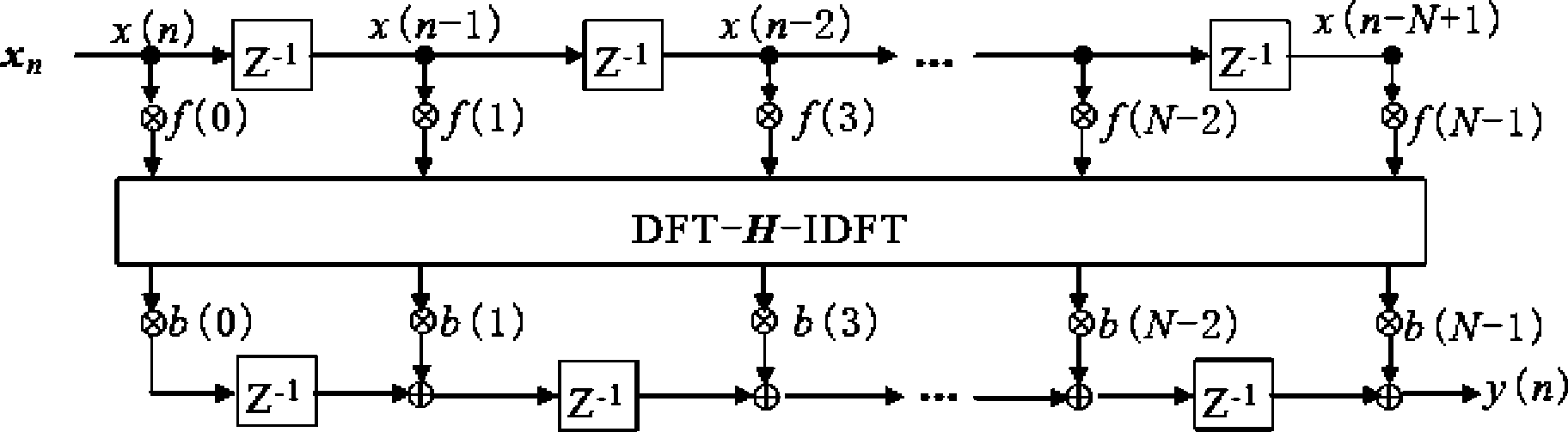
图1 带双窗的全相位滤波器
Fig.1 All-phase Digital Filter with double-window
图中xn是输入信号序列, f是前基窗,b是后基窗,DFT/IDFT表示傅里叶/反傅里叶变换,H是系统特性序列,y(n)表示系统在n时刻的输出,它由下式(1)求出。
(1)
上式中,
(2)
CN等于全相位数字滤波器前窗和后窗镜像的卷积即卷积窗。当前后窗均为矩形窗、前或后窗为矩形窗、前后窗均不为矩形窗时对应的全相位滤波器称为无窗、单窗和双窗系统。与图1等效的FIR结构如下:
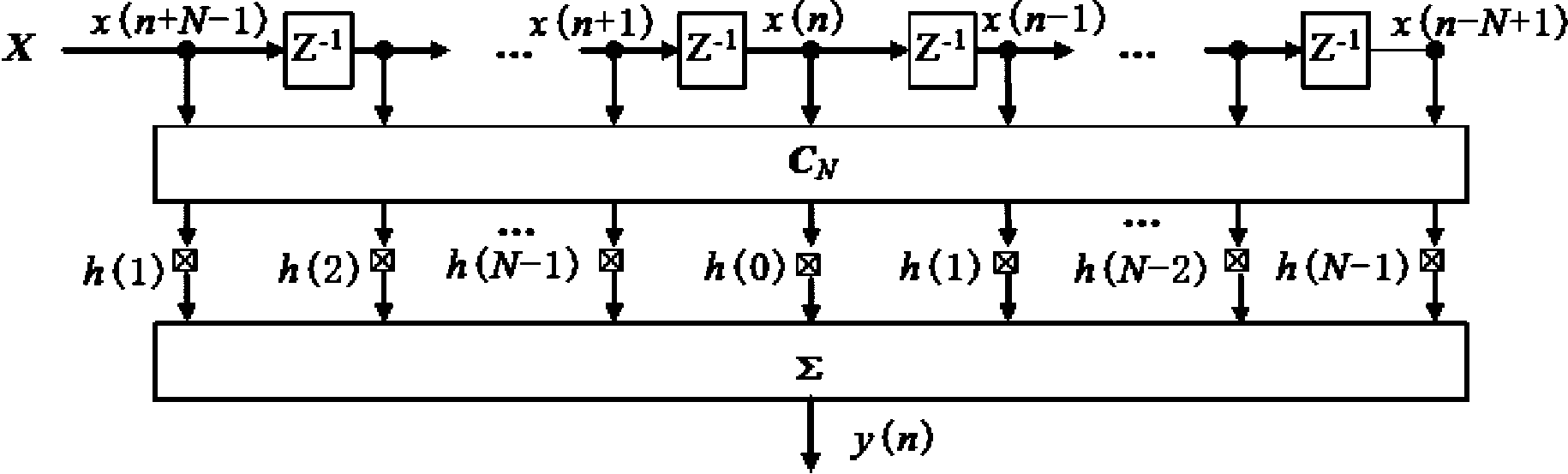
图2 与图1系统等效的FIR滤波器结构
Fig.2 Equivalent FIR structure to All-phase System
对(1)两端进行傅里叶变换并经过整理得到系统传输特性:

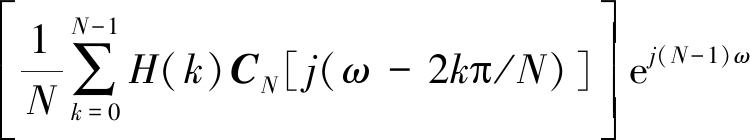
(3)
(3)表明,全相位频率响应函数幅频特性等于频率采样向量的离散卷积,即全相位滤波器的频率响应函数可通过频率采样值内插实现,其内插函数为卷积窗的频谱函数。且可以证明[12],系统1具有线性相位的充要条件是H和前/后窗均为中心对称或前窗与后窗相等。
2.1 无窗全相位系统
这时f=b=RN,即前后窗均为长度为N的矩形窗,卷积窗可以表示如下:
cN(n)=RN(n)⊗RN(n) n∈[-N+1,N-1]
(4)
结合(2)和(4)得到移位的卷积窗谱函数(归一化)如下:
(5)
显然,无窗全相位系统的卷积窗是归一化插值函数的平方,这样使旁瓣的能量进一步降低,从而主瓣的能量占比提高。在频率采样点处:
(6)
即无窗全相位系统幅频曲线通过传输特性H的频率抽样点,采样点之间的频率幅度由(5)插值函数确定。
2.2 单窗全相位系统
前窗或者后窗为矩形窗,假定f=RN,且后窗满足一般窗函数的3个条件,即:
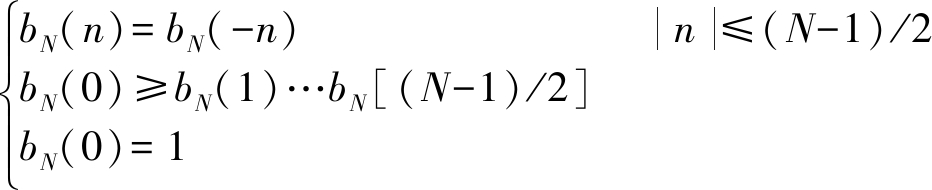
(7)
对于有限长度为N的后窗b可以表示为:
(8)
假设边界点b[(N-1)/2+1]=0。(8)说明满足条件的长度为N的窗b可以表示(N-1)/2+1个变长矩形窗之和。通过下面示意图说明:
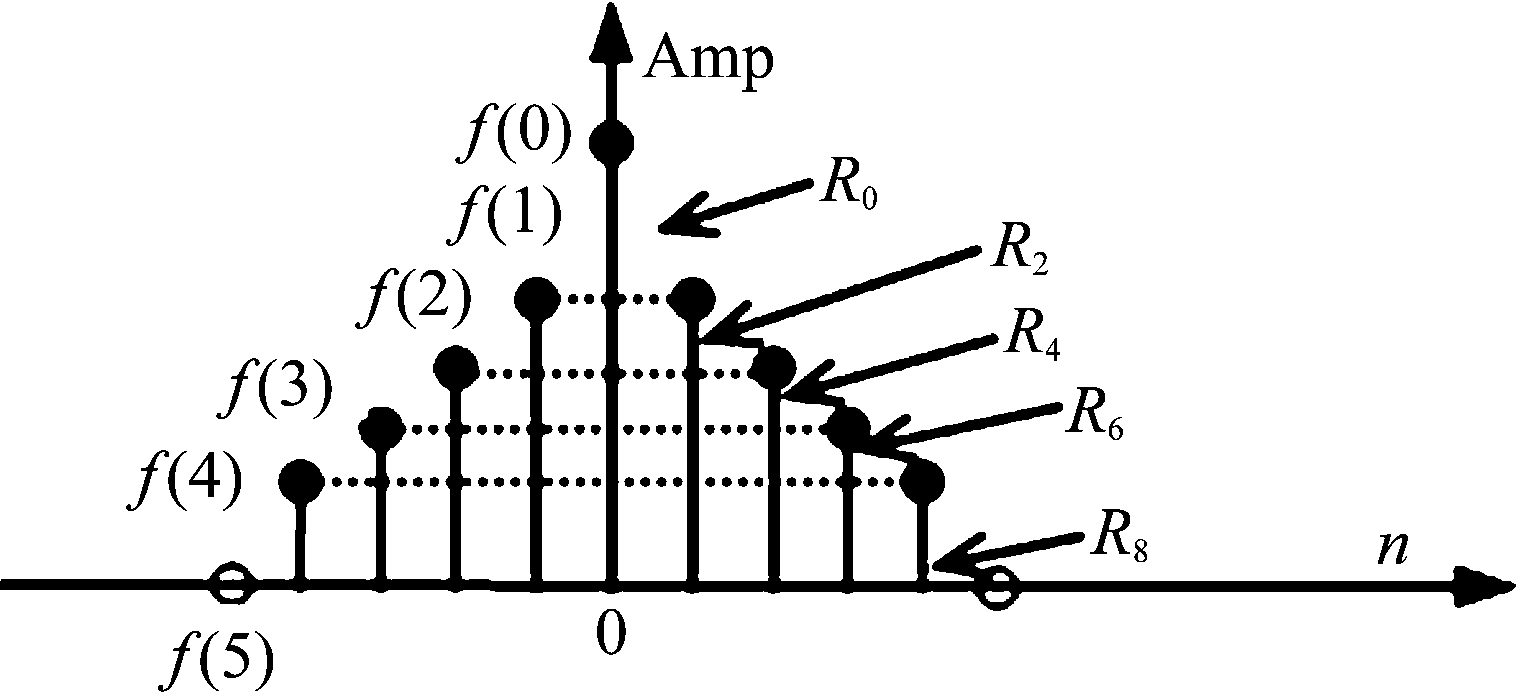
图3 后窗矩形基分解图
Fig.3 Rear Base Rectangular Window Analysis
由上图可以看出,幅度和长度均可变长的矩形窗序列{R2n(n)}中各元素相互正交,即{R2n(n)}构成非完备正交系。结合(2)和(8)得到移位的卷积窗谱函数(归一化)如下:
CN[j(ω-2kπ/N)]|ω=j·2kπ/N=
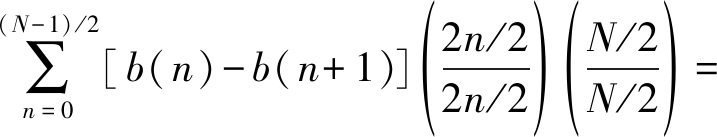
(9)
单窗系统的卷积窗是由若干个可变长度的插值函数之和构成。且增加了零值点,所以旁瓣的能量比单窗时更为降低,主瓣的能量占比提高,由于第一零值点不变仍为2π/N,所以过渡带并未变宽。在频率采样点处:
ΦS[j(ω-2kπ/N)]|ω=j·2k′π/N
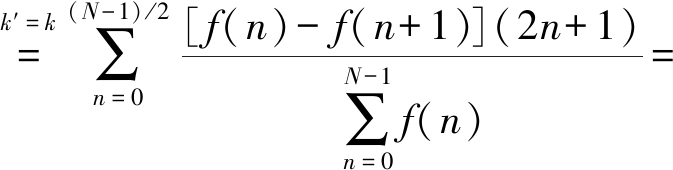

(10)
即单窗全相位系统结论同无窗系统。
2.3 双窗全相位系统
与分析单窗系统类似,可得到双窗系统移位的归一化卷积窗谱函数如下:
(11)
对于具有线性相位的系统f=b且为正交系,所以在频率采样点处:
CN[j(ω-2kπ/N)]|ω=j·2kπ/N=
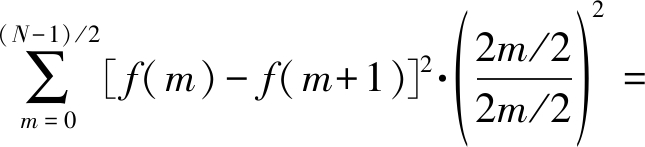
(12)
显然,(12)满足下列不等式:
(13)
基窗f不是矩形窗使得(13)不具备相等的条件。因此,双窗系统的归一化卷积窗谱在采样点处的值小于在系统取样序列对应时刻处的取样值。由双窗系统插值函数(11)可以看出,旁瓣在小于1的幅值平方作用下降低了很多,主瓣能量占比得到提升;另一方面,由(11)确定的插值函数使主瓣的宽度得到增加。
综上,无窗及单窗全相位系统对应的卷积窗构成的频率采样函数通过H各个频点,而双窗全相位系统的频率采样函数总是低于在系统取样序列对应时刻错的取样值。但是(12)表明,频点k处的幅值是与k无关的常量,因此可以通过再次归一化而得到提升。
3 基窗设计与实验
3.1 算法设计
对于满足线性条件的双窗全相位系统结合(2)可知cn=c-n,系统传输特性可以表示为下式。
(14)
其中h是系统单位冲激响应。令:
(15)
则(14)可表示为:
(16)
假定系统特性序列为H,则偏差平方和为:
(17)
上式中H是系统传输特性序列。假定对应的基窗f满足中心对称,则卷积窗满足:
(18)
不失一般性,设N为奇数(偶数可以作类似讨论),重新整理(16)如下:
(19)
式中ωk=2kπ/N,再令:
(20)
则(19)的误差可以表示为:
(21)
考虑到H的对称性,重新整理(21)可得:
(22)
上式的结果是cn的函数,为取得最小值有:
(23)
整理上式得:
(24)
用矩阵表示(24),分别记:
P=
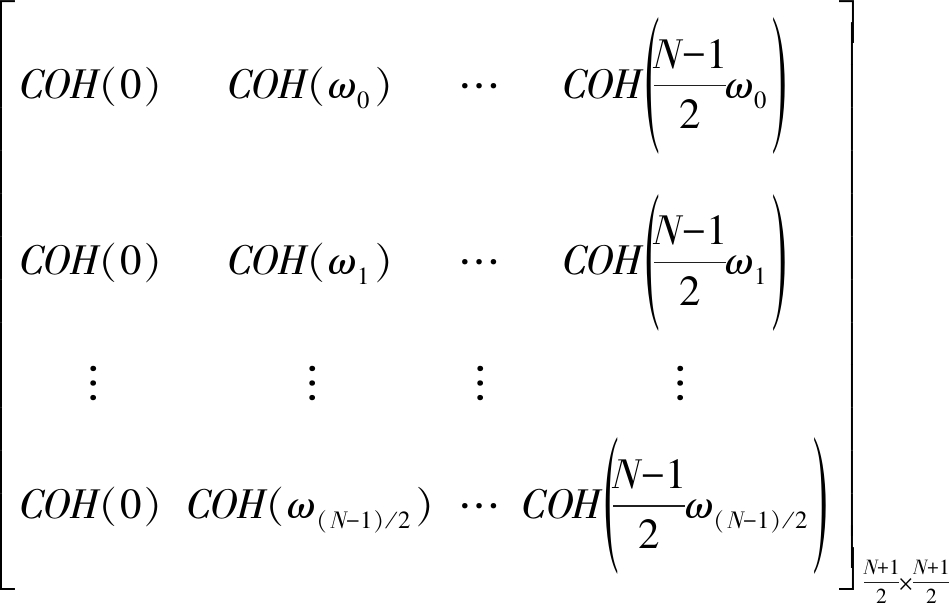
V=
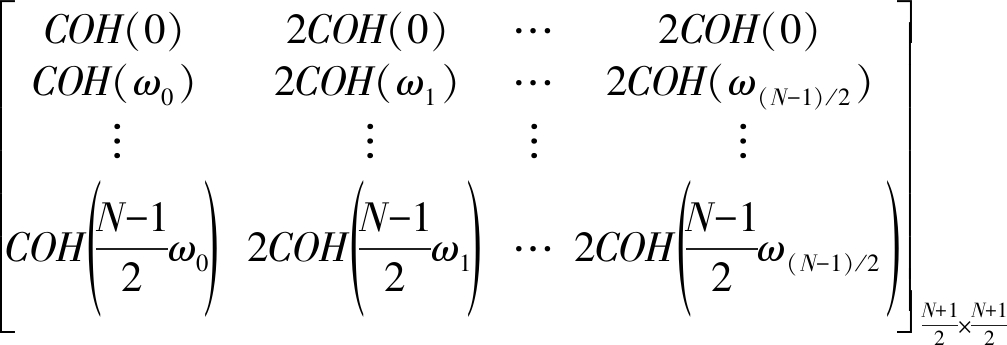
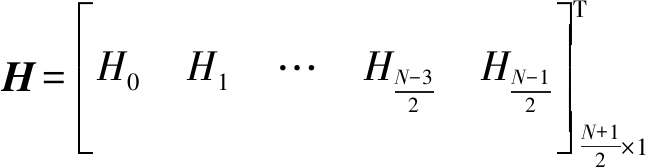
(25)
则(24)可以表示为:
VPC=VH
(26)
从而可以求得窗C:
C=(VP)-1VH
(27)
3.2 实验与讨论
取N=17,低通滤波器的截止频率为π/2,即传输特性序列H=[1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1],则频率取样点为ωk=2kπ/17,单位响应序列h=[0.52940.3188-0.0299-0.10750.03150.0660-0.0346-0.04880.03980.0398-0.0488-0.03460.06600.0315-0.1075-0.02990.3188],则按(25)构造各个矩阵代入(26)求得窗C=[0.5000 0.5000 0.5000 0.5000 0.5000 0.5000 0.5000 0.5000 1.0000 0.5000 0.5000],以窗C为基窗形成的双窗卷积窗图形及对应的系统曲线如下图4所示。卷积窗的参数B=0.2165Δω,A=-24 dB,D=-10.15 dB。
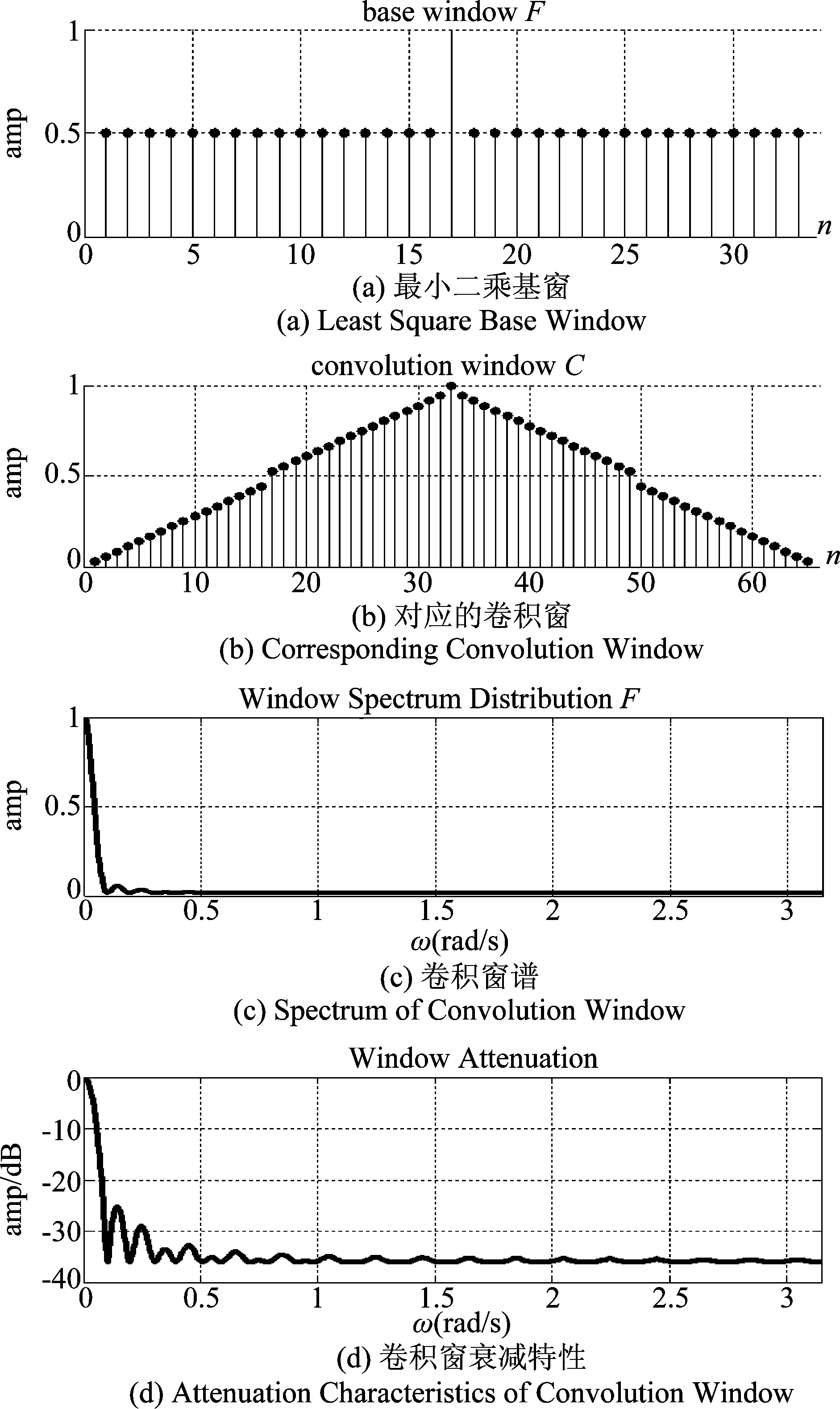
图4 实验得到的最小二乘卷积窗特性
Fig.4 Characteristics of Novel Convolution Window
作为对比,我们仿真并画出Bartlett窗的3 dB宽度B,最大旁瓣衰减和衰减速度D。
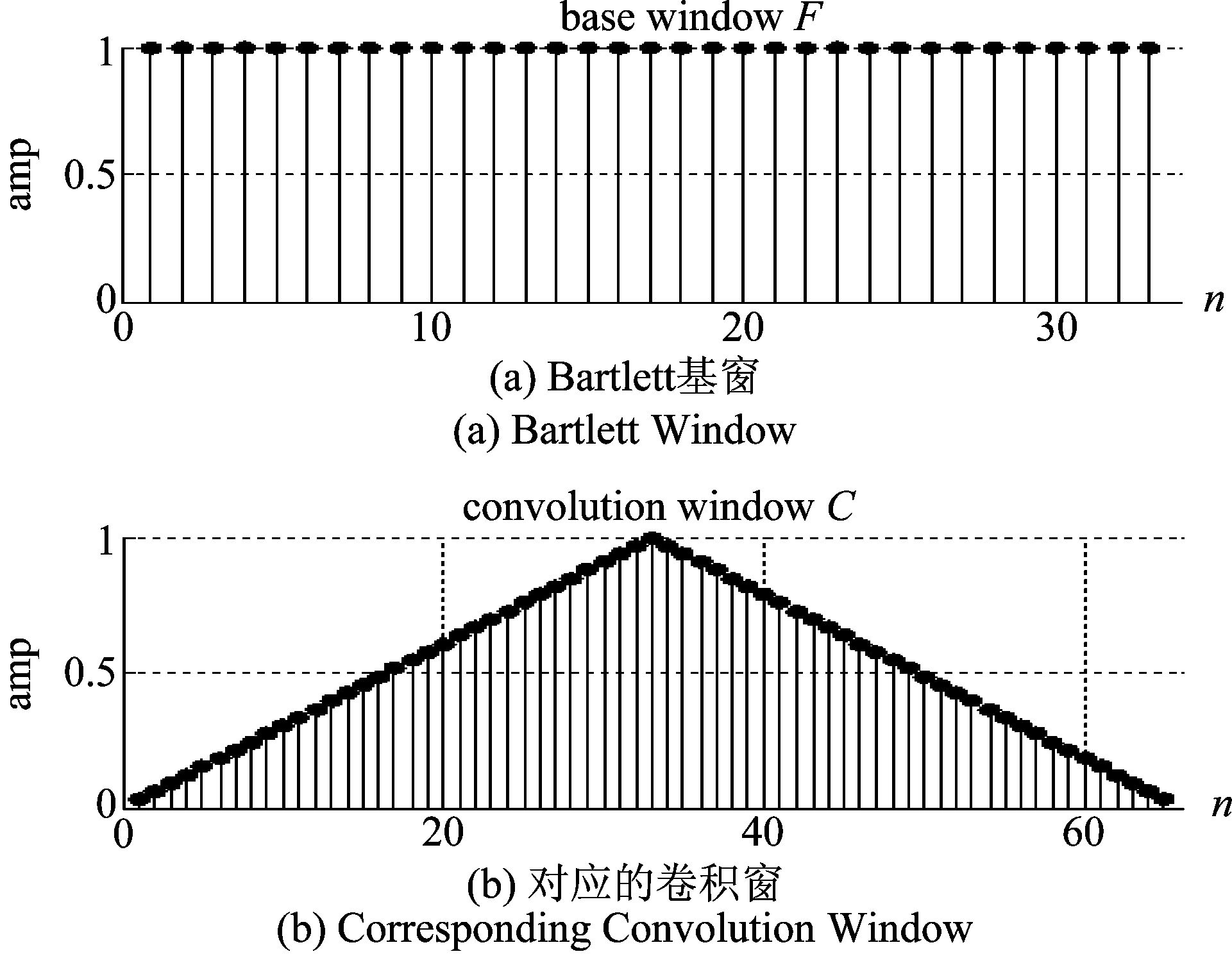
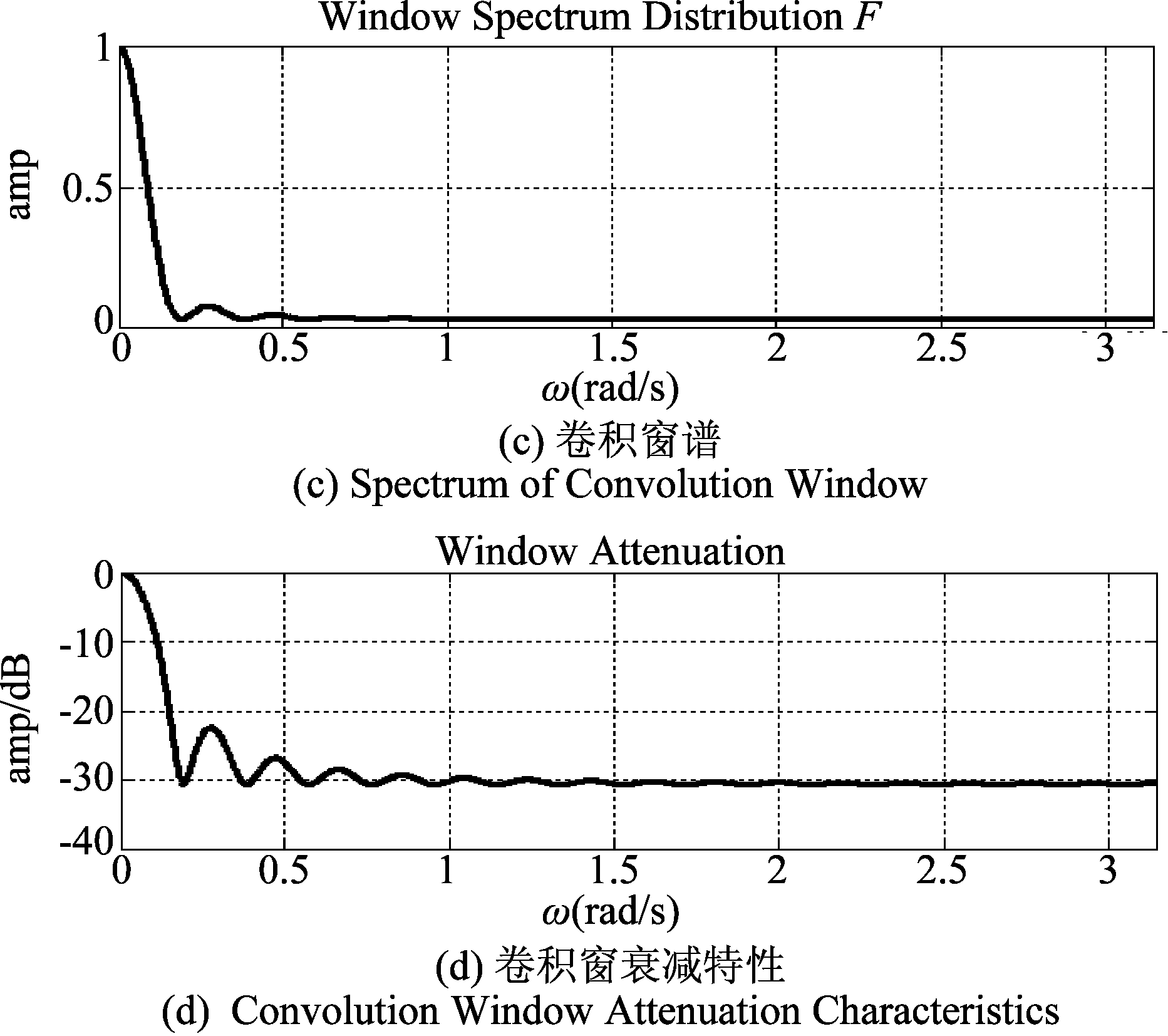
图5 Bartlett卷积窗特性
Fig.5 Characteristics of Bartlett Convolution Window
计算得到Bartlett窗的参数分别为:B=1.2837,A=-25.7022 dB,D=-25.8864 dB/oct。按照最小二乘准则得到的新型卷积窗虽然在过渡带方面得到很大得改善,但A和D都较低,但这却换来的最小的均方误差。作为对比,传统基窗的参数如下表1。
表1 七种传统窗的参数
Tab.1 Parameters of Seven Traditional Windows
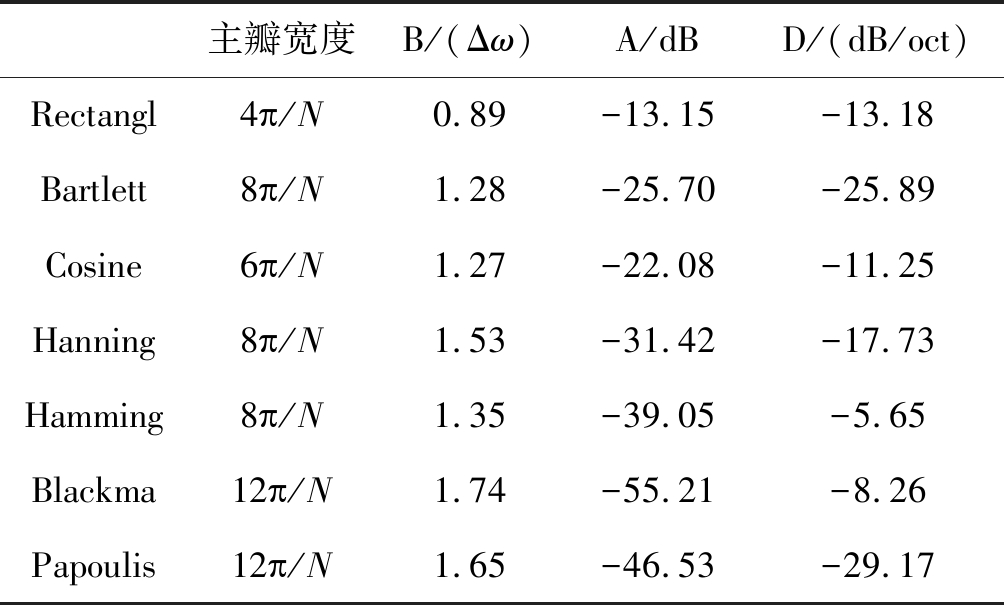
主瓣宽度B/(Δω)A/dBD/(dB/oct)Rectangl4敥/N0.89-13.15-13.18Bartlett8敥/N1.28-25.70-25.89Cosine6敥/N1.27-22.08-11.25Hanning8敥/N1.53-31.42-17.73Hamming8敥/N1.35-39.05-5.65Blackma12敥/N1.74-55.21-8.26Papoulis12敥/N1.65-46.53-29.17
可以看出,在相同的阶数情况下,该新型窗具有最小的过渡带。基于此新型窗函数,作者还设计得到了双窗低通滤波器,其传输特性曲线如下图6。
由实验结果可以看出,按照MSE准则得到的卷积窗作用于系统特性使得在通带及阻带内波较均匀分布,且通带幅度小于1而阻带幅度大于0,比较好的效果是系统整体谱泄露误差为0.2117,比最优的Bartlett窗泄露误差降低2%。
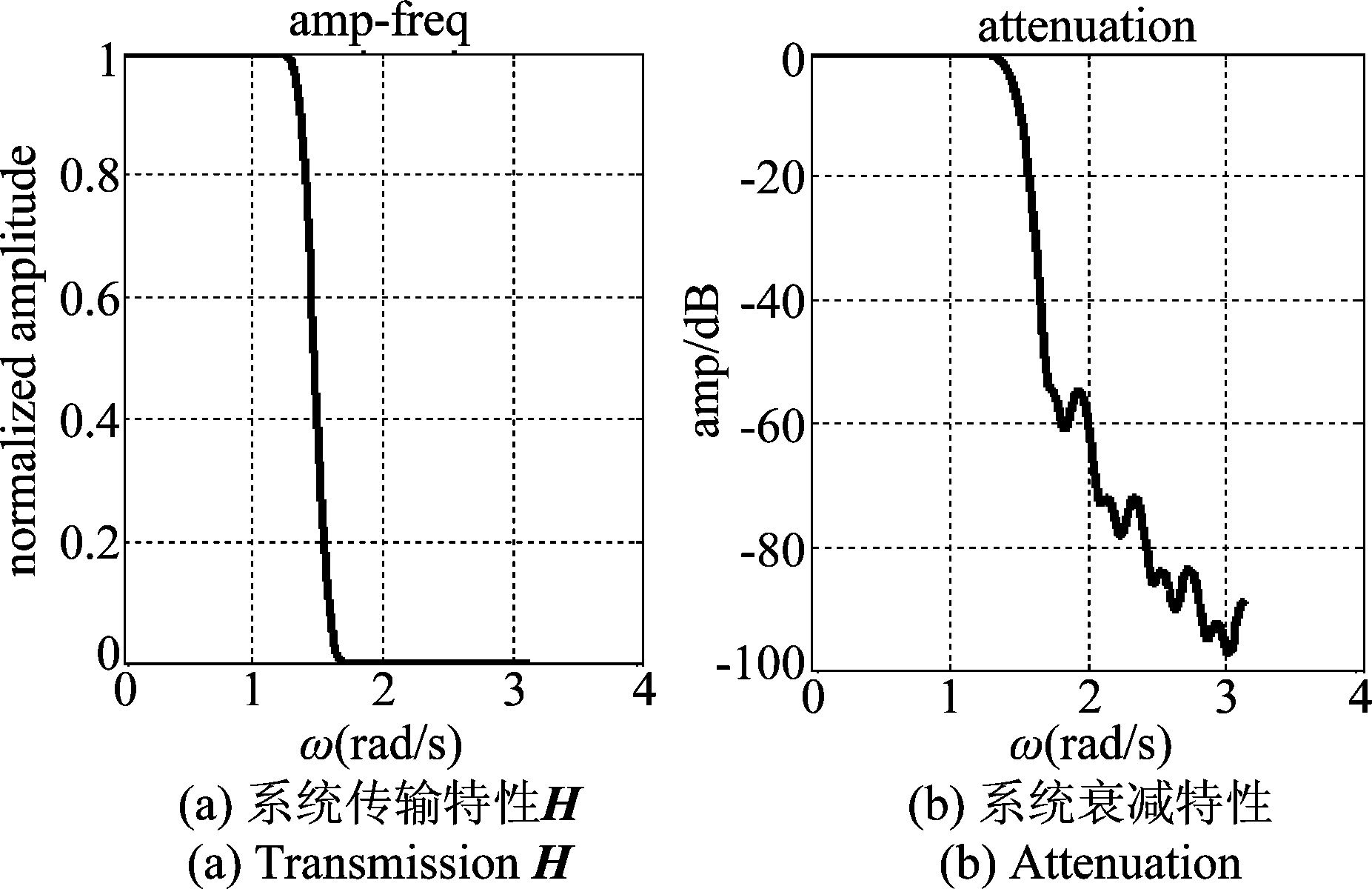
图6 系统特性
Fig.6 Transform Characteristic of System
4 结论
基于全相位数字滤波器的前后基窗卷积就是对应的FIR滤波器的卷积窗。本文在此基础上构建了无窗、单窗及双窗条件下的卷积窗特性及相应的频率抽样定理形式。双窗卷积窗具有最佳的设计性能,但引入了采样误差,实验分析得到Bartlett是具有最小误差的基窗。最后,用最小二乘法求得具备最小谱取样误差的基窗,比Bartlett降低2%。
窗函数特性B、A和D是相互制约的参数,不能同时得到改善。但是窗函数的设计是与信号的特性相关的,所以应根据信号的统计特性和传输特性的需求侧重提高某个参数以达到最佳的期望输出,如何建立具有动态调节机制的窗函数设计是今后需要研究的内容。
[1] 肖唐良. 数字信号处理中的Gibbs效应及其抑制算法的研究[J]. 电子测量技术, 2016, 39(11): 71-74. DOI:10.3969/j.issn.1002-7300.2016.11.017.
Xiao Tangliang. Study on Gibbs effect and its suppression algorithm in Digital signal processing[J]. Electronic Measurement Technology, 2016, 39(11): 71-74. DOI:10.3969/j.issn.1002-7300.2016.11.017.(in Chinese)
[2] 褚晶辉, 王晓娜, 黄翔东, 等. 一种基于全相位预处理有效消除图像Gibbs伪迹的方法[J]. 数据采集与处理, 2017, 32(5): 861- 868. DOI:10.16337/j.1004-9037.2017.05.02.
Chu Jinghui, Wang Xiaona, Huang Xiangdong, et al. A method based on full phase preprocessing to effectively eliminate Gibbs artifacts from images[J]. Data Acquisition and Processing, 2017, 32(5): 861- 868. DOI:10.16337/j.1004-9037.2017.05.02.(in Chinese)
[3] 肖唐良. 基于迭加窗的时频门抑制算法研究[J]. 中国科技投资, 2018(26): 9-10.
Xiao Tangliang. Research on time-frequency gate suppression algorithm based on overlapping Windows[J]. China Science and Technology Investment, 2018(26): 9-10.(in Chinese)
[4] 欧巧凤, 熊邦书. 窗函数的奇数阶约束问题探讨[J]. 教育教学论坛, 2018(34): 200-201.
Ou Qiaofeng, Xiong Bangshu. Discussion on odd-order constraint of window function[J]. Education Teaching BBS, 2018(34): 200-201.(in Chinese)
[5] 郭虎, 许发诺, 孙超. 用窗函数法设计FIR数字滤波器[J]. 信息与电脑: 理论版, 2017(13): 56-58.
Guo Hu, Xu Fanuo, Sun Chao. FIR digital filter design using window function method[J]. Information and Computer: Theory Edition, 2017(13): 56-58.(in Chinese)
[6] 王艳芬, 张晓光, 王刚, 等. 关于FIR滤波器窗函数设计法的若干问题讨论[J]. 电气电子教学学报, 2017, 39(2): 83- 88.
Wang Yanfen, Zhang Xiaoguang, Wang Gang, et al. Discussion on several problems of FIR filter window function design method[J]. Journal of Electrical and Electronic Education, 2017, 39(2): 83- 88.(in Chiese)
[7] Mahrokh G. Shayesteh, Mahdi Mottaghi-Kashtiban. FIR Filter Design Using A New Window Function[J]. Proceeding 6th International Conference of Digital Signal Processing, 2009: 978-983.
[8] Zierofer C M. Data window with tunable side lobe ripple decay[J]. IEEE Signal Processing Letters, 2007, 14(11): 1109-1118.
[9] Jascula M. New windows family based on modified Legendre polynomials[C]∥Poland, 2002, 19th IEEE IMTC, 2002: 553-556.
[10]Huang X, Jing S, Wang Z, et al. Closed-Form FIR Filter Design Based on Convolution Window Spectrum Interpolation[J]. IEEE Transactions on Signal Processing, March1, 2016, 64(5): 1173-1186.
[11]苏飞, 孙杰. 全相位半带滤波器设计与实现[J]. 信号处理, 2015, 31(2): 194-200.
Su Fei, Sun Jie. Design and implementation of full phase half-band filter[J]. Journal of Signal Processing, 2015, 31(2): 194-200.(in Chinese)
[12]Huang Xiangdong, Cui Haitao, Wang Zhaohua. Mechanical Fault Diagnosis Based on All-phase FFT Parameters Estimation[C]∥2010 IEEE 10th International Conference on Signal Processing, ICSP2010 paper, Vol.1: 307-310.
