1 引言
近些年来,世界各国对风电产业的投资日益扩大,全球风力发电累计装机容量呈指数上升趋势[1]。随着全球范围内的风电场的大规模建设,风电场会对空中交通管制系统、防空预警监视系统、气象观测系统等一次或二次雷达设备产生严重的影响[2- 6]。当雷达波束照射到风轮机叶片上时,风轮机叶片旋转产生微多普勒现象,因此风轮机叶片回波被当做一种杂波(Wind Turbine Clutter,WTC)。这些杂波具有目标信号相似性,会造成虚警问题。WTC还可能干扰或者掩盖目标信号,产生掩蔽和阴影效应,造成雷达系统的探测盲区。另外,风轮机杂波还会导致目标检测跟踪性能的下降。
WTC的干扰问题目前已经成为各国雷达系统的难题。文献[7]提出对风轮机叶片加涂纳米吸波材料,以减小风轮机叶片的RCS达到抑制杂波产生的效果,但是该方法不仅成本较高,还增大了风轮机叶片重量,将造成电能转化率降低。文献[8]通过部署补盲雷达,利用信息融合来抑制WTC。文献[9]提出通过优化风轮机的部署来减小WTC对雷达系统的影响,但是该方法依赖于地形因素。文献[10]提出在风轮机上增设应答器,通过特定方式调制雷达信号以达到抑制效果。上述方法都是通过增加设备或者优化布置来达到杂波抑制效果,对现有已部署风电场干扰问题的解决效率不高。
在信号处理层面,由于风轮机回波在频域上存在微多普勒,产生频谱展宽效应,导致这类杂波频率范围大,MTI、MTD抑制效果很差。文献[11]提出一种利用形态差异对海上微动目标信号和海杂波分别在chirp 字典和FT字典上进行稀疏表示以达到抑制海杂波的方法,但是WTC与海杂波信号有着明显差异,因此难以在chirp字典或FT字典进行有效稀疏表示。文献[12]提出对风轮机的杂波进行重构,然后从回波信号中将重构的杂波滤除,既保留了目标信号,又实现了对WTC的抑制。但是,以上几种重构方法为了保证精确度需要生成数目庞大的固定原子字典,运算量大、字典冗余度高但重构精确度较低。因此,本文提出了一种对WTC进行栅格化稀疏重构抑制的方法。该方法依据风轮机杂波信号形态特征对其进行重构,通过栅格化将字典“由粗到细”逐级生成、逐级更新,再利用OMP算法匹配最佳原子实现对杂波信号的重构来实现杂波抑制。理论分析和仿真结果均表明该方法可以实现对杂波信号的精准重构,可以达到对风轮机杂波有效抑制,且该方法具有重构精度高、运算量小和字典冗余度低的特点。
2 风轮机杂波信号建模分析
WTC主要由桅杆、引擎舱等产生的静态杂波和由叶片旋转产生的动态杂波两部分组成。其中静态杂波可通过MTI滤波器滤除,因此本文只针对由风轮机叶片产生的动态杂波进行研究。为简化分析,假设风轮机与雷达处于同一个平面(若不在同一平面,可将其投影到同一平面,具体流程见附录)。以风轮机旋转中心为原点O,建立如图1坐标系。其中,B为雷达站,r为雷达视线(LOS),θ为叶片旋转角,R为雷达中心距离风轮机旋转中心距离,li为风轮机上散射点距离叶片旋转中心的长度,li≪R。
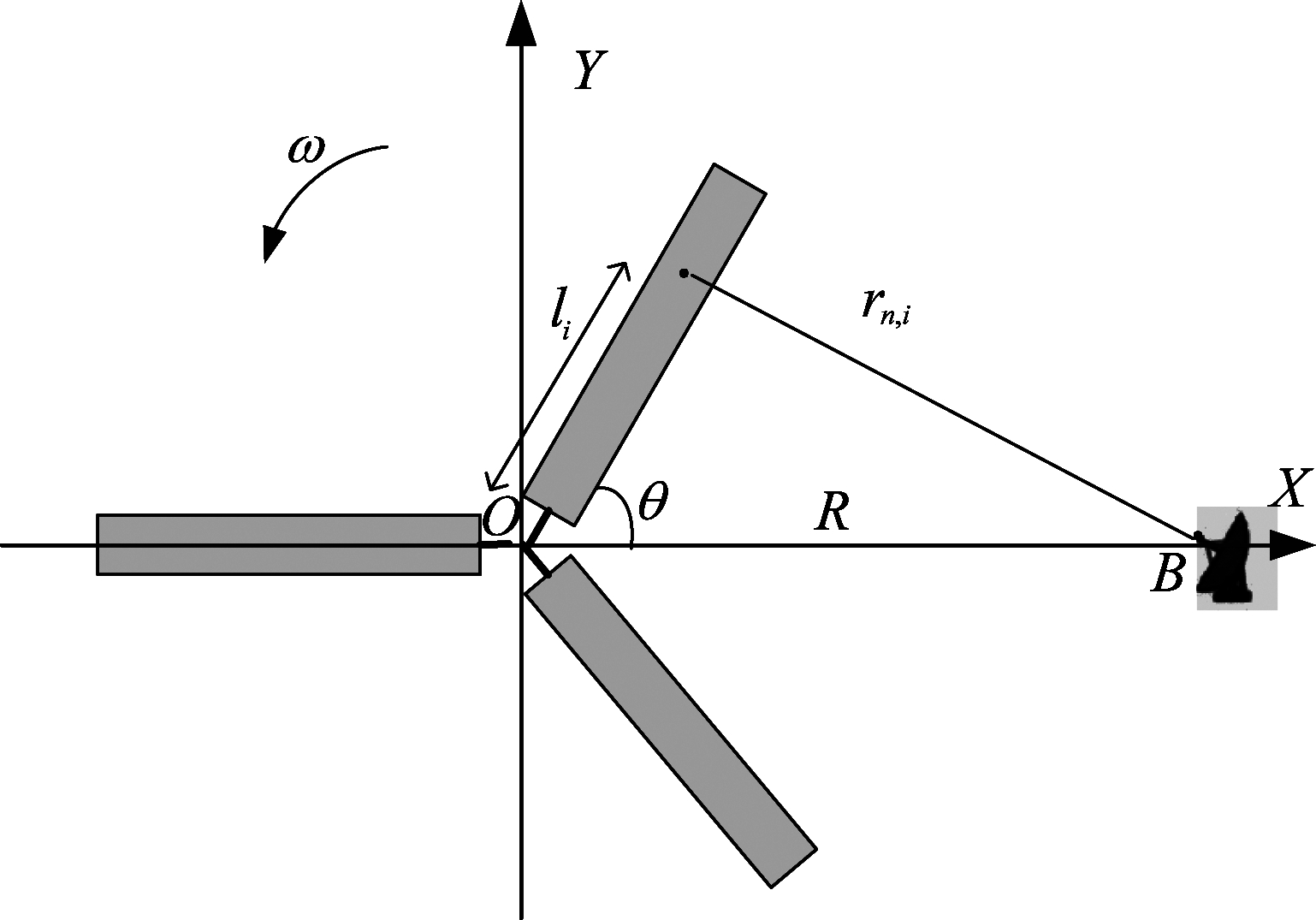
图1 风轮机杂波模型
Fig.1 Wind turbine clutter model
假设雷达发射信号p(t)=exp(-j2πfct), fc为载频,则风轮机散射点的基带回波信号可表示为:
(1)
其中N为叶片数,M为单个叶片上的散射点数,σn,i为第n个叶片上第i个散射点的散射系数,rn,i(tm)为第n个叶片上第i个散射点到雷达的距离。
由于li≪R,则雷达到叶片散射点间的距离rn,i可近似为[13]:
(2)
其中,根据空间几何关系可知:
cos θ(t)=cos(θ0+ωt+2π(n-1)/N)
(3)
θ0为该叶片初始旋转角,ω为叶片旋转角速度,单位为rad/s。
假设风电场附近有一以径向速度νtar匀速运动的目标,则目标的回波基带信号为[14]:
star(t)=σtarexp(j4π(Rtar-νtart)/c)
(4)
式中σtar为目标散射系数,Rtar为目标初始距离。
因此,混合回波信号可表示为:
σtarexp(j4π(Rtar-νt)/λ)+n(t)=
σtarexp(j4πRtar/λ)·exp(-j2πfd-tart)+n(t)
(5)
式中,exp(j4πR/λ)和exp(j4πRtar/λ)为常数项,exp(-j4πlicos θ(t)/λ)和exp(-j2πfd-tart)为多普勒项,分别包含了风轮机和目标的多普勒信息,其中目标多普勒fd-tar=2νtar/λ,σw为整个风轮机叶片的等效散射系数,n(t)为线性噪声。
由多普勒项可知,风轮机散射点的多普勒频率可以表示为:
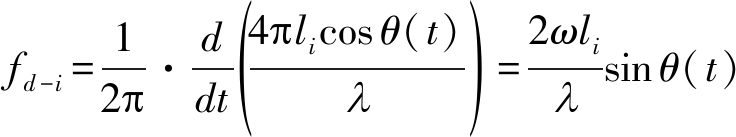
(6)
由式(6)可知,散射点的微多普勒频率受正弦函数调制,且正弦周期与风轮机的旋转周期一致,同一叶片上的散射点都具有相同的初相,但是不同叶片的微多普勒具有不同的初相[15]。同时,当|sin θ(t)|=1且li=L时,风轮机瞬时多普勒频率达到最大值,此时:
fd-max=2ωL/λ
(7)
因此叶片的多普勒频率在[-fd-max, fd-max]之间变化。
假设风轮机旋转角速率为ω=π rad/s,风轮机叶片为L=20 m,雷达波长为λ=0.3 m,脉冲重复频率为1000 Hz,则风轮机瞬时多普勒频率最大值为fd-max=418 Hz,因此风轮机多普勒频率在[-418 Hz,418 Hz]之间,并且其变化规律收到正弦函数调制。由于该风轮机多普勒频率展宽,其频率占据了脉冲重复频率的92%。而假设某目标径向速度为60 m/s,其多普勒频率fd-tar为400 Hz。目标频率落在风轮机多普勒频率范围内,此时目标频率与风轮机频率混叠,无法从频谱图上将两者区分,因此常规的频域滤波方法如MTI等无法有效抑制WTC。同时,尽管叶片旋转速率很低,但是其叶尖速度为62.8 m/s,与该运动目标速度接近,处于飞机的速度范围内[16],因此风轮机叶片还可能造成雷达的虚警。
3 栅格化稀疏重构WTC的原理
基于栅格化稀疏重构风轮机杂波的原理,首先通过风轮机回波和目标信号的信号形态差异性,构建基于WTC特征的栅格化过完备字典;然后将混合回波信号投影到字典各原子上,通过OMP算法选择最佳原子线性组合,实现对杂波的稀疏重构,通过混合信号滤去稀疏重构的WTC,进而得到目标信号,完成杂波抑制,处理基本流程如图2。
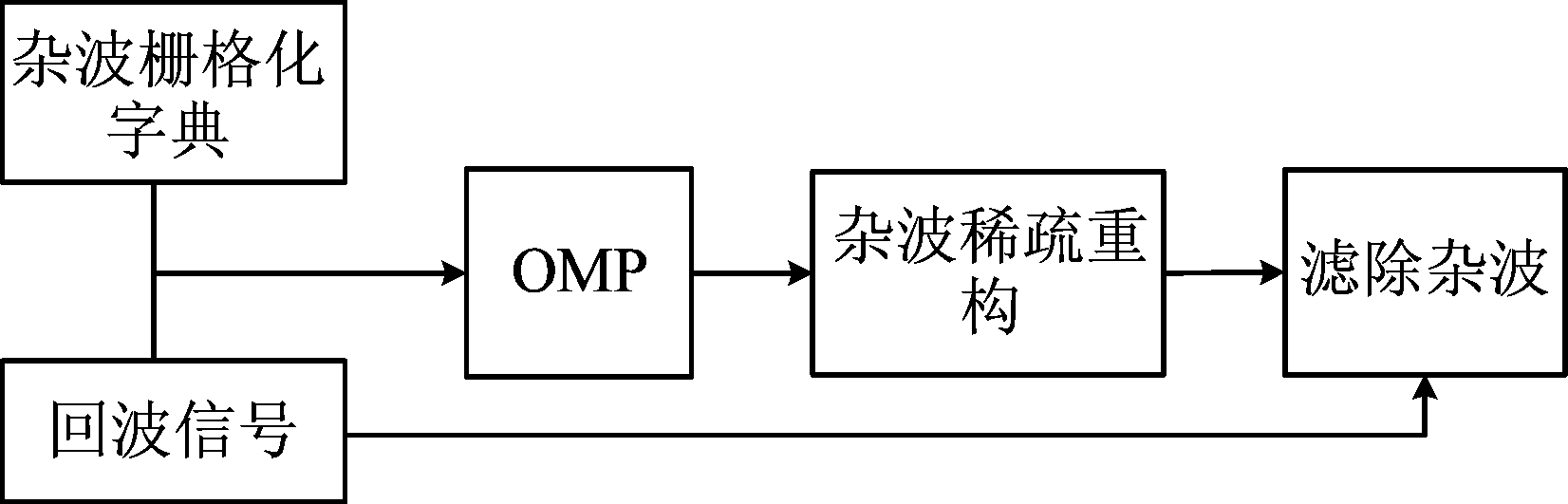
图2 稀疏重构WTC抑制处理流程图
Fig.2 WTC suppression process of sparse reconstruction
3.1 栅格化字典构造
字典的精准度直接关系到稀疏重构结果的好坏。由式(1)、(2)可知,风轮机杂波信号sblade与风轮机叶片长度L、叶片转速ω、叶片初始旋转角θ0+2π(n-1)/N有关。且根据第2节分析可知风轮机回波信号具有微多普勒特征,其频率随时间变化受到正弦函数的调制,而目标信号不具备这种时频变化特征,因此可以根据WTC信号的微动特征构造过完备字典原子[15]:
d(t)=sin c(Acos(υt+μ))exp(iAπcos(υt+μ))
(8)
其中A=2L/λ为尺度因子,υ为旋转因子,与风轮机转速ω有关,
为相位因子,与风轮机叶片初始旋转角有关。D={dk}为基于风轮机杂波信号的过完备字典,dk原子的长度与信号长度相同。一般地,为了满足稀疏分解的条件,需要对dk作进一步归一化处理。
对字典进行过完备构建,实际上是对参数{L,ω,θ}离散化表示。对参数{L,ω,θ}的离散化越精细,其与风轮机杂波信号的匹配度越高,但是原子数目越多,字典也会越大,收敛速度越慢,对运算内存也提出了更高的要求。
本文提出一种栅格化字典(Rasterized Dictionary, RD)构造方法,栅格化的本质也是离散化。该方法采取对相关参数均匀离散化{iΔL, jΔω,kΔθ},1≤i≤M1, 1≤j≤M2,1≤k≤M3,离散的栅格步长为Δdλ{ΔL,Δω,Δθ}。基于OMP算法可选出本级栅格字典中与WTC信号匹配度最高的原子dr1,当残差大于设定阈值T时,可在该原子基础上进行新一级的栅格字典重构更新。在区间dr1±Δdλ内,离散的栅格步长更新为
Δω/M2,Δθ/M3},重构新一级的栅格字典Dnew,在新的字典上再进行进一步的OMP算法,找出Dnew中与风轮机杂波信号最匹配的原子,循环往复,直到匹配的原子的残差小于设置的阈值T,如图3所示。此时可完整的稀疏重构出杂波信号
在混合信号中滤除重构的WTC信号,即可达到抑制的结果。其中,阈值T的选取会关系杂波重构误差的大小,若阈值T选取过大,会造成WTC重构不完全,误差过大而无法有效抑制WTC;阈值T选取过小,会造成过度迭代,影响算法收敛速度。因此,阈值T选取要适当选小,并可以结合设置栅格化级数上限来具体实施。
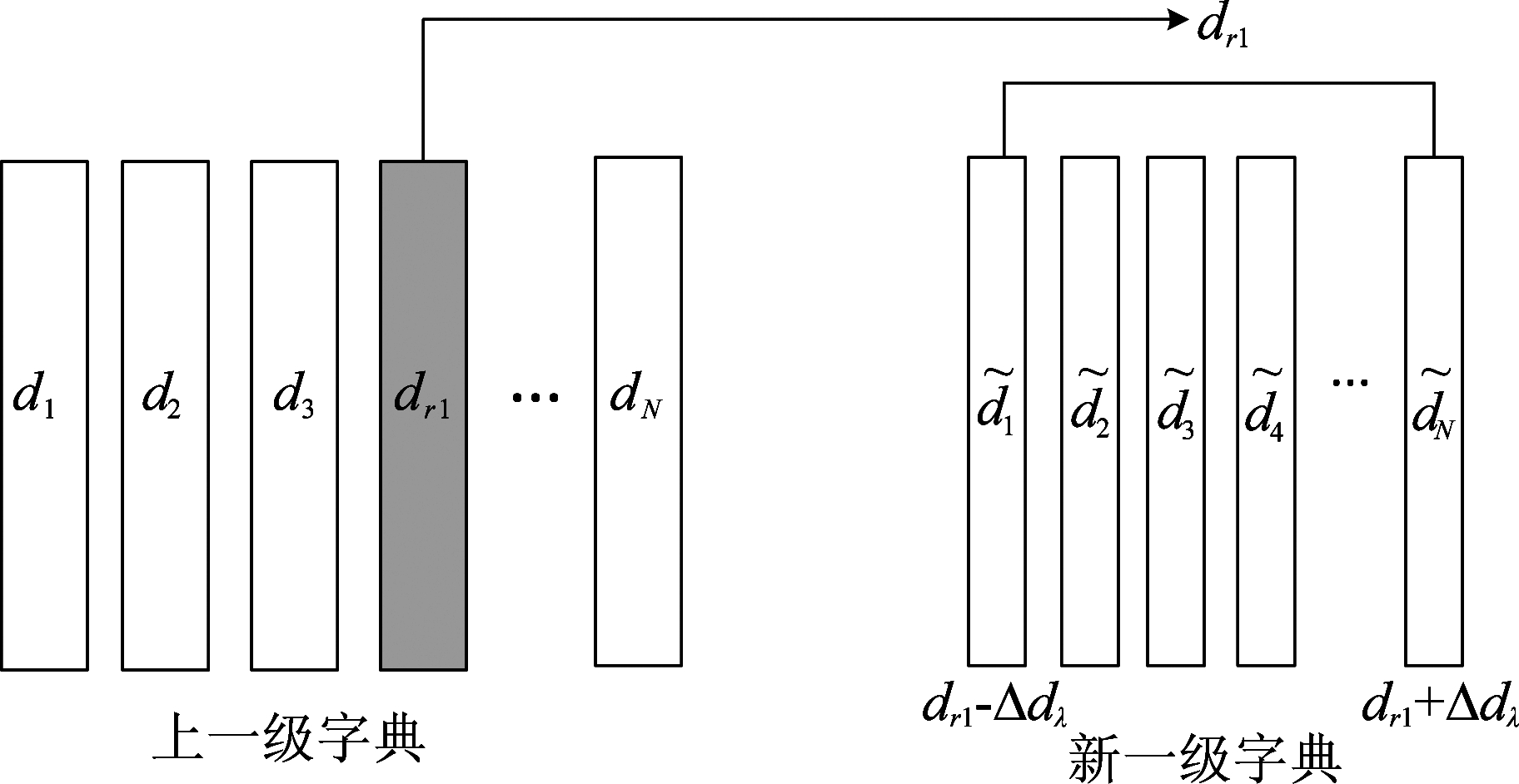
图3 栅格化字典构造原理
Fig.3 Construction principle of RD
3.2 OMP算法
OMP算法通过对信号s(t)在过完备字典D{d1,d2,d3,…,dK}上进行分解,每一步分解都对所选择的原子进行正交化处理,这使得在相同的精度要求下,OMP算法的收敛速度要比MP算法更快[17],而且被匹配过的原子不会被再次匹配。利用OMP算法选择的与信号s(t)最匹配的原子,可以构建出一个稀疏逼近,通过求出残差信号后继续选择与残差最匹配的原子,反复迭代直到达到停止准则。因此,信号s(t)可以由每次迭代的原子以及残差来线性表示:
(9)
其中αr为稀疏系数,dr为OMP选择的匹配原子,sr为残差。
由于本文仅是对WTC信号进行重构,因此其稀疏度spark(s)=N,因此WTC信号可以进行稀疏表示。另外,只有混合回波信号内的WTC信号部分能够在特定过完备字典上稀疏分解,因此目标信号和噪声信号作为残差被保留下来。
OMP算法步骤如下[18]:
Step 1 初始化残差sr0=s;
Step 2 在字典D中选择与残差sr0内积绝对值最大的原子,该原子即为最匹配的原子,表示为dr1;
dr1=arg{sup|〈s,dk〉|}
(10)
Step 3 每一个匹配原子实际为一个单位列向量,将所选择的匹配原子作为列组成匹配原子矩阵Φt,Φt所在空间的正交投影矩阵为:
(11)
其中,pinv为矩阵求伪逆,通过从sr0减去其在Φt所张成空间上的正交投影得到新的残差sr1
sr1=sr0-P0sr0=(I-P0)sr0
(12)
Step 4 更新残差,迭代执行(2)、(3)步
srm+1=srm-Pmsrm=(I-Pm)srm
(13)
Step 5 当迭代次数大于N,跳出迭代,计算稀疏系数矩阵。
采用栅格化原子字典构造可以将原子数一直控制在K=M1·M2·M3个,并不会因为原子划分更加细分而增加原子个数,而且栅格化原子构建实质上是对目标参数的迭代匹配,每一次构建新一级字典都建立在上一级字典所匹配的最佳原子的基础上,在不增加运行内存的前提下实现了可原子更精准的构建,从而实现了对WTC更加精准的稀疏重构,可以达到更好的杂波抑制效果。
从上述分析可知,通过分析风轮机杂波信号与目标信号间的特性与区别,构造特定WTC栅格化字典,再通过OMP算法匹配最佳原子实现对WTC信号的稀疏重构,从而可以达到抑制杂波、保留目标信号的目的,其重构整体流程图如图4所示。循环1生成本级栅格字典,循环2在本级栅格字典中匹配最佳原子,循环3实现重构风轮机杂波信号的稀疏重构。
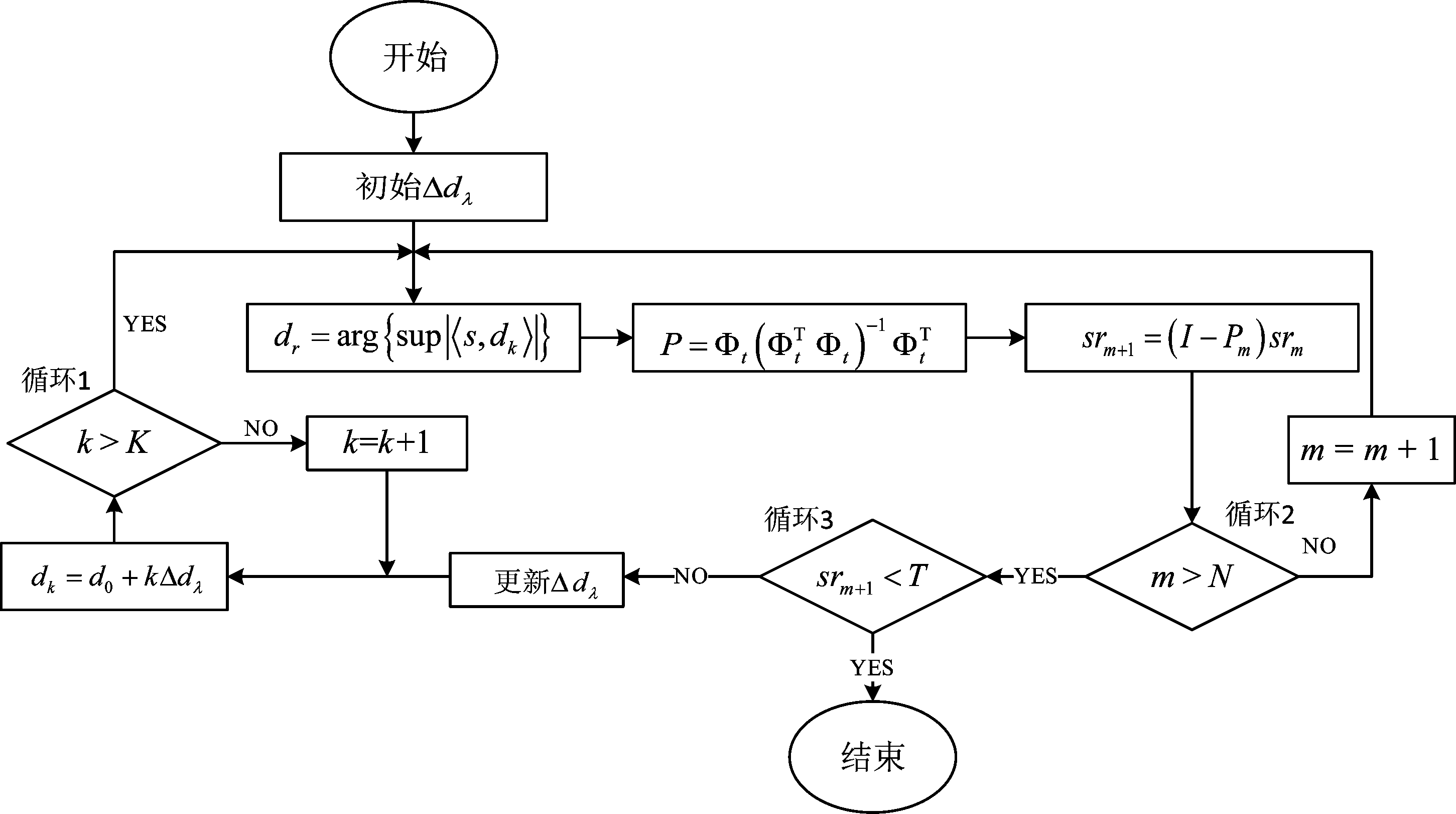
图4 WTC重构流程图
Fig.4 Reconstruction flow chart of WTC
4 仿真结果及分析
为了验证本文方法对风轮机杂波信号的抑制作用,本文仿真参数设置如表1。其中雷达相关参数依据某型引进中程空管雷达相关参数,假设信号在传播过程中不受地球曲率影响。
表1 参数设置
Tab.1 Parameter settings
参数值单位脉冲重复率1000Hz观测时间2s载波频率1GHz叶片数3个叶片长度20m风轮机距离10km目标距离9.9km目标速度30m/s杂噪比30dB信杂比-20dB
4.1 回波信号建模
设定叶片转速为ω=3.1428 rad/s,叶片初始相位为θ0=0.141 rad,回波信号建模仿真如图5所示,图(a)为回波频谱图,图(b)为回波时频图。
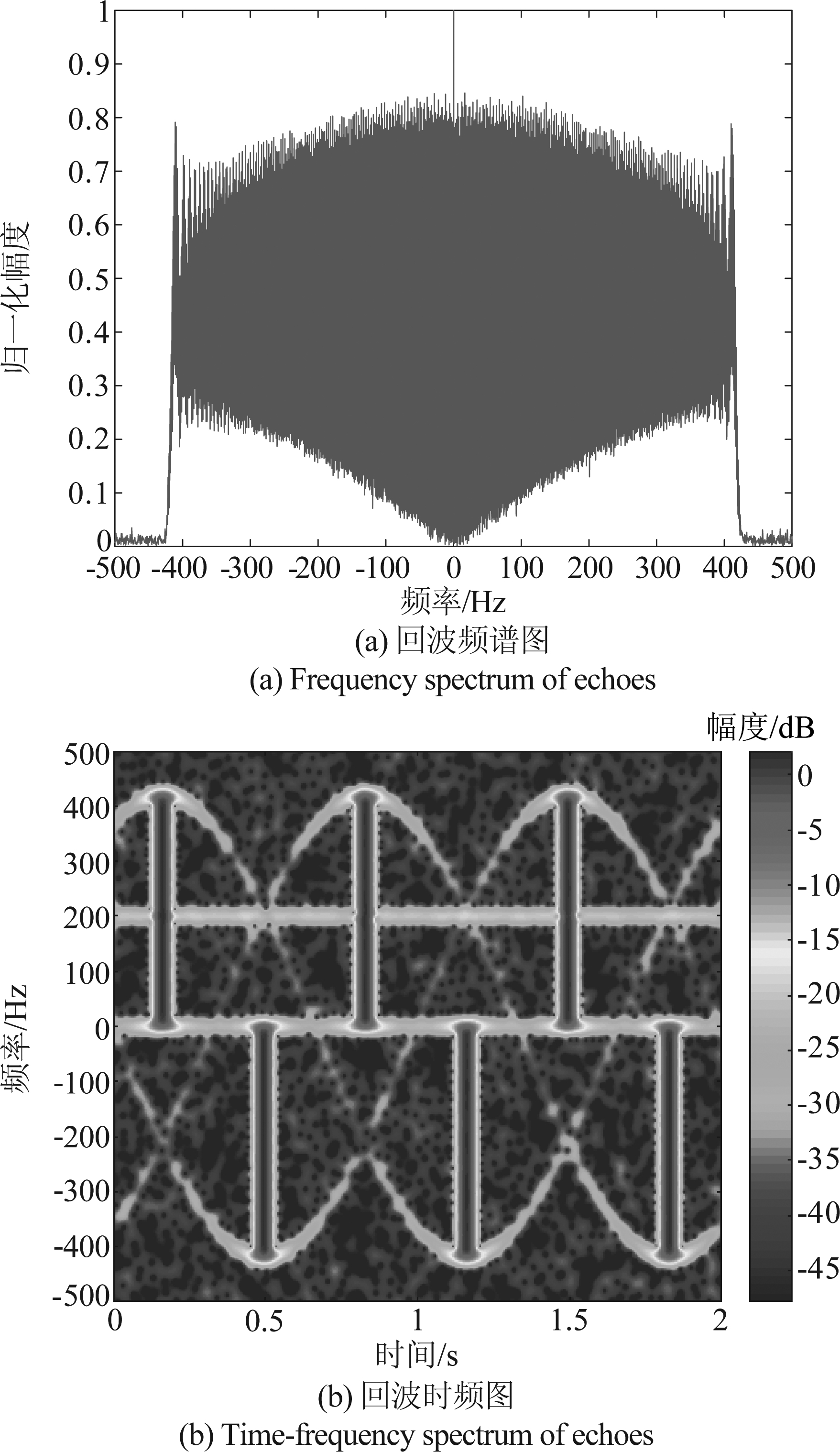
图5 回波仿真结果
Fig.5 Simulation results of echoes
从图5(a)可以看出风轮机杂波频谱图是一个在[-418 Hz,418 Hz]的频率带,目标回波频率被淹没在风轮机杂波频率中,无法在频域将目标频率与风波频率有效分离。图(b)可以看出WTC信号与目标信号在时频域的区别,WTC受到微动特征影响其频率随时间受到正弦函数调制,且在叶片与雷达视线垂直时产生“闪烁”,在观察时间内3个风轮机叶片共与雷达LOS垂直6次,因此共有6次“闪烁”,当叶片转向远离雷达方向时,闪烁频率在[-418 Hz,0 Hz]区间;当叶片转向靠近雷达方向时,闪烁频率在[0 Hz,418 Hz]内。而目标信号不存在微多普勒频率,其频率固定在200 Hz,且无正弦函数调制现象,噪声充满整个时频域。
4.2 杂波抑制性能仿真与分析
4.2.1 CFD与RD稀疏重构对比实验
对4.1中仿真回波进行杂波抑制。根据文献[5]可知,风轮机叶片一般在15～45 m之间,叶片转速不超过π rad/s。假设初始原子间步长间隔Δdλ为{1 m,π/100 rad/s,π/20 rad},根据先验信息,常规固定字典(Conventional Fixed Dictionary, CFD)和栅格化字典大小均设置为K=30×100×20个原子。WTC抑制性能仿真如图6、图7所示。图6(a)～(c)是采用CFD对WTC重构的时频图、杂波抑制后的时频图和杂波抑制后的频谱图;图7(a)～(c)是利用本文所提栅格化字典对WTC重构的时频图、杂波抑制后的时频图和杂波抑制后的频谱图。表2给出了两种方式的重构参数。
由图6可以看出,由于常规固定字典原子间隔无法达到预设理论值精度要求,利用OMP算法匹配的原子的转速和初相就近匹配,重构的杂波信号与原杂波信号存在失配现象,由失配造成的重构信号误差达到79.0239,从图6(b)、(c)可以看出当重构信号出现失配时,该方法只能抑制部分WTC,对零频附近杂波信号的抑制性能较好,但是对高频部分抑制性能较差,因风轮杂波而产生的频带依然存在,无法实现目标与杂波的有效分离。
图7采用本文所提的栅格化稀疏重构方法,由于字典精度通过迭代更新逐级精准,匹配原子的转速和初相与理论值达到误差允许范围内。图7(a)可以看出利用本文方法可以很好地对WTC信号进行稀疏重构,并且重构杂波信号与回波信号中的杂波信号误差极小,只有0.0698,该误差的产生是由于稀疏重构时目标信号和噪声信号的存在会对稀疏系数造成一定的影响,但是由于噪声信号和目标信号无法在WTC特定字典上完全分解,因此这种影响是微小的。由图7(b)、(c)可以看出本文方法对WTC信号进行有效抑制。
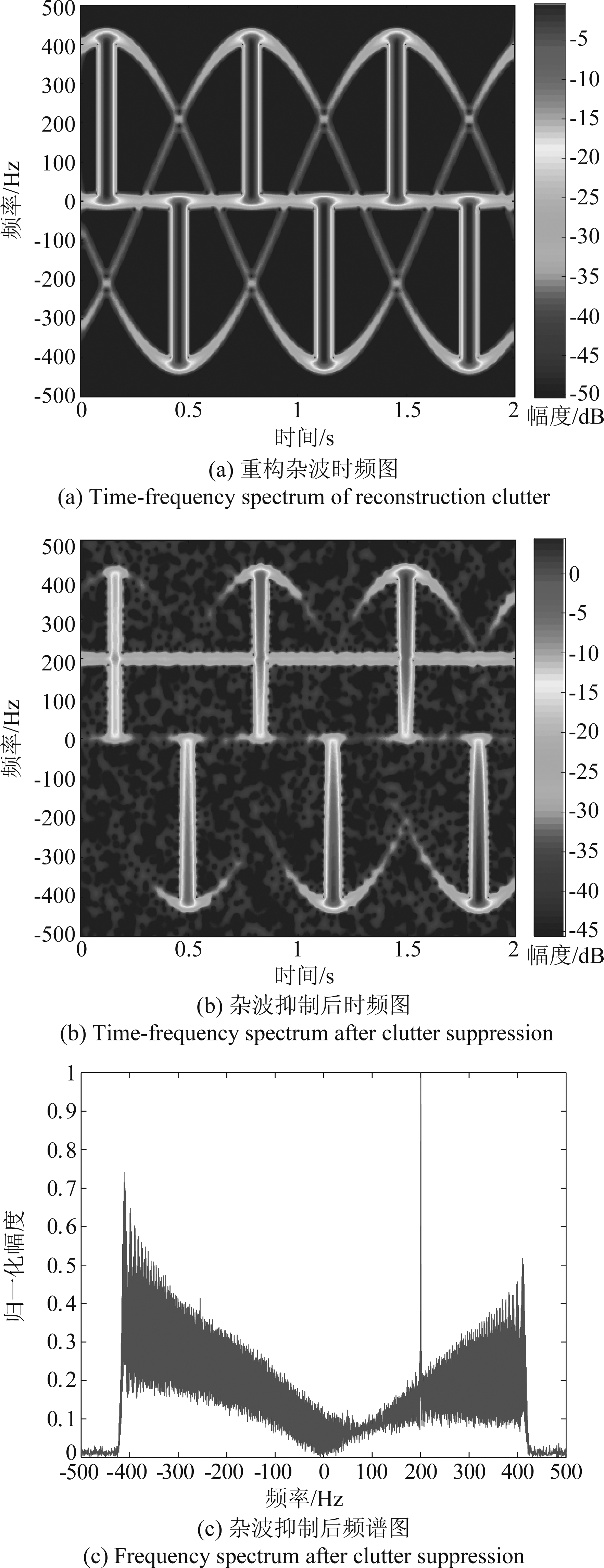
图6 常规固定字典算法的杂波抑制性能
Fig.6 Clutter suppression performance of CFD
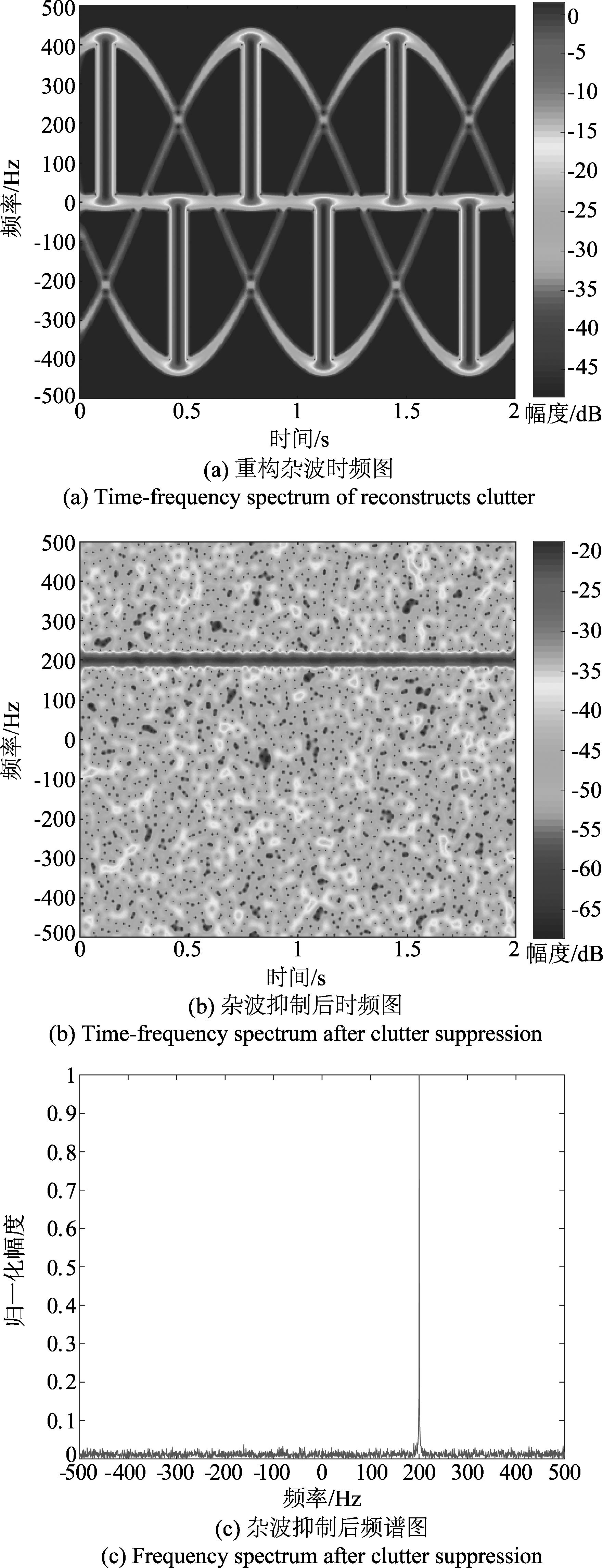
图7 栅格化字典算法的杂波抑制性能
Fig.7 Clutter suppression performance of RD
该仿真是在常规字典和栅格化字典原子数均为K=30×100×20个下进行的,对比图6、图7,可知该条件下栅格化算法可对WTC有效抑制。而若在同样先验条件下,用常规固定字典对WTC达到如图7栅格化字典效果的有效抑制,则至少需要K=30×10000×10000个原子,固定字典大小远大于栅格化字典,且在固定字典运算量也远大于栅格化字典。因此本文所提方法与常规方法相比,在同样信息条件下具有运算量小,字典冗余度小的特点;在字典大小固定条件下,本文所提方法具有精确度高的优点。
表2 常规固定字典与栅格化字典重构对比
Tab.2 Comparison of CFD and RD
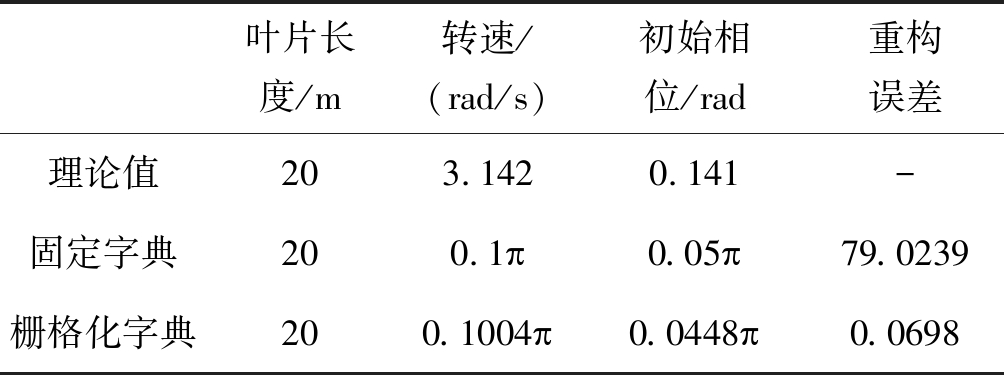
叶片长度/m转速/(rad/s)初始相位/rad重构误差理论值203.1420.141-固定字典200.1敥0.05敥79.0239栅格化字典200.1004敥0.0448敥0.0698
4.2.2 阈值与栅格化级数选择仿真实验
在3.1分析中提出,阈值的选取会影响栅格化级数,进而影响到WTC信号的重构精度。针对本文设定仿真条件,阈值选取与栅格化级数对应关系由实验可得,如表3所示,其中Es为回波总能量。
栅格化级数越高,WTC重构精度也越高,但是同时会增加算法迭代次数,进而增加算法的运行时间。不同栅格化级数与重构误差的关系如图8所示。由图8可知,第一级字典的重构误差相对较大,但是对其栅格化一次后,重构相对误差大幅度减小,当栅格化级数达到三级以上时,重构相对误差基本收敛,保持相对稳定,因此本文提出阈值选取应采取适当较小原则,即阈值T范围应为回波信号总能量Es的0.07～0.1倍之间,当残差信号能量小于阈值T或当栅格化级数大于3级以上时,可采取跳出栅格化迭代。
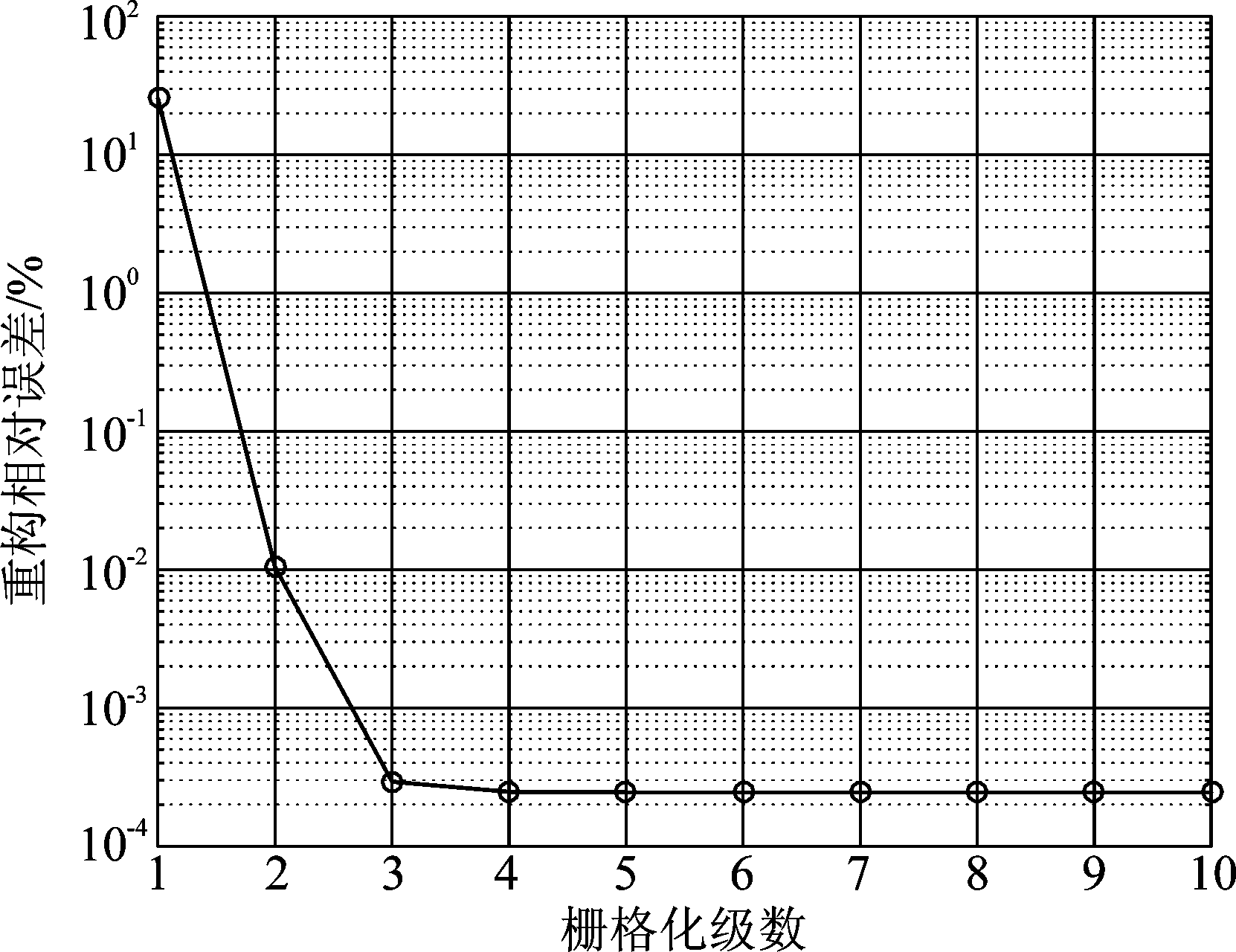
图8 不同栅格化级数的重构相对误差
Fig.8 The relative error of reconstruction in different grid series
表3 阈值选取与栅格化级数对应关系
Tab.3 The corresponding relationship between the threshold and grid series
阈值0.05Es0.06Es0.07Es0.08Es0.09Es0.10Es0.11Es0.12Es栅格化级数10以上10以上333322
4.2.3 多风轮机杂波信号干扰抑制实验
本文算法同时可用于探测区域内有多个风轮机场景下的WTC抑制。假设探测区域内有三台同类型风轮机,叶片长度均为20 m,其叶片转速为ω1=3.267 rad/s,ω2=3.079 rad/s,ω3=3.142 rad/s初始相位对应为θ1=0.214 rad,θ2=1.212 rad,θ3=0.725 rad,其他条件保持不变,阈值选取为0.1Es。其风轮机杂波抑制实验结果如图9所示。其重构杂波的相关参数如表4所示。
由图9及表4可知,该栅格化重构算法对于多来源的风轮机杂波也可达到有效抑制,其重构误差为1.620。其中,由于三台风轮机的转速十分接近,其叶片的微多普勒频率范围区别不大,但该栅格化稀疏重构算法依然对三台风轮机的转速达到了精确地匹配,由此可证明该栅格化稀疏重构算法具有
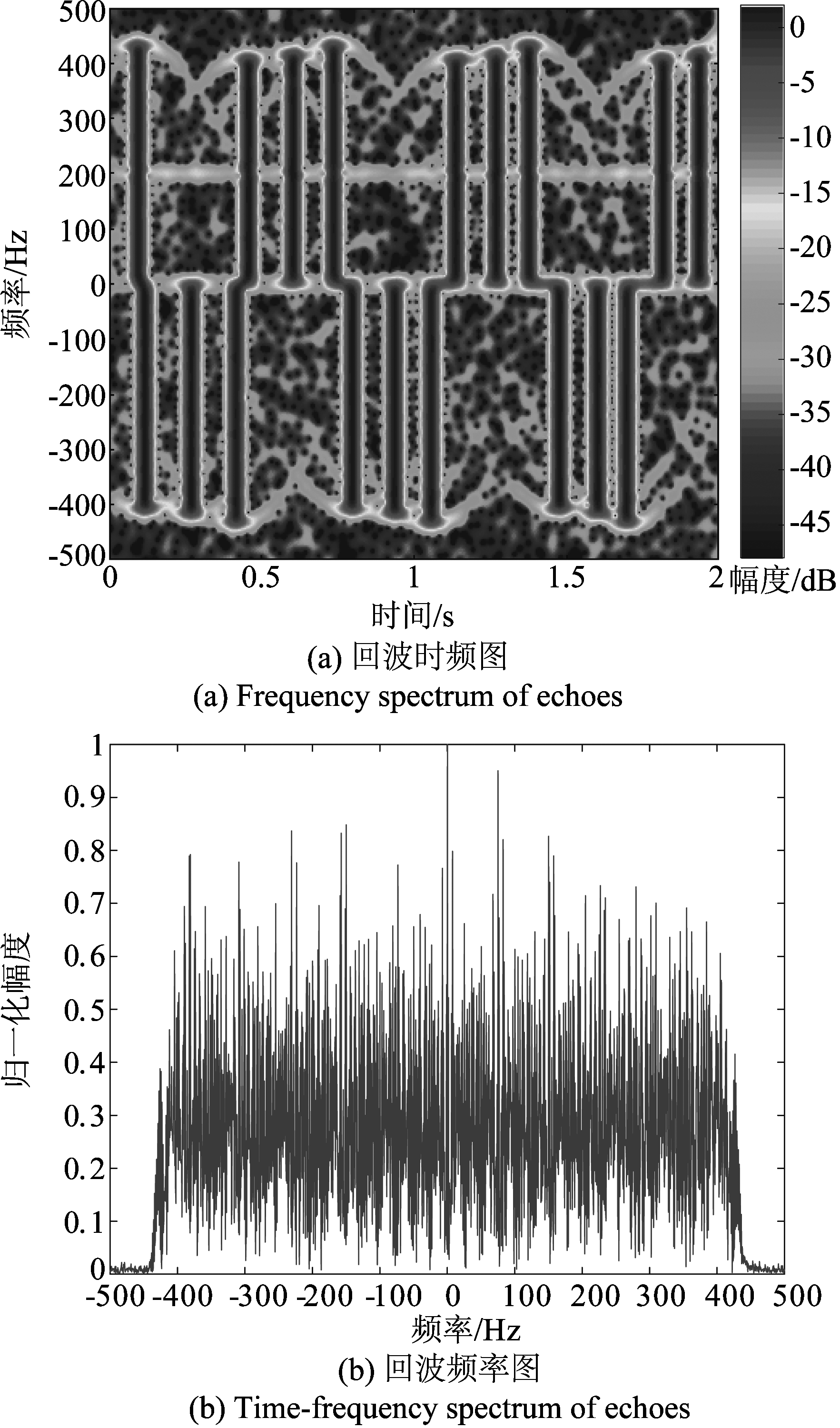
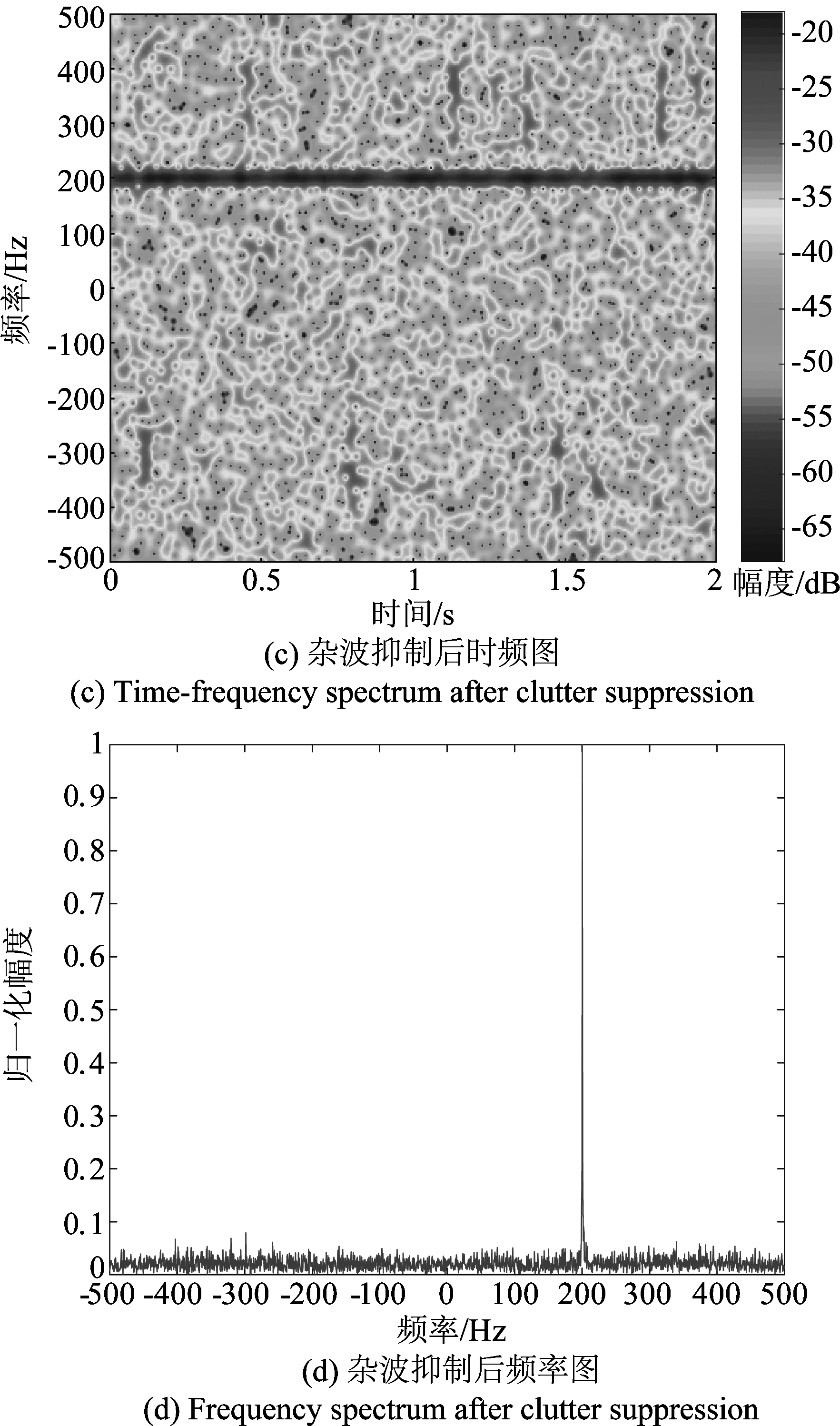
图9 多风轮机杂波抑制 Fig.9 Clutter suppression of multi-wind turbines
表4 多风轮机重构参数
Tab.4 Reconstruction parameter of multi-wind turbines
风轮机重构L/m重构ω/(rad/s)重构θ0/rad1232020201.040敥0.980敥1.000敥0.0681敥0.3858敥0.2308敥
很高的精度。
4.3 算法稳定性分析
图10通过蒙特卡罗实验仿真了不同杂噪比CNR和不同信杂比SCR情况下该重构抑制算法的平均相对误差,其中雷达、风轮机相关参数与4.1相同,蒙特卡罗次数为100次,平均相对误差求解公式为:
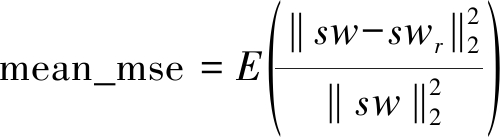
(14)
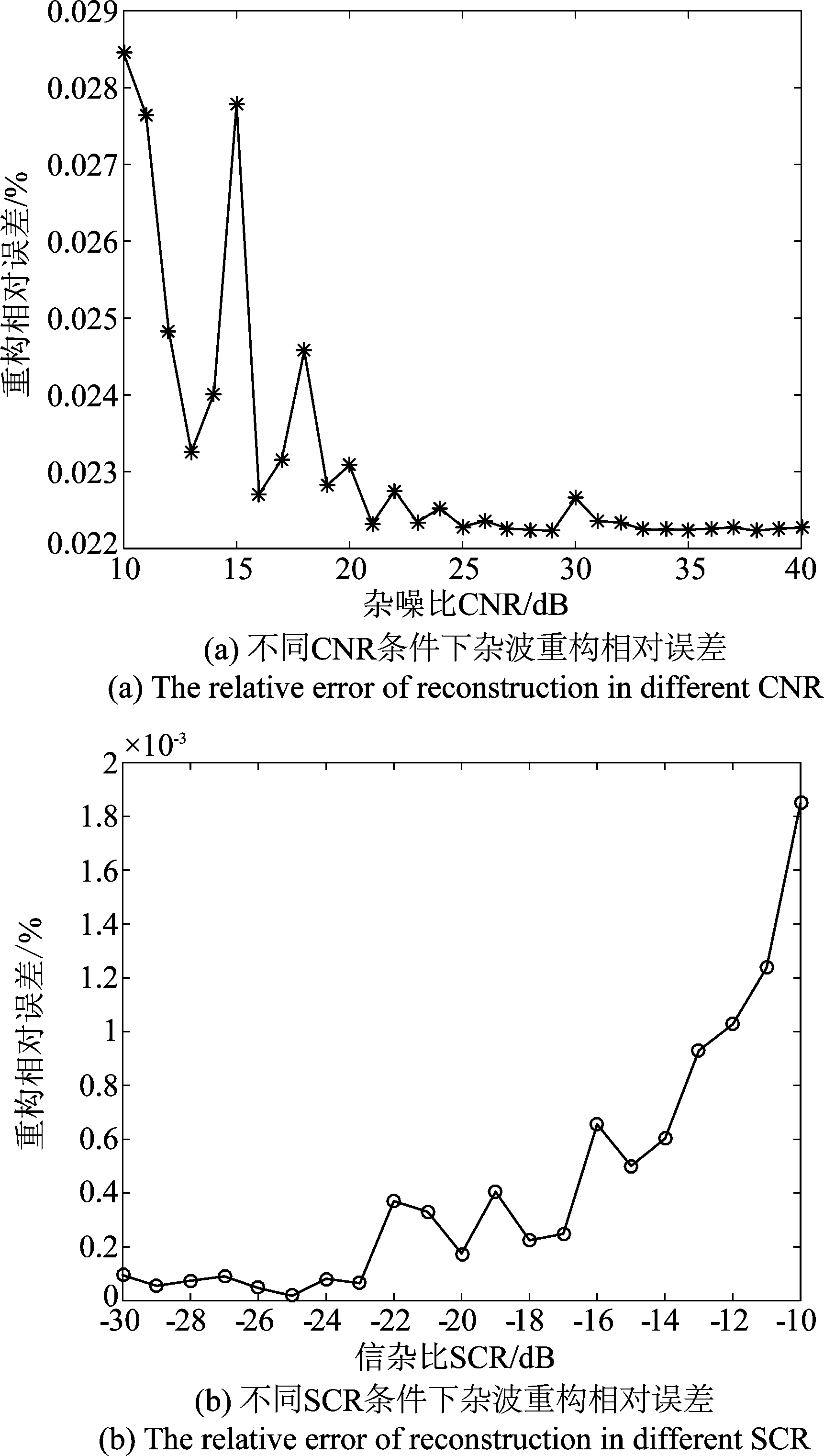
图10 算法稳定性分析 Fig.10 Algorithm stability analysis
通过图10(a)可以看出,噪声功率相对于WTC功率越小,其重构杂波信号的相对误差也越小。当CNR大于18 dB之后,该重构算法的相对误差区域稳定。CNR的大小在对重构的精准度会有一定的影响,不同杂噪比情况下重构误差均小于0.029%,该误差对WTC的抑制效果影响很小,因此可以说明该算法较为稳定且对噪声有一定的容忍度。同时,由图10(b)可以看出,目标信号功率与WTC功率相差越大,其重构杂波的相对误差越小,目标信号对WTC重构有一定的影响,但是一般情况下风轮机杂波功率要远大于目标信号功率,由(b)可知SCR在[-30 dB,-10 dB]之间时,重构相对误差不超过0.002%,因此这种影响很小且该重构误差小于噪声对抑制算法的影响。由此,可以说明本文所提算法相对稳定,SCR对算法的影响很小,且该算法具有一定的抗噪性能。
5 结论
本文根据WTC区别于目标信号的微动特征的特点,通过构建栅格化字典,利用OMP算法进行匹配最佳原子,在最佳原子基础上对字典进一步生成更新,实现对WTC信号的栅格化稀疏重构,从而达到抑制杂波的目的。实验结果显示,在字典大小固定的前提下,常规字典的重构杂波会出现失配现象,严重影响抑制效果,而本文所提栅格化字典可以在上级最佳原子的基础上进行逐级重构,通过三级以上的栅格化可实现对WTC的精准重构。由对比仿真实验可得栅格化字典的重构方法与常规字典重构方法相比,具有运算量小、字典冗余度低和精确度高的优点。同时仿真证明该算法对在多个风轮机场景下依然可以有效抑制WTC。实验分析该算法稳定性高,噪声的变化对抑制性能的影响在误差范围内。
附 录
假设雷达视线间存在方位角α,如图11所示。
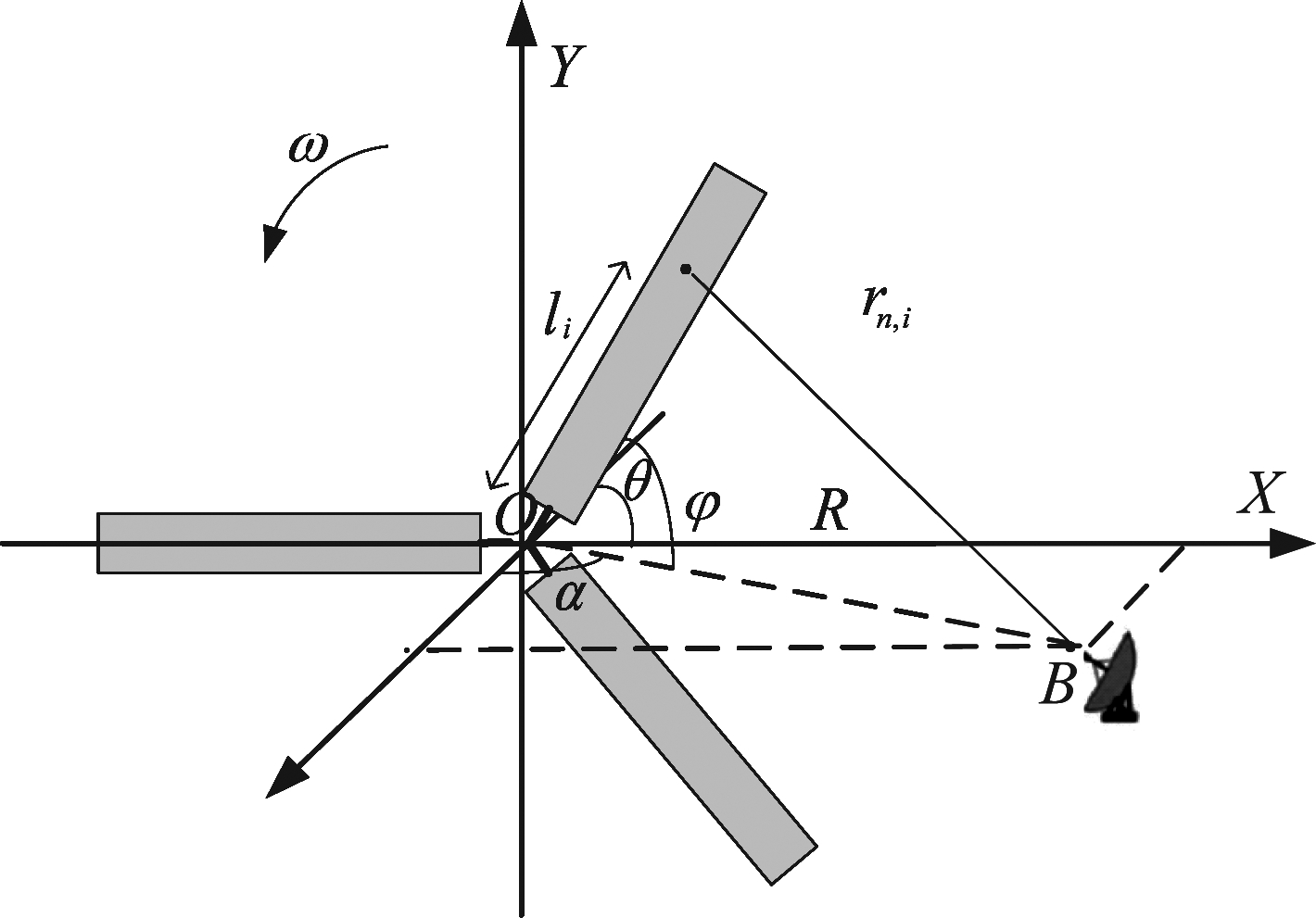
图11 WTC模型
Fig.11 WTC model
叶片直线的方程为:
雷达视线LOS的方程为:
根据空间直线夹角公式,雷达视线LOS与叶片间的夹角φ可表示为:
(15)
则风轮机叶片的基带回波信号表示为:
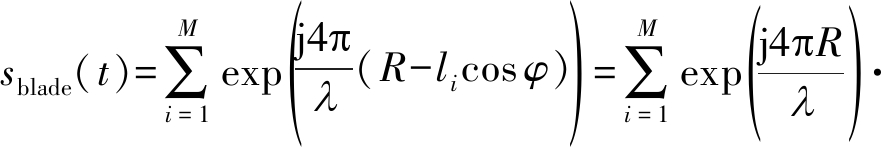
(16)
令
为将风轮机叶片与雷达投影至同一平面时的散射点离叶片旋转中心的等效长度。此时,风轮机回波信号表达式为:
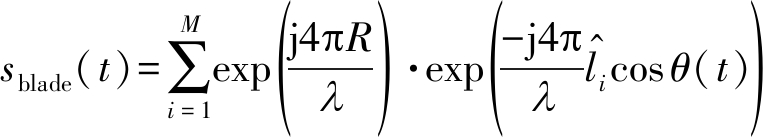
(17)
与式(6)中风轮机回波信号部分形式相同,因此本文所提风轮机杂波抑制方法依旧适用。不过在OMP算法中匹配到的是风轮机叶片的投影等效长度
并非实际长度,对算法的抑制性能并不造成影响。
[1] 何炜琨, 窄秋苹, 郭双双, 等. 基于微多普勒特征的风轮机雷达杂波检测[J]. 信号处理, 2017, 33(4): 496-504.
He Weikun, Zhai Qiuping, Guo Shuangshuang, et al. Wind turbine radar clutter detection method based on Micro-Doppler character-istics of wind turbine[J]. Journal of Signal Processing, 2017, 33(4): 496-504.(in Chinese)
[2] 何炜琨, 吴仁彪, 王晓亮, 等. 风电场对雷达设备的影响评估与干扰抑制技术研究现状与展望[J]. 电子与信息学报, 2017, 39(7): 1748-1758.
He Weikun, Wu Renbiao, Wang Xiaoliang, et al. The review and prospect on the influence evaluation and interference suppression of wind farms on the radar equipment[J]. Journal of Electronics & Information Technology, 2017, 39(7): 1748-1758.(in Chinese)
[3] Crespo-Ballesteros M, Antoniou M, Chernia-kov M. Wind Turbine Blade Radar Signatures in the Near-Field: Modelling and Experimental Confirmation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(4): 1916-1931.
[4] Uysal F, Selesnick I, Isom B M. Mitigation of Wind Turbine Clutter for Weather Radar by Signal Separation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(5): 2925-2934.
[5] Poupart G J, Qineti Q. Wind Farms Impact on Radar Aviation Interests-Final Report: FESW/14/00614/00/REP[R]. London, UK, 2003.
[6] Osman Karabayir, Mustafa Unal, Ahmet Faruk Coskun, et al. CLEAN based wind turbine clutter mitigation approach for pulse-Doppler radars[C]∥2015 IEEE Radar Conference. Arlington, VA, USA: IEEE, 2015: 1541-1544.
[7] Wang J, Lok Y F, Hubbard O, et al. Impact of wind turbines On ATC radars and mitigation results[C]∥2013 IEEE Radar Conference. Arlington, VA, USA: IEEE, 2013: 1- 4.
[8] Rashid L, Brown A. Partial treatment of wind turbine blades with radar absorbing materials (RAM) for RCS reduction[C]∥In Proceedings of the 4th European Conference on Antennas and Propagation, Barcelona, Spain, 2010: 1-5.
[9] Theil, Schouten, Jong D. Radar and Wind Turbines: A Guide to Acceptance Criteria[C]∥In Proceedings of the 2010 IEEE International Radar Conference, Arlington, VA, USA, 2010: 1355-1361.
[10]Wang Wenqin. Detecting and Mitigating Wind Turbine Clutter for Airspace Radar Systems[J]. The Scientific World Journal, 2013, 2013(Article ID 385182): 1- 8.
[11]陈小龙, 关键, 董云龙, 等. 稀疏域海杂波抑制与微动目标检测方法[J]. 电子学报, 2016, 44(4): 860- 867.
Chen Xiaolong, Guan Jian, Dong Yunlong, et al. Sea clutter suppression and Micro-motion target detection in sparse domain[J]. Acta Electronica Sinica, 2016, 44(4): 860- 867.(in Chinese)
[12]Naqvi A, Ling H. Signal filtering technique to remove Doppler clutter caused by wind turbines[J]. Microwave & Optical Technology Letters, 2012, 54(6): 1455-1460.
[13]陈永彬, 李少东, 杨军, 等. 旋翼叶片回波建模与闪烁现象机理分析[J]. 物理学报, 2016, 65(13): 281-291.
Chen Yongbin, Li Shaodong, Yang Jun, et al. Rotor blades echo modeling and mechanism analysis of flashes phenomena[J]. Acta Physica Sinica, 2016, 65(13): 281-291.(in Chinese)
[14]Bassem R. Mahafza. 雷达系统分析与设计(MATLAB版)[M]. 陈志杰, 罗群, 沈齐, 译, 北京: 电子工业出版社, 2008: 89-91.
Bassem R. Mahafza. Radar Systems Analysis and Design Using MATLAB[M]. Chen Zhijie, Luo Qun, Shen Qi, translate. Beijing: Publishing House of Electronics Industry, 2008: 89-91.(in Chinese)
[15]陈永彬, 李少东, 杨军, 等. 一种旋翼叶片微动特征提取新方法[J]. 雷达科学与技术, 2017, 15(1): 13-28.
Chen Yongbin, Li Shaodong, Yang Jun, et al. A new method for Micro-Motion signature extraction of Rotor Blades[J]. Radar Science and Technology, 2017, 15(1): 13-28.(in Chinese)
[16]Victor C. Chen. 雷达中的微多普勒效应[M]. 吴顺君, 杜兰, 刘宏伟, 译, 北京: 电子工业出版社, 2013: 93-109.
Victor C. Chen. The Micro-Doppler effect in radar[M]. Wu Shunjun, Du Lan, Liu Hongwei, translate. Beijing: Publishing House of Electronics Industry, 2013: 93-109.(in Chinese)
[17]周伟栋, 杨震, 于云. 改进的正交匹配追踪语音增强算法[J]. 信号处理, 2016, 32(3): 287-295.
Zhou Weidong, Yang Zhen, Yu Yun. Speech enhancement by using modified orthogonal matching pursuit algorithm[J]. Journal of Signal Processing, 2016, 32(3): 287-295.(in Chinese)
[18]刘学文, 肖嵩, 王玲, 等. 迭代预测正交匹配追踪算法[J]. 信号处理, 2017, 33(2): 178-184.
Liu Xuewen, Xiao Song, Wang Ling, et al. Iteration forecast orthogonal matching pursuit algorithm[J]. Journal of Signal Processing, 2017, 33(2): 178-184.(in Chinese)
