1 引言
单个次用户频谱感知受隐藏终端、低信噪比以及深度衰落等影响严重,协作感知可一定程度克服此问题,适用于独立同分布的相关信号检测。近年来随着随机矩阵理论的发展,利用信号协方差矩阵的协作频谱感知算法不断被提出,例如利用最大最小特征值检测法[1](Maximum-minimum Eigenvalue,MME)、最大最小特征值之差法[2](the Difference between the Maximum Eigenvalue and the Minimum Eigenvalue,DMM)、最大最小特征值之差与几何平均特征值之比[3](Difference between the Maximum-Minimum and Geometric mean eigenvalue,DMMG)等。通常在高斯噪声背景下推导得到这类算法的检测统计量概率密度函数和检测门限。但是,实际环境中噪声并不一定服从高斯分布,因此上述门限值只是近似结果,所以检测性能有待改善。
为克服以上传统协作感知所存在的问题,学者们研究了利用机器学习进行频谱感知的相关算法。该类算法首先建立合适的学习模型,然后通过训练确定分类器参数,利用此分类器就能准确分类信号,无需理论推导准确的检测门限,且对不同噪声环境的适应度高。文献[4] 提取信号循环谱特征参数,利用随机森林(Random Forest,RF)进行感知判决,但该方法是单点感知,无法克服多径和衰落等影响。文献[5]利用能量检测进行本地感知,并将每个协作点的感知结果构成训练序列,在融合中心利用反向传播神经网络(Back Propagation Neural Network,BPNN)调整每个协作节点的融合权重,从而提高频谱感知的整体检测性能。文献[6]提出了基于支持向量机(Support Vector Machine,SVM)和加权K近邻(k-Nearest Neighbor,kNN)监督学习算法的协作频谱感知方法,该方法无需设计融合规则,但其使用能量向量作为特征进行训练和识别,在低信噪比时识别效果不佳。文献[7]利用采样协方差矩阵的特征值作为特征向量,并使用K均值聚类(K-means)和混合高斯模型(Gaussian Mixture Model,GMM)的非监督学习框架进行频谱感知,相比于能量特征向量,具有更高的噪声鲁棒性。文献[8]利用协方差矩阵的3种检测统计量构造特征向量,然后采用SVM完成感知任务。虽然上述利用机器学习的协作频谱感知方法能够克服传统频谱感知的检测门限确定的准确性和困难的问题,但这些方法需要构造特征参数,该过程往往会丢失大量原始信号信息,而且频谱感知性能受所构造的特征参数影响。
卷积神经网络(Convolutional Neural Network,CNN)提取二维图像特征性能通常优于其他机器学习算法,文献[9]利用接收到的OFDM信号获得循环自相关信息,并使用卷积神经网络对信号进行检测,但该方法与文献[4]相同,也是非协作感知算法。对此,本文利用CNN提取输入采样协方差矩阵高层次特征,进行协作频谱感知。该方法无需确定检测门限,无需提取特征参数,充分地利用了信号原始信息,对不同噪声环境具有更好的适应性。
2 系统模型与理论基础
假设认知网络由M个次用户和1个主用户组成,yi(n)是第i个次用户的接收信号,s(n)是主用户的发射信号,hi(n)是第i个次用户与主用户之间的信道系数;第i个次用户接收到的有用信号为xi(n)=s(n)hi(n)、噪声是νi(n),且该噪声服从均值为0、方差为σ2的高斯分布。第i个次用户进行频谱感知的二元假设检验可以表示成:
(1)
H0、H1是主用户信号不存在以及存在的假设。M个次用户接收到的第k个采样数据序列为:
y(k)=[y1(k),y2(k),...,yM(k)]T
(2)
接收信号矩阵为:
(3)
其中N为采样点数。接收信号统计协方差矩阵R可以使用N点采样信号矩阵Y进行估计,得到相对应的采样协方差矩阵为:
(4)
当N→∞时,R(N)→R。当次用户数为M时,R(N)矩阵大小为M×M。
以40个协作用户为例,H0、H1假设下采样协方差矩阵灰度图分别如图1(a)和(b)所示,颜色越深代表的数值越小。可见,当不存在主用户信号时,除对角线外,整个灰度图颜色比较均匀,且数值很小;当存在主用户信号时,除对角线外,灰度图颜色不太均匀,呈灰色,数值变大。因此,根据两种不同假设下灰度图的区别,可以利用卷积神经网络提取图像中的特征对两种假设进行检验,实现频谱感知。
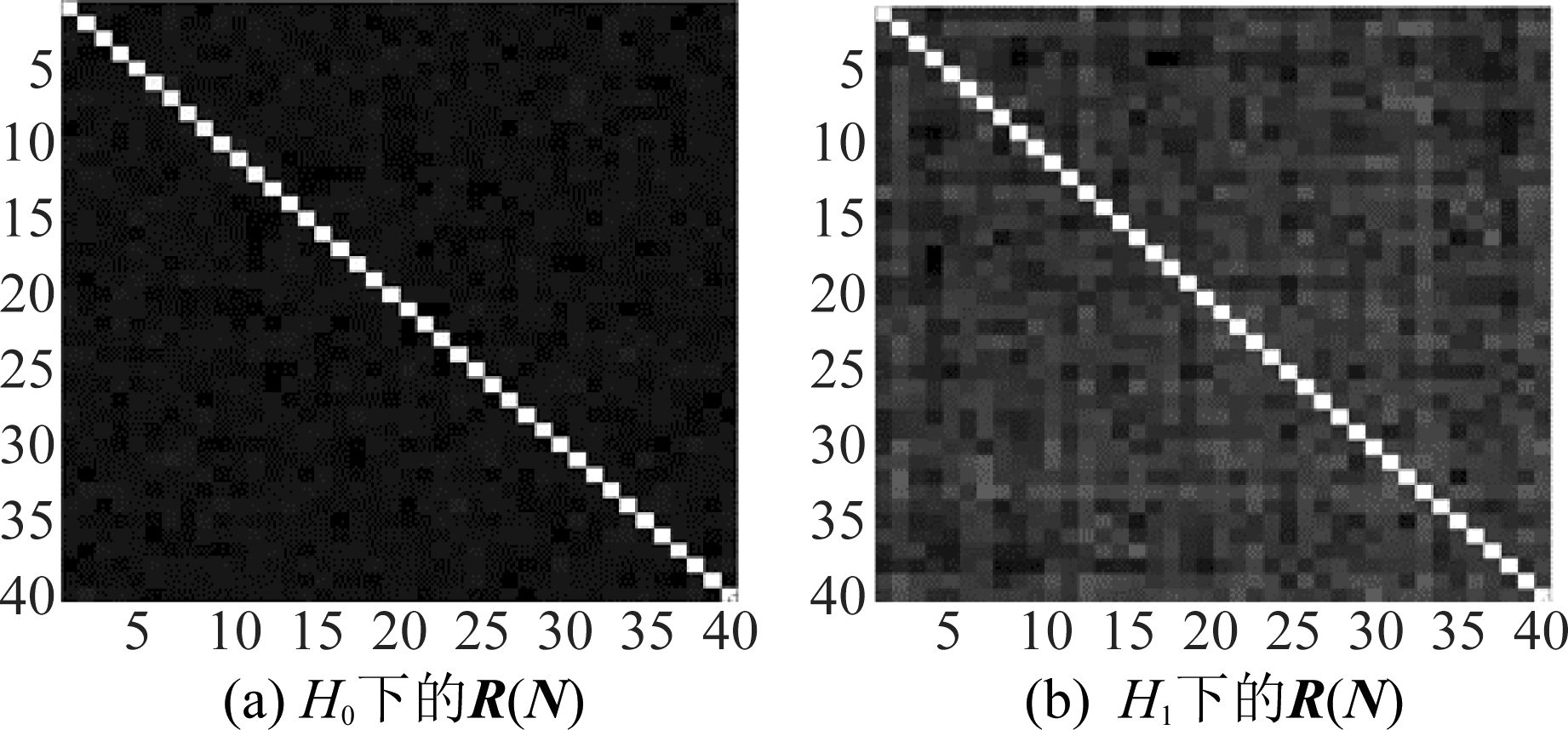
图1 采样协方差矩阵灰度图
Fig.1 Gray scale of sampling covariance matrix
3 基于卷积神经网络的频谱感知模型
本文频谱感知方法的处理过程由数据预处理和频谱感知模型训练两部分构成,如图2所示。
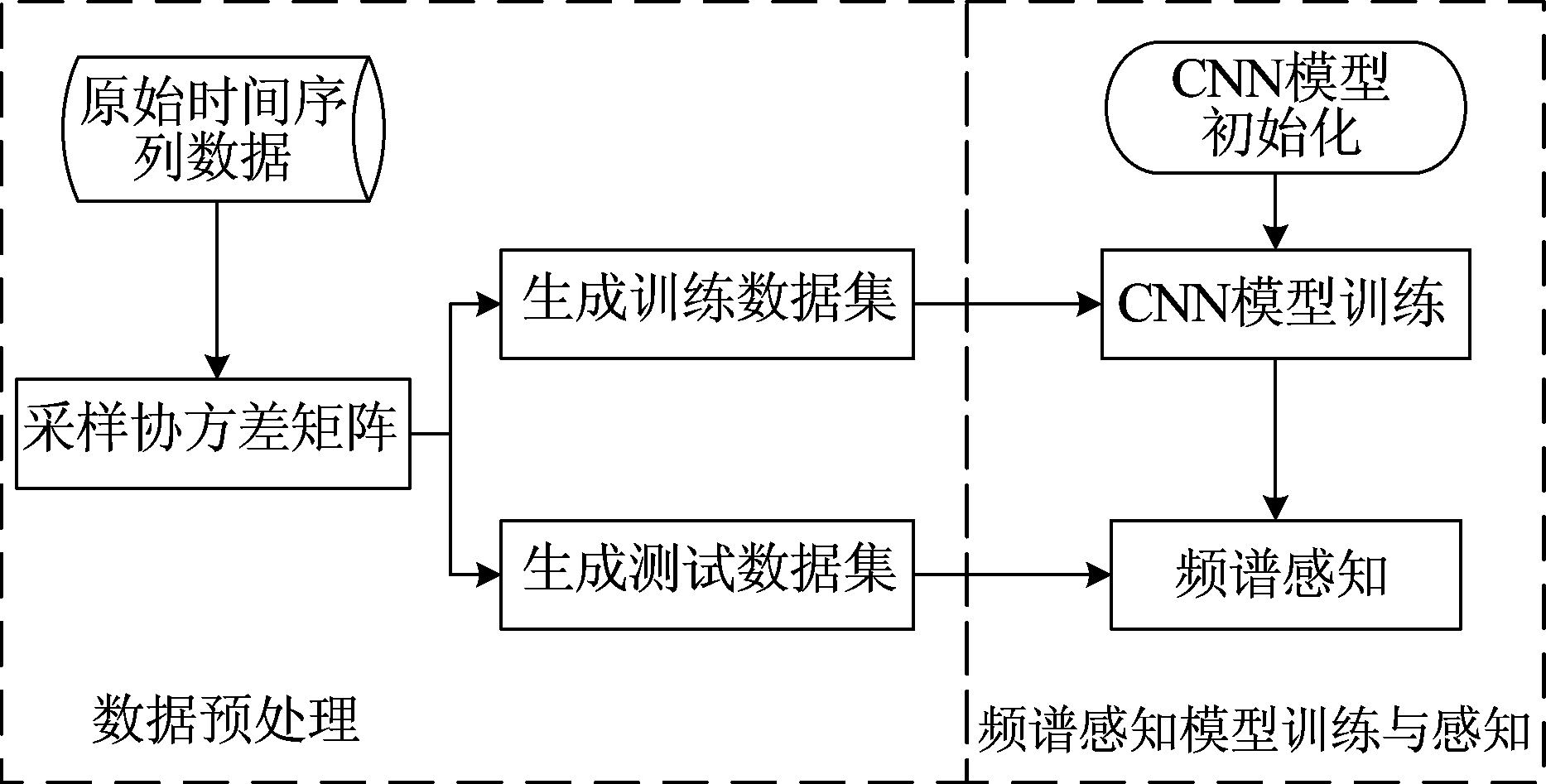
图2 基于CNN的频谱感知模型
Fig.2 Spectrum sensing model based on CNN
3.1 数据预处理
接收信号通过正交解调和采样得到I、Q双路基带信号,然后构成模型的原始数据,即:
yi(n)=Ii(n)+jQi(n)
(5)
其中,Ii(n)和Qi(n)分别为第i个次用户接收到的I路信号和Q路信号。该两路信号都包含有原始信号的信息,因此在训练和测试数据集的生成过程中需要充分使用两路信息。
对M个次用户接收到的数据进行分段,每段长度是N。将这M个长度为N的序列的实部和虚部分别组成两个矩阵:
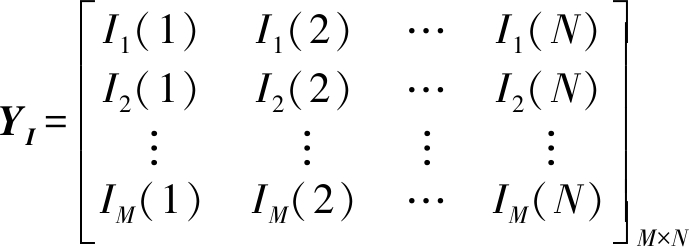
(6)
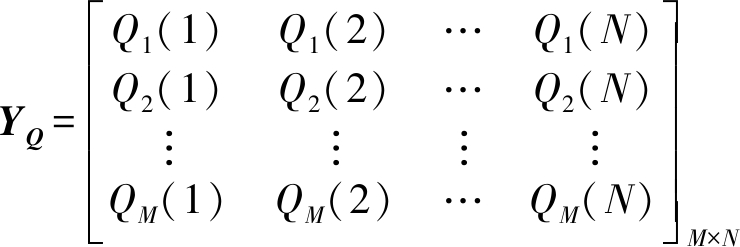
(7)
令实部及虚部的采样协方差矩阵为RI和RQ,且
根据式(4)、(6)和(7)可得:
(8)
将RI和RQ归一化处理并组合成双通道矩阵,作为频谱感知模型的输入。
3.2 频谱感知模型训练与感知
卷积神经网络将采样协方差矩阵RI和RQ作为输入,通过卷积层(Convolution Layer)、池化层(Pooling Layer)和全连接层(Full Connection Layer)等提取特征,最终利用所提取的特征进行频谱感知,即判断主用户信号存在与否,也就是对原始信号进行两种类型的分类。
3.2.1 CNN网络结构
卷积层由卷积核和相应的特征图组成,卷积核与上一层的特征图进行卷积运算,利用激活函数产生当前层的特征图。整个卷积层的运算过程为:
X(L)=f(W(L)⊗X(L-1)+b(L))
(9)
其中,L表示层序号;X(L-1)表示上一层输出的特征图;X(L)表示本层特征图输出;W(L)表示本层卷积核;b(L)表示本层偏置值; f(·)为激活函数,能够增强网络非线性,本文均采用relu为各个隐藏层的激活函数,即:
(10)
池化层可以降低特征图维数,减少训练参数,同时也可以相对缓解训练模型的过拟合情况。本文使用均值池化。
全连接层一般位于最后,它将本层以及上一层的特征图进行全连接,把多次卷积和池化所得到的特征转化为输出的分类结果。
本文使用图3所示的CNN网络结构。网络的输入是3.1节中得到的RI和RQ组成的双通道矩阵。每个通道的矩阵大小为M×M,这里取M为40进行CNN网络结构的分析。其中C代表卷积层,S代表池化层。
C1是首个卷积层,通过数量为N1的3×3×2的卷积核,对输入采样协方差矩阵进行处理,移动步长为1,得到N1个38×38大小的特征图。
S2是池化层,将C1所得到的特征图进行池化。使用2×2的窗口进行均值池化,移动步长取2,得到降低维数后的N1个19×19大小的特征图。
C3是卷积层,使用数量为N2的2×2的卷积核对通过S2池化后所得到的特征图进行处理,得到N2个18×18大小的特征图。
S4是池化层,池化过程与S2相同,最终得到N2个9×9的特征图。
C5是最后一个卷积层,利用数量为N3的9×9的卷积核对上一层的特征图卷积,获得N3个1×1大小的特征图。
F6为全连接层,两个全连接单元分别表示主用户存在与不存在的分类,每个分类点都与C5层的N3个特征图一一相连,最后通过softmax函数得到最终的结果。
3.2.2 CNN网络训练
假设有n对用于训练的数据
表示第n个双通道采样协方差矩阵,
表示
的真实标签。前向传播从输入层开始,经过多层的卷积、池化等操作,得到最终的输出映射关系为:
(11)
其中,W和b是CNN中需要训练的参数,分别表示权值和偏置值,
表示
经过CNN后的输出映射。
由于前向传播所得到的结果
与所期望的结果标签存在误差,本文使用交叉熵作为误差损失函数,其可表示为:
(12)
为了降低最终预测值与实际值之间的误差损失函数Loss值,利用反向传播算法,逐层调整CNN中W和b的参数值。
3.2.3 模型性能测试
CNN网络经过多次训练,得到最终的频谱感知网络模型,用此网络模型可以进行频谱感知。为评估所得到模型频谱感知性能,使用测试数据进行测试。
测试数据不重复使用训练数据集,假设有n对测试样本
表示测试集中的第n个协方差矩阵,
为
的真实标签。
当存在主用户时生成n对测试样本,对于每对数据样本,将作为CNN模型输入,得到输出结果
将其与真实标签对比得到误差为:
(13)
设定误差门限errth,统计err(n)
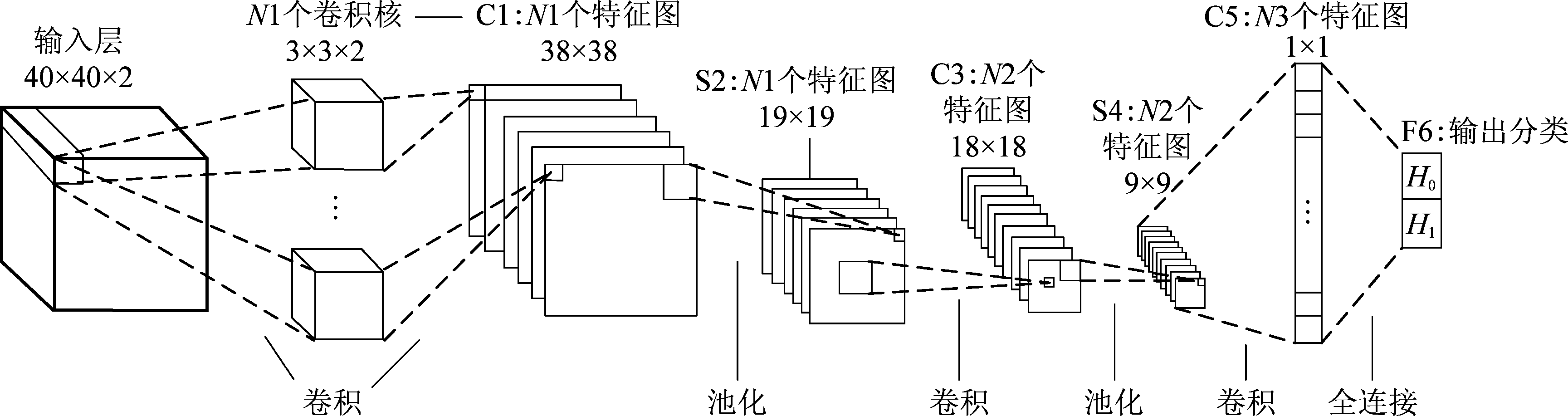
图3 CNN网络结构
Fig.3 The network architecture of CNN
同理,当不存在主用户时生成n对测试样本,可得到在误差门限errth下的虚警概率(Probability of False alarm,Pf)为(1-kc/n)。
4 实验分析
本节训练与测试数据集均由Matlab仿真产生;在ubuntu16.04操作系统下,使用Python3.6、scikit-learn库以及Keras深度学习框架编程实现算法;硬件CPU采用Intel Core i7-7700,GPU采用GeForce GTX 1080,运行内存16Gb。
4.1 数据集生成
在Matlab中分别生成用于训练和测试的数据集,主用户信号为QPSK信号,每个码元采样点数8,噪声是均值为0、方差为1的高斯白噪声。通过调整产生的QPSK信号幅度,得到不同信噪比(Signal-to-noise Ratio,SNR)下的主用户信号数据。
协方差矩阵的大小是M×M,随着次用户数M的改变,CNN输入层所使用的数据维度也相应变化。因此,不同协作次用户数需要训练不同的CNN模型。本文训练了协作次用户数M为10、20和40的CNN模型。
针对每种不同的协作次用户数量,均生成SNR为-20 dB～0 dB、间隔1 dB的数据。每种SNR下产生1000对数据,每对数据采样点数N为1000,计算得到归一化的采样协方差矩阵作为CNN的输入数据,标签设置为[1, 0]T。另外还需生成无主用户信号下的纯噪声数据,数据处理方法同上,标签设置为[0, 1]T。测试数据生成过程与训练数据相同,最终分别产生样本数量为21000的测试和训练数据集。
4.2 CNN结构参数对频谱感知性能影响
卷积核的数量和大小以及激活函数的选择都影响模型的频谱感知性能,本节训练和测试均使用40个次用户协作的数据集。根据数据集的设置,当标签为[1, 0]T时得到的是主用户存在的情况,但是softmax所输出的结果并非[1, 0]T或[0, 1]T,而是由两个相加和为1的实数组成的二维向量,设定误差门限errth=1,根据式(13)计算err(n),并判定主用户信号存在与否。
(1) 卷积核对频谱感知性能的影响
隐藏层激活函数使用relu,同时改变C1和C3卷积核的个数、大小以及C5卷积层的神经元数量,训练20次,重复实验十次取平均,得到CNN模型的频谱感知性能如表1所示。
表1 卷积核对频谱感知性能影响
Tab.1 The effect of convolution kernel on spectrum sensing performance
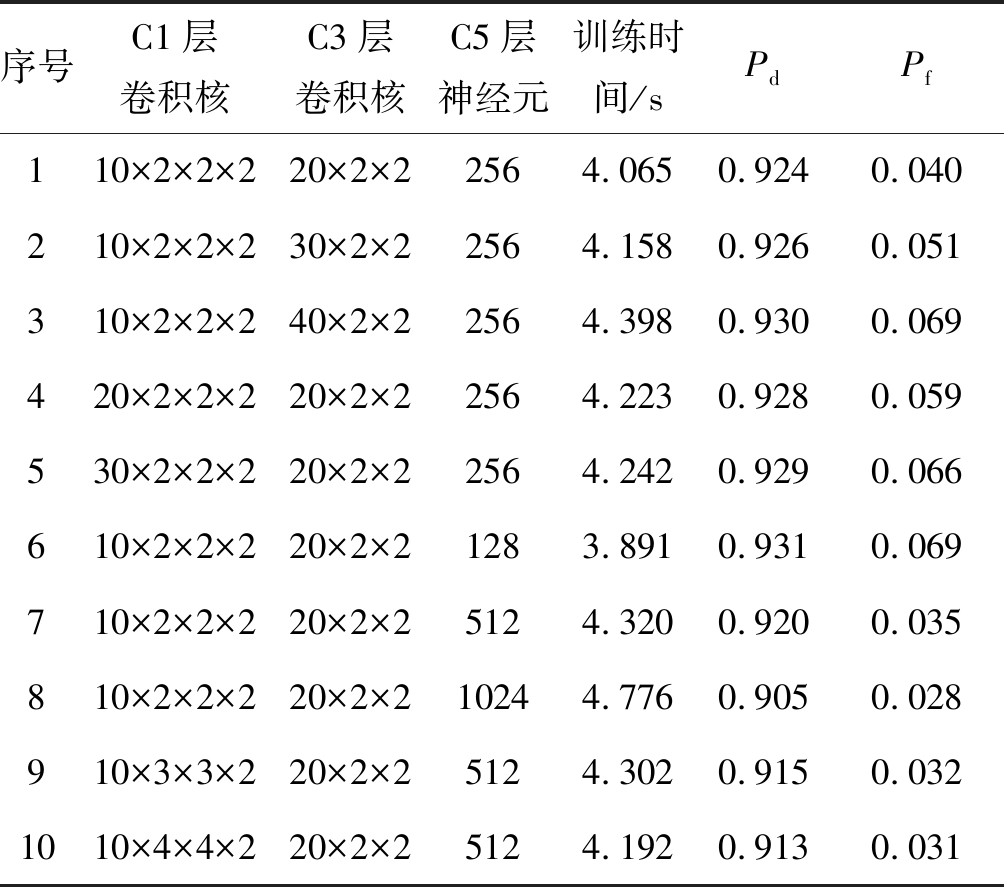
序号C1层卷积核C3层卷积核C5层神经元训练时间/sPdPf110×2×2×220×2×22564.0650.9240.040210×2×2×230×2×22564.1580.9260.051310×2×2×240×2×22564.3980.9300.069420×2×2×220×2×22564.2230.9280.059530×2×2×220×2×22564.2420.9290.066610×2×2×220×2×21283.8910.9310.069710×2×2×220×2×25124.3200.9200.035810×2×2×220×2×210244.7760.9050.028910×3×3×220×2×25124.3020.9150.0321010×4×4×220×2×25124.1920.9130.031
由表1的序号1～5可得,随着C1、C3的卷积核数量增加,训练时间增加,检测概率与虚警概率也升高;由序号7、9和10可得Pf和Pd对卷积核大小的改变都不敏感;由序号6～8可得C5全连接层神经元数量的增加能降低虚警概率,但增长了训练时间,降低了检测概率。
综合考虑频谱感知性能,下文仿真中选择序号1模型的参数。
(2)激活函数对频谱感知性能的影响
激活函数能增加模型的非线性,提高复杂函数的建模准确性,同时缓解过拟合。使用sigmoid、linear、tanh及relu作为隐藏层的激活函数,利用该4种函数对网络分别训练5次、10次、15次及20次,得到的频谱感知的Pd和Pf如表2所示。
由表2可得,将relu作为激活函数得到的模型收敛较快,在训练次数达到10次左右,模型已经基本收敛;训练20次后的Pd为0.922,Pf为0.044,可见随着训练次数的增加,在保证较高检测概率的同时,也能拥有较低的虚警概率。因此本文选用relu作为模型隐藏层的激活函数。
表2 激活函数对频谱感知性能影响
Tab.2 Effect of activation function on spectrum sensing performance
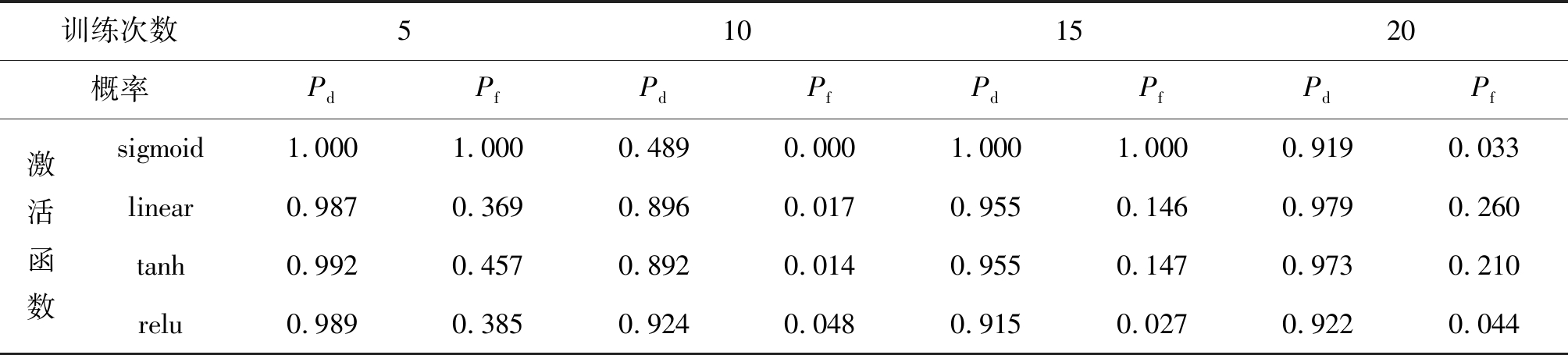
训练次数5101520概率PdPfPdPfPdPfPdPf激活函数sigmoid1.0001.0000.4890.0001.0001.0000.9190.033linear0.9870.3690.8960.0170.9550.1460.9790.260tanh0.9920.4570.8920.0140.9550.1470.9730.210relu0.9890.3850.9240.0480.9150.0270.9220.044
4.3 算法性能分析
根据4.2节仿真结果,综合考虑模型的整体性能,C1和C3分别采用10个和20个2×2大小的卷积核,C5采用256个神经元,每层卷积步长为1;S2和S4池化层使用2×2均值池化,池化步长为2;输出层的激活函数使用softmax。以下将本文所提方法(简记为CNN)与文献[3]的DMMG算法、文献[8]的基于SVM的算法和文献[10]的ED算法进行对比。
(1)训练次数对频谱感知性能的影响
CNN的Pd与训练次数之间的关系如图4。
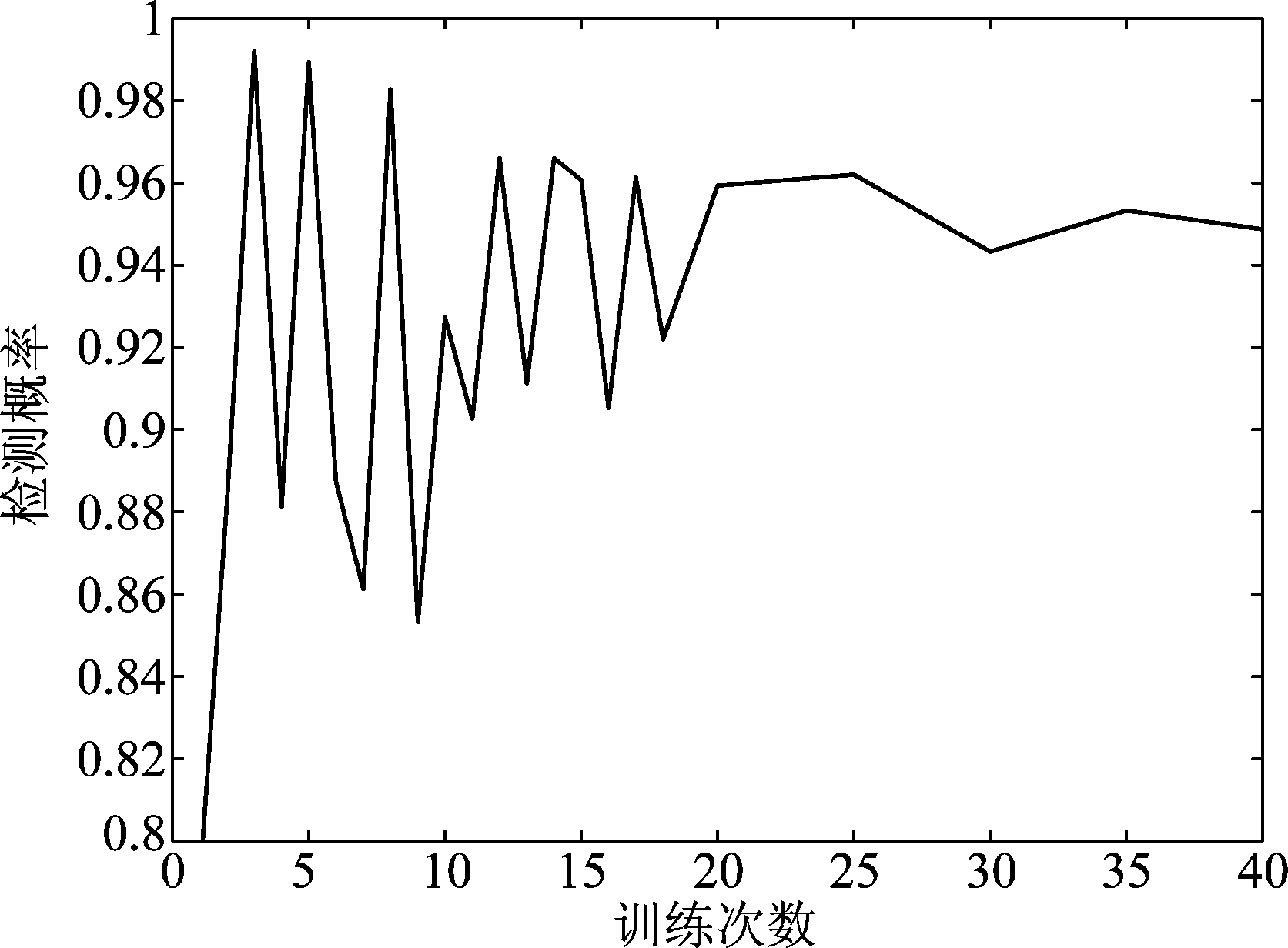
图4 检测概率收敛情况
Fig.4 Detection probability convergence
由图4可得,当训练次数低于20时,本文使用的频谱感知算法的Pd起伏大;同时当训练次数大于20时,Pd逐渐稳定在0.95左右。因此,下文的模型训练次数选择25次。
(2)离线训练和在线检测时间
CNN与SVM算法都需要通过离线训练来建立模型,DMMG和ED算法则不存在训练过程,能够直接进行在线检测。三种协作用户数下,使用21000组训练数据离线训练本文算法模型和SVM,使用2100组测试数据在线测试上述四种算法,四种算法所需的离线训练和在线检测时间分别如表3所示。
由表3可见,CNN方法的离线训练时间大于SVM,但是在线检测时间却少于SVM。这是由于CNN所需训练的参数数量远多于SVM,所以训练时间长;在线检测阶段,CNN仅需计算协方差矩阵并将其输入到训练完成的网络中,而SVM方法还需根据协方差矩阵提取多种特征参数,因此数据预处理时间比CNN更长,从而增加了在线检测时间。DMMG算法直接从协方差矩阵中提取特征参数进行检测,而ED算法通过累加信号能量作为检测统计量进行检测,因此均不存在离线训练过程。同时,CNN和DMMG在线检测时间相近,而CNN具有更高的检测性能,虽然ED算法在线检测时间短,但检测性能却远不如CNN。
四种算法的在线检测复杂度分析如下。由于CNN、SVM和DMMG算法均需使用采样协方差矩阵,因此只分析各算法后续步骤的复杂度,其中n表示测试样本数,m表示次用户数。ED算法不涉及矩阵运算,它的复杂度为O(nm);DMMG算法需求解m×m的矩阵特征值,因此复杂度为O(nm3+n);SVM算法在求解矩阵特征值的基础上还需要进行复杂度为O(n3)的SVM分类[11],因此总复杂度为O(nm3+n3)。CNN算法的复杂度为
其中,Pk、Gk、Uk 分别表示第k个卷积层的输出特征图的边长、卷积核边长和输出通道数,U0表示网络输入样本通道数。当次用户数m小于40时,算法复杂度排序为SVM>CNN>DMMG>ED。
(3)算法性能对比
表3 四种算法的离线训练及在线检测时间
Tab.3 Offline training and online detection time of the four algorithms
CNNSVMDMMGED协作用户离线训练在线检测离线训练在线检测离线训练在线检测离线训练在线检测1075.612.96642.823.866—2.841—0.55920119.786.08775.357.102—5.323—1.01240204.8911.287138.0913.365—10.870—2.635
对于CNN和SVM算法,使用SNR为-20 dB～-1 dB的数据训练网络模型;在测试过程中,分别调节两种方法的误差门限errth,使两种方法的Pf为0.10;最后利用调节得到的门限进行测试。对于DMMG和ED算法,利用Pf=0.10直接计算相应的检测门限。当SNR为-20 dB～-1 dB,次用户数量分别为10、20和40时,上述四种算法的Pd曲线如图5所示。
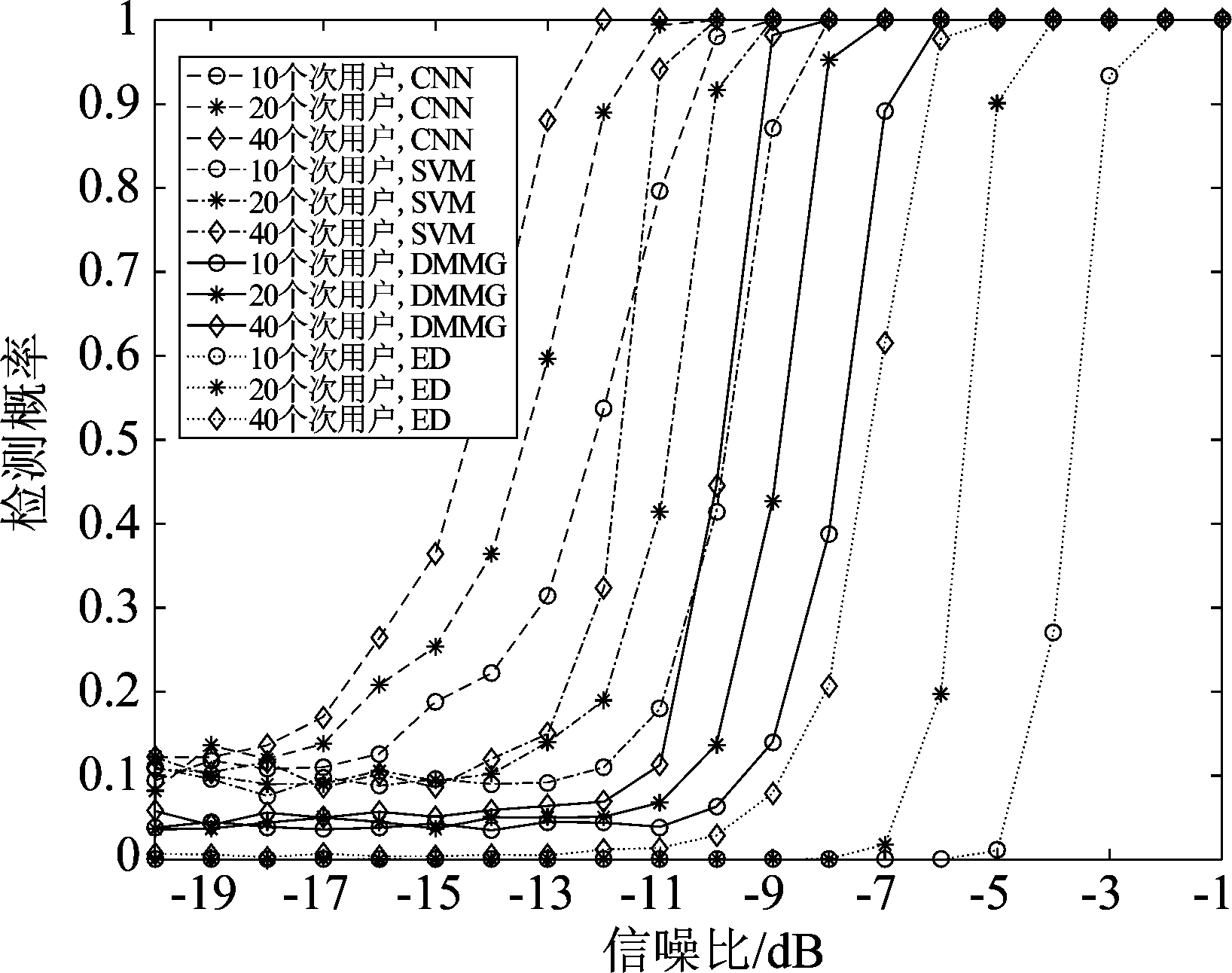
图5 四种算法在不同信噪比下的检测概率
Fig.5 Detection probabilities of four algorithms under different SNR
根据图5可得,CNN性能优于三种对比算法。当SNR为-12 dB、次用户数为40时,CNN的Pd达到1,SVM、 DMMG和ED算法的Pd分别约为0.32、0.07和0.01。当信噪比为-11 dB,次用户数为20时,CNN的Pd达到1,而SVM、 DMMG和ED算法的Pd分别约为0.41、0.11和0.00。当SNR是-10 dB、次用户数10,CNN的Pd达到1,而SVM、 DMMG和ED算法的Pd分别约0.41、0.06和0.00。
当SNR为-13 dB时,四种算法在次用户数分别为10、20和40时的ROC(Receiver Operating Characteristic)曲线如图6所示。
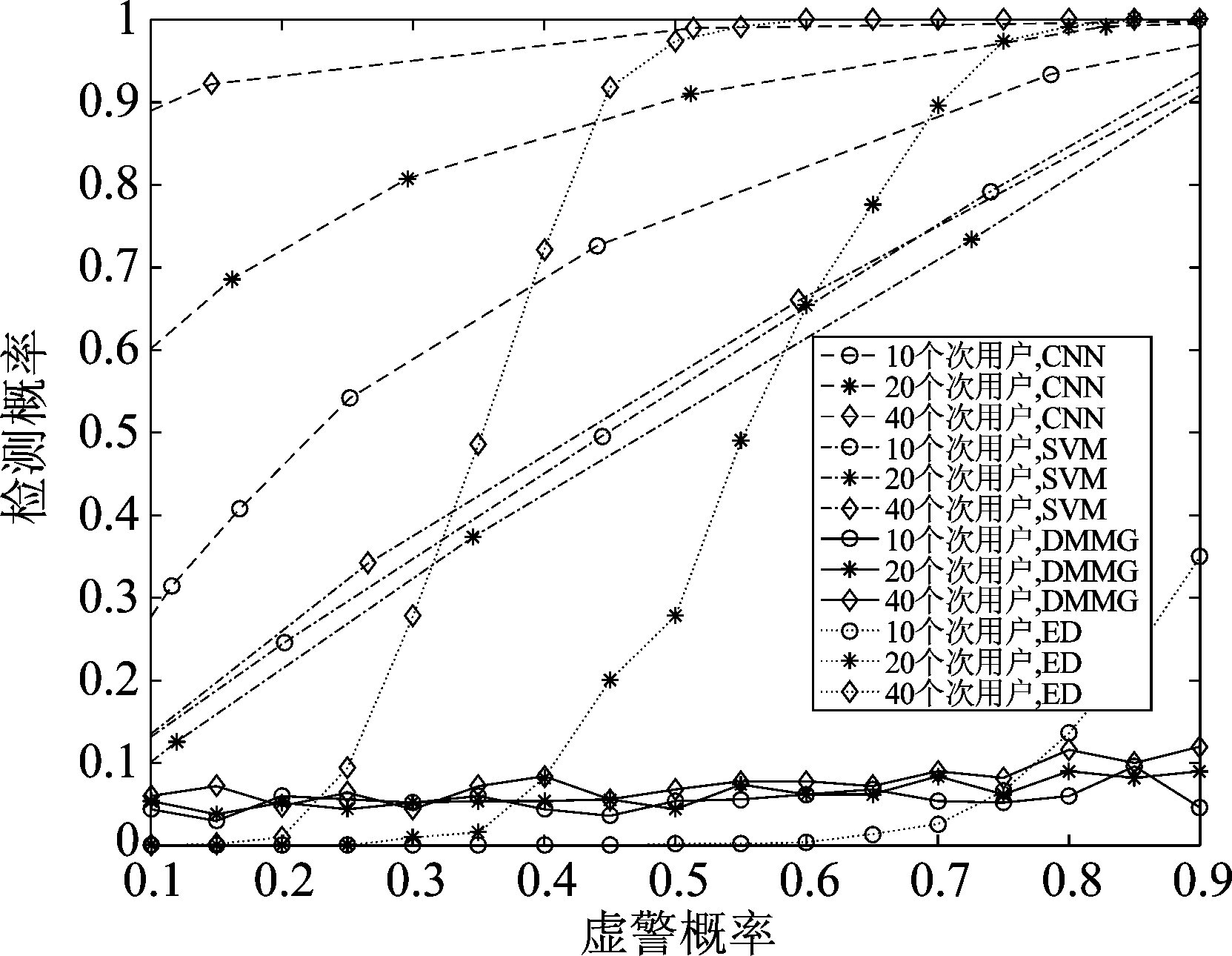
图6 -13 dB时四种算法的ROC曲线
Fig.6 ROC curves of four algorithms at -13 dB
实际系统希望在虚警概率尽可能低的情况下,达到尽可能高的检测概率。由图6可见,CNN的性能明显高于SVM、DMMG和ED算法。在SNR=-13 dB, Pf=0.30,次用户数量为10个、20个和40个时,CNN的Pd分别约为0.61、0.80和0.94,而其他三种算法的Pd都在0.4以下。由于次用户数量的增加,利用四种算法进行频谱感知所表现出的性能均得到提升。
5 结论
本文使用卷积神经网络以及接收信号协方差矩阵进行频谱感知。首先计算多个节点接收的I、Q两路数据协方差矩阵,然后使用卷积神经网络从协方差矩阵中提取出有用的特征对信号进行检测。仿真结果表明,相比对比算法,本文算法在SNR较低的条件下具有更高的Pd,且当次用户的数量增加时,频谱感知算法性能提升明显。
[1] Wael C B A, Armi N, Rohman B P A. Spectrum sensing for low SNR environment using maximum-minimum eigenvalue (MME) detection[C]∥International Seminar on Intelligent Technology & Its Applications, Lombok, 2016: 435- 438.
[2] 王颖喜, 卢光跃. 基于最大最小特征值之差的频谱感知技术研究[J]. 电子与信息学报, 2010, 32(11): 2571-2575.
Wang Yingxi, Lu Guangyue. Spectrum sensing technology based on the difference between maximum and minimum eigenvalues[J].Journal of Electronics and Information, 2010, 32(11): 2571-2575.(in Chinese)
[3] 杨雪梅, 徐家品, 何希. 基于特征值对数分布的频谱感知算法[J]. 电子技术应用, 2018, 44(1): 79- 83.
Yang Xuemei, Xu Jiapin, He Xi. Spectrum sensing algorithm based on logarithmic eigenvalue distribution[J]. Application of Electronic Technology, 2018, 44(1): 79- 83.(in Chinese)
[4] 王鑫, 汪晋宽, 刘志刚, 等. 基于随机森林的认知网络频谱感知算法[J]. 仪器仪表学报, 2013, 34(11): 2471-2477.
Wang Xin, Wang Jinkuan, Liu Zhigang, et al. Random forest-based cognitive network spectrum sensing algorithms[J]. Journal of Instruments and Instruments, 2013, 34(11): 2471-2477.(in Chinese)
[5] 陈易, 张杭, 胡航. 基于BP神经网络的协作频谱感知技术[J]. 计算机科学, 2014, 42(2): 43- 45.
Chen Yi, Zhang Hang, Hu Hang. Cooperative spectrum sensing technology based on BP neural network[J]. Computer Science, 2014, 42(2): 43- 45.(in Chinese)
[6] Thilina K M, Choi K W, Saquib N, et al. Machine learning techniques for cooperative spectrum sensing in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(11): 2209-2221.
[7] Sobabe G C, Song Y, Bai X, et al. A cooperative spectrum sensing algorithm based on unsupervised learning[C]∥International Congress on Image & Signal Processing, Shanghai, 2017: 1- 6.
[8] 姚迪, 刘会杰, 刘洁, 等. 基于支持向量机的认知无线电频谱感知[J]. 电子设计工程, 2018, 26(21): 1-5.
Yao Di, Liu Huijie, Liu Jie, et al. Cognitive radio spectrum sensing based on support vector machine[J]. Electronic Design Engineering, 2018, 26(21): 1-5.(in Chinese)
[9] 张孟伯, 王伦文, 冯彦卿. 基于卷积神经网络的OFDM频谱感知方法[J]. 系统工程与电子技术, 2019, 41(1): 178-186.
Zhang Mengbo, Wang Lunwen, Feng Yanqing. OFDM spectrum sensing method based on convolutional neural network[J]. Systems Engineering and Electronic Technology, 2019, 41(1): 178-186.(in Chinese)
[10]黄浩, 吴利民.基于能量和协方差的两步频谱感知[J].无线电通信技术, 2014, 40(6): 29-32, 57.
Huang Hao, Wu Limin. Two-step spectrum sensing based on energy and covariance[J]. Radio Communication Technology, 2014, 40(6): 29-32, 57.(in Chinese)
[11]陈丽, 陈静, 高新涛, 等.基于支持向量机与反K近邻的分类算法研究[J].计算机工程与应用, 2010, 46(24): 135-137, 188.
Chen Li, Chen Jing, Gao Xintao, et al. Research on classification algorithm based on support vector machine and anti-k nearest neighbor[J]. Computer Engineering and Application, 2010, 46(24): 135-137, 188.(in Chinese)
[12]孙月驰, 李冠.基于卷积神经网络嵌套模型的人群异常行为检测[J].计算机应用与软件, 2019, 36(3): 196-201, 276.
Sun Yuechi, Li Guan. Detection of crowd abnormal behavior based on nested model of convolutional neural network[J]. Computer Application and Software, 2019, 36(3): 196-201, 276.(in Chinese)
