1 引言
中国民航局在全国机场运输生产指标统计中指出,截止到2018年12月,我国当年累计旅客吞吐量已达到12亿多人次,起降架次达到1108.9万,比上年同期增长8.2%。随着我国民航事业的发展,伴随着民航技术,尤其是导航监视技术的不断进步,越来越多的飞机装载有ADS-B系统进行实时监测,使得ADS-B的空域流量逐渐增多。当多条ADS-B报文同时到达接收机时,信号之间可能发生部分信息混叠,即交织现象,从而对飞机的监视造成了极大困难[1]。文献[2]表明,当信号不发生交织的概率为95%时,飞机数量最多为121架;而当概率为99%时,数量下降至24架。如果将发生交织的信号分离开,则概率为95%和99%的飞机数量将分别增加至2284架和984架。可见,对ADS-B信号进行解交织将极大提高接收机范围内的飞机数量。
关于ADS-B解交织问题,国内外众多学者进行了相关研究。在空域解交织方面,Gong等人[3]采用扩展投影(Extended Projection Algorithm, EPA)算法和主成分分析(Principle Component Analysis, PCA)算法分离ADS-B交织信号,但应用EPA算法需要预处理混合信号。文献[4]提出了一种高增益稳健正交投影(Project Algorithm, PA)算法,该算法在保证稳健性的同时提高了信号的输出信噪比。Zhang等人[5]把PCA-FastICA算法应用于ADS-B信号解交织中,FastICA算法具有收敛速度快且鲁棒性好等优点,同时不需要阵列校准,上述这些方法都是基于阵列信号处理进行的,但在实际应用过程中,阵列天线存在着与现有接收设备兼容性不好等问题,所以近年来单天线成为了国内外研究热点。在单天线解交织方面,文献[1]提出了一种时域解交织方法,即通过K-means算法对不同区间上的ADS-B信号进行累加分类(Accumulation Classification, AC),该方法需交织信号之间存在一定功率差时才能有较好的分离效果。Yu等人[6]提出了一种自适应阈值调整算法用于ADS-B解交织,该方法通过估计重叠信号的功率来分离ADS-B信号。文献[7]将经验模态分解(Empirical Mode Decomposition, EMD)和独立分量分析(ICA)算法应用于单天线雷达信号的分离中。EMD算法有较好的稳健性,可用于将单通道接收到的非平稳信号自适应分解出其高频分量和低频分量,且无需知道信号的先验信息,对ADS-B交织信号相对时延不敏感,但该算法在当接收到的信号大于两条及以上且其频率比值为0.5~1.5时,会出现模态混叠的现象。
考虑到经验模态分解[8]可将单天线接收到的ADS-B信号进行升维,并且可实现交织信号个数自检测,本文提出了一种基于经验模态分解的单天线盲解交织算法。该算法首先对单天线接收到的ADS-B观测信号进行EMD分解,采用能量检测法估计出ADS-B交织数目,针对EMD分解中出现的模态混叠现象构造动态嵌入矩阵,利用独立分量分析算法进行解混叠,将与交织信号相关性大的分量信号同交织信号组成新的多维信号,最后利用FastICA算法实现单天线ADS-B信号的解交织。
2 信号模型
ADS-B信号采用振幅键控(Amplitude Shift Keying, ASK)调制方式将信号调制到1090 MHz进行广播,每帧信号的长度固定为120 μs,由8 μs报头和112 μs数据位组成[9]。报头中含有4个脉冲,在数据位采用的是脉冲位置调制(Pulse Position Modulation, PPM)方式,数据位中包含有飞机的高度、经纬度等信息,ADS-B信号格式如图1所示。

图1 ADS-B信号格式
Fig.1 ADS-B signal format
设每架飞机广播的ADS-B信号为sl(t),l=1,2,…,L,则单天线接收到的ADS-B信号模型可表示为:
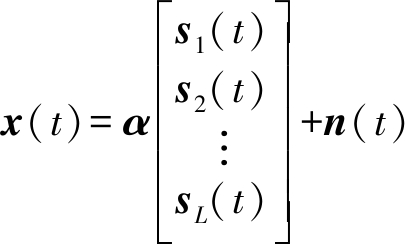
(1)
其中,n(t)表示加性高斯白噪声。单天线接收条件下信号解交织的目标是在系数矩阵α=[a1,a2,…,aL]未知的情况下分离出原始信号s1(t),s2(t),…,sL(t),这属于欠定盲分离问题,而EMD算法可以对单通道接收到的ADS-B信号进行自适应分解来构造多维信号,这样就把欠定分离问题转化为正定分离问题,同时可利用EMD分解实现ADS-B交织信号个数的自检测。
3 基于EMD的解交织算法
3.1 经验模态分解(EMD)
经验模态分解(EMD)是一种自适应分解处理方法,可以将接收到的非平稳信号分解为一系列线性本征模态函数(Intrinsic Mode Function,IMF)。EMD的具体过程如下:
(a)对交织信号x(t),取其局部最大值和最小值,利用插值函数分别对这些值进行插值得到交织信号的上包络u(t)和下包络l(t),求得包络均值为:
d1(t)=[u(t)+l(t)]/2
(2)
(b)用x(t)减去d1(t)得:h1(t)=x(t)-d1(t),对h1(t)重复进行步骤(a),直到:
h1k(t)=h1(k-1)(t)-d1k(t)
(3)
满足IMF的特征[8],并令imf1(t)=h1k(t),则imf1(t)为筛分出的第一个IMF分量;
(c)用x(t)减掉imf1(t),得到:
x1(t)=x(t)-imf1(t)
(4)
把x1(t)当做原始信号,重复步骤(a)~(c),依次得到imf2(t),…,imfm(t)和残差rm(t)。
ADS-B信号本身具有非平稳特性,所以可以采用EMD算法分解出ADS-B信号的高频分量部分,从而对单通道信号进行升维。
3.2 信源数目检测
由于ADS-B信号帧长为120 μs,则根据其特点对接收到的信号进行预检测,判断是否存在交织问题。具体做法为:在检测到ADS-B信号有效脉冲位置(Valid Pulse Position,VPP)后继续做脉冲检测,当出现连续3个脉冲区间无有效脉冲时认为信号结束[10],从而得到信号总时长,若总时长大于120 μs,则判定为存在交织问题。交织信号x(t)经EMD分解后得到m个IMF分量imfi(t)和残差rm(t)之和,即:
(5)
其中m=[log2N]-1,N为交织信号的采样点数[8]。
每一个本征模态函数imfi(t)是交织信号x(t)在每个原始信号频率段上的分量,随着i的增大,imfi(t)所对应的频率是逐渐降低的[11]。由于分离出的每一个IMF的能量都来自于原信号,其中前L个分量的能量值与ADS-B信号能量值相对应,后m-L个分量对应于噪声等干扰信号的能量,其能量值小于前L个分量的能量值[12],而残差rm(t)的能量很小,可忽略不计。因此,可以把IMF的能量值作为门限值,并与每一帧ADS-B信号能量值相结合进行信源个数的判别。经EMD分解得出的每一个IMF分量的能量为:
(6)
依次对分解出来的IMF分量求其能量并设置门限值进行检测,门限值K为第一个IMF能量的1/8倍,即:
(7)
若EMD分解出的IMF能量值Ei大于K,则可认定其为一条ADS-B信号,从而对每一个IMF分量的能量值进行判决直到检测出所有的ADS-B信号。该方法利用EMD的分解特性,直接求分解出来的每一个IMF的能量值,并对每一个能量值进行阈值检测来识别信源个数,无需采用其他附加方法来进行检测。
3.3 解交织算法
对ADS-B信号进行盲解交织的目标是确定分离矩阵,从而获得每一个源信号的估计值。交织的ADS-B信号x(t)通过EMD算法自适应的分解为有限个IMF分量imfi(t)(i=1,2,…,m)和残差rm(t),如式(5)所示。采用设定阈值法对分解出来的单分量信号进行能量判别来检测交织信号个数,取前L-1个与交织信号x(t)相关性较大的IMF分量同交织信号x(t)组成新的多维信号:
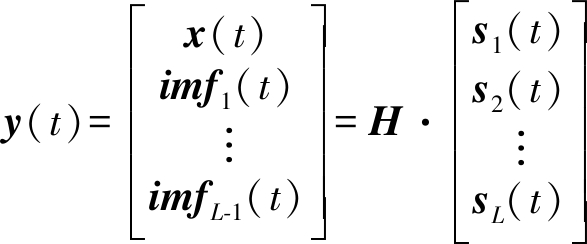
(8)
从而将欠定解交织问题转化为正定解交织问题。
然而单天线接收到的ADS-B交织信号由于受到多普勒频移和噪声等因素影响,多条原始信号之间的频率比值在0.5~1.5之间,导致EMD分解出来的一个IMF分量中包含交织信号的多个频率特征,即模态混叠现象,从而无法直接利用FastICA算法对多通道信号y(t)进行解交织。本文采用相空间重构法[13]和独立分量分析来进行解混叠,即对混叠分量imfi(t)中的N-(M-1)τ个采样点分别延迟时间τ,从而构成动态嵌入矩阵[14]:
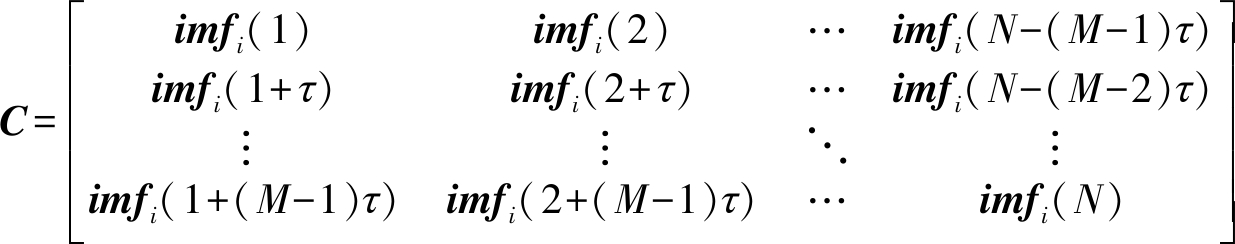
(9)
其中,M和τ分别为矩阵的行数和延迟点数,其值为:M=2L+1,τi=fs/fci, fs为采样频率, fci为混叠分量的频率。本文采用独立分量分析对虚拟多维矩阵C进行解混叠,假设分离后的信号为gi1(t),gi2(t),…,giM(t),但其中可能存在虚假分量[15],从而影响最终分离结果,则采用式(10)来计算解混叠出来的各分量与交织信号x(t)之间的相关性来消除虚假分量。
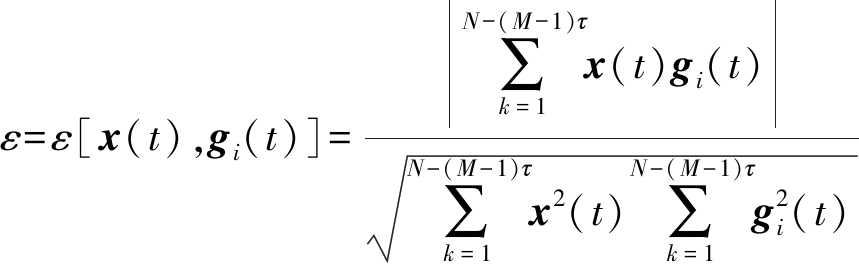
(10)
其中:ε越小,则x(t)与gi(t)相关性越小;反之,x(t)与gi(t)相关性越大。
分别计算对多维矩阵C解混后的分量gi1(t),…,giM(t)与交织信号x(t)的相似系数,将其中相似系数大的信号与x(t)构成新的多维信号,记为:
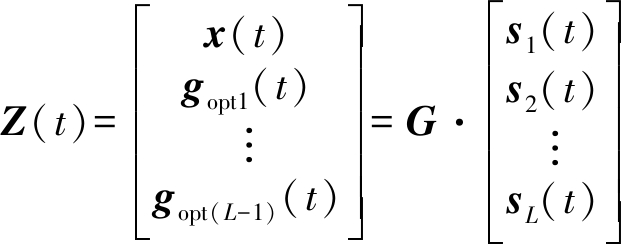
(11)
至此,本文所提的单天线ADS-B解交织算法步骤如下:
(1)对单天线接收到的ADS-B信号x(t)进行预检测,若信号时域长度大于120 μs,则判定存在交织问题;
(2)对交织信号x(t)进行经验模态分解得到IMF分量ximf=(imf1,imf2,…,imfm,rm)T;
(3)利用能量判别法估计信号交织个数,根据信源数目构造动态嵌入矩阵消除模态混叠现象;
(4)计算解混叠后的分量gi1(t),…,giM(t)与交织信号x(t)的相似系数,取与交织信号x(t)相关性大的L-1条信号分量与其构成新的多路信号,记为Z(t)=[x(t),gopt1(t),…,gopt(L-1)(t)]T;
(5)针对新的多维信号Z(t),应用FastICA算法实现盲解交织,得到源信号s的估计值y。

图2 原理框图
Fig.2 The principle block diagram
4 仿真实验结果
仿真实验中分别采用2条、3条和4条ADS-B信号进行验证信源数目自检测性能。信号1经纬度为(117.5,37.5),高度为34100 ft;信号2经纬度为(117.8,37.4),高度为32100 ft;信号3经纬度为(118.0,37.6),高度为33000 ft;信号4经纬度为(118.2,37.3),高度为33100 ft,采样频率为80 MHz,信噪比分别为19 dB、20 dB、20 dB和21 dB。
依次对ADS-B信号x(t)的三种交织情形进行EMD分解,得到IMF分量ximf=[imf1(t),imf2(t),…,imf13(t),r13(t)]T,其中imf1(t),…,imf5(t)的波形如图3所示,依次计算每一个IMF的能量,得到其能量分布如图4所示。由图4可知:采用能量判别法对交织信号个数检测,有对应的信源个数大于设定的门限值K,从而估计为相应的信源数目。图5为信源检测正确率与信噪比之间的关系曲线。
在民航应用中,出现两条信号交织的概率最大[16],所以本实验采用单天线接收信号1和信号2这两条ADS-B信号进行解交织,设置相对时延为10 μs,单天线接收到的ADS-B交织信号时域波形如图6所示。对交织信号x(t)进行EMD分解,取分解后的第一个IMF分量imf1(t)对其进行构造动态嵌入矩阵C,并采用独立分量分析对矩阵C进行分离,得到各分量与交织信号x(t)的相似系数如表1所示,选择阈值μ=0.6,于是消除虚假分量g12(t),由交织信号x(t)和g11(t)构成二维矩阵Z(t)进行FastICA盲解交织,得到分离后的信号时域波形如图7所示。
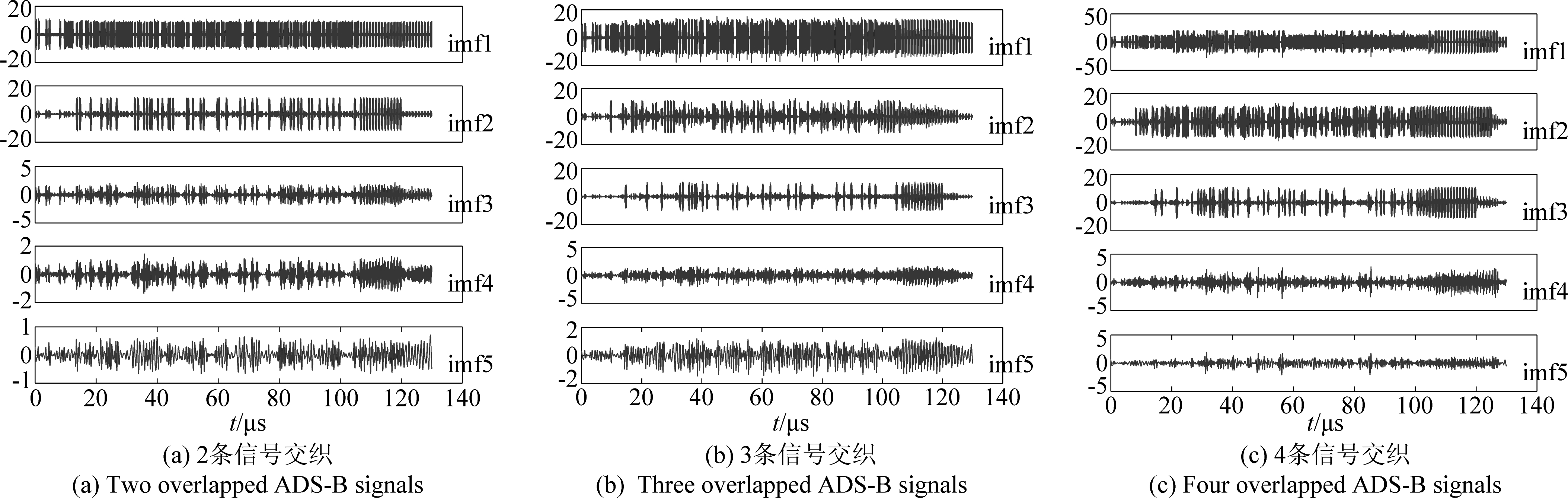
图3 各IMF时域波形图
Fig.3 Time domain waveform diagram to each IMF
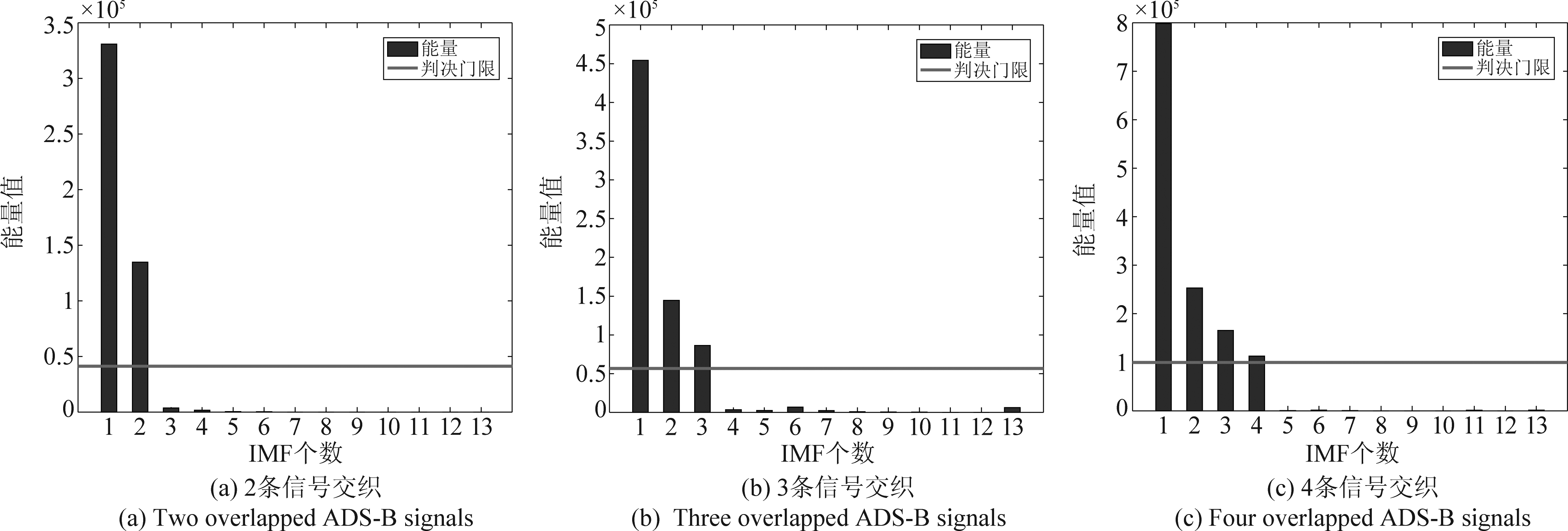
图4 各IMF所对应的能量值
Fig.4 Energy value corresponding to each IMF
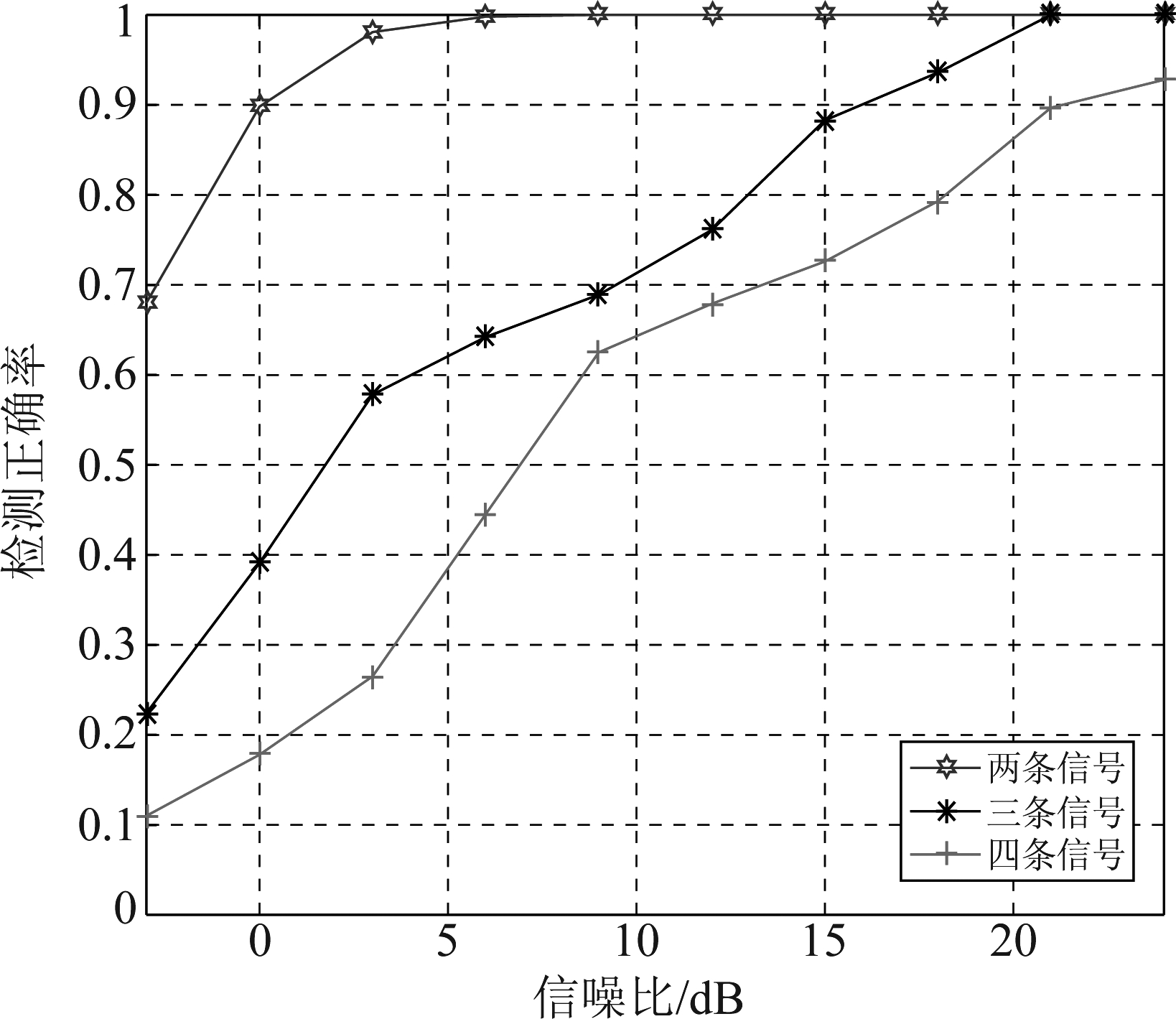
图5 检测概率与信噪比关系曲线
Fig.5 Detection probability and SNR Curve
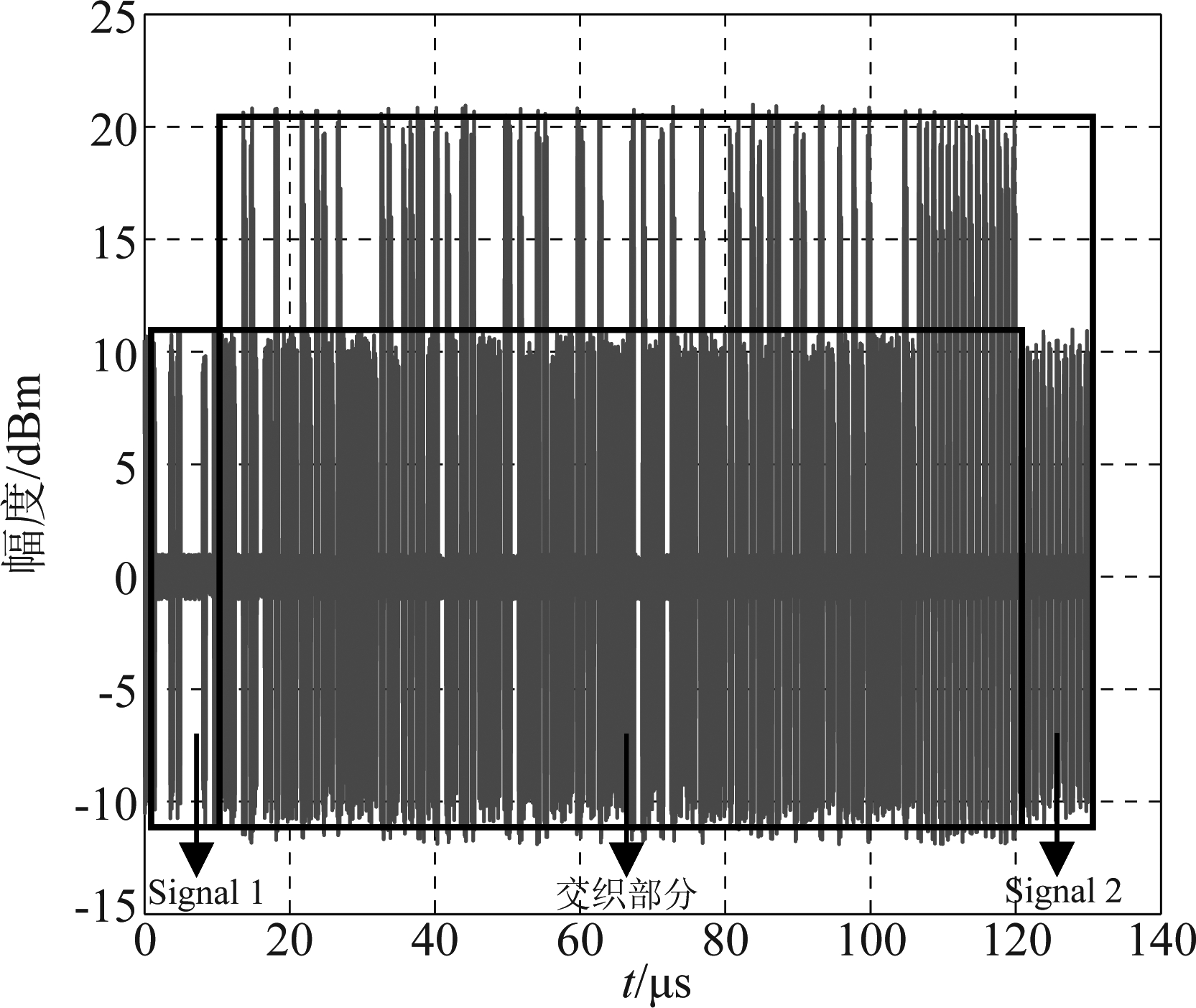
图6 交织信号时域波形
Fig.6 Overlapping signal in time domain
表1 相似系数
Tab.1 Similarity coefficient

x(t)g11g1210.73260.4765
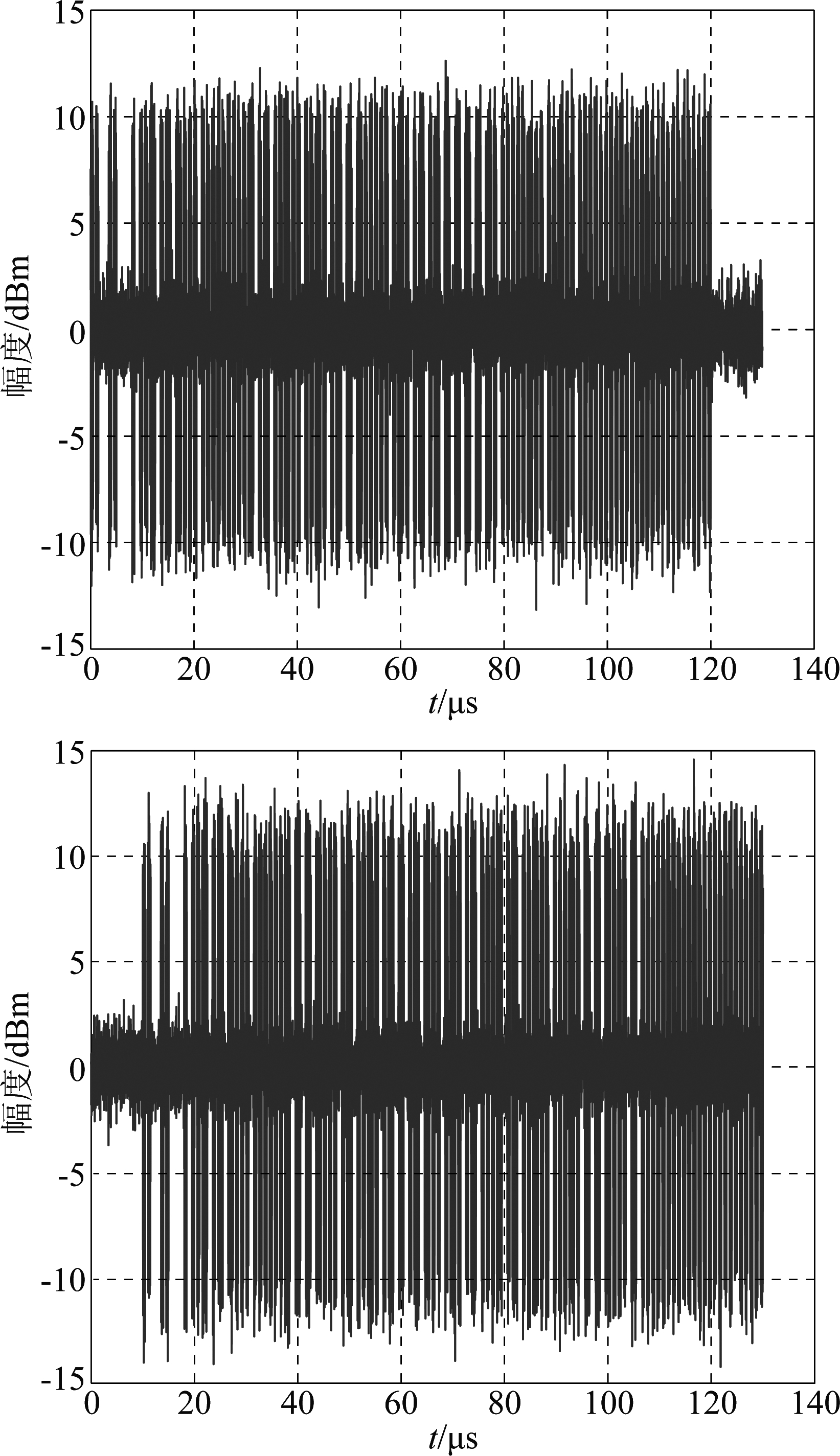
图7 解交织信号时域波形
Fig.7 Separated signal in time domain
由图7可以看出,两条ADS-B交织信号得到了很好的分离。由此得出,利用EMD算法不仅可以将单通道信号升维转为多通道信号,从而使用相应的盲源分离算法将升维后的多通道信号分离,而且还可以实现交织信源个数的自检测。将解交织后的信号放入ADS-B接收机中进行解码,结果如表2所示:解码结果与仿真的ADS-B信号相同,可以得到飞机的识别码等信息。
表2 解码结果
Tab.2 Decoding result

信号识别码(AA)经度(Lon)纬度(Lat)高度(Alt)信号1780123117.5037.5034100 ft信号2780ABC117.8037.4032100 ft
为了进一步验证算法性能,本次实验利用两条ADS-B信号交织来进行数据对比测试,对比方法为基于累加分类[1]的解交织算法和基于置信度判决(Confidence Declaration, CD)[17]的解交织方法,其中基于累加分类算法中信号1对应功率较高的信号,信号2对应功率较低的信号,两信号功率相差3 dBm,基于置信度判决算法是取接收到的信号中的一条来进行处理,对其中一条解交织出来则认为解码正确,三种解交织方法正确解码率与信噪比的变化关系曲线如图8所示。解码正确率随两条信号功率差的变化曲线如图9所示,可以看出基于EMD-ICA解交织方法几乎不受功率差变化影响。通过上述实验验证,本算法可成功应用于单天线ADS-B信号解交织中。

图8 解码正确率随信噪比变化关系曲线
Fig.8 The curve of decoding accuracy changing with SNR
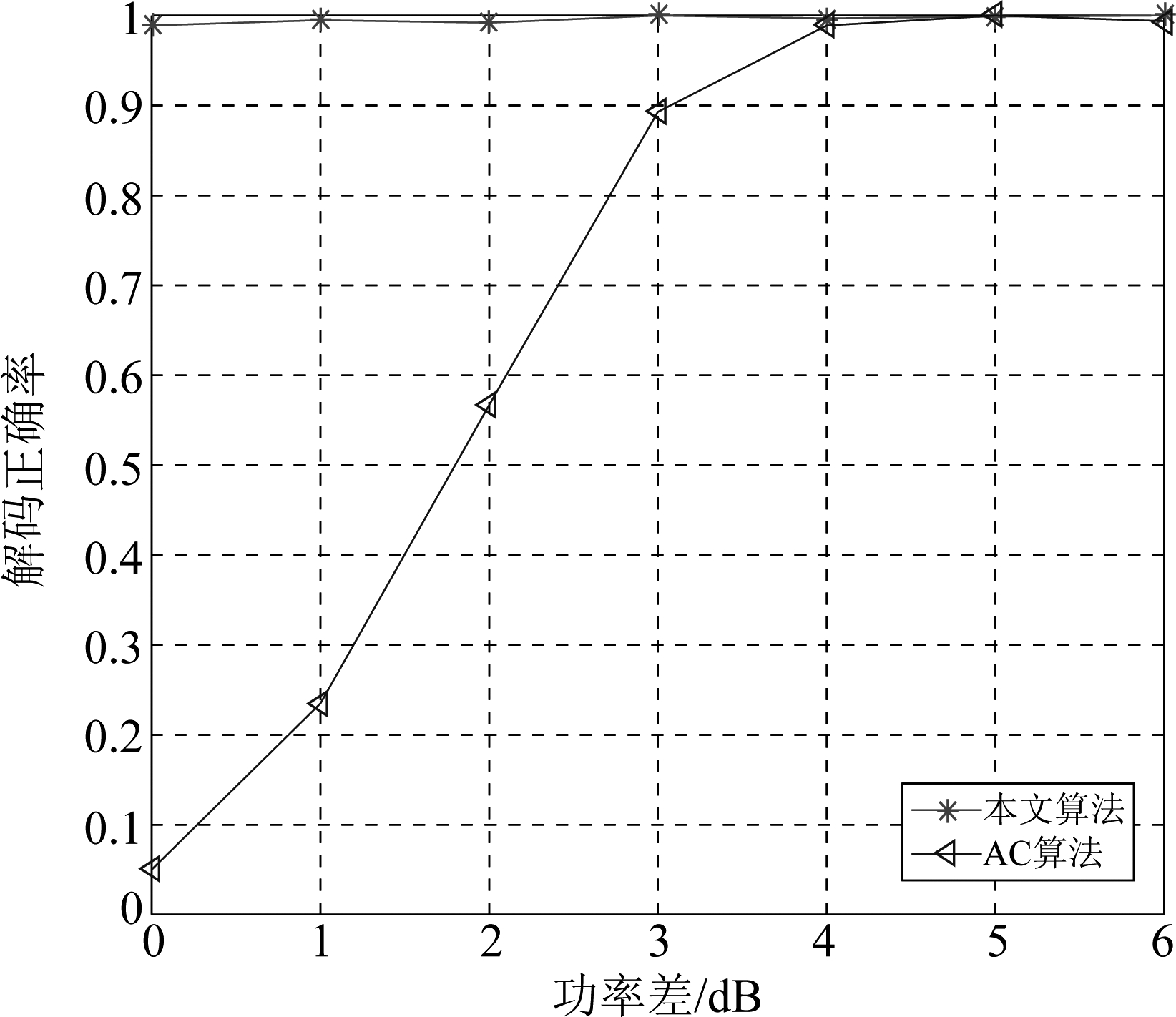
图9 解码正确率随功率差变化关系曲线
Fig.9 The curve of decoding accuracy changing with power difference
此外,本实验还研究了两条信号的相对时延对于信号解交织的影响程度,设置信噪比为18 dB,对比方法为基于四阵元的PA算法,设置两交织信号的相对时延从0 μs到10 μs,进行500次蒙特卡洛实验得出的解码正确率随信号的相对时延关系曲线如图10所示,可以看出,PA算法在对于两条交织信号时延差较小时影响大,其原因是PA算法需要两条信号之间存在一定的时延差来求信号的导向矢量估计值,即需要采用其中一条信号来估计导向矢量,而本算法在除完全重叠时正确率差别不大,因此本算法对单天线接收的ADS-B交织信号相对时延不敏感。
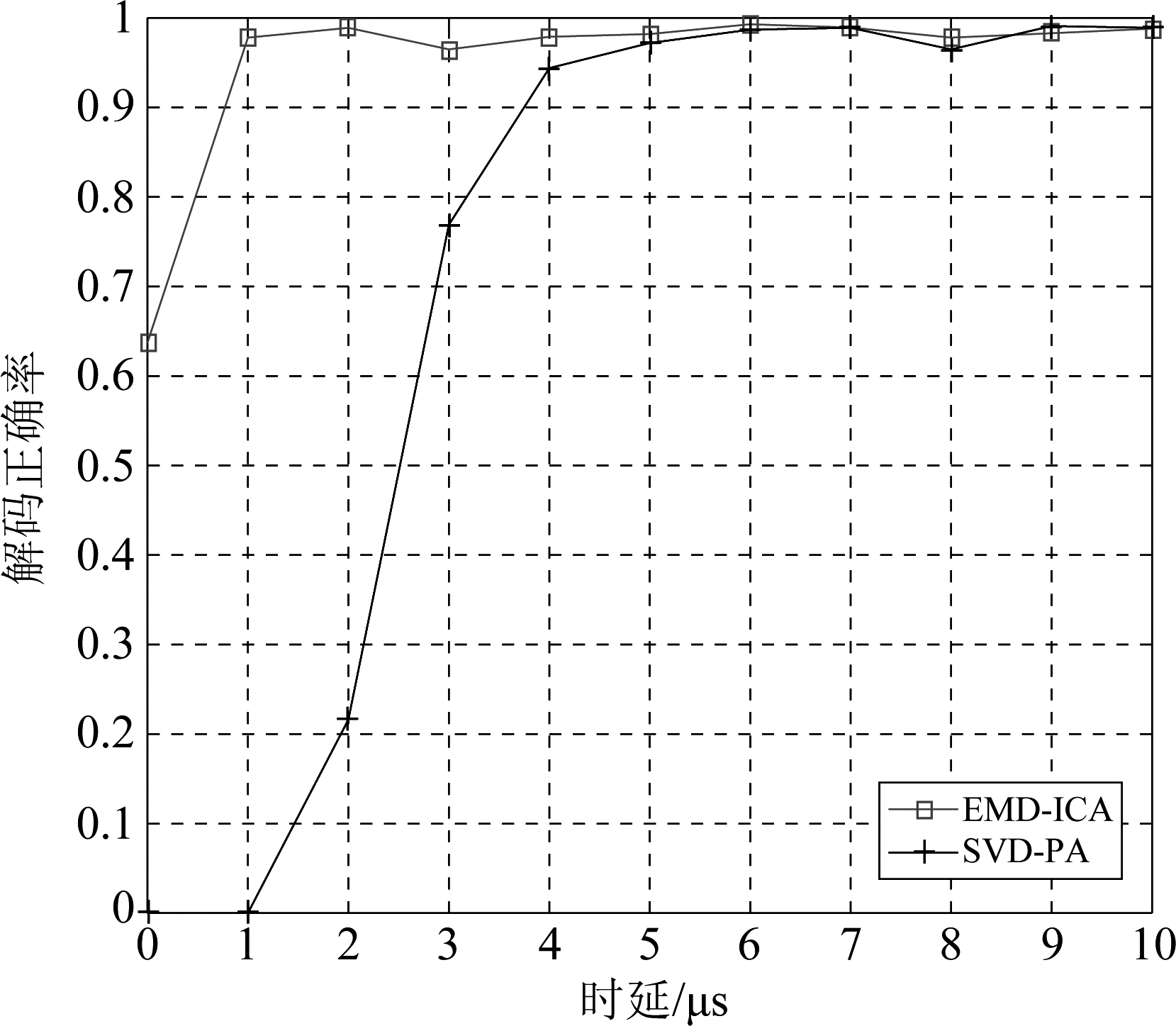
图10 解码正确率随时延变化关系曲线
Fig.10 The curve of decoding accuracy changing with time delay

图11 单天线接收实物图
Fig.11 Single antenna receiving physical chart
5 实采数据结果
为了进一步验证算法的有效性,本小节通过接收的实采数据来验证算法的性能。单天线接收实物如图11所示,通过(a)图中接收机测试系统产生ADS-B交织数据并调制到10 MHz中频,由(b)图中两条发射天线发送数据,通过(c)图中单天线接收数据,送至(d)图下变频器得到交织时域波形如(e)图所示,其中采样频率为80 MHz,发射天线与接收天线的位置关系如图(f)所示。
图12为实采数据经EMD分解后得到的前5个IMF分量,求得所有的IMF分量的能量如图13所示,可以看出有两个信号能量大于门限值,所以观测信号由两条ADS-B信号交织。图14为将(e)图中的ADS-B交织信号通过EMD-ICA进行解交织得到的时域波形,可以看到此算法可以解出原始信号,且幅度与原始信号基本相等。将交织信号实采数据和解交织后的两条ADS-B信号经接收机解码并进行CRC校验,得到结果如表3所示,由表可知:交织信号无法通过CRC校验,而经该算法解交织后的数据可以通过CRC校验,能够正确解出飞机的信息,证明该方法能够有效地解决ADS-B信号交织问题。

图12 各IMF时域波形图
Fig.12 Time domain waveform diagram to each IMF
表3 解码结果
Tab.3 Decoding result

信号识别码(AA)下行链路格式(DF)高度(Alt)CRC校验交织信号2320111731296 ft×信号10001021732379 ft√信号21011121733623 ft√
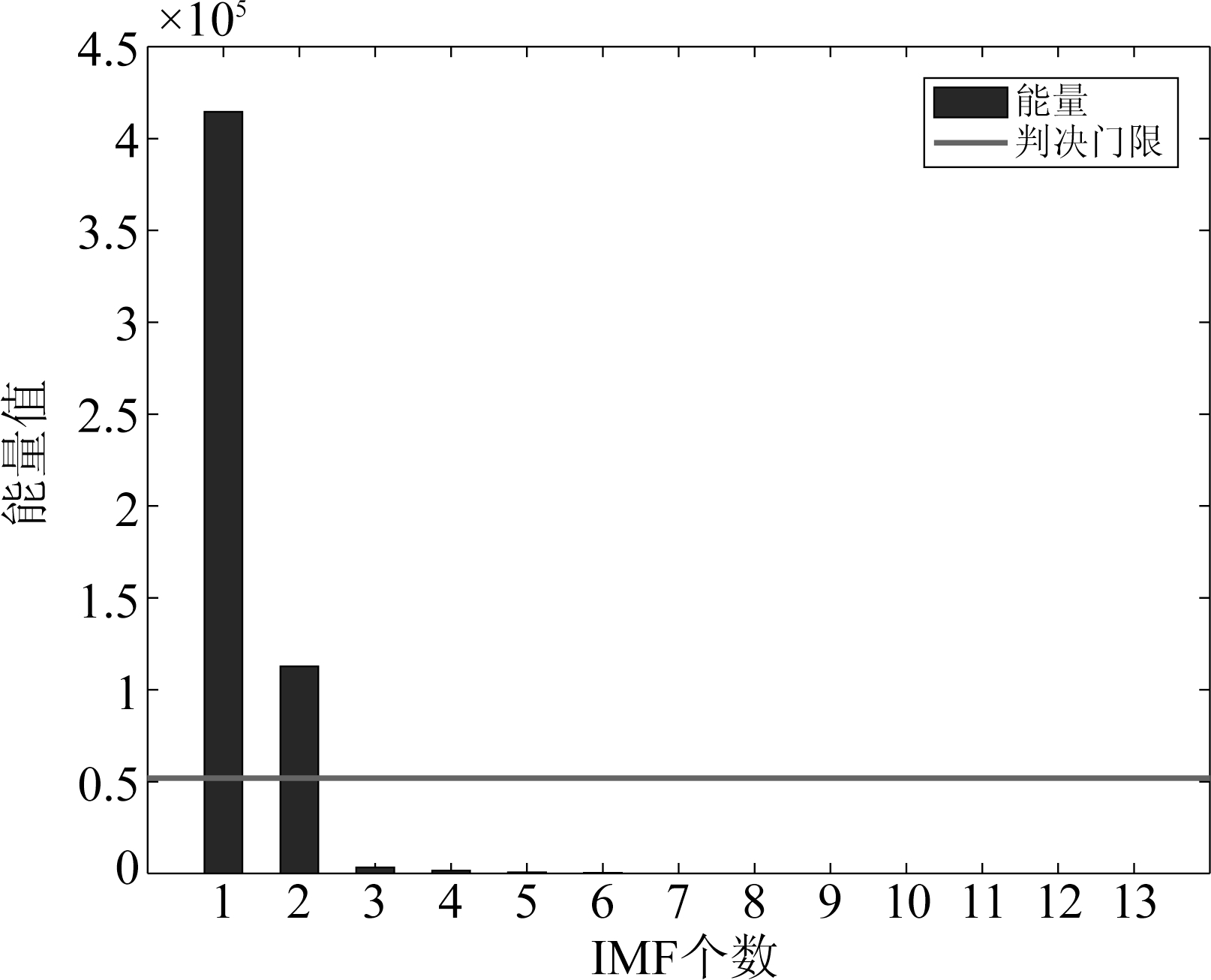
图13 各IMF所对应的能量值
Fig.13 Energy value corresponding to each IMF
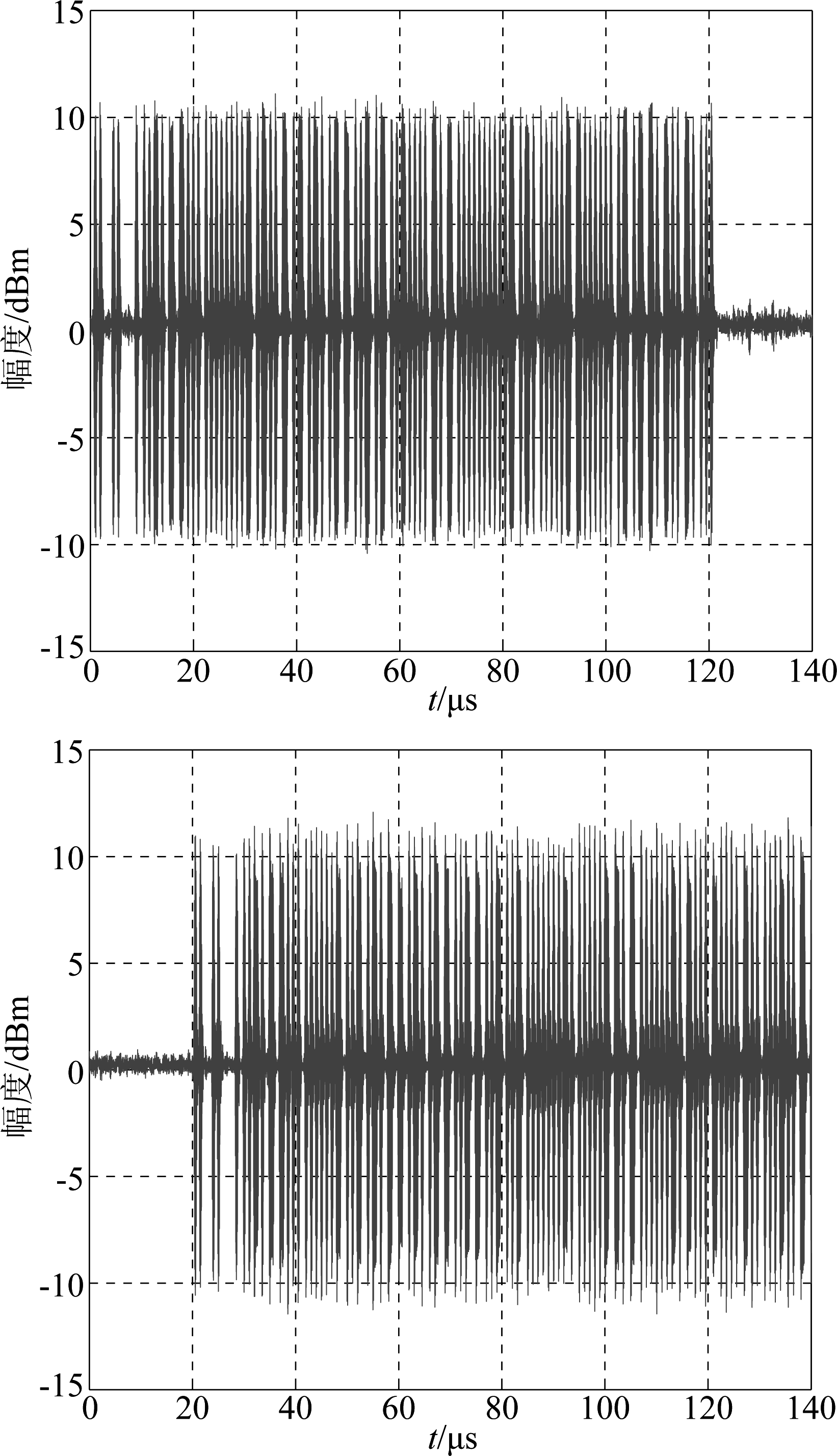
图14 解交织信号时域波形
Fig.14 Separated signal in time domain
6 结论
本文结合了经验模态分解和盲源分离各自的优点,提出了基于EMD-ICA的单天线ADS-B信号解交织方法。该方法将单天线接收到的ADS-B信号进行经验模态分解并根据分解得到的IMF分量特点及ADS-B信号特征相结合识别出信源个数,通过构造动态嵌入矩阵消除模态混叠现象的影响,并依据信号个数重组多维混合信号,将欠定盲源分离问题转化为正定问题,从而利用FastICA算法对多维混合信号进行分离。本文中所介绍的方法是针对于单天线接收来进行的,该方法可以实现信源数目自检测,且有较好的稳健性。本文通过大量的仿真实验及实采数据来进行测试,并与其他解交织算法进行了对比,证明此算法可成功应用于单天线ADS-B信号解交织中。
[1] 吴仁彪, 吴琛琛, 王文益. 基于累加分类的ADS-B交织信号处理方法[J]. 信号处理, 2017, 33(4): 572-576. doi: 10.16798/j.issn.1003- 0530.2017.04.017.
Wu Renbiao, Wu Chenchen, Wang Wenyi. A method of overlapped ADS-B signal processing based on accumulation and classification[J]. Journal of Signal Processing, 2017, 33(4): 572-576. doi: 10.16798/j.issn.1003- 0530.2017.04.017.(in Chinese)
[2] Petrochilos N, Galati G, Piracci E. Separation of SSR Signals by Array Processing in Multilateration Systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982.doi: 10.1109/TAES.2009.5259177.
[3] Gong Fengxun, Wang Kai, Ma Yanqiu. An Algorithm to Separate 1090ES ADS-B Signals[J]. Advanced Materials Research, 2014, 875- 877: 2158-2163.
[4] 卢丹, 赵敏同. 用于ADS-B解交织的高增益稳健PA算法[J]. 信号处理, 2018, 34(9): 1060-1067. doi: 10.16798/j.issn.1003- 0530.2018.09.006.
Lu Dan, Zhao Mintong. A Robust and High Gain Algorithm for Separating Overlapped ADS-B Signal Based on PA[J]. Journal of Signal Processing, 2018, 34(9): 1060-1067. doi: 10.16798/j.issn.1003- 0530.2018.09.006.(in Chinese)
[5] Zhang Zhaoyue. Optimization Performance Analysis of 1090ES ADS-B Signal Separation Algorithm based on PCA and ICA[J]. International Journal of Performability Engineering, 2018, 14(4): 741-750. doi: 10.23940/ijpe.18.04.p17.741750.
[6] Yu Sunquan, Chen Lihu, Li Songting. Separation of space-based ADS-B signals with single channel for small satellite[J]. 2018 IEEE 3rd International Conference on Signal and Image Processing, July 2018, doi: 10.1109/SIPROCESS.2018.8600464.
[7] 郑伟然. 基于EMD和ICA的混合信号分离算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
Zheng Weiran. Research on Hybrid Signal Separation based on Empirical Mode Decomposition and Independent Component Analysis[D]. Harbin: Harbin Institute of Technology, 2018.(in Chinese)
[8] Norden E Huang, Zheng Shen, Steven R Long, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. The Royal Society, 1998, 454: 903-995.
[9] RTCA DO-260B. Minimum Operational Performance Standards for 1090 MHz Extended Squitter Automatic Dependent Surveillance-Broadcast(ADS-B) and Traffic Information Services-Broadcast(TIS-B)[S]. 2009.
[10]吴琛琛. ADS-B系统解交织算法研究[D]. 天津: 中国民航大学, 2017.
Wu Chenchen. Overlapped Signals Separation for ADS-B System[D]. Tianjin: Civil Aviation University of China, 2017.(in Chinese)
[11]Wang Yung-hung, Hu Kun, Lo Men-Tzung. Uniform Phase Empirical Mode Decomposition: An Optimal Hybridization of Masking Signal and Ensemble Approaches[J]. IEEE Access, 2018, 6: 34819-34833.
[12]Dong Y L, Zhang J, Guan J, et al. Weak target detection based on the Membership Degree of the IMFs Energy[C]∥Proceedings of 2011 IEEE CIE International Conference on Radar, 2012. doi: 10.1109/CIE-Radar.2011.6159588.
[13]He Pengju, She Tingting, Li Wenhui, et al. Single channel blind source separation on the instantaneous mixed signal of multiple dynamic sources[J]. Mechanical Systems and Signal Processing, 2018, 113: 22-35. doi: 10.1016/j.ymssp.2017.04.004.
[14]Sauer T, Yorke J A, Casdagli M. Embedology[J]. Journal of Statistical Physics, 1991, 65(3- 4): 579- 616.
[15]赵知劲, 黄艳波. 基于经验模态分解的单通道盲源分离算法[J]. 计算机应用研究, 2017, 34(10): 3010-3012. doi: 10.3969/j.issn.1001-3695.2017.10.029.
Zhao Zhijin, Huang Yanbo. Single-channel blind source separation algorithm based on empirical mode decomposition[J]. Application Research of Computers, 2017, 34(10): 3010-3012. doi: 10.3969/j.issn.1001-3695.2017.10.029.(in Chinese)
[16]Liu Kai, Zhang Tao, Ding Yang. Blind signal separation algorithm for space-based ADS-B[C]∥International Conference on Mechatronics Engineering and Information Technology(ICMEIT): Beijing, China, 2016: 384-390.
[17]RTCA, DO-260B 1090 Minimum Operational Performance Standard for ADS-B and TIS-B[I]. 2006, 7.

