1 引言
跳频通信网台分选是截获敌方通信,产生最佳干扰信号的首要前提。现有的跳频信号网台分选主要利用跳频信号的持续时间、方位信息、功率以及信号时间相关性等参数实现跳频信号的网台分选识别。文献[1]通过计算跳频信号的方向信息来实现网台分选。文献[2]通过对跳频信号的功率、时间和方位等参数进行聚类分选,实现对跳频信号的分类。但是,随着跳频模式的增多,仅靠以上特征难以实现跳频信号的正确分选。考虑到跳频电台在生产过程中所用的元器件性能、生产工艺以及安装调试等方面的差异性,使其自身辐射的跳频信号具有和其他跳频电台信号不同的细微特征[3],因此可以利用不同跳频电台信号特有的细微特征,即“指纹”特征,实现跳频信号的网台分选和识别。文献[4]通过固有时间尺度分解算法分解原始信号,再提取信号分量的近似熵、样本熵和排列熵,采用支持向量机分类器实现信源的分类识别。文献[5]利用发射功率放大器在瞬态响应过程中所表现的的不同细微特征,实现跳频电台分选。但是瞬态信号持续时间短,易受噪声干扰,识别难度大[6-7]。文献[8-9]均采用高阶谱特征实现辐射源个体识别,但是提取特征的计算量大,所需样本数量较多,算法实时性较差。文献[10]通过提取辐射源信号的时频能量谱多维特征实现了手机辐射源的个体识别。但是由于特征集的信息冗余较多,其识别正确率很低。文献[11]通过提取固定尺度时频能量谱的一、二阶矩和能量谱熵组成特征集,但是并未考虑在不同分块条件下,跳频信号的时频能量谱具有不同的能量分布特征,导致分类识别正确率不高。
现有研究跳频电台细微特征识别算法大多是在大样本和高信噪比条件下进行的,没能有效克服样本数量和信噪比对分类识别率的不良影响。针对上述问题,本文提出一种基于多尺度时频能量谱分形和瑞利熵特征的跳频电台细微特征识别方法。首先通过稀疏重构算法得到跳频信号的时频能量谱,然后将时频能量谱看作为由时间、频率和能量三维坐标组成的复杂曲面。该曲面的能量分布变化情况包含了用于分类识别跳频电台的细微特征信息。为了能有效提取该时频能量谱曲面的细微特征,本文是在多种不同分割尺度条件下,分别计算表征时频能量谱曲面变化规律的时频能量谱瑞利熵、多重分形维数和差分盒维数三种特征并组成特征集。最后采集四部不同型号跳频电台的跳频信号数据,用支持向量机分类器分别对本文和文献[10-11]方法所提取的特征集进行分类识别。实验结果对比表明,本文方法所提取特征集具有较强的可分性,特征之间冗余较小,在少训练样本数量条件下,识别正确率高于文献[10-11]方法。
2 算法流程
基于稀疏重构的时频能量谱特征分类算法流程如图1所示。
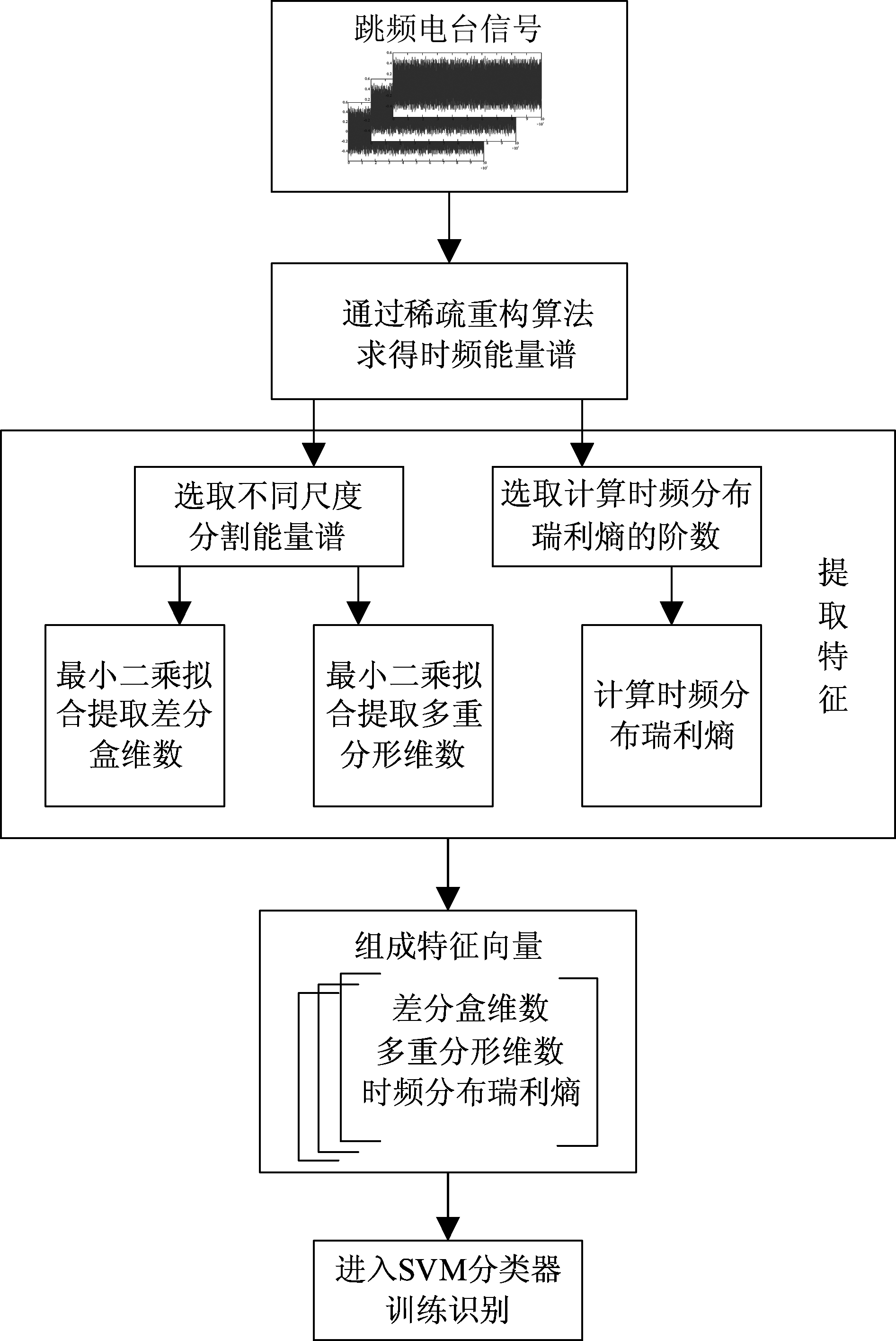
图1 算法流程图
Fig.1 Algorithm flowchart
首先通过近似l0范数(AL0)算法得到跳频信号的时频能量谱曲面,然后计算不同分割尺度条件下的时频瑞利熵、多重分形维数和差分盒维数三种特征组成特征集,最后通过支持向量机分类器进行分类识别。
2.1 基于稀疏重构的时频能量谱算法原理
假设在观测时间T内跳频信号sk(t)在观测时间内共有B跳,幅度为ak,跳周期为Tk,则其表达式为:
(1)
其中fk,b和φk,b分别为sk(t)第b跳的载频和初相,t′=t-(b-1)Tk-Δtk0,Δtk0为观测开始非完整跳的持续时间,rect(t)为单位矩形脉冲。
功率放大器是跳频电台最主要的器件,电台细微特征的主要来源于功率放大器的系统响应,由于功率放大器是典型的非线性系统,因此跳频电台辐射的跳频信号通常采用泰勒多项式来近似表示,即
(2)
其中ai为泰勒多项式系数,包含了跳频电台的细微特征,m为泰勒多项式阶数。
在实际跳频信号传输过程中,会受到噪声的影响,在高斯白噪声信道下,接收机接收到信号为
y(t)=φ(sk)+ν(t),0≤t<T
(3)
其中0≤t<T,ν(t)表示均值为0、方差为σ2的加性高斯白噪声。
由于AL0稀疏重构算法具有分辨精度高、计算量小和所需样本点少等特点而得到广泛应用[12]。AL0算法主要原理是将平滑高斯函数近似l0范数,采用最速下降法求解近似l0范数,实现稀疏信号重构。
假设跳频信号的有限频率集为w,接收信号频率集为{ωm}⊂w,根据算法对时间精度的要求,将跳频段等间隔划分为P个频点,接收的跳频信号y等间隔划分为K段,每段数据yk的长度为P,则有
yk=y(k•L:k•L+P-1)
(4)
其中,1≤k≤K,L为分段间隔。观测矩阵Y=[y1,y2,...,yK]可表示为
Y=WX+V
(5)
其中, W=[ω0,...,ωP-1],ωi=[ejωi1,...,ejωiP],X为时频矩阵,V为噪声矩阵,
由于跳频信号在时频域的稀疏性,X中的时频点即是稀疏的,同时非零点又全部在各跳频点对应的行上,X也是行稀疏的。因此可假设带惩罚函数的无约束优化函数:
(6)
其中,xk表示X第k行, μ1是X点稀疏惩罚因子, μ2是X行稀疏惩罚因子。
AL0算法引入高斯函数来近似l0范数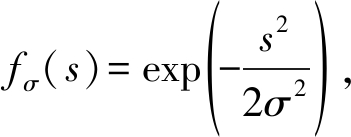
当σ近似为0时,有
(7)
其中,si表示向量s的第i行,可用式(7)近似l0范数,则稀疏重构问题即可转化为求解高斯和函数的最小化问题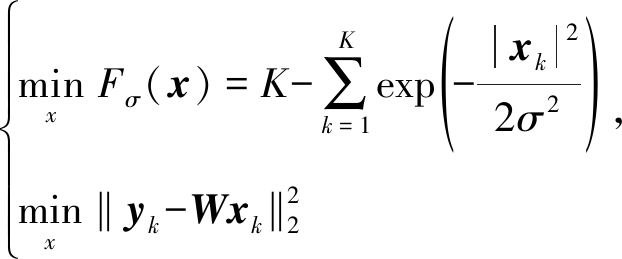
其中Fσ(x)表示跳频信号的l0范数,引入惩罚因子λ,将l0范数最小化问题转化为最优化问题,即
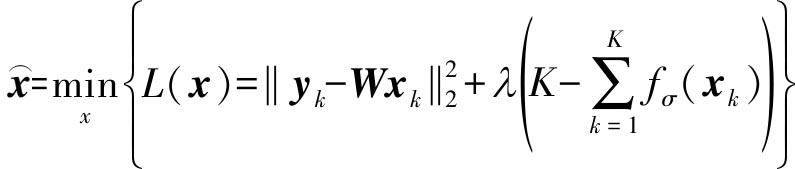
(8)
最速下降方向是L(x)的共轭梯度方向
L(x)。
(9)
其中x*为x的共轭。根据复数变量的共轭梯度定义可得
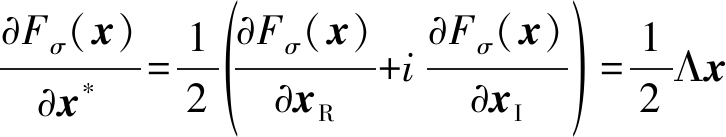
(10)
其中,xR表示x的实部,xI表示x的虚部,对角阵Λi,i=exp(-|xk|2/2σ2)/σ2。
根据
可得:
(11)
将式(10)和(11)代入式(9)中,可得
(12)
则计算式(9)中的L(x)共轭梯度方向为
(13)
其中,Λ1=fσ(X)/σ2;Λ2是对角矩阵,其第n个对角元素是
则AL0算法详细算法步骤如下,其中σ取值依次为[2,1,0.5,0.2,0.1,0.05]:
输入: 矩阵W,测量值向量y。
Step1 令初始值x(0)=WT(WWT)-1y。
Step2 选取下降序列[σ1σ2,...,σJ],令ε为收敛准则,ε表示均值为0,方差为σ2的高斯白噪声。选择合适的λ参数。
Step3 最速下降法求解。
For j=1,2,...,J
σ=σj;
While norm(L(x))>σjε
Fσ(x-uL(x))<Fσ(x);(确定步长u);
x=x-uL(x);(沿梯度方向更新);
End
x(j)=x;
End
Step4 输出结果
通过AL0算法稀疏重构得出的两部同步组网跳频电台的时频能量谱如图2所示。
图2 两部跳频电台的时频能量图
Fig.2 Time-frequency energy diagram of two frequency hopping stations
由图2可知,型号和工作方式相同的两部跳频电台,由于来自不同的辐射源,携带着各自的细微特征信息。通过提取各部电台信号时频能量谱曲面的能量变化和频点分布等特征规律,即可实现跳频电台的个体识别。
2.2 分形特征提取
由数学家Mandelbrot创建的“分形”理论为自然界中形形色色的复杂信号和结构的研究提供了非常简便的手段和方法。该理论表明,分形维数既能度量物体形状的复杂程度,而且具有多尺度、多分辨率变化的不变性特点。本文正是在不同的分块尺度条件下,提取跳频信号时频能量谱曲面的差分盒维数和多重分形维数特征。
(1)差分盒维数
采用文献[13]计算图像的差分盒维数方法,将稀疏重构出的跳频信号时频能量谱的时频轴看作平面,能量谱值看作图像灰度值。
跳频信号时频能量谱曲面的差分盒维数计算步骤:
Step1 假设时频能量谱F的尺寸大小为N×N,S是M×M的网格,F被S分割成若干子块(1≤M≤N/2,M∈Z+),每个网格S中都有大小M×M×M′的盒子柱,r=
,其中G为时频能量谱的最大值,⎣•」为向下取整运算符。
Step2 设在第(μ,ν)个网格中,gmax和gmin分别表示时频能量谱的最大值和最小值,在尺度M下,第(μ,ν)个网格的盒子数为:
nM(μ,ν)=
+1
(14)
Step3 利用式(14),计算出在M尺度下所有网格的盒子数。
(15)
Step4 改变网格S的尺度M,重复上述Step1～3,计算出不同分块尺度M条件下的NM。
Step5 通过最小二乘方法拟合估计出差分盒维数。
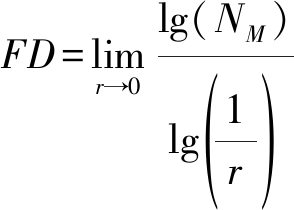
(16)
(2)多重分形
单重分形在描述大多数客观存在的分形物体时,并不能完整地度量其复杂性和非线性特征,在一定程度上,无法充分体现其全部特性。多重分形能够从局部出发研究其整体特征,提高了对物体几何特征和局部尺度行为刻画的精细程度。为了更加有效的表征时频能量谱局部特征,本文提取跳频信号时频能量谱的多重分形维数作为第二维特征。从文献[14]中可知,多重分形MD可以表示为:
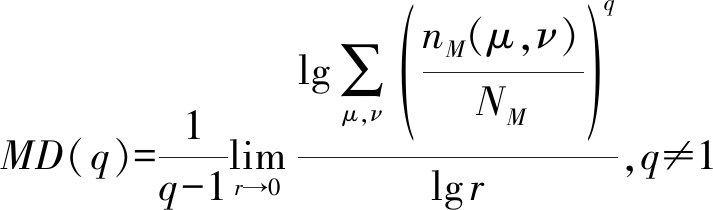
(17)
其中q提供了对奇异测度不同区域的微观测度,在实际应用中,q值的不同选择,影响MD的稳定性。根据差分盒维数算法Step 1～3,计算出不同分块尺度M条件下的NM,再结合式(17),利用最小二乘法拟合得到跳频信号时频能量谱的多重分形特征。
2.3 时频能量谱瑞利熵特征提取
熵可以定义成一个度量混乱无规律、不确定等无序状态的量。由图2可知,两部跳频电台信号的的时频能量分布规律具有一定的差异性,这种分布的差异正好可通过统计时频能量谱瑞利熵来进行度量,即从直观上的不同转化为了数值上的差异,因此为了保证特征集的充分可分性,本文提取时频能量谱瑞利熵作为第三维特征。
假设随机变量J的概率密度分布为P={p1,p2,...,pT},满足条件w(p)=∑pt≤1,则J的瑞利熵定义如式:
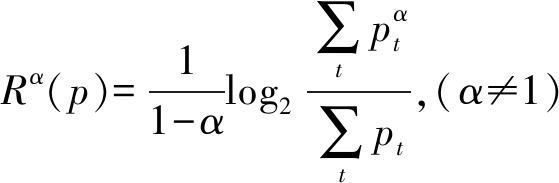
(18)
其中α为瑞利熵阶数。
连续形式的α阶瑞利熵如式:
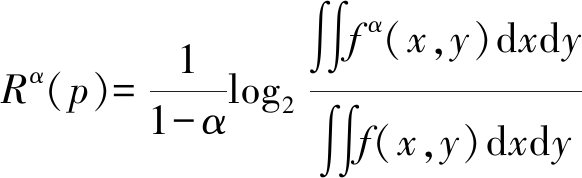
(19)
其中, f(x,y)是连续二维概率密度分布。
对跳频信号s(t)稀疏重构后,得到的时频能量谱P(t, f )具有时频边缘特性和能量保持特性,如式(20)、(21)所示:
(20)
(21)
其中,s( f )是s(t)的傅里叶变换。由此可知时频能量谱P(t, f )同式(19)的二维概率密度分布f(x,y)性质相同,因此可用P(t, f )定义跳频信号的时频能量谱瑞利熵,如式:
(22)
式(22)的稳定条件是
为了计算方便,时频能量谱瑞利熵的离散表达式:
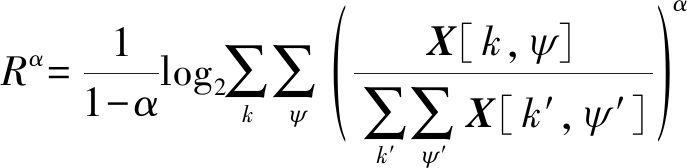
(23)
其中,X为时频矩阵,1≤k≤K,1≤k′≤K,ω0≤ψ′≤ωP-1,ω0≤ψ≤ωP-1。
最后将上述三种特征组成特征集V=[FD,MD(q),Rα],再利用支持向量机分类器进行分类识别。
3 实验结果与分析
3.1 多尺度特征提取与分析
本文实验数据采集于四部跳频电台,其电台型号和工作方式如表1所示。
表1 电台型号和工作方式
Tab.1 Radio model and working method
制造商电台工作频率/MHz跳速型号/(hop/s)HarrisRF5800H-MP1.6～6020Q-MACHF-902～305GrintekTR24001.6～3010ThalesSysteme30001.5～10820
考虑到在对稀疏重构后的时频能量谱进行分块时,如果尺度L值过大,则无法完全利用能量谱的边界信息,导致提取的特征不能完全反应信号的本质信息;如果尺度L值过小,则会增加计算的运算量。因此在本文仿真实验中,分块尺度L选取4、8、12、16、20五个值。
从式(17)可知,参数q影响MD(q)值的稳定性,采用RF5800H-MP电台的跳频信号数据样本,计算不同q值条件下的MD(q),其变化规律如图3所示。
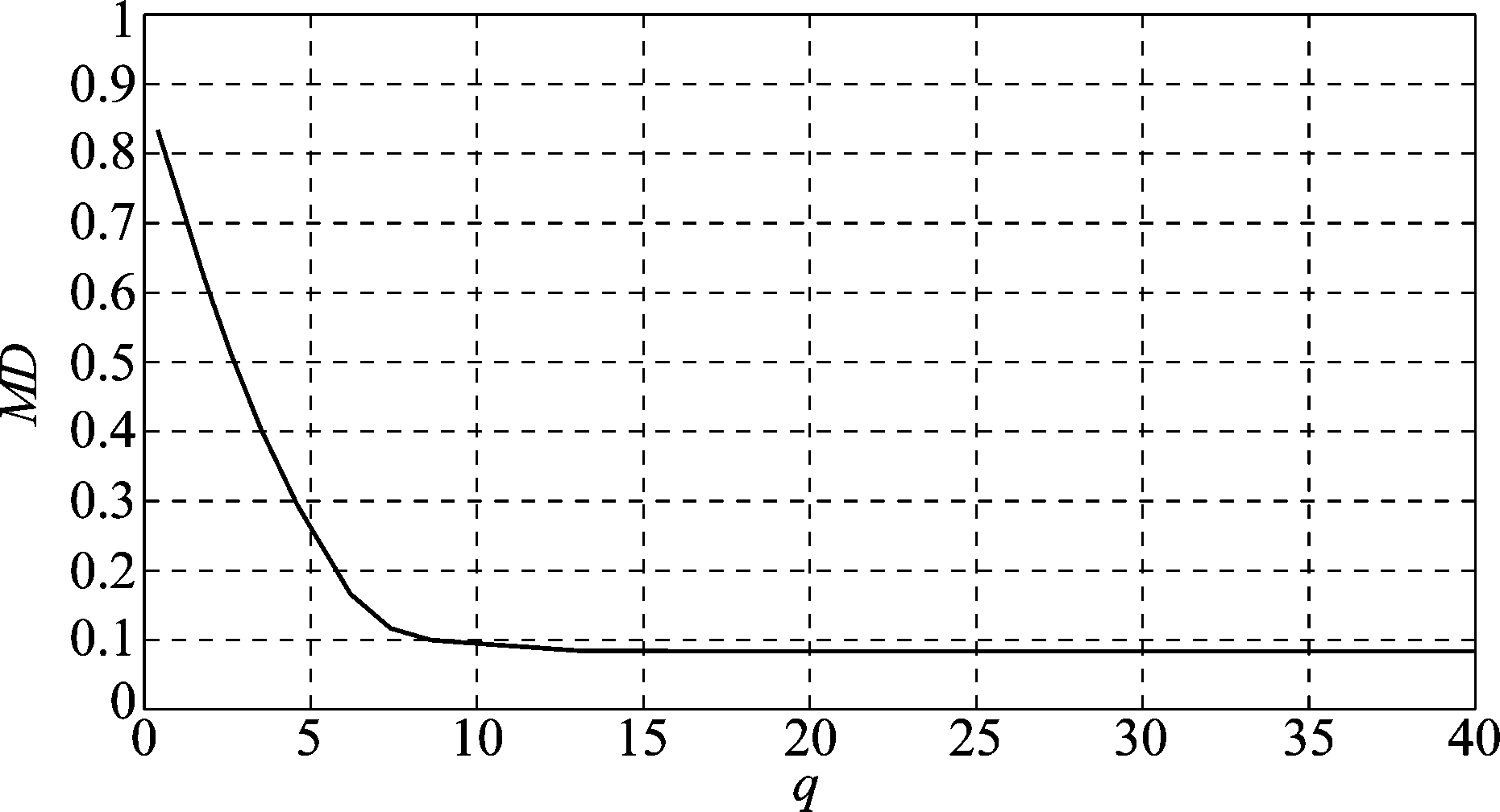
图3 MD变化规律
Fig.3 MD change law
由图3可知,只有当10<q时,MD(q)受q值影响较小。经反复实验观察,4部电台的跳频信号的MD(q)值均在q=13时趋于稳定,为了保证所提取特征的稳定性,选取q=13。
3.2 时频能量谱瑞利熵特征提取与分析
时频能量谱瑞利熵可以很好地反映各跳频信号的时频能量谱规律和复杂度,但从式(23)可知,阶数α的取值对时频能量谱瑞利熵特征的提取影响很大。本文选取4部电台的跳频信号样本数据,分别计算了阶数α在0～30的整数阶时频能量谱瑞利熵,如图4所示。
图4 时频能量谱熵随阶数变化规律
Fig.4 Time-frequency energy spectral entropy changes with order
从图4中可知,4部电台的跳频信号时频能量谱瑞利熵随着阶数α的增大逐渐变小。当α=14时,不同电台跳频信号的时频能量谱瑞利熵值还有一定的差异性,当α>16时,其差异性越来越小。当α=3时,各跳频电台信号的时频能量谱瑞利熵值差异性最大,具有较强的可分度。同时,在文献[15]中验证当阶数α=3时瑞利熵的稳定性最好。因此本文时频能量谱瑞利熵特征的阶数选取3。
3.3 不同信噪比条件下的功率放大器识别结果分析
为了分析本文所提取特征集的抗噪性能,在不同信噪比条件下生成三种泰勒级数功率放大器的训练和测试样本,实验中采用的三种9阶泰勒系数功率放大器具体表达式如下:
yo1=450.8s-540.0s2+230.0s3-
0.07006s4+0.2501s5-0.5267s6+
0.6486s7-0.4318s8+0.1200s9
(24)
yo2=457.9s-539.6s2+220.80s3-
0.06474s4+0.2311s5-0.4876s6+
0.5944s7-0.3991s8+0.1109s9
(25)
yo3=467.7s-550.4s2+222.2s3-
0.07058s4+0.2519s5-0.5306s6+
0.6535s7-0.4351s8+0.1209s9
(26)
本实验在高斯信道下,跳频信号跳速50 hop/s,频率集为[10294.72048957739]MHz,采样率为200 MHz,在同一信噪比条件下每台生成500个样本,其中随机选取100个作为训练样本,400个作为测试样本,在信噪比0～20 dB条件下,每间隔2 dB生成一次样本数据,则每台共有1100个训练样本,4400个测试样本。在不同信噪比条件下,采用本文算法以及文献[10]、[11]的算法提取特征向量,再利用支持向量机分类器进行训练分类识别,三种算法各统计50次分类识别实验的平均识别正确率如图5所示。
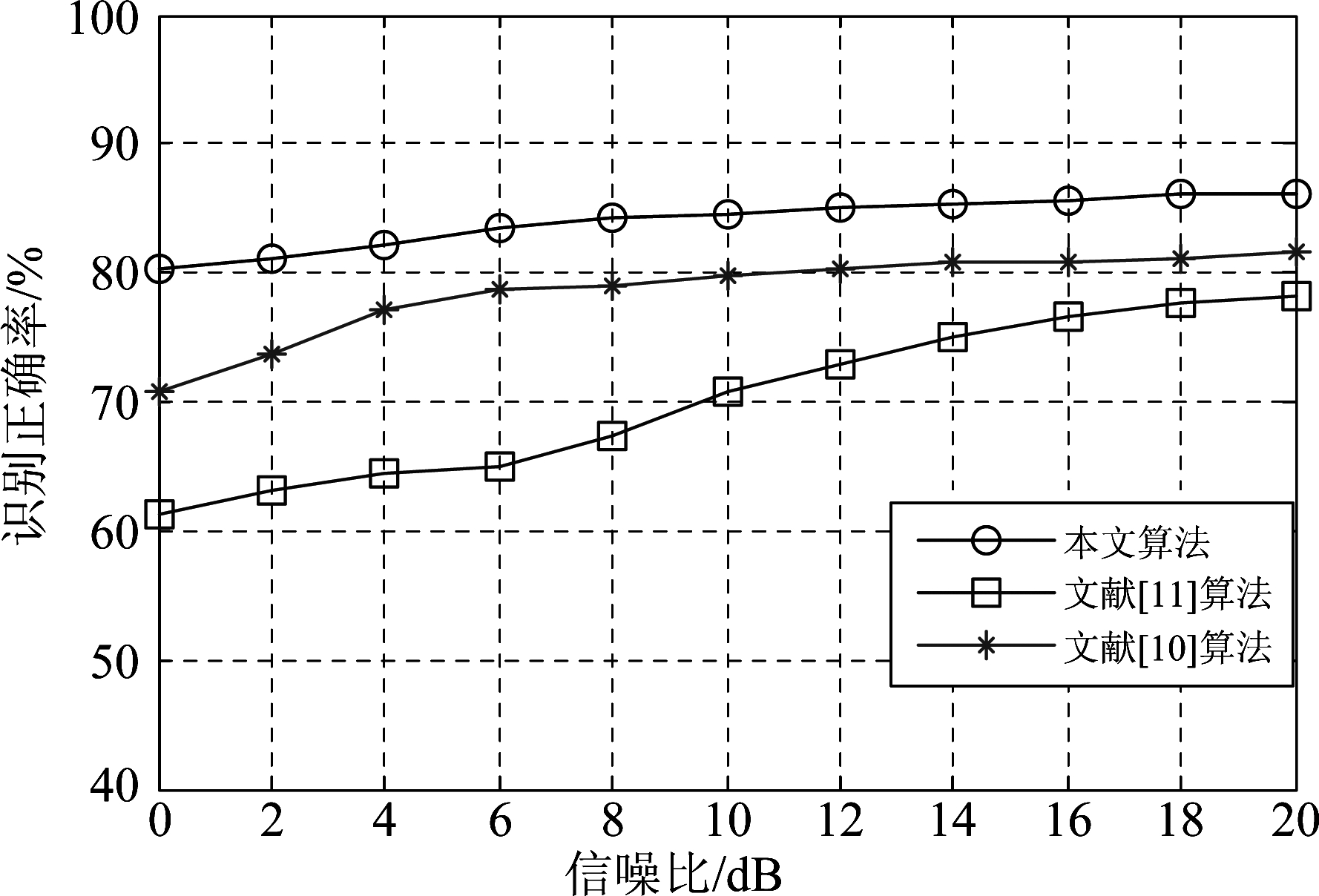
图5 识别正确率随信噪比变化规律
Fig.5 The correct rate of recognition varies with the signal-to-noise ratio
从图5中可知,随着信噪比的增加,三种算法的识别正确率均有所增加,但本文算法的识别正确率始终高于文献[10]和[11]算法。而且本文算法的识别正确率受信噪比变化影响较小,在信噪比从0 dB增加到20 dB后,本文算法的识别正确率增加了6%,而文献[10]和[11]算法的识别正确率分别增加了12%和17%。其主要原因是本文算法所提取特征向量的特征稳定性和表征能力更强,不易受噪声影响。
3.4 不同型号的跳频电台个体识别结果分析
为了验证本文算法的实用性,分别对采集于表1的四部不同型号电台的数据进行截取,首先从采样数据的头部截取200段数据作为训练样本,每段训练样本数据的采样点数是1024,各段间隔200点。然后采用同样的方法,从采样数据的尾部截取200段数据作为测试样本。在不同训练样本数条件下,分别采用本文算法以及文献[10]、[11]的算法提取特征向量,再利用支持向量机分类器进行分类识别,对比分析三种算法对实际电台的识别性能。三种算法各统计50次分类识别实验的平均识别正确率如图6。
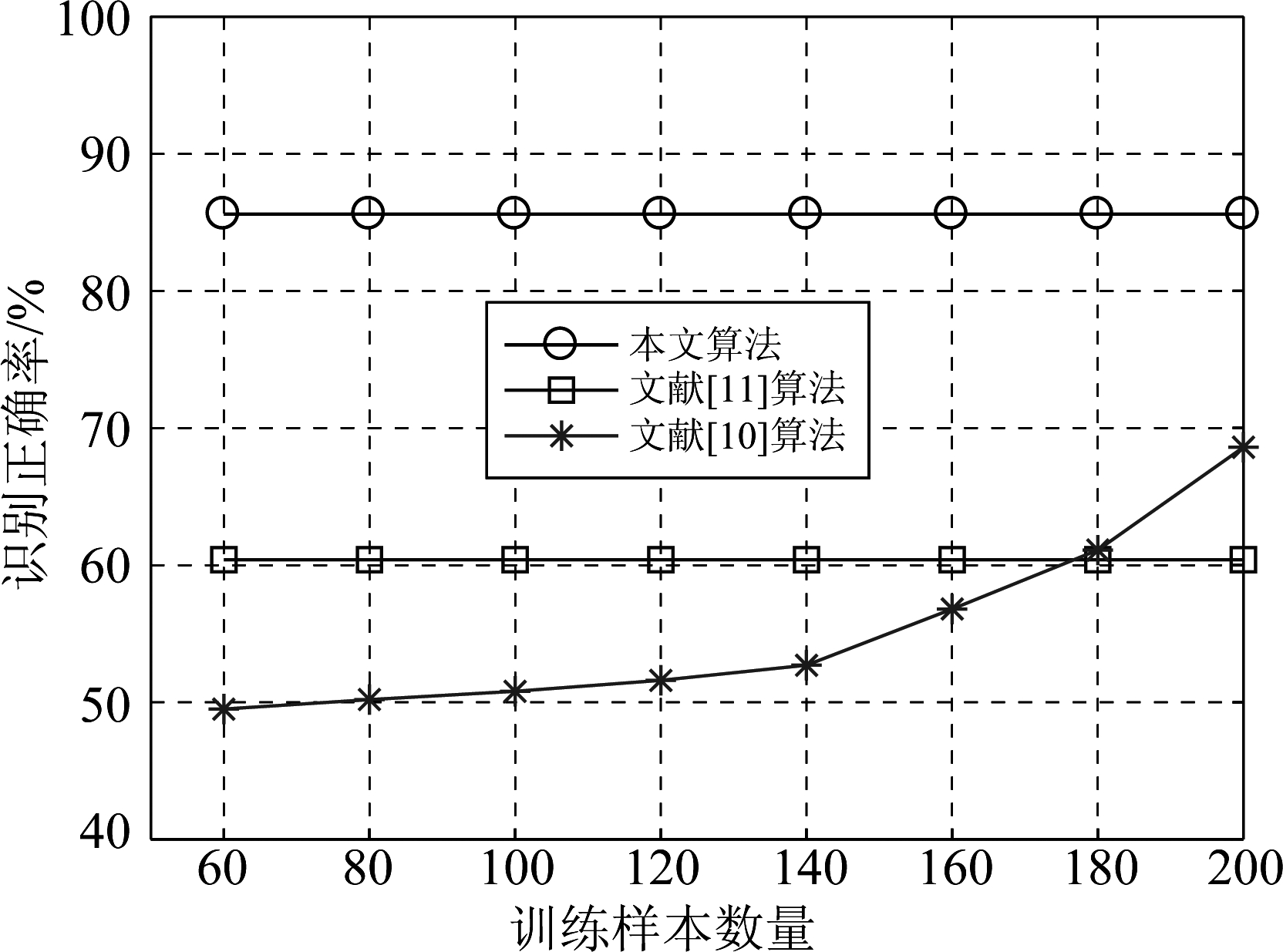
图6 识别正确率随训练样本数变化规律
Fig.6 The correct rate of recognition varies with the number of training samples
从图6中可知,文献[10]算法的识别正确率随着训练样本数量的增加而逐渐增加,当训练样本数量增加到200时,文献[10]的识别正确率达到最大为68.6%。而本文算法和文献[11]算法的识别正确率不受训练样本数量变化的影响,始终保持在85.6%和60.4%。其主要原因是本文算法提取的三种特征能定量描述时频能量谱的能量变化、时频能量谱复杂度和规律性,避免了由于单一特征的相似性而造成的误判问题。
为了方便分类效果的可视化,文献[10]和[11]利用主成分分析[16]算法对提取出来的多维特征向量进行降维处理,将前三个主元构造成为新的特征向量。在训练样本数为200条件下,本文算法、文献[10]和文献[11]算法得出的三维特征分类效果如图7所示。
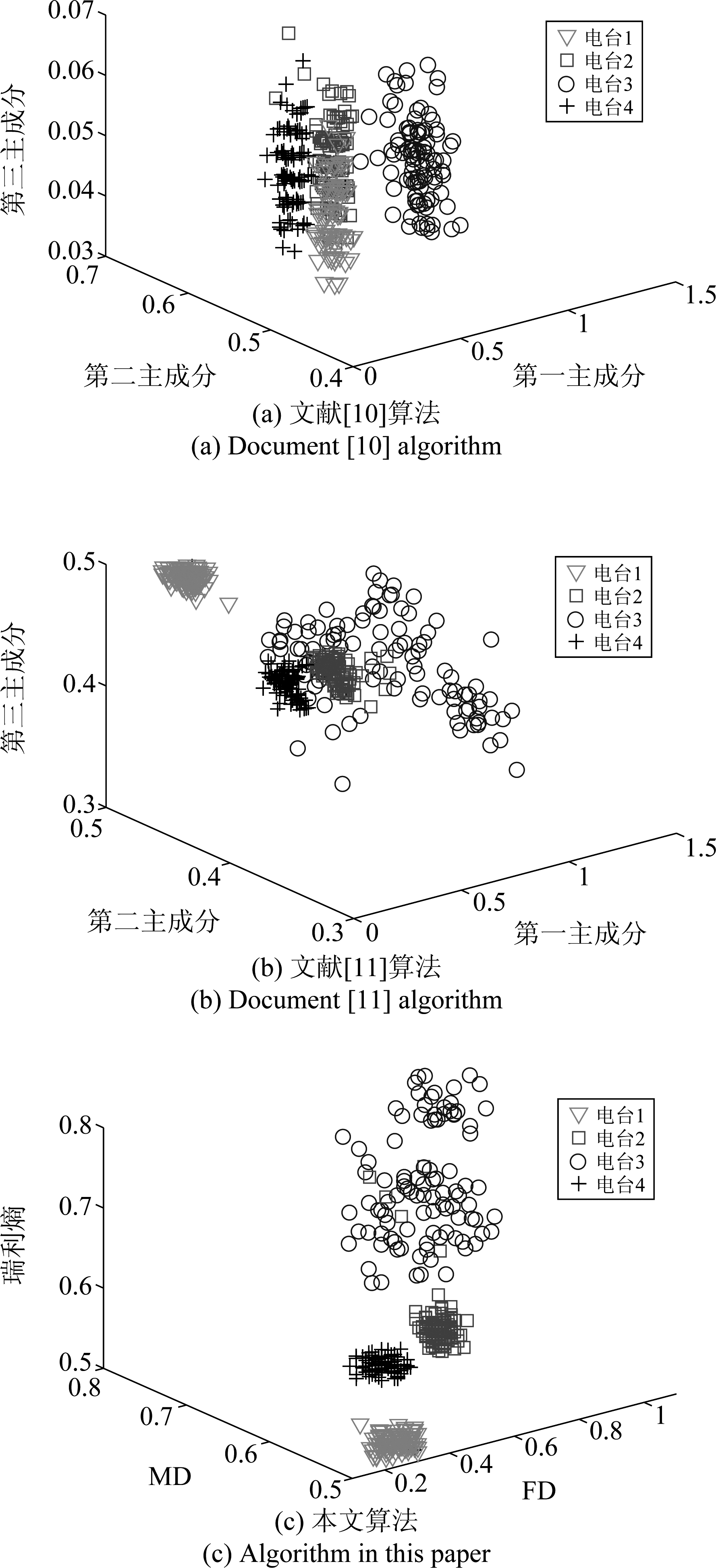
图7 分类效果图
Fig.7 Classification effect chart
从图7中可知,文献[10]和[11]算法的分类特征均有较严重的重叠,聚类效果差,而本文算法的分类特征只有少部分重叠,具有明显的聚类效果,符合图6的识别结果。
4 结论
本文提出了一种基于跳频信号时频能量谱的特征提取方法。该方法首先对跳频信号稀疏重构得到时频谱,分别提取其差分盒维数、多重分形维数和时频能量谱瑞利熵三种特征,避免了由单一特征的相似性而造成的误判问题。通过分类识别实验表明,本文算法的识别性能受训练样本数量和信噪比影响较小,能够在较少训练样本数量条件下,具有较高的识别正确率。AL0稀疏重构算法的字典网格疏密对跳频能量谱提取的质量和算法复杂度有较大影响,当跳频带宽较大时,字典网格数变多,算法复杂度增加明显,同时本实验是在高斯信道条件进行的,对于多径、衰落等实际信道环境并不完全适用,因此如何降低提取能量谱算法复杂度和适应多种信道条件下的跳频电台识别是下一步研究重点。
[1] Eric M, Dukic M L. Frequency hopping signal separation by spatio-frequency analysis based on MUSIC method[J]. Spread Spectrum Techniques and Applications, 2000, 66(1): 78- 82.
[2] 王斌, 陈秋华, 王翠柏. 基于聚类的跳频信号分选[J]. 北京邮电大学学报, 2009, 32(2): 80- 84.
Wang Bin, Chen Qiuhua, Wang Cuibai. Identification of Frequency Hopping Signals Based on Clustering[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(2): 80- 84.(in Chinese)
[3] Bibile M A, member, Karmakar N A. Moving Chipless RFID Tag Detection Using Adaptive Wavelet Based Detection Algorithm[J]. IEEE Transactions on Antennas and Propagation, 2018, PP(99): 1-1.
[4] 任东方, 张涛, 韩洁. 结合ITD与非线性分析的通信辐射源个体识别方法[J]. 信号处理, 2018, 34(3):331-339.
Ren Dongfang, Zhang Tao, Han Jie. Approach of specific Communication emitter identification combining ITD and nonlinear analysis[J]. Journal of Signal Processing, 2018, 34(3):331-339.(in Chinese)
[5] 骆振兴, 赵知劲. 基于功放瞬态响应的跳频电台分选方法[J]. 杭州电子科技大学学报, 2009, 29(1): 29-32.
Luo Zhenxing, Zhao Zhijin. Individual HF Transmitter Identification Based on Transient Response of Power Amplifier[J]. Journal of Hangzhou Dianzi University, 2009, 29(1): 29-32.(in Chinese)
[6] Wachowski N, Azimi M R. Detection and Classification of Nonstationary Transient Signals Using Sparse Approximations and Bayesian Networks[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2017, 22(12): 1750-1764.
[7] Hashemi F, Mohammadi M, Kargarian A. Islanding detection method for microgrid based on extracted features from differential transient rate of change of frequency[J]. Iet Generation Transmission & Distribution, 2017, 11(4): 891-904.
[8] Zaccaria V, Melzani F, Bertoni G. Spectral features of higher-order side-channel countermeasures[J]. IEEE Transactions on Computers, 2018, PP(99): 1-1.
[9] Zak G, Wylomanska A, Zimroz R. Local damage detection method based on distribution distances applied to time-frequency map of vibration signal[J]. IEEE Transactions on Industry Applications, 2018, PP(99): 1-1.
[10]Yuan Y, Huang Z, Wu H, et al. Specific emitter identification based on Hilbert-Huang transform-based time-frequency-energy distribution features[J]. Communications Iet, 2014, 8(13): 2404-2412.
[11]Zhang J, Wang F, Dobre O A, et al. Specific Emitter Identification via Hilbert-Huang Transform in Single-Hop and Relaying Scenarios[J]. IEEE Transactions on Information Forensics & Security, 2016, 11(6): 1192-1205.
[12]王军华, 黄知涛, 周一宇, 等. 基于近似l0范数的稳健稀疏重构算法[J]. 电子学报, 2012, 40(6): 1185-1189.
Wang Junhua, Huang Zhitao, Zhou Yiyu, et al. Robust Sparse Recovery Based on Approximate l0 Norm[J]. Acta Electronica Sinica, 2012, 40(6): 1185-1189.(in Chinese)
[13]Sarkar N, Chaudhuri B B. An efficient differential box-counting approach to compute fractal dimension of image[J]. IEEE Trans. Syst. Man Cybern, 1994, 24(1): 115-120.
[14]Soares F, Janela F, Pereira M, et al. 3D lacunarity in multifractal analysis of breast tumor lesions in dynamic contrast-enhanced magnetic resonance imaging[J]. IEEE Transactions on Image Processing, 2013, 22(11): 4422- 4435.
[15]Baraniuk R G, Flandrin P, Janssen A J E M, et al. Measuring time-frequency information content using the Renyi entropies[J]. Information Theory IEEE Transactions on, 2001, 47(4): 1391-1409.
[16]杨洁. 基于PCA的间歇过程监测及故障诊断方法研究[D]. 东北大学, 2010.
Yang Jie. Research on Batch Process Monitoring and Fault Diagnosis Method Based on PCA[D]. Northeastern University, 2010.(in Chinese)
