1 引言
随着数字通信的发展,直接序列扩频(Direct Sequence Spread Spectrum, DSSS)信号因其抗干扰能力强,保密性能好,截获率低在军事和民用通信领域中,得到了广泛应用。在军事通信侦察、民用信号管控等非合作通信系统中,由于接收方接收的是未知的PN码调制的信号,因此对PN码的估计是进行信息获取、解扩及分析的前提和关键。直扩信号的PN码盲估计研究日趋成熟,但绝大多数的研究都是先对接收机端的载波调制信号进行载频估计,然后进行下变频得到基带直扩信号,最后对基带信号进行PN码的估计。但实际上,对信号参数的估计总是存在误差的,且接收端的本振频率稳定度有限,这样利用本振对信号下变频时,总会有一个较小的残余频偏[1],其对应的载波称为残余载波,这在很大程度上增加了PN码盲估计的难度。就目前公开发表的文献来看,对带有残余载波的直扩信号PN码的盲估计研究极少。
周期长码直扩(Periodic Long-code Direct Sequence Spread Spectrum, PLC-DSSS)信号是指一周期的PN码调制整数个信息码,PN码的周期遭到严重破坏,故针对已经研究成熟的短码直扩(Short-code Direct Sequence Spread Spectrum, SC-DSSS)信号PN码盲估计的方法[2-3]不能够直接用在PLC-DSSS信号上。针对PLC-DSSS信号PN码盲估计,文献[4- 8]首先将PLC-DSSS信号建模为等效的虚拟多用户SC-DSSS信号,然后分别用矩阵特征分解结合模糊酉矩阵的方法[4-5]、约束投影逼近子空间跟踪(Constrained Projection Approximation Subspace Tracking, CPAST)算法[6]、Fast-ICA算法[7]、Viterbi算法[8]估计各虚拟用户PN码,最后按照一定顺序进行拼接得到完整的周期长码PN码序列,事实证明这种将PLC-DSSS信号建模为多用户SC-DSSS信号的方法是有效可行的。文献[9]提出基于重叠分段MCMC-UKF(Markov Chain Monte Carlo-Unscented Kalman Filter)的盲估计算法,能够实现对LC-DSSS信号PN码的有效估计。随着研究的深入,又出现了高阶统计分析中的m序列三阶相关函数法(Triple correlation function, TCF)[10-13],根据TCF峰值出现位置找到PN码本原多项式从而恢复出PN码序列。上述针对LC-DSSS信号PN码估计方法,都只针对的是基带信号,并不适用于这里讨论的复信号。文献[14]提出利用线性调频Z变换的方法,对未知载频进行估计,但由于系统的频率稳定性往往是有限的,载频的估计误差也是不可避免的。文献[15-16]利用DPLL对自相关矩阵的主特征向量中残留的载波进行跟踪、消除,取得了理想的效果,但文章并未对长码直扩(Long-code Direct Sequence Spread Spectrum, LC-DSSS)信号进行深入讨论。
针对带残余载波的周期长码直扩信号PN码盲估计难度大的问题,本文提出一种结合矩阵特征分解和DPLL的方法,完成对PN码的估计。首先将信号等效建模为多用户SC-DSSS信号,然后将信号按照PN码的周期长度进行分段构成相关矩阵,对此矩阵进行特征分解并去除酉模糊得到带有残余载波的PN码,最后将带有残余载波的PN码送到DPLL对载波进行跟踪消除,最终估计出正确的PN码。
2 信号模型
假设信号的PN码周期,码片速率可事先估计得到[17-18],载波频率为fc的LC-DSSS信号在接收端经过正交下变频后可表示为
x(t)=s(t)exp[j(2πfΔt+φ)]+n(t)
(1)
其中
s(t)=d(t-τ)c(t)
(2)
式中,s(t)为基带信号,残余频偏fΔ=f0-fc, f0为本振频率, fΔ≪ f0,φ为均匀分布的随机相位,n(t)为方差为σ2的复高斯白噪声;
为信息序列波形,d(i)∈{±1}为独立同分布的信息序列,Td为信息码宽度,q(t)为矩形门函数;
为PN码序列波形,c(j)∈{±1}为PN码序列,Tcp为码片宽度;τ为接收端存在的随机时延,假设时延τ已被估计得到[1,6],即已完成信号盲同步,不失一般性假定τ=0;PN码周期T=LTcp,L表示一周期PN码中包含的码片个数;扩频调制比G=T/Td,当G为整数时,表示一周期PN码调制G个信息码,即T=GTb=LTcp,此时x(t)表示带有残余载波的PLC-DSSS信号。
将PLC-DSSS信号建模为虚拟多用户SC-DSSS信号模型,令A(t)=exp[j(2πfΔt+φ)],x(t)还可以表示为
kT<t≤(k+1)T
(3)
其中
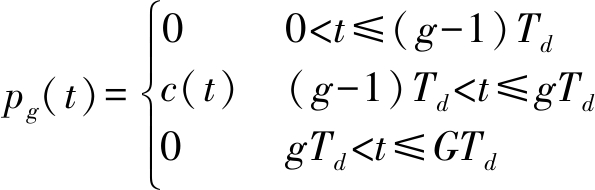
(4)
G表示虚拟用户数,对信号以采样间隔Ts(Ts≤Tcp)进行采样,并将信号以T为宽度进行分段,构成观察矩阵
X=[x1x2…xK]
(5)
分段后每一段向量xk(k=1,2,…,K)内采样点数目n=T/Ts,一个信息码元内包含的采样点数目m=Tb/Ts,则n=mG,且当Ts=Tcp时,L=n。 xk可表示为
(6)
其中
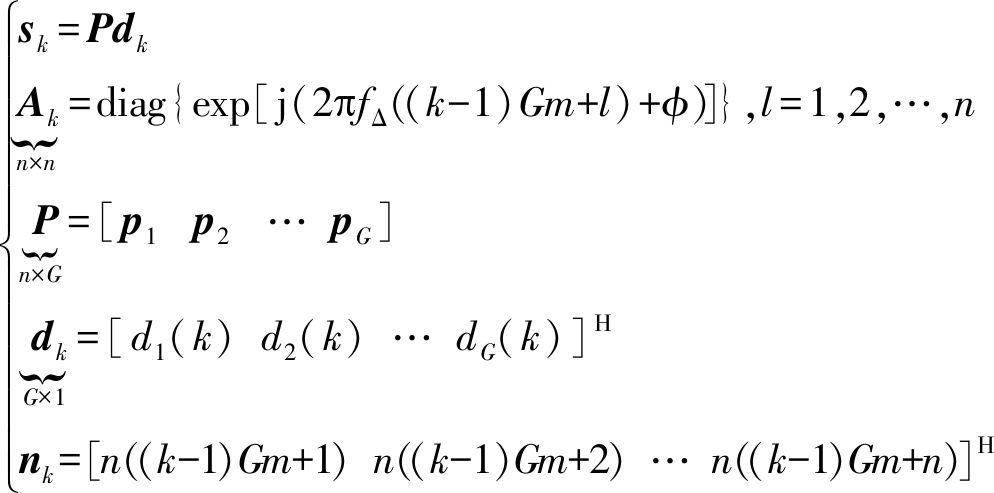
(7)
式(7)中,dg(k)和pg(g=1,2,…,G)分别表示第g个虚拟用户的信息码(码速率为1/T)和PN码序列,其中pg可表示为
(8)
PLC-DSSS信号等同的虚拟多用户SC-DSSS信号模型如图1所示。
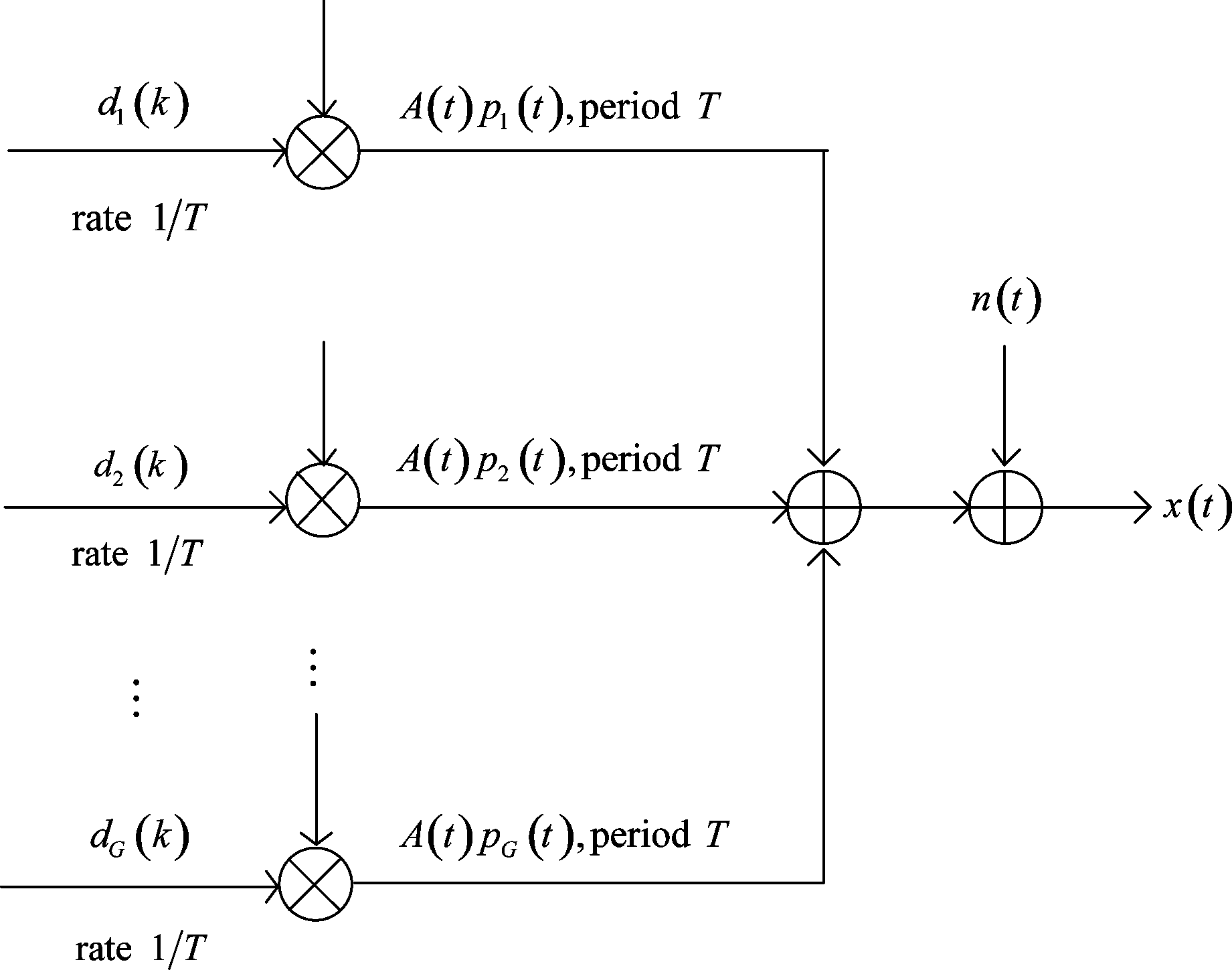
图1 PLC-DSSS信号的虚拟多用户模型
Fig.1 Virtual multiuser mode for PLC-DSSS signals
3 残余载波下PN码盲估计
3.1 带残余载波的周期长码直扩信号的特征分解方法
接收信号向量的自相关矩阵可以表示为
(9)
其中,E[·]表示取期望,将式(6)代入到式(9)可得到
(10)
考虑到Ak=exp[j2πfΔ(k-1)Gm]A1,其中A1=diag {exp[j(2πfΔl+φ)]},l=1,2,…,n。则式(10)可展开为
(11)
由式(6)和式(7)可知,sk=Pdk=p1d1(k)+p2d2(k)+…+pGdG(k),将pg作幅度归一化,有
由式(8)可知,ug是正交归一化向量,故式(10)可展开为
(12)
其中,
为信息序列的方差,
为PN码序列能量,
为有用信号方差,信噪比
由式(8)可知
故有用信号特征值分别为
将(12)写成特征值分解的形式为
(13)
式(13)中,Λ=diag(λs,1,λs,2,…,λs,G)为有用信号的特征值对角矩阵,A1Us是其对应的特征向量矩阵。
根据特征值分解的性质可知,由于Λ内包含了G个相等的特征值,所以无法按照由大到小的次序取出这G个相等的特征值对应的特征向量,也就无法得到各虚拟用户对应的PN码信息,即A1Us≠A1P。实际上,A1Us与A1P存在一种模糊关系[19]:
(14)
其中,Q为模糊酉矩阵,为方便起见,令
则式(14)可写为
(15)
接下来用数学处理算法[20]来求解Q, 假设
Q=[q1q2…qG]
(16)
将式(15)表示为
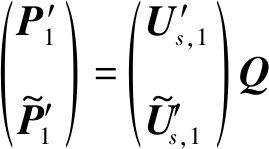
(17)
其中,矩阵
和
分别为P′和
的前(G-1)m行构成。由于的最后一列元素全为0,故
表示求秩运算。由式(17)可得
(18)
由于Q为满秩矩阵,所以
比较式(18)等式两边矩阵的最后一列,可知
(19)
则qG可表示为
(20)
由于矩阵
只有一个零特征值,所以qG是的最小特征值对应的特征向量。
当估计qG-g+1(g=2,3,…,G)时,类似于式(17)有
(21)
其中,矩阵
和
分别为P′和的前(G-g)m行构成,此时,
同理比较式(21)两边最后g列列向量,可得
(22)
从而有
(23)
由式(22)可知,
故
有g个零特征值,所以也就不能从的特征分解中确定qG-g+1。下面再令
(24)
其中,Λg为的特征值对角矩阵,Vg为对应的特征向量矩阵。Vg可表示为
(25)
其中,
是零空间对应的特征向量。因此,
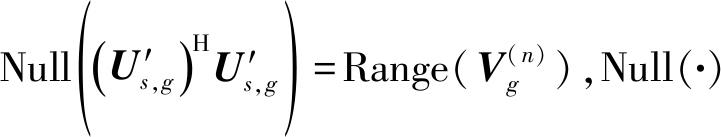和Range(·)分别表示零空间和范围。假定存在g×1维列向量z,且
则qG-g+1可由下式给出
(26)
定义Qg如下
Qg
[qG-g+2q2…qG], g=2,3,…,G
(27)
因为Q为酉矩阵,所以有
(28)
将式(26)带入到式(28)中有
(29)
因为
是(g-1)×g的满秩矩阵,所以
只有一个零特征值,从而z可以表示为
(30)
将z代入式(26)便可得到qG-g+1。
为了得到Q的第一列,可利用下式
(31)
则q1可表示为
(32)
即q1为
最小特征值对应的特征向量。
到此,整个Q便求解出来了,将Q代入式(14)中便可求得P′,即各虚拟用户对应的各段PN码。但由于P′中A1的存在,导致估计出的各段PN码是经过残余载波调制后的PN码,如果直接对其进行符号判决的话,会出现严重误码的情况。为此,需要一种有效的方法来消除残余载波对PN码的影响,下面研究如何通过DPLL来解决该问题。
3.2 DPLL消除残余载波
记P′的估计为
(33)
显然,
中包含了G个虚拟用户的PN码信息。由式(8)不难看出,对于第g个虚拟用户来说,只有第(g-1)m+1到(g-1)m+m个数据包含所需要的数据,其他数据可以忽略。因此,对于求得的矩阵
来说,只需截取其第g(g=1,2,…,G)列的第(g-1)m+1行到第(g-1)m+m行元素,并对其进行依次拼接就可得到残余载波调制下的一周期PN码估计值,记为
这样进行处理,减少了算法的运算量,可以一次性将数据送入到DPLL进行载波的跟踪、消除,避免了逐个用户的数据处理。
可以写为
(34)
其中,
表示最终要得到的周期PN码的估计值。式(34)可展开为
(35)
由式(35)可知,由于残余载波存在于PN码的估计值
之中,影响对的准确估计,接下来利用锁相环消除残余载波。
锁相环(PLL)是一个能跟踪输入信号频率(相位)的闭环自动控制系统,其主要用途是在收、发通信双方建立载波同步或位同步,本文主要运用DPLL来估计、跟踪和消除残余载波从而实现对
的解调。式(35)可写为如下形式
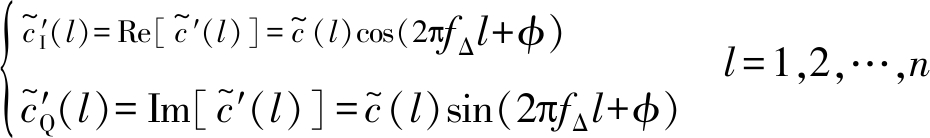
(36)
对式(36)进行相位旋转
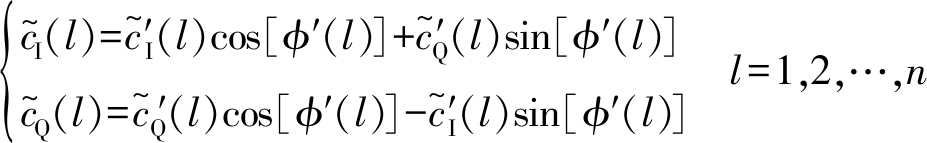
(37)
将式(36)代入式(37),有
(38)
当DPLL的跟踪相位φ′(l)→(2πfΔl+φ),即Δφ→0时,DPLL完成锁定时,此时
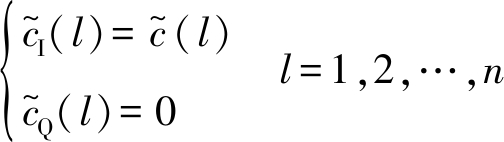
(39)
最终便得到PN码的估计值
图2是用于消除残余载波的DPLL。
图2中的鉴相器(Phase detector, PD)为反正切PD,用来计算相位差Δφ,该相位差经过环路滤波器(Loop Filter, LF)滤波后,用于控制压控振荡器(Voltage Controlled Oscillator, VCO)的瞬时输出相位φ′(l),
图2 用于消除残余载波的DPLL
Fig.2 The DPLL for removing residual carrier
最后将φ′(l)送入到正余弦信号发生器产生sin[φ′(l)]和cos[φ′(l)]用于相位旋转。其中,滤波器系数KI和KP用于控制锁相环带宽和阻尼系数,VCO采用直接数字同步器(Direct Digital Synchronizer, DDS)的形式,DDS包括累加器和正弦信号发生器。图2中DPLL一方面可以用来估计和跟踪输入信号的残余载波,另一方面也可用来消除残余载波实现信号的解调,是常见数字通信系统中实现频率和载波相位同步的重要组成部分。
由图2可知,相位差Δφ的计算由PD完成,其输出为
(40)
实际上,相位旋转操作和鉴相操作合在一起,在相位运算上等效为
φi(l)-φ′(l)=Δφ
(41)
其中,φi(l)=2πfΔl+φ表示DPLL输入信号
和
残余频偏和相位。
DPLL的相位跟踪在LF和DDS的累加器中完成,通过如下形式实现
φ′(l+1)=φ′(l)+KI f ′(l)+KPe(l)
(42)
f ′(l+1)=f ′(l)+e(l)
(43)
为防止φ′(l+1)溢出,使
φ′(l+1)=φ′(l+1)%2π
(44)
其中,%表示求余运算,由式(40)至(42)可得整个环路滤波器的传递函数为
(45)
其中,Φ′(Z)为φ′(l)的Z 变换,Φi(Z)为φi(l)的Z 变换,滤波器系数KI和KP的确定可根据文献[21]的方法,通过调节滤波器参数搜索出最佳环路相位误差响应曲线来得到。
由式(34)可知,利用DPLL对输入信号的残余载波进行跟踪消除后,得到的
为一周期PN码的估计。由于
是由G段PN码组合而成,而每段PN码都会独立的取正负号,因此对于组合序列来说有2G种可能,从而产生相位模糊,对此,利用PN码的性质去除相位模糊从而得到正确的码序列[22]。例如:根据m序列周期自相关函数的旁瓣具有单一值“-1”,Gold序列的周期自相关函数为三值函数且与码序列长度有关,来搜索出正确的组合序列
4 仿真实验与分析
不失一般性,实验中信息码采用随机产生的BPSK调制序列;PN码采用m序列,平均误码率计算公式为
(46)
式(46)中,n表示经采样后的一周期PN码长度,nr表示第r次蒙特卡洛仿真中估计的一周期PN码中错误的位数,R表示蒙特卡洛仿真次数。
实验1 验证本文算法的可行性。PN码采用长度L=255 bit的m序列,采样速率为一个码片采样一个点,即Ts=Tcp,则对信号进行分段后的每组数据长度n=L,数据组数K=500,扩频调制比G=3,即一PN码周期含有3个信息码元,则一个信息码元内包含的采样点数目m=L/G=85,信噪比SNR=-10 dB。残余频偏采用归一化形式fΔ=0.02,表示一个残余载波周期内包含50个采样点,随机初始相位φ∈[0,2π]。
图3是经特征值分解和去酉模糊后估计出的一周期PN码序列,图4是将图3的PN码序列送入到DPLL后输出的数据,其中图4(a)是DPLL输出的I路数据
图4(b)是DPLL输出的Q路数据
图5是最终估计的PN码同真实PN码对比图。
图3 经特征值分解估计的PN码序列
Fig.3 PN code sequence estimated by eigenvalue decomposition
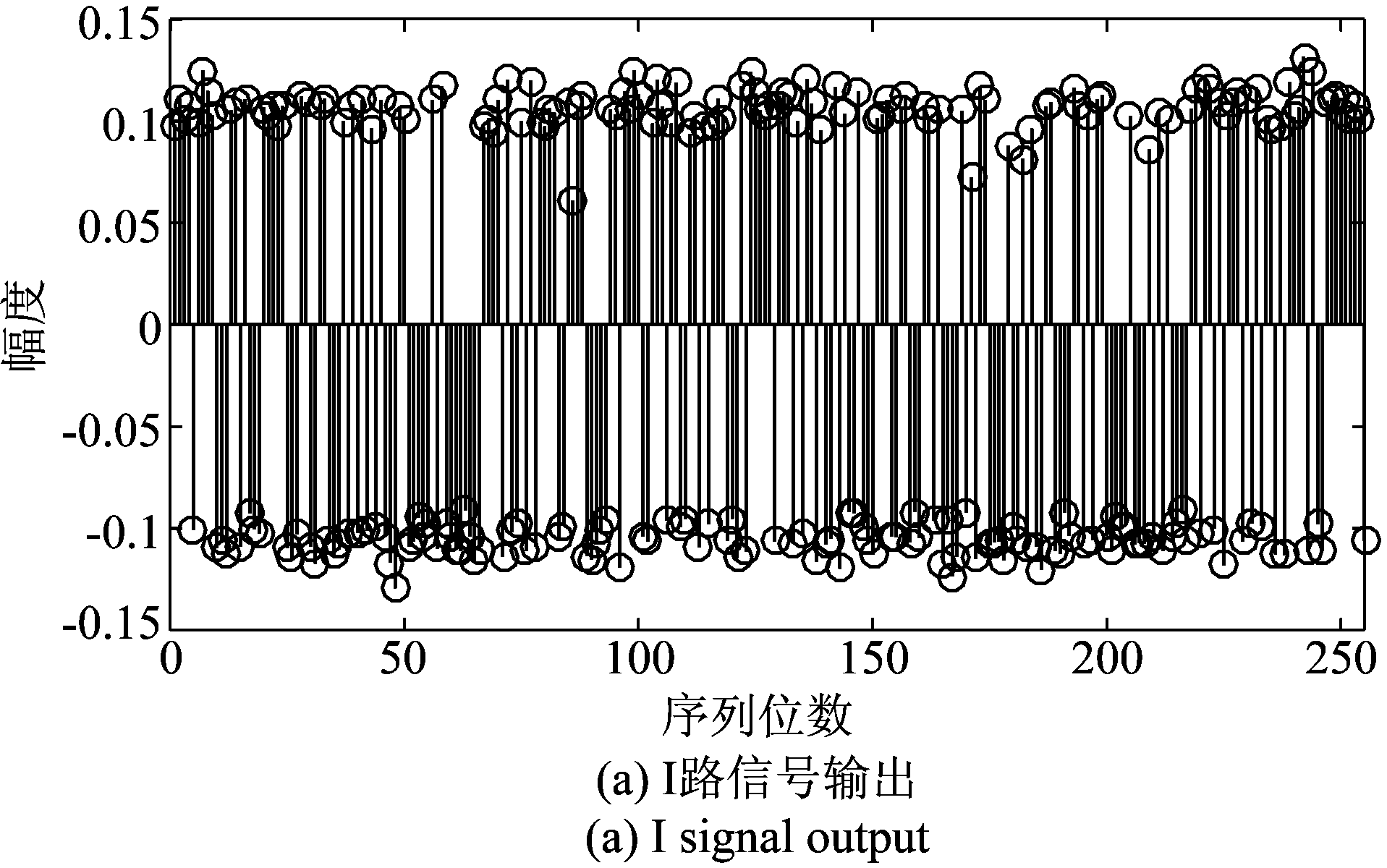
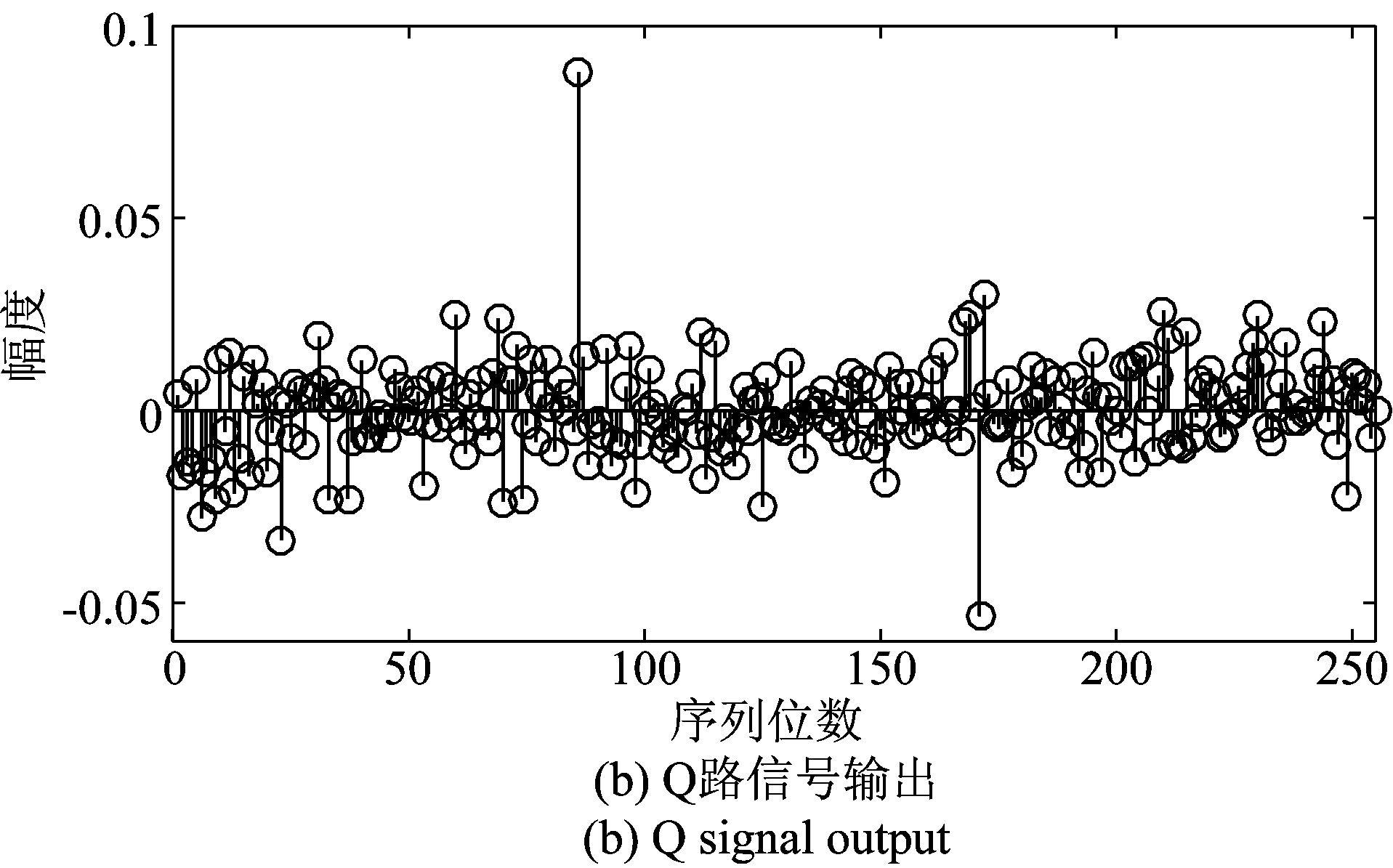
图4 DPLL输出
Fig.4 DPLL output
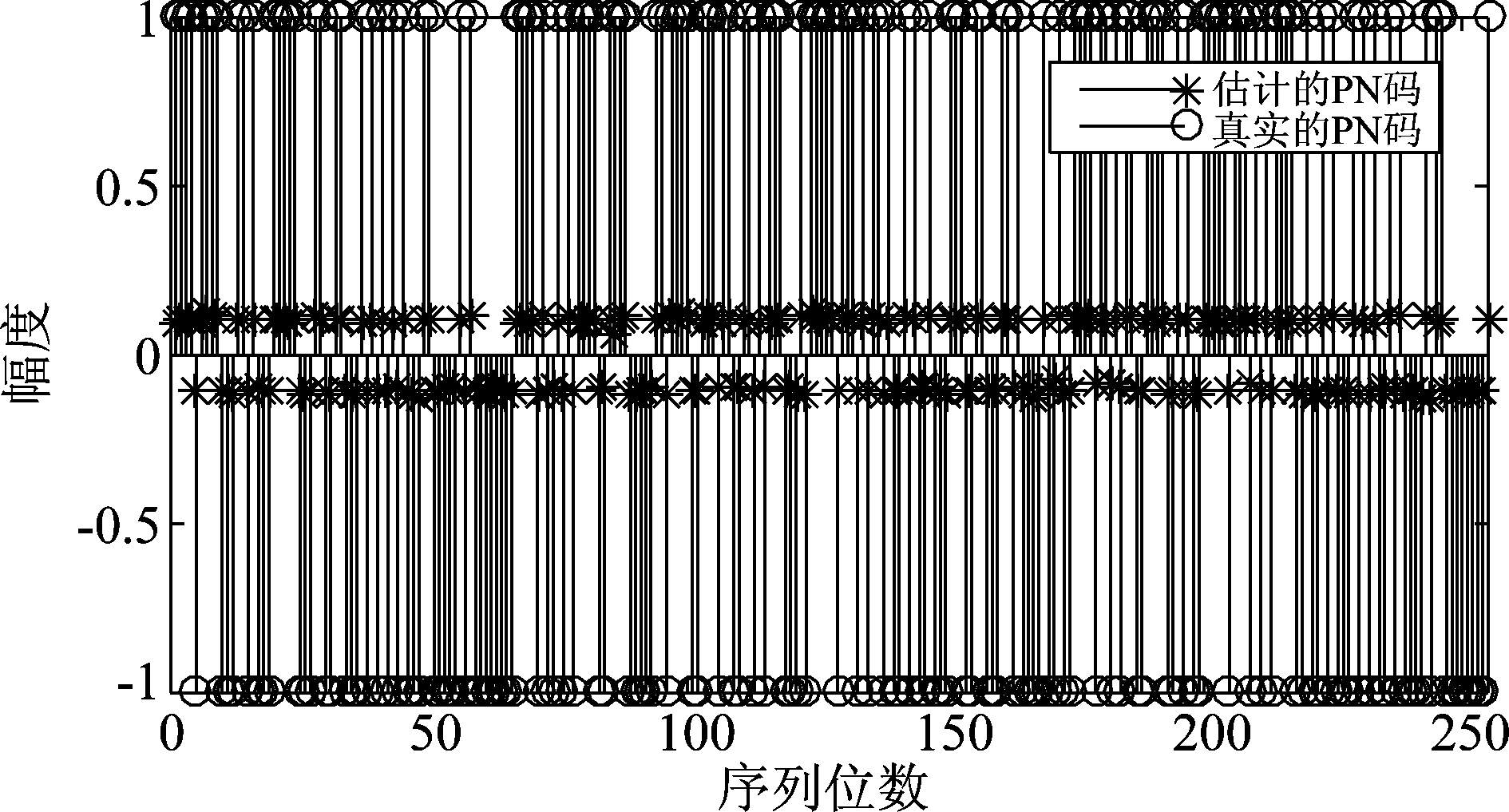
图5 估计的PN码与真实PN码对比图
Fig.5 Comparison of estimated PN codes and real PN codes
由图3可知,利用特征值分解后估计出的PN码含有残余载波,无法直接从其中恢复出原始PN码序列。由图4可知,I路输出
去除了图3中载波的影响,恢复出了PN码序列,Q路输出
基本都在0值附近,但在序列的第86位和第171位,幅值有突变情况,这是因为这两个位置正好是各虚拟用户PN码之间的拼接点会出现相位突变的情况,DPLL不能够立刻对突变的相位进行锁定而导致输出幅值突变,由于相位突变值一般会在[-π/2,π/2]区间内,并结合式(38)可知,相位差的突变并不会影响对这两处PN码估计值的符号判决。说明了本文算法的可行性。由图5可看出,根据m序列的周期函数性质去除相位模糊后,本文算法能够在信噪比为-10 dB下准确地估计出PN码。
实验2 比较不同PN码长度L和不同扩频调制比G对PN码估计性能的影响。PN码分别采用长度L=255的m序列和长度L=60的截断m序列,扩频调制比分别为G=3和G=5,信噪比变化范围从-20 dB～-10 dB,变化间隔为1 dB,其余实验条件同实验1,蒙特卡洛仿真500次得到PN码的误码率曲线如图6所示。
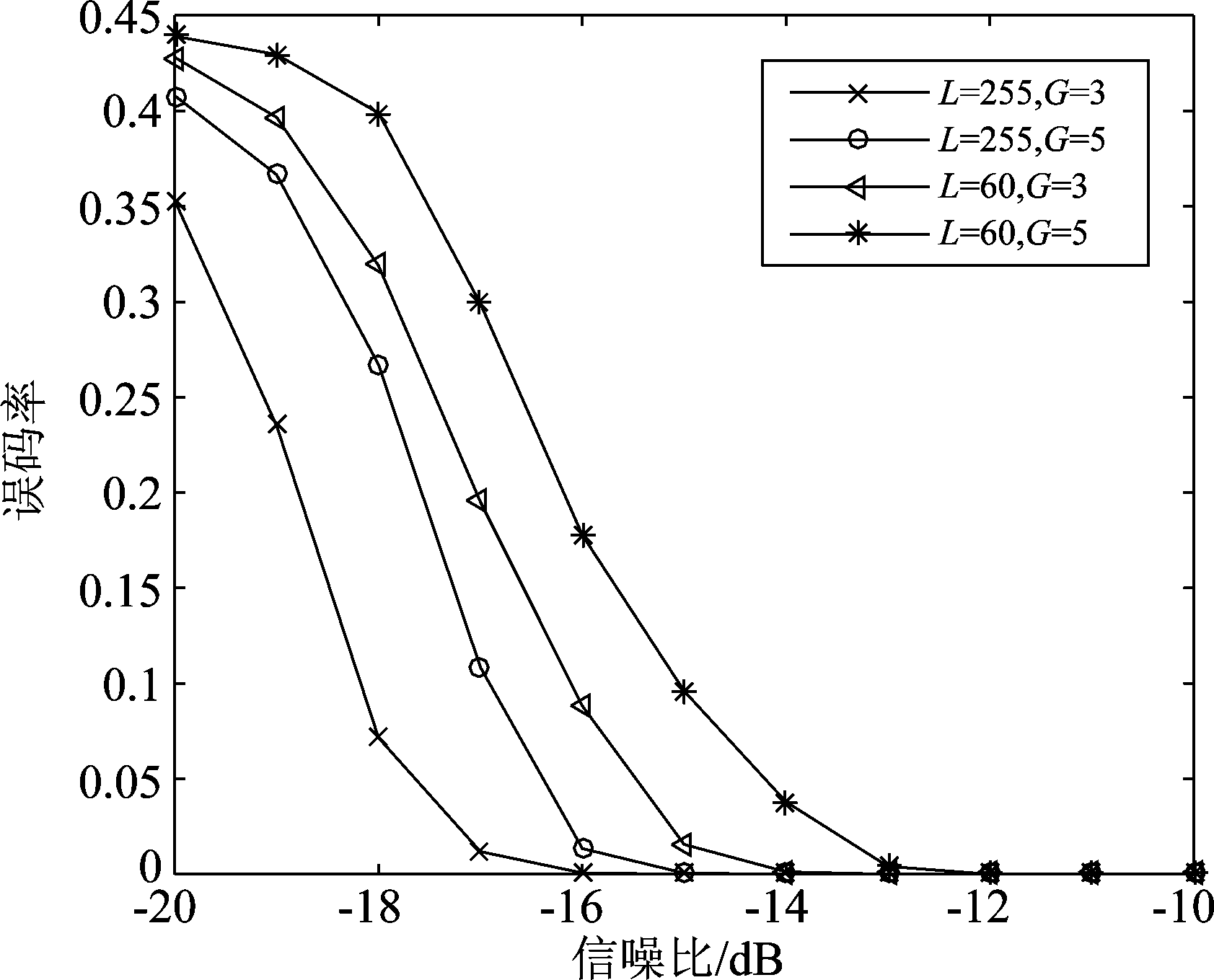
图6 不同PN码长度和不同扩频调制比下的 PN码估计性能
Fig.6 Estimation performance of PN codes under different PN codes lengths and different spread spectrum modulation ratios
由图6可看出,在扩频调制比相同条件下, PN码长度越长,PN码序列越接近白噪声,抗干扰性能越好,在PN码长度L=255条件下,无误码估计的信噪比门限低至-16 dB 和-15 dB;在PN码长度相同的条件下,扩频调制比越大,意味着一周期长度的PN码内包含的信息码元越多,对PN码周期性破坏程度越大,算法的估计效果越差,误码率越高,因此在样本长度不够长的情况下,扩频调制比对码序列的估计有一定的影响。
实验3 比较不同残余频偏fΔ对PN码的估计性能的影响。PN码分别采用长度L=255的m序列,扩频调制比分别为G=3,归一化频偏分别为fΔ=0.002、 fΔ=0.02、 fΔ=0.04、 fΔ=0.06,信噪比变化范围从-20 dB～-10 dB,变化间隔为1 dB,其余实验条件同实验1。除了对不同频偏下PN码的估计性能进行分析比较外,在相同实验条件下,还对文献[4]中无残余频偏的周期长码直扩信号的PN码估计性能进行了比较,比较结果如图7所示。
从图7中可以看出,当归一化频偏低至fΔ=0.002时,通过合理调节滤波器系数,本文算法对PN码的估计性能优于文献[4],说明DPLL在一定程度能提升PN码估计性能。随着频偏增大,估计性能有所下降,当频偏fΔ=0.02、 fΔ=0.04、 fΔ=0.06时,可以看出误码率曲线基本一致,且不同条件下实现PN码准确估计的信噪比门限都能低至-16 dB,说明本文设计的DPLL在去除频偏时,没有带来较大的误差传播,适应性广,稳定性高,具有很强的实用价值。
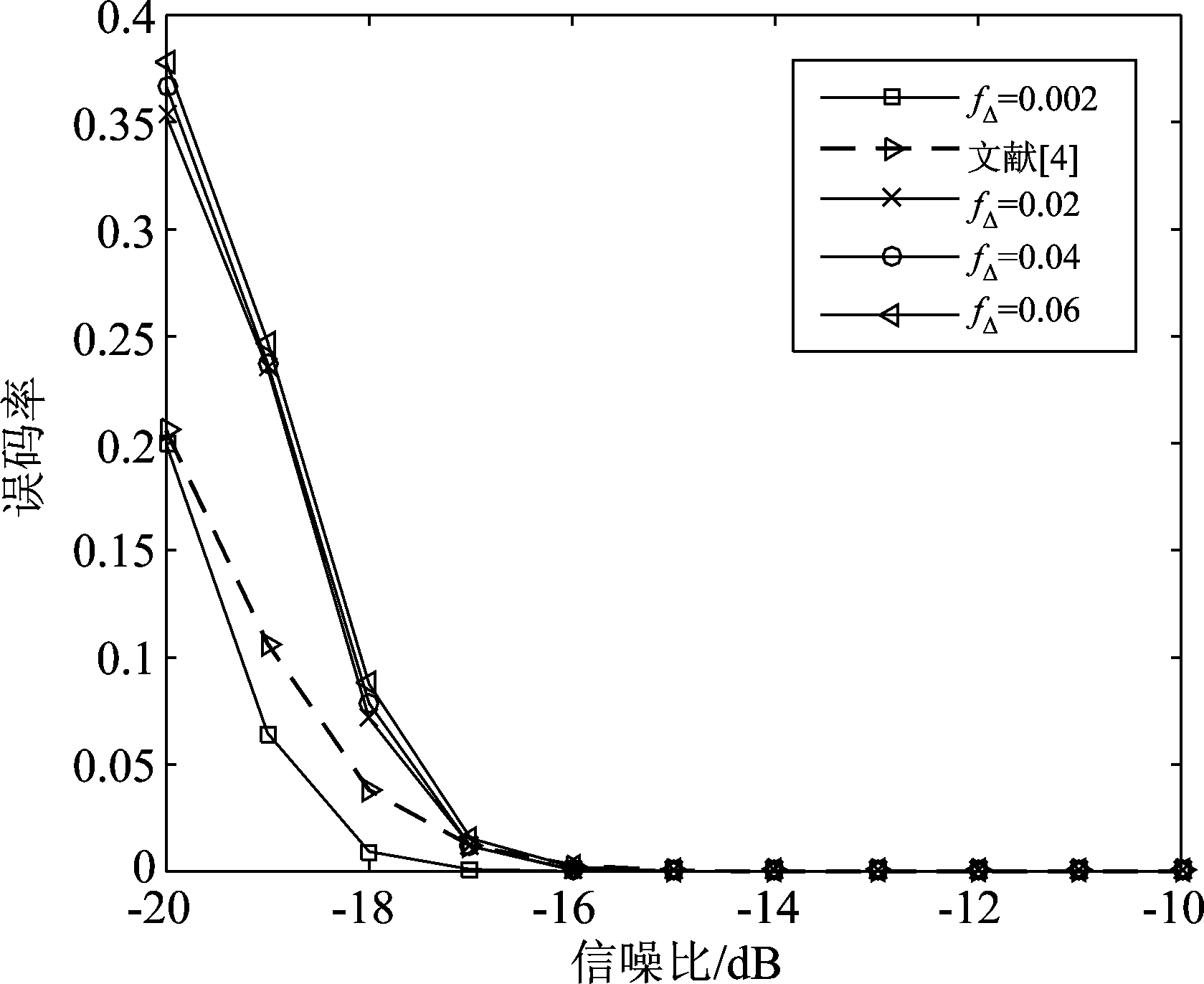
图7 不同频偏下的PN码估计性能
Fig.7 PN code estimation performance at different frequency offsets
实验4 本文算法与文献[6]所提算法的PN码估计性能比较。PN码采用长度L=255的m序列,扩频调制比G=5,数据组数分别为K=500、K=1000,其余实验条件同实验1。得到不同算法在不同数据组数下的PN码误码率曲线如图8所示。
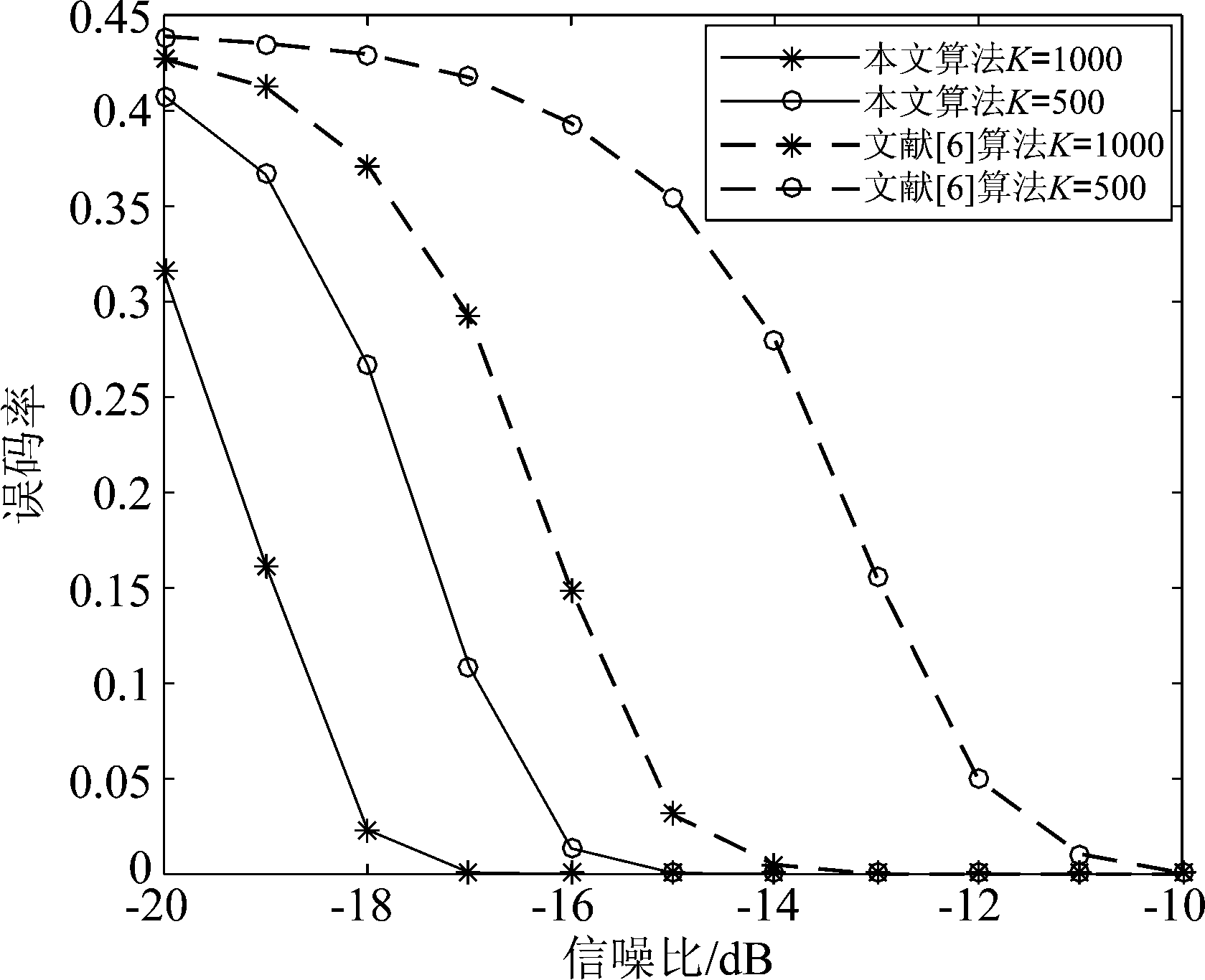
图8 算法性能对比
Fig.8 Algorithm performance comparison
从图8可看出,本文算法对PN码估计性能优于文献[6]的算法。在数据组数分别为K=500和K=1000,误码率低于1%时,本文算法同文献[6]相比信噪比分别提升了约4 dB 和5 dB。文献[6]利用CPAST算法对PN码序列分段迭代求解,当分的段数较多时,每段的数据量较少,迭代性能下降,且在迭代过程中,估计效果还受参数初始化的影响。从图8还可看出,随着数据组数的增加,包含的有用信息越多,PN码序列估计效果也越好。
实验5 比较在不同信噪比下,数据组数K对PN码的估计性能的影响。PN码采用长度L=63 bit的m序列,采样速率为一个码片采样2个点,即Ts=Tcp/2,则对信号进行分段后的每组数据长度n=2L,扩频调制比G=3,即一PN码周期含有3个信息码元,则一个信息码元内包含的采样点数目m=2L/G=42,设置信噪比SNR 分别为-17 dB、-15 dB、-13 dB、-11 dB,数据组数K变化范围从50～1000,变化间隔为50,蒙特卡洛仿真500次,其他条件同实验1,得到不同信噪比下的收敛曲线如图9所示。
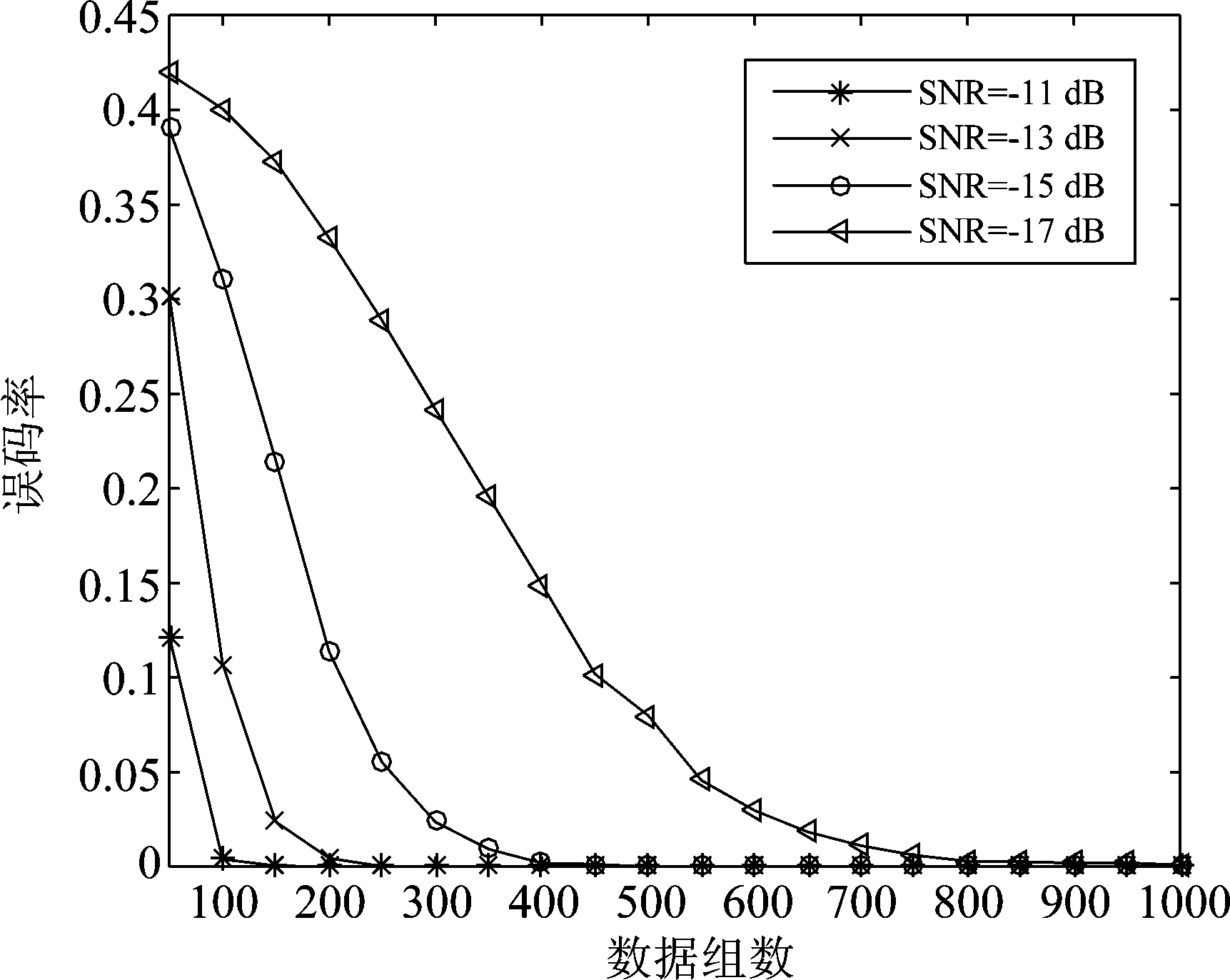
图9 不同信噪比下的收敛曲线
Fig.9 The convergence curves under different SNR
从图9可以看出,随着数据组数增加,误码率逐渐降低,最终达到0。且信噪比越高,曲线收敛速度越快,无误码时需要的数据组数越少。在信噪比为-11 dB时,只需要150组数据就能够实现PN码的正确估计,因此可以通过增加数据组数来进一步降低信噪比。
5 结论
针对带有残余载波的周期长码直扩信号PN码盲估计问题,本文提出一种矩阵特征分解结合数字锁相环的方法。首先将信号等效建模为虚拟多用户SC-DSSS信号,然后按照PN码的周期长度进行分段构成相关矩阵,对此矩阵进行特征值分解并去除酉模糊得到带有残余载波的PN码,最后将带有残余载波的PN码送到DPLL对载频进行跟踪消除。理论分析及仿真结果表明,本文方法能够在数据组数为500,信噪比为-16 dB下,实现不同频偏下PN码的正确估计,且在相同条件下,本文算法的估计性能优于文献[6],实现了低信噪比环境下PN码的正确估计,具有较高的工程应用价值,为进一步解决复杂环境下的直扩信号PN码估计提供了良好的解决思路和方法。
[1] 牟青, 魏平. 未知频偏下长码直扩信号的盲解扩[J]. 电子与信息学报, 2010, 32(8): 1797-1801.
Mou Qing, Wei Ping. Blind dispreading of Long-code DS-SS signals with unknown carrier offset[J]. Journal of Electronics & Information Technology, 2010, 32(8): 1797-1801.(in Chinese)
[2] 张天骐, 杨强, 宋玉龙, 等. 基于相似度的直扩信号盲解扩方法[J]. 系统工程与电子技术, 2017, 39(7): 1451-1456.
Zhang Tianqi, Yang Qiang, Song Yulong, et al. Similarity based blind despread method of DS-SS signal[J]. Systems Engineering and Electronics, 2017, 39(7): 1451-1456.(in Chinese)
[3] 强幸子, 张天骐, 赵军桃, 等. 非合作直扩信号伪码及信息序列联合盲估计[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(4): 468- 472.
Qiang Xingzi, Zhang Tianqi, Zhao Juntao, et al. Blind estimation of non-cooperative direct sequence spread spectrum signals and information sequence[J]. Journal of Chongqing University of Post and Telecommunications: Natural Science Edition, 2016, 28(4): 468- 472.(in Chinese)
[4] 白娟, 张天骐, 赵德芳, 等. 基于虚拟多用户模型的长码直扩信号伪码估计[J]. 电讯技术, 2011, 51(8): 29-35.
Bai Juan, Zhang Tianqi, Zhao Defang, et al. PN sequence estimation of Long-code DSSS signals based on virtual multiuser model[J]. Telecommunication Engineering, 2011, 51(8): 29-35.(in Chinese)
[5] 朱照阳, 高勇. 短码、周期长码直扩信号伪码序列盲估计[J]. 电讯技术, 2017, 57(11): 1313-1319.
Zhu Zhaoyang, Gao Yong. Blind estimation of PN sequence of short-code and periodic long-code DSSS signals[J]. Telecommunication Engineering, 2017, 57(11): 1313-1319.(in Chinese)
[6] 王猛, 李迟生. 基于谱范数和CPAST算法的周期长码直扩信号PN序列估计[J]. 科学技术与工程, 2018, 18(10): 59- 64.
Wang Meng, Li Chisheng. Estimation of PN sequence of periodic long code direct sequence spread spectrum based on the spectral norm and CPAST algorithm[J]. Science Technology and Engineering, 2018, 18(10): 59- 64.(in Chinese)
[7] 周德强, 康一丁, 陈卫东. 基于Fast-ICA的周期长码直扩信号盲扩频码估计[J]. 无线电通信技术, 2013, 39(6): 55-59.
Zhou Deqiang, Kang Yiding, Chen Weidong. Blind estimation for spread spectrum codes of PLC-DSSS signals based on Fast-ICA[J]. Radio Communications Technology, 2013, 39(6): 55-59.(in Chinese)
[8] 王建雄, 张立民, 马超. 周期长码直扩信号扩频序列的盲估计[J]. 计算机与数字工程, 2016, 44(6): 1035-1040.
Wang Jianxiong, Zhang Limin, Ma Chao. Blind estimation of spread spectrum sequence of periodic Long-code DSSS signal[J]. Computer & Digital Engineering, 2016, 44(6): 1035-1040.(in Chinese)
[9] 马超, 张立民. 基于MCMC-UKF 的直扩信号盲估计[EB/OL]. 计算机工程. https:∥doi.org/10.19678/j.issn.1000-3428.0050464, 2018, 06.
Ma Chao, Zhang Limin. Blind estimation of DSSS signal based on MCMC-UKF[EB/OL]. Computer Engineering. https:∥doi.org/10.19678/j.issn.1000-3428.0050464, 2018, 06.(in Chinese)
[10]Gu Xiaowei, Zhao zhijin, Shen Lei. Blind estimation of pseudo-random codes in periodic long code direct sequence spread spectrum signals[J]. IET Communications, 2016, 10(11): 1273-1281.
[11]赵知劲, 强芳芳, 顾骁伟, 等. 利用三阶相关特征信息的周期长码扩频信号伪码盲估计[J]. 信号处理, 2016, 32(6): 739-745.
Zhao Zhijin, Qiang Fangfang, Gu Xiaowei, et al. Blind estimation of pseudo-random codes in period long code spread spectrum signals by using triple correlation feature information[J]. Journal of Signal Processing, 2016, 32(6): 739-745.(in Chinese)
[12]赵知劲, 顾骁伟, 沈雷, 等. 非周期长码直扩信号的伪随机码盲估计[J]. 通信学报, 2015, 36(5): 23-30.
Zhao Zhijin, Gu Xiaowei, Shen Lei, et al. Blind estimation of pseudo-random codes in non-periodic long code direct-sequence spread-spectrum signals[J]. Journal on Communications, 2015, 36(5): 23-30.(in Chinese)
[13]尹辉, 赵知劲. 利用FastICA和三阶相关函数的多天线辅助NPLC-DS-CDMA扩频码盲估计[J]. 信号处理, 2018, 34(3): 289-295.
Yin Hui, Zhao Zhijin. Blind estimation of spreading codes for multi-antenna NPLC-DS-CDMA signals based on FastICA and third order correlation function[J]. Journal of Signal Processing, 2018, 34(3): 289-295.(in Chinese)
[14]沈斌, 王建新. 窄带干扰条件下含有未知载频的直扩信号的伪码序列估计[J]. 电子与信息学报, 2015, 37(7): 1556-1561.
Shen Bin, Wang Jianxin. Estimation of PN sequence in DSSS signals with unknown carrier frequency under narrow band interference[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1556-1561.(in Chinese)
[15]Zhang Tianqi, Dai Shaosheng, Ma Guoning, et al. Approach to blind estimation of the PN sequence in DS-SS signals with residual carrier[J]. Journal of Systems Engineering and Electronics, 2010, 21(1): 1- 8.
[16]Zhang Tianqi, Dai Shaosheng, Zhang Wei, et al. Blind estimation of the PN sequence in lower SNR DS-SS signals with residual carrier[J]. Digital Signal Processing, 2012, 22(1): 106-113.
[17]张天骐, 李雪松, 代少升, 等. 一种同时估计直扩信号伪码周期及码片速率的方法[J]. 舰船电子对抗, 2008, 31(3): 77- 83.
Zhang Tianqi, Li Xuesong, Dai Shaosheng, et al. An approach to estimate the pseudo-code period and chip rate of direct sequence spread spectrum signals simultaneously[J]. Shipboard Electronic Countermeasure, 2008, 31(3): 77- 83.(in Chinese)
[18]金艳, 孙玖玲, 姬红兵. 基于相关熵的扩频周期估计方法[J]. 系统工程与电子技术, 2018, 40(1): 17-22.
Jin Yan, Sun Jiuling, Ji Hongbing. PN sequence period estimation method based on correntropy[J]. Systems Engineering and Electronics, 2018, 40(1): 17-22.(in Chinese)
[19]Daneshmand S, Aghaeinia H, Tohidian M, et al. Blind estimation of signal in periodic long-code DSSS communications[C]∥2009 IEEE International Conference on Sarnoff Symposium. Princeton, NJ, USA, 2009: 1- 6.
[20]Farid A A, Luo Zhiquan, Ding Zhi. Blind channel equalization based on second order statistics[C]∥2005 IEEE International Conference on Acoustics, Speech, and Signal Processing. Pennsylvania, USA, 2005: 557-560.
[21]魏选平, 姚敏立, 张周生. 锁相环的时域跟踪性能及MATLAB仿真分析[J]. 电子测试, 2010, 1(7): 60- 62.
Wei Xuanping, Yao Minli, Zhang Zhousheng. PLL tracking performance and time-domain simulating analysis of MATLAB[J]. Electronic Test, 2010, 1(7): 60- 62.(in Chinese)
[22]尹辉, 赵知劲, 姜显扬. 利用BCH码纠错和Fast-ICA的长码直扩CDMA信号扩频码盲估计[J]. 信号处理, 2017, 33(11): 1436-1442.
Yin Hui, Zhao Zhijin, Jiang Xianyang. Blind estimation of spread spectrum codes for LC-DS-CDMA signals based on BCH code error correction and Fast-ICA[J]. Journal of Signal Processing, 2017, 33(11): 1436-1442.(in Chinese)
