1 引言
Polar码作为一种新型信道编码,自Arikan[1]提出以来,引起了广泛的关注[2-3],它是唯一被证明能够达到香农限的信道编码方法。为了提升Polar码在有限码长时的性能,学者们提出和改进了很多有效的译码算法[4-5],文献[4]提出的BP-CRC与基于生成矩阵G的早期终止准则,有效降低BP译码器的时延和能耗。文献[5]提出了一种混合逻辑SC解码器,它结合了组合解码器的有利方面和顺序逻辑解码器的低复杂性。然而,在实际的通信系统中,信道可能会出现衰落和相关性的噪声导致译码性能并不理想[6-7]。相关噪声的产生有多种原因,接收机处过采样产生的噪声[8]以及数字系统中的设备噪声[9]都具有相关性;在电力线通信中,有色噪声往往是由普通建筑物和住宅电子设备引起的[10];在10 GBASE-t以太网中,需要使用各种滤波方案来对抗相关噪声导致的符号间干扰[11]。
相关性噪声会严重影响信道编码的性能[11-12],解决这个问题的最有效方法就是白化[13],即把有色噪声转化为白噪声,但是这种方法由于需要矩阵乘法,所以对于长码来说是高度复杂的。因此,我们希望设计出一种低复杂度和鲁棒性的译码方法,能够利用噪声相关特性而不依赖于其特定结构。由于神经网络善于寻找特征,所以把深度学习应用在相关性噪声问题的解决上具有非常好的效果[14]。最近,深度学习特别是神经网络被认为是替代或帮助Polar码译码的潜在解决方案[15-19],因为他们具有强大的预测模型和单次译码属性[20]。但是深度学习译码存在局限性[21],对于k个信息比特,神经网络需要区分2k个不同的码字[20],学习空间的指数复杂性导致了基于神经网络的译码器只能实现短码长度的最大后验概率(MAP)性能。一种解决方法是通过分块进行译码[20,22]。Cammerer等人[20]利用神经网络辅助组件取代了一些置信度传播(Belief Bropagation, BP)译码器的子块,并通过剩余BP阶段来耦合这些子快,文献[22]提出了神经网络串行抵消译码(Neural Successive Cancellation,NSC),NSC译码器由与SC译码码树连接的多个神经网络译码器构成,但是以上两种方法的可译码长度依然限于短码。另一种解决方法是使用神经网络的回归功能对信道噪声进行估计,2018年,沈聪等人[14]使用标准BP译码估计信道噪声,然后用CNN消除估计误差,获得更准确的信道噪声估计,但是该结构在估计信道噪声阶段引入了BP迭代,增加了计算复杂度,使得译码时延上升。
针对目前神经网络译码的指数复杂性,本文利用神经网络的回归功能预测信道噪声,使其可以应用在长码上;针对噪声估计阶段需要使用BP译码算法,复杂度较高,本文设计了一种新型的前置预判-卷积神经网络结构。通过前置预判深度优化神经网络,使其准确估计信道噪声并使残余噪声分布尽可能遵循高斯分布,再根据信道的残余噪声分布统计修正对数似然比(Logarithm Likelihood Ratio, LLR),更可靠的似然比信息能帮助使得译码器进行更准确的译码,提升Polar码的性能,有效地解决了Polar码在相关噪声信道下性能严重下降的问题。
2 Polar码与卷积神经网络
2.1 Polar码编译码原理
信道极化作为Polar码的理论基础,就是将N个相同的二进制离散无记忆信道(B-DMC)W的独立拷贝信道,变成N个相关的比特信道的集合
在这个信道集合中有两类比特信道,即信道容量趋近于1和趋近于0的信道。当码长N趋于无限大时,正好存在占总信道比例为I(W)的比特信道容量趋于1,其中I(W)表示W的信道容量。Polar码的构造就是选取信道容量趋近于1的比特信道来传输信息,所以Polar码理论上可以达到香农限。
Polar码作为线性分组码,码长为N的Polar码编码过程可以写为
(1)
其中,GN是Polar码的N阶生成矩阵,GN=BNF⊗n,BN是比特翻转矩阵,
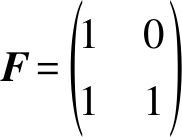
(2)
信息位通常用A来表示,A⊂{1,2,…,N},公式(1)可以改写为
(3)
其中,GN(A)是生成矩阵GN中A集合对应的行构成的矩阵,Ac是A的补集。通常,Polar码表示为P(N,K,A,uAc),其中K表示A中元素的个数,K/N为码率,A是信息位,uAc为冻结位信息。
Polar码的译码算法主要有连续消除(Successive Cancellation,SC)译码算法和置信度传播(BP)译码算法。Polar码的BP译码是基于因子图表示的,码长为N的Polar码通过一个n阶段的因子图迭代译码,其中N=2n,因子图包含N(n+1)个节点,每个阶段有N/2个处理单元(Processing Elements,PE)。第一阶段的节点与信息位有关,初始化为
(4)
第n+1阶段的节点信息与信道的接收值有关,把计算好的LLR输入到该节点
Ln+1, j=LLRj
(5)
节点(i, j)中,i代表因子图中的阶段,取值范围为1≤i≤n, j代表因子图中的行。在译码器每个PE单元中,节点(i, j)中有两种信息在传递:从左到右传递的信息Ri, j,从右向左传递的信息Li, j。信息以对数似然比的形式先从右向左更新,再左到右更新,循坏一次为BP译码的一次迭代。每个PE单元中L和R的计算公式为:
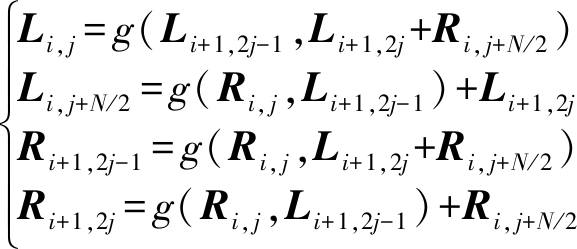
(6)
其中,1≤i≤n,1≤j≤N/2,且g(x1,x2)=2arctanh(tanh(x1/2)tanh(x2/2))。
达到设定好的迭代次数或停止条件后,得到最终的节点置信度,如果j∈Ac,该节点为冻结位
否则按照下式判断各个节点并得到译码结果:
(7)
2.2 CNN原理及设计
深度学习是一种包含多级非线性变换的机器学习方法,深层神经网络是目前的主要形式,神经网络利用类似于人脑的分层模型结构,从底层到高层对输入数据逐级提取特征,在底层信号到高层语义之间建立起映射关系。CNN是其中一种经典且普遍应用的神经网络结构。CNN的权值共享、局部连接以及池化等操作有效地降低了网络的复杂度,具有强鲁棒性和容错能力,并且易于训练和优化。基于这些优越的特性,它被广泛应用于各种信号和信息处理的任务中。
CNN的结构如图1所示,网络的第一层可以看出,一列数据n通过卷积核的卷积操作,生成f1个特征映射,可以表示为:
(8)
其中,Z1, j是第一层网络输出的第j个特征映射,h1, j是第j个卷积核,它本质上是长度为k1的一维向量,b1, j是对应的标量偏差,ReLU(•)是激活函数。在神经网络中,卷积运算由*表示,并定义为
(9)
第i层(i>1)的卷积操作在上一层网络的输出上进行,可以看成是二维卷积,网络的输出为
Zi, j=ReLU(hi, j*Zi-1+bi, j)
(10)
其中,Zi, j是第i层网络的第j个特征映射,hi, j是第j个大小为ki×si-1的卷积核,其中si-1是前一层的卷积核数量。使用L来表示总层数。在最后一层,输出信道噪声的最终估计:
n′=hL*ZL-1+bL
(11)
在本文所提出的PD-CNN译码算法中,定义每一层卷积的方式为same,使得卷积操作的输入和输出尺寸保持一致。CNN的结构取决于网络的层数,卷积核的大小和数量,在训练之前将CNN结构设为四层{4;9,3,3,15;64,32,16,1}。
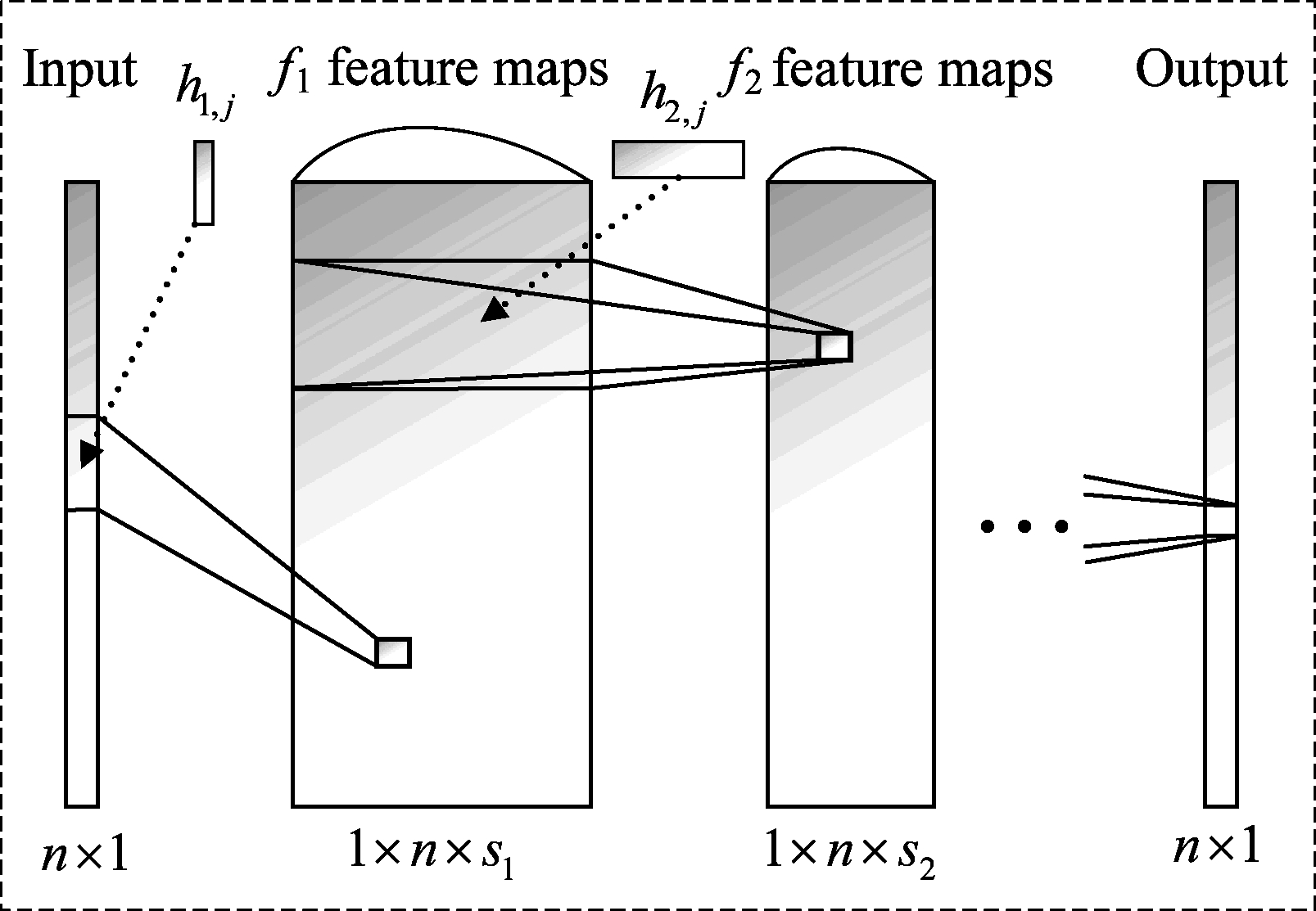
图1 CNN结构图
Fig.1 The adopted CNN structure
因为本文中CNN的输入是信道噪声的估计值,是一维向量,所以用keras库里的快速开始序贯(Sequential)模型[23],第一层网络的卷积核数量为64,卷积核大小为9,卷积的方式选择为same,所以第一层的输出为64列n行。同理,第二层卷积核数量为32,卷积核大小为3,第三层网络的卷积核数量为16,卷积核大小为3,第四层卷积核数量为1,卷积核大小为15。前三层的激活函数为RELU,第四层的激活函数设为Linear,目的是通过四层网络之后,CNN的输出结果为信道噪声准确的估计值。
3 基于PD-CNN的Polar码译码算法
本文提出的基于PD-CNN的Polar码译码算法流程如图2所示,在发送端,长度为K的信息比特u通过Polar码编码器被编码为长度为N的二进制Polar码x,码字x通过二进制相移键控(Binary Phase Shift Keying, BPSK)调制,映射到符号向量s,BPSK调制后的信号s将通过具有加性噪声的信道传递,信道噪声n为自相关的高斯随机向量。
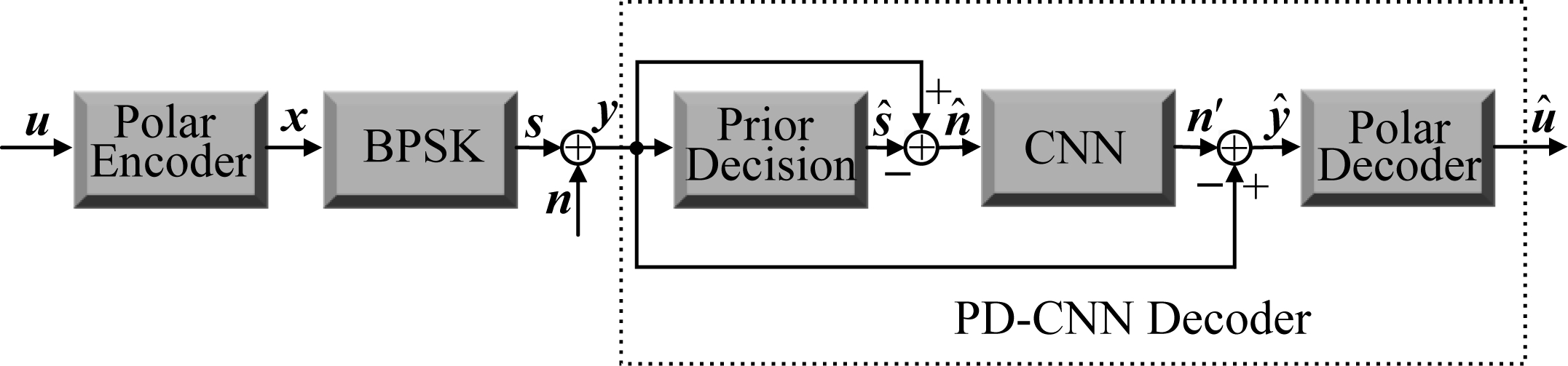
图2 基于PD-CNN的Polar码译码算法流程图
Fig.2 The process diagram of the decoding algorithm for Polar based on PD-CNN
在接收端,接收到的信息y表示为
y=s+n
(12)
通过前置预判,用
表示预判结果,可以得到噪声估计值
(13)
是对信道噪声的初步估计。由于前置预判可能存在错误,所以重写
(14)
其中,ε表示初步噪声估计的误差。把输入到CNN,得到对噪声的更准确估计并使残余噪声尽可能遵循高斯分布,用n′表示CNN的输出,得到噪声受到抑制的接收向量
(15)
通过公式(15),接收值减去信道估计值,抑制了信道噪声的功率,等价于提高了信噪比;使残余噪声遵循高斯分布,相当于对信道的相关噪声进行白化,便于计算出更可靠的LLR。在译码之前,要根据
和信道的残余噪声分布修正LLR值,
(16)
其中, p0,i和p1,i表示y′的第i个元素为-1或1的概率。计算公式如下,
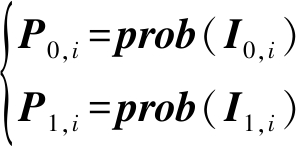
(17)
其中, prob为真实信道噪声减去神经网络估计的信道噪声后的残余噪声的分布统计,在训练网络时产生并保存,
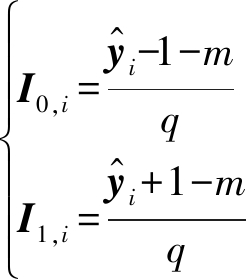
(18)
其中,
表示的第i个元素,m=-10,q=0.01。
最后将更可靠的LLR输入到Polar码译码器,得到最终的信息估计
本文设计的PD-CNN结构,通过前置预判,可以高效的对信道噪声进行第一次估计,不引入BP迭代,降低了复杂度。CNN被设计为输出噪声的准确值,利用的是其回归功能对信道噪声进行估计,所以突破了传统神经网络译码的局限性,可以应用在较长的码字上。通过残余噪声的分布更新出的可靠的似然比信息能帮助译码器进行更准确的译码,有效的解决了相关噪声下传统Polar码译码性能下降的问题。
本文以BP译码算法为例,提出了基于PD-CNN的Polar码译码算法,如算法1所示。
3.1 生成训练数据
为了训练网络,需要前置预判估计的信道噪声和信道的实际噪声作为训练样本。如果已知噪声相关函数的信道模型,就能够生成足够的信道噪声样本来训练网络。在给定(20)中的信道相关矩阵,可以生成信道的噪声样本:
n=A1/2nω
(19)
其中,nω为独立同分布的标准高斯随机向量。本文使用的是标准的相关模型进行模拟[8]。 相关矩阵A由下式给出:
(20)
其中,Ai, j是A的第(i, j)个元素,η是|η|≤1的相关系数。
信道条件即信噪比(Signal-Noise Rate, SNR)也是产生数据的一个因素,它将决定前置预判错误的严重性并关系到CNN的输出,如果信道条件非常好,则存在非常少的错误,CNN就可能无法学习信道噪声的鲁棒特征。如果信道条件非常糟糕,则中存在许多错误,它们将掩盖信道噪声特征,对网络训练也是不利的。本文生成训练数据的信噪比范围是0 dB到8 dB,间隔为0.5 dB,每个SNR值生成10万条训练数据。通过生成随机的二进制比特u,执行Polar码编码,BPSK调制,模拟信道干扰和前置预判,可以获得信道的估计噪声
虽然CNN的训练需要大量的数据,并且训练网络的好坏也取决于训练数据,具有高复杂性,但是这些影响因素不会妨碍本文所提出的算法用于实际系统。因为网络的训练是离线完成的,可以通过GPU等强大的计算设备来完成复杂的训练过程。
3.2 损失函数的定义以及训练网络
在深度学习中,损失函数的选择将直接影响CNN的性能,损失函数表示的是神经网络的实际输出与期望输出之间的差异,应该根据神经网络要实现的具体任务定义。在本文的译码算法中,CNN的作用是估计信道噪声,它的输出将直接影响到后面LLR的计算,所以要充分考虑CNN与后面LLR计算之间的关系来选择合适的损失函数。在这里,根据参考文献[14]中的定义,使用了损失函数的正态性检验,以便测量残余噪声样本遵循高斯分布的可能性,便于之后的LLR修正。损失函数定义为:
(21)
其中,λ为平衡因子,偏度D和峰度S定义如下:
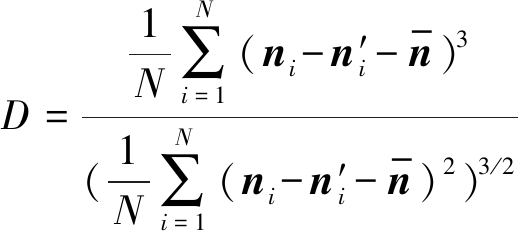
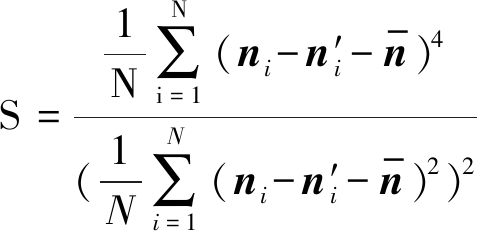
(22)
其中,ni表示真实噪声向量中的第i个元素,
是CNN输出向量的第i个元素,
表示的是样本的均值。通过仿真实验可以发现,这个损失函数可以提供非常理想的训练输出。
本文采用的是批量梯度下降法(Stochastic Gradient Descent, SGD)来训练网络,每个批量包含500组数据,每个SNR中的数据在一个批量中都占有相同的比例,使用adam优化方法,每50次迭代检查一次损失值,直到持续一段时间没有下降。
4 仿真及性能分析
本文通过数值仿真来分析基于PD-CNN的Polar码译码算法的性能,以验证该算法的有效性。Polar码码长N为512,码率R分别为0.5,0.75,0.8,0.9。噪声自相关强度η为0.5和0.8,BP迭代都为30次。图3(a)表示在码率0.5的条件下,本文提出的译码算法在不同噪声相关强度下的译码性能,从图中可以看出,随着噪声相关强度的增大,译码性能会下降,当噪声没有相关性的时候,译码性能和标准BP没有差距。图3(b)表示在自相关系数η=0.8强相关下条件下,本文提出的译码算法在不同码率下的性能对比,从图中可以看出随着SNR的增大,BER下降明显,且随着码率的提高,Polar的性能会降低。在高信噪比处出现BER曲线下降缓慢的现象,这是因为噪声功率的降低导致CNN可识别的特征减少,所以在高信噪比处CNN识别的特征随SNR的增大变化缓慢。
为了体现Polar码的译码算法在不同噪声相关强度下性能表现的差异性,本文对不同码率的Polar码在不同噪声相关强度下不同译码算法的性能进行对比。从图4中可以看出,由于彩色噪声的功率谱密度不平坦,其对信号会有更大的干扰,所以传统译码器在彩色噪声下的性能并不理想,且噪声相关性越强,Polar码的性能会越差。从图4(d)中可以看出,当BER为10-4时,相比于高斯白噪声,标准BP译码算法在噪声自相关系数η=0.5中等相关下有1.3 dB的衰减,而在图4(a)噪声自相关系数η=0.8强相关下有3.2 dB的衰减;当SNR为5 dB时,与高斯白噪声信道相比,中等相关噪声信道下的标准BP算法BER有近2个数量级的衰减,而强相关噪声信道下BER有3个数量级的衰减。因此传统的Polar译码算法不适用于具有相关性噪声的信道。
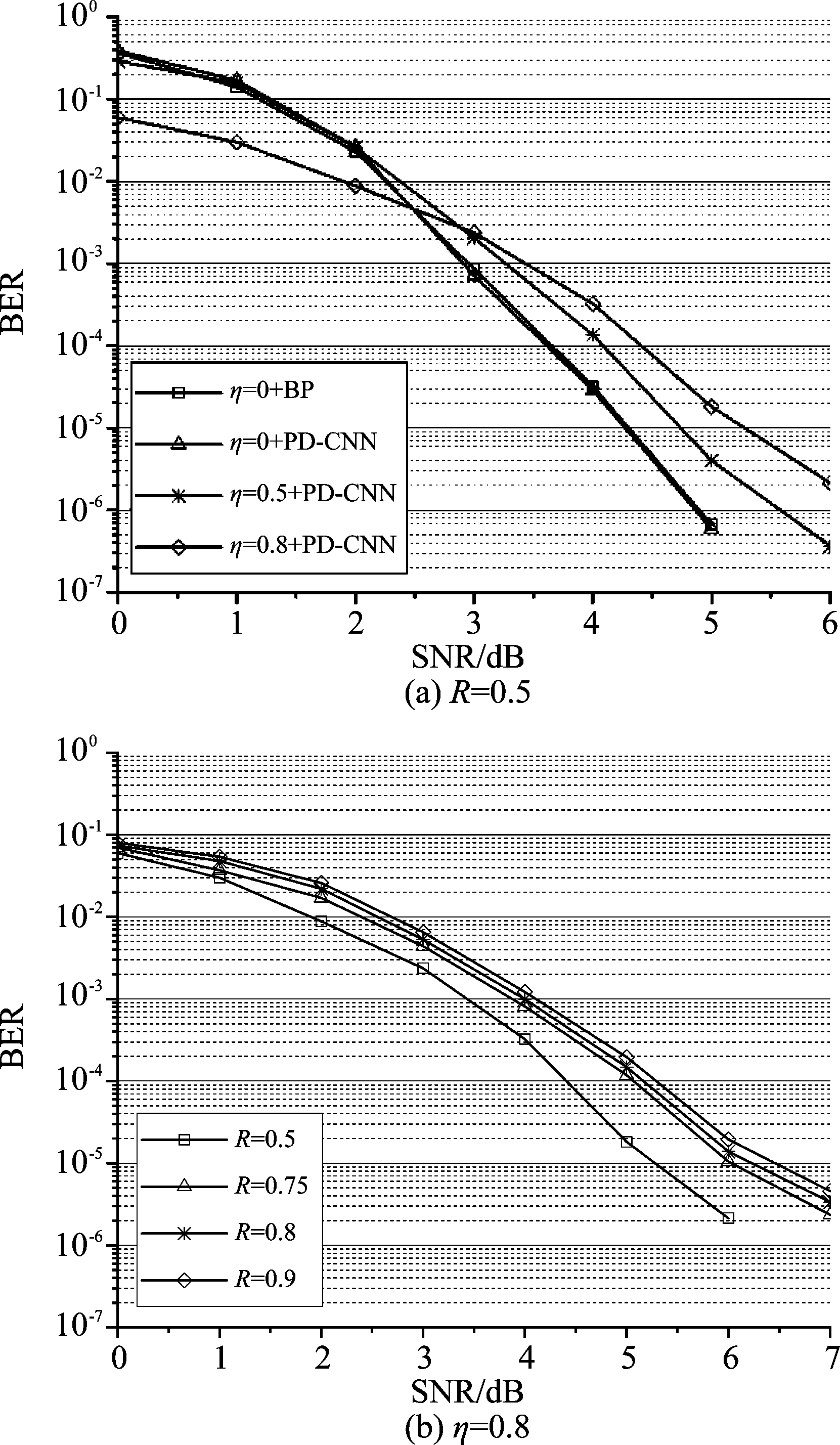
图3 本文提出的译码算法在不同码率 不同噪声下的性能对比
Fig.3 Performance comparison of the decoding algorithm proposed in this paper under different bit rates and different noises
针对上述问题,本文提出的基于PD-CNN的译码算法,通过CNN的前置预判,有效的估计了信道噪声,降低了相关噪声对Polar码的影响,计算出了更加可靠的似然比信息,有效地解决了相关噪声信道下Polar码性能下降的问题。从图4(a)可以看出,当码率为0.5时,和标准BP算法相比,本文提出的译码算法在BER为10-4时有2.2 dB的增益,BER在信噪比为6 dB时有近2个数量级的提升。随着码率的提高,增益逐渐增大,从图4(c)可以看出,当码率为0.9时,和标准BP算法相比,本文提出的译码算法在BER为10-4时有3 dB的增益,BER在SNR为6 dB时有3个数量级的提升。
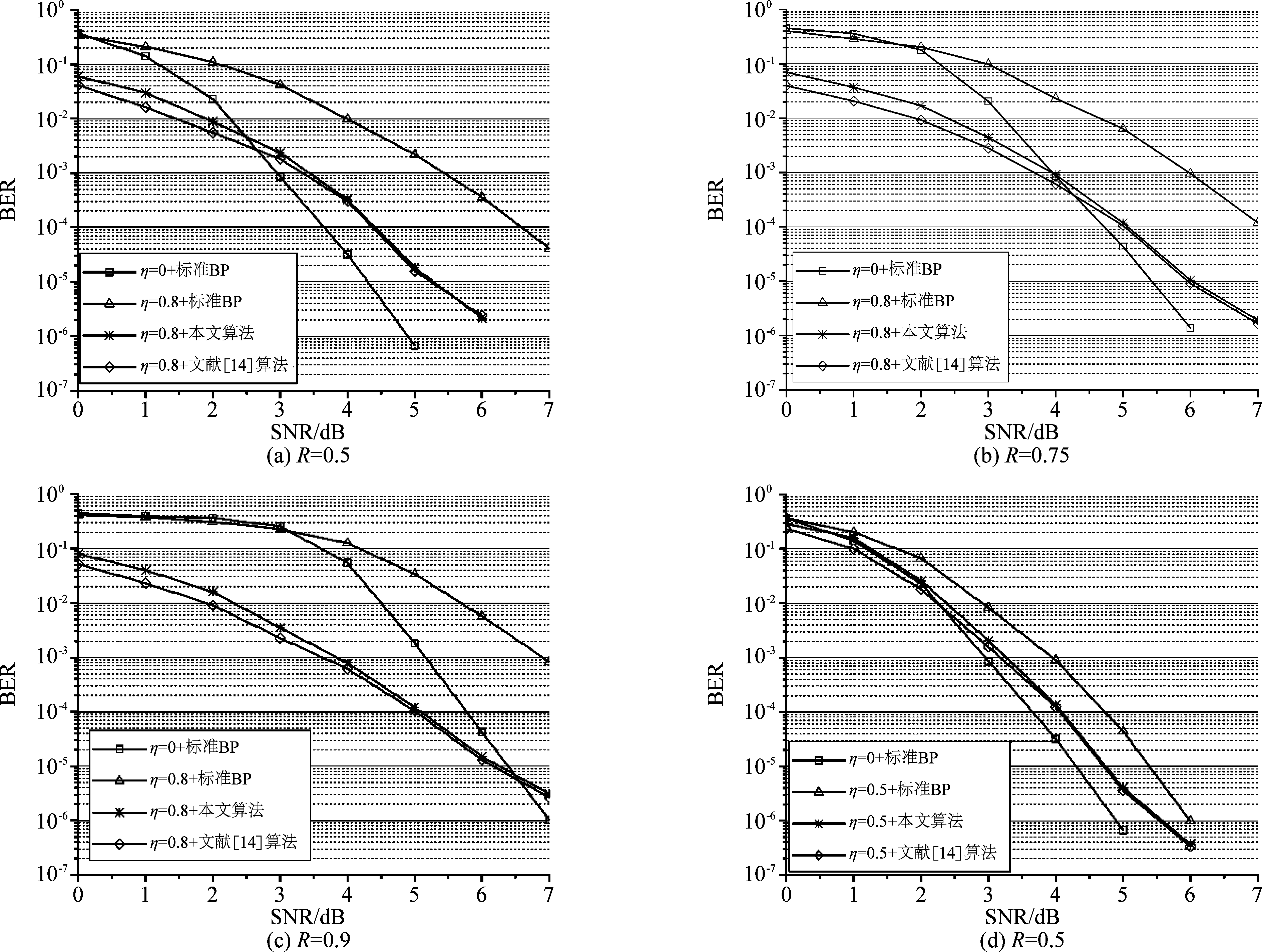
图4 不同码率和噪声相关强度下各种译码算法性能比较
Fig.4 Performance comparison of various decoding algorithms under different bit rates and noise correlation intensities
从图4可以看出,在低SNR时,本文提出的算法在相关噪声下的性能优于高斯白噪声下标准BP译码算法的性能,但是在高SNR时性能略差。这是由于在低SNR时噪声功率大,CNN有效的估计了噪声,计算出更可靠的似然比信息,而在高SNR时噪声的功率过小,CNN识别的特征不够,导致Polar码受相关噪声影响较大,所以和高斯白噪声下的标准BP相比性能略差。另外,随着码率的提高,两者BER曲线的交点逐渐后移,这是因为在有限码长时,信道极化不完全,随着码率的提高,有些信息位受噪声影响增大,而CNN有效的识别了噪声。
噪声相关性的强弱会影响到本文提出的译码算法的性能增益。从图4(d)可以看出,在噪声自相关系数η=0.5中等相关下,本文提出的译码算法和标准BP译码算法相比在BER为10-4时只有0.8 dB的增益。噪声相关性降低一方面导致标准BP算法性能下降较小,另一方面使得CNN识别的特征减少,所以与噪声强相关时相比,增益变小。
本文提出的基于PD-CNN的译码算法复杂度明显低于参考文献[14]中的BP-CNN算法。因为前置预判只是对接收序列进行简单的1和-1的判决,而BP迭代具有非常复杂的非线性操作,如astanh,arctanh,exp和log,此外前置预判直接得到的是s的估计值,而BP译码在得到的信息估计值
后还要进一步映射到s进行下一步的计算,导致了复杂度和译码延迟的增加。
从图4中可以看出,在低信噪比时,本文的译码算法效果略差,这是因为低信噪比时噪声较大导致前置预判的错误率较高,在高信噪比的情况下,两种译码算法的效果几乎一致。表1表示两种译码算法在不同码长下的译码时延以及两者的译码时延差,从图中可以看出,随着码长的增加,两者的译码时延差呈指数增加。本文提出的译码算法和文献[14]中的译码算法相比译码时延最大可降低42%。
表1 译码延迟(秒·103)
Tab.1 The delay of Polar decoding (second·103)
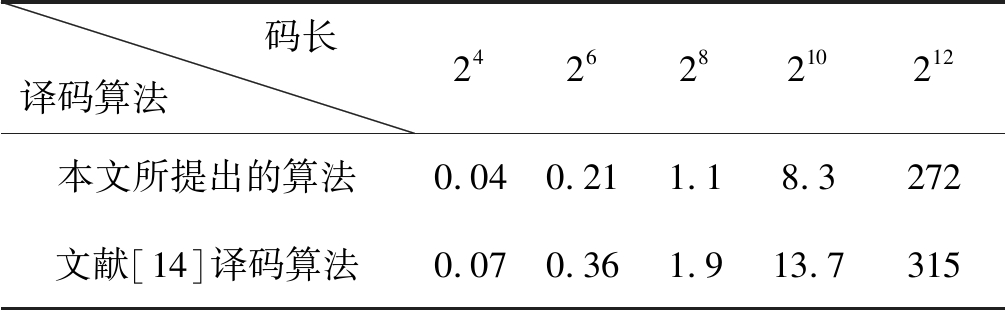
码长译码算法 242628210212本文所提出的算法0.040.211.18.3272文献[14]译码算法0.070.361.913.7315
CNN以较低的复杂度实现性能增益:除了用相同的BP迭代次数提高译码性能,还可以以更低的总体复杂度,使其性能优于标准BP译码。通过设置BP迭代次数,使本文的算法和标准BP算法具有相同的复杂度,然后比较BER性能。虽然运行时间对于复杂性比较并不完全准确,因为它们在很大程度上取决于实现架构,但是这种方法可以作为近似比较,并可作为未来研究的基础[14]。而且,在TensorFlow,keras等其他神经网络库中高度优化和支持CNN的执行,这是基于PD-CNN算法架构的重要优势。随着AI芯片的快速发展,复杂性不会成为CNN在未来通信系统中应用的主要问题。
运行前置预判和结构为{4; 9,3,3,15; 64,32,16,1}的CNN大致相当于3次BP迭代。图5表示不同BP迭代次数对译码性能的影响,BP(5)中的数字代表迭代5次。从图5(a)中可以看出,PD-CNN-BP(5)译码算法的复杂度远远低于标准BP(30),但是在BER为10-4时依然有1.6 dB的增益。当译码器复杂度相同时,PD-CNN-BP(5)和PD-CNN-BP(15)的译码性能都优于标准BP(18)和BP(8)。在图5(a)噪声强相关条件下大概有2.5 dB左右的增益。在图5(b)噪声中等相关下有1 dB左右的增益。
图5 BP迭代次数对译码性能的影响
Fig.5 The figure of the influence of different BP iterations on decoding performance
5 结论
根据相关噪声信道的特点,本文提出了一种基于PD-CNN的Polar码译码算法,利用CNN识别噪声的相关特性,准确估计和白化信道噪声,计算出可靠的LLR,有效降低了相关噪声对Polar码的影响。同时将本文提出的译码方法在不同码率不同噪声相关强度下的译码性能进行比较。仿真结果表明:在相关噪声信道下,本文提出的译码算法的BER曲线随着SNR的增加具有良好的下降趋势。在同等条件下,本文提出的译码算法与传统译码算法相比具有更加优异的性能,在BER为10-5时可获得约2.5 dB的增益。与BP-CNN算法相比具有相同的纠错性能,但复杂度更低,译码延迟最多可降低42%,且易于硬件实现。此外,本文以BP为例给出了基于PD-CNN的译码算法,同时也可推广到Polar码的其他译码算法。
[1] Arikan E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073.
[2] 张孝甜, 赵生妹, 郑宝玉. 无线信道中的Polar码协商[J]. 信号处理, 2018, 34(7): 793-798.
Zhang Xiaotian, Zhao Shengmei, Zheng Baoyu. Key Reconciliation Using Polar Code in Wireless Channel[J]. Journal of Signal Processing, 2018, 34(7): 793-798.(in Chinese)
[3] 范海玲, 赵生妹, 郑宝玉. 莱斯信道中Polar码的构造及性能分析[J]. 信号处理, 2015, 31(9): 1062-1066.
Fan Hailing, Zhao Shengmei, Zheng Baoyu. Construction and Analyses Corresponding Performance of Polar Codesin Rician Channels[J]. Journal of Signal Processing, 2015, 31(9): 1062-1066.(in Chinese)
[4] 邢超, 赵生妹, 郑宝玉. 极化码置信传播算法早期终止准则的研究[J]. 信号处理, 2016, 32(3): 253-259.
Xing Chao, Zhao Shengmei, Zheng Baoyu. The Study on the Early Stopping Criteria for Polar Belief-Propagation Decoders[J]. Journal of Signal Processing, 2016, 32(3): 253-259.(in Chinese)
[5] Dizdar O, Arikan E. A High-Throughput Energy-Efficient Implementation of Successive Cancellation Decoder for Polar Codes Using Combinational Logic[J]. IEEE Transactions on Circuits & Systems I Regular Papers, 2016, 63(3): 436- 447.
[6] Shiu D S, Foschini G J, Gans M J, et al. Fading Correlation and Its Effect on the Capacity of Multielement Antenna Systems[J]. IEEE Transactions on Communications, 2000, 48(3): 502-513.
[7] Chen Pingping, Shi Long, Yi Fang, et al. A Coded DCSK Modulation System over Rayleigh Fading Channels[J]. IEEE Transactions on Communications, 2018, PP(99): 1-1.
[8] Sharma S K, Chatzinotas S, Ottersten B. SNR Estimation for Multi-dimensional Cognitive Receiver under Correlated Channel Noise[J]. IEEE Transactions on Wireless Communications, 2013, 12(12): 6392- 6405.
[9] Hajimiri A, Lee T H. A General Theory of Phase Noise in Electrical Oscillators[J]. IEEE Journal of Solid-state Circuits, 1998, 33(2): 179-194.
[10]Bert L D, Caldera P, Schwingshackl D, et al. On Noise Modeling for Power Line Communications[C]∥IEEE International Symposium on Power Line Communications & Its Applicationss. IEEE, 2011: 283-288.
[11]Tehrani S S, Cockburn B F, Bates S. On the Effects of Colored Noise on the Performance of LDPC codes[C]∥IEEE Workshop on Signal Processing Systems Design & Implementation. IEEE, 2006: 226-231.
[12]Wang J D, Chung H Y. Trellis Coded Communication Systems-Colored Noise and the Swapping Technique[J]. IEEE Transactions on Communications, 1990, 38(9): 1549-1556.
[13]Monk A M, Davis M, Milstein L B, et al. A Noise-whitening Approach to Multiple Access Noise Rejection. I. Theory and background[J]. IEEE Journal on Selected Areas in Communications, 1994, 12(5): 817- 827.
[14]Liang Fei, Shen Cong, Wu Feng. An Iterative BP-CNN Architecture for Channel Decoding[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 144-159.
[15]Lugosch L, Gross W J. Neural Offset Min-Sum Decoding[C]∥International Symposium on Information Theory (ISIT). IEEE, 2017: 1361-1365.
[16]Nachmani E, Marciano E, Lugosch L, et al. Deep Learning Methods for Improved Decoding of Linear Codes[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 119-131.
[17]Xu Weihong, Wu Zhizhen, Ueng Y L, et al. Improved Polar Decoder Based on Deep Learning[C]∥Signal Processing Systems (SiPS). IEEE, 2017: 1- 6.
[18]Gruber T, Cammerer S, Hoydis J, et al. On Deep Learning-Based Channel Decoding[C]∥2017 51st Annual Conference on Information Sciences and Systems (CISS). IEEE, 2017: 1- 6.
[19]Lyu W, Zhang Zhaoyang, Jiao Chunxu, et al. Performance Evaluation of Channel Decoding with Deep Neural Networks[C]∥International Conference on Communications (ICC). IEEE, 2018: 1- 6.
[20]Cammerer S, Gruber T, Hoydis J, et al. Scaling Deep Learning-Based Decoding of Polar Codes Via Partitioning[C]∥Global Communications Conference(GLOBECOM). IEEE, 2017: 1- 6.
[21]Wang Xiaoan, Wicker S B. An Artificial Neural Net Viterbi Decoder[J]. IEEE Transactions on Communications, 1996, 44(2): 165-171.
[22]Doan N, Hashemi S A, Gross W J. Neural Successive Cancellation Decoding of Polar Codes[C]∥International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). IEEE, 2018: 1-5.
[23]Lee J H, Kim D, Jeong S N, et al. Diagnosis and prediction of periodontally compromised teeth using a deep learning-based convolutional neural network algorithm[J]. Journal of Periodontal & Implant Science, 2018, 48(2): 114-123.
