1 引言
如果能够预测移动用户在未来一至几分钟内每秒的平均信道增益或平均数据率,则预测资源分配可以充分利用网络的残余资源和用户的移动性,以主动服务非实时业务的方式在不降低用户服务质量的前提下大大提升蜂窝网络的吞吐量或降低网络能耗[1-7]。根据在第四代移动通信网络中实测的数据和基于线性预测得到的未来数据率所进行的分析表明,相对于只根据当前估计的信道进行资源分配的传统方法,预测资源分配的节能增益可高达180%[1]！
多数研究预测资源分配的现有方法假设需要预测的信息(如数据率、平均信道增益和残余带宽等)在未来一段时间窗(称为预测窗)内每帧(取决于用户位置变化速度,如1 s)的值都已知或其预测误差的统计特性已知[2-5],通过优化分配给请求视频点播(Video on Demand,VoD)或文件下载等非实时业务用户的未来时频资源,在使用户对服务质量满意的前提下提升网络性能。未来平均信道增益可以根据预测的用户轨迹[6]和信道地图[7]得到[2-3,5],未来的残余带宽可以根据预测的网络流量由排队论导出[4]。尽管不少文献对移动轨迹和网络流量预测进行了研究[8],但目前很少有文献研究在分钟级的预测窗内未来秒级分辨率的信息是否可预测及如何预测。文献[1]采用一个简单的线性时间序列模型对未来半分钟时间窗内每秒的数据率进行了预测,结果表明预测误差很大,给预测资源分配带来了不小的性能损失。文献[6]采用长短时记忆(long-short-term memory,LSTM)循环神经网络对城市道路的车辆用户未来每秒的位置进行了预测,结果表明可以预测未来一分钟时间窗内的移动轨迹,90%的预测误差小于6 m。为了降低需要的预测分辨率,文献[9]提出一种只需预测粗略的移动轨迹和网络流量来计算信道和带宽门限、并基于门限值制定传输规划的低复杂度策略,简称为双门限策略;在此基础上,文献[10]进一步设计了深度神经网络(deep neural network,DNN),直接从蜂窝网络里可以测量的、不同分辨率的多源数据学习双门限策略所需要的信息,发现有预测误差时双门限算法的性能依然与无预测误差时的最优预测资源分配方法的性能非常接近。
如果对所需的信息能够预测得足够远,那么预测窗长应该等于VoD视频的播放时长加上用户允许卡顿的总时间[10]。随着预期卡顿时间的增加,预测资源分配的吞吐量也增长[9]。由于求解优化问题的计算复杂度随着预测窗长和用户数急速增长,现有方法通常给定预测窗,如半分钟[1]、一到三分钟[2-5,9-10],很少研究预测窗的长短不同时卡顿时间对预测资源分配性能的影响。对蜂窝网络实测数据的分析表明[8],不同基站的负载有很大的差异,这意味着不同基站的残余带宽可能相差很大;但现有文献很少研究网络负载的空间差异对预测资源分配的影响。另外,除了文献[5]在假设未来秒级平均信道增益已知的前提下、针对文件下载业务研究了通过优化基站静默和用户接入对异构网中的小区间干扰进行协调,所有的文献都考虑同构网络、假设用户就近接入、且把干扰当作噪声。文献[5]的研究表明,在负载很重的异构网络中,不进行干扰协调的预测资源分配在文件下载完成率方面的性能急剧下降。
本文旨在研究预测窗长、残余带宽差异、不同的信息预测算法和用户接入方法对同构、异构网络中预测资源分配性能的影响。鉴于双门限策略的计算复杂度低、且在有/无预测误差时都能接近最优预测资源分配的性能,我们考虑面向同构网提出的双门限策略。由于在由宏、微小区重叠覆盖的异构网络中就近接入性能较差,我们设计一个基于残余带宽门限的用户接入方法,在同构网中退化为就近接入。双门限策略需要预测信道门限、带宽门限、用户未来接入的基站集合及其残余带宽,这些信息即可以通过端到端的方式预测[10]、也可以通过非端到端的方式间接预测,本文还分析了这两种不同预测方法的影响。
本文后续部分安排如下。第2节介绍业务、信道和传输模型,第3节介绍如何得到双门限预测资源分配策略所需的信息和用户接入方法,第4节设计DNN来预测双门限算法所需的几种信息,第5节通过仿真分析业务、系统参数等关键因素对预测资源分配性能的影响,最后总结全文。
2 系统模型
考虑一个有Nb个小区的蜂窝网络,各基站都连接到一个中心处理器、能收集各基站和用户的历史数据、预测所需要的信息并把这些信息提供给各个基站。所考虑的蜂窝网络既可以是同构网、即各基站都是宏基站,也可以是异构网、即由重叠覆盖的宏基站和微基站构成。为了简化符号,下面不区分宏、微基站。
2.1 业务模型
网络需要同时服务低延时容忍度的实时业务(如电话和游戏)和有一定延时容忍度的非实时业务(如VoD和文件下载)。本文仅考虑对请求VoD业务的移动用户进行预测资源分配,但研究结果同样适用于其他非实时业务。由于实时业务有更高的优先级,因此基站在满足实时业务的需求后、利用残余传输资源服务非实时业务。
与VoD业务不同,实时业务请求的数据无法提前传输,其数据包随机到达基站后在基站的缓冲队列中等待传输。为了满足用户服务质量(Quality of Service,QoS)的要求,这些数据包在队列中等待的时间应该依照一定的概率小于给定值。实时业务的QoS需求可以用延时界和超时概率衡量,如果在第k个用户队列中的等待时间超过Dmax的概率小于
则满足第k个实时用户的QoS需求[11-12]。
非实时用户的请求异步到达基站,所请求的视频文件可以被分为多个独立编码的片段。用户一旦接收到一个完整的片段,则该片段可以被解码和播放。若每个片段能在上一个片段播放完之前传输给用户,则不会产生播放中断。假定基站能够预先缓存用户将要观看的视频。
2.2 信道模型
时间被离散化为长度为Δ(如1 s)的帧,每帧包括Ts个单位长度(如1 ms)的时隙;二者的长度取决于用户运动导致的大尺度衰落(包括路径损耗与阴影衰落)和小尺度衰落(如瑞利衰落)信道的时变特性。假设大尺度信道增益(也称为平均信道增益)在同一帧内保持不变、在不同帧间可能不同,小尺度信道增益(也称为瞬时信道增益)在同一时隙内保持不变、在不同时隙内统计独立同分布。假设阴影衰落服从对数正态分布、小尺度衰落服从瑞利分布。
2.3 传输模型
考虑多输入多输出正交频分多址系统,每个基站采用最大比传输的方式在每个子载波上服务所接入的用户。令
和
分别为第j帧第k个用户与其所接入基站之间的平均信道增益和距离,则第k个用户在第j帧第t个时隙的可达数据率为:
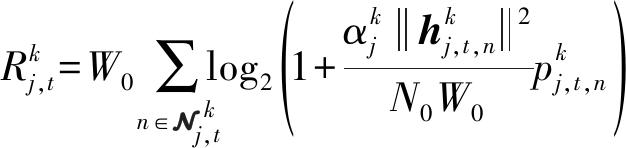
(1)
其中W0为子载波间隔,
为在第j帧第t个时隙分配给用户k的子载波集合,N0为噪声功率谱密度,
为在第j帧第t个时隙分配给用户k的第n个子载波的功率,
为瞬时信道向量,在不同子载波、不同发射天线间瞬时信道统计独立同分布,Ntx为基站的发射天线数。
当Ntx很大时,不难导出接入第m个基站(记作BSm)的第k个用户在第j帧的平均可达数据率为[10]:
(2)
其中,
为噪声功率,
为BSm在第j帧的残余带宽,Pmax为最大发射功率。
3 双门限预测资源分配策略
预测资源分配通过预测用户行为合理制定传输规划,达到提高网络吞吐量的目的。对于非实时用户,其基本原理是在用户数据率高时给其多传数据[1-3],这可以通过寻找两个门限来实现[9]:为了提高吞吐量,基站应该在用户信道好时为其传输数据,因此需要一个信道门限衡量信道条件的好坏;为了减小卡顿时间,空闲基站应当提前给那些即将进入繁忙基站的移动用户传输数据,因此需要一个带宽门限衡量基站剩余资源的多少。利用这两个门限值,各基站能够决定优先服务哪些用户。这种双门限策略只需预测粗略的移动轨迹和网络流量计算信道和带宽门限,并基于门限值制定传输策略。如果仅采用一个信道门限、即用户信道好时多传,则称为单门限算法[9]。
下面首先介绍如何得到两个门限,而后介绍用户接入方法。
3.1 门限与残余带宽预测
把用户发起请求后需要进行预测资源规划的一段未来时间窗称为预测窗。令预测窗的长度为Tf帧。移动用户在预测窗内各帧的大尺度信道既可以通过先预测用户轨迹再通过查询信道地图得到[2-3,5]、也可以进行直接预测。为了提高对预测误差的鲁棒性,文献[9]采用各用户在预测窗内各帧大尺度信道增益的中位数作为信道门限。对于第k个用户,信道门限为:
(3)
文中还导出了在Ntx足够大、非实时用户的瞬时信噪比较高且用户在以基站为中心的圆环上均匀分布时的带宽门限。对于第m个基站,带宽门限为:
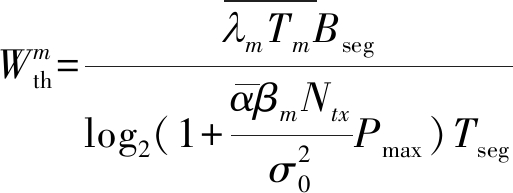
(4)
其中,
是预测窗内BSm的平均VoD请求到达率,
为预测窗内用户接入BSm的平均时间,
为非实时用户与该基站的平均距离,hb为基站高度,Rb为小区半径,βm为第m个小区的路径损耗因子,Bseg为一个视频片段大小、即所包含的字节数。在异构网中,由于宏、微小区覆盖范围不同、且受到接入原则的影响,对于宏基站和微基站和有所不同;进一步由于宏、微基站的发射功率和基站高度等系统参数不同,两类基站的带宽门限有所不同。同时,由于同构网络中所有基站的网络拓扑结构相同,而异构网络中基站的拓扑不同,因此同构网中所有基站的带宽门限相同,而异构网中每个基站的带宽门限都不相同。
残余带宽等于总带宽Wmax减去被实时用户占用的带宽,后者可用有效容量与有效带宽理论计算得到。当数据包到达服从均值为
的泊松过程、包大小服从均值为
的指数分布、且瞬时信噪比较低时,BSm在第j帧的平均残余带宽可由下式计算[10]:
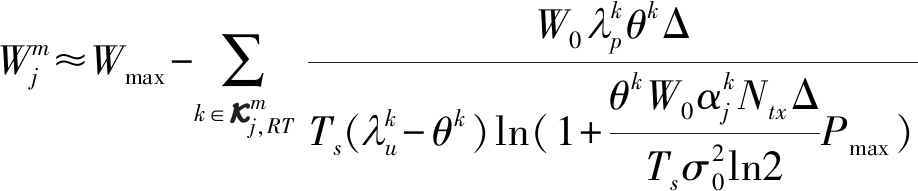
(5)
其中,
为QoS指数[11-12]
为在第j帧接入BSm的实时用户的集合。由此,可以计算第m个基站在预测窗内的平均残余带宽:
(6)
其中,Ji为用户发起请求的时刻。
实时用户所占用的带宽也可以直接利用排队论得到。如果到达各基站的实时用户请求服从泊松分布,则各基站在第j帧的平均残余带宽等于不同值的概率为[4]:
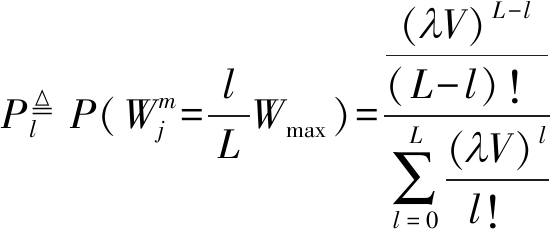
(7)
其中,L为基站能同时服务的最大实时用户数,V为每个实时业务被服务的平均时间,λ为实时业务的请求到达率。利用式(7)不难导出第m个基站在第j帧的平均残余带宽为:
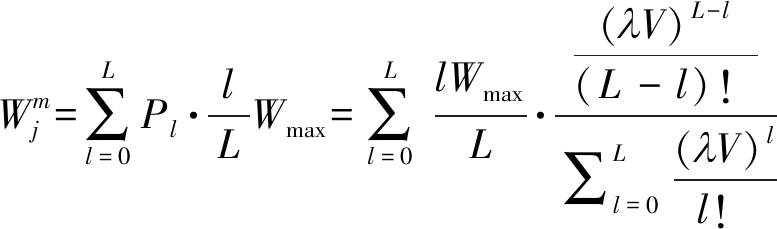
(8)
由此,第m个基站在预测窗内的平均残余带宽可以根据式(6)计算得到。当实时业务请求到达率λ较低时(如0.3个请求/秒),不难得到残余带宽与λ的关系近似呈线性,此时也可以通过如下方式近似计算BSm在预测窗内的平均残余带宽:
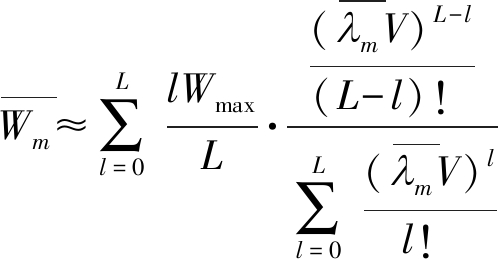
(9)
其中,为预测窗内到达BSm的实时业务平均请求到达率。
3.2 基于带宽门限的用户接入
文献[9-10]采用了传统的用户接入原则——接收功率最大,即在每一帧开始时、用户k被能够提供最大接收信号功率的基站服务。然而,由于宏、微基站发射功率和天线数不同、繁忙程度不同,这种接入方式并不适于异构网。
为了充分利用异构网中的残余资源,我们设计一个基于带宽门限的用户接入方法如下。
在每一帧开始时刻,令用户k可能接入的候选基站(该用户附近的宏基站或微基站)集合为SB,其中,残余带宽大于带宽门限的基站集合为SW。若SW非空,则用户k被该集合中能提供最大接收信号功率的基站服务;否则,若用户k的候选基站集中没有基站的残余带宽大于带宽门限,则该用户被SB中能提供最大接收信号功率的基站服务。在同构网中,这种接入方法退化为接收功率最大的传统方法。
3.3 基于门限的预测资源分配
一个非实时业务发出请求的时刻即为这个用户的预测窗开始时刻,此时中心处理器根据收集的历史数据预测出每个基站的带宽门限值,预测这个用户在预测窗内即将接入哪些基站、以及这些基站在预测窗内的平均残余带宽,然后预测这个用户的信道增益门限,最后把预测值发送给这些基站。
在每一帧和每个时隙开始时,其中的各个基站按照文献[10]的步骤进行资源规划、分配和传输。
4 预测所需信息的神经网络设计
本节以同构网场景为例,设计DNN来预测双门限算法所需的信道门限、带宽门限、未来接入基站集合和残余带宽等信息,分别考虑端到端预测和非端到端预测两种方法。对于异构网,DNN的设计类似。不同之处在于,由于带宽门限用于决定用户在当前时刻的接入方式、而不是用于判决用户未来接入的基站是否平均剩余带宽较低,因此不需要预测用户未来即将接入的基站及其平均剩余带宽。
4.1 端到端预测
文献[10]设计了四个子DNN分别预测各用户在预测窗内将接入的多个基站和信道门限、以及各基站的残余带宽和带宽门限,并对所有子DNN共用同一个学习率和正则化参数、使四个子网络的输出与预期输出之间的均方误差之和最小。这种联合优化方法不能保证每个子网络都达到各自的最优性能。
因此,我们分别训练四个独立的DNN,从而使每个DNN都能达到最优的预测性能。每个DNN都是一个全连接网络,输入为在用户发起请求前一段时间内无线网络记录的历史数据,输出为预测窗内的未来信息。具体地,DNN-1和DNN-2的输入均为离某用户最近三个基站的大尺度信道增益,输出分别为该用户即将接入的基站和信道门限值;DNN-3的输入为实时业务流量,输出为基站的残余带宽;DNN- 4输入为VoD请求到达率与用户在某小区的平均接入时间,输出为该小区的带宽门限值。各个DNN的训练目标是最小化一个由其输出与期望输出之间的均方误差和正则化项组成的代价函数,即:
(10)
其中
是DNN在l-1层与l层之间的权重矩阵,b[l]是DNN在l层的偏置,y(n)是DNN的期望输出,
是输入x(n)时的DNN输出,N为样本个数,ν为正则化参数。训练集和测试集样本的产生方式及DNN训练过程的反向传播与学习率自适应更新算法与文献[10]一致。
4.2 非端到端预测
若已知预测窗内实时业务的平均请求到达率,则可以由公式(9)计算出预测窗内基站的平均残余带宽。可以采用与4.1节中类似的全连接DNN,输入为在一定的观测时间内(如45分钟)以一定周期(如15分钟)记录的实时业务请求到达率,输出为预测窗内实时业务的平均请求到达率,带入(9)即可得到残余带宽的预测值。利用类似的DNN也可以预测VoD业务的平均请求到达率,而后根据(4)得到带宽门限的预测。
为了预测信道门限,可先利用LSTM预测非实时用户在预测窗内每帧的轨迹[6],再与信道地图相结合得到预测窗内各帧的大尺度信道增益,取其中值即可得到信道门限。根据通过上述方法间接预测的大尺度信道,既可以确定用户在预测窗内将接入的基站集合。
5 仿真和数值结果
下面分别在同构和异构网络中评估已知需预测的信息以及采用不同方法预测这些信息时预测资源分配算法的性能。
考虑一个由几个半径为250 m的宏小区构成的同构网或一个由宏、微基站构成的异构网。每个宏、微基站的最大发射功率分别为40 W和1 W,最大残余带宽均为10 MHz,小区边缘信噪比均为5 dB(把小区间干扰视为噪声)。路径损耗模型为α0+βlog10(d),其中d为基站和用户之间的距离,β为路径损耗因子,α0=36.8[13]。为反映各个小区间信道环境的差异,各小区的β在36.6～36.8间随机选取。阴影衰落服从相关距离在40 m～60 m间均匀选取的对数正态分布,其中宏基站的标准差在6 dB～8 dB间均匀分布、微基站的标准差为10 dB。
用户以平均速度20 m/s、随机加速度1 m/s2沿着直线道路移动。为了避免边缘效应,用户到达道路的终点后将会从道路的另一侧重新进入。
每一帧的长度为1 s,每一帧包含100个时隙,即每个时隙长度为10 ms。预测窗长为Tf,与视频的播放时长相同,所有非实时用户的请求在1～Tf秒内到达,且请求的到达服从泊松分布。每个视频包含多个播放时长为10 s、大小为Bseg兆字节(Mbytes,MB)的片段。
仿真结果由100次蒙特卡洛得到。在每次仿真中,用户发起请求时间、地理位置、移动速度和移动方向都随机,小尺度信道根据瑞利衰落随机生成。但对于多次仿真,路径损耗和阴影衰落只生成一次、存为文件,每次仿真根据用户的位置查表得到,从而模拟信道地图。
下面分别在平均残余带宽不同的网络中,评估给定用户满意率为95%(即网络中95%的用户播放视频的总卡顿时间不大于期望的卡顿时间)时的蜂窝网络吞吐量或可支持的最大非实时业务请求到达率,以及预测资源分配相对于一种也考虑了QoS需求的非预测资源分配方法[14]的吞吐量增益。定义蜂窝网络吞吐量为网络中所有基站在单位时间可以传输的数据量总和,即为可支持的最大VoD请求到达率乘以VoD文件的大小。吞吐量增益指的是预测资源分配达到的吞吐量与非预测资源分配的吞吐量之比。考虑到用户对播放时长不同的视频能容忍的总卡顿时间不同,为了与文献中经常考虑的一分钟长度视频[3]相比较,用户预期的卡顿时间设为每播放一分钟允许的总卡顿时间。
5.1 同构网络
在同构网络的仿真场景中,每个宏基站有8个天线。用户沿三条到基站最近距离分别为50 m、100 m、150 m的直线道路行驶,途经位于道路一侧的六个宏基站。每条道路在离第一个基站最近的位置设有红绿灯,用户会在红绿灯处随机停车5～20 s。Bseg=2 MB。
5.1.1 无预测误差时双门限算法的性能
本节在信息理想已知、即没有预测误差时,分析预测窗长、用户预期的卡顿时间与网络残余带宽的均值和方差对双门限算法的影响。当改变预测窗长时,所请求视频的播放时长和片段数量也相应改变。例如,当预测窗长为60 s时,视频文件大小为12 MB,每个视频由6个片段组成,总播放时间为60 s。考虑到预测窗过长时计算复杂度过高、且预测窗最短不能短于一个传输片段,因此在仿真中分别设定预测窗长度为20 s,30 s,60 s,120 s,180 s,240 s,300 s。
图1 吞吐量随预测窗长的变化
Fig.1 Throughput versus prediction window
当网络的平均残余带宽为80%(此时六个基站的平均残余带宽分别为9、8、7、9、8、7 MHz)、用户期望的卡顿时间分别为每分钟卡顿2、5和10 s时,采用双门限和非预测资源分配策略[14]时网络吞吐量随预测窗长度的变化如图1所示。结果表明,采用双门限算法时,随着预测窗长的增加,网络吞吐量持续上升,但吞吐量的提升速度逐渐降低。无论采用哪种资源分配方法,用户每分钟允许的卡顿时间越长,能够支持的吞吐量越大;当采用非预测方法时,增加期望的卡顿时间对于吞吐量的提升更明显;由于图中的卡顿时间指的是播放一分钟允许的卡顿时间,当预测窗更长时,达到同样的吞吐量需要用户在整个视频播放过程中允许的总卡顿时间更长。双门限方法相对于非预测资源分配的吞吐量增益在预测窗长不同时随着期望卡顿时间的变化如图2所示。可以看出,当期望的卡顿时间相同时,双门限算法的吞吐量增益随预测窗长而提升;当预测窗长相同时,吞吐量增益随着预期卡顿时间的增加而下降;在Tf=60 s时,双门限算法的吞吐量增益大于150%,Tf=300 s时、预期卡顿时间为2 s时的吞吐量增益可达到250%。
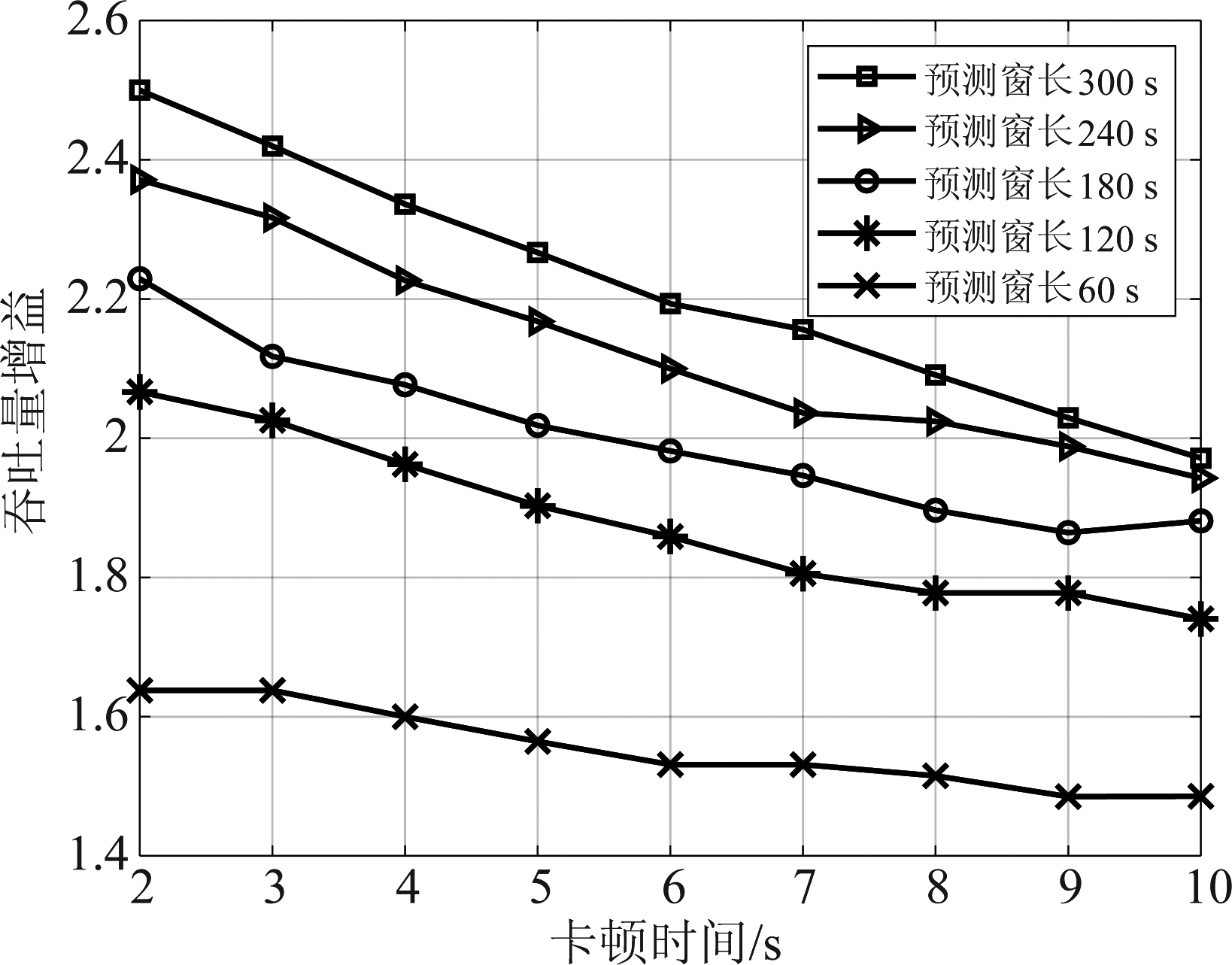
图2 吞吐量增益随卡顿时间的变化
Fig.2 Throughput gain versus stalling time
当网络的平均残余带宽不同时双门限算法的吞吐量增益随预测窗长的变化如图3所示。在用户预期的卡顿时间和预测窗长相同时,残余带宽为50%(六个基站的平均残余带宽分别为7、5、3、7、5、3 MHz)时的吞吐量增益略高于残余带宽为80%的情况,也就是说在残余带宽相对较少时,双门限算法取得吞吐量增益更高。这个结果似乎与直觉相反。然而,当网络残余带宽更大时,双门限算法和非预测方法能支持的吞吐量都更大、且双门限算法的吞吐量提升大于非预测方法的提升,但由于吞吐量增益是二者吞吐量的比值,所以增益反而有所降低。
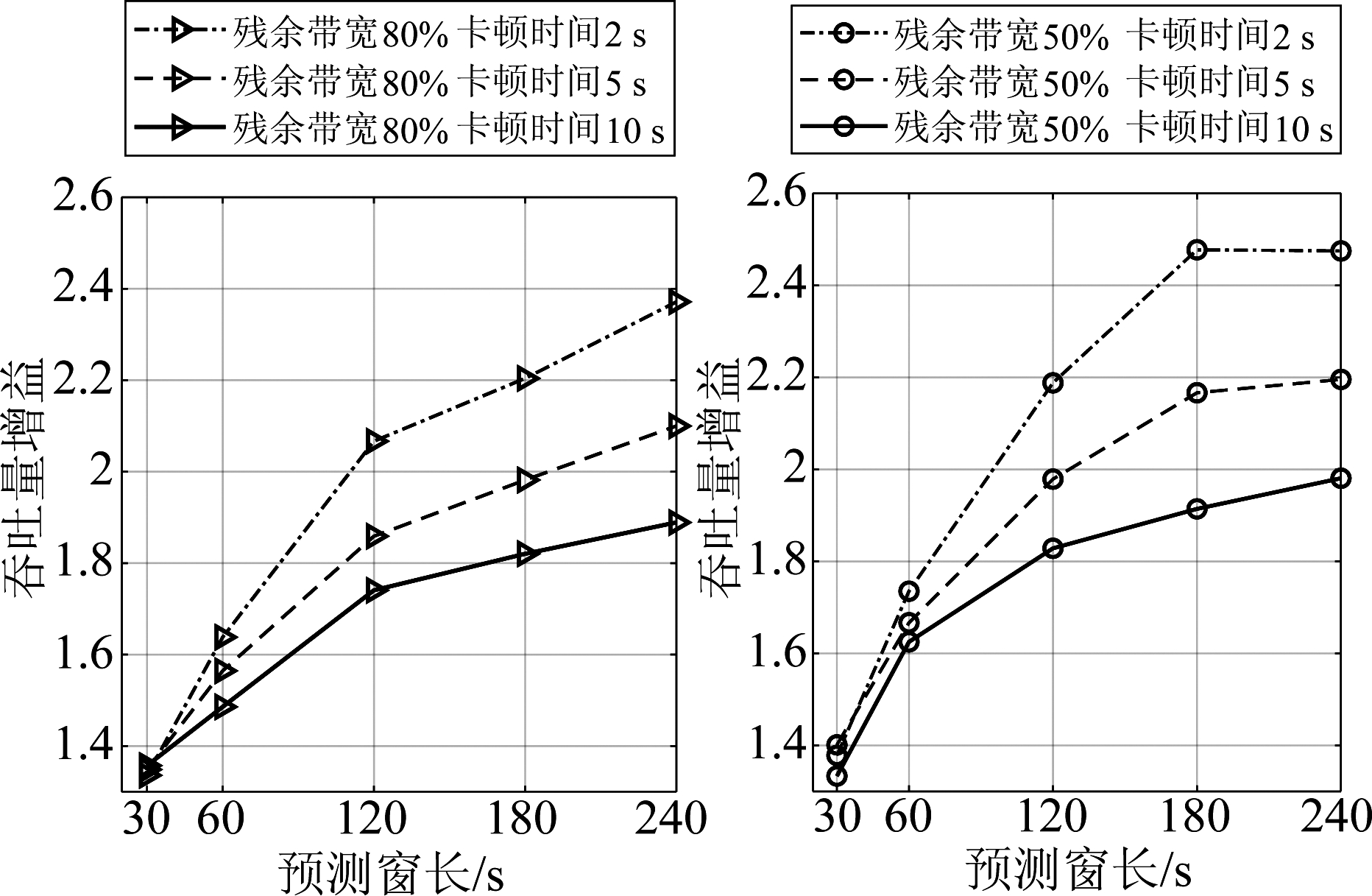
图3 平均残余带宽不同时吞吐量增益随预测窗长度的变化
Fig.3 Throughput gain versus prediction window when the average residual bandwidth is different
在双门限算法中,通过带宽门限选择出即将进入繁忙小区的用户,优先对其进行服务。基站的繁忙程度可通过残余带宽衡量,不同基站繁忙程度的差异可通过残余带宽方差来衡量。下面分析残余带宽的标准差对双门限算法性能的影响。在仿真中,设六个基站在预测窗内的平均残余带宽为均值是5 MHz、标准差为1～2 MHz间不同数值的高斯随机变量(因基站带宽最大为10 MHz,故平均残余带宽为50%)。为了分析采用带宽门限的必要性,图4中还给出了在卡顿时间为10 s时、双门限和单门限策略相对于非预测资源分配能支持的吞吐量增益。从仿真结果可见,预测资源分配的吞吐量增益随着残余带宽标准差的增加而提高。当残余带宽的标准差较小、即不同基站的繁忙程度相差不大时,双门限与单门限策略性能几乎相同;只有当残余带宽标准差较大时,优先服务即将进入繁忙基站的用户才有意义,从而使双门限策略性能更好。
图4 预测窗长不同时吞吐量增益随残余带宽标准差的变化
Fig.4 Throughput gain versus residual bandwidth standard deviation when prediction window is different
5.1.2 预测误差对双门限算法性能的影响
本节分析在把可预测信息转化为双门限算法需要预测信息的过程中相应预测误差的变化及最终预测误差对双门限方法的影响。仿真中预测窗长为60 s。
采用各个DNN单独训练的方法可以利用更少的训练样本达到与文献[10]中的联合训练方法相同的性能1，在DNN训练过程中,训练集中有500个样本,测试集中有300个样本。训练各个DNN的超参数如表1所示。其中,DNN-1,2,3,4为端到端预测方法,训练和测试样本的生成方法与文献[10]相同(即根据式(5)为DNN-3生成标签数据);DNN-RT为4.2节中用于预测实时业务平均请求到达率的神经网络,其训练和测试样本也根据某校园网网关实测数据合成的数据得到,具体合成方法如下:为了保证基站能够有一定的剩余资源服务非实时用户,令基站最小残余带宽为Wmin,则根据式(8)可以计算出此时实时业务的请求到达率λmax_sim;令实测数据集中的最大请求到达率为λmax_real;合成的数据集为实测数据集中的每个数据记录除以λmax_real/λmax_sim,从而保证在请求到达率最高时基站的残余带宽为Wmin。
在DNN训练过程中,使用小批量的方法处理训练集数据[16],批大小为128,训练迭代次数为200次。在采用端到端预测时,通过式(5)生成各个小区残余带宽的标签数据,各参数的取值与文献[10]一致,即数据包的平均到达率为1000个包/秒,包的平均大小为
为
为1%。在采用非端到端预测时,通过式(7)生成各小区残余带宽的标签数据,仿真中设置基站能服务的最大实时业务数L为100,每个实时业务被服务的平均时间V为300 s。通过调整式(5)中每个小区实时用户的个数以及式(7)中每个小区实时业务的请求到达率λ,可以使通过二种方法计算出的残余带宽保持一致,而且对于60 s以上的预测窗,两种预测方法的预测误差对预测资源分配的影响也一致(由于篇幅限制,这里不提供仿真结果)。
端到端预测方法的训练和测试低复杂度,但在视频的播放时间较短时性能极差。例如,当用户请求的视频播放时长为40 s时,双门限算法的预测窗长度为40 s。由于用户在红绿灯处会随机停车5～20 s、且仿真中红绿灯位于离基站最近的位置,停车时将处于信道条件极好的环境,而均值为12.5 s的停车时间占预测窗总长度的30%以上,从而导致用户的信道门限值大幅度提高。图5给出了预测窗长40 s时信道门限值的累计分布函数(cumulative distribution function,CDF)。可以看出90%左右的样本分布在0～6*10-12以内,由于停车导致的数值很大的信道门限值虽只占总样本数的10%、但最大值高达10-9,即训练数据不平衡。在DNN-2的训练集中,信道门限值为训练样本的标签,这些极端的门限值导致DNN只能学习到10%的极端值,无法学习到在非停车时的信道门限值,从而造成信道门限预测误差很大。这一问题的根本原因是:用户在预测窗内的停车时间随机且与历史轨迹不相关,因此DNN-2无法学习到历史信息和预测值之间的关系。这一问题可以通过给样本输入中加入反映用户未来停车时间的额外特征来解决。
1在文献[10]中，联合训练DNN需要1000个训练样本，是本文中各DNN单独训练方法所需要样本数的2倍。
表1 预测窗长Tf=60 s时,DNN的超参数
Tab.1 Hyperparameters of DNN when prediction window Tf =60 s
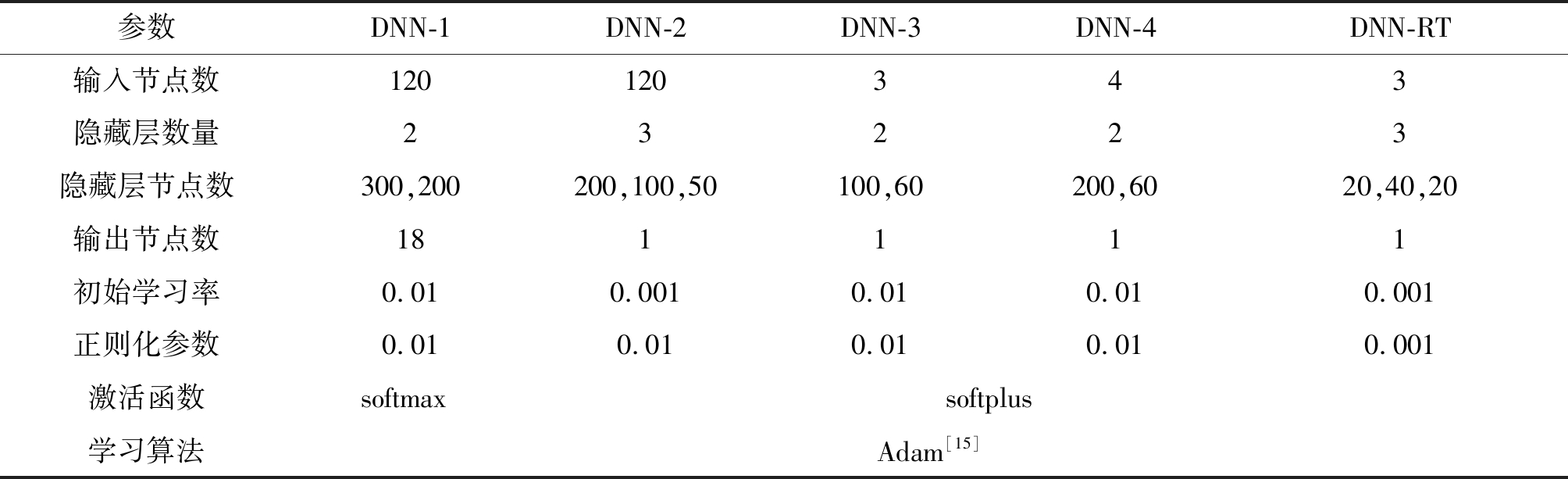
参数DNN-1DNN-2DNN-3DNN-4DNN-RT输入节点数120120343隐藏层数量23223隐藏层节点数300,200200,100,50100,60200,6020,40,20输出节点数181111初始学习率0.010.0010.010.010.001正则化参数0.010.010.010.010.001激活函数softmax softplus 学习算法Adam[15]
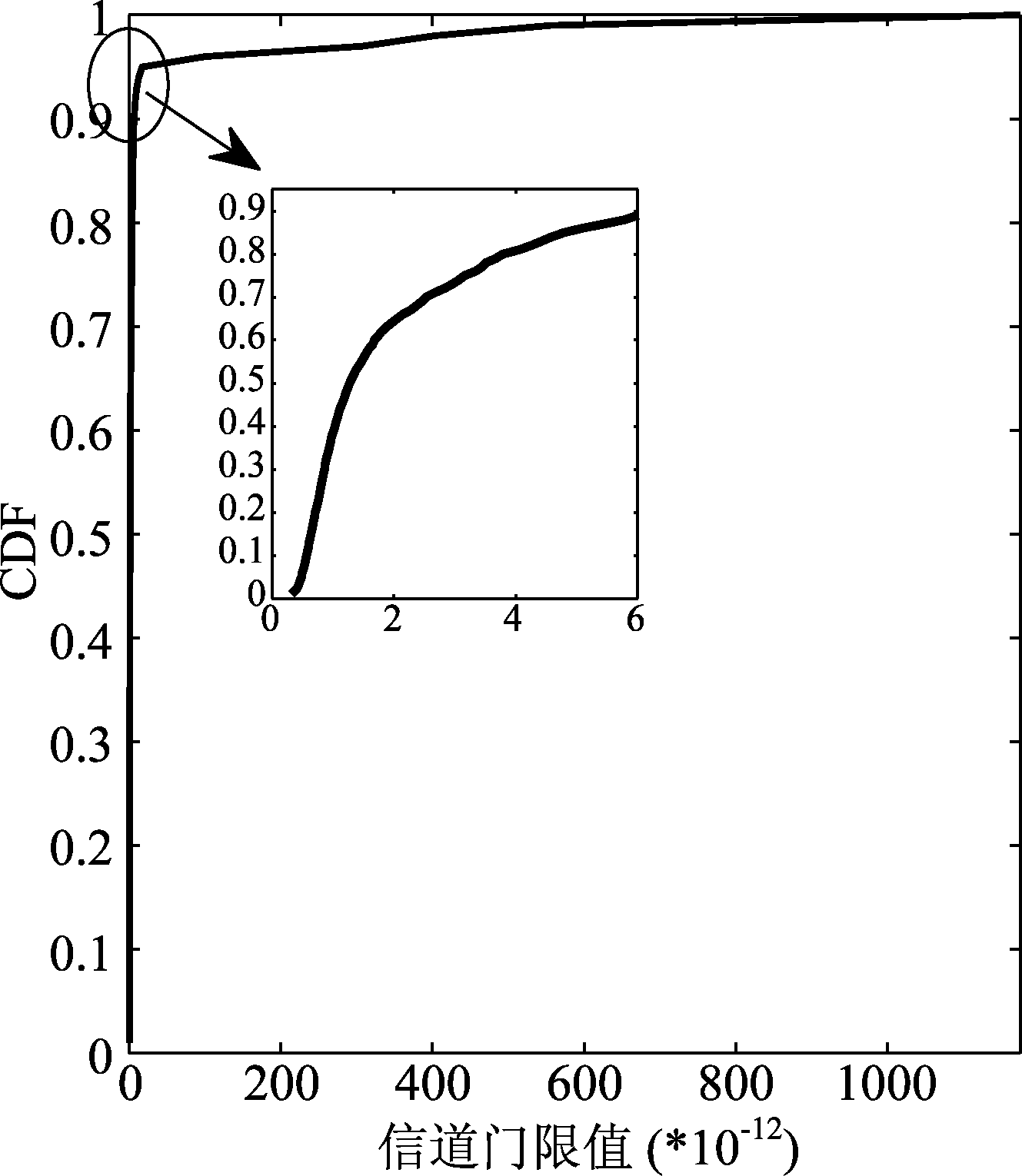
图5 端到端方法,DNN-2训练集信道门限的CDF
Fig.5 CDF of the threshold for average channel gain in training set
当用户请求视频的播放时长较长、即停车时间相对于预测窗长较短时,DNN-2预测得到的信道门限均值将与真实的信道门限值较为接近。
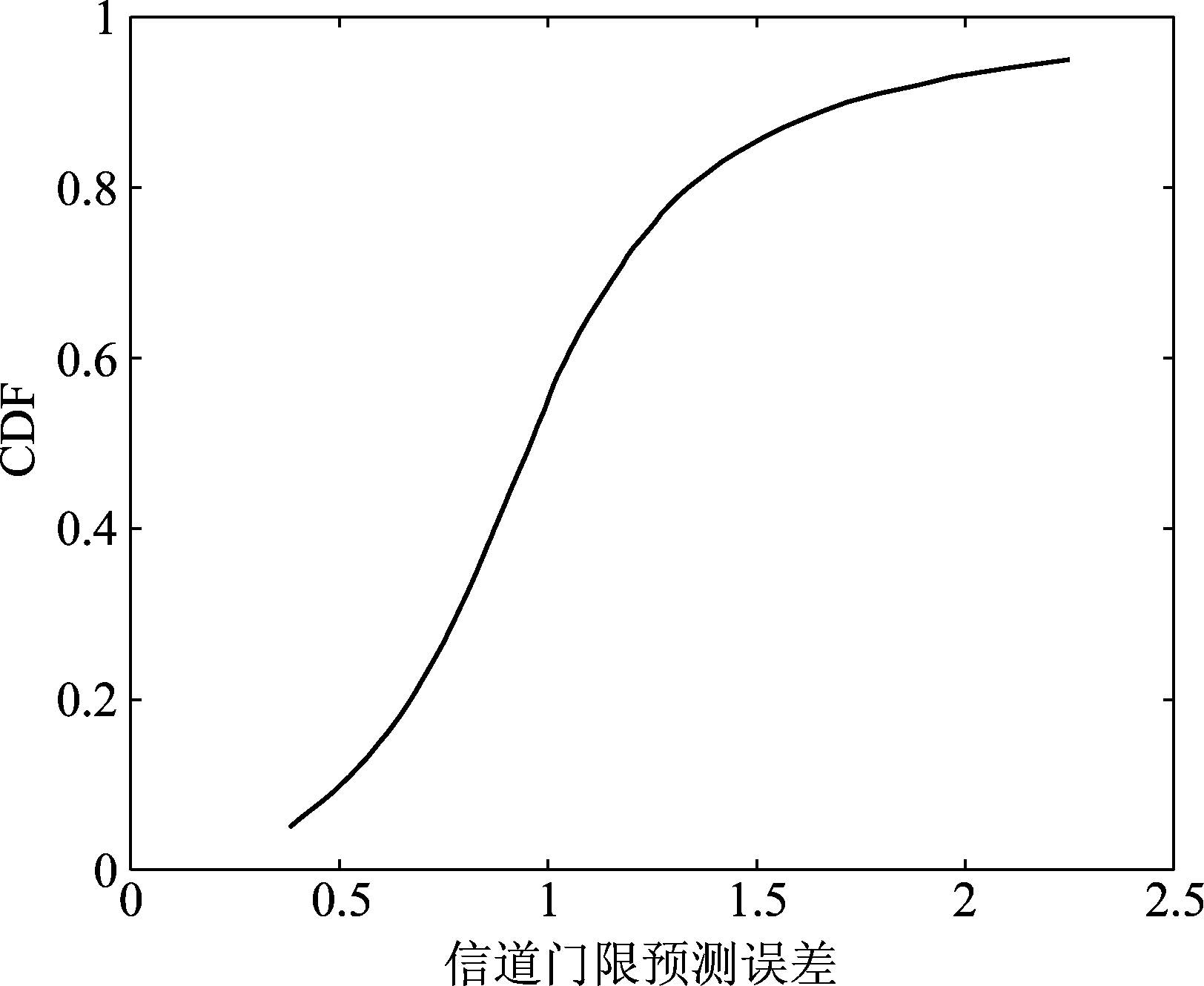
图6 非端到端方法,信道门限预测误差的CDF
Fig.6 CDF of the threshold error for average channel gain
在非端到端预测中,对于信道门限值的预测是通过把轨迹预测与信道地图相结合的方式完成的,而LSTM的输入输出数据都为用户轨迹,所以即使无法预测车辆在何处停车和停车时间多长、只能预测停车时间的均值,也不会出现端到端预测中训练数据存在极端标签数据污染训练样本的现象。图6给出了预测窗长40 s时,采用非端到端预测方法得到的信道门限预测误差的CDF,此时由于随机停车导致的轨迹预测误差高达百米、由于阴影衰落导致的大尺度信道预测误差有10%高于15 dB(由于篇幅限制,此处不给出相应的预测误差统计特性),但是对其取中值后对门限预测的影响大大减小。
为了评估预测误差对双门限算法的影响,图7给出了有、无预测误差时双门限算法能支持的非实时业务的最大请求到达率,其中采用非端到端的方式预测所需要的信息(对于下面预测窗长为60 s的场景,采用端到端方式预测所需信息时的仿真结果与图7几乎相同)。从仿真结果中可见,无论是轨迹预测误差还是残余带宽预测误差,均未对双门限算法的性能造成明显的影响。值得一提的是,有误差的算法性能在部分情况下略高于无误差算法的性能,这是因为双门限算法中门限值的设定并非最优值。
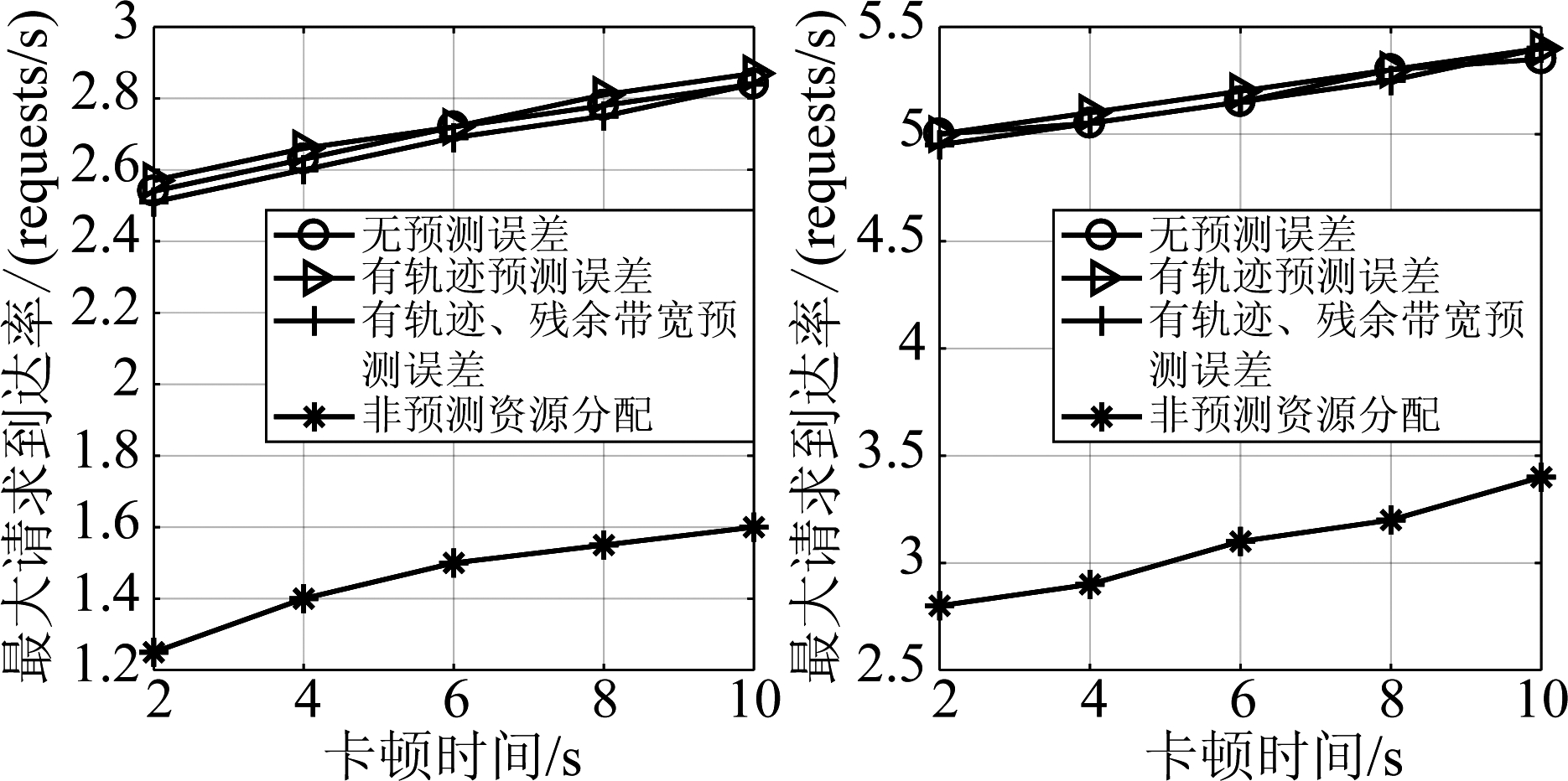
图7 残余带宽为50%(左)和80%(右)时双门限算法的性能
Fig.7 The performance of threshold-based scheme
5.2 异构网络
在异构网络的仿真场景中,每个宏基站有4个天线,每个微基站有2个天线。用户沿一条到宏基站最近距离120 m的直线道路行驶,途经位于道路一侧的四个宏基站和30个随机分布在道路两侧的微基站。微基站之间的最小距离为80 m,微基站与道路的距离在40 m～60 m之间均匀分布。每个用户请求大小为60或120 MB、播放时长为60 s的视频;每个视频包括6个片段、即Bseg =10 MB或20 MB,每个片段播放时长为10 s。与同构网的仿真场景相比,为了分析不同用户接入方法的影响,我们部署了较多的微基站;由于部署的总基站数更多、服务能力更强,故此处减小了宏基站的个数和基站天线数、并考虑清晰度更高的视频。当Bseg的值更大时,网络负载更重。仿真中基站的平均残余带宽服从平均值为5 MHz、标准差为2 MHz的高斯分布、即网络的平均残余带宽为50%。
下面评估当采用基于带宽门限的用户接入(图例为“基于带宽门限的接入”)时双门限策略能够支持的最大请求到达率,并与当采用接收功率最大用户接入原则时双门限策略(图例为“接收功率最大的接入”)以及用户接入方案为接收功率最大原则时的非预测资源分配算法[14](图例为“非预测方法”)进行比较。用户请求的视频大小为不同值时的结果分别如图8和图9所示。
图8 用户请求的视频大小为60 MB
Fig.8 Video with size of B=60 MB
图9 用户请求的视频大小为120 MB
Fig.9 Video with size of B=120 MB
仿真结果表明,当采用不同的用户接入方法时,预测资源分配与非预测资源分配算法相比都有很大的性能增益,但基于带宽门限的接入方法增益更大。当预期的卡顿时间为10 s时,若视频大小为60 MB,则基于带宽门限的接入与接收功率最大的接入相比有125%的增益、与非预测资源分配相比有154%的增益,若视频大小为120 MB,则基于带宽门限接入与基于接收功率最大接入的预测资源分配与非预测资源分配相比分别有145%和173%的性能增益。可见当网络负载较重时(即用户请求清晰度更高的视频),基于带宽门限的接入方法性能提升更大。
6 结论
本文分析了预测窗长、卡顿时间、残余带宽、信息预测方法、用户接入和小区间干扰对预测资源分配性能的影响。利用对城市道路上车辆用户移动轨迹的合成数据、以及根据局部区域的实测网络流量合成的数据,采用典型的信息预测算法,在同构和异构网络中对一种基于门限的预测资源分配策略相对于非预测资源分配在保证用户满意率前提下可支持的吞吐量增益进行了评估。研究结果表明:(1)即使对于20 s之短的预测窗,预测资源分配也有130%以上的增益,增益随着预测窗而增长、但增速渐趋缓慢;(2)网络残余带宽均值越大、预测资源分配可支持的吞吐量也越大、但吞吐量增益减小,残余带宽方差越大,可支持的吞吐量增益越大;(3)当预测窗较长时,端到端和非端到端信息预测的误差对预测资源分配的性能影响不大;(4)用户接入对于异构网络中的预测资源分配性能有很大的影响,当采用基于残余带宽的接入时,网络负载越高、这种接入方法的性能增益越大。
[1] Bui N, Widmer J. Data-driven evaluation of anticipatory networking in LTE networks[J]. IEEE Trans. Mobile Comput., 2018, 17(10): 2252-2265.
[2] Yao C, Yang C, Xiong Z. Energy-saving predictive resource planning and allocation[J]. IEEE Trans. on Commun., 2016, 64(12): 5078-5095.
[3] Atawia R, Hassanein H S, Ali N A, et al. Utilization of stochastic modelling for green predictive video delivery under network uncertainties[J]. IEEE Trans. on Green Commun. and Netw., 2018: 1-1.
[4] Yao C, Yang C, Chih-Lin I. Data-driven resource allocation with traffic load prediction[J]. Journal of Communications and Information Networks, 2017, 2(1): 52- 65.
[5] Guo K, Liu T, Yang C, et al. Interference coordination and resource allocation planning with predicted average channel gains for HetNets[J]. IEEE Access, 2018, 6: 60137- 60151.
[6] Zhang W, Liu Y, Liu T, et al. Trajectory prediction with recurrent neural networks for predictive resource allocation[C]∥IEEE ICSP 2018, 2018: 1- 6.
[7] Chen J, Yatnalli U, Gesbert D. Learning radio maps for UAV-aided wireless networks: A segmented regression approach[C]∥IEEE ICC 2017, 2017: 1- 6.
[8] Wang J, Tang J, Xu Z, et al. Spatiotemporal modeling and prediction in cellular networks: A big data enabled deep learning approach[C]∥IEEE INFOCOM 2017, 2017: 1-9.
[9] Guo J, She C, Yang C. Predictive Resource Allocation with Coarse-Grained Mobility Pattern and Traffic Load Information[C]∥IEEE ICC 2018, 2018: 1- 6.
[10]Guo J, Yang C, Chih-Lin I. Exploiting Future Radio Resources with End-to-end Prediction by Deep Learning[J]. IEEE Access, 2018, 6(1): 75729-75747.
[11]Helmy, Amir, Le-Ngoc T, et al. Energy-Efficient Power Adaptation over a Frequency-Selective Fading;Channel with Delay and Power Constraints[J]. IEEE Trans. Wireless Commun., 2013, 12(9): 4529- 4541.
[12]She C, Yang C, Liu L. Energy-Efficient Resource Allocation for MIMO-OFDM Systems Serving Random Sources With Statistical QoS Requirement[J]. IEEE Trans. Commun., 2015, 63(11): 4125- 4141.
[13]3GPP TSG RAN. Further advancements for E-UTRA physical layer aspects[S]. Tech.Rep.36.814 v9.0.0, 2010.
[14]Su D, Yang C. User-Centric Downlink Cooperative Transmission With Orthogonal Beamforming Based Limited Feedback[J]. IEEE Trans. Commun., 2015, 63(8): 2996-3007.
[15]Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv: 1412.6980, 2014.
[16]Goodfellow I, Bengio Y, Courville A, et al. Deep Learning[M]. Cambridge: MIT Press, 2016.
