1 引言
双向中继网络(TWRN)能够借助中继节点实现信息交换,克服单向中继造成的半双工复用损失,在提高网络频谱利用率,扩大网络覆盖范围等方面具有极高的研究潜力[1- 4],而多输入多输出(MIMO)技术可以充分利用空间域实现多路数据传输,使得网络容量得到非常可观的提升[5]。因此,通过在终端和中继配置多天线的方式使得MIMO技术与TWRN的融合已然成为研究热点,这种技术融合被认为是构建高速率覆盖的网络框架中最具价值的改进[6-7]。
双向中继通过两个时隙实现终端之间的信息交互,在第一时隙,两终端同时向中继发送信号,根据放大转发(AF)的中继策略,中继将接收的叠加信号向两终端进行广播。目前,现有的研究主要集中在系统优化,包括最佳天线选择,预编码优化设计[8-10]等热点问题上,文献[8]提出了一种低复杂度天线选择的优化算法,通过最大化系统可达速率实现中继天线的选择,文献[9]进一步研究了AF-MIMO双向多中继系统中预编码与天线选择的联合优化问题,通过特征值分解方法最小化均方误差(MSE)获得最佳的检测性能,文献[10]从中继预编码不同优化角度出发,推导了最小MSE、最大信道容量、最大最小限制条件数四种目标函数下的性能优化。
然而,当前针对双向MIMO中继网络的研究多数基于理想的信道状态信息(CSI)和完全消除自干扰的条件。实际应用环境中,受非理想信道估计的影响,这种理想假设下的自干扰抵消及其优化处理技术的性能会大打折扣。目前自干扰处理技术多数是围绕基于信道估计的干扰抵消方案(EIC)[11-14]进行研究的。与MIMO技术相结合后中继网络会使各链路信道信息获取难度和开销大大提高,受天线间干扰、信道空间相关性、信道时变、反馈时延及非高斯复合噪声等因素影响,通信终端无法获取精确的链路信道参数,非理想信道估计带来的信道估计误差会引入剩余自干扰,严重恶化网络性能。国内外众多学者对双向网络中非理想信道估计引入的剩余自干扰进行了大量的有意义的研究[11-13]。在文献[11]中,作者推导了单天线条件下平坦衰落信道估计方案的平均误比特率(BER)闭合表达式以及中断概率的渐进表达式,在此基础上设计了自适应功率分配算法,能够显著提高中继网络性能,不可避免地在非理想信道估计情况下,中断概率和BER性能在高SNR时会出现平台;文献[12]中,作者采用叠加训练的方案较好地解决了MIMO网络中的信道估计问题,并进一步解决了信道估计误差对TWRN中和速率性能的影响的问题;在文献[13]中作者对正交空时编码框架下的MIMO-TWRN进行了存在信道估计误差的网络性能分析,推导了平均BER的理论值。多天线条件下,剩余自干扰会造成和速率和BER的性能损失。综上所述,消除非理想信道估计引入的剩余自干扰可以有效改善TWRN的系统性能和传输容量。
本文针对AF模式下双向MIMO中继网络中的自干扰抵消问题,从消除非理想信道估计带来的剩余自干扰着手,提出一种低复杂度采用信道独立预编码的盲干扰抵消(BIC)方案。新方案在源节点对信息进行预编码操作,实现行空间映射,构建与MIMO信道独立的目标信号子空间以及自干扰子空间,在接收端设计对应的解码矩阵,实现未知信道状态下自干扰抵消和目标信号分离,避免受到信道估计误差的影响,具有较好的鲁棒性。同时,以最大有效信噪比为准则设计最佳预编码,推导了可达和速率的闭合表达式。仿真实验比较不同方案下信道估计误差分别对BER及可达和速率的影响,验证了方案的有效性。
本文所用的标记说明:大写(小写)黑体字母代表矩阵(列向量),上标H,*,†和T分别代表共轭转置,共轭,伪逆及转置。![]() 表示a×b维复数空间;N×N维的单位矩阵和全零矩阵可以分别表示为IN和0N;tr{·}为求矩阵的迹操作而
表示a×b维复数空间;N×N维的单位矩阵和全零矩阵可以分别表示为IN和0N;tr{·}为求矩阵的迹操作而![]() 为求统计期望操作;
为求统计期望操作;![]() 表示克罗内克积。
表示克罗内克积。
2 系统模型
考虑一个基于AF协议的单中继MIMO-TWRN,如图1所示,包括源节点![]() 和
和![]() 以及中继节点
以及中继节点![]() 其中
其中![]() 和
和![]() 均配备NS根天线,
均配备NS根天线,![]() 配备NR根天线,且满足NR≥NS使得中继网络支持NS个独立数据流。假设所有的天线工作模式为半双工模式,且两节点
配备NR根天线,且满足NR≥NS使得中继网络支持NS个独立数据流。假设所有的天线工作模式为半双工模式,且两节点![]() 和
和![]() 之间的直传链路由于较大的链路损耗不能用于传输数据,仅通过
之间的直传链路由于较大的链路损耗不能用于传输数据,仅通过![]() 进行数据交互。两节点间的双向通信分为两个时隙,在第一时隙内,
进行数据交互。两节点间的双向通信分为两个时隙,在第一时隙内,![]() 和
和![]() 通过NS根天线向中继节点广播数据;在第二时隙内,
通过NS根天线向中继节点广播数据;在第二时隙内,![]() 通过NR根天线对接收到的来自
通过NR根天线对接收到的来自![]() 和
和![]() 的叠加信号进行放大并且分别转发至
的叠加信号进行放大并且分别转发至![]() 和
和![]()
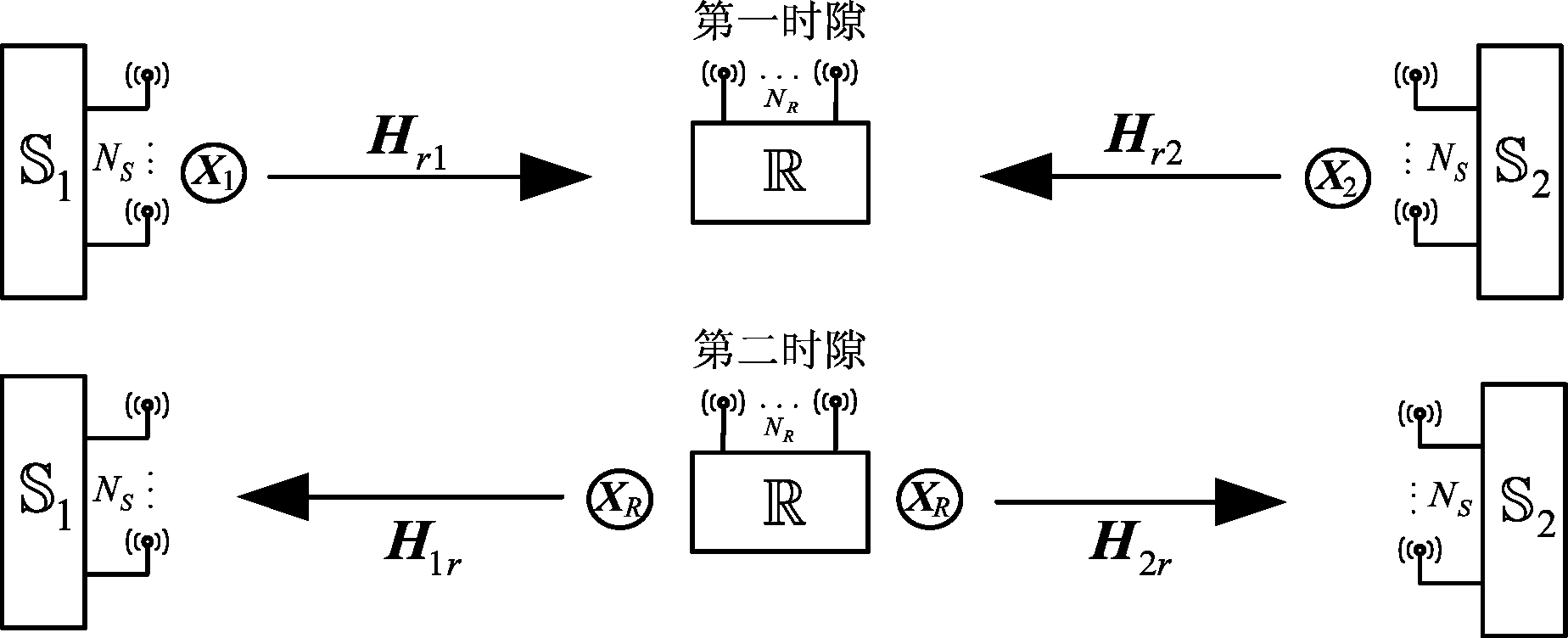
图1 三节点式双向MIMO中继网络示意图
Fig.1 Schematic diagram of relay network for two-way MIMO with three nodes
在![]() 和
和![]() 采用块传输模式,传输的每个信息符号块分为固定长度为NS的K个子块,表示为
采用块传输模式,传输的每个信息符号块分为固定长度为NS的K个子块,表示为![]() k=0,1,…,K-1,然后排列组成信息矩阵
k=0,1,…,K-1,然后排列组成信息矩阵![]() 信息符号假设为相互独立的随机变量,取自零均值、单位符号功率的调制信号符号集。对源信息矩阵S1,S2分别进行信道独立预编码操作,预编码矩阵为
信息符号假设为相互独立的随机变量,取自零均值、单位符号功率的调制信号符号集。对源信息矩阵S1,S2分别进行信道独立预编码操作,预编码矩阵为![]() 经过预编码后的数据块可以表示为:
经过预编码后的数据块可以表示为:
(1)
其中,预编码矩阵为行满秩的正交矩阵且满足
(2)
公式(2)中的限制条件保证预编码前后信号功率保持不变[14]。在第一时隙,Xi中的每行在对应的传输天线上串行传输,将数据块传输至![]() 在源节点
在源节点![]() 的平均传输功率可以表示为:
的平均传输功率可以表示为:
(3)
在![]() 的接收信号可以用矩阵形式表示为:
的接收信号可以用矩阵形式表示为:
R=Hr1S1P1+Hr2S2P2+NR
(4)
其中,![]() 和
和![]() 分别为
分别为![]() 到
到![]() 与
与![]() 到
到![]() 的MIMO信道矩阵,其所有元素服从相对独立的循环对称复高斯随机变量(CSCG,cyclic symmetric complex Gaussian),分别服从
的MIMO信道矩阵,其所有元素服从相对独立的循环对称复高斯随机变量(CSCG,cyclic symmetric complex Gaussian),分别服从![]() 以及
以及![]() 其中d1,R和d2,R分别表示节点
其中d1,R和d2,R分别表示节点![]() 和
和![]() 与节点
与节点![]() 和
和![]() 之间的距离,ε表示路径损耗指数,
之间的距离,ε表示路径损耗指数,![]() 为与天线增益和波束长度相关的常量。而加性白噪声
为与天线增益和波束长度相关的常量。而加性白噪声![]() 中所有元素相互独立,均服从
中所有元素相互独立,均服从![]() 在第二时隙,中继对接收到的来自
在第二时隙,中继对接收到的来自![]() 和
和![]() 的叠加信号进行放大转发,即XR=βR,其中β为中继放大因子,满足中继的传输功率限制条件。在中继的平均传输功率可以表示为:
的叠加信号进行放大转发,即XR=βR,其中β为中继放大因子,满足中继的传输功率限制条件。在中继的平均传输功率可以表示为:
(5)
将公式(4)带入(5),可以给出:
(6)
不失一般性地,以![]() 作为接收端进行研究,其接收信号可以表示为:
作为接收端进行研究,其接收信号可以表示为:
(7)
其中,i∈{1,2}且![]() 时i=2以及
时i=2以及![]() 时
时![]() 为
为![]() 到
到![]() 的MIMO信道矩阵,服从
的MIMO信道矩阵,服从![]() 且
且![]() 为加性白噪声,服从
为加性白噪声,服从![]()
3 最佳预编码设计
本文提出的BIC方案其新颖性主要体现在对源信息矩阵进行信道独立预编码操作,预编码矩阵为![]() 从矢量空间的角度分析,“右乘”预编码属于行空间映射[15],它将发送信息S1和S2分别映射到预编码矩阵P1和P2各行矢量张成的子空间,经信道传输后目标信号所在的行子空间与自干扰信号所在的行子空间保持正交且与CSI相互独立,通过在接收端设计简单的解码矩阵
从矢量空间的角度分析,“右乘”预编码属于行空间映射[15],它将发送信息S1和S2分别映射到预编码矩阵P1和P2各行矢量张成的子空间,经信道传输后目标信号所在的行子空间与自干扰信号所在的行子空间保持正交且与CSI相互独立,通过在接收端设计简单的解码矩阵![]() 即可实现未知信道条件下的干扰消除与混叠信号分离,在接收端
即可实现未知信道条件下的干扰消除与混叠信号分离,在接收端![]() 对接收信号Yi进行解码操作:
对接收信号Yi进行解码操作:
(8)
其中,等效噪声包括中继传输噪声及接收端引入噪声Wi=βHirNR+Ni,为了实现对端信号的可靠检测,解码矩阵Qi需要满足下述特性:
(9)
因此,解码矩阵Qi可以表示为:
(10)
另一方面,为了消除公式(8)中的自干扰信号,解码矩阵Qi的设计需要考虑包含预编码矩阵Pi的零空间,即:
PiQi=0K
(11)
根据公式(9)和公式(11),在![]() 采用不同的预编码矩阵,需要保证P1和P2行矢量张成的子空间相互正交,即:
采用不同的预编码矩阵,需要保证P1和P2行矢量张成的子空间相互正交,即:
span{P1}∩span{P2}={0}
(12)
其中span{·}表示矩阵行矢量张成的线性子空间。考虑最大化公式(8)中接收信号的有效信噪比(SNR,signal-to-noise ratio),实现最佳的预编码矩阵设计,有效SNR可以定义为:
(13)
根据公式(10),通过最大化有效SNR获取最佳的解码矩阵Qi等效于最佳的预编码矩阵![]() 的设计。考虑公式(2)和公式(12)给出的预编码矩阵满足条件,因此,
的设计。考虑公式(2)和公式(12)给出的预编码矩阵满足条件,因此,
![]()
span{P1}∩span{P2}={0}
(14)
实际上,公式(14)中的优化问题可以简化为最小化等效噪声![]() 可以表示为:
可以表示为:
(15)
引理:对于L×L的正定矩阵M,具有不等式性质tr(M)tr(M-1)≥L2。其中,对于某非零常数λ,当且仅当M=λ IL时等式成立。根据上述引理,![]() 为正定矩阵,因此当且仅当
为正定矩阵,因此当且仅当![]() 时,
时,![]() 取得最小值,即:
取得最小值,即:
(16)
最佳预编码和解码矩阵可以借助任意正交矩阵![]() 进行设计,即:
进行设计,即:
(17)
其中O(i:j,:)表示正交矩阵O中的第i行至第j行,一般在对称传输中设定M=2K。
4 可达速率分析
根据公式(8),可以发现通过在接收端进行解码操作,在未知MIMO-CSI的情况下,消除了剩余自信息干扰,在![]() 的接收信号可以重新表示为:
的接收信号可以重新表示为:
(18)
从公式(18)中可以判断,采用BIC方案后,能够完全消除剩余自干扰,双向MIMO中继网络可以看作两部分互不干扰的单向MIMO中继网络组合。为了反映信道估计误差对双向MIMO中继网络不同自干扰抵消方案的可达速率性能的影响,假设MIMO信道矩阵表示为![]() 其中,
其中,![]() 和
和![]() 中的所有元素服从相对独立的CSCG,即
中的所有元素服从相对独立的CSCG,即![]() 与
与![]() 表示对应MIMO矩阵的信道估计精度,公式(18)可以进一步表示为:
表示对应MIMO矩阵的信道估计精度,公式(18)可以进一步表示为:
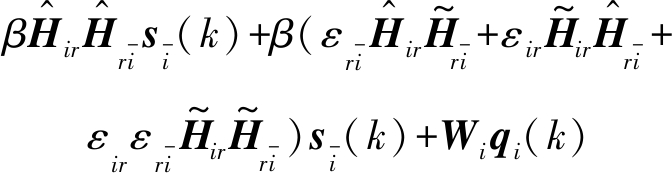
(19)
其中,![]() 分别为
分别为![]() 和Qi的第k列,由于在高SNR环境下,
和Qi的第k列,由于在高SNR环境下,![]() 因此公式(19)可以简化为:
因此公式(19)可以简化为:
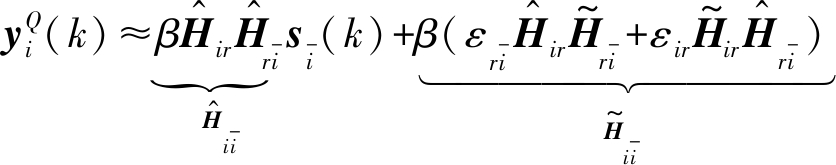
(20)
根据公式(3)与公式(17),可以获得![]() 第k列信息矢量的可达速率可以表示为:
第k列信息矢量的可达速率可以表示为:
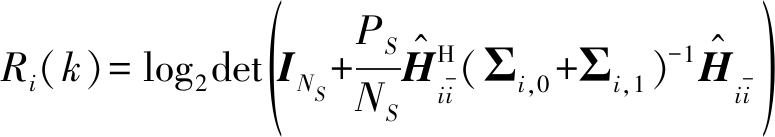
(21)
对于任意随机变量![]() 厄米特矩阵
厄米特矩阵![]() 存在
存在![]() 则:
则:
![]()
![]()
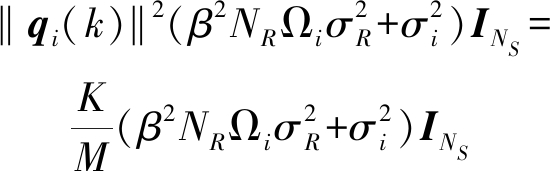
(22)
![]()
![]()
(23)
由于源节点S1和S2之间通过中继节点![]() 进行数据交互,其传输单位信息块的平均可达和速率可以表示为
进行数据交互,其传输单位信息块的平均可达和速率可以表示为
(24)
5 仿真实验与分析
针对AF协议下的三节点MIMO-TWRN进行仿真实验,从误比特率(bit error rate, BER)和可达和速率两方面对采用信道独立预编码的BIC方案进行系统性能分析,并且与文献[11-13]中提出的EIC方案进行对比。假定AF中继网络中MIMO信道为相互独立的平坦瑞利衰落信道,中继位置dA,R=dB,R=0.5且G=3,信道为对称信道。信息数据采用QPSK的调制方式,源节点![]() 和
和![]() 设置为对称的数据业务,即以相同的信息速率进行传输,预编码矩阵的参数设置M=2K。仿真实验中,假设源节点和中继节点的平均传输功率设置为Ps=Pr=1,中继节点
设置为对称的数据业务,即以相同的信息速率进行传输,预编码矩阵的参数设置M=2K。仿真实验中,假设源节点和中继节点的平均传输功率设置为Ps=Pr=1,中继节点![]() 和
和![]() 节点配备NS=NR=2根天线,其信噪比分别定义为
节点配备NS=NR=2根天线,其信噪比分别定义为![]() 且SNR=SNRR=SNRi。假设传输信息块长度为N=64,传输的每个信息块以固定长度NS=2分为K=32个子块,预编码矩阵P1和P2(K=32,M=64),正交矩阵O设定为64×64的Walsh-Hadamard矩阵。
且SNR=SNRR=SNRi。假设传输信息块长度为N=64,传输的每个信息块以固定长度NS=2分为K=32个子块,预编码矩阵P1和P2(K=32,M=64),正交矩阵O设定为64×64的Walsh-Hadamard矩阵。
5.1 BER分析
首先,假设单跳信道具有相同的信道估计性能,信道估计误差的精度![]() 与误差比率ω=f(ε,SNR)(dB)相关。不失一般性地,以
与误差比率ω=f(ε,SNR)(dB)相关。不失一般性地,以![]() 作为接收端,进行基于最小均方误差的符号检测[12]。图2对比了两种干扰消除方案在不同的估计误差下的BER曲线。可以明显看出,本文提供的BIC方案在不同的误差比率ω下,相比文献[11-13]中广泛应用的EIC方案具有更好的BER性能。原因在于,本文提出的BIC方案通过在源节点实现行空间映射来分别构建目标信号子空间以及自干扰子空间,并且在传输过程中与MIMO中继网络中的CSI相互独立,因此干扰消除不受信道估计误差影响。非完美信道状态信息下(ω=-20 dB,-30 dB),EIC方案中的剩余自干扰恶化了信息检测性能,在理想情况下(无自干扰影响的情况)的BER性能与BIC方案完美契合,说明BIC方案能够完全消除剩余自干扰。从图中可以判断,EIC方案的BER曲线相比BIC方案对于信道估计误差更加敏感,即使在较小的信道估计误差下(ω=-30 dB),也会损害双向中继网络的符号检测性能。因此相比EIC方案,本文提出的BIC方案不受信道估计误差的影响,具有更好的鲁棒性。
作为接收端,进行基于最小均方误差的符号检测[12]。图2对比了两种干扰消除方案在不同的估计误差下的BER曲线。可以明显看出,本文提供的BIC方案在不同的误差比率ω下,相比文献[11-13]中广泛应用的EIC方案具有更好的BER性能。原因在于,本文提出的BIC方案通过在源节点实现行空间映射来分别构建目标信号子空间以及自干扰子空间,并且在传输过程中与MIMO中继网络中的CSI相互独立,因此干扰消除不受信道估计误差影响。非完美信道状态信息下(ω=-20 dB,-30 dB),EIC方案中的剩余自干扰恶化了信息检测性能,在理想情况下(无自干扰影响的情况)的BER性能与BIC方案完美契合,说明BIC方案能够完全消除剩余自干扰。从图中可以判断,EIC方案的BER曲线相比BIC方案对于信道估计误差更加敏感,即使在较小的信道估计误差下(ω=-30 dB),也会损害双向中继网络的符号检测性能。因此相比EIC方案,本文提出的BIC方案不受信道估计误差的影响,具有更好的鲁棒性。
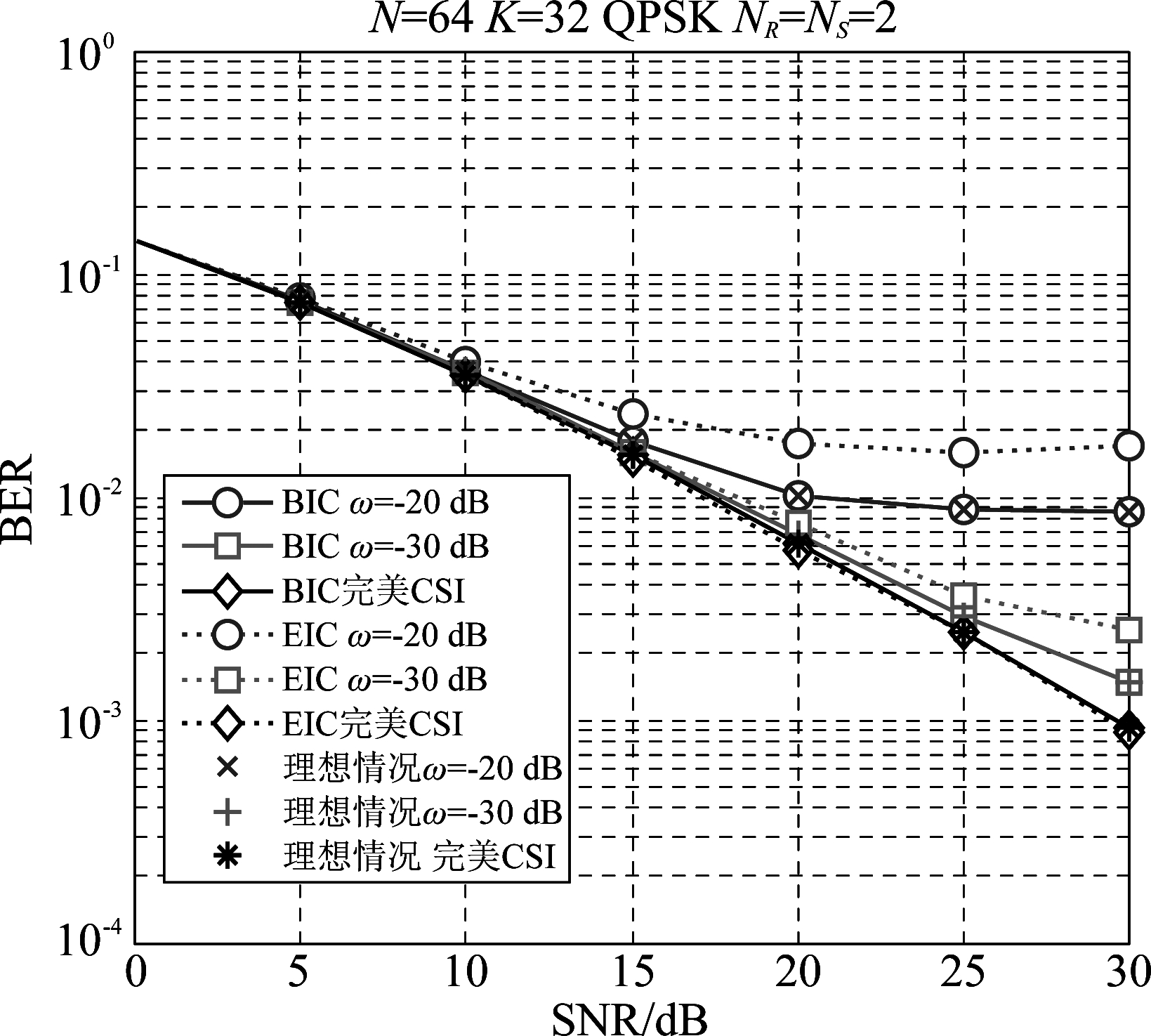
图2 不同方案下BER性能与SNR关系曲线
Fig.2 Curve of BER performance vs SNR of different schemes
然后,依然以![]() 作为接收端,考虑单跳信道估计性能不同的两种情况。第一种情况,理想Hr1信道,即Hr1信道估计误差的精度εr1=0,而H2r信道估计误差比率ω2r=f(ε2r,SNR)(dB)相关;第二种情况,理想H2r信道,即H2r信道估计误差的精度ε2r=0,而Hr1信道估计误差比率ωr1=f(εr1,SNR)(dB)相关。如图3所示,分别对比了两种情况下两种干扰消除方案受信道估计误差影响的BER曲线。可以明显发现,在理想Hr1信道情况下,考虑不同的估计误差时,BIC方案相比EIC方案其BER性能更加优越,而在理想H2r信道情况下,考虑不同的估计误差时,BIC方案与EIC方案的BER性能几乎相同。根据公式(8),主要原因在于EIC方案中的剩余自干扰受H2r信道估计误差影响而与Hr1无关,而BIC方案能够完全消除与H2r信道相关的剩余自干扰。由于信号的可靠检测受等效噪声的影响,根据公式(8),包含中继传输噪声在内的等效噪声是与H2r信道的估计性能相关的非高斯白噪声。如图3所示,考虑相同的估计误差时,理想H2r信道情况下的BER性能较理想Hr1信道情况更好。为了实现信息的可靠检测,在双向中继网络中,H2r信道的估计相对Hr1信道更为重要。
作为接收端,考虑单跳信道估计性能不同的两种情况。第一种情况,理想Hr1信道,即Hr1信道估计误差的精度εr1=0,而H2r信道估计误差比率ω2r=f(ε2r,SNR)(dB)相关;第二种情况,理想H2r信道,即H2r信道估计误差的精度ε2r=0,而Hr1信道估计误差比率ωr1=f(εr1,SNR)(dB)相关。如图3所示,分别对比了两种情况下两种干扰消除方案受信道估计误差影响的BER曲线。可以明显发现,在理想Hr1信道情况下,考虑不同的估计误差时,BIC方案相比EIC方案其BER性能更加优越,而在理想H2r信道情况下,考虑不同的估计误差时,BIC方案与EIC方案的BER性能几乎相同。根据公式(8),主要原因在于EIC方案中的剩余自干扰受H2r信道估计误差影响而与Hr1无关,而BIC方案能够完全消除与H2r信道相关的剩余自干扰。由于信号的可靠检测受等效噪声的影响,根据公式(8),包含中继传输噪声在内的等效噪声是与H2r信道的估计性能相关的非高斯白噪声。如图3所示,考虑相同的估计误差时,理想H2r信道情况下的BER性能较理想Hr1信道情况更好。为了实现信息的可靠检测,在双向中继网络中,H2r信道的估计相对Hr1信道更为重要。

图3 理想单跳信道情况不同方案下 BER性能与SNR关系曲线
Fig.3 Curve of BER performance vs SNR of different schemes with perfect single-channel state information
5.2 可达和速率分析
图4对比了两种干扰消除方案在不同的估计误差下的平均可达和速率曲线。可以明显发现,在完美CSI状态下,本文提出的BIC方案与EIC方案可以获得相同的可达和速率,而非完美CSI状态下(ω=-20 dB,-30 dB),BIC方案相比EIC方案可以获得更高的平均可达和速率。而EIC方案依赖信道估计来抑制自干扰,其信道估计误差会产生剩余自干扰,从而降低系统容量。即使在较小的信道估计误差下(ω=-30 dB),EIC仿真中由于不完美的干扰抵消导致的速率损失也非常明显。
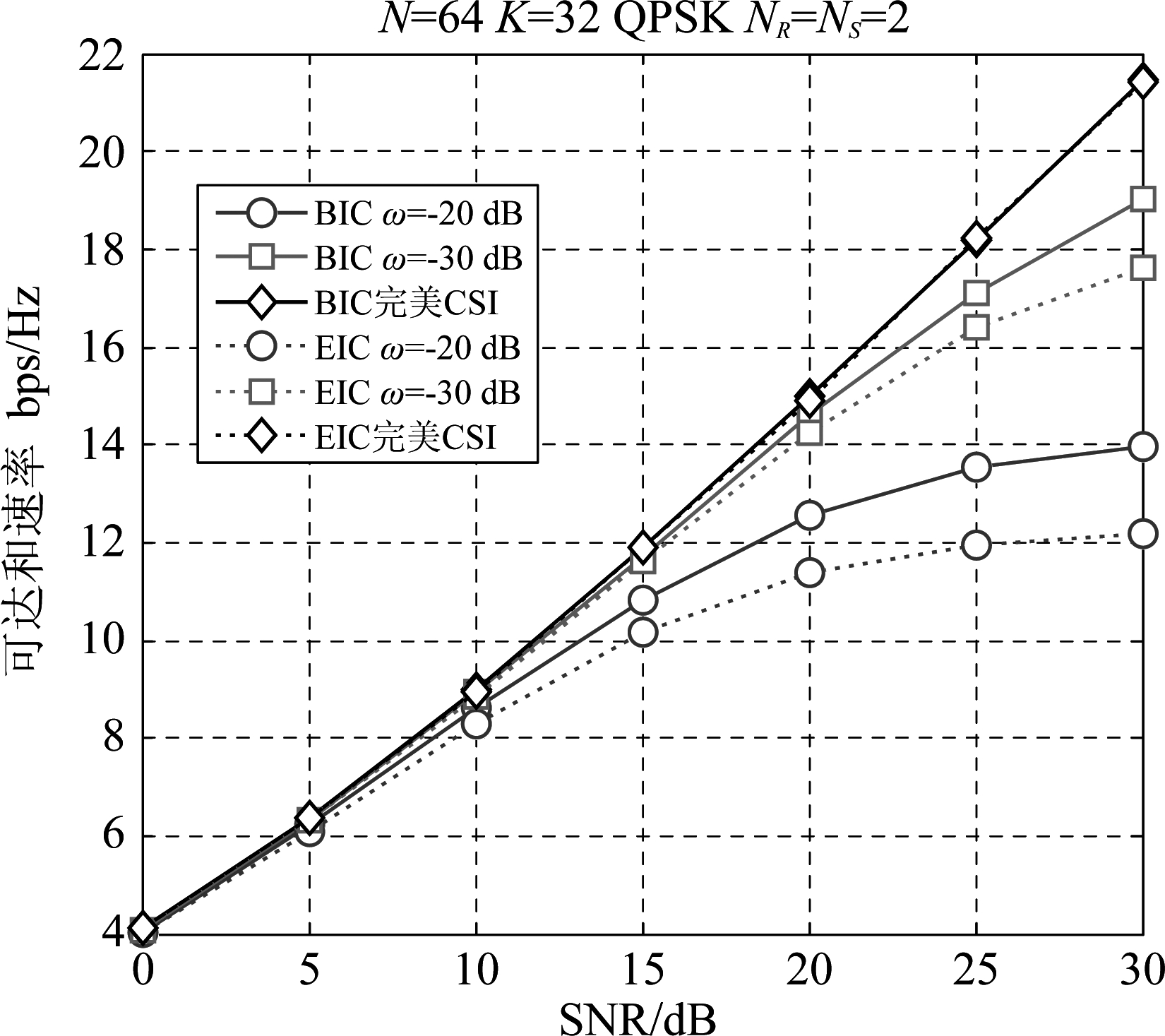
图4 不同方案下可达和速率性能与SNR关系曲线
Fig.4 Curve of achievable sum rate vs SNR of different schemes
6 结论
本文针对AF模式下双向MIMO中继网络中的自干扰抵消问题,提出一种基于行空间映射的盲干扰抵消(BIC)方案。通过在源节点对信息进行行空间预编码,从而构建不依赖于MIMO信道矩阵的期望信号子空间和自干扰子空间,实现未知信道状态下自干扰抵消和期望信号分离,从而消除非理想信道估计带来的剩余自干扰信号。仿真实验比较了BIC方案与EIC方案中信道估计误差分别对BER及可达和速率的影响,验证了BIC方案的有效性。新方案一方面突破了传统依赖信道估计进行干扰消除的传统思路;另一方面通过将信道估计与自干扰抵消解耦,消除多天线空间相关性和非理想信道估计对自干扰消除的影响,提高干扰消除的灵活性和鲁棒性,为多天线中继干扰消除提供新的解决思路。本文提出的盲干抵消除方案,能够进一步扩展到双路径中继网络中,通过采用交替预编码的策略,能够在未知信道状态信息的条件下抑制中继间干扰信号和中继噪声,从而消除信道估计误差引起的剩余自干扰和中继噪声对系统的影响。
[1] Nguyen K, Rong Y, Nordholm S. Simplified MMSE precoding design in interference two-way MIMO relay systems[J]. IEEE Signal Processing Letters, 2016, 23(2): 262-266.
[2] You J, Liu E, Wang R, et al. Joint source and relay precoding design for MIMO two-way relay systems with transceiver impairments[J]. IEEE Communication Letters, 2017, 21(3): 572-575.
[3] Dai Y, Dong X. Power allocation for multi-pair massive MIMO two-way AF relaying with linear processing[J]. IEEE Transactions on Wireless Communications, 2016, 15(9): 5932-5946.
[4] 赵睿, 傅友华, 李春国, 等. 多天线双向中继中的中继处理与资源分配策略[J]. 电子与信息学报, 2010, 32(4): 763-769.
Zhao R, Fu Y H, Li C G, et al. Relay processing and resource allocation strategies for multi-antenna two-way relay system[J]. Journal of Electronics and Information Technology, 2010, 32(4): 763-769.(in Chinese)
[5] Chiong C, Rong Y, Xiang Y. Channel training algorithms for two-way MIMO relay systems[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3988-3998.
[6] He Z, Lang Z, Rong Y, et al. Joint transceiver optimization for two-way MIMO relay systems with MSE constraints[J]. IEEE Wireless Communication Letters, 2014, 3(6): 613- 616.
[7] Luo Z, Leung S, Yu X. Robust precoder design for MIMO relay networks over double correlated Rician channel[J]. IEEE Transactions on Signal Processing, 2015, 63(9): 2295-2305.
[8] Park H, Chun J, Adve R. Computationally efficient relay antenna selection for AF MIMO two-way relay chennels[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 6091- 6097.
[9] Hu C, Liu G, Chen B. Joint relay/antenna selection and precoding design for two-way MIMO amplify-and-forward relaying systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 4854- 4864.
[10]Wang C, Chen J, Peng Y. Relay precoder designs for two-way amplify-and-forward MIMO relay systems: an eigenmode-selection approach[J]. IEEE Transactions on Wireless Communications, 2016, 15(7): 5127-5137.
[11]Wang C, Liu T, Dong X. Impact of channel estimation error on the performance of amplify-and-forward two-way relaying[J]. IEEE Transactions on Vehicular Technology, 2012, 61(3): 1197-1207.
[12]Panah A, Heath R. MIMO two-way amplify-and-forward relaying with imperfect receiver CSI[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4377- 4386.
[13]Arti M, Manav R. Performance analysis of two-way AF MIMO relaying of OSTBCs with imperfect channel gains[J]. IEEE Transactions on Vehicular Technology, 2014, 63(8): 4118- 4124.
[14]Tran N, Pham D, Tuan H, et al. Orthogonal affine precoding and decoding for channel estimation and source detection in MIMO frequency-selective fading channel[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 1151-1162.



