1 引言
随着近年来社会与科技的发展,通信设备的数量以及通信数据都呈爆发式增长,从而导致对通信性能需求也不断提高。具体而言,即将到来的下一代通信技术对通信提出了高可靠低延时,高数据吞吐量以及密集连接等要求[1]。为了满足这些需求,诸如非正交多址接入(NOMA)、多输入多输出(MIMO)等新技术受到广泛关注[2-3]。而在这些技术的推广应用中,通信信号的处理是不可或缺的部分[4]。然而,传统的通信信号处理方法面临着复杂度与通信性能之间相互制约的问题。因此,针对通信信号的处理方法需要引入新的思想和方法去研究。
在通信信号处理中,信道估计和多用户检测是两个十分重要的问题。首先对于信道估计,利用导频信号进行信道估计的方法是最重要的方法之一[5- 6]。之后论文[7- 8]指出针对MIMO-OFDM系统,利用导频信号的联合信道估计和多用户检测方法能够获得比单纯的信道估计更好的通信性能。然而,这些方法具有很高的计算复杂度。为了降低联合信道估计与多用户检测的复杂度,改进的算法被应用于低复杂度的解决方法研究中,如加权增强算法[8]、遗传算法[9]、粒子群算法[10]等。虽然以上方法获得了良好的效果,然而降低其计算复杂度依然是一个亟待解决的问题。
对于多用户检测,其在各个不同的通信系统均是十分重要的研究课题。例如,正交多址接入的码分多址(CDMA),空分多址(SDMA),以及非正交多址接入(NOMA)范畴内的稀疏码多址接入(SCMA)、交织多址接入(IDMA)等。在多用户检测的方法中,最大后验概率(MAP)的多用户检测具有最优的误码率性能,然而随着用户数增加而呈指数递增的计算复杂度使得该方法难以被实际运用[11]。因此,针对各个通信系统的低复杂度多用户检测方法一直是热门的研究课题,如SCMA低复杂度多用户检测技术[12]。以多输入多输出(MIMO)系统为例,迫零检测等方法具有远低于MAP方法的计算复杂度[13-14]。然而,这些计算复杂度的降低是以牺牲系统通信性能为代价的。因此,保证通信性能的低复杂度通信信号处理方法一直是通信设计所追求的目标。
而在计算复杂度理论与理论物理的研究中发现,量子计算得益于量子叠加效应和量子并行原理展示出了巨大的计算潜能[15-21]。具体而言,量子计算最早由理论物理学家费曼最早构思并提出[22],针对特定的问题,其能够以远低于经典算法的复杂度获得结果。例如,著名的量子算法Shor算法[23]能够快速进行大数分解,量子搜索算法[24]能够快速在无序数据库中搜索得到特定目标。由于搜索问题所具有的基础性与广泛性,量子搜索算法进一步被拓展为实现未知解个数情况下的搜索[25]和对数据库最小值的搜索[26]。与此同时,关于量子搜索等量子算法的理论在后续文献中被进一步研究[27-29]。由于量子计算所蕴含的巨大潜能,量子计算在通信中被认为具有十分广阔的应用前景[30]。区别于[30]中仅针对量子搜索算法本身进行归纳,本文从经典通信领域中存在的信号处理问题着手,讨论了已有工作中量子搜索算法对于这些问题的启发和帮助。我们对于几个典型的经典通信问题,从时间角度来纵向展开量子搜索算法的作用,在这里面,量子搜索算法或是独立地作为一种工具,或是与其他类似近似公式等方法一起构成组合计算工具。特别地,对于通信信号处理的问题,目前已经有文献研究运用量子计算进行通信信号处理的方法,以期实现比经典处理方法更低的计算复杂度。具体而言,运用量子计算实现联合信道估计与信号检测的方法[31]和基于量子计算的多用户检测方法等一系列研究,使得量子通信信号的处理方法可以从一个全新的角度得到分析。但是目前该领域的研究尚处于起始阶段,缺少系统化的研究方法。因此,对该领域的研究进行总结和综述显得尤为重要。为了给后续研究者提供一个参考,本文对经典通信信号的量子化处理方法进行一个综述。
本文第2节首先介绍了量子计算的基础,并且在此基础上总结了通信信号的量子处理这个领域中相关的量子算法。之后,第3节介绍量子计算在信道估计问题上的应用。紧接着,针对量子计算在通信中另一重要应用,第4节总结了针对各个不同的通信系统中基于量子计算的多用户检测方法。最后,对本文的总结以及未来展望将在第5节给出。
2 量子计算与量子搜索算法
由于量子计算的原理与经典计算采用的原理存在根本性差异,量子计算具有许多经典计算所不具备的特性,如态叠加、量子并行效应等。所以量子算法在通信中的使用方式也是多种多样的。因此，如图1所示，我们调研了该领域近年来主要研究成果随时间的发展进程。最近也有研究工作从不同的方面讨论了量子计算与经典通信的结合方式[32]。为使本文更加清晰易懂,本节将首先介绍量子计算的基础。基于此,我们进一步介绍量子计算中与通信信号处理相关的量子算法。其中,我们将该领域相关的量子算法总结于表1中,并将其与对应的经典算法进行复杂度上的比较。本文所涉及的量子算法主要包括量子搜索算法、量子神经网络和量子计数算法。
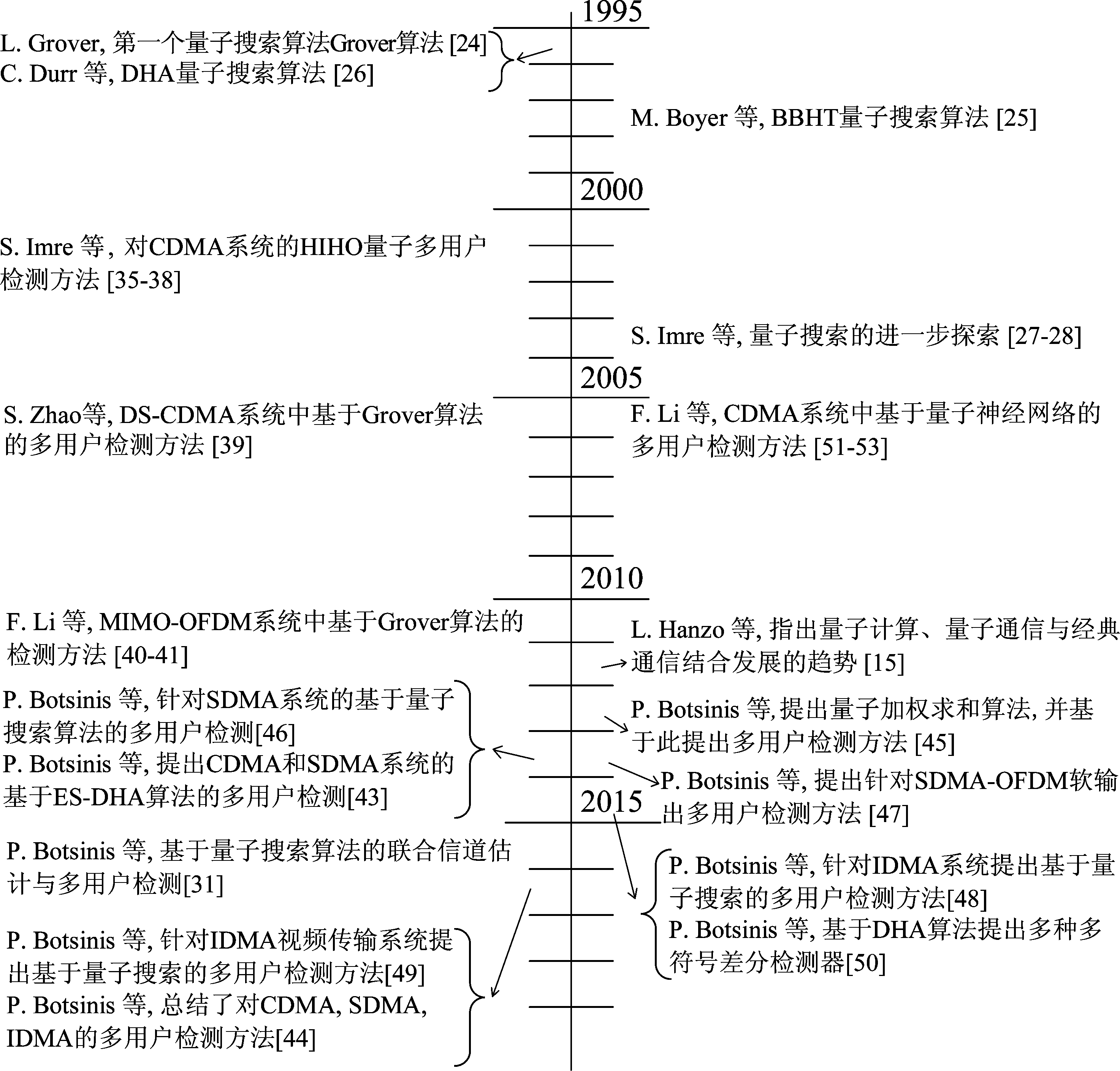
图1 通信信号的量子处理主要研究成果时间轴
Fig.1 The main contributions on quantum processing for communication signals
2.1 量子计算基础
本小节介绍量子计算的理论基础。量子领域与经典领域有相同也有差异:与经典领域的比特类似,量子领域中的基本单位我们称之为量子比特,记作qubit,而量子态表示的则是每个qubit的状态。量子态被分为纯态和混合态两种,其中纯态又可分为单一态和叠加态。在纯态中,每种量子态依概率出现,对于叠加态|ρ〉=α|0〉+β|1〉,所有状态出现的概率和为1,即|α|2+|β|2=1。而在混合态中,则是有多种纯态按照概率出现。同时,量子比特的数量可以是单个,也可是多个,由n个qubit组成的量子系统状态是2n个基态的叠加态或者混合态,而多个量子态之间存在量子纠缠,量子纠缠使得量子与量子之间存在联系。量子纠缠本身是因为在粒子之间存在相互作用力,从而导致单个粒子的状态不能独立拆分出来,而是作为整个系统的一部分,表现出的效果就是牵一发而动全身。也正因为量子纠缠,量子计算机能够储存远多于经典计算机的信息。
表1 用于通信信号处理的量子算法
Tab.1 The quantum algorithms used for communication signal processing
量子算法功能量子复杂度对应经典算法经典复杂度Grover算法搜索含N元素的无序数据库中特定的解,其中解个数已知O(N) 穷搜算法O(N) BBHT算法搜索含N元素的无序数据库中特定的解,其中解个数未知O(N)穷搜算法O(N)DHA算法在含N元素的无序数据库中搜索代价函数最大值(最小值)的元素O(N)穷搜算法O(N)量子神经网络函数计算-神经网络-量子计数算法统计数据库中符合条件的解个数,其中使用c个辅助qubitO(2c) 经典计数O(N)
为了利用这种强大的信息存储能力,需要设计合适的量子算法用以操控量子系统的状态。而对于量子计算,量子存储器的状态可以通过幺正算符U来操控,幺正算符满足U-1=U+。因此,通过设计由幺正算符表示的量子算法,可以控制量子系统状态发生改变,从而实现特定的计算目标。在下文中,我们将介绍与通信信号的量子处理相关的量子算法。特别地,对于穷搜问题,量子搜索具有比经典算法具有更低的复杂度,是量子计算中一类重要的算法。其中应用最为广泛的三个量子搜索算法分别是Grover量子搜索算法,Boyer-Brassard-Hoyer-Tapp (BBHT)量子搜索算法和Durr-Hoyer (DHA)量子搜索算法,而随着神经网络的日渐成熟,对于量子神经网络的研究也随之产生。
2.2 Grover量子搜索算法
作为由L.Grover于1996年提出的第一个量子搜索算法[24],Grover算法能够实现在N个无序的量子态中找到满足条件的有限个解的功能,并且此时要求已知解的个数。为了在N个元素中找到满足f(x0)=δ的元素x0,Grover提出了用量子算子G进行Gover迭代,其中G=HPH·O,而H表示Hadamard算子,P=|0〉〈0|-I,HPH的作用是使得满足条件的元素以更高的概率被观测到;最后O则表示Oracle算子,其作用是在量子域以量子并行的方式衡量数据库中所有元素对应的f(x)值,并且将所有满足f(xo)=δ的|xo〉处理成为-|xo〉。
Grover算法的操作过程主要分为初始化,Grover迭代和结果观测三个步骤。初始化的目的是产生N个概率等同的不同量子态,即初始化之后得到:
(1)
随后用G算子对这N个量子态进行Grover迭代,由于G算子本身的构成,所以在经过特定次数的迭代之后,可以使所有满足条件f(x0)=δ的元素x0实现相位翻转;最后经过观测能够以接近1的概率得到满足条件的解。同时由于迭代次数已知,成功搜索的概率可以确定性地给出,此时的计算复杂度为
2.3 BBHT量子搜索算法
前面提及的Grover算法要求已知满足条件的解的个数,而作为Grover算法的改进,BBHT算法则不需要提前知道解的个数,同时BBHT算法可以以更接近于1的概率在最后观测的阶段得到满足条件的解[25]。但由于具体解的个数未知,所以无法计算精确的成功概率。
作为Grover算法的改进版本,BBHT算法增加了对于Grover迭代次数的估计过程,通过初值设定,Grover迭代和结果观测来进行量子搜索。其中初值设置是为了能够在迭代之前给出需要迭代的次数,当在此次搜索中没有找到所有满足条件的解时,则增大迭代次数重新进行搜索,一般地,迭代次数在
以下,所以当迭代次数超过时,算法停止迭代并认为没有满足条件的解。
由于BBHT算法的复杂度仍是由G算子决定的,所以BBHT算法的复杂度仍为
2.4 DHA量子搜索算法
前面两种量子搜索算法是为了求得满足条件的解,而DHA量子搜索算法则是在全部的N个元素中找到使f(x)取得最大值(或最小值)的元素xmax(或xmin)[26]。由于此时需要将所有元素的函数值进行比较,所以DHA算法在BBHT算法的基础上需要进一步地提前选定一个函数值作为阈值用于比较,也即Δ=f(xi),而BBHT算法则用于搜索满足条件f(xs)>Δ(或f(xs)<Δ)的元素xs,若找到新的阈值,则重新进行搜索,一般地,Grover迭代的次数ΩDHA满足
若在迭代次数达到
的时候仍旧没有结束搜索,则认为当前的阈值为最大值(或最小值),并确定对应的xmax(或xmin)。同样地,DHA算法的计算复杂度为
2.5 量子神经网络
量子神经网络是人工神经网络在量子计算上的拓展,其作用是提升人工神经网络的计算能力。由于经典的神经网络涉及大量的信息存储和函数计算,因此需要消耗巨大的计算资源。将人工神经网络与量子计算结合,可以利用量子叠加效应和量子并行效应大幅提升计算效率。具体而言,量子神经网络运用n个qubit能够存储2n个比特的信息,而经典神经网络只能表示n比特的信息。通过设计特定的量子算符,则可以实现所有函数值的并行计算。量子神经网络目前被认为具有高效率,存储能力强,高稳定性等特性而有望在未来人工智能领域获得应用[33]。
2.6 量子计数算法
针对经典领域中的穷搜问题,G Brassard等人在振幅放大中采用了Grover迭代的算法,观察到量子搜索算法可以以更低的复杂度解决经典领域的部分穷搜问题,并进一步结合了Grover和Shor的量子算法用于近似计数,这也可以视为一种对于振幅的近似估计。这种量子计数算法可以用于计数而非上述方法中的寻找满足条件的解。
3 基于量子计算的联合信道估计与数据解码
信道估计是通信中一个基本问题。在上行多用户多载波通信系统中,基站会进行信道估计的操作,以期能够准确地判断信道对传输信号的影响。并且,信道估计的准确性会直接影响接收端多用户检测的性能。目前已有许多不同的文献研究了提高信道估计与多用户检测性能的方法,特别地,联合信道估计与数据解码方法能够在提高信道估计的准确性的同时降低多用户检测的误检测率[8-9]。然而,精确的信道估计以及多用户检测都面临着复杂度过高的问题。因此,运用量子计算去解决这个问题是一个非常有价值的方向。
经典的联合信道估计与数据解码的方法是决策导向信道估计(DDCE),该方法分为五个部分,分别是导频信道估计,信道脉冲响应(CIR)滤波器,信道估计,多用户检测和信道解码。具体而言,首先根据导频信道估计的结果,CIR滤波器预测下一个符号的信道状态。之后,关于信道状态和解码的软输出信息在信道估计模块,多用户检测模块和信道解码模块之间进行迭代,不断更新信道估计的结果和多用户检测的结果。通过使用进化算法,可以较快地获得信道估计结果和多用户检测结果。然而,该方法的复杂度依然过高。
针对经典的联合信道估计和数据检测,在空分多址正交频分复用(SDMA-OFDM)系统中,P. Botsinis等人[31]提出基于量子计算的联合信道估计与数据解码方案。具体而言,文献[31]运用DHA量子搜索算法去加速进化算法中的Repeated Weighted Boosting Search(RWB)算法,得到一个新的量子辅助算法——Quantum Repeated Boosting Search (QRWBS)算法。通过利用该算法去进行最优的信道参数搜索,同时利用DHA算法去进行多用户检测部分的最优码字搜索过程,即可显著地降低经典解法的复杂度。并且,由于量子搜索的准确性接近概率1,因此基于量子计算的多用户检测步骤相比经典多用户检测不会造成误码率性能损失。与此同时,论文[32]指出该方法可以在略微降低复杂度的情况下,获得更好的信道估计结果。
4 基于量子计算的信号检测方法
如何准确高效地进行信号检测同样是通信系统中一个亟待解决的问题。而传统的通信技术中,信号检测的复杂度与误码率性能是相互制约的。因此,降低通信系统中多用户检测算法的复杂度是一个重要的研究课题。依据原理的不同,我们将基于量子计算的多用户检测方法在表2进行了分类总结,每一行包含了有关各个检测方法的自提出以来最具代表性的工作。具体而言,其原理主要分为基于量子搜索的方法,结合量子搜索和近似公式的方法,基于量子加权和算法的方法,以及基于量子神经网络的方法。量子搜索算法解决的问题范围较广,本文仅介绍与解决多用户信号检测问题相关的量子搜索算法。本节中,我们根据原理的不同分别针对以上不同类别的多用户检测方法进行介绍。在Hanzo等人的一篇综述文章中同样提及了量子搜索算法在通信中的运用[30]。而我们把重点放在量子搜索算法对于经典通信信号处理的应用,因此对这个部分的相关文献进行了更为全面透彻的调研,以期给读者更明确的调研思路。特别地,由于量子搜索算法不仅仅可以单独作为一种简化计算的工具,更可以与其他数学手段结合使用,以达到简化计算的效果。所以本部分以各个工作出现的时间为线索,介绍量子搜索算法在经典通信中信号检测领域的使用情况。
表2 量子多用户检测方法
Tab.2 The quantum-aided multiuser detection methods
量子多用户检测原理通信系统文献来源基于Grover算法的方法运用Grover算法搜索,替代经典方法中的穷搜部分CDMA,MIMO-OFDM[35-42]基于DHA算法的方法将经典算法中需要穷搜的部分直接运用DHA量子算法进行代替CDMA,SDMA[43-45]加权和与量子搜索算法结合的方法针对多用户检测的计算,提出新的量子加权求和算法(QWSA)进行公式的高效计算SDMA-OFDM[46-47]近似方法与量子搜索算法结合的方法将经典算法中的计算公式进行近似,使得问题能够运用DHA算法进行穷搜IDMA,SDMA,MIMO[48-50]基于量子神经网络的方法用量子神经网络代替经典多用户检测中的神经网络DS-CDMA[51-53]
4.1 基于Grover算法和DHA算法的多用户检测方法
我们首先介绍基于Grover算法和DHA算法的多用户检测方法,该类方法的原理是直接运用量子算法代替经典算法的公式。在上行OMA系统中,每个用户发送的信息将由不同的信道发送给基站。给定发射信号x,基站接收到的信号y表示为:
y=Hx+n
(2)
其中H是信道参数矩阵,n是信道噪声。
对于码分多址(CDMA),空分多址(SDMA)和正交频分多址(OFDMA)等系统,经典的多用户检测方法是基于最大似然估计(ML)的硬输入硬输出方法。当基站接收得到信号y时,该方法的目标函数是
f(x)=‖y-Hx‖2
(3)
通过穷搜发射端的所有码字组合,得到使得f(x)最大的码字组合x。该方法的误码率性能是最优的,然而该方法的复杂度高达O(MK)。为了降低该方法的复杂度,同时保证误码率性能损失有限,基于量子计算的信号检测方法相继被提出。
最早的基于量子计算的多用户检测方案由Imre等人在文献[35-38]中提出,该方法考虑直序扩频CDMA(DS-CDMA)系统的多用户检测问题。在多用户检测领域,最初的方式是在总的K个用户中解码某一个用户k的信息。其中每一个用户都可以发送两种量子态的信息到基站,即+1和-1,各个不同的状态产生的码字的组合,存储在量子寄存器中用于进行以后的搜索和解码。当需要检测用户k的信息的时候,则运用Grover搜索算法对存储于两个量子寄存器中的其余用户所发送的信号,时延等信息进行排查,从而获得目标用户k的信息。运用上述方法,可以得益于Grover算法较低的复杂度提升检索效率,最后得到用户的解码数据。但是这个最初提出的多用户检测方法具有很大的局限性,例如每次搜索只能针对一个目标用户进行检测,没有给出通信性能方面的研究等。因此,在此方法的出现之后,研究人员提出了一系列改进的量子计算和多用户检测相结合的方法。
后来的研究人员主要针对量子多用户检测中的通信性能,以及量子技术的应用上进行了扩展。针对上面提到的DS-CDMA系统,目前已经有人提出了可以在K个用户中同时检测出不止一个用户信息的方法,并且这个方法适用于多种通信系统[39]。也有文献改进使得其能够不局限于二相相移键控(Binary Phase Shift Keying, BPSK)的多用户检测[18]。同时针对SDMA相关的量子多用户检测,也存在相关的工作,采用ES-DHA进行对目标函数的检索,从而获得远低于最大似然方法的计算复杂度,提升了原本的DHA算法的性能,也带来了更高的通信质量[43- 45]。Fi等人[40- 41]以及Abdulnabi等人[42]则在多输入多输出正交频分复用(MIMO-OFDM)系统的基础上应用了Grover算法,从而进一步发挥了量子算法简化计算的优势。
4.2 基于量子加权和算法(QWSA)和量子搜索的多用户检测方法
在有U个用户,L个发射天线的SDMA系统中,对于经典的MAP算法,每个比特或者符号的后验概率的对数似然比(LLR)都会被计算。设用户为u,则该用户发送信息的第m位的LLR计算方法如下:
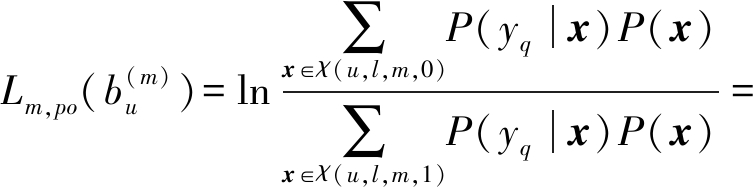
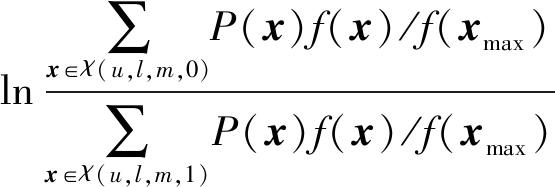
(4)
其中
f(x)=P(yq|x)=exp(-‖yq-Hx‖/2σ2)
(5)
为了降低其计算复杂度,文献[46- 47]提出了一种量子加权算法(QWSA),结合此算法与DHA算法提出一种新的量子多用户检测方案。具体而言,该方法首先运用DHA算法搜索得到了使得f(x)取得最大值的xmax。之后,该方法运用QWSA算法进行每个比特分子和分母LLR的计算,从而获得每个比特最终的LLR计算结果。相比于经典的最优算法,该方法的复杂度明显降低,同时具有次优的误码率性能。
4.3 基于近似公式和量子搜索算法的多用户检测方法
在多用户检测技术中,基于MAP的多用户检测是一类重要的技术。基于MAP的多用户检测能够获得最优的误码率性能,但是它的计算复杂度非常高,使得该技术的应用受到很大制约。因此,降低MAP多用户检测技术的复杂度成为了一个重要的研究课题,特别地,基于量子计算的低复杂度MAP多用户检测是近年来一个非常有创新性的方法。
对于经典的MAP算法,每个比特或者符号的后验概率的LLR都会被计算。设用户为u,则该用户发送信息的第m位的LLR计算方法如下:
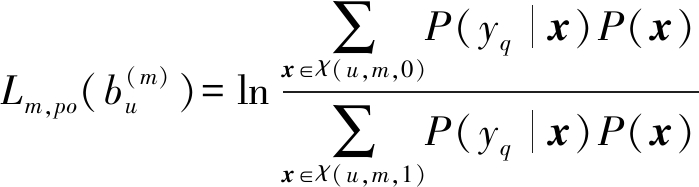
(6)
根据上式可知,虽然MAP能够实现最优的误码率性能,但却同时具有O(MU)的过高的计算复杂度。为了在不同的场景降低MAP算法的复杂度,Botsinis等在文献[48-50]中针对不同的情形,研究多种基于量子搜索算法的低复杂度多用户检测方法。具体而言,文献[48]中针对多载波交织多址接入系统(MC-IDMA),提出了两种能够降低MAP算法复杂度的量子多用户检测器。第一种被称为DHA-MAA多用户检测器,其原理是将DHA算法与LLR的最大近似方法(Maximum Approximation,MAA)相结合。设定目标函数f(x)=P(yq|x)P(x),那么LLR的MAA近似如下
(7)
在此基础上,对于发送信息的每一位,DHA-MAA检测器运用DHA算法去寻找上式中的使得目标函数最大的输入,并计算其相应的LLR。因此完成多用户检测器的任务。第二种量子多用户检测器被称为DHA-MUA检测器,因为其将DHA算法和多输入近似方法(MUA)相结合。采用了MUA近似的LLR公式如下
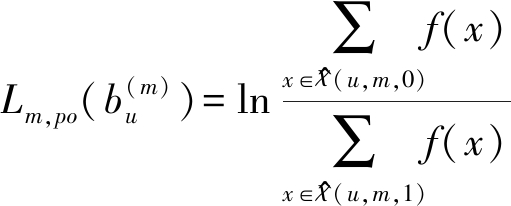
(8)
DHA-MUA从每次发送的码块所有比特的第一位开始,运用DHA算法在包含所有可能码字组合的集合中搜索目标函数最大值。每次确定了一位的值之后,更新集合,使得剩下的码字组合与已经计算得到的结果相符,直到所有位均计算完毕。两种方法中,DHA-MUA的方法能够降低复杂度的同时逼近MAP的误码率性能,而DHA-MAA的误码率性能则不如前者。之后Botsinis等在文献[49]中将DHA-MUA多用户检测器应用于IDMA系统的视频流多用户检测中。在IDMA的视频流传输系统中,每个用户将向基站传输多层次的视频文件,每个层对应视频不同的清晰度。
4.4 基于量子神经网络的多用户检测方法
基于量子计算的多用户检测方法中,上文已述方法的主要思想是利用量子算法加速经典多用户检测的计算过程。除了上文中的涉及量子搜索的多用户方法,我们最后介绍量子神经网络和量子进化算法在多用户检测问题上的应用。
量子神经网络是一种将量子计算与经典的人工神经网络相结合的新技术,该技术借助量子计算的并行特性,有潜力获得快速学习和高速信息处理能力,且具有较高的稳定性和可靠性[34,52]。针对CDMA系统的多用户检测,Li等在文献[51-53]中研究了基于量子神经网络的多用户检测方法。针对经典的CDMA系统,Verdu证明了,CDMA最优多用户检测公式如下,
(9)
其中,b为发射的信息比特向量,y为接收的信号,R为信道参数。该方法由于需要穷搜所有可能的码字,因此复杂度是无法适合推广使用的。在这个背景下,相比经典方法中运用Hopfield神经网络(HNN)的多用户检测器,文献[51-53]中提出的量子神经网络多用户检测方案能够在降低算法复杂度的同时更接近最优检测器的误码率性能。具体而言,将匹配滤波器输出的接收信号存储在一个量子寄存器中,此时该量子寄存器的位数与接收信号的维度一致。之后将存储在量子寄存器中的信息输入到一个带反馈的量子神经网络中。通过设计量子神经网络中的参数,可以使得量子寄存器的状态在量子神经网络的影响下状态演化得到系统的末态。同时,通过设定一个特定的观测算符,使得对量子神经网络的末态进行观测即能够获得公式(7)中的计算结果,从而获得对原始信号的估计。在[52-53]中,作者的仿真结果证明该方法也具有较好的抗远近效应的能力。
5 结论
经典通信信号处理面临着复杂度过高等问题,近年来高速发展的量子计算理论为解决该问题提供了崭新的思路,并形成了一个新的通信研究领域。为了方便后续研究者参考,本文总结了迄今为止基于量子计算的通信信号处理理论与方法。具体而言,我们阐述了这个领域涉及的主要量子计算原理,运用到的量子算法以及性能上的提升。针对通信信号的量子处理,其主要应用包括基于量子计算的联合信道估计与数据解码,多用户检测技术。我们分别针对这两个领域,总结了基于量子计算的新解决方法。由于量子计算独特的并行特性和叠加特性,量子算法能够获得比经典算法更低的复杂度。由于量子计算近年来不断提出新的方法,更多的通信信号处理问题具有可能性借助量子计算的方法获得比经典处理更具优势的解法。然而,量子计算的硬件实现与量子算法的模拟依然是物理学上一个难题,这也会对运用量子计算去处理通信信号的方法相应地产生影响。对于量子计算与经典通信信号处理的融合,在未来发展中取决于两方面,一方面是更加深入地挖掘量子计算与经典通信信号处理的关系,另一方面是量子计算技术本身的理论与实验发展。如果将视野扩展到通信信号处理之外的领域,量子计算也能够在各种不同的路由优化问题[55-57],可见光通信系统中室内定位问题[58],以及NOMA系统中信息传输发挥作用[59],对于现在炙手可热的社交网络中通信性能的优化也能起到简化计算的作用。如今,高精尖技术正在飞速发展,在通信技术之外,还有覆盖面广,准确度高的雷达监测系统等[60- 61],所以量子计算在未来或可以应用在更加广泛的先进技术中,从而进一步推动人类社会的发展。
[1] Andrews J G, Buzzi S, Choi W, et al. What will 5g be?[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1065-1082.
[2] Gupta A, Jha R K. A survey of 5g network: Architecture and emerging technologies[J]. IEEE Access, 2015, 3: 1206-1232.
[3] Luo F L, Zhang C. Signal processing for 5g: algorithms and implementations[M]. [S.l.]: John Wiley & Sons, 2016.
[4] Li Y, Nambi S, Sirikiat A. Channel estimation for OFDM systems with transmitter diversity in mobile wireless channels[J]. IEEE Journal on Selected Areas in Communications, 1999, 17(3): 461- 471.
[5] Li Y. Simplified channel estimation for OFDM systems with multiple transmit antennas[J]. IEEE Transactions on Wireless Communications, 2002, 1(1): 67-75.
[6] Ghosh M, Weber C L. Maximum-likelihood blind equalization[J]. Optical Engineering, 1992, 31(6): 1224-1229.
[7] Chen S, Wu Y. Maximum likelihood joint channel and data estimation using genetic algorithms[J]. IEEE Transactions on Signal Processing, 1998, 46(5): 1469-1473.
[8] Zhang J, Chen S, Mu X, et al. Joint channel estimation and multiuser detection for sdma/ofdm based on dual repeated weighted boosting search[J]. IEEE Transactions on Vehicular Technology, 2011, 60(7): 3265-3275.
[9] Jiang M, Akhtman J, Hanzo L. Iterative joint channel estimation and multi-user detection for multiple-antenna aided ofdm systems[J]. IEEE Transactions on Wireless Communications, 2007, 6(8): 2904-2914.
[10]Zhang J, Chen S, Mu X, et al. Evolutionary-algorithm-assisted joint channel estimation and turbo multiuser detection/decoding for ofdm/sdma[J]. IEEE Transactions on Vehicular Technology, 2013, 63(3): 1204-1222.
[11]Verdu S, et al. Multiuser detection[M]. [S.l.]: Cambridge University Press, 1998.
[12]Bayesteh A, Nikopour H, Taherzadeh M, et al. Low complexity techniques for scma detection[C]∥2015 IEEE Globecom Workshops (GC Wkshps), 2015: 1- 6.
[13]Hanzo L, Alamri O, El-Hajjar M, et al. Near-capacity multi-functional mimo systems: sphere-packing, iterative detection and cooperation: volume 4[M]. [S.l.]: John Wiley & Sons, 2009.
[14]Hanzo L, Akhtman Y, Akhtman J, et al. Mimo-ofdm for lte, wifi and wimax: Coherent versus non-coherent and cooperative turbo transceivers[M]. [S.l.]: John Wiley & Sons, 2010.
[15]Hanzo L, Haas H, Imre S, et al. Wireless myths, realities, and futures: from 3g/4g to optical and quantum wireless[J]. Proceedings of the IEEE, 2012, 100(Special Centennial Issue): 1853-1888.
[16]Imre S. Quantum communications: Explained for communication engineers[J]. IEEE Communications Magazine, 2013, 51(8): 28-35.
[17]Imre S, Balazs F. Quantum computing and communications: an engineering approach[M]. [S.l.]: John Wiley & Sons, 2005.
[18]Imre S. Quantum computing and communications-introduction and challenges[J]. Computers & Electrical Engineering, 2014, 40(1): 134-141.
[19]Imre S, Gyongyosi L. Quantum-assisted and quantum-based solutions in wireless systems[J]. arXiv preprint arXiv: 1206.5996, 2012.
[20]Nielsen M A, Chuang I. Quantum computation and quantum information[Z]. [S.l.]: AAPT, 2002.
[21]余文斌, 郑宝玉, 赵生妹. 多方计算任务的量子通信复杂度[J]. 信号处理, 2014, 30(12): 1473-1478.
Yu Wenbin, Zheng Baoyu, Zhao Shengmei. Quantum Communication Complexity of Multi-Party Computation Task[J]. Journal of Signal Processing, 2014, 30(12): 1473-1478.(in Chinese)
[22]Feynman R P. Simulating physics with computers[J]. International Journal of Theoretical Physics, 1982, 21(6): 467- 488.
[23]Shor P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]∥Proceedings 35th Annual Symposium on Foundations of Computer Science. [S.l.]: Ieee, 1994: 124-134.
[24]Grover L K. A fast quantum mechanical algorithm for database search[J]. arXiv preprint quantph/9605043, 1996.
[25]Boyer M, Brassard G, Høyer P, et al. Tight bounds on quantum searching[J]. Fortschritte der Physik: Progress of Physics, 1998, 46(4-5): 493-505.
[26]Durr C, Hoyer P. A quantum algorithm for finding the minimum[J]. arXiv preprint quantph/9607014, 1996.
[27]Imre S, Bal
zs F. The generalized quantum database search algorithm[J]. Computing, 2004, 73(3): 245-269.
[28]Imre S. Quantum existence testing and its application for finding extreme values in unsorted databases[J]. IEEE Transactions on Computers, 2007, 56(5): 706-710.
[29]Toyama F, Van Dijk W, Nogami Y. Quantum search with certainty based on modified grover algorithms: optimum choice of parameters[J]. Quantum Information Processing, 2013, 12(5): 1897-1914.
[30]Botsinis P, Alanis D, Babar Z, et al. Quantum algorithms for wireless communications[J]. IEEE Communications Surveys & Tutorials, 2018.
[31]Botsinis P, Alanis D, Babar Z, et al. Joint quantum-assisted channel estimation and data detection[J]. IEEE Access, 2016, 4: 7658-7681.
[32]Ye W, Chen W, Guo X, et al. Quantum Search-Aided Multi-User Detection for Sparse Code Multiple Access[J]. IEEE Access, 2019, 7: 52804-52817.
[33]孙健, 张雄伟, 孙新建. 一种新的量子神经网络训练算法[J]. 信号处理, 2011, 27(9): 1306-1312.
Sun Jian, Zhang Xiongwei, Sun Xinjian. A New Quantum Neural Network Training Algorithm[J]. Signal Processing, 2011, 27(9): 1306-1312.(in Chinese)
[34]李飞, 郑宝玉, 赵生妹. 量子神经网络及其应用[D]. 南京邮电大学通信与信息工程学院, 2004.
Li Fei, Zheng Baoyu, Zhao Shengmei. On the Features of Quantum Neuron[D]. Institute of Signal & Information Processing, Nanjing University of Posts and Telecommunications, 2004.(in Chinese)
[35]Imre S, Balzs F. Quantum multi-user detection[C]∥Proc. 1st. Workshop on Wireless Services & Applications, Paris-Evry, France. [S.l.:s.n.], 2001: 147-154.
[36]Imre S, Balzs F. Non-coherent multi-user detection based on quantum search[C]∥2002 IEEE International Conference on Communications. Conference Proceedings. ICC 2002 (Cat. No.02CH37333): volume 1. [S.l.]: IEEE, 2002: 283-287.
[37]Imre S, Balzs F. Performance evaluation of quantum based multi-user detector[C]∥IEEE Seventh International Symposium on Spread Spectrum Techniques and Applications, volume 3. [S.l.]: IEEE, 2002: 722-725.
[38]Imre S, Balazs F. A tight bound for probability of error for quantum counting based multiuser detection[J]. arXiv preprint quant-ph/0205138, 2002.
[39]Zhao S M, Yao J, Zheng B Y. Multiuser detection based on grover’s algorithm[C]∥2006 IEEE International Symposium on Circuits and Systems. [S.l.]: IEEE, 2006: 4735-4738.
[40]Li F, Zhou L, Liu L, et al. A quantum search based signal detection for mimo-ofdm systems[C]∥2011 18th International Conference on Telecommunications. [S.l.]: IEEE, 2011: 276-281.
[41]周立志, 李飞. 基于 Grover 算法的通信系统信号检测[D]. 南京邮电大学通信与信息工程学院, 2010.
Zhou Lizhi, Li Fei. Signal Detection of Communication Systems Based on Grover Algorithm[D]. Institute of Signal & Information Processing, Nanjing University of Posts and Telecommunications, 2010.(in Chinese)
[42]Abdulnabi S H, Taha S M. Grover’s qsa based mc-cdma detector[J]. International Journal of Computer Applications, 2015, 975: 8887.
[43]Botsinis P, Ng S X, Hanzo L. Fixed-complexity quantum-assisted multi-user detection for cdma and sdma[J]. IEEE Transactions on Communications, 2014, 62(3): 990-1000.
[44]Botsinis P, Alanis D, Babar Z, et al. Coherent versus non-coherent quantum-assisted solutions in wireless systems[J]. IEEE Wireless Communications, 2017, 24(6): 144-153.
[45]Botsinis P, Ng S X, Hanzo L. Quantum search algorithms, quantum wireless, and a lowcomplexity maximum likelihood iterative quantum multi-user detector design[J]. IEEE Access, 2013, 1: 94-122.
[46]Botsinis P, Ng S X, Hanzo L. Low-complexity iterative quantum multi-user detection in sdma systems[C]∥2014 IEEE International Conference on Communications (ICC). [S.l.]: IEEE, 2014: 5592-5597.
[47]Botsinis P, Alanis D, Ng S X, et al. Low-complexity soft-output quantum-assisted multiuser detection for direct-sequence spreading and slow subcarrier-hopping aided sdma-ofdm systems[J]. IEEE Access, 2014, 2: 451- 472.
[48]Botsinis P, Alanis D, Babar Z, et al. Iterative quantum-assisted multi-user detection for multicarrier interleave division multiple access systems[J]. IEEE Transactions on Communications, 2015, 63(10): 3713-3727.
[49]Botsinis P, Huo Y, Alanis D, et al. Quantum search-aided multi-user detection of idma-assisted multi-layered video streaming[J]. IEEE Access, 2017, 5: 23233-23255.
[50]Botsinis P, Alanis D, Babar Z, et al. Noncoherent quantum multiple symbol differential detection for wireless systems[J]. IEEE Access, 2015, 3: 569-598.
[51]Li F, Xie C, Zheng D, et al. Feedback quantum neuron for multiuser detection[C]∥The 2006 IEEE International Joint Conference on Neural Network Proceedings. [S.l.]: IEEE, 2006: 2967-2971.
[52]李飞, 赵生妹, 郑宝玉. 量子神经网络及其在CDMA多用户检测中的应用[J]. 信号处理, 2005, 21(6): 555-559.
Li Fei, Zhao Shengmei, Zheng Baoyu. Quantum Neural Networks and its application in CDMA Miltiuser Detection[J]. Signal Processing, 2005, 21(6): 555-559.(in Chinese)
[53]Li F, Zhao S, Zheng B. Quantum neural network for cdma multi-user detection[C]∥International Symposium on Neural Networks. [S.l.]: Springer, 2005: 338-342.
[54]Song X, Shi J, Chi Y, et al. Multi-user detection on ds-cdma uwb system using qdpso algorithm[M]∥Advances in Multimedia, Software Engineering and Computing Vol.2. [S.l.]: Springer, 2011: 77- 83.
[55]Alanis D, Botsinis P, Babar Z, et al. Non-dominated quantum iterative routing optimization for wireless multihop networks[J]. IEEE Access, 2015, 3: 1704-1728.
[56]Alanis D, Botsinis P, Babar Z, et al. A quantum-search-aided dynamic programming framework for pareto optimal routing in wireless multihop networks[J]. IEEE Transactions on Communications, 2018, 66(8): 3485-3500.
[57]Alanis D, Botsinis P, Ng S X, et al. Quantum-assisted routing optimization for self-organizing networks[J]. IEEE Access, 2014, 2: 614- 632.
[58]Botsinis P, Alanis D, Feng S, et al. Quantum-assisted indoor localization for uplink mm-wave and downlink visible light communication systems[J]. IEEE Access, 2017, 5: 23327-23351.
[59]Botsinis P, Alanis D, Babar Z, et al. Quantum-aided multi-user transmission in non-orthogonal multiple access systems[J]. IEEE Access, 2016, 4: 7402-7424.
[60]毛二可, 曾涛, 胡程, 等. 基于地球同步轨道合成孔径雷达的双基地探测系统: 概念及潜力[J]. 信号处理, 2013, 29(3): 285-292.
Mao Erke, Zeng Tao, Hu Cheng, et al. Bistatic detection based on Geosynchronous SAR: Concept and Potentiality[J]. Journal of Signal Processing, 2013, 29(3): 285-292.(in Chinese)
[61]Mao Erke, Long Teng, Zeng Tao, et al. State-of-art of Geosynchronous SAR[J]. Signal Processing, 2012, 28(4): 451- 462.
