1 引言
无线传感器网络[1-2]是由大量空间分布的传感器节点组成的分布式网络系统,能够协同地实时监测、感知和采集网络区域中各种环境信息,在环境监测、军事国防和目标跟踪等领域有着重要的意义和广阔的应用前景。基于不同传感器节点的测量值,实现对感兴趣物理量未知参数的准确估计是无线传感器网络的一个重要应用。在传感器网络中,每个传感器节点通常具有有限的计算、通信和存储能力[3- 4],传感器网络所使用节点的性能不同,成本也不同。近年来,基于二值传感器网络的理论与应用研究获得了广泛的关注,该网络中的每个节点只能提供低精度的1比特测量值,与能够提供模拟测量值(无限精度)的传感器相比,二值传感器有较低的使用成本。如何从二值传感器网络的1比特测量中获得较好的参数估计性能是一个值得研究的问题。
另一方面,在传感器网络中,集中式和分布式是两类主要的信号处理方式。根据传感器节点的协作方式,分布式信号处理又分为增量式和扩散式等[5]。相对于集中式的信号处理方法,分布式方法不需要强大的计算与存储中心,并且具有更好的鲁棒性,因此得到了较广泛的研究,近年来提出了大量的分布式信号参数估计算法,如分布式稀疏估计算法[6-9]、权重自适应的分布式估计算法[10]、基于删失回归模型的分布式算法[11]等等,我们在这方面也有部分研究成果,如[6,11]。然而,值得注意的是,这些算法并非基于传感器网络的1比特测量。基于1比特测量,目前有许多关于标量参数的估计算法[12-13],在这些算法中,每个1比特测量值被建模为一个比较器的输出,输入为受加性噪声干扰的未知标量参数。此外,基于1比特测量的矢量参数估计算法也有不少文献报道,如1比特线性回归[14-15],1比特系统辨识[16]和1比特压缩感知[17-18]等等。这些现有的算法都有其各自的优点,但值得注意的是,大部分这些算法都是基于批处理的,而非自适应在线估计。相对于批处理算法,自适应算法具有较低的复杂性和存储要求,并且能够适应慢变参数的估计。尽管文献[19]提出了一种具有1比特自适应滤波方法,但该算法没有考虑测量噪声,并且正如[15]中所指出的那样,在存在噪声的情况下,该算法不能保证收敛。另外,在目前提出的1比特参数估计算法中,大多数算法没有考虑待估计参数的稀疏性。稀疏性是自然界中的许多信号(包括人造信号)的本质特征,充分利用这一稀疏性能够有效提高参数估计的精度和鲁棒性。
鉴于目前提出的传感器网络1比特参数估计算法的缺点,本文推导了一种新的基于二值传感器网络1比特测量的分布式稀疏自适应LMS参数估计算法。该算法采用稀疏惩罚最大似然优化,并结合期望最大化和最小均方(LMS)方法,获得稀疏信号的在线估计。新提出的算法放宽了许多现有算法中涉及的一些假设要求,如量化器的输入不含噪声[17-18]、模型中使用的量化阈值为零[15]等等。通过一系列的仿真实验表明,尽管只采用1比特测量,提出的算法仍具有较好的收敛性,且能够获得与采用非1比特测量(模拟测量)的同类算法相近的估计误差。
2 传感器网络模型和问题描述
2.1 二值传感器网络信号参数估计模型
考虑一个由N个节点构成的二值传感器网络,如图1。每个节点k在每个时刻i能够获得某一感兴趣信号yk,i的二进制测量值dk,i:
dk,i=sign(yk,i)∈{-1,1},其中
(1)
式(1)中,νk,i表示节点的测量噪声,并假设νk,i是方差为
的零均值高斯过程,uk,i为信号模型的输入矢量,并独立于νk,i,sign(x)为符号函数,当x>0时,sign(x)=1,当x≤0时,sign(x)=-1。该网络的目的是,通过这些分布式节点采集到的有关yk,i的二进制测量值dk,i,获得对未知参数w0的准确估计,在本文中,我们考虑w0是一稀疏矢量。
此外,在二值传感器网络中,连接到节点k的节点集(包括k本身)由Nk表示,称为节点k的邻域。连接到节点k的节点数(包括k本身)称为节点k的度(即Nk的基数),并由nk表示。每个节点只被允许与其邻居节点合作。如图1所示,节点k的邻域为Nk={1,2,k,l},节点k的度为nk=4。
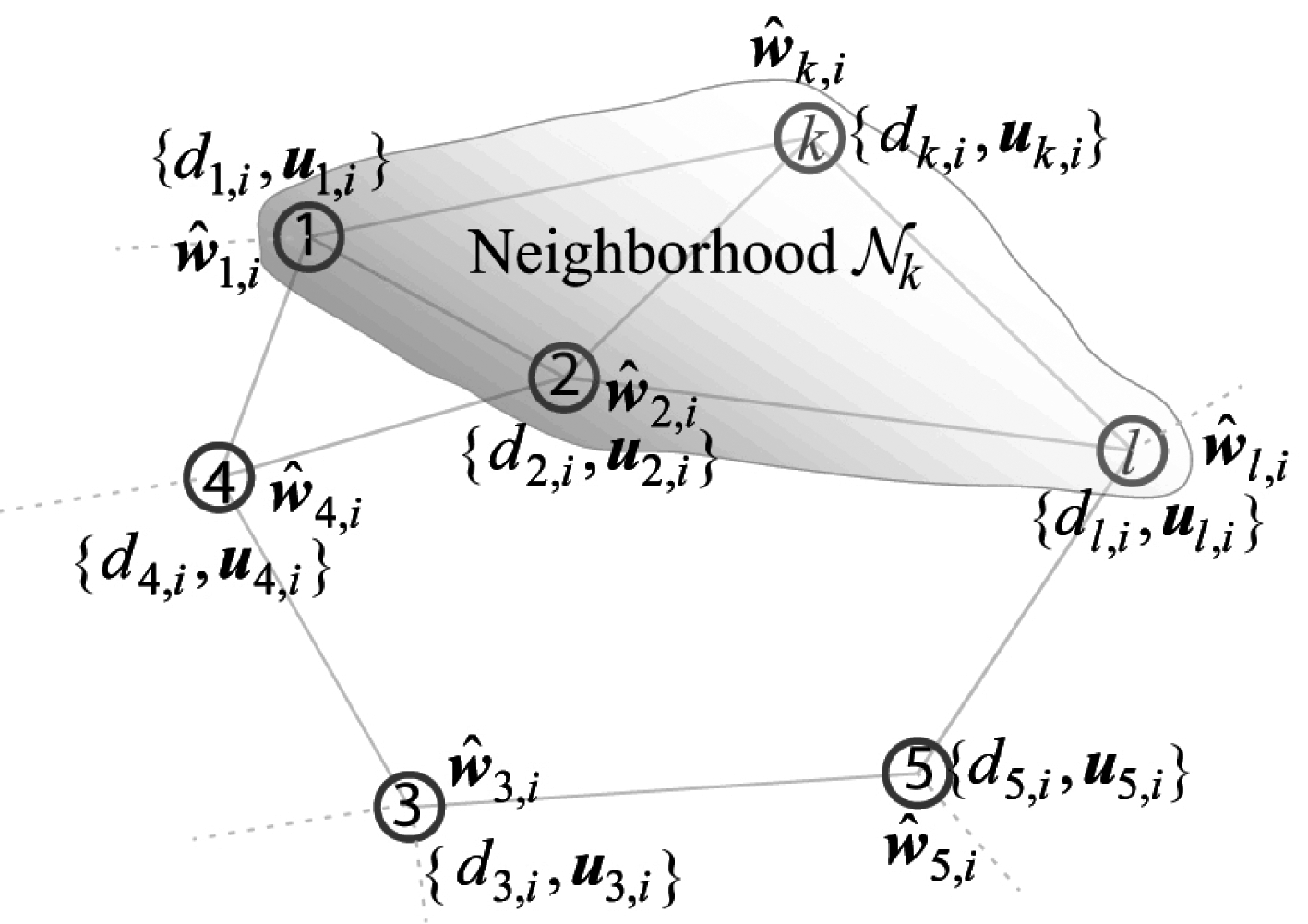
图1 分布式二值传感器网络
Fig.1 Distributed binary sensor network
2.2 问题描述
基于该二值传感器网络,我们考虑采用分布式处理的方式获得稀疏参数w0的估计
每个节点k首先使用各自的测量数据{dk,i,uk,i},生成各自的局部估计
然后通过信息交换得到其邻居节点的局部估计
∈Nk},根据以下规则更新
(2)
其中c,k为加权系数并满足以下公式:
且当∉Nk时c,k=0
(3)
考虑到矢量w0是稀疏的,我们可以在代价函数中引入稀疏约束项作为零吸引因子,迭代的每一步都吸引估计值向零值靠近,可以显著加快算法的收敛速度和减小估计误差。最常用的稀疏约束项是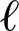0、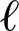1 范数,以及加权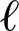p范数等[20-21]。根据这一思想,并正如文献[18]一样,考虑局部优化问题:
(4)
并采用分布式LMS算法可以得到:
(5)
其中μ表示步长参数,用于控制梯度下降的步长,ρ和ε为平衡因子,控制着零吸引因子对代价函数的影响。然而,上述分布式稀疏LMS算法忽略了测量值dk,i只是yk,i的1比特采样,因此无法获得有效的参数估计。自然地,文献[18]替代(4),考虑如下的优化问题:
(6)
并用S形联系函数
代替符号函数sign(x)。在这种情况下,分布式LMS算法变为:
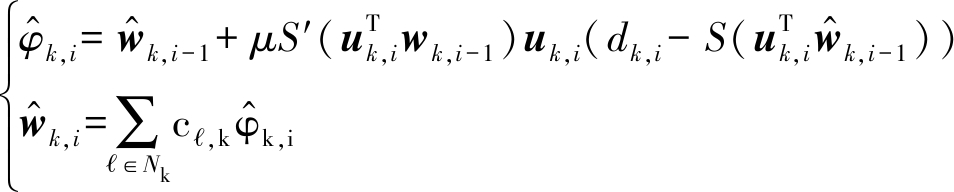
(7)
然而,这种替代算法需要非常小的步长,收敛速度也非常慢。
3 1-Bit分布式稀疏LMS算法
为了克服现有算法的缺点,在本节中,我们将推导一种新的1比特分布式稀疏参数估计算法。该算法的基本思想为:由于测量值dk,i是yk,i的1比特采样,因此我们可以将yk,i视作系统中的隐变量,采用期望最大(EM)思想对含隐变量的问题进行迭代求解,并推导出了在给定当前参数估计
和当前数据{dk,i,uk,i}的情况下yk,i的期望值的计算公式,最后利用梯度下降的方法实现对稀疏矢量的估计。
3.1 最大似然估计
考虑最大似然估计问题:
(8)
对于每个节点k,噪声νk,i为方差为
的零均值白高斯过程,可知概率密度函数满足
因此上述最大似然估计问题等同于以下惩罚最小均方问题:
(9)
由于系统采用的1比特测量,因此测量值为{dk,i}而不是{yk,i},因此很难直接找到(9)或(8)的解。在(1)中,我们注意到dk,i与w0相关,而条件概率p(dk,i|yk,i)则不依赖于w0。然而,
(10)
表明问题(8)也等同于:
(11)
因此,由于问题(8)难以解决,我们将它转换成了问题(11)。接下来,我们将采用期望最大化(EM)算法来解决(11)。
3.2 EM算法
为了解决问题(11),EM算法通过交替的两个步骤产生一个估计序列。在第一步,即E步,我们计算对数似然函数
在给定当前参数估计
和当前数据{dk,i,uk,i}的情况下相对于yk,i的期望值。在第二步,即M步,通过使yk,i的期望值最大化来更新关于参数w的估计
具体过程如下:
E步:
其中Ey[·]表示关于yk,i的期望。
M步:
在E步中,依据(8),(9)和(11)之间的等价关系以及公式(10)可以得到:
(12)
其中
是yk,i的条件期望并被定义为:
(13)
因此,M步可推出如下形式:
(14)
其中:
(15)
此外,可以通过梯度下降过程求解
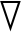
(16)
其中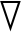
是的梯度:
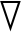
(17)
利用扩散合作策略组合上述EM算法,得到基于以下框架的1-Bit分布式稀疏LMS算法:
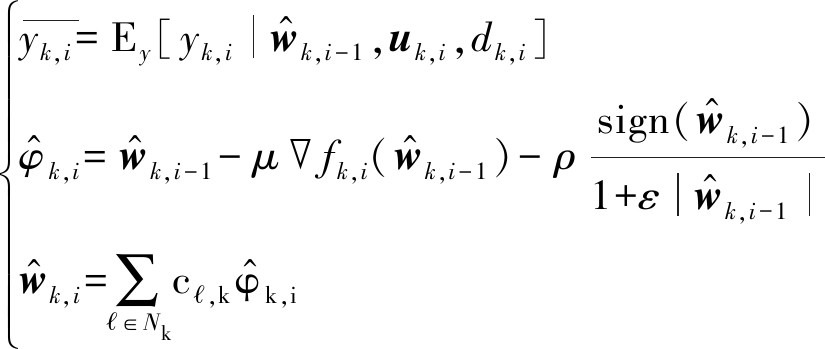
(18)
在(18)中,
可以被视为yk,i的替代输出,将在下一小节讨论。
3.3 计算替代输出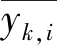
为了计算替代输出
我们知道dk,i=-1 和dk,i=1是一对互补事件,且分别等效于yk,i≤0和yk,i>0。因此,根据
的定义和模型(1),我们得到:
(19)
为了继续讨论问题,我们先介绍以下引理[22]:
引理:给定具有标准正态分布的随机数υ和一个常数a,有如下公式
(20a)
(20b)
其中φ(·)表示标准正态分布的概率密度函数,Φ(·)表示分布函数,
根据(20a)和(20b),我们可以得到:
E[υ|υ≤a]=-E[-υ|-υ>-a]=-Ω(a)
E[υ2|υ≤a]=E[(-υ)2|-υ>-a]=1-aΩ(a)。
使用该引理,并注意到
我们可以得出:
(21)
同理:
(22)
组合(21)和(22),我们得到条件期望为:
(23)
由此,我们得到1-Bit分布式稀疏LMS算法:
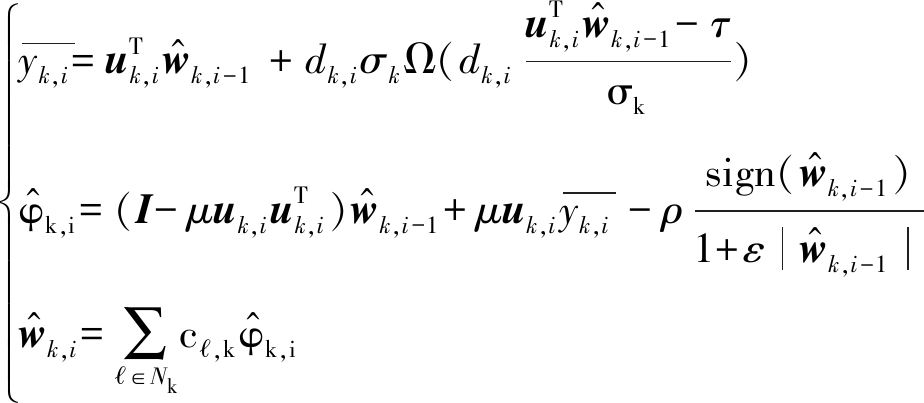
(24)
可以看出,假如
我们提出的1-Bit分布式稀疏LMS算法(24)等同于分布式稀疏LMS算法[7]。
4 性能仿真
在这一节中,我们将通过MATLAB仿真实验来验证我们提出的1-Bit分布式稀疏LMS算法的性能,并与标准的分布式LMS算法[7]以及非稀疏的1-Bit分布式LMS算法进行比较。假设二值传感器网络包含N=20个节点(如图2),随机分布在10×10的面积区域,并且节点间的通信距离为2.5,各个节点噪声方差如图3。待估计的未知真实参数是一个长度为M=16的矢量,且仅仅包含2个非零参数,具有较明显的稀疏性
的初始值
设置为一个16×1且值全为0.001的向量。步长μ取0.02, 阈值τ取0。定义节点k对应的稳态均方误差(MSD)为:
(这里,i取算法达到稳定状态的值),并定义网络的瞬态平均MSD为:
以下所有的仿真结果是通过200次重复试验获得的。
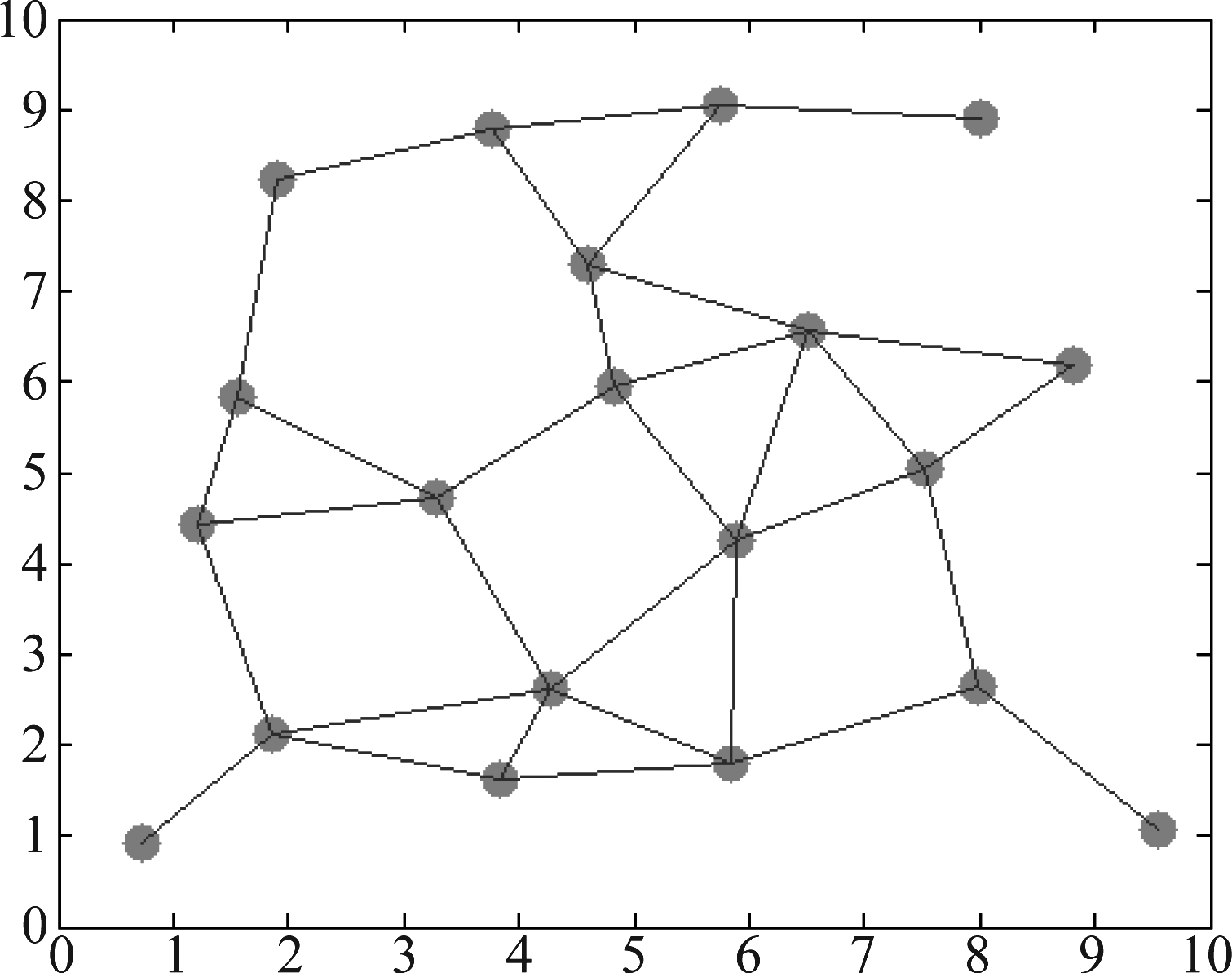
图2 网络拓扑结构
Fig.2 Network Topology
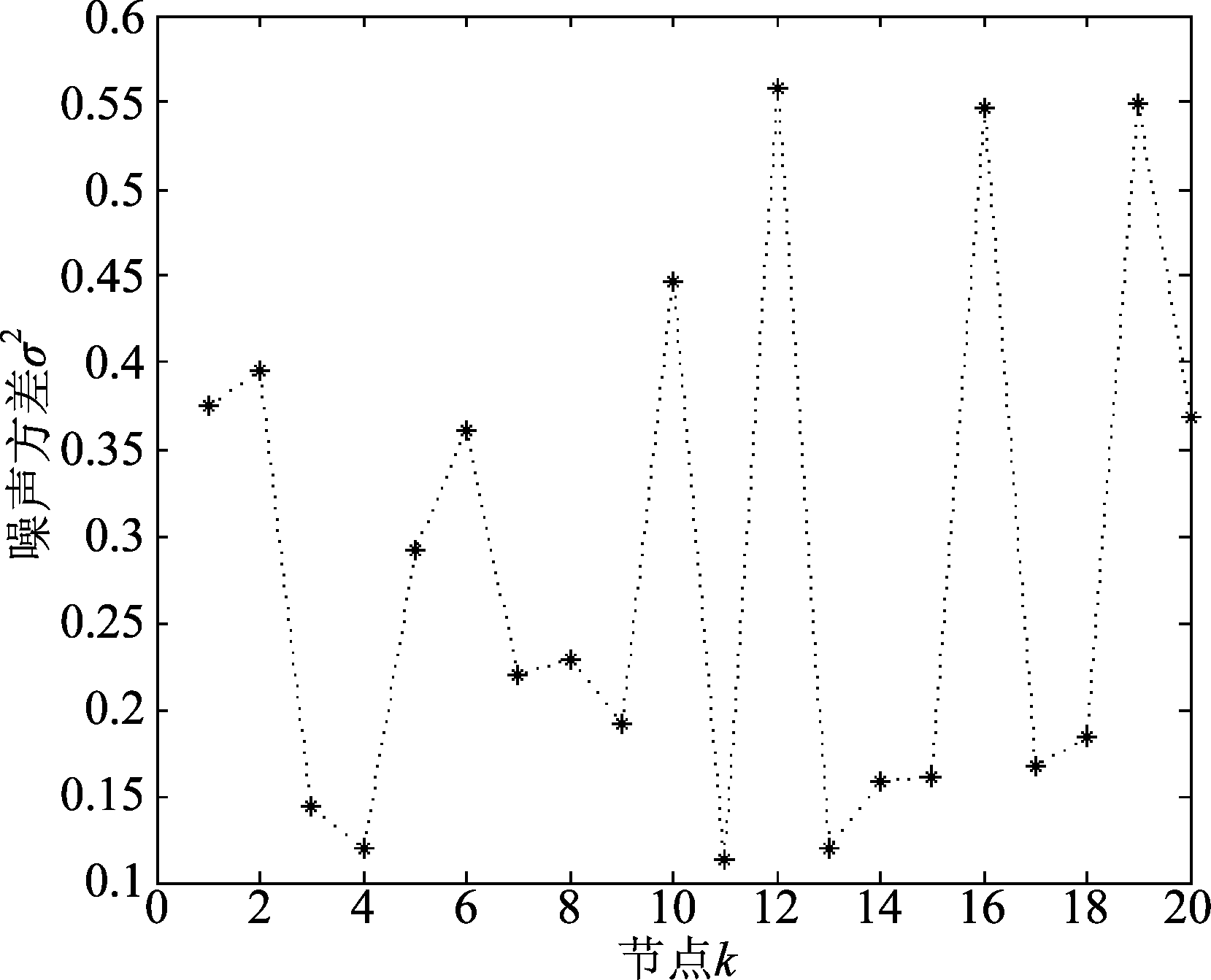
图3 各个节点的输入噪声方差
Fig.3 Input noise variance of each node
图4给出了几种算法(1-Bit分布式LMS、1-Bit集中式 LMS、传统分布式LMS和传统集中式LMS)的瞬态MSD与时间i的关系；图5进一步给出了这四种算法的稳态MSD。四种算法均未引入稀疏约束,从图中可以看到采用非1比特测量的传统分布式LMS算法相比采用1比特测量的算法更早的收敛,随着迭代次数的增加,最终采用1比特测量的算法与采用非1比特测量的算法达到基本相同的估计误差,因此尽管只采用了1比特测量,但新提出的算法仍具有良好的收敛性和较低的估计误差。此外,我们还加入了两种分布式算法对应的集中式算法进行比较,从结果中我们也可以注意到,1比特测量的集中式算法相比两种分布式算法有着更优误差表现,而非1比特测量集中式算法则有着更低的均方偏差。虽然仿真中显示集中式策略有着更低的估计误差,但实际应用中的鲁棒性较差,不如分布式策略。
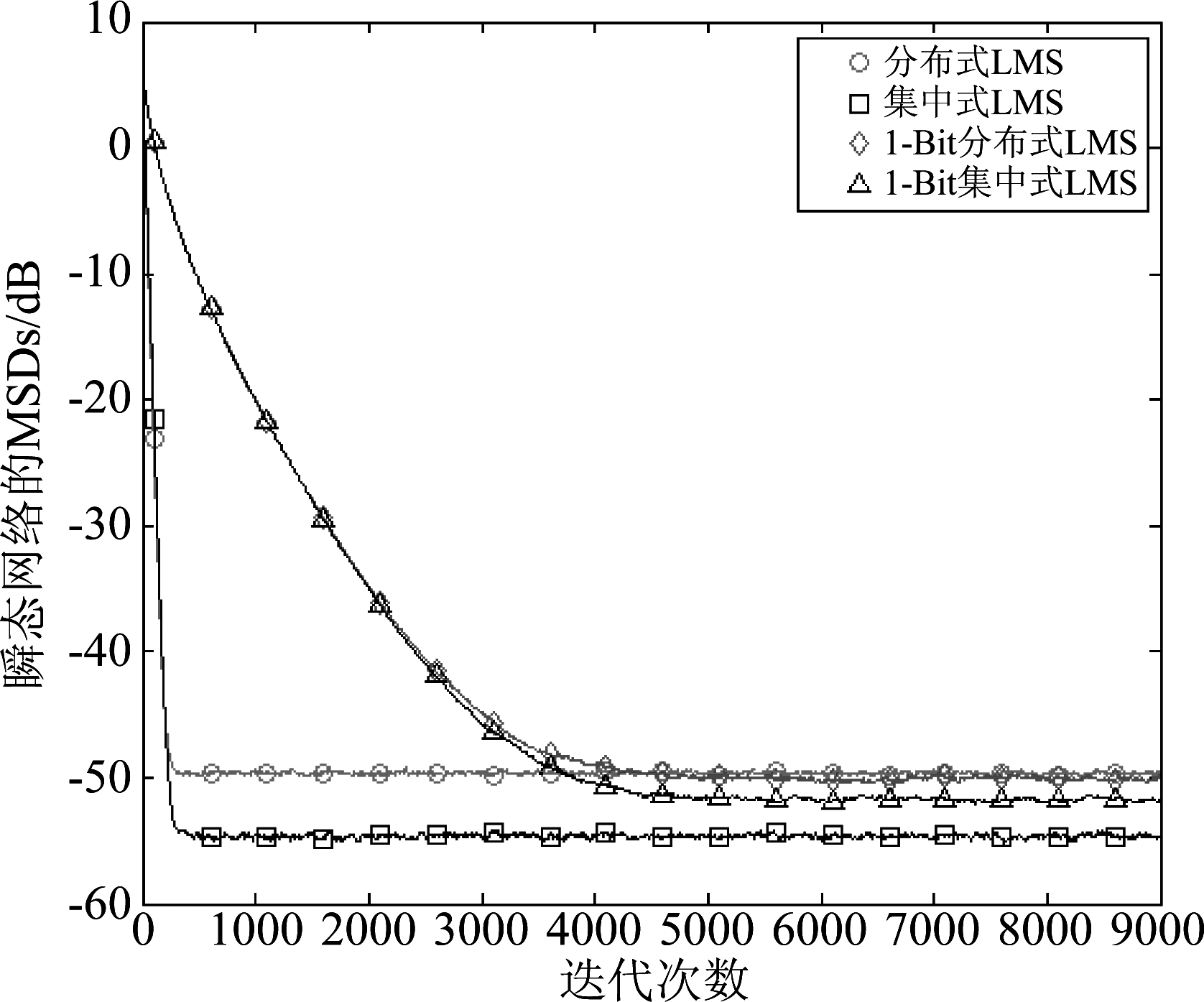
图4 瞬态网络平均MSD与时间i:1-Bit 分布式/集中式LMS与传统分布式/集中式LMS
Fig.4 Transient network average MSD and time i: 1-Bit distributed/centralized LMS and traditional distributed/centralized LMS
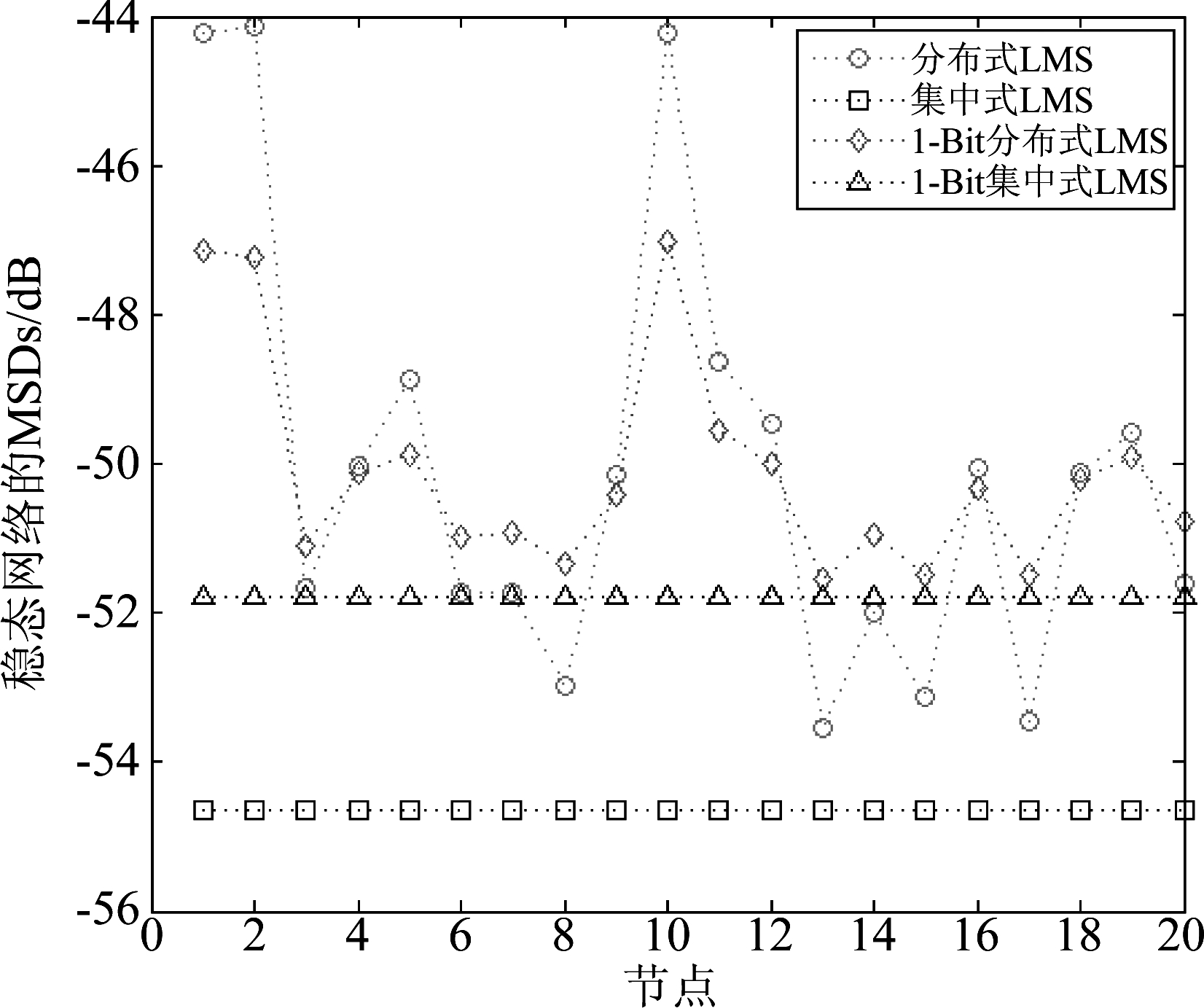
图5 稳定状态时各个节点的MSD:1-Bit 分布式/集中式 LMS与传统分布式/集中式LMS
Fig.5 MSD of each node in steady state: 1-Bit distributed/centralized LMS and traditional distributed/centralized LMS
图6对比了未引入稀疏约束项与引入了稀疏约束项的四种算法(1-Bit分布式LMS、1-Bit集中式 LMS、1-Bit分布式稀疏LMS和1-Bit集中式稀疏LMS)的瞬态MSD；图7则给出了这四种算法的稳态MSD。其中1-Bit分布式稀疏LMS与1-Bit集中式稀疏LMS引入了稀疏约束项,约束因子ρ和ε分别取0.00015和20,从图中可以看到与没有引入稀疏约束项的算法相比,引入稀疏约束项的算法在稳态误差方面有着更好的表现。此外,我们同样加入了两种分布式算法对应的集中式算法进行比较,仿真结论与之前相同。
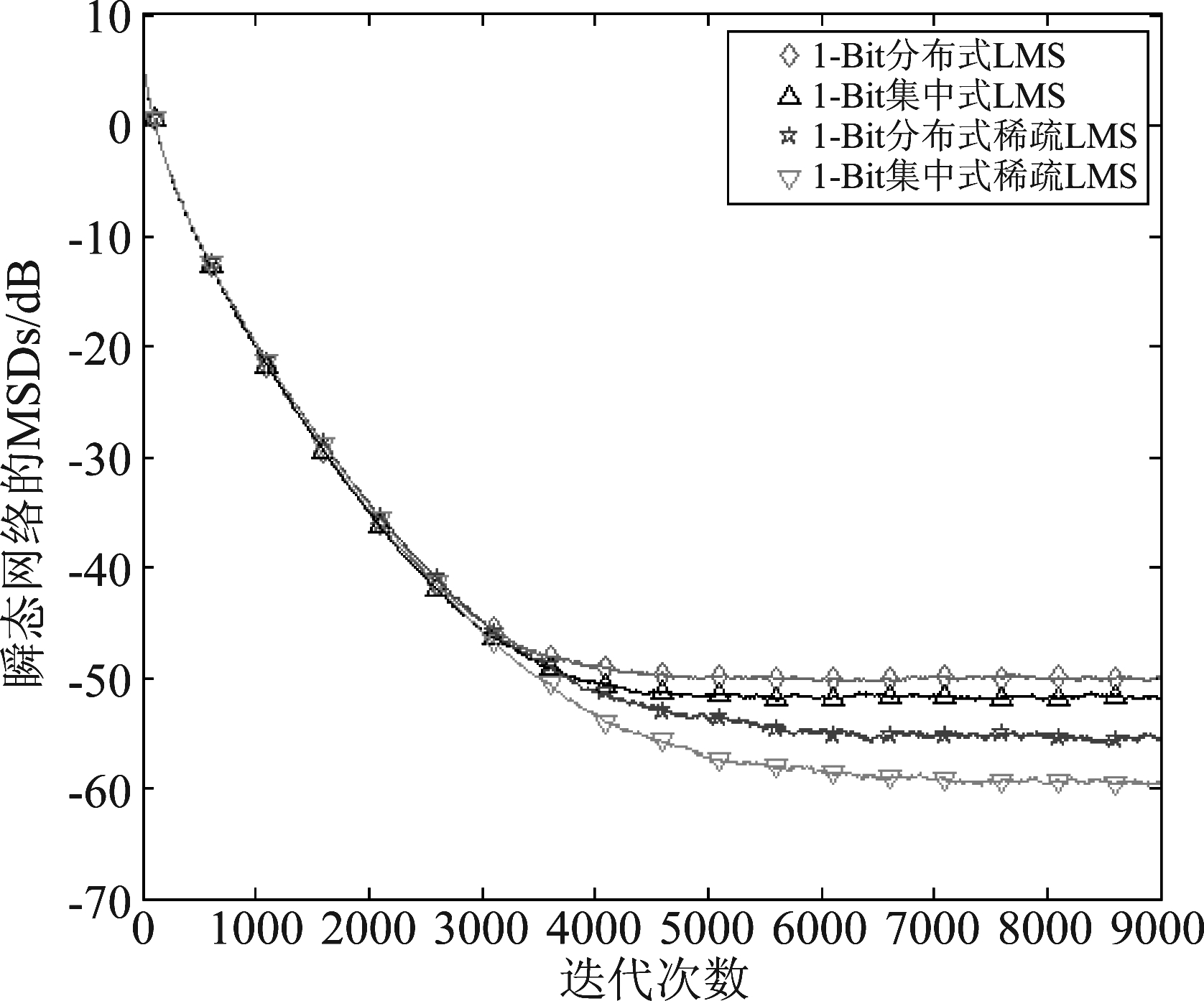
图6 瞬态网络平均MSD与时间i:1-Bit 分布式/集中式 LMS与1-Bit分布式/集中式稀疏LMS
Fig.6 Transient network average MSD and time i: 1-Bit distributed/centralized LMS and 1-Bit distributed/centralized sparse LMS
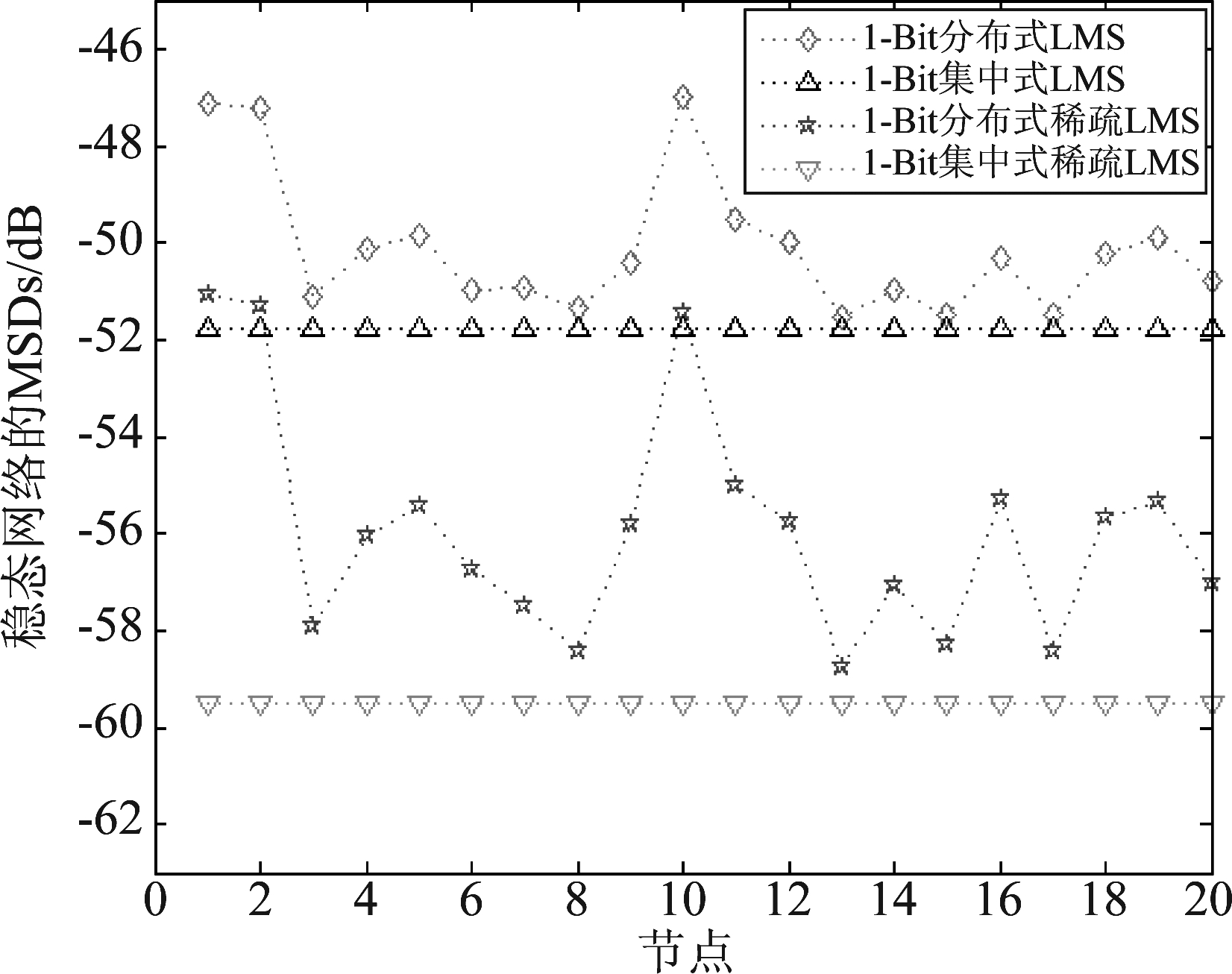
图7 稳定状态时各个节点的MSD:1-Bit 分布式/集中式 LMS与1-Bit分布式/集中式稀疏LMS
Fig.7 MSD of each node in steady state: 1-Bit distributed/centralized LMS and 1-Bit distributed/centralized sparse LMS
5 结论
本文在分析传统的基于传感器网络分布式LMS参数估计算法的基础上,考虑一种采用低成本二值传感器网络的分布式参数估计问题,提出了1比特分布式稀疏LMS算法。该算法基于稀疏惩罚最大似然优化,并结合期望最大(EM)和最小均方(LMS)思想,能够使用1比特测量值获得较好的参数估计性能。仿真实验表明,尽管只采用1比特的测量信号,提出的1比特分布式稀疏LMS算法仍具有良好的收敛性,并且在稳定状态时的均方误差与传统分布式稀疏LMS算法相当。此外,由于对信号进行了1比特的采样,只保留其符号信息,因此算法本身就具有较好的鲁棒性和实用性。
[1] 孙利民. 无线传感网络[M]. 北京: 清华大学出版社, 2005.
Sun Limin. Wireless sensor network[M].Beijing: Tsinghua University Press, 2005.(in Chinese)
[2] Ma L, Wang Z, Lam H, et al.Distributed Event-Based Set-Membership Filtering for a Class of Nonlinear Systems with Sensor Saturations Over Sensor Networks[J].IEEE Transactions On Signal Processing, 2017, 47(11): 3892-3905.
[3] 康莉, 谢维信, 黄建军, 等. 无线传感器网络中的分布式压缩感知技术[J]. 信号处理, 2013, 29(11): 1560-1567.
Kang Li, Xie Weixin, Huang Jianjun, et al.Distributed Compressive Sensing for Wireless Sensor Networks[J]. Journal of Signal Processing, 2013, 29(11): 1560-1567.(in Chinese)
[4] Maheswari M, Malathi M. Wireless Sensor Networks-A Survey[J]. Imperial Journal of Interdisciplinary Research, 2017, 11(3): 487- 490.
[5] Liu Y, Li L. Distributed Blind Estimation over Sensor Networks[J]. IEEE Access, 2017, 5(99): 18343-18355.
[6] Liu Z, Liu Y, Li C. Distributed Sparse Recursive Least-Squares Over Networks[J]. IEEE Transactions on Signal Processing, 2014, 62(6): 1386-1395.
[7] Liu Y, Li C, Zhang Z. Diffusion Sparse Least-Mean Squares Over Networks[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4480- 4485.
[8] Zheng Z, Liu Z, Huang M. Diffusion least mean square/fourth algorithm for distributed estimation[J]. Signal Processing, 2017, 134: 268-274.
[9] Lorenzo P D, Sayed A H. Sparse Distributed Learning Based on Diffusion Adaptation[J]. IEEE Transactions on Signal Processing, 2013, 61(6): 1419-1433.
[10] Takahashi N, Yamada I, Sayed A H. Diffusion Least-Mean SquaresWith Adaptive Combiners: Formulation and Performance Analysis[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4795- 4810.
[11] Liu Z, Li C, Liu Y. Distributed Censored Regression Over Networks[J]. IEEE Transactions on Signal Processing, 2015, 63(20): 5437-5449.
[12] Zhao W, Chen H F, Tempo R, et al. Recursive Nonparametric Identification of Nonlinear Systems with Adaptive Binary Sensors[J]. IEEE Transactions on Automatic Control, 2017, 62(8): 3959-3971.
[13] Zhu J, Lin X, Blum R S, et al. Parameter Estimation From Quantized Observations in Multiplicative Noise Environments[J]. IEEE Transactions on Signal Processing, 2015, 63(15): 4037- 4050.
[14] Zhu J, Wang X, Lin X, et al. Maximum Likelihood Estimation From Sign Measurements With Sensing Matrix Perturbation[J]. IEEE Transactions on Signal Processing, 2014, 62(15): 3741-3753.
[15] Colinet E, Juillard J. A Weighted Least-Squares Approach to Parameter Estimation Problems Based on Binary Measurements[J]. IEEE Transactions on Automatic Control, 2010, 55(1): 148-152.
[16] Guo J, Wang L Y, Yin G, et al. Identification of Wiener systems with quantized inputs and binary-valued output observations[J].Automatica, 2017, 78(C): 280-286.
[17] Knudson K, Saab R, Ward R. One-Bit Compressive Sensing With Norm Estimation[J]. IEEE Transactions on Information Theory, 2016, 62(5): 2748-2758.
[18] Zayyani H, Korki M, Marvasti F. A Distributed 1-bit Compressed Sensing Algorithm Robust to Impulsive Noise[J]. IEEE Communications Letters, 2016, 20(6): 1132-1135.
[19] Wigren T. Adaptive filtering using quantized output measurements[J]. IEEE Transactions on Signal Processing, 1998, 46(12): 3423-3426.
[20] 金坚, 谷源涛, 梅顺良.用于稀疏系统辨识的零吸引最小均方算法[J]. 清华大学学报: 自然科学版, 2010(10): 1656-1659.
Jin Jian, Gu Yuantao, Mei Shunliang. Adaptive algorithm for sparse system identification: Zero-attracting LMS[J]. Journal of Tsinghua University: Science and Technology, 2010(10): 1656-1659.(in Chinese)
[21] Gu Y, Hero A O. Sparse LMS for system identification[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE Computer Society, 2009: 3125-3128.
[22] Liu Z, Li C. Recursive Least-Squares for Censored Regression[J]. IEEE Transactions on Signal Processing, 2017, 65(6): 1565-1579.
