1 引言
变换域通信系统(transform domain communication system,TDCS)是一种由美国军方提出能够利用频谱空洞进行信息传输的新型认知无线抗干扰通信系统[1- 4]。V.Chakravarthy在WCNC2005会议上提议将TDCS作为认知无线电(Cognitive radio,CR)候选技术[5]。TDCS通过对电磁频谱环境估计,利用幅度谱将信号能量避开干扰所在频段,从而具有很强的抗干扰性能,同时对幅度谱进行伪随机编码,确保了TDCS的基函数具有低截获(Low Probability of Intercept,LPI)和低检测(Low Probability of Detection,LPD)特性,也是迄今为止最符合认知电子战概念的通信方式[6-7]。
幅度谱设计直接决定TDCS的抗干扰性能,目前大多学者关注干扰门限剔除算法的研究,依然采用由“0”、“1”构成的传统二元幅度谱[8-10],但是传统幅度谱一方面,没有充分利用干扰频谱分布信息以增强TDCS抗干扰性能,另一方面任何干扰门限剔除算法,都无法完全彻底的规避干扰频段。文献[11]通过频谱估计得到两个门限阈值(即低门限λ1和高门限λ2),将频谱估计结果大于λ2的幅度谱Ak设置为0,小于λ1的幅度谱Ak设置为1,介于λ1和λ2之间的幅度谱Ak设置为0.5,可见该文献提出了一种三元幅度谱设计方案,相比之下传统二元幅度谱,性能确实有所改善,但是该方法仍然没有足够充分地利用频谱估计所得到的干扰频谱信息,其幅度谱结构设计方案和抗干扰性能有待改进。文献[12]针对频谱失配情况下,在干扰频段进行幅度谱编码,实际上由于将传输信息能量注入到干扰频段而导致TDCS抗干扰性能减弱。分析现有算法,对干扰频谱分布情况考虑较少,误码率未能达到最优结果。针对以上问题,本文将最优化理论[13-15]应用到TDCS幅度谱编码问题中,提出变换域通信系统最优误码率多元幅度谱编码算法,通过理论推导将求解系统最优误码率多元幅度谱编码转换成约束条件多维最优化问题,利用拉格朗日函数设置增广目标函数,迭代求解得出最优误码率多元幅度谱编码,以最大化程度增强TDCS的抗干扰性能。
2 TDCS原理
如图1所示,TDCS首先通过频谱估计对环境采样, 对所估计的干扰信号频谱进行门限判决,与预先设置好的门限值ψth进行比较,如公式(1)所示:
(1)
式(1)中R为干扰频谱幅值。将高于门限值的频段设置为“0”,表示该频段被干扰,不再注入信号能量,低于门限值的频段置设为“1”表示该频点可用,形成一个由“0”,“1”组成的幅度谱Ak。其次将幅度谱Ak如公式(2)所示进行伪随机编码,使基函数具有良好的LPI/LPD性能,实现射频隐身:
Bk=Ak·ejθk,k=1,2,…,N
(2)
经过能量调整后,再经过IFFT变换,得到时域基函数,其离散形式表示为:
(3)
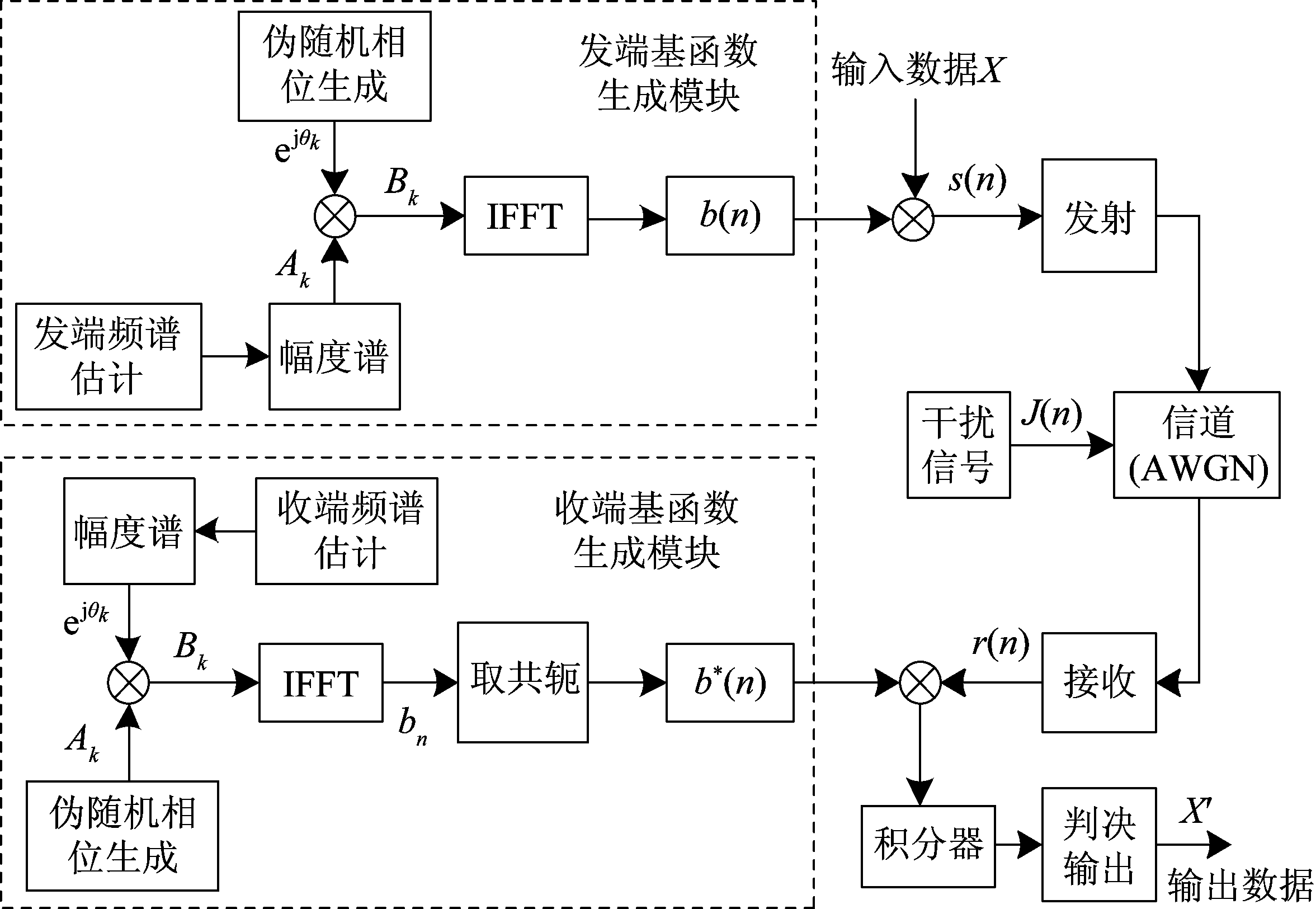
图1 TDCS原理框图
Fig.1 Principle block diagram of TDCS
式(3)中,调整因子
其中N为基函数长度,NA表示可用频谱载波的个数。由于TDCS的基函数具有类噪声特征,因此通常采样循环移位键控(Cyclic Shift Keying,CCSK)调制,基于CCSK调制的TDCS信号波形为:
(4)
其中mi代表了第i个发送信息的十进制数,Mary为CCSK调制阶数。
通过分析不难得出传统二元幅度谱抗干扰性能依赖于门限值ψth的设置,但是任何门限判决算法都无法将干扰完全彻底的检测和剔除。下面将对本文提出的多元幅度谱编码算法进行介绍和分析。
3 设计方案
3.1 抗干扰性能分析
调制后的TDCS信号经过信道到达发射机,接收信号的模型如下:
r(n)=S(n)+J(n)+n0
(5)
式中S(n)为发射信号,J(n)为没有被完全剔除的干扰信号,n0表达高斯白噪声。接收到信号后,进行相关接收后,解调信号为:
z=r(n)×b*(n)=[S(n)+J(n)+n0]×b*(n)
(6)
此时将公式(3)、(4)代入公式(6)可以得到:
z=S(n)×b*(n)+J(n)×b*(n)+
(7)
式(7)中,解调后的信号被分解成信号分量、干扰分量和噪声分量三个部分,因此TDCS接收信号的输出信号干扰噪声比表示为:
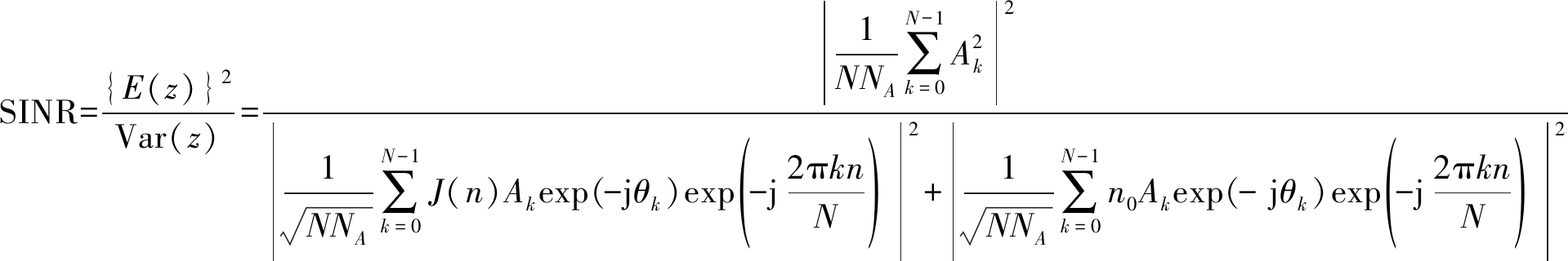
(8)
基于CCSK调制的TDCS误码率表示为[11]:
(9)
式(9)中Q(x)表达是为:
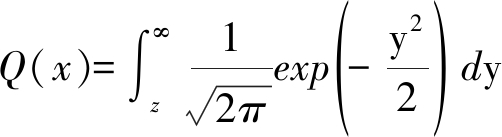
(10)
联合式(8)、(9)、(10)可以得出变换域通信系统误码率、幅度谱和干扰频谱信息的动态关系式。本文重点研究多元幅度谱Ak的编码问题,所做工作应当在有用信号能量
不变情况下完成的,任何改变信号能量以提升或者降低信噪比的情况是不被允许的。在此条件下,从误码率表达式可以得到
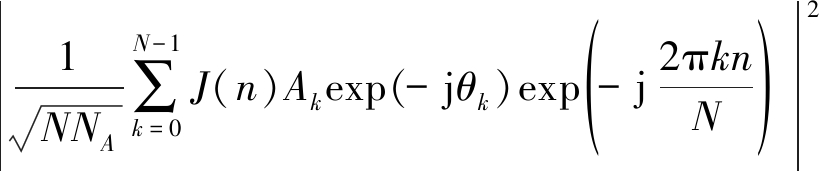
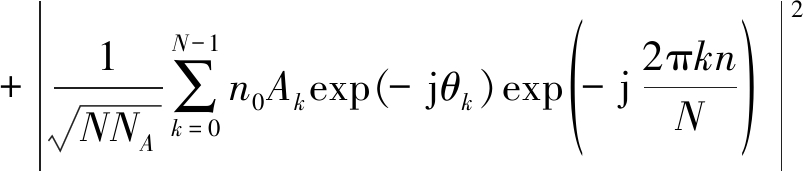
直接反映了TDCS的抗干扰性能,当幅度谱Ak确定之后,相应的TDCS误码率Pber就可以求解出来。
3.2 幅度谱编码方案
实际上在高干信比情况下,噪声对误码率的影响极小,可以忽略不计。因此要想达到最优误码率性能的情况,只需要计算出
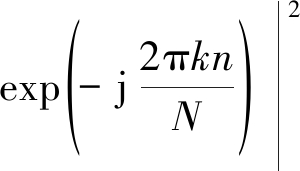的最小值即可。综合以上分析,可以将幅度谱编码问题转化成:
(11)
其中,Dk代表传统二元幅度谱,因为Dk为仅含有0、1的序列,所以只要干扰剔除门限确定, 相应的
值就可以得到,故假设
可以看出本文将TDCS幅度谱编码算法,转换成约束条件多维最优化计算问题。
记可行域
则式(11)的拉格朗日函数为:
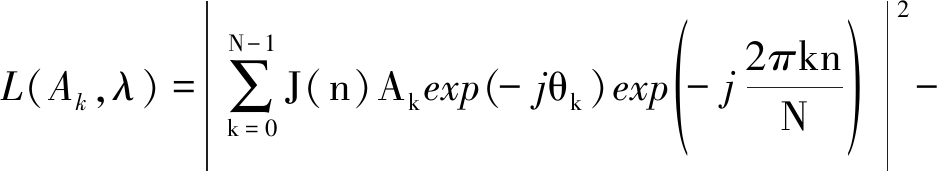
(12)
增广目标函数设置为:
(13)
其中M为惩罚因子,式(13)将式(11)转化成无约束多维优化minψ(Ak,λ,M)问题。假设λ=λ′,可以求出相应的ψ(Ak,λ,M)极值点,通过不断的更新λ和Ak,直到求解出符合要求的λ*和
根据无约束极值必要条件得到:
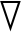Akψ(Ak,λ,M)=0
(14)
根据卡罗需-库恩-塔克(Karush-Kuhn-Tucjer)条件的向量对
可以得到:
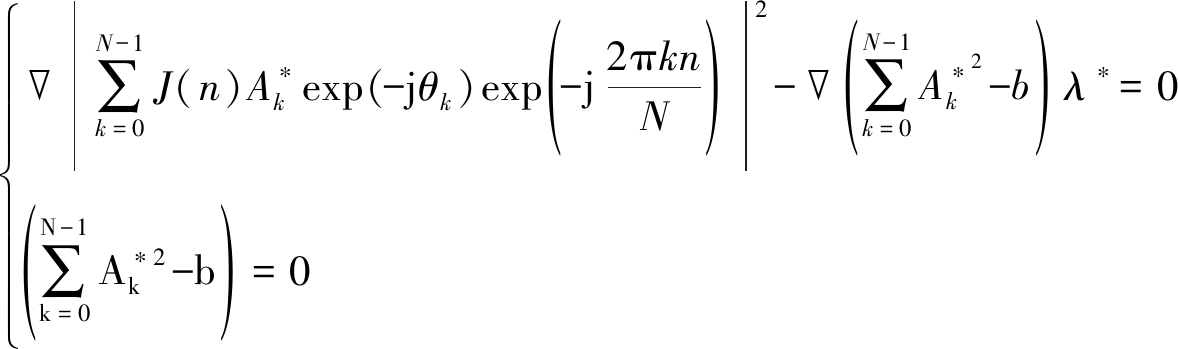
(15)
根据式(14)、(15),将乘子向量更新规则制定为:
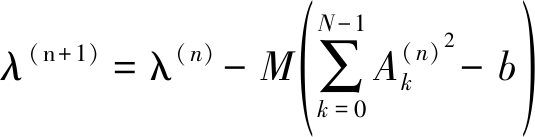
(16)
式(16)可以看出当
趋近与0时,乘子向量λ(n)收敛。
表1 多元幅度谱编码算法
Tab.1 Multiple amplitude spectrum coding algorithm
可见传统二元幅度谱编码算法空间复杂度为O(n),本文所提多元幅度谱编码算法的空间复杂度为O(n2),因此本文所提多元幅度谱编码算法虽然降低系统误码率,但是以增加系统复杂度为代价。不过随着数字处理器的飞速发展,相关硬件的计算能力不断地提升,并且本文所提多元幅度谱编码算法在高干信比情况下抗干扰增益极其明显,进一步提升了TDCS在复杂电磁环境下的通信有效性和可靠性,具有一定的理论价值和工程实践意义。
3.3 相关性分析
TDCS接收机通过对本地基函数取共轭,将其作为参考信号与接收信号进行相关解调,因此导致基函数相关性减弱的幅度谱编码算法会导致信号失真,严重影响系统抗干扰性能。基函数自相关函数定义为:
R(u)=E[b(n)b(n+u)]
(17)
对其υ值进行分类分析,当υ≠0的情况时,由于基函数具有伪随机特性,b(n+u)进行了循环移位,与b(n)几乎不相关,故R(u)≈0；
当υ=0的情况下:
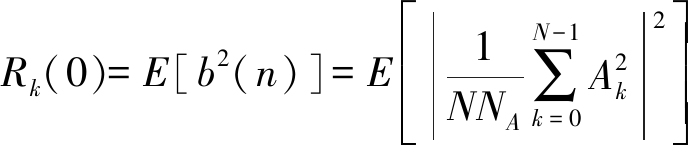
(18)
式中Rk为多元幅度谱编码后的基函数自相关值。又因为:
(19)
将式(19)代入式(18)可以得到:
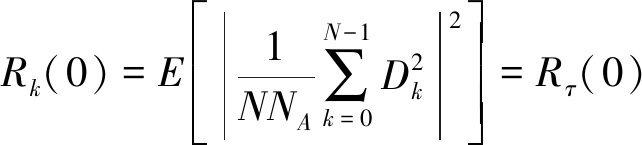
(20)
式中Rτ为传统二元幅度谱编码的基函数自相关值。可以看出多元幅度谱编码不影响基函数的相关特性。
4 仿真验证
仿真参数设置:仿真建立在收发双方电磁环境一致情况,收、发两端基函数相同；信道模型为加性高斯白噪声信道；基函数长度为512 bit；选取本原多项式系数向量为[1 1 1 0 1 1 0 0 1]、移位寄存器初始状态为[0 0 0 0 0 0 0 0 1]的m序列作为伪随机编码序列；调制方式采用CCSK(Mary=2)调制；选取子载波数为64位且频谱幅度值偶对称的干扰,将前32位子载波幅度列出,如表2所示。
表2 初始干扰等效基带频谱幅度
Tab.2 Initial interference equivalent base band spectral amplitude
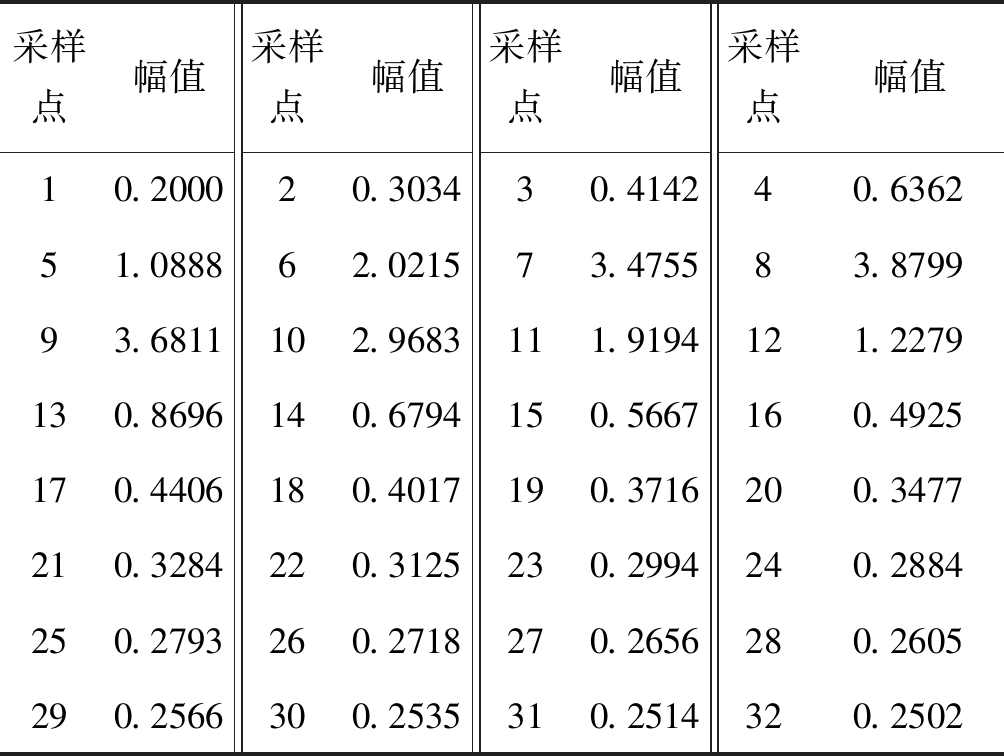
采样点幅值采样点幅值采样点幅值采样点幅值10.200020.303430.414240.636251.088862.021573.475583.879993.6811102.9683111.9194121.2279130.8696140.6794150.5667160.4925170.4406180.4017 190.3716200.3477210.3284220.3125230.2994240.2884250.2793260.2718270.2656280.2605290.2566300.2535310.2514320.2502
根据表1设定初始干扰等效基带频谱幅度,对传统二元幅度谱编码算法和本文提出的多元幅度谱编码算法生成的幅度谱进行比较。由于本文不对干扰门限剔除算法重点研究,故设定门限值ψth=0.4×max(R)[8]。
图2最为直观地表现出本文采用的多元幅度谱编码算法和传统二元幅度谱编码算法之间的区别。可以看出本文提出的多元幅度谱算法充分体现出子载波信道之间的质量差别,有效地考虑干扰的频谱信息,生成的幅度谱值更加丰富,在信道增益大的频段可以分配到更多的功率；反之,给予较小的功率,充分利用较好的频段进行传输信息,以保证有较好的误码率。
图2 干扰信号以及幅度谱频谱幅度值
Fig.2 Amplitude of interference and amplitude spectrum
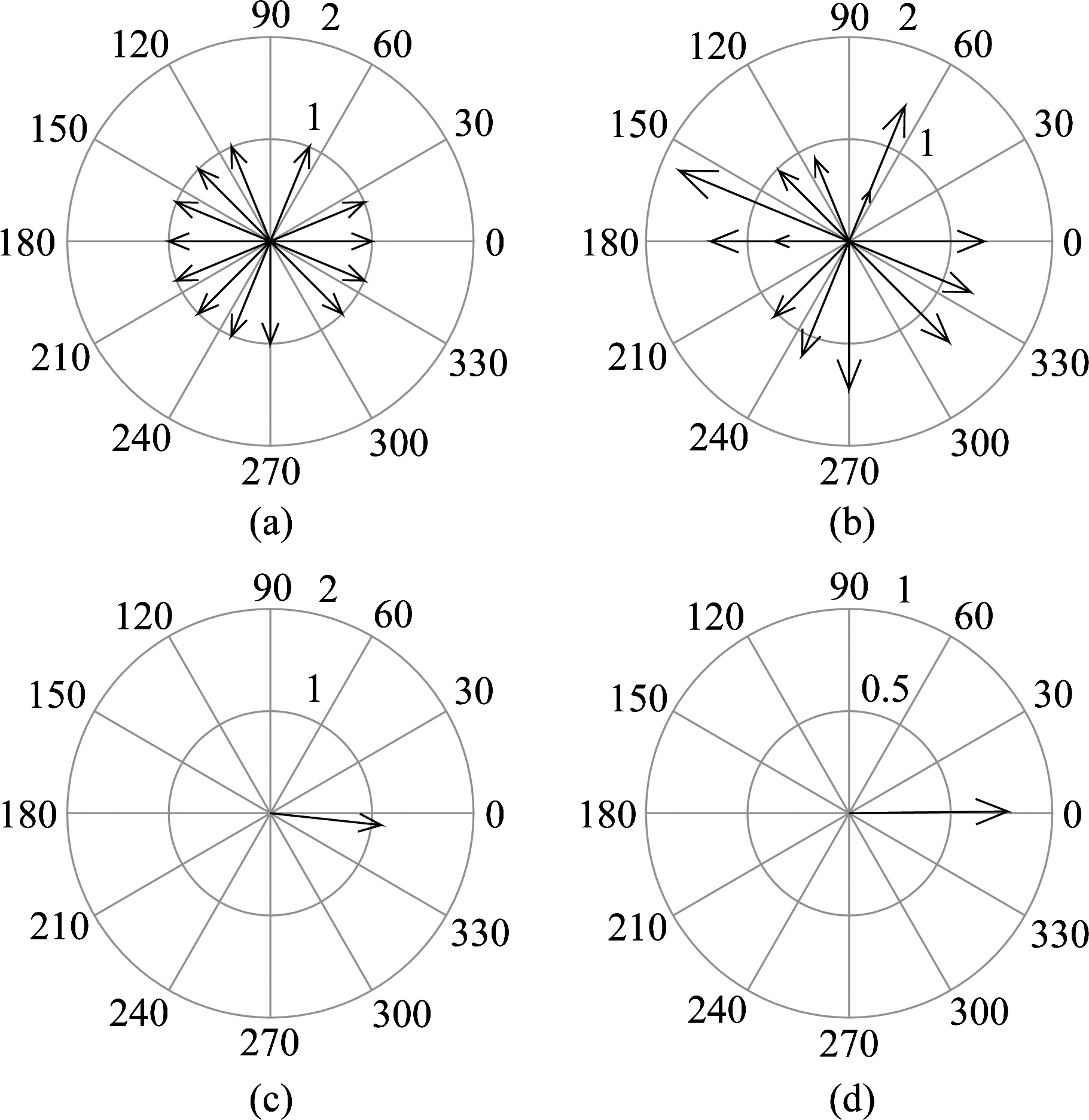
图3 基函数与干扰信号相乘后的序列以及其和的向量图
Fig.3 The sequence of the basis function multiplied by the interference and its sum vector graph
分析式(8)、(9)可以得到,随着基函数与干扰信号相乘之后得到向量和的模值减小,TDCS系统误码率就相应降低,抗干扰性能就会随之提升。图3(a)、(b)分别给出了传统二元幅度谱生成的基函数和本文提出多元幅度谱生成的基函数向量图,可以看出传统二元幅度谱生成的基函数频谱向量图模值大小相同,分布相对均匀,本文提出多元幅度谱生成的基函数频谱向量图模值及其分布变化相对较大。图3(c)、(d)分别给出了传统二元幅度谱生成的基函数和本文提出多元幅度谱生成的基函数与干扰信号相乘得到向量和的模值,可以看出本文提出多元幅度谱算法在误码率性能上优于传统二元幅度谱编码算法。
图4可以看出,本文提出的多元幅度谱编码生成的基函数和传统二元幅度谱生成的基函数在时域上同样具有明显的类噪声特征,具有较好的LPI/LPD性能。
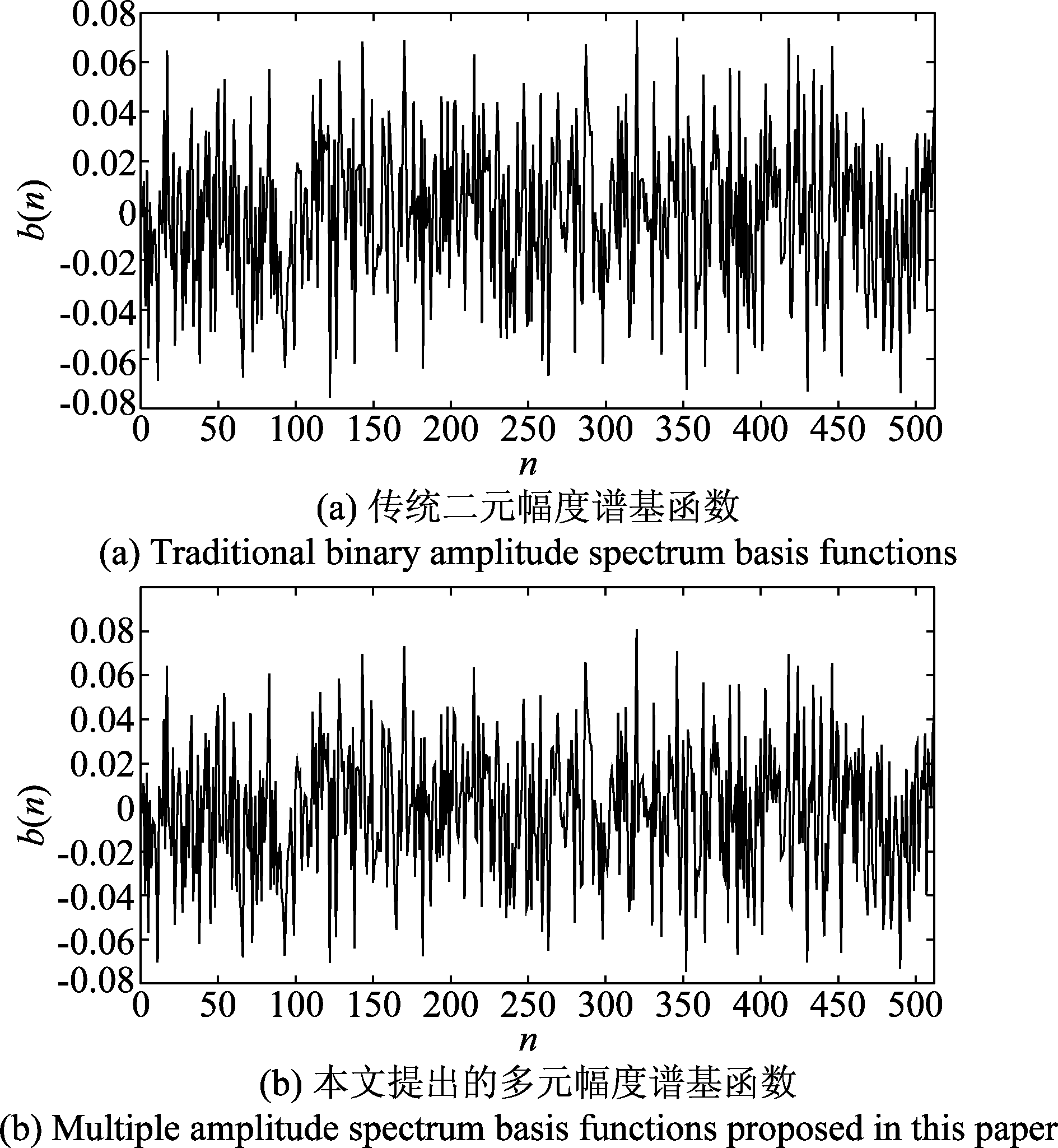
图4 基函数时域图
Fig.4 Time domain diagram of basis functions
为进一步分析论证式(20)的正确性,需要对基函数自相关性进行仿真。图5可以看出,本文提出的多元幅度谱编码并不影响基函数的自相关性,因此不会影响TDCS相关解调,保证算法的抗干扰性能。
TDCS的LPI/LPD性能源于其基函数的类噪声特征,一般意义上认为高斯白噪声服从正态分布(亦称为高斯分布),具有最好的LPI/LPD性能[16]。图6(a)、(b)分别仿真验证了传统二元幅度谱和本文提出多元幅度谱基函数实部和虚部的正态分布概率图。如图6所示,一方面传统二元幅度谱和本文提出的多元幅度谱基函数实部和虚部的采样曲线大致沿各自的正态概率基准线出现,可以认为数据样本服从正态分布；另一方面可以看出,本文所提多元幅度谱算法与传统二元幅度谱编码算法相比,对基函数时域波形的概率分布影响不大,甚至可以忽略。可以认为本文提出多元幅度谱编码算法对TDCS的LPI/LPD性能没有影响。
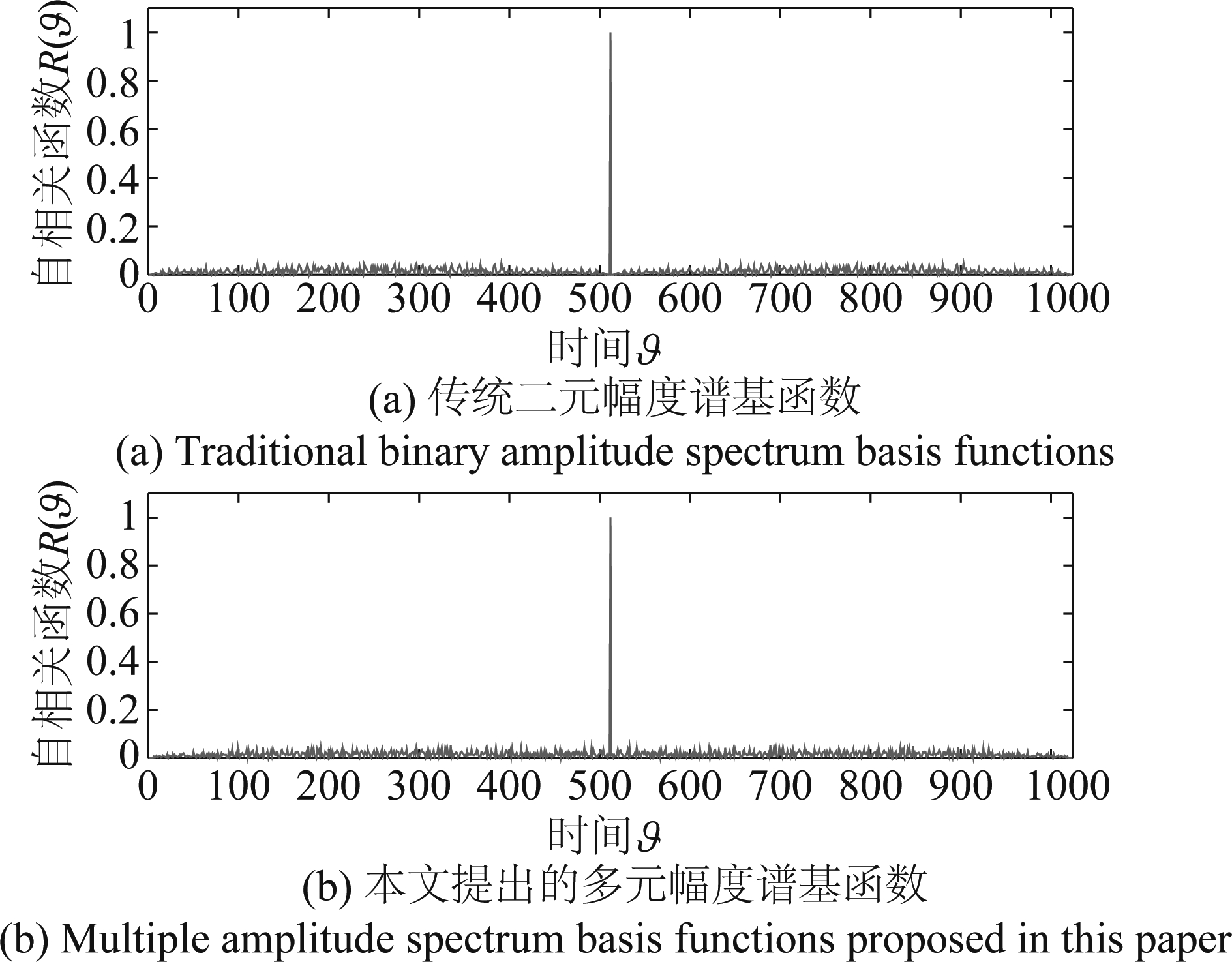
图5 自相关性对比图
Fig.5 Autocorrelation comparison diagram
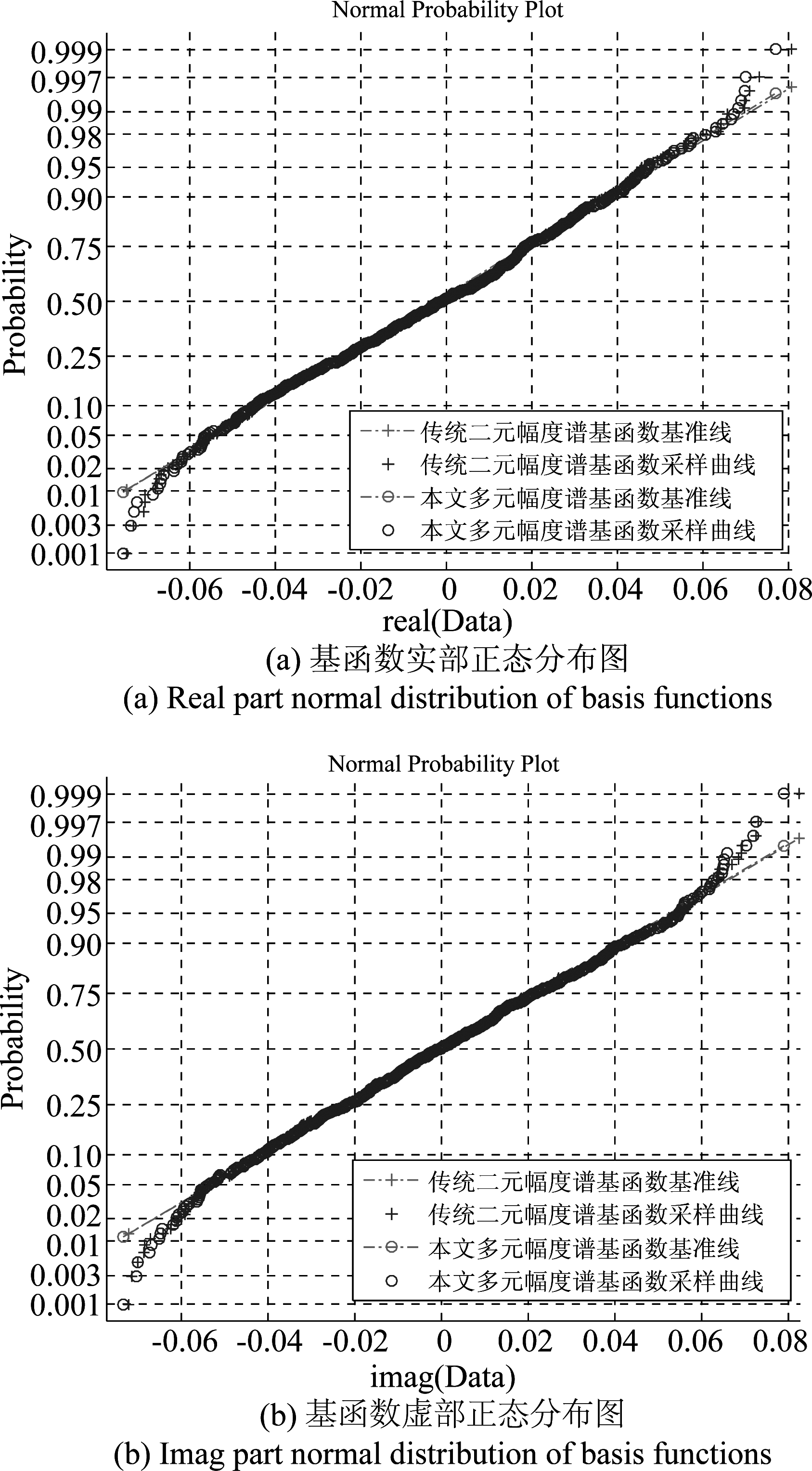
图6 正态分布概率图
Fig.6 Autocorrelation comparison diagram
式(9)可以得到,干信比(JSR)和信噪比(SNR)直接决定TDCS系统误码率。因此有必要对两者和误码率的关系进行仿真分析,图7给出了信噪比分别固定为4 dB、8 dB情况下,干信比和误码率之间的关系。其中理想值为干扰完全剔除的情况下TDCS误码率情况。可以看出在干信比低于15 dB时,干扰能量较少,由于TDCS本身具备一定的扩频增益,所以误码率差距体现并非十分明显。但是随着干信比的不断增大,干扰能量超过系统的干扰容限时,系统误码率迅速恶化。可以明显看出并且本文所提出的多元幅度谱编码算法相比之传统二元幅度谱编码算法抗干扰性能提升约3 dB。
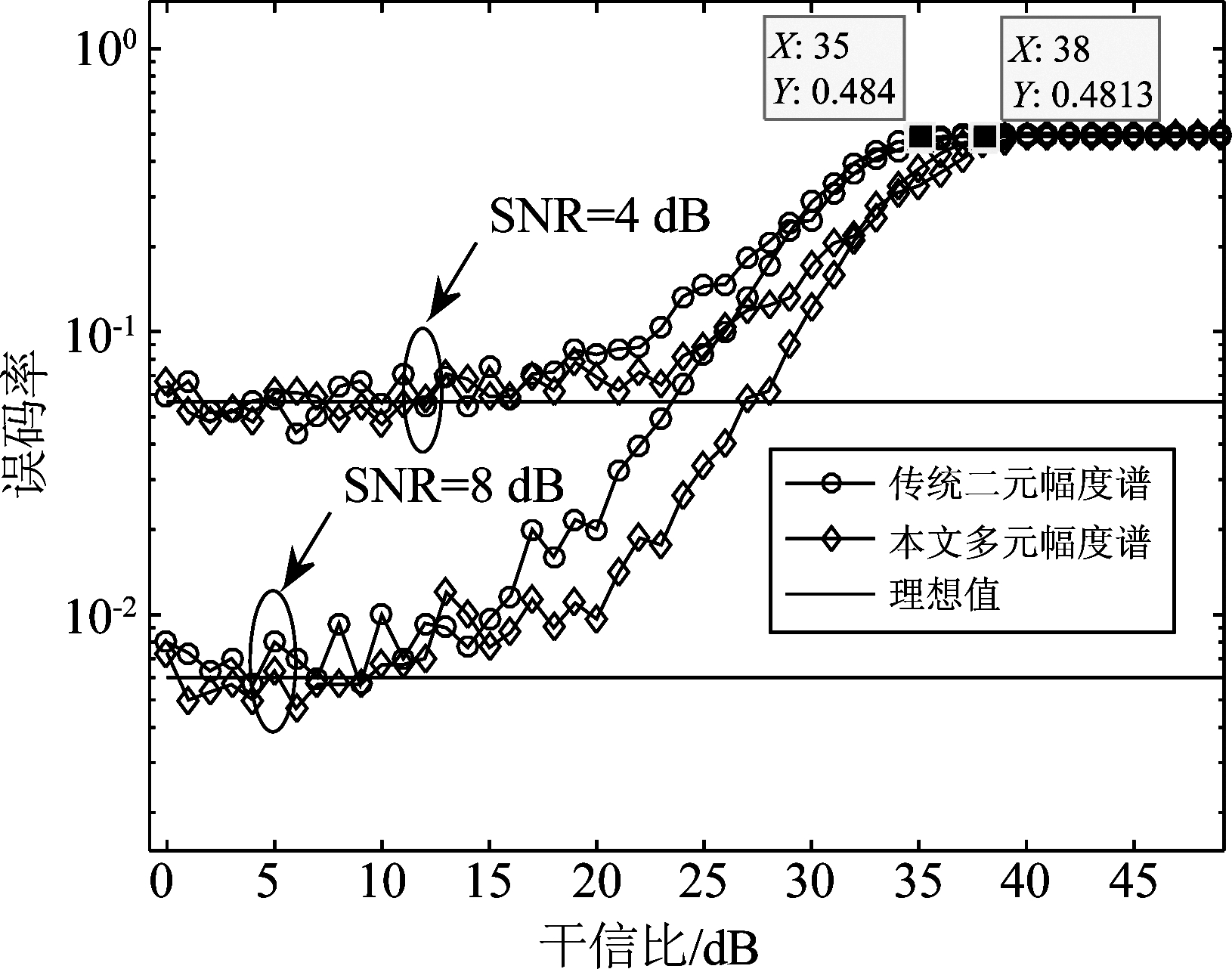
图7 干信比与误码率关系图
Fig.7 Relationship between JSR and bit error rate
图8是干信比分别为35 dB、25 dB、15 dB情况下,信噪比与TDCS系统误码率的关系图。可以看出本文提出的多元幅度谱编码算法与传统二元幅度谱编码算法比较,误码率均有一定的改善,并且随着干扰能量的增大,当干信比为35 dB时,无论信噪比增大到多少,传统二元幅度谱编码算法都无法正常通行,此时TDCS系统误码率性能出现了平底现象,然而多元幅度谱编码算法,可以有效缓解误码率平底现象。与传统二元幅度谱编码算法比较,本文方法在高干信比情况下改善尤其明显。因此本文方法具有更好的误码率性能,提升系统的抗干扰性能,尤其在高干信比情况下,保证发射机和接收机依然能够建立通信链路。
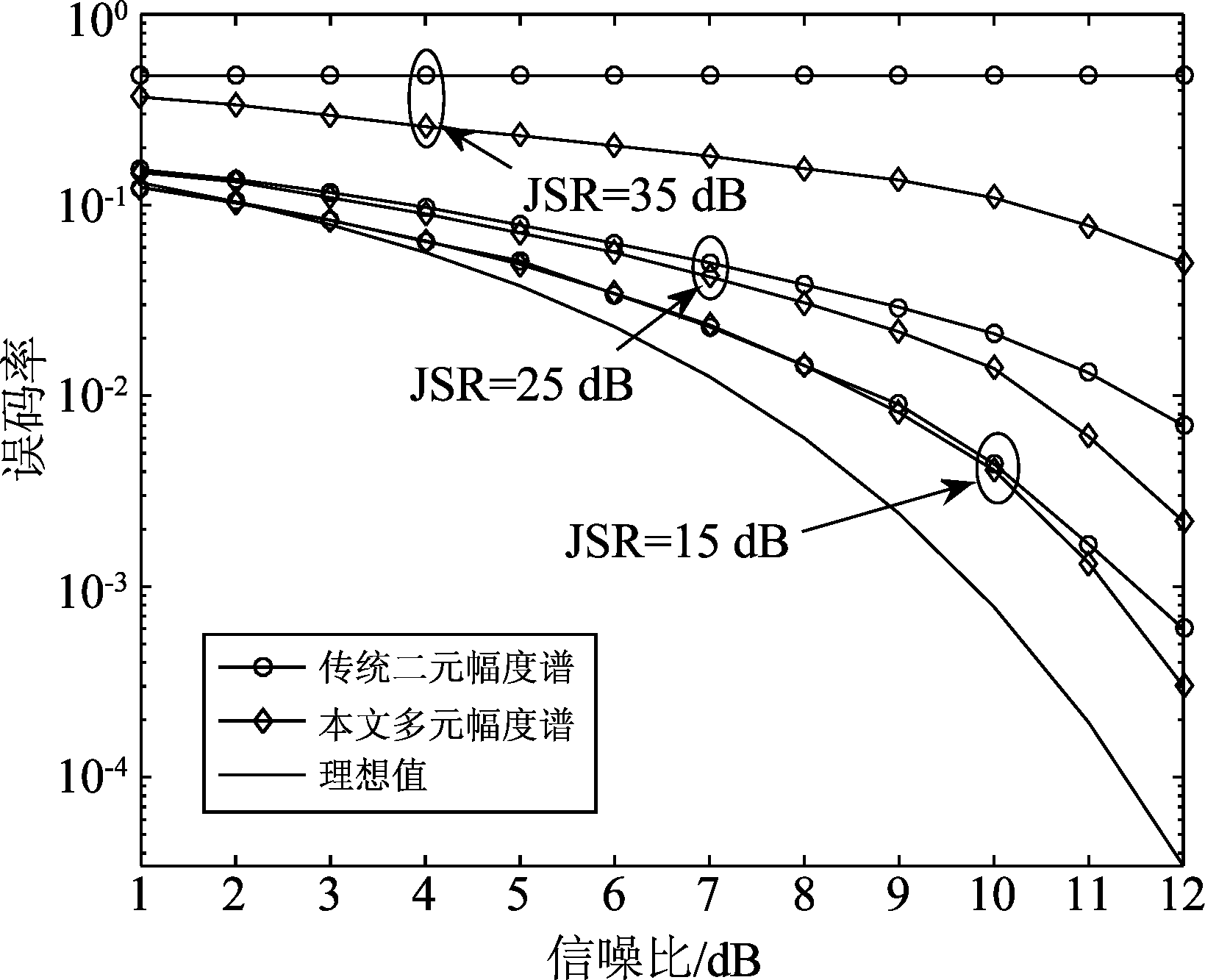
图8 信噪比与误码率关系图
Fig.8 Relationship between SNR and bit error rate
5 结论
本文详细推导了在干扰情况下TDCS信号干扰噪声比和误码率之间的关系,建立了幅度谱和干扰频谱信息的动态关系式,不受限于传统的二元幅度谱编码方式,根据求解系统最优误码率,将TDCS多元幅度谱编码问题转化成约束条件下多维极值最优化问题,利用拉格朗日函数将其转化成无约束条件下minψ(Ak,λ,M)迭代求最优解计算。理论分析和仿真结果表明,本文提出多元幅度谱编码算法相比较传统二元幅度谱编码算法,更加充分地利用了干扰频谱背景信息,将传输信息的能量更多地注入到信道增益大的频段,尤其在干扰能量较强的情况下,具有更加理想的抗干扰性能。
[1] Hu S, Li F, Guo H, et al. TDCS-IDMA System for Cognitive Radio Networks with Cloud[J]. IEEE Access, 2018, 6(6): 20520-20530.
[2] Liu Z, Guan Y L, Parampalli U, et al. Spectrally-Constrained Sequences: Bounds and Constructions[J]. IEEE Transactions on Information Theory, 2018, 64(4): 2571-2582.
[3] Chang C, Hao H, Guo J, et al. Complementary peak reducing signals for TDCS PAPR reduction[J]. Iet Communications, 2017, 11(6): 961-967.
[4] Jin C, Hu S, Huang Y, et al. On Transform Domain Communication Systems under Spectrum Sensing Mismatch: A Deterministic Analysis[J]. Sensors, 2017, 17(7): 1594-1594.
[5] Chakravarthy V D, Shaw A K, Temple M A, et al. Cognitive radio-an adaptive waveform with spectral sharing capability[C]∥IEEE Wireless Communications and NETWORKING Conference. IEEE, 2005, 2(2): 724-729.
[6] 张春磊, 杨小牛. 认知电子战与认知电子战系统研究[J]. 中国电子科学研究院学报, 2014, 9(6): 551-555.
Zhang C L, Yang X N. Research on Cognitive Electronic Warfare and Cognitive Electronic Warfare System[J].Journal of Chinese Academy of Electronic Sciences, 2014, 9(6): 551-555.(in Chinese)
[7] 张春磊, 杨小牛. 认知电子战初探[J]. 通信对抗, 2013, 32(2): 1- 4.
Zhang C L, Yang X N. Cognitive electronic warfare[J]. Communication Countermeasure, 2013(2): 1- 4.(in Chinese)
[8] 谢铁城, 达新宇, 褚振勇, 等. 变换域通信系统基函数的最佳门限设计[J]. 系统工程与电子技术, 2013, 35(10): 2204-2207.
Xie T C, Da X Y, Chu Z Y, et al. Optimal Threshold Design of Base Function for Transform Domain Communication Systems[J]. Systems Engineering and Electronic Technology, 2013, 35(10): 2204-2207.(in Chinese)
[9] Science S O C. A Complex Network Clustering Algorithm based on Gene Expression Programming and Information Theory[J]. Wireless Personal Communications, 2014, 79(2): 1301-1320.
[10] Fumat G, Chargé P, Zoubir A, et al. Transform domain communication systems from a multidimensional perspective, impacts on bit error rate and spectrum efficiency[J]. Iet Communications, 2011, 5(4): 476- 483.
[11] 刘鑫, 贾敏, 李秀华, 等. 双门限频谱估计的变换域通信系统[J]. 哈尔滨工业大学学报, 2013, 45(7): 103-108.
Liu X, Jia M, Li X H, et al. Transform domain communication system based on double-threshold spectrum estimation[J]. Journal of Harbin Institute of Technology, 2013, 45(7): 103-108.(in Chinese)
[12] 刘立, 张衡阳, 毛玉泉, 等. 变换域通信系统抗干扰编码幅度谱成型算法[J]. 西安交通大学学报, 2017, 51(2): 91-96.
Liu L, Zhang H Y, Mao Y Q, et al. Anti-interference coding amplitude spectrum shaping algorithm for transform domain communication systems[J].Journal of Xi′an Jiaotong University, 2017, 51(2): 91-96.(in Chinese)
[13] Jia L, Yao F, Sun Y, et al. Bayesian Stackelberg Game for Antijamming Transmission With Incomplete Information[J].
IEEE Communications Letters, 2016, 20(10): 1991-1994.
[14] Lin C H, Ma F, Chi C Y, et al. A Convex Optimization-Based Coupled Nonnegative Matrix Factorization Algorithm for Hyperspectral and Multispectral Data Fusion[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 52(3): 1652-1667.
[15] 李周, 崔琛. 压缩感知中观测矩阵的优化算法[J]. 信号处理, 2018, 34(2): 201-209.
Li Z, Cui C. An Optimization Algorithm for Observation Matrix in Compressive Sensing[J]. Journal of Signal Processing, 2018, 34(2): 201-209.(in Chinese)
[16] 王旭东, 陆威, 闫贺. 基于KL散度的雷达信号波形抗截获性能评估[J]. 电子与信息学报, 2017, 39(8): 1894-1898.
Wang X D, Lu W, Yan H. Anti-interception Performance Evaluation of Radar Signal Waveform Based on KL Divergence[J]. Journal of Electronics & Information Technology, 2017, 39(8): 1894-1898.(in Chinese)
