1 引言
在自适应信号处理领域,由于最小均方(Least mean square, LMS)算法和归一化LMS(Normalized LMS, NLMS)具有复杂度低且容易实现的特点,因此已经被广泛应用于自适应系统识别、信道估计和回波消除中[1-7]。LMS及NLMS算法的应用均是以输出噪声服从高斯分布假设为前提,但在许多实际情况下输出噪声往往具有非高斯特性,这将影响上述算法性能。鉴于此,目前研究者提出了许多鲁棒自适应滤波算法(Robust adaptive filtering algorithms, RAFAs),例如基于最大互相关熵准则(Maximum correntropy criterion, MCC) [8-11]的自适应滤波算法,最小平均混合范数(LMMN)算法[12]和最小平均绝对偏差(LMAD)[13]算法等。上述算法可用于解决非高斯测量噪声环境下的信号处理问题。其中,以MCC为代价函数的算法应用最广,可根据许多不同领域的实际问题而设计出不同形式的新算法,包括扩散MCC[14],核 MCC[15],广义 MCC[16],组约束 MCC和加权组约束MCC[17]算法。
虽然上述基于MCC的算法在非高斯输出噪声中具有良好的鲁棒性,但其对于解决稀疏系统辨识(Sparse System Identification, SSI)问题仍存在一定缺陷,这是由于其并没有有效利用系统稀疏的先验知识。对于SSI问题,目前主要存在两种解决方法,包括压缩感知理论[18-21]和比例更新两种机制[22]。基于压缩感知的算法主要是在原自适应滤波算法中添加稀疏惩罚约束项来应用系统稀疏特性,如零吸引算法(Zero Attraction)和加权零吸引类(Reweight Zero Attraction)算法[23-25]。而基于比例更新机制的AFAs,则是通过引入一个增益矩阵来成比例的自适应调节算法的步长以改进算法性能,主要包括proportionate NLMS[22]、proportionate NLMF[26]、proportionate MCC[27]等。虽然上述算法可充分利用系统的稀疏性,但这些算法并未考虑到输入信号受噪声干扰的问题。为了解决由于输入噪声所产生的偏差,近年研究者们提出了许多基于偏差补偿(Bias-compensated)的自适应滤波算法,如偏差补偿归一化最小均方(BCNLMS)算法[28-30],偏差补偿归一化最小平均四阶(BCNLMF)算法[31],以及偏差补偿NMCC(BCNMCC)算法[32]。尽管上述算法可以有效解决输入信号受噪声干扰的系统辨识问题,但是其并未考虑SSI问题。
根据以上分析,本文将以SSI问题为研究重点,且同时考虑输入信号含有噪声和输出噪声具有非高斯的条件,将比例更新机制和偏差补偿思想引入到NMCC算法,设计偏差补偿比例更新归一化互相关熵算法(BCPNMCC)。
2 偏差补偿比例更新互相关熵算法
2.1 归一化互相关熵算法(NMCC)
本节以FIR模型为基础给出NMCC算法,模型输入和输出关系由式(1)表示:
d(n)=u(n)Two+ν(n)
(1)
其中u(n)=[u(n),u(n-1),...,u(n-M+1)]T表示系统输入信号,wo=
...,
T为系统最优权重向量,M表示系统参数向量长度。ν(n)是与u(n)相互独立的加性背景噪声。基于上述模型,可定义MCC代价函数为:
(2)
其中e(n)=d(n)-uT(n)w(n)表示系统瞬时误差,w(n)=[w1(n),w2(n),...,wM(n)]T为对系统最优权重向量在第n次迭代时的估计。σ核宽度。基于公式(2)并应用梯度法,可得到NMCC算法的权重迭代公式为:
(3)
其中ε为一个正参数,其目的是为了保证分母不为零；μ为步长因子,其主要是控制算法收敛速度和稳态精度的重要参数。
当遇到脉冲离群点时,误差e(n)会变得特别大,在传统的自适应滤波算法中很难解决这个问题从而导致算法的鲁棒性不佳,但是在NMCC算法中由于指数项的存在,当有大的离群点出现,即产生较大的误差e(n)时,公式(3)中第二项的指数项将趋近于0,也就是可以衰减脉冲点所带来的影响。
2.2 比例更新归一化互相关熵算法(PNMCC)
文献[25]提出了比例更新互相关熵算法(PMCC),其权重更新方程为:
(4)
其中G(n)=diag(g1(n),g2(n),...,gM(n))表示一个对角增益矩阵,它可以自适应地更新每个权重的步长,其中第n个权重向量的增益gl(n)可表示为:
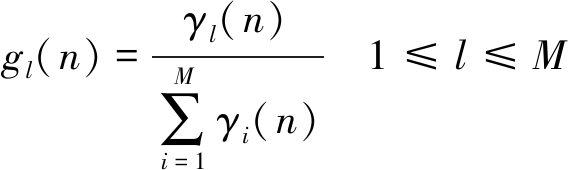
(5)
其中
γl(n)=max(ξmax(δ,|w1(n)|,|w2(n)|,...,
|wM(n)|),|wl(n)|)
(6)
ξ和δ均是正参数,一般取值分别为ξ=5/M,δ=0.01。
结合公式(3)和(4)得出:
w(n+1)=w(n)+
(7)
式(7)则是比例更新NMCC算法的迭代公式,记为PNMCC。
2.3 偏差补偿比例更新互相关熵算法(BCPNMCC)
本节将主要设计偏差补偿PNMCC (BCPNMCC)算法以增强PNMCC算法在输入信号含有噪声环境下的鲁棒性。为了补偿输入噪声带来的偏差,引入偏差补偿项B(n)到公式(7)中,则
w(n+1)=w(n)+
(8)
由于输入信号含有噪声,所以输出信号误差可定义为:
(9)
式中
表示先验误差,为了计算偏差项B(n)需要定义权值估计误差(WEV)为
结合(8)和WEV可得:
(10)
若使自适应滤波器估计的权值w(n)逼近于期望结果的wo,理想条件是在算法接近稳态时
趋近于0。建立如下无偏准则[26]:
(11)
此时为了计算补偿项B(n),对公式(10)左右两边同时求在输入信号存在噪声的条件下的期望,即:
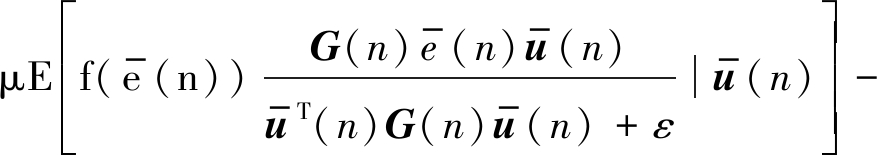
(12)
结合(11)和(12),可得:
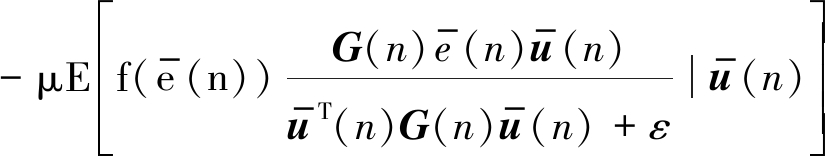
(13)
其中
表示一个非线性带噪误差函数,即:
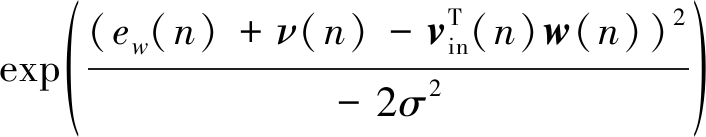
(14)
为了进一步获得偏差补偿项需要做出以下假设[31]:
假设1:假设信号ν(n),vin(n),u(n)和彼此之间都是相互独立的。
假设2:假设f(ν(n)),vin(n),G(n)和
之间都是相互独立的。
假设3:权重,误差,输入信号之间也相互独立。
为了便于计算
本文对
在点ν(n)处进行泰勒展开得到:
(15)
利用公式(14)可得:
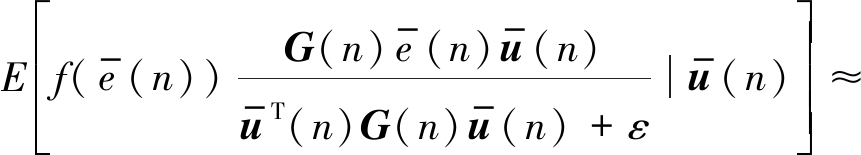
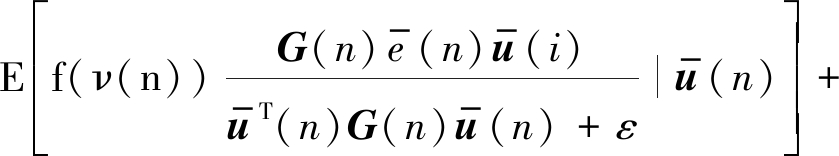
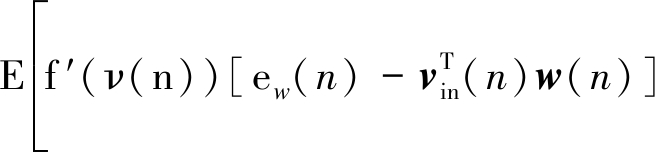
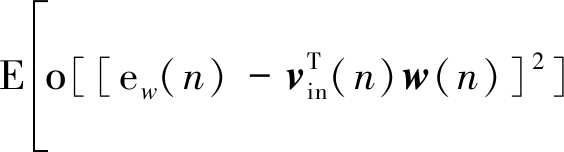
(16)
通常来说,当算法趋于稳定时,先验误差ew(n)是一个非常小的值,且当步长因子很小的时候ew(n)与输出的噪声相比是一个可以忽略的值。结合假设1、2、3下,公式(16)中的第二部分可以近似为:
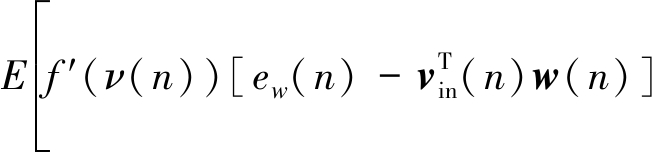
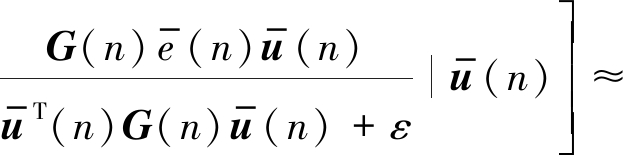
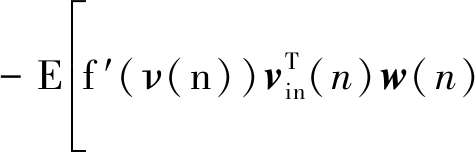
(17)
进一步,公式(16)中第三部分可近似为:
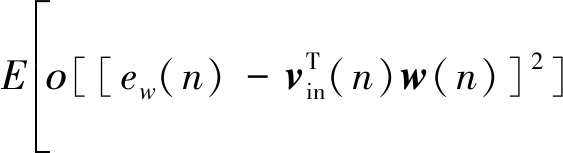
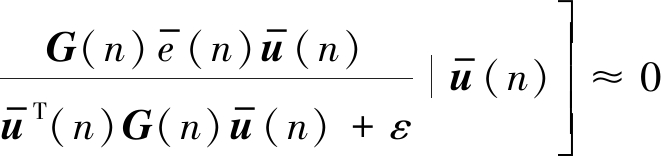
(18)
结合(16)～(18)和假设3,可以将(16)重写为:
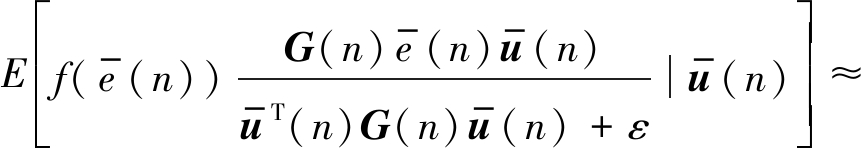
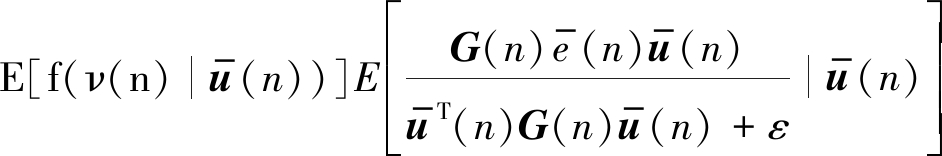
(19)
将
带入到(19),则有:
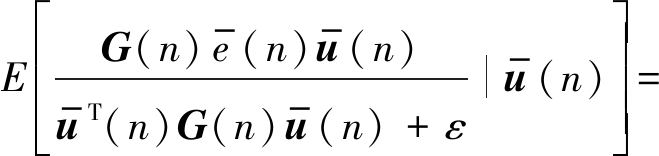
(20)
这里
(21)
(22)
且
(23)
(24)
将式(21)～(24)带入(20)可得:
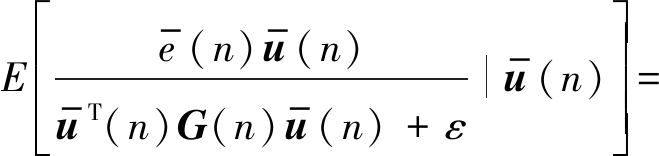
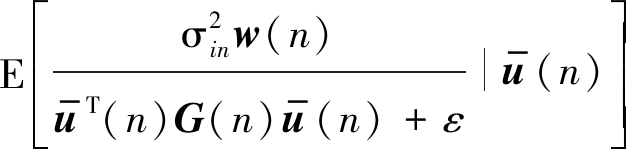
(25)
由(20)、(25)和(13)可得:
(26)
进一步基于逼近理论,可得:
(27)
将公式(27)代入(8)可以得到:
w(n+1)=
(28)
公式(28)则为BCPNMCC算法的迭代方程。
注记:公式(28)的结构与BCNMCC算法相似,当增益矩阵为单位矩阵时,BCPNMCC算法将退化为BCNMCC算法。此外,当输入噪声方差为0时,BCPNMCC等价于PNMCC算法。因此,本文提出的BCPNMCC算法同时具有BCNMCC和PNMCC算法的优点。
2.4平均收敛性分析
由于输入噪声与输出噪声的存在,且在该算法中包含指数项,在算法的收敛性分析方面会有较大的困难。基于此,本文在此仅给出BCPNMCC算法的平均收敛性能分析,在仿真实验中通过选择不同的步长因子也对本文所提算法的收敛性进行了仿真验证。结合公式(9)和(28)以得到:
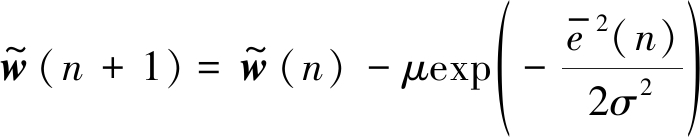
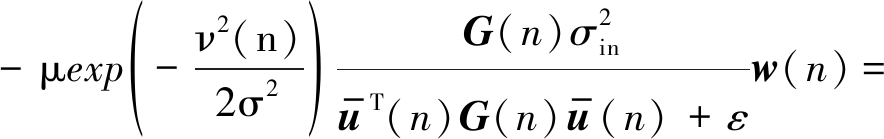
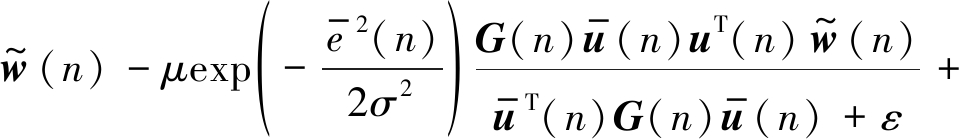
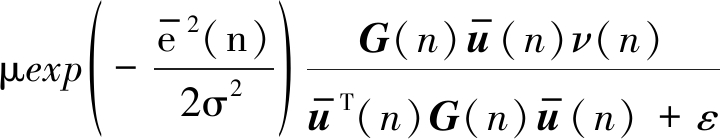
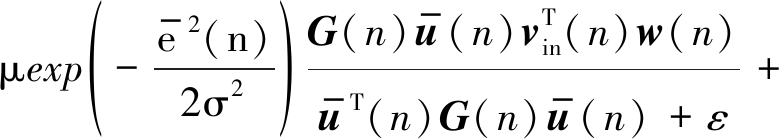
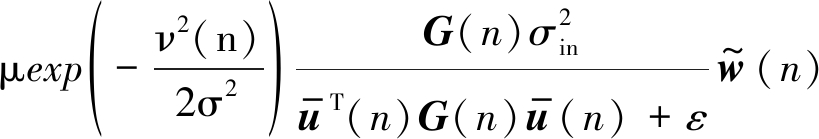
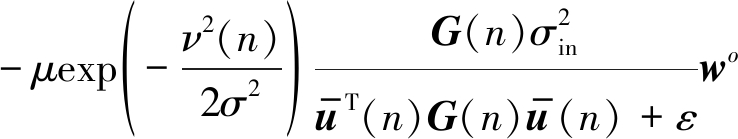
(29)
对公式(29)取期望并且根据假设1～3,和公式(10)可得:
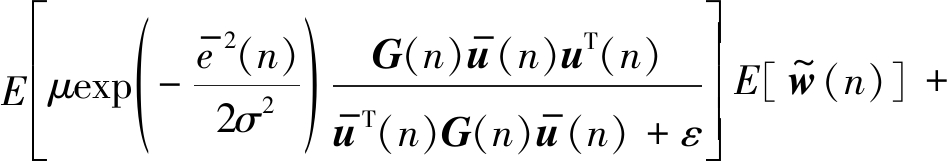
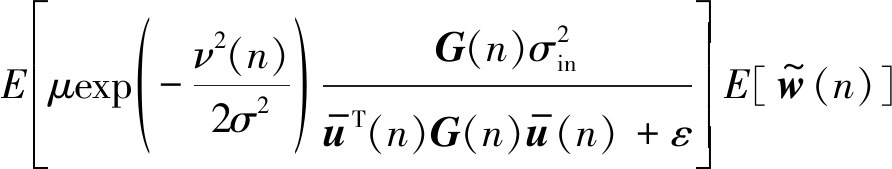
(30)
根据(30),可知要使得BCPNMCC算法满足平均收敛性,需满足如下不等式:
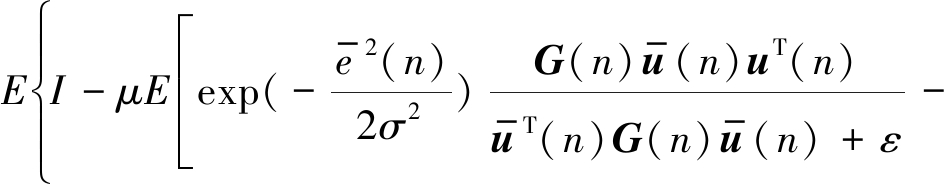
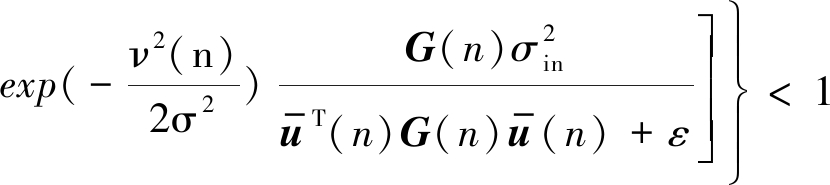
(31)
通过公式(31)可进一步得到步长需满足的范围为
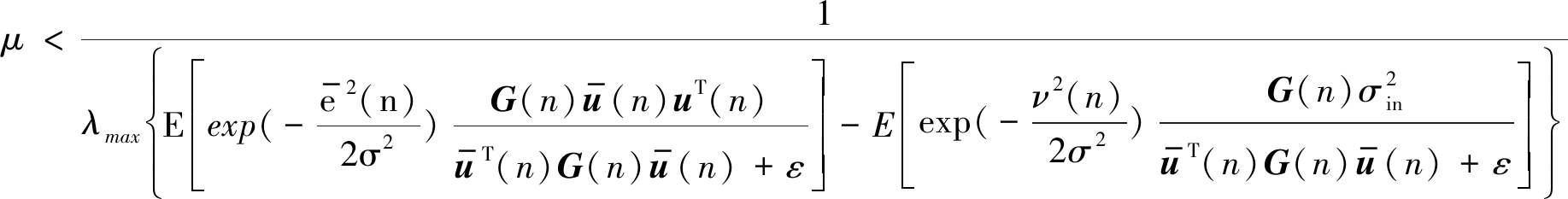
(32)
其中λmax表示输入自相关矩阵的最大特征值参数。
2.5 计算复杂度
在本小节,对所提算法的计算复杂度进行分析。这里仅分析在一次迭代过程中,算法的主要更新公式所产生的计算复杂度问题。为了更好的分析该算法的复杂度,将更新公式(28)重新写为:
w(n+1)=
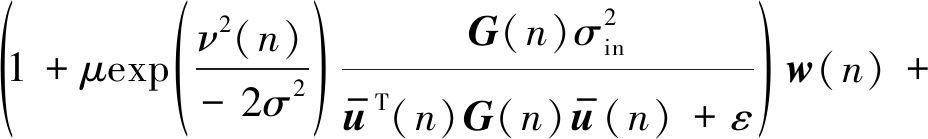
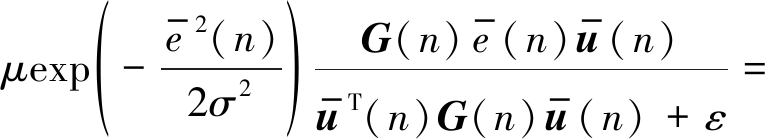
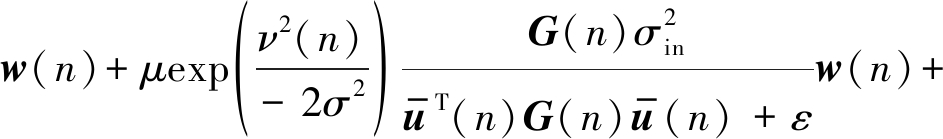
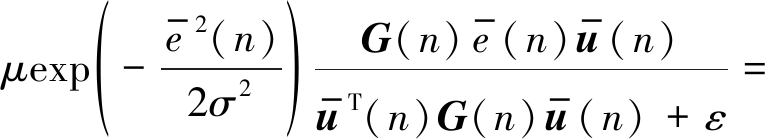
w(n)+A(n)+B(n)
(33)
其中
则如表1所示给出了该算法的计算复杂度分析过程。
表1 计算复杂度
Tab.1 Computation Complexity
公式加法乘法除法指数计算A(n)1M2+M+5M+1MB(n)12M2+6M+1Mw(n)+A(n)+B(n)2MNANANA总体计算复杂度2M+23M2+M+112M+22M
注记:BCPNMCC算法与传统的PNMCC算法相比其计算复杂度中多了偏差补偿项B(n)的计算；与BCPNLMS算法相比多了一项指数项的计算。
3 计算机仿真分析
本节将利用MATLAB软件编程进行计算机仿真实验,来比较分析所提算法BCPNMCC鲁棒性,将主要与NMCC、PNMCC和BCNMCC算法进行比较研究。在仿真中,设置未知时变系统的参数向量如图1所示。
图1中设定wo的长度为M,取值分别为32,64,128。定义稀疏度SR为:
(34)
这里的Nnon-zeros为wo中非零参数的个数。本文为了研究所提算法的鲁棒性,由α稳态分布来模拟产生脉冲随机序列作为系统观测噪声。α稳态分布的特征函数的定义:
f(t)=exp{jθt-γ|t|α[1+jβsgn(t)S(t,α)]}
(35)
其中
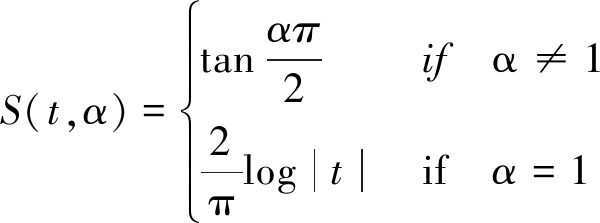
(36)
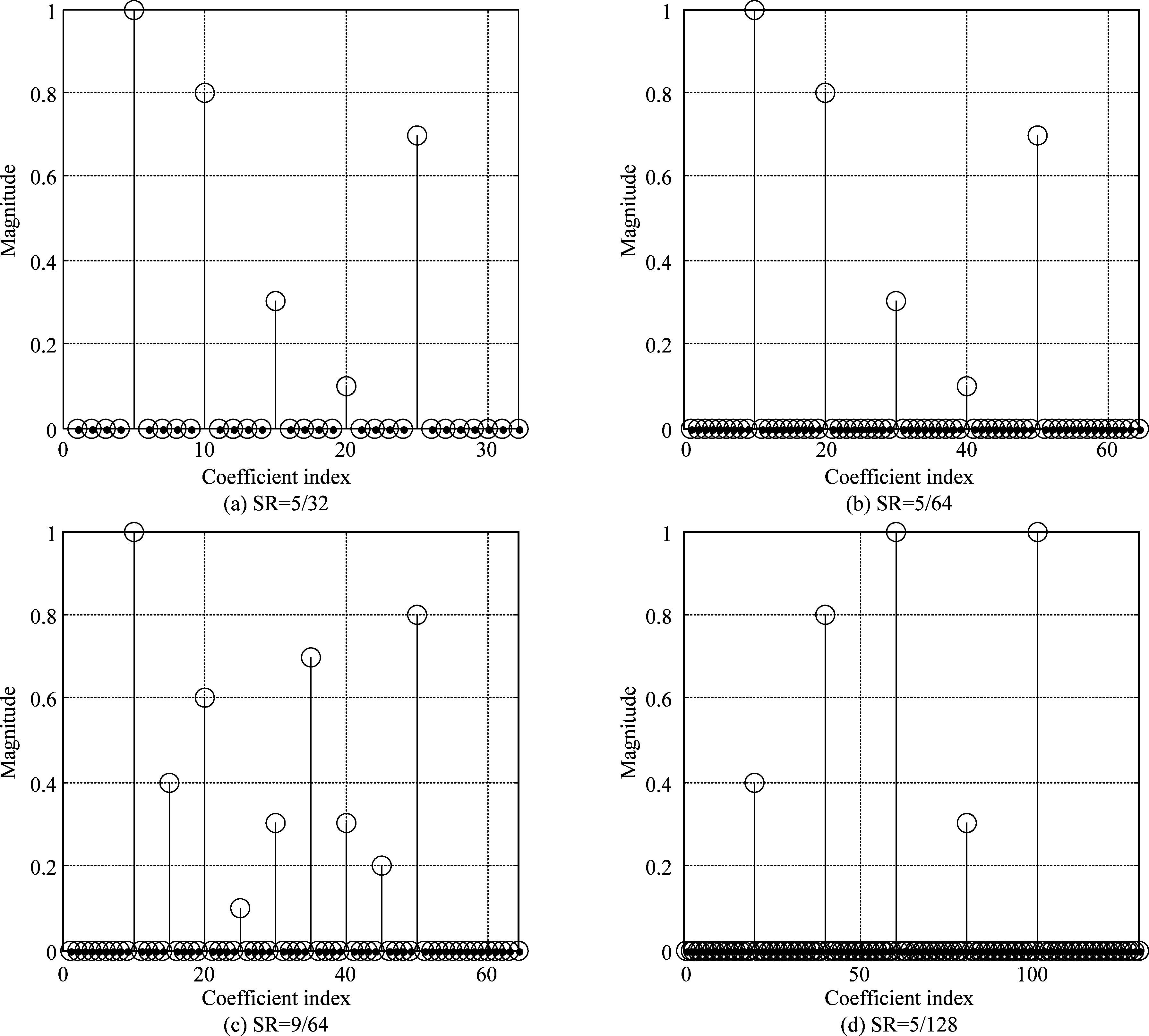
图1 稀疏脉冲响应参数
Fig.1 Impulsive response parameters of the sparse system
这里的α∈(0,2]是特征参数,-
<θ<+被定义为位置参数,β∈[-1,1] 为对称参数,而γ>0表示扩散参数。 特征参数α用来衡量分布的重尾特性,α越小,脉冲越大。定义噪声模型的参数向量为Vα-stable(α,β,γ,θ)。α噪声模型常被应用于稳健自适应滤波算法性能的验证中[32-33]。文中每项试验,都是通过进行200次的独立蒙特卡洛(MC)实验,且每次实验所迭代数千次来获得相应的实验结果。本文使用均方偏差(MSD)来衡量算法性能,其定义如下:
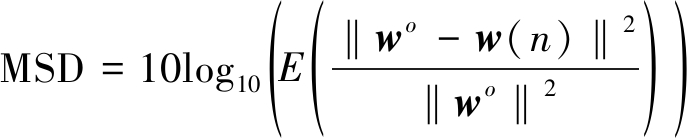
(37)
本文在仿真验证过程中选择不同稀疏度的最优权重向量来验证所提算法的性能,而其他参数的设定均保证各算法可获得最优性能。其中NMCC算法中的σ=20；输入噪声方差和输入信号的方差均为1,而输出噪声向量为Vα-stable(1.2,0,0.4,0)。正参数ε=0.001。
3.1 算法收敛性仿真分析
首先,研究所提算法与其他算法在拥有相同收敛速度条件下稳态精度的性能。图2给出了各算法在不同稀疏度((a) SR=5/32, (b) SR=5/64, (c) SR=5/128)下的收敛曲线图。从该结果中可看到新算法在稀疏度递减的情况下始终保持着最好的性能。图3则是当系统参数向量长度一致,而稀疏度不同时的各算法的收敛曲线结果,从该结果中可知随着稀疏度的增大,各个算法的性能都在变差,但是新算法(BCPNMCC)始终都是效果最好的算法。图3与图2相结合,可以得到新算法在相同稀疏环境下与其他三种算法相比当收敛速度相同时始终保持着最好稳态精度。
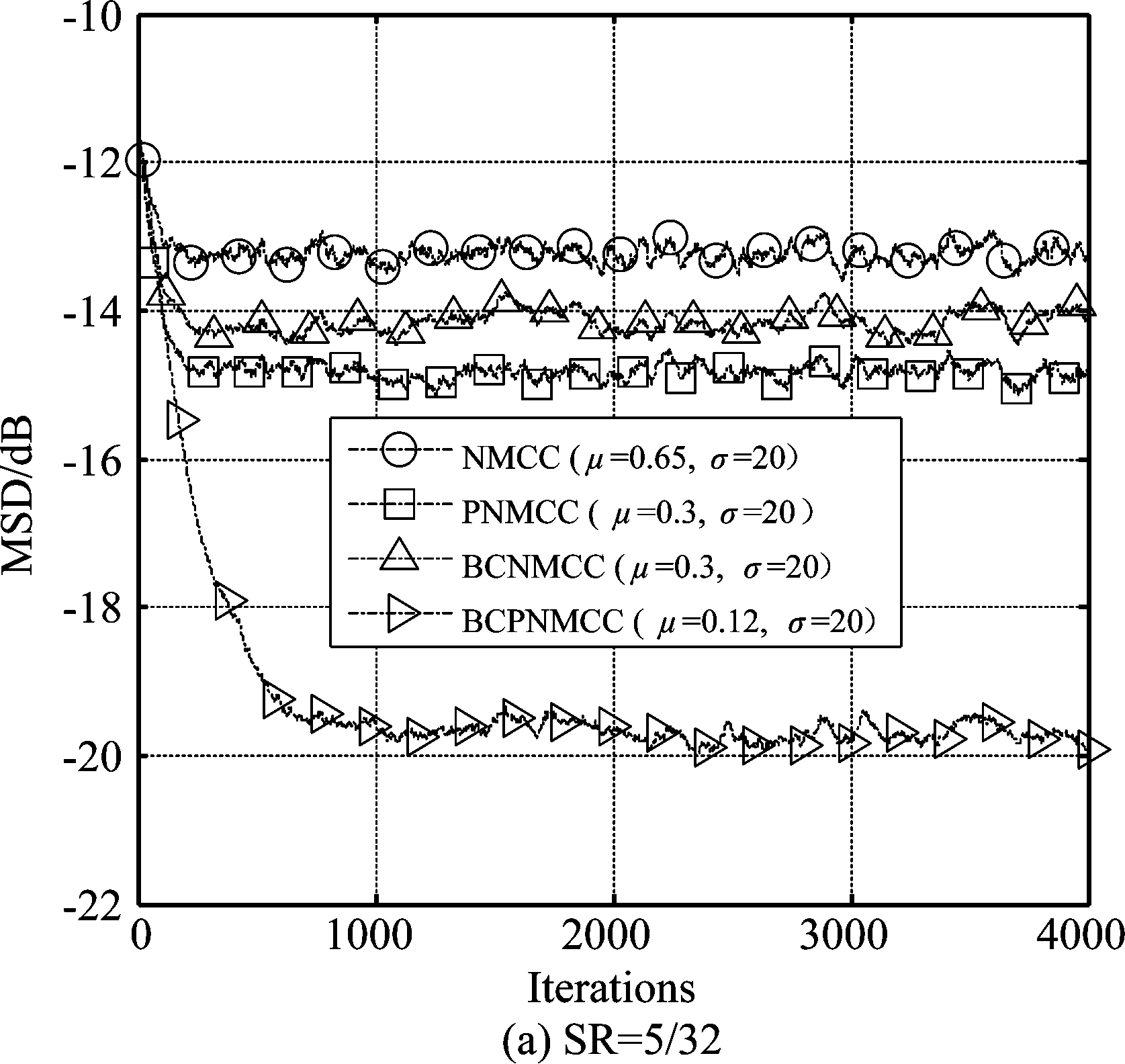
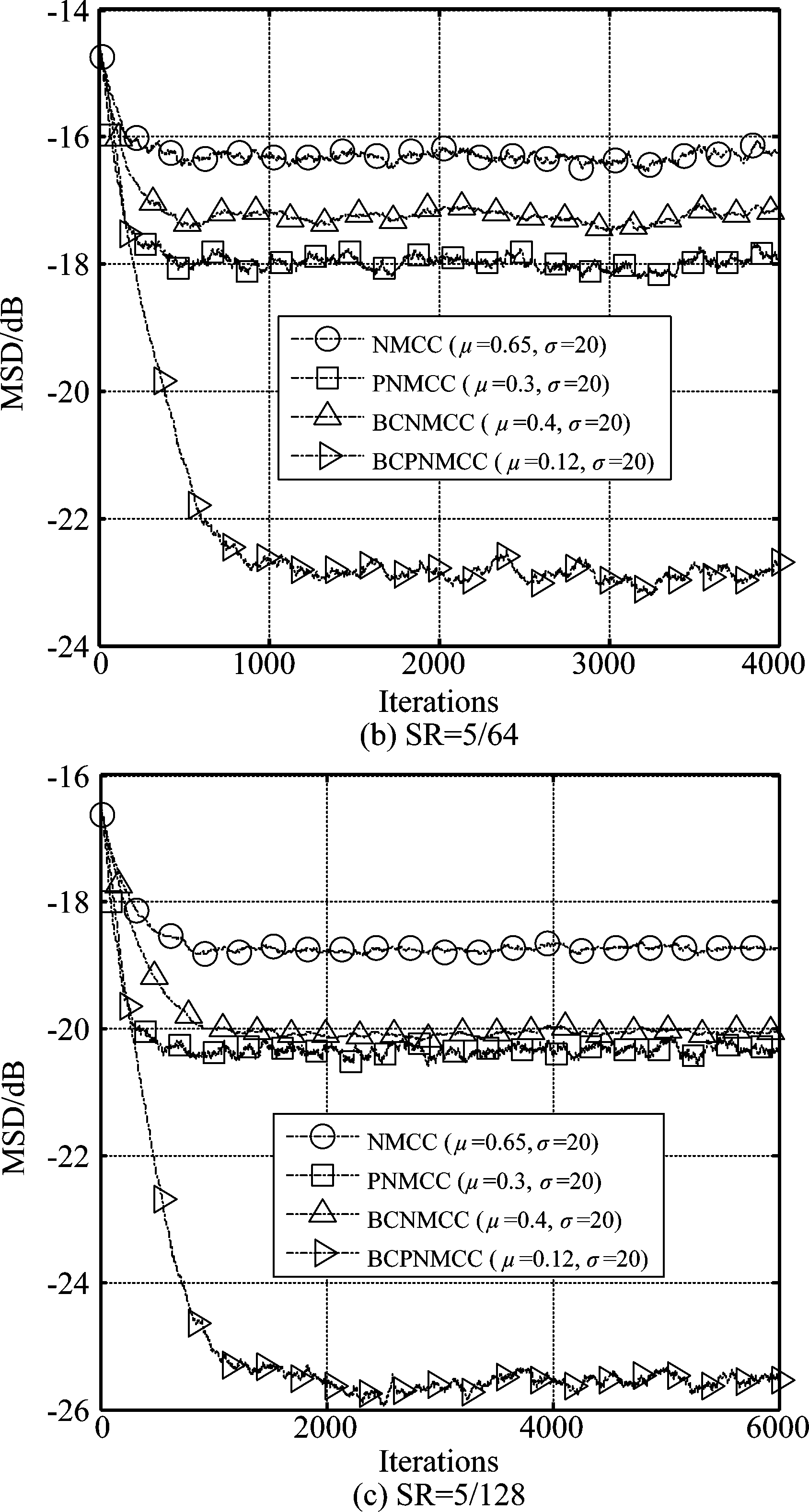
图2 相同收敛速度下四种算法就MSD的收敛曲线对比图
Fig.2 Convergence curves of four algorithms keep the similar initial convergence speed in term of MSD
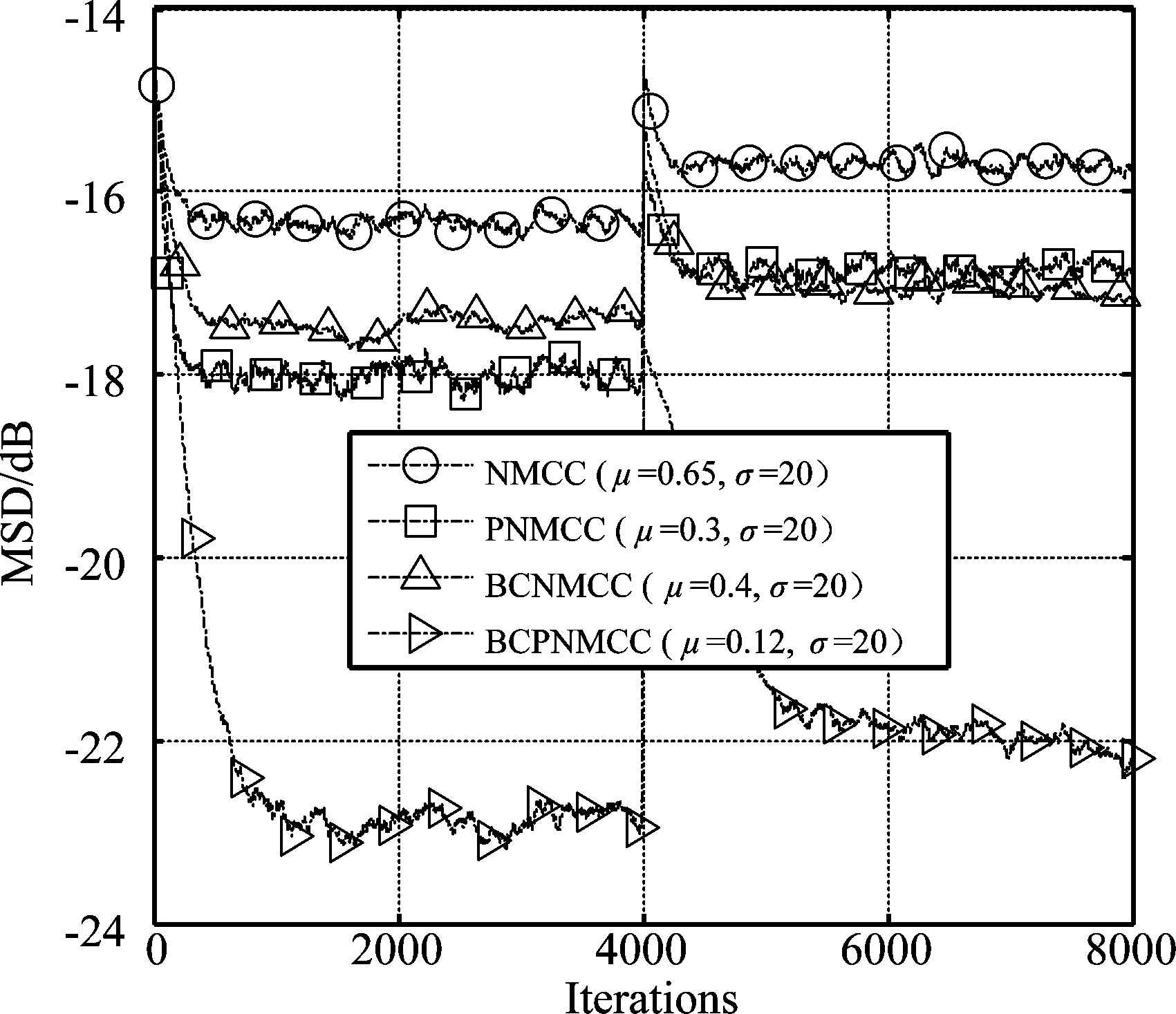
图3 四种算法在不同SR下的收敛曲线对比图.
第一阶段SR=5/64；第二阶段SR=9/64
Fig.3 Convergence curves of four algorithms under different SR.
The first stage SR=5/64; the second stage SR=9/64
其次,研究所提算法的收敛速度和稳态精度。在本实验中,步长因子设置是以满足各算法能够获得相同稳态精度为前提的。如图4所示为算法的收敛曲线,从中可看出与BCNMCC算法相比,新算法有更好的收敛速度,这主要是因为新算法中包含了增益矩阵,其可以自适应更新步长；而与PNMCC算法对比,新算法在相同收敛速度下有着PNMCC算法所不能达到的高稳态精度,因为新算法包含了偏差补偿项可以有效步长输入噪声带来的偏差。
图4 四种算法保证相同稳态精度下的收敛速度对比图. SR=5/64
Fig.4 Convergence curves of four algorithms to the similar initial convergence speed and the similar steady-state accuracy respectively. SR=5/64
3.2 各参数对算法性能的影响分析
首先,选择不同的
值(0.3,0.5,0.65,0.8,1.0)进行仿真来进一步验证算法的鲁棒性。其他参数设置不变。图5为各算法的稳态MSD,从中可知,当增大到一定程度时,偏差补偿算法(包括BCNMCC和BCPNMCC)要比原来的算法(即NMCC和PNMCC)表现得更好,PNMCC和BCPNMCC算法则比NMCC和BCNMCC算法具有更高的稳态精度,这与上述实验结果一致。此外,还进一步研究了核宽度σ对算法性能的影响。分别设置σ为(10,20,30,40,50)。图6给出了每一个算法的稳态MSD结果。显然,1)BCPNMCC算法优于NMCC、PNMCC和BCNMCC算法； 2)BCPNMCC算法在σ=20时达到最佳性能,算法的性能与σ值之间不存在明显的线性关系,这意味着在不同应用中应选择合适的核宽度以达到预期性能。
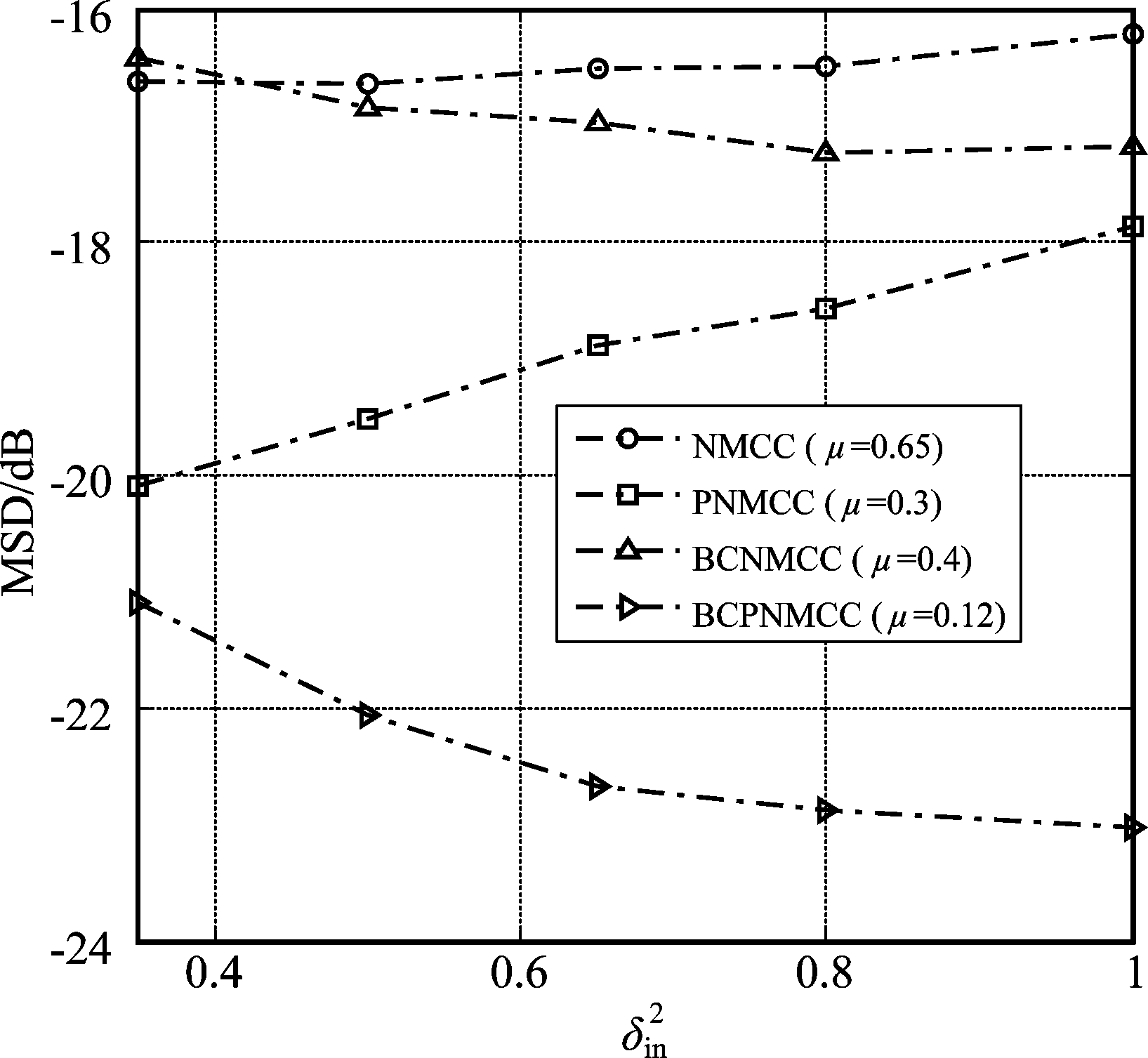
图5 不同输入噪声方差下的稳态精度曲线. σ=20, SR=5/64
Fig.5 Steady-state MSDs with different values of 
σ=20, SR=5/64
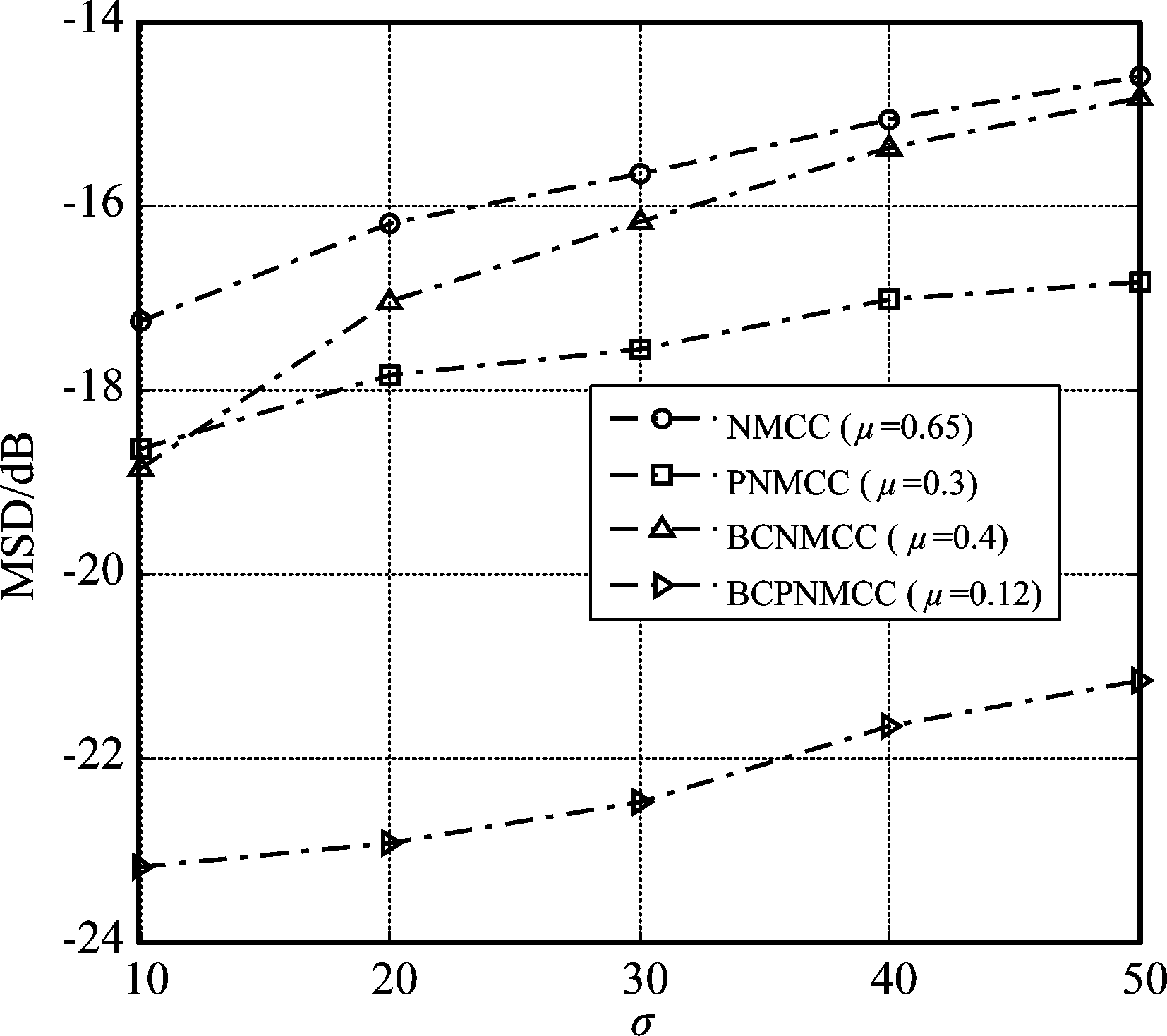
图6 不同σ下稳态精度的对比.
Fig.6 Steady-state MSDs with different values of σ.
其次,考虑算法在不同能量脉冲噪声的性能,即选取不同的噪声模型参数产生噪声。本实验中设置系统稀疏度仍然为5/64,步长为0.12,核宽度为20。在α稳态分布模型中,特征参数α用来衡量分布的重尾特性,α越小,脉冲越大；与此相反γ越大则脉冲越大,为了验证在脉冲噪声下新算法的鲁棒性,本实验对所提新算法分别作了当α(1.0,1.1,1.2,1.3,1.4)变化而γ=0.4和γ(0.2,0.3,0.4,0.5,0.6)变化而α=1.2的仿真验证,结果如图7(a)、(b)所示。从该结果可知随着脉冲逐渐增大,算法的稳态性能也在减弱,但是算法仍然能表现出收敛特征,未出现大的波动。
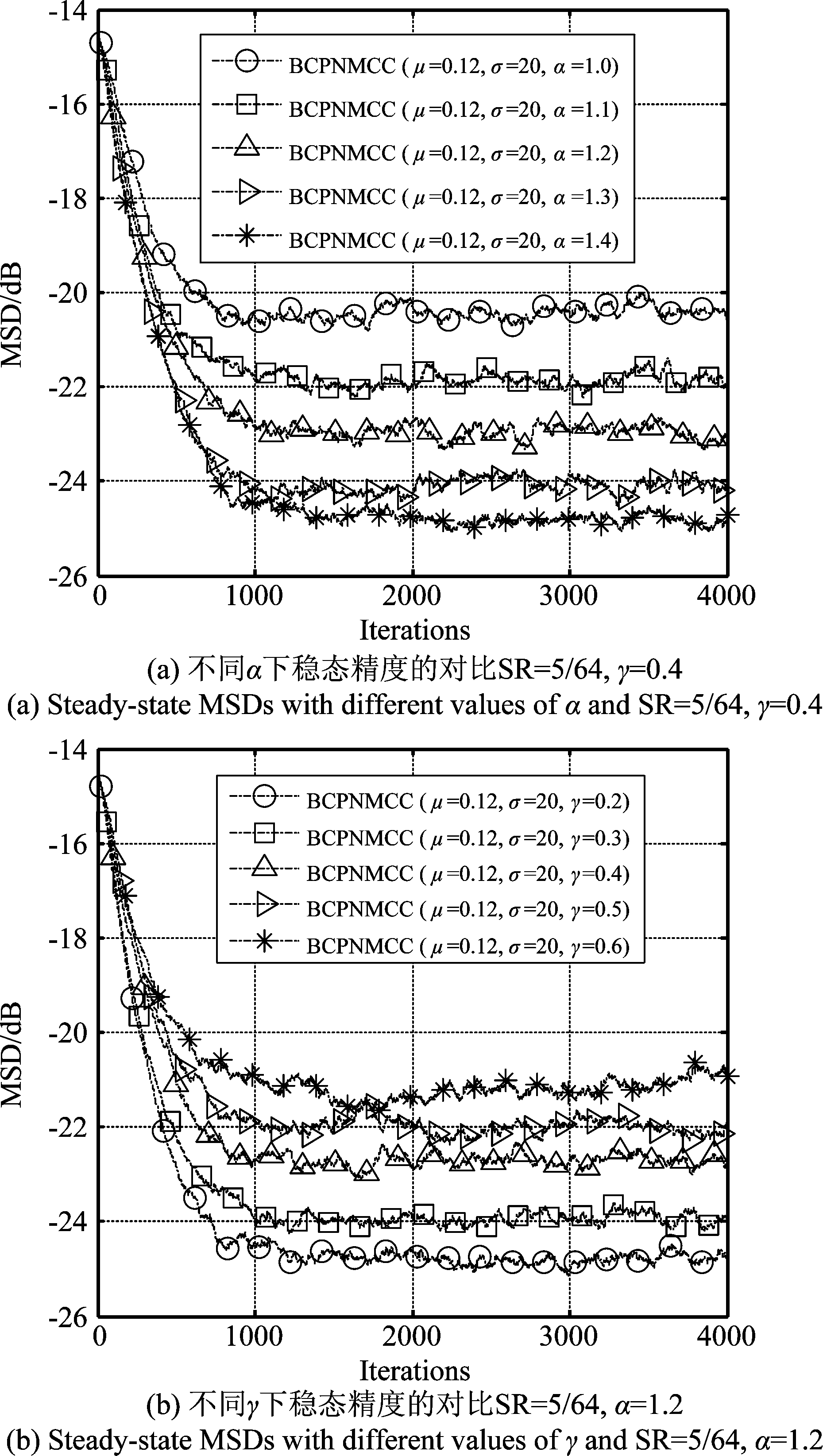
图7 不同α和γ下的性能对比
Fig.7 Steady-state MSDs with different values of α and γ respectively
最后,在其他参数均未发生改变的前提下验证步长μ(0.01,0.02,0.04,0.07,0.1和0.7)对算法收敛性影响分析。本仿真中核宽度设置为20。如图8所示为算法在不同步长μ值下的收敛曲线图。从图中可以看到当步长越大时则收敛速度越快但稳态精度越差,相反当步长越小时收敛速度越慢稳态精度越高。根据该结果可知,如其他自适应滤波算法一样,要保证该算法具有理想的收敛性,需要使选择的步长满足一定条件,即其值要在特点的范围内。
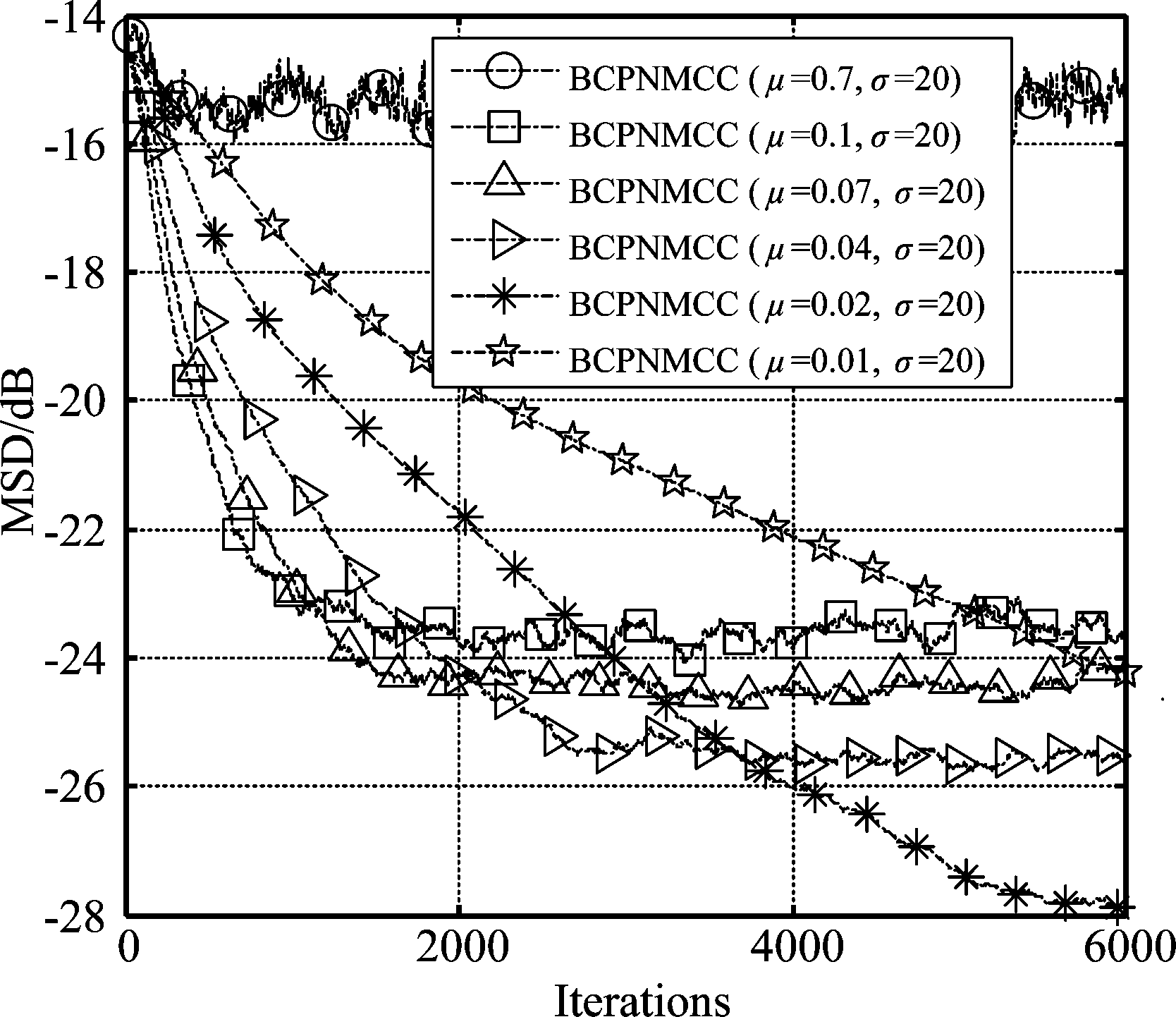
图8 不同μ下BCPNMCC算法的稳态精度对比
Fig.8 Steady-state MSDs with different values of μ
4 结论
本文针对含噪输入和输出噪声具有非高斯特征的稀疏系统辨识问题,将比例更新机制和偏差补偿准则引入到NMCC算法,提出了BCPNMCC算法。所提算法具有比BCNMCC算法更快的收敛速度,这是由于增益矩阵可自适应调整步长。另外,通过在BCPNMCC算法中引入无偏准则而导出了偏差补偿项,该项可以有效解决由于输入噪声所带来的偏差,从而具有理想的辨识精度。仿真结果表明:1)BCPNMCC算法在稀疏系统中优于PNMCC算法。2)无论步长因子和内核宽度为多大,BCPNMCC算法都能保持最佳性能。当输入噪声方差比较大时偏差补偿算法也将随着方差的变大效果也越明显。
[1] Kalouptsidis N, Mileounis G, Babadi B. Adaptive algorithms for sparse system identification[J]. Signal Process., 2011, 91(8): 1910-1919.
[2] Slock D T M. On the convergence behavior of the LMS and the normalized LMS algorithms[J]. IEEE Trans. Signal Process., 1993, 41(9): 2811-2825.
[3] 李方伟, 张浩. 一种新的变步长LMS自适应滤波算法及其仿真[J]. 重庆邮电大学学报: 自然科学版, 2009, 21(5): 1385-1388.
Li F W, Zhang H. A new LMS adaptive filtering algorithm for variable step length and its simulation[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2009, 21(5): 1385-1388.(in Chinese)
[4] Walach E, Widrow B. The least mean fourth (LMF) adaptive algorithm and its family[J]. IEEE Trans. Inf. Theory, 1984, 30(2): 275-283.
[5] Zerguine A. Convergence and steady-state analysis of the normalized least mean fourth algorithm[J]. Digit. Signal Process., 2007, 17: 17-31.
[6] 王敏强, 郑宝玉. 一种新的可变步长LMS自适应滤波算法[J]. 信号处理, 2004, 20(6): 613- 618.
Wang M Q, Zheng B Y. A novel variable step size LMS adaptive filtering algorithm[J]. Signal Processing, 2004, 20(6): 613- 618.(in Chinese)
[7] 靳翼, 邵怀宗. 一种新的变步长LMS自适应滤波算法及其仿真[J]. 信号处理, 2010, 26(9): 1385-1388.
Jin Y, Shao H Z. A novel variable step size LMS adaptive filtering algorithm and its simulation[J]. Signal Processing, 2010, 26(9): 1385-1388.(in Chinese)
[8] Liu W, Pokharel P, Principe J C. Correntropy: Properties and applications in non-Gaussian signal processing[J]. IEEE Trans. Signal Process., 2007, 55(11): 5286-5298.
[9] Chen B, Xing L, Liang J, et al. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J]. IEEE Signal Process. Lett., 2014, 21(7): 880- 884.
[10] Chen B, Principe J C. Maximum correntropy estimation is a smoothed MAP estimation[J]. IEEE Signal Process. Lett., 2012, 19(8): 491- 494.
[11] Chen B, Wang J, Zhao H, et al. Convergence of a fixed-point algorithm under maximum correntropy criterion[J]. IEEE Signal Process. Lett., 2015, 22(10): 1723-1727.
[12] Chambers J, Avlonitis A. A robust mixed-norm adaptive filter algorithm[J]. IEEE Signal Process. Lett., 1997, 4(2): 46- 48.
[13] Breidt F J, Davis R A, Trindade A A. Least absolute deviation estimation for all-pass time series models[J]. Ann. Stat., 2001, 29(4): 919-946.
[14] Ma W, Chen B, Duan J, et al. Diffusion maximum correntropy criterion algorithms for robust distributed estimation[J]. Digit. Signal Process., 2016, 58: 10-19.
[15] Wu Z, Shi J, Zhang X, et al. Kernel recursive maximum correntropy[J]. Signal Process., 2015, 117: 11-16.
[16] Chen B, Xing L, Zhao H, et al. Generalized correntropy for robust adaptive filtering[J]. IEEE Trans. Signal Process., 2016, 64(13): 3376-3387.
[17] Wang Y, Li Y, Albu F, et al. Group-constrained maximum correntropy criterion algorithms for estimating sparse mix-noised channels[J]. Entropy, 2017, 19(8): 432.
[18] 李少东, 杨军, 胡国旗. 一种改进的压缩感知信号重构算法[J]. 信号处理, 2012, 28(5): 744-749.
Li S D, Yang J, Hu G Q. A modified signal reconstruction algorithm via compressive sensing[J]. Signal Processing, 2012, 28(5): 744-749.(in Chinese)
[19] Donoho D L. Compressed sensing[J]. IEEE Trans. Inf. Theory, 2006, 52(4): 1289-1306.
[20] Baraniuk R G. Compressive sensing[C]∥IEEE Signal Process. Mag., 2008, 56(4): iv-v.
[21] 周千, 马文涛, 桂冠. 基于l1范数约束的递归互相关熵的稀疏系统辨识[J]. 信号处理, 2016, 32(9): 1079-1086.
Zhou Q, Ma W T, Gui G. Recursive Maximum Correntropy Criteria Algorithm with l1-norm Constraints for Sparse System Identification[J]. Journal of Signal Processing, 2016, 32(9): 1079-1086.(in Chinese)
[22] Duttweiler D L. Proportionate normalized least-mean-squares adaptation in echo cancelers[J]. IEEE Trans. Speech Audio Process., 2000, 8(5): 508-518.
[23] Gu Y, Jin J, Mei S. l0norm constraint LMS algorithm for Sparse system identification[J]. IEEE Signal Process. Lett., 2009, 16(9): 774-777.
[24] Gui G, Adachi F. Sparse least mean fourth algorithm for adaptive channel estimation in low signal-to-noise ratio region[J]. Int. J. Commun. Syst., 2015, 27(11): 3147-3157.
[25] Li Y, Wang Y, Albu F, et al. A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification[J]. Symmetry, 2017, 9(10): 229.
[26] Sayin M O, Yilmaz Y, Demir A. The Krylov-proportionate normalized least mean fourth approach: Formulation and performance analysis[J]. Signal Process., 2015, 109: 1-13.
[27] Ma W, Zheng D, Zhang Z. Robust proportionate adaptive filter based on maximum correntropy criterion for sparse system identification in impulsive noise environments[J]. Signal Image Video Process., 2017(3): 1- 8.
[28] Jung S M, Park P G. Normalized least-mean-square algorithm for adaptive filtering of impulsive measurement noises and noisy inputs[J]. Electron. Lett., 2013, 49(20): 1270-1272.
[29] Yoo J W, Shin J W, Park P G. An improved NLMS algorithm in sparse systems against noisy input signals[J]. IEEE Trans. Circuits Syst. II Express Briefs, 2015, 62(3): 271-275.
[30] Ma W, Zheng D, Tong X, et al. Proportionate NLMS with Unbiasedness Criterion for Sparse System Identification in the Presence of Input and Output Noises[J]. IEEE Trans. Circuits Syst. II Express Briefs, 2017, 65(11): 1808-1812.
[31] Zheng Z, Liu Z, Zhao H. Bias-compensated normalized least-mean fourth algorithm for noisy input[J]. Circuits Syst. Signal Process., 2017, 36(9): 3864-3873.
[32] Ma W, Zheng D, Li Y, et al. Bias-compensated normalized maximum correntropy criterion algorithm for system identification with noisy Input[J]. Signal Process., 2018, 152: 160-164.
[33] 张斌, 冯大政, 刘建强. α噪声环境下整体最小平均P-范数IIR自适应滤波算法[J]. 信号处理, 2010, 26(3): 473- 476.
Zhang B, Feng D Z, Liu J Q. Total least mean lp-norm algorithm for adaptive IIR filtering in α-stable noise environments[J]. Signal Processing, 2010, 26(3): 473- 476.(in Chinese)
