1 引言
OFDM技术因其频谱利用率高、抗衰落能力强,在民用和军事通信领域均得到了广泛应用[1]。从军事侦察、信息安全、电子对抗的角度来看,研究OFDM信号的非协作侦收具有重要的意义[2-3]。在非协作通信系统中,由于侦听方对于接收信号无先验信息,为实现准确的盲解调,需先对OFDM信号时间参数进行精确的估计。OFDM信号时间参数包括有用符号长度、循环前缀(Cyclic prefix,CP)长度、OFDM符号总长度等,信号参数盲估计是信号盲同步和盲解调的前提。
为实现非协作通信中OFDM时间参数的精确估计,国内外学者对此做了大量研究。文献[4]利用OFDM信号的自相关函数和符号能量之间的关系估计出循环前缀长度；文献[5]分析OFDM循环自相关函数的三维结构,基于循环自相关谱峰特性估计OFDM时间参数；文献[6]针对短循环前缀的OFDM信号,提出了一种基于符号峰态的OFDM信号参数盲估计方法,该算法解决了短循环前缀和符号数目较少情况下OFDM时间参数的估计；文献[7]提出一种在任意过采样率盲接收场景下的OFDM拦截接收机,基于迭代循环平稳特性的检测进行参数估计,大大降低估计过程的计算复杂度；文献[8]基于OFDM信号循环平稳特性,分析了多径衰落、定时偏移、载波频率偏移和叠加高斯噪声等非协作通信场景中参数盲估计性能；文献[9]基于循环自相关算法,实现了NC-OFDM信号的参数盲估计以及ZP-OFDM信号的盲识别。
以上的文献为OFDM的时间参数估计提供了很好的思路和算法,但并未考虑OFDM信号中含导频的情况。在实际的OFDM通信系统中,因为接收端的信道估计和相干解调,OFDM信号中通常包含导频信号[10],而导频信号的存在对OFDM的循环自相关性能有较大影响,而且该影响还和导频类型、导频间隔以及导频信号与信息数据的功率比有关,因此,本文考虑OFDM信号非协作侦收的实际应用场景,分析了包含导频的OFDM信号的二阶循环特性,基于循环自相关算法,改进了OFDM时间参数的估计算法,同时适应非整数倍采样情况,使OFDM的时间参数估计算法更加鲁棒。
本文内容安排如下:第2节描述信号模型；第3节介绍了OFDM信号循环自相关特性；第4节针对实际应用场景,分析了含导频OFDM信号的二阶循环谱特征,并考虑了实际场景中的非整数倍采样情况,改进了基于循环自相关的时间参数估计算法；第5节仿真对比分析改进前后的OFDM时间参数估计算法性能；最后总结全文。
2 信号模型
OFDM信号经过加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道之后的接收复基带信号为
r(t)=s(t)+n(t)
(1)
其中,s(t)为OFDM基带信号, n(t)为零均值高斯白噪声,n(t)～CN(0,2σ2),2σ2为噪声功率,并与信号s(t)相互独立。从t0时刻起的接收复基带信号数学模型如下
r(t)=s(t-t0)ej2πf0t+n(t)
(2)
其中,信号模型时间t>t0, f0为收发频偏。OFDM信号模型如下
(3)
其中,G为OFDM符号总长度(样点数),G=N+D,N为有用符号长度(样点数),D为循环前缀长度(样点数),Tc=1/ft为样点周期, ft为发端采样频率,Ts为OFDM符号周期,g(t)为矩形成型脉冲,对应第k个OFDM符号信号模型时间取值范围t0+(k-1)(N+D)Tc≤t≤t0+(N+D)kTc,ck,l为加入循环前缀后第k个OFDM符号的第l个样点,其时域表达式如下
,l=0,1,…,G-1
(4)
其中,ak,n为频域上第k个OFDM符号第n个子载波上的调制数据,n=0,1,…,N-1。
3 OFDM信号的循环自相关特性
信号第k个OFDM符号中,延迟样点为nτ(0≤nτ≤N)的时域数据ck,l的自相关为:
(5)
根据上式,则有:
(6)
这里的相关特性是由于循环前缀所引入的,不考虑初始时延、频偏和噪声,则接收信号的自相关函数为:
Rr(t,τ)=E[r(t)·r*(t-τ)]=
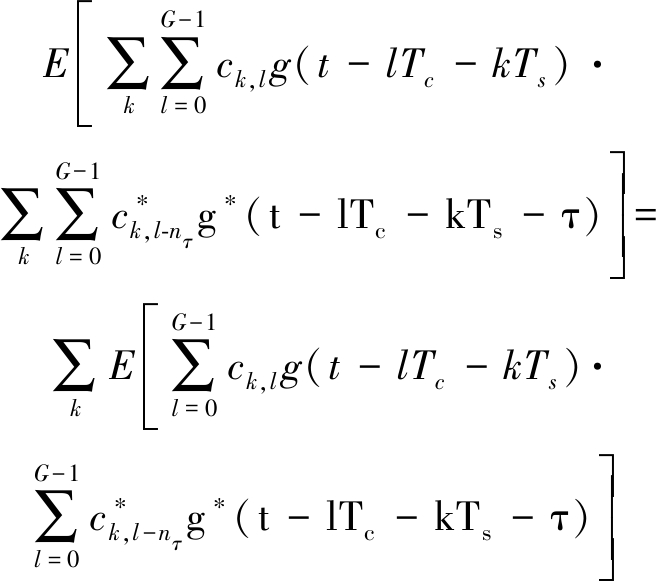
(7)
其中,延时τ=nτTc。
由式(7)可知,OFDM信号的循环周期有两个,表达式如下所示:
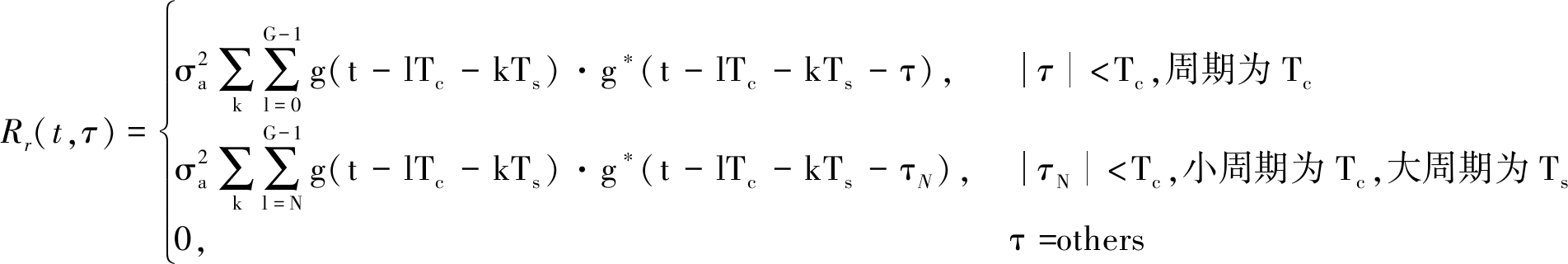
(8)
其中,τN=|τ|-NTc。由以上证明可知OFDM信号具有二阶循环平稳特性,OFDM信号有Tc和Ts两个循环周期,Rr(t,τ)存在周期性,根据傅里叶变换的性质,其对t的傅里叶变换则会出现离散谱线,谱线位置在α=m/Tc或α=m/Ts,m∈Z处,这里α被称作循环频率。对Rr(t,τ)做关于t的傅里叶变换可得
(9)
图1为无导频OFDM信号的循环自相关谱,谱特征对应公式(9),OFDM信号循环前缀为1/8有用符号长度,512个子载波,无导频。在循环频率α=0截面,存在相关谱峰,基于谱峰位置可估计OFDM有用符号长度。在时延τ=Tu截面,在基准频率α=m/Ts位置存在谱峰,可估计OFDM符号周期。为更加清晰分析谱特征,对应参数估计流程,给出循环自相关谱的二维剖析。
图2为发端无导频OFDM信号的循环自相关谱(不同截面)。在非协作通信中,对于未知信号的接收采样频率通常为符号速率的非整数倍,设接收采样频率为fs=Rsamft,Rsam为收发采样频率的比值。由式(6)和式(9)以及图 2,则可总结出利用无导频OFDM信号(含循环前缀)的循环自相关函数估计其时间参数的步骤如下:
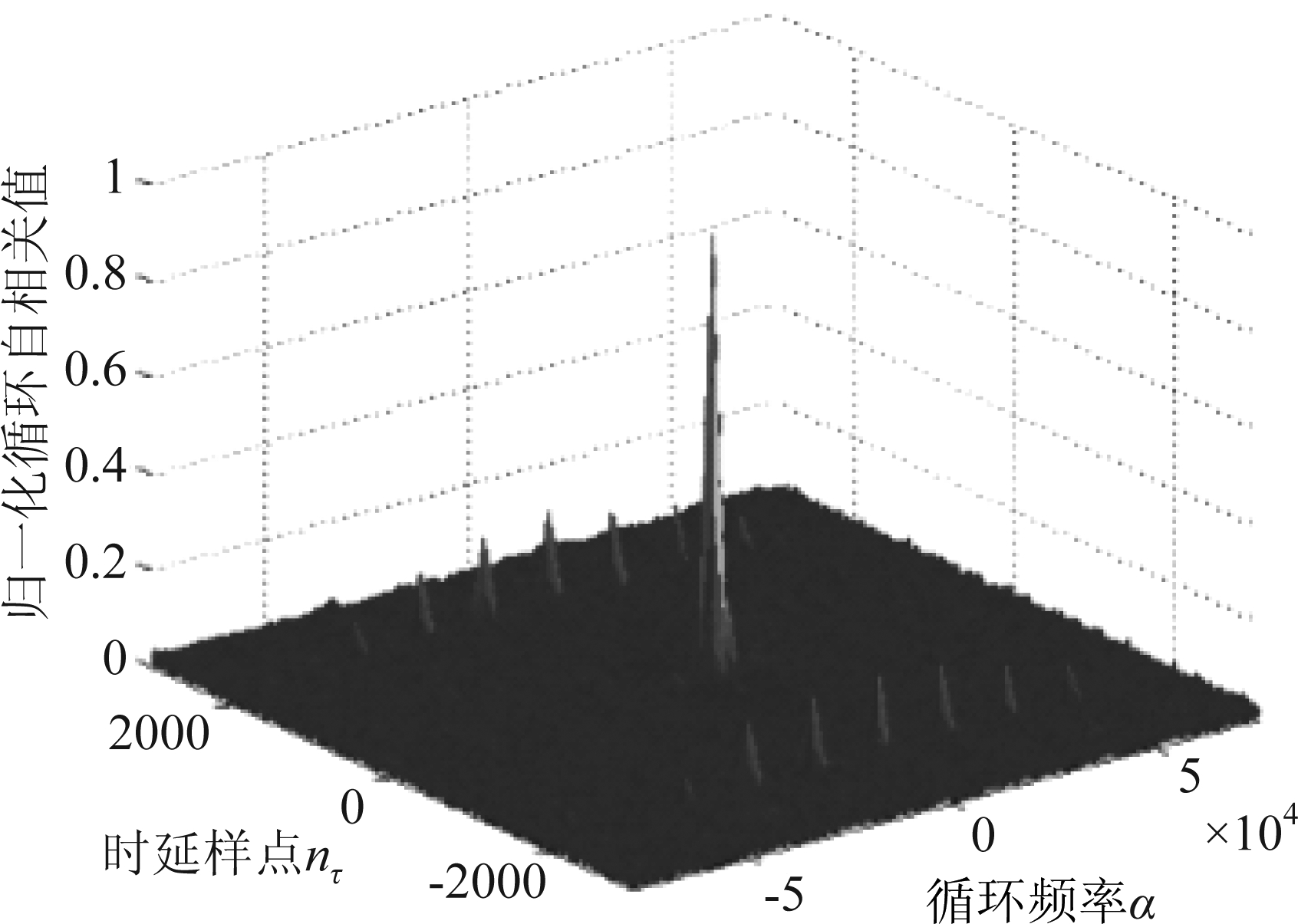
图1 无导频OFDM信号循环自相关谱
Fig.1 Cyclic autocorrelation spectral of OFDM signals without pilots
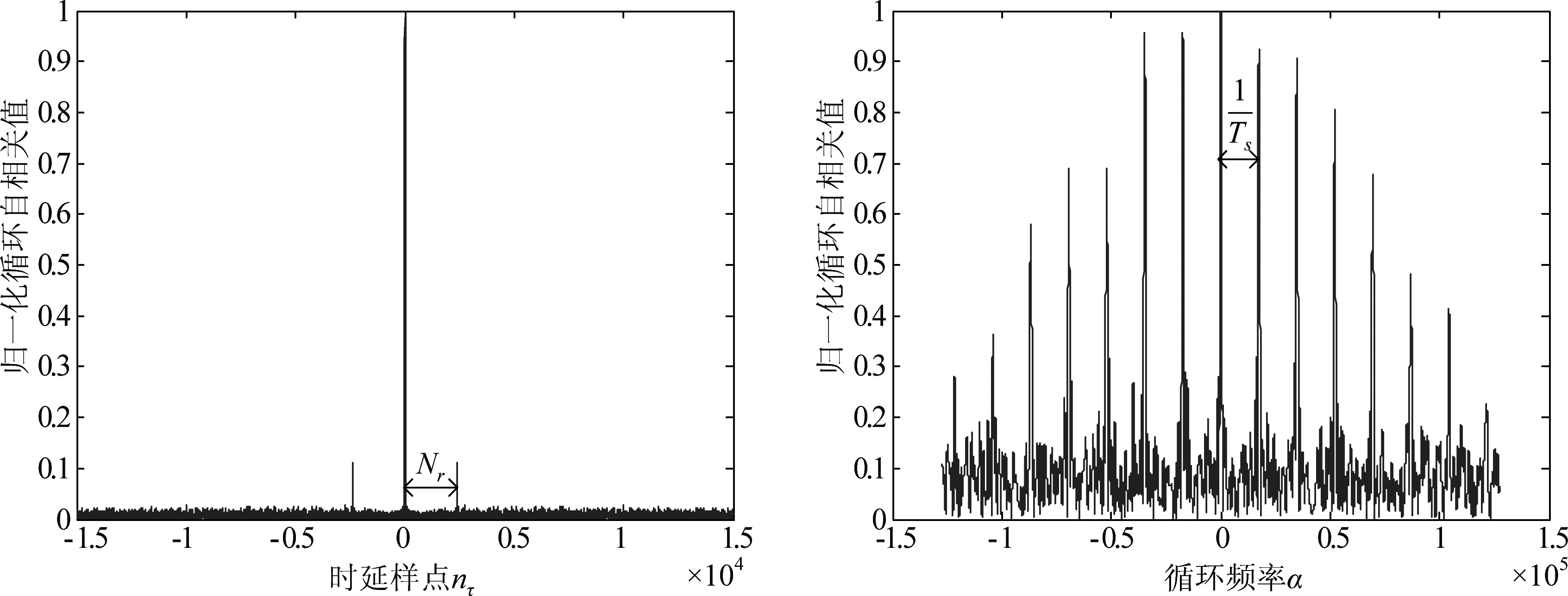
图2 无导频OFDM信号循环自相关谱(不同截面)
Fig.2 Cyclic autocorrelation spectral of OFDM signals without pilots (different sections)
1)由图2中循环频率α=0截面,计算截面上两峰值之间的距离Nr,结合采样频率fs,则可估计出OFDM信号的有用符号周期
2)计算时延τ=0的截面图,搜索截面上相邻两谱线的距离,即能估计出OFDM信号的码片时宽
3)根据1)中估计出的有用符号周期
由图2中时延
的截面图,搜索截面上相邻两谱线的距离得基准频率
即能估计出OFDM信号的符号周期
4 基于循环自相关的OFDM时间参数改进算法
在实际OFDM通信系统中,为使接收方实现准确的信道估计和符号定时,通常会加入导频。如图3为常见的导频图案,其中图(c)为矩形型星状导频,图(d)为菱形型星状导频。相邻导频间隔子载波数为M,每I个OFDM符号插入相同导频序列。无论是块状导频,梳状导频,还是星状导频[11],均会引起二阶循环特征的变化。对于块状导频,在时域插入导频,时域导频块间存在相关性,从而引入新的相关谱峰。由于相邻块状导频间隔I个OFDM符号,所以引入谱峰位置对应τ值较大,可被当做异常簇删除。但对于梳状导频和星状导频,导频引入的周期相关性造成特征谱变化,从而影响了OFDM信号的时间参数估计。当导频与数据的功率比值较高时,传统基于循环自相关的时间参数估计算法已不适用。因此为了使基于循环自相关的OFDM时间参数估计算法更适合实际应用场景,必须对时间参数估计算法进行改进。本文重点研究含梳状导频或星状导频OFDM信号的时间参数估计。
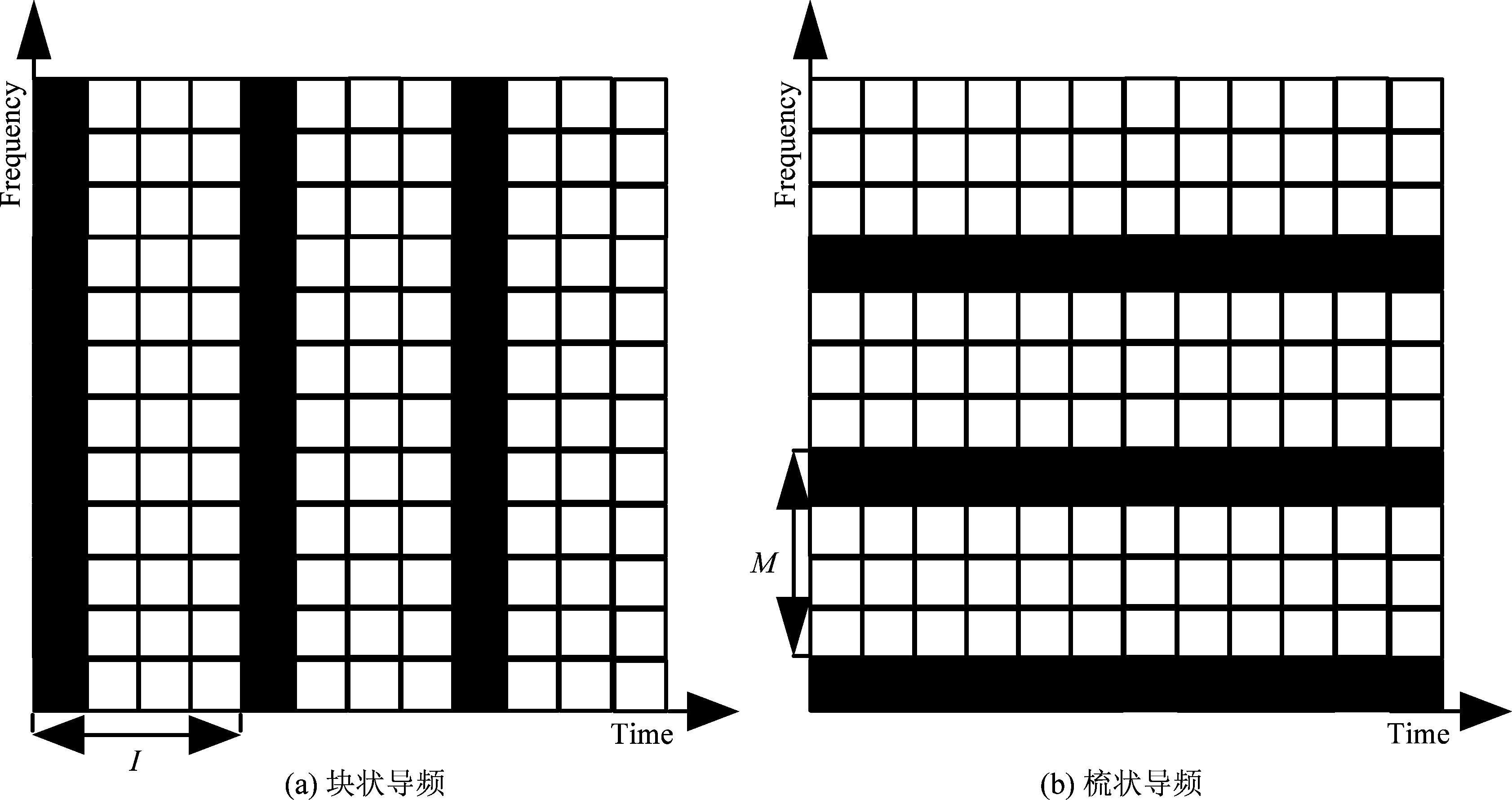
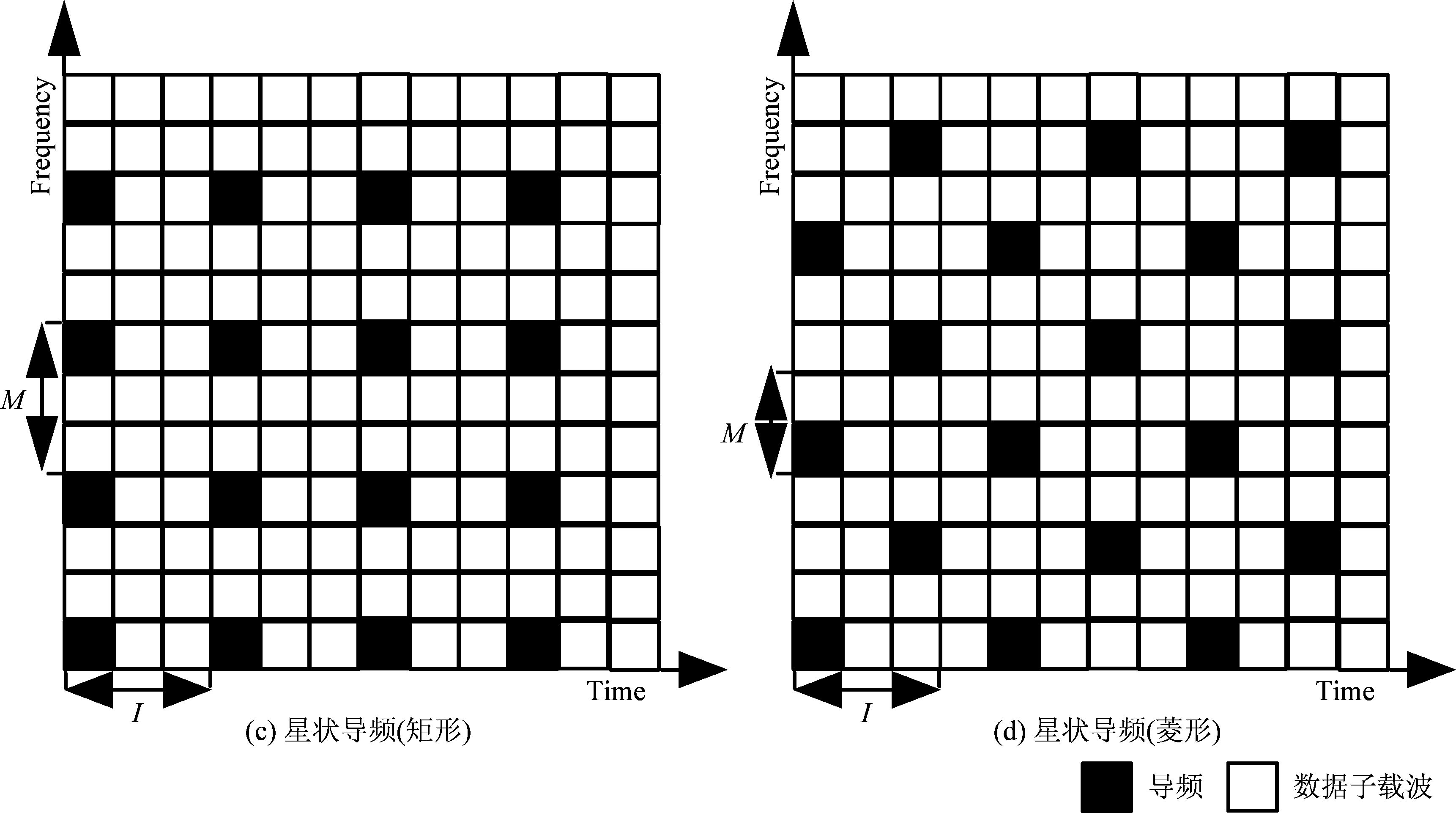
图3 导频图案
Fig.3 The pattern of pilots
4.1 含导频的OFDM信号二阶循环特性分析
在实际通信系统中,通信方为实现良好的信道估计[10-11],在信号中插入导频,此时符号间的导频数据具有相关性。对于侦听方,在盲解调过程中基于循环自相关进行OFDM时间参数估计会受到符号间导频相关带来的影响,此时在循环频率α=0截面会出现多个峰值,下面给出理论分析。
假设OFDM信号在频域每M个子载波插入一个导频,pk,n表示第k个OFDM符号上的第n个子载波上的导频数据,对应导频序列为[pk,1,…,pk,(np-1)M+1,…,pk,(Np-1)M+1],np=1,2,…,Np,Np表示导频数目,假设仅导频子载波上存在导频数据,其他子载波为空。此时对应的时域数据如下
l=1,2,…,G-1
(10)
对时域数据自相关
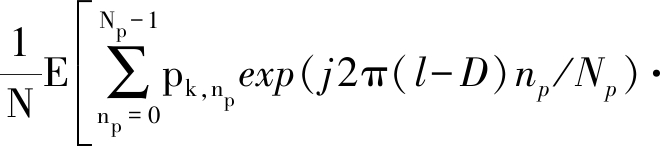
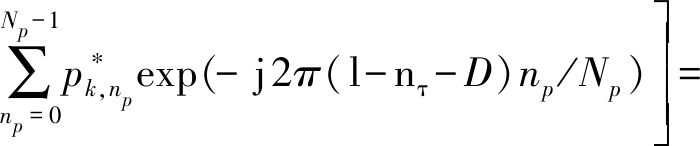
(11)
对应在时延nτ=0,Np,2Np，…,(M-1)Np会出现峰值。
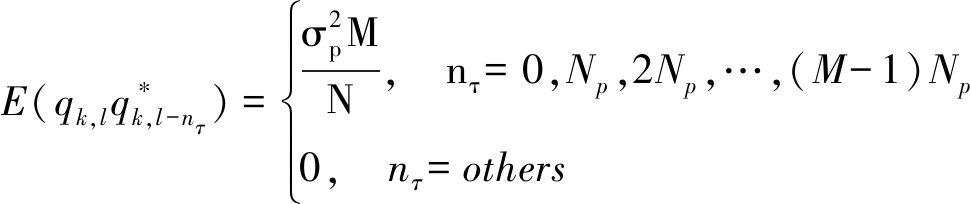
(12)
经过脉冲成型,得到等效的基带输出,可得到对应自相关函数
Rp(t,τ)=E[r(t)·r*(t-τ)]=
(13)
简化推导,此处忽略成型脉冲,分析循环频率α=0的循环自相关截面中导频引入的相关特性。
(14)
当循环频率α=0时,在一个OFDM符号长度范围内,对应时延
存在峰值,峰值幅度为
此时,对于式(9),式(14)为循环频率α=0时引入的干扰项。引入的周期性谱线峰值受导频功率
和频域相邻导频间隔M影响。
假设OFDM信号循环前缀为1/8有用符号长度,512个子载波,其中星状导频采用图3中(c)导频图案,每I=2个OFDM符号导频序列相同,带内信噪比为10 dB。相邻导频间隔的子载波数M=N/Np,导频与信号数据的功率比为Ratio。
图4为含导频OFDM信号的循环自相关谱(三维)。由于导频的存在,循环自相关谱α=0截面谱特征发生变化,循环自相关谱τ=Tu截面谱特征则保持不变。为更加清晰分析谱特征变化,对比不同导频类型、导频间隔和导频功率的谱特征,给出α=0截面的OFDM循环自相关谱谱特征。
图5为含导频图案的OFDM信号循环自相关谱(α=0截面)。在含导频的OFDM信号中,星状导频每I=2个OFDM符号插入相同导频序列。对比图(a)和图(c),无论是梳状导频还是星状导频均会引起谱特征变化；对比图(b)和(c)可知,当导频功率较高时,引入的周期性谱线更加明显,影响有用符号长度N值的估计；对比图(c)和图(d),在一个OFDM符号内nτ=0,Np,2Np,…,(M-1)Np位置存在谱线,导频间隔越大,导频数目越少,谱线间隔越小,谱线峰值越小。如图5中(b)、(c)、(d),|nτ|=IG位置均会出现大周期性峰值谱线,在|nτ|=kN/M,k∈Z位置均出现小周期性峰值谱线。这一周期性特性受导频数目和导频功率的影响,导频的间隔越大(即导频数目越少),谱线间隔越小,而功率越大,引入的谱线值越高。图(c)、(d)的大周期和小周期谱线更为明显,此时会影响目标峰值谱线的检索,从而造成有用符号长度N的错误估计。
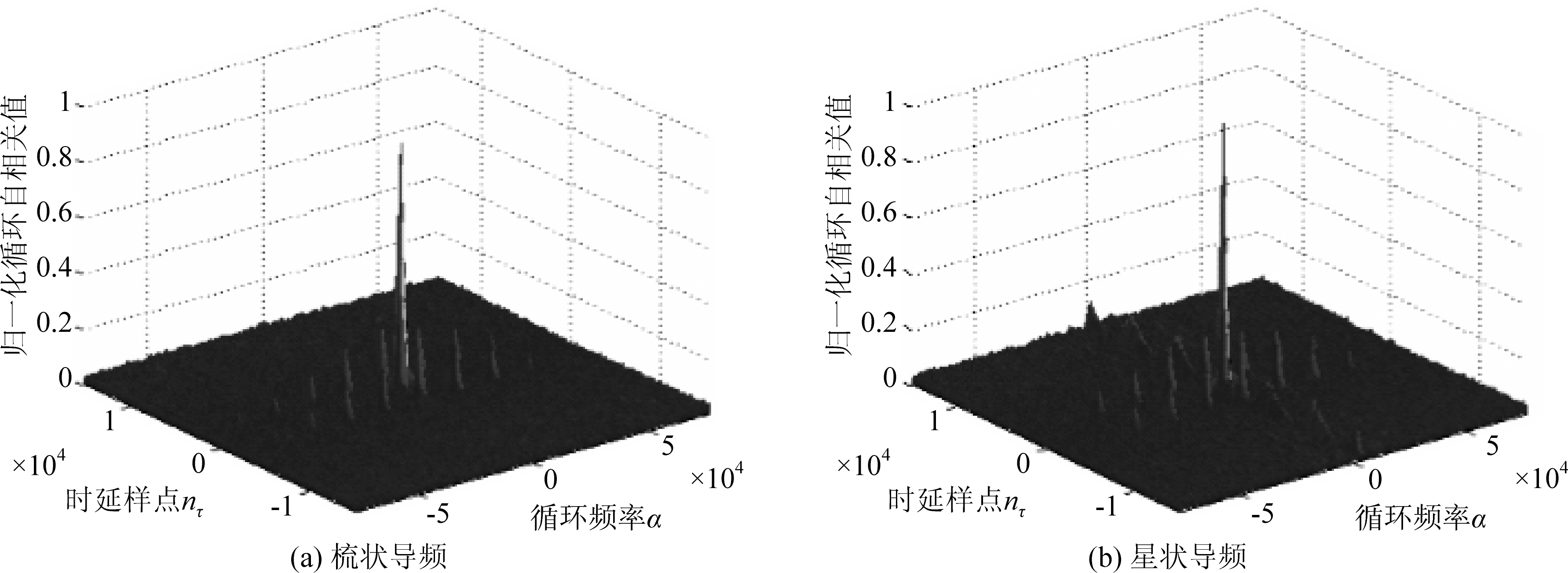
图4 含导频的OFDM信号循环自相关谱
Fig.4 Cyclic autocorrelation spectrum of OFDM signals with pilots
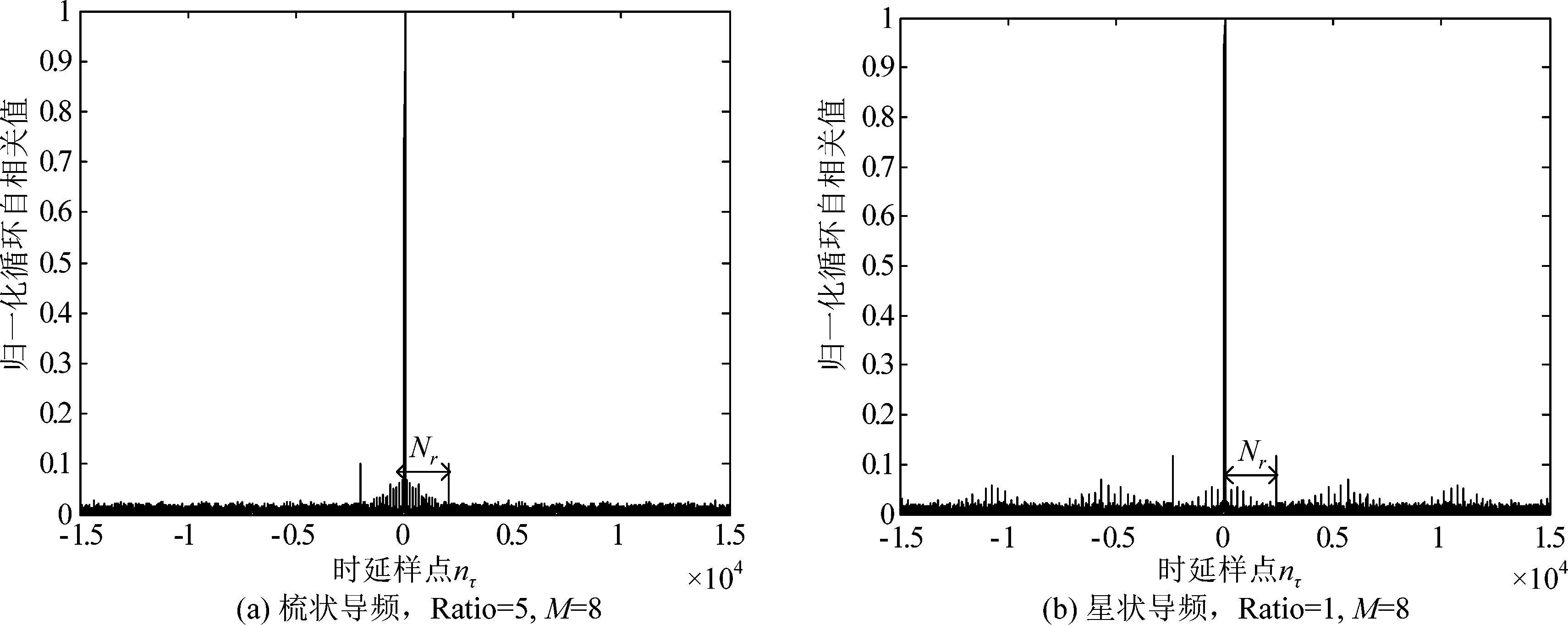
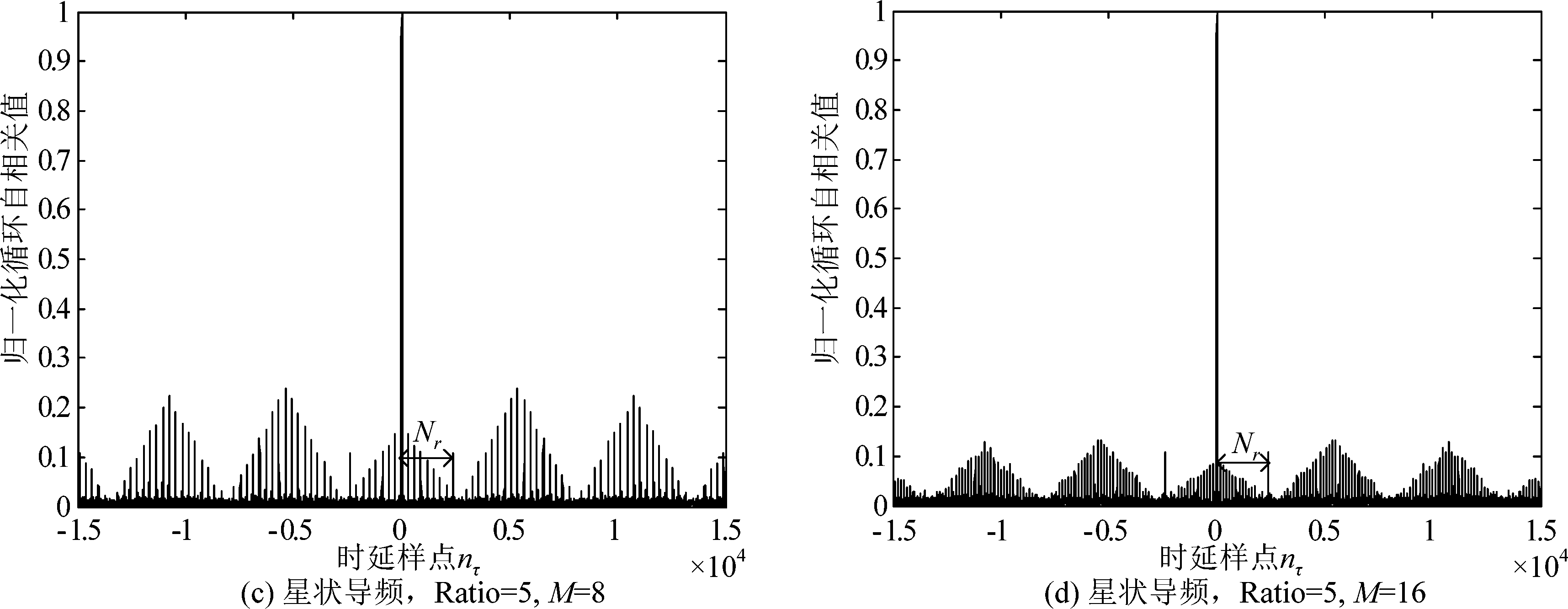
图5 含导频的OFDM信号循环自相关谱α=0截面
Fig.5 Cyclic autocorrelation spectrum of OFDM signals with pilots when α=0
4.2 基于循环自相关的OFDM时间参数估计算法改进
4.1小节分析了OFDM信号(含循环前缀)中由未知导频引起的循环自相关函数α=0截面的谱特征变化。本小节结合实际应用,对传统算法进行改进。定义门限T为循环自相关函数α=0截面的谱密度乘以门限因子,设置不同门限因子对应动态门限。具体算法流程如下:
(1)通过预处理估计出信号带宽
(2)分析循环自相关函数α=0截面的峰值谱线,检索大于门限T的谱线,对谱线进行分簇,相邻位置的峰值谱线为一簇,每一簇的最高值对应该簇值,每一簇最高值位置对应该簇的位置。
(3)改进目标峰值检索机制。分析簇的数目和簇的分布规律,删除异常簇,检索有用符号长度位置
1)由图 2和图5(a)可知,当簇的数目较少且相邻簇间隔不存在等间隔规律,说明此时导频与信号数据的功率比Ratio较小或不存在导频,零点外最大峰值谱线的簇位置对应有用符号长度位置
2)由图 5(b)、(c)、(d)可知,当簇的数目较多且相邻簇间隔存在等间隔规律,说明此时导频与信号数据的功率比Ratio较大,引入的周期性峰值明显。若存在比相邻等间隔簇值小的异常簇(噪声引入),则删除,同时删除由导频周期相关引入的等间隔的簇,则保留簇中最大值簇的位置对应有用符号长度位置若异常簇删除后保留的簇集合为空,且门限更新次数小于动态门限最大更新次数Imax,则更新门限T,重新返回步骤(1)。
(4)对谱峰值位置多次修正和插值,估计有用符号长度和有用符号周期。修正
得到
使其为值最接近于
的2的幂次方,即
相应得到
并对接收信号插值,然后根据信号带宽
再次修正,得到发端采样频率的估计值
最后估计出有用符号长度
有用符号周期
或
(5)多谱线联合估计符号总长度和符号周期
截面上不同谱线对应循环频率
联合不同m值对应的循环频率α求相邻谱线间隔平均值得
求得OFDM符号周期为
符号总长度
5 性能仿真分析
本节仿真对比改进前后OFDM信号时间参数估计的性能,首先仿真分析对于无导频的OFDM信号在算法改进前后的时间参数估计性能,然后以星状导频OFDM信号为例,分析含导频的OFDM信号参数估计性能。其中有用符号长度平均误差样点数(符号级)定义为
符号总长度平均误差样点数(符号级)定义为
有用符号周期归一化均方根误差
符号周期归一化均方根误差
OFDM信号为复基带信号,仿真参数设置如下:
表1 仿真参数设置
Tab.1 Simulation parameter setting
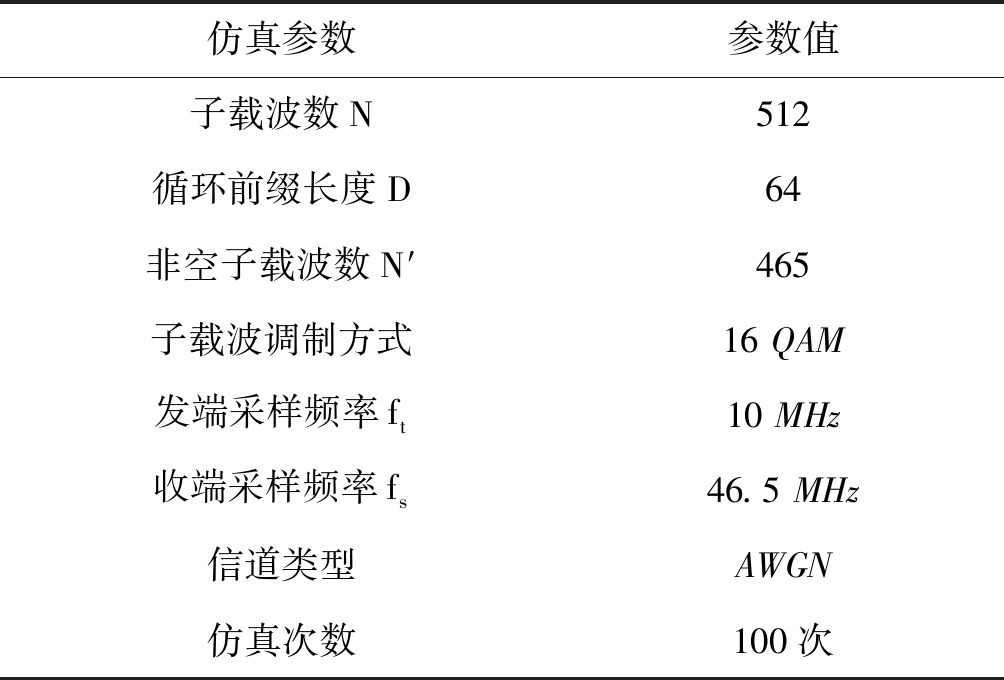
仿真参数参数值子载波数N512循环前缀长度D64非空子载波数N′465子载波调制方式16 QAM发端采样频率ft10 MHz收端采样频率fs46.5 MHz信道类型AWGN仿真次数100次
5.1 无导频OFDM信号参数估计性能仿真分析
图6为AWGN信道环境下、用传统算法(改进前)和改进后算法对无导频OFDM信号的有用符号长度N和OFDM符号总长度G的估计性能对比,其中带内信噪比SNR为信号平均功率与噪声平均功率的比值。带内信噪比SNR大于1 dB时,改进前后算法对N的估计均无误差,改进后对G的估计误差可降低一个数量级。改进后的算法引入多次插值,精估计发端采样频率
并联合不同m值对应循环频率α估计
估计精度更高。
图7为AWGN信道环境下、改进前后算法对无导频OFDM信号的有用符号周期Tu和OFDM符号周期Ts的估计性能。当带内信噪比大于1 dB时,改进后算法的NRMSETu和NRMSETs比改进前性能均可降低一个数量级。符号总长度G是基于nτ=N循环自相关截面进行估计,在有用符号长度N精确估计的前提下,才能准确估计G,因此图6和图7中G和Ts的估计误差大于N和Tu的估计误差。由于采样频率的估计存在误差,即使N估计误差为0,Tu的估计依然存在误差,但改进算法通过对峰值位置的多次修正,比传统算法的估计更准确,Tu和Ts的NRMSE较改进前降低一个数量级。
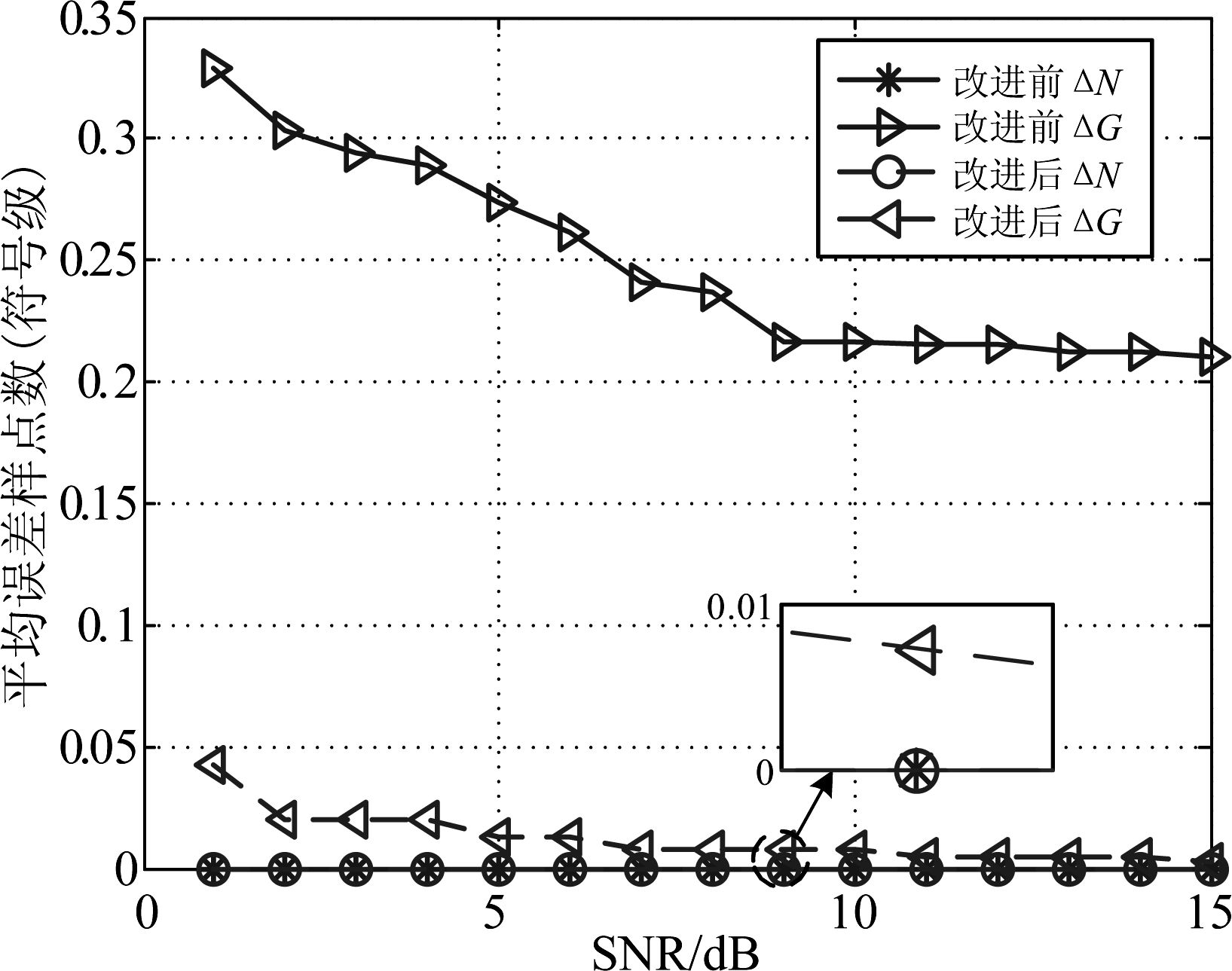
图6 无导频OFDM信号的N和G的估计误差
Fig.6 Estimation error of N and G of OFDM signals without pilots
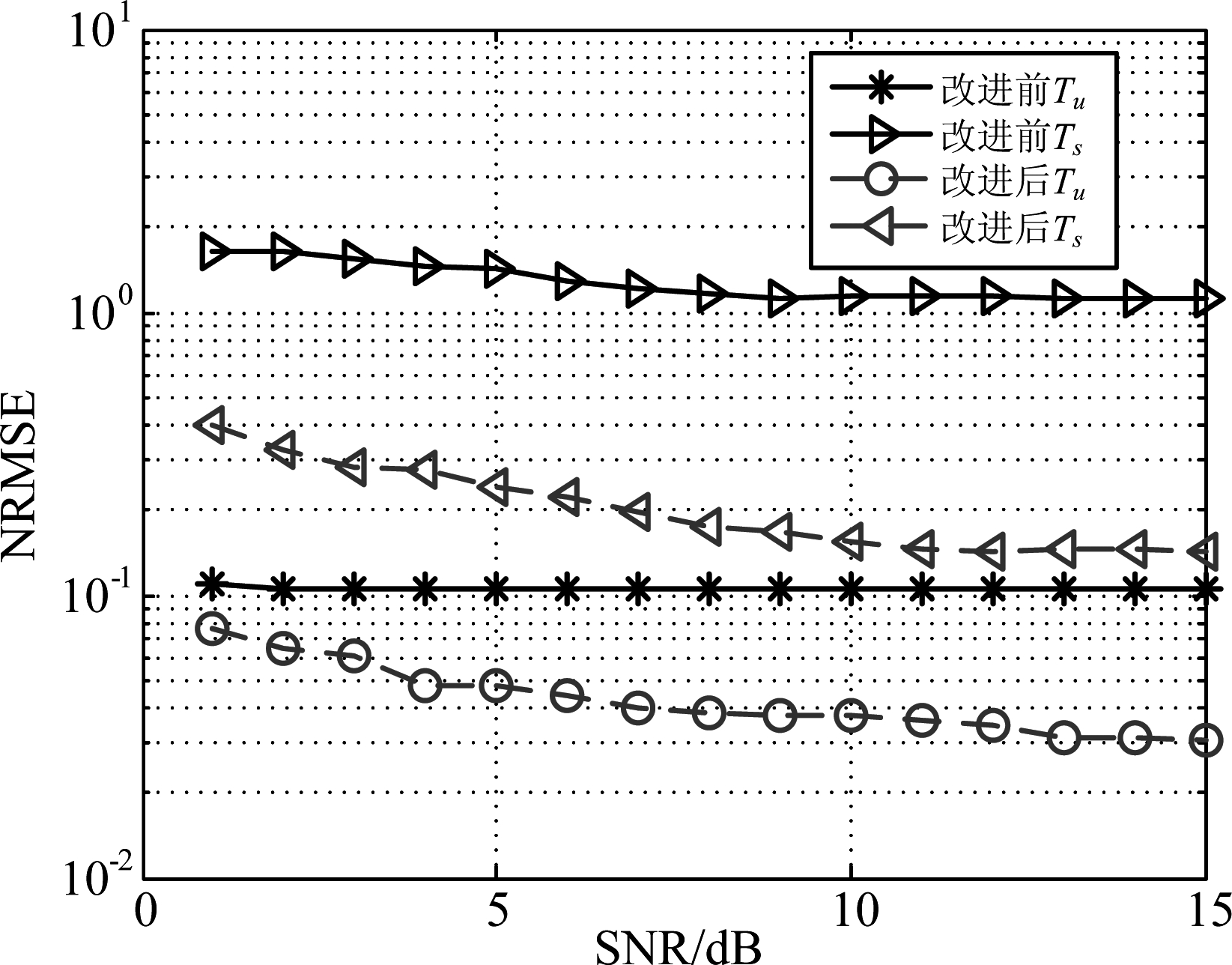
图7 无导频OFDM信号的Tu和Ts归一化均方根误差
Fig.7 Normalized root mean square error of Tu and Ts of OFDM signals without pilots
5.2 含导频OFDM信号参数估计性能仿真分析
由图5可见,无论是梳状导频还是星状导频,导频均会引入更多的周期性谱线,当导频功率较高且导频数目较多时,引入的周期性谱线更加明显。此时用改进前的时间参数估计算法无法估计时间参数N、G、Tu和Ts,此时需采用改进后算法。在实际通信系统中,为降低开销,提高信息传输效率,导频图案多采用星状导频。为了更好地反映实际场景,本文仿真时采用了一种常见的星状导频图案:奇数符号采用一组导频调制序列和子载波位置,偶数符号采用另一组导频序列和子载波位置,相邻导频间隔子载波数M=16,导频调制方式为QPSK,此时带内信噪比SNR为信号(含信号数据和导频)平均功率与噪声平均功率的比值,其中导频与数据功率比为5,其他参数见表1。
图8为AWGN信道环境下、改进后算法对含导频OFDM信号的N和G的估计性能。此时改进前算法已无法有效估计OFDM时间参数。基于改进后算法,当带内信噪比大于1 dB时,OFDM有用符号长度N的估计误差为0；当带内信噪比大于10 dB时,OFDM符号长度G的平均采样点误差降至0.01以下。改进后的算法同样适用于含导频OFDM信号的时间参数估计且性能并未降低。
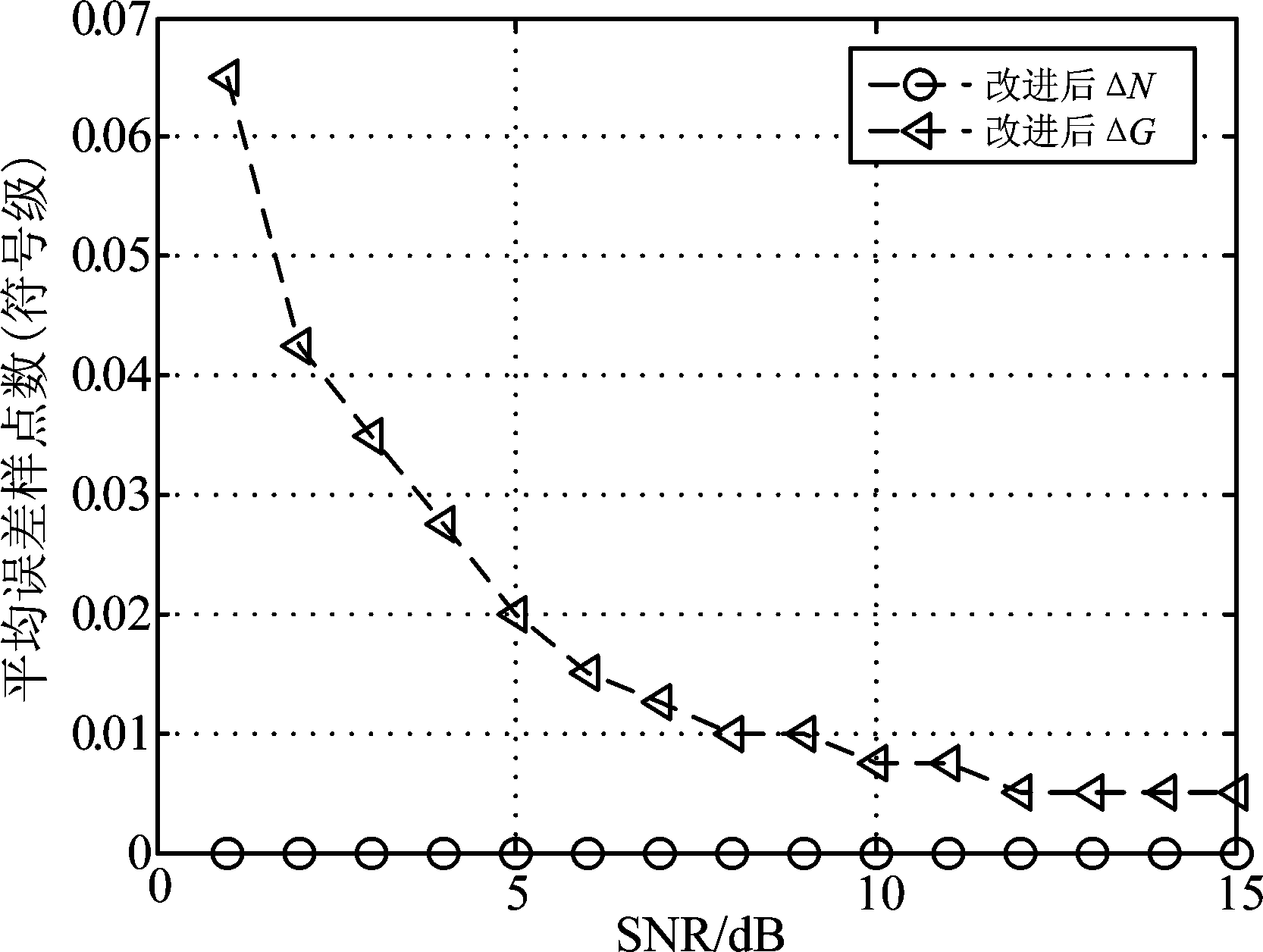
图8 含导频OFDM信号的N和G的估计误差
Fig.8 Estimation error of N and G of OFDM signals with pilots
图9为AWGN信道环境下基于改进后算法含导频OFDM信号的Tu和Ts的估计性能。基于改进后算法,带内信噪比大于1 dB时,有用符号周期Tu的均方根误差小于0.5个样点,符号周期Ts的均方根误差小于0.1个样点。对比无导频OFDM信号和含导频OFDM信号的仿真结果,改进后算法均可有效估计OFDM时间参数且性能一致,同样适用于含导频OFDM信号。改进后算法增加了峰值检索机制,有效避免了导频引入二阶谱峰的影响,更适用于实际应用场景。
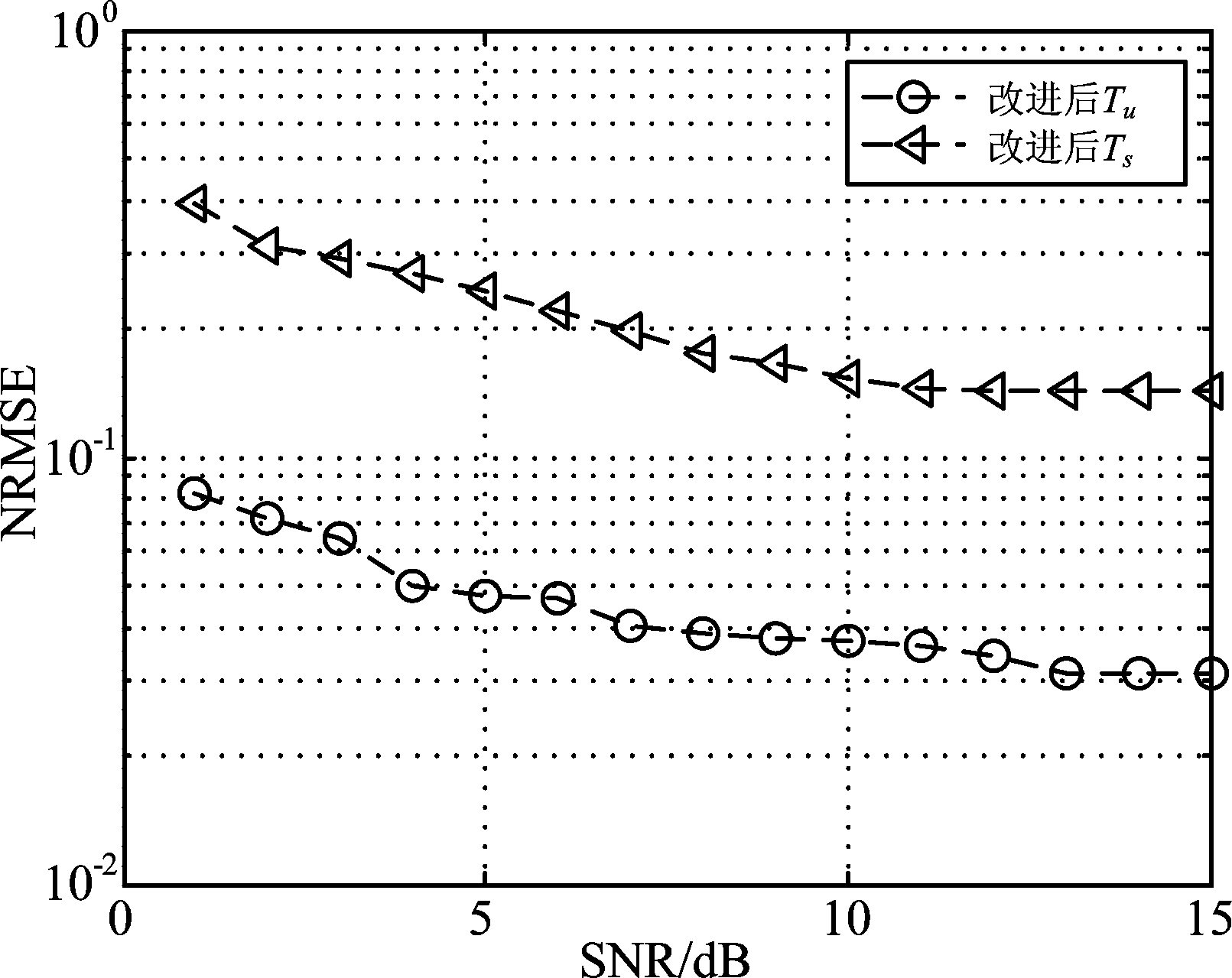
图9 含导频OFDM信号的Tu和Ts归一化均方根误差
Fig.9 Normalized root mean square error of Tu and Ts of OFDM signals with pilots
6 结论
本文研究了基于循环自相关的OFDM时间参数估计算法在实际非协作系统中的应用,分析了含导频OFDM信号的循环自相关谱,改进了时间参数估计算法。改进后算法既适用于无导频OFDM信号的时间参数盲估计,比传统算法性能更优,Tu和Ts的NRMSE降低一个数量级；又克服了传统算法无法用于含导频OFDM信号侦收的问题,对于含导频OFDM信号时间参数盲估计,具有很好的估计性能,同时满足非整数倍采样应用场景,算法更加鲁棒,适用范围更广,具有很好的应用价值。
[1] 丁凌琦, 穆道生, 蒋太杰. OFDM技术应用现状分析[J]. 软件, 2016, 37(10):130-134.
Ding Lingqi, Mu Daosheng, Jiang Taijie. Analysis of Application Actuality of OFDM Technology[J]. Computer Engineering & Software, 2016, 37(10): 130-134.(in Chinese)
[2] 霍凯, 赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11):2776-2789.
Huo Kai, Zhao Jingjing. The Development and Prospect of the New OFDM Rsdar[J]. Journal of Electronics and Information Technology, 2015, 37(11): 2776-2789.(in Chinese)
[3] Arslan H, Mahmoud H A, Yücek T. OFDM for Cognitive Radio: Merits and Challenges[J]. Wireless Communications IEEE, 2009, 16(2):6-15.
[4] Zou Li. Detection of the guard interval length in OFDM systems[C]∥Consumer Communications and NETWORKING Conference, 2006. Ccnc. IEEE Xplore, 2006:1048-1051.
[5] Tang N J, Li B B, Liu M Q. A modified blind OFDM systems parameters estimation method[C]∥IEEE International Conference on Communication Technology. IEEE, 2011:1279-1282.
[6] 张海川, 雷迎科. 短循环前缀OFDM信号参数估计方法研究[J]. 信号处理, 2016, 32(12):1489-1496.
Zhang Haichuan, Lei Yingke. Study on Parameter Estimation for the Short Length Cyclic Prefix OFDM Signal[J]. Journal of Signal Processing, 2016, 32(12): 1489-1496.(in Chinese)
[7] Liu J G, Wang X, Nadeau J, et al. Blind parameter estimation for OFDM interception receiver with iterative cyclostationary analysis[C]∥Military Communications Conference, 2011-Milcom. IEEE, 2012:2211-2215.
[8] Punchihewa A, Bhargava V K, Despins C. Blind Estimation of OFDM Parameters in Cognitive Radio Networks[J]. IEEE Transactions on Wireless Communications, 2011, 10(3):733-738.
[9] 王胜, 张天骐, 袁帅. 基于循环自相关的NC-OFDM信号参数的盲估计[J]. 计算机应用研究, 2019(5).
Wang Sheng, Zhang Tianqi， Yuan Shuai． Parameter blind estimation based on cyclic autocorrelation of NC-OFDM signals [J]． Application Research of Computers， 2019(5).(in Chinese)
[10] 张继东, 郑宝玉. 基于导频的OFDM信道估计及其研究进展[J]. 通信学报, 2003(11):116-124.
Zhang Jidong, Zheng Baoyu. Overview of pilot-aided channel estimation in OFDM[J]. Journal of China Institute of Communications, 2003(11): 116-124.(in Chinese)
[11] 魏雍, 苏立焱, 杨晨阳. 利用数据和导频的多小区Massive MIMO系统信道估计[J]. 信号处理, 2017, 33(6):781-791.
Wei Yong, Su Liyan, Yang Chenyang. Data and Pilot-Aided Channel Estimation for Multi-cell Massive MIMO System[J]. Journal of Signal Processing, 2017, 33(6):781-791.(in Chinese)
[12] 何雪云, 赵天, 梁彦. 大规模MIMO-OFDM系统结构化压缩感知信道估计中导频优化方法研究[J]. 信号处理, 2017, 33(1):87-94.
He Xueyun, Zhao Tian, Liang Yan. Optimizing Pilots for Structured Compressive Sensing Based Channel Estimation in Massive MIMO-OFDM Systems[J]. Journal of Signal Processing, 2017, 33(1): 87-94.(in Chinese)
