1 引言
调制方式识别和参数估计在认知无线电、频谱监测与管理、电子侦察、干扰识别、非合作通信等军用和民用通信领域具有广泛的应用[1-2],其中参数的盲估计是调制方式识别的前提和基础,多进制数字相位调制(Multiple Phase Shift Keying,MPSK)和多进制正交幅度调制(Multiple Quadrature Amplitude Modulation,MQAM)等星座类调制信号具有较高的频谱利用率,是数字通信系统中的典型调制方式[3],对MPSK/MQAM调制信号的盲识别和盲解调是近些年的研究热点[4],其中,频偏和符号速率是星座类调制信号盲识别和盲解调过程中需要估计的重要参数[5- 6]。
在目前的研究中,载波频偏的估计算法主要包括:频率中心法[7]、最大似然法[8]以及多次方谱载波估计算法[9]等。频率中心法直接以信号带宽的中心频点作为载波频率,计算简单,在带宽估计的同时估计载波频偏,精度较低,通常作为频偏粗估计值;最大似然载波估计算法具有较好性能,但其估计范围因受接收信号长度和采样速率影响,估计范围较小;多次方谱估计算法适用于星座类调制信号,并且低阶调制信号的载波提取特征明显,且复杂度低,估计范围较最大似然法大,但传统多次方谱算法估计精度仍不够高;为此,本文基于多次方谱算法,提出了频偏估计的改进算法:结合新的频率估计方法[10],提高了频偏估计精度,同时提出一种基于谱峰指数的置信度准则,提高了频偏估计的可靠性,获得了优于传统算法的估计性能。
目前符号速率盲估计算法主要有带宽估计法、循环谱法[11]、IFFT法[12]以及二次小波变换算法[13]。带宽估计法是将带宽估计结果作为符号速率估计结果,复杂度低,但精度低;循环谱法是根据接收信号的循环谱,在特定频点位置得到载频及符号速率的特征谱线,计算复杂度较高,且估计误差较大;IFFT算法利用根升余弦滤波器的形状特点,通过计算时域信号两次过零点的样点间隔,并结合采样频率估计符号速率,当小数采样时,符号速率估计不准确;二次小波变换可以放大信号的局部变化特性,使得信号的瞬时特性变得明显,并且此算法具有较好的鲁棒性。本文在传统基于二次小波变换的符号速率估计算法的基础上,结合新的频率估计算法[10],减小了估计误差,提高了算法性能。
本文内容安排如下:第2节介绍现有单载波MPSK/MQAM信号的载波频偏和符号速率盲估计算法原理;第3节阐述单载波MPSK/MQAM信号的载波频偏估计算法和符号速率估计算法的改进思路和实现步骤;第4节仿真分析了QPSK和16QAM的载波频偏和符号速率估计性能,并对改进前后算法的估计性能进行了对比分析;最后全文总结。
2 现有单载波MPSK/MQAM信号参数盲估计算法原理
2.1 载波频偏估计算法原理
2.1.1 基于多次方谱的频偏估计算法
对星座类调制信号求N次幂,可以去除调制信息的影响,使信号中产生与载波频率相关的单频分量,频谱中将产生较为突出的谱线。对于MPSK/MQAM这类抑制载波的单载波信号,常用多次方谱的方法估计其载波。
首先,对接收信号r(t)建模如下:
r(t)=s(t)+n(t)
(1)
其中n(t)为均值为0、方差为σ2的加性高斯白噪声,s(t)为MPSK/MQAM调制信号:
s(t)=Re[Amg(t)ej(2πfot+θm)]
m=1,2,…,M
(2)
式中Am和θm分别是承载了调制信息的载波幅度和相位,g(t)为低通脉冲波形, fo为收发载波频偏,定义为接收机中心频率减去发射机中心频率。由于r(t)不存在离散的信号载频,为了较精确估计频偏,现对接收信号进行N次幂,得到rN(t),使其含有与信息无关的频偏分量,即根据rN(t)在N倍载波频偏处存在离散谱线的特征,可以估计信号的频偏fo。常用MPSK/MQAM突出谱线位置对应关系如表1所示。
表1 调制方式及突出谱线位置对应表
Tab.1 Corresponding table of modulation mode and prominent line position

调制样式所需N次幂运算突出谱线位置BPSK2次幂2foQPSK4次幂4foQAM4次幂4fo
2.1.2 基于最大似然的频偏估计算法
最大似然(ML)估计是频偏估计中最常用的方法,其同样需要先求接收信号N次方去除接收信号中的相位调制信息,然后根据最大似然准则使得N次方信号的周期图取得最大值。L&R算法[15]是一种基于样本自相关函数的复正弦信号的估计算法,可以用于频偏的最大似然估计,L&R算法的载波频偏估计式为:
(3)
其中,![]() 为频偏估计值,Ts为采样时间间隔,L为接收信号采样长度。RN(τ)为接收信号N次幂的相关函数,为了降低运算复杂度常用时间平均代替统计平均,即:
为频偏估计值,Ts为采样时间间隔,L为接收信号采样长度。RN(τ)为接收信号N次幂的相关函数,为了降低运算复杂度常用时间平均代替统计平均,即:
![]()
(4)
Aτ为常数,γ(τ)为时间平均代替统计平均所引入的误差。
2.2 符号速率估计算法原理
2.2.1 基于IFFT的符号速率估计算法
基于IFFT的符号速率估计算法利用根升余弦滤波器的形状特点,通过观测时域相关信号的过零点位置的样点间点数求得过采样倍数,然后结合收端采样频率确定符号速率。
2.2.2 基于二次小波变换的符号速率估计算法
小波变换具有局部显微特性,对信号的瞬时特性具有较强的捕获能力,采用二次小波变换可对数字调制信号进行符号率估计。根据文献[13]对小波变换的定义可知当噪声忽略不计时,MPSK/MQAM信号经过二次小波变换(Harr小波基)后的包络为:
(5)
其中,a为尺度,Td为符号周期,Ai为小波变换幅度。
对二次小波变换的包络CWT 2r(t)(a,τ)进行傅里叶变换得:
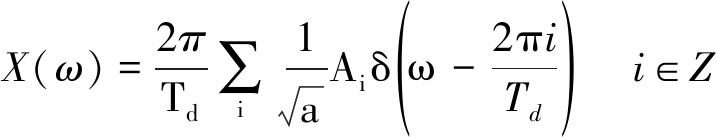
(6)
则X(ω)零频之外的第一个尖峰所在位置即为符号速率Rs=1/Td。
3 单载波MPSK/MQAM信号参数盲估计改进算法
3.1 改进思路1:更精确的频率估计
多次方谱频偏估计法和小波变换符号速率估计法均需要进行DFT变换,然后根据谱峰的位置进行参数估计,但是由于DFT的结果为离散谱线,当频偏为DFT分辨率的小数倍时,通过只寻找谱峰会造成估计误差,因此本文采用一种新的频率估计方法,结合2L-DFT和迭代校正进行频偏的精确估计[10],估计出小数频偏,再在整数倍频偏估计值的基础上补偿小数频偏,从而提高频偏估计的精度。
假设载波收发频偏fo为:
fo=fr+fp
(7)
其中fr为频偏fo的DFT分辨率整数倍估计值, fp为小数倍估计值。整数频偏位置km可以通过搜索最大值进行估计,小数频偏位置δ则通过2L-DFT和迭代校正进行精确估计[10]。首先通过Fang算法得到δ的初始估计值![]() 为:
为:
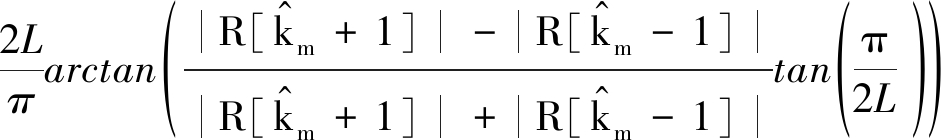
(8)
其中R[k]为接收信号的2L-DFT变换,![]() 为突出谱峰的位置。然后采用功率最高的两根谱线对频率估计值进行多次迭代校正,迭代第i+1次的估计值
为突出谱峰的位置。然后采用功率最高的两根谱线对频率估计值进行多次迭代校正,迭代第i+1次的估计值![]() 为:
为:
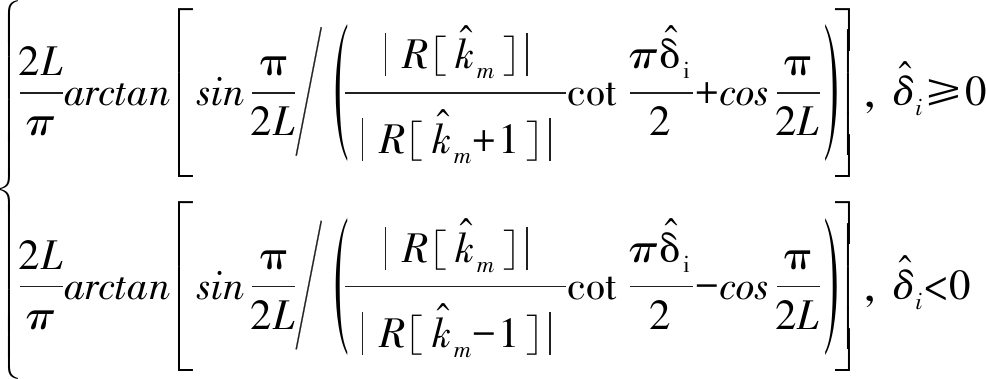
(9)
其中i=0,1,…,T-1,T为设定的迭代次数。最后得到的频偏估计值为:
(10)
其中Δf=Fs/2L为2L-DFT变换后的频率分辨率,Fs为采样频率。
3.2 改进思路2:结合信噪比的谱峰指数置信度准则
当信噪比(Signal to Noise Ratio,SNR)较低时,频偏估计值的可靠性大大降低,因此,本文提出了一种基于信噪比和谱峰指数的置信度准则,通过SNR和谱峰指数值判断频偏估计的可靠性:若谱峰指数大于门限,则认为本次频偏估计置信度较高,估计值可靠;否则,认为不可靠,此时频偏估计失效,保留预处理的粗估计值作为载波频偏估计值,谱峰指数的门限设置与信噪比有关。
在此先给出峰值谱线的定义:若某一谱线在其左右邻域内为最大值,则称该谱线为峰值谱线,即若|R[k]|为峰值谱线(k为谱线的位置),则满足|R[k]|≥|R[k+Δk]|且|R[k]|≥|R[k-Δk]|,其中Δk为邻域参数。谱峰指数[14]计算方法:
(1)找出待测信号带宽内所有峰值谱线;
(2)将峰值谱线从大到小排列;
(3)取峰值最大的前2·Δk+1条谱线,求和为SMax1;
(4)在(3)之外的剩余谱线,再取峰值最大的前2·Δk+1条谱线,求和为SMax2;
(5)求比值SPI=SMax1/SMax2,SPI则是谱峰指数。
通常当谱峰指数SPI越大、SNR越高,频偏估计的置信度越高,反之当谱峰指数SPI越小、SNR越低,频偏估计的置信度越低,因此根据这个特点,本文设计了基于SNR和谱峰指数的置信度准则,低信噪比时,SPI波动较大,此时设置较高的SPI判决门限;较高信噪比时,此时的谱峰位置可靠,频偏估计对SPI值的依赖性减小,可设置较低的SPI门限,从而保证频偏估计结果的可靠性。
3.3 频偏估计改进算法实现步骤
(1)对接收信号进行预处理,粗估计得到信号带宽、频偏和信噪比等参数,并根据频偏粗估计值对信号进行下变频;
(2)根据带宽粗估计值对信号进行滤波,减小噪声影响;
(3)计算滤波后信号的N次幂,突出载频分量;
(4)进行DFT操作,得到信号的N次方谱;
(5)搜索突出谱峰,并结合改进思路1进行频偏精估计;
(6)结合改进思路2,验证估计结果的可靠性,若可靠则输出频偏精估计结果,若不可靠则保留频偏粗估计结果。
3.4 符号速率估计改进算法实现步骤
(1)对接收信号进行预处理、滤波、频偏精估计等操作后进行下变频为基带信号;
(2)对基带信号进行二次小波变换,放大其局部特性;
(3)进行DFT操作,得到信号的N次方谱;
(4)结合改进思路1,精确找出经过二次小波变换后的信号的谱峰位置,该频点所对应的频率值便是符号速率估计值。
4 仿真性能分析
本文以单载波QPSK和16QAM信号为例,仿真分析了改进前后频偏和符号速率的估计性能。系统仿真参数如表2所示。
表2 仿真参数设置
Tab.2 Simulation parameter settings
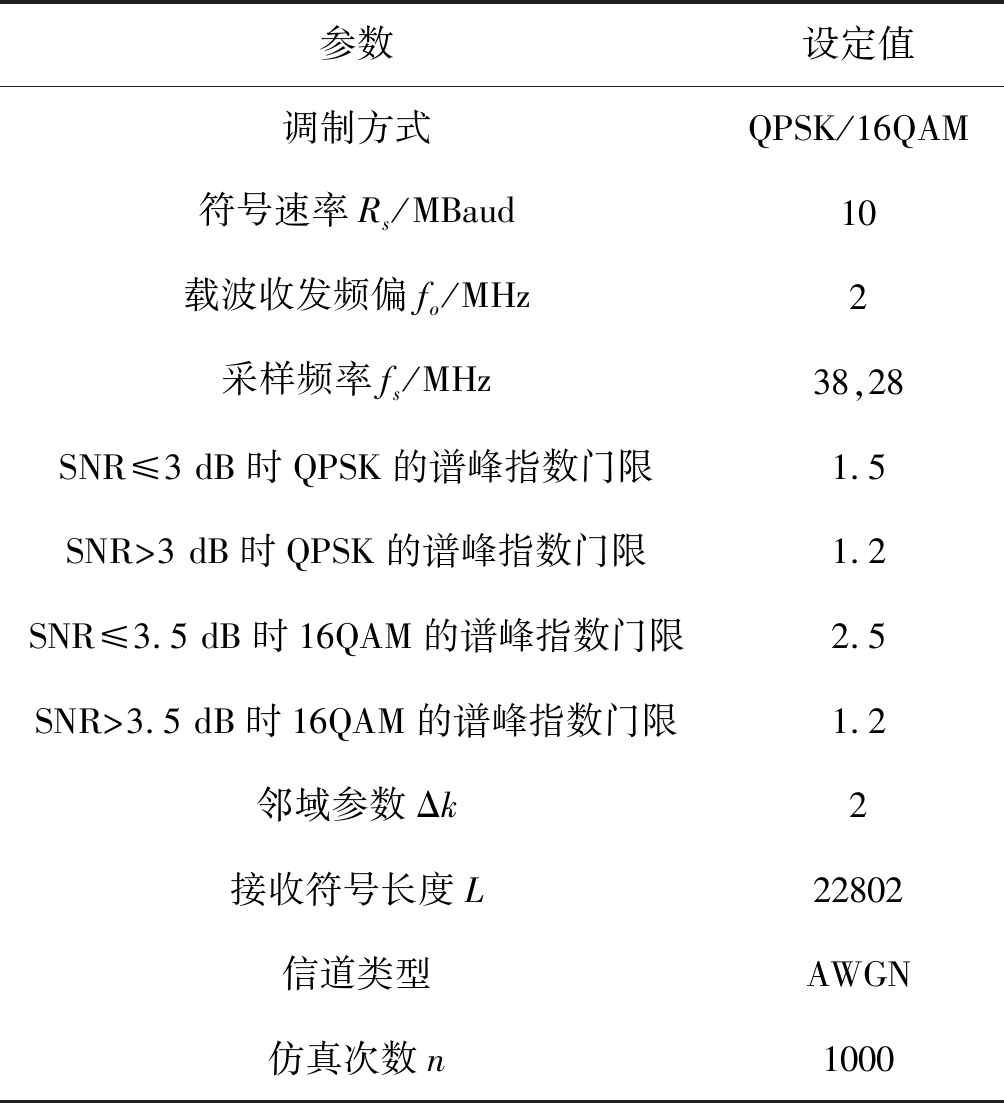
参数设定值调制方式QPSK/16QAM符号速率Rs/MBaud10载波收发频偏fo/MHz2采样频率fs/MHz38,28SNR≤3 dB时QPSK的谱峰指数门限1.5SNR>3 dB时QPSK的谱峰指数门限1.2SNR≤3.5 dB时16QAM的谱峰指数门限2.5SNR>3.5 dB时16QAM的谱峰指数门限1.2邻域参数Δk2接收符号长度L22802信道类型AWGN仿真次数n1000
经过4次幂运算后,QPSK在4fo上主要集中在1个相位上,相比于QPSK信号,16QAM在4fo上会有3个不同的相位,彼此影响,并且其调制幅度也会对其造成影响,导致其谱线没有QPSK的突出,尤其在低信噪比下噪声对其谱线的影响更大,因此二者确定频偏估计可靠性的信噪比门限略有不同,所以16QAM以SNR=3.5 dB为阈值、QPSK以SNR=3 dB为阈值进行谱峰指数(SPI)门限的设置;另外,在低SNR下,为了提高SPI的可靠性,16QAM SPI门限高于QPSK的情况。随着信噪比的增大,QPSK和16QAM的SPI都比较高,频偏估计结果对SPI依赖性降低,因此QPSK和16QAM在高SNR下的SPI门限相同。其中,SNR的大小可通过信噪比估计得到。
频偏估计和符号速率估计的性能通常用归一化均方根误差(Normalized Root Mean Square Error,NRMSE)表征,分别定义如下:
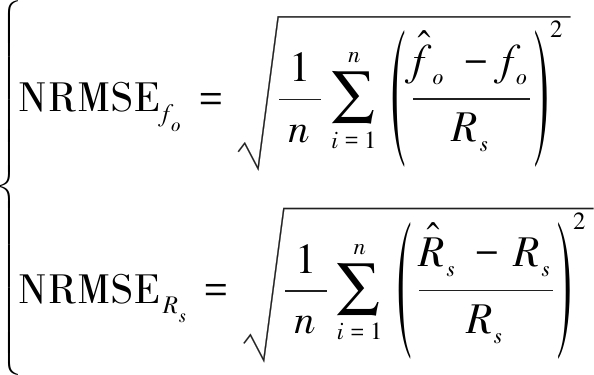
(11)
其中![]() 为符号速率估计值。
为符号速率估计值。
4.1 频偏估计性能
在进行频偏精估计之前,首先使用频率中心法[7]在预处理时得到频偏的粗估计,然后进行频偏精估计。使用改进思路2,即采用基于SNR和谱峰指数的置信度准则,对传统的基于多次方谱的频偏估计算法增加频偏精估计值的可靠性判断,基于QPSK和16QAM的仿真结果如图1所示。
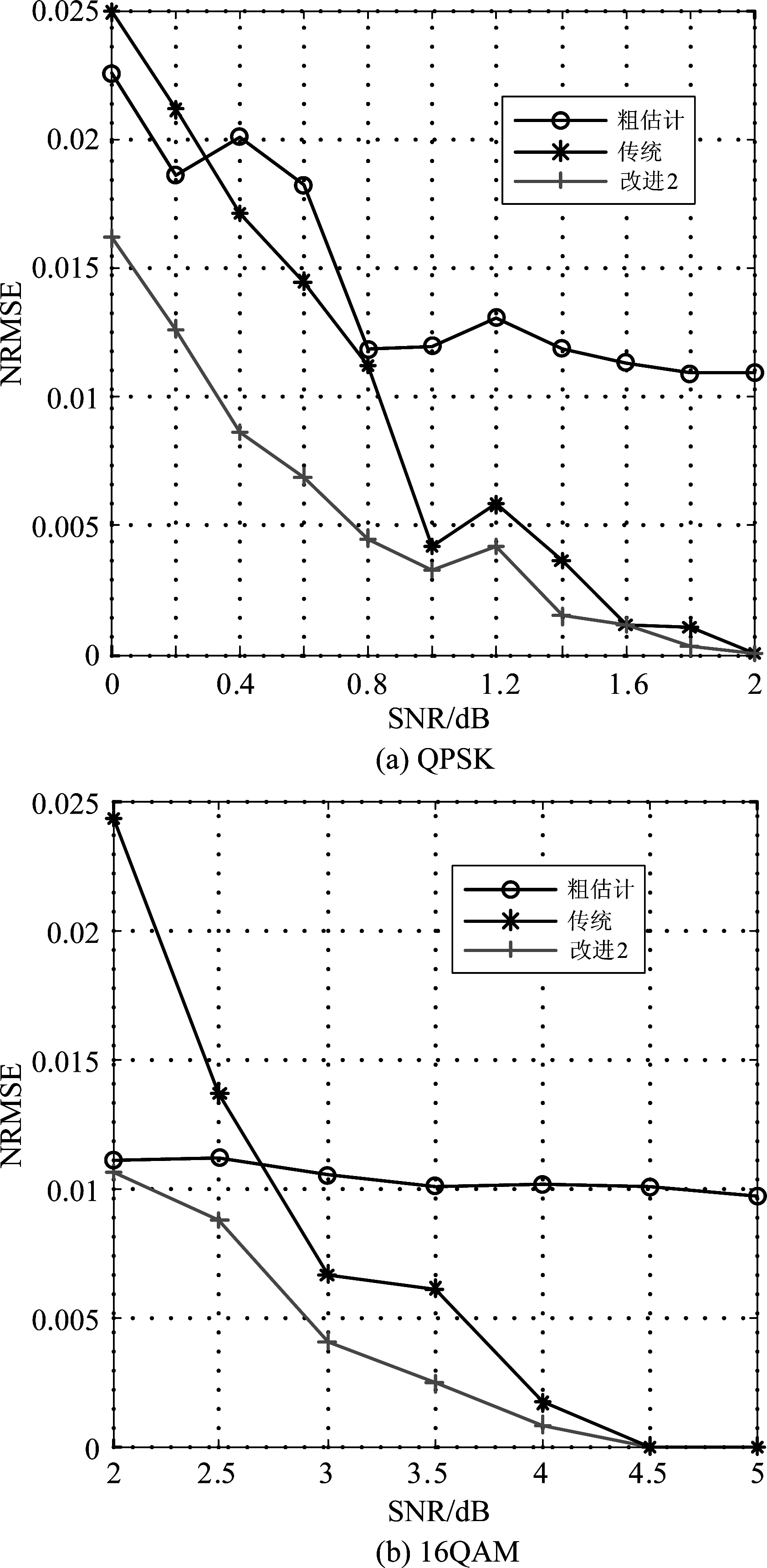
图1 低信噪比下的频偏估计性能
Fig.1 Performance of frequency offset estimation at low signal-to-noise ratio
从图1可以看出,在低信噪比环境中,对于MPSK/MQAM信号,采用传统的基于多次方谱的频偏估计算法,频偏估计误差较大,甚至可能会高于粗估计误差,这是由于在信噪比较低时,受噪声影响,峰值谱线位置可能并不是频偏所对应的位置,从而会导致频偏估计误差较大;采用改进思路2,增加谱峰指数的置信度判断,只保留可靠的频偏估计,而通过不可靠的峰值谱线得到的频偏估计值不予采纳(此时保留上一级预处理的频偏粗估计值),从而降低了频偏估计的误差,提高了低信噪比下的频偏估计可靠性。随着SNR的逐渐增大,峰值谱峰的值更为可靠,频偏估计对其的依赖性减小,改进思路2与传统算法性能的频偏估计性能将趋于一致,16QAM和QPSK仿真性能趋势类似,但16QAM需要更高的信噪比。
峰值谱峰位置估计可靠的基础上采用改进思路1,根据峰值谱峰及其相邻的谱线进行更精确的频偏估计,不同算法的频偏估计性能仿真结果如图2所示。
从图2可以看出,当发送信号为QPSK时,由于利用时间平均代替统计平均带来了误差以及小数采样的影响,基于最大似然的频偏估计NRMSE约为10-4,并且在信噪比大于3 dB时出现性能平层;传统基于N次方谱的频偏估计通过直接提取谱线,其性能优于最大似然频偏估计算法,其频偏估计的NRMSE平层约为10-5,但是由于DFT的栅栏效应,在信噪比大于3 dB时同样出现了性能平层;相比于传统的N次方谱频偏估计算法,改进算法克服了栅栏效应,在信噪比约大于2 dB时频偏估计NRMSE小于10-5,随着信噪比的增大,其NRMSE约为10-6,相比传统N次方谱算法降低了一个数量级,同时克服了另外两种算法的性能平层,提高了估计的精确性。16QAM信号在不同算法的频偏估计性能趋势与QPSK类似,但需要更高的信噪比才能达到与QPSK相同的估计性能,改进算法需要5 dB的信噪比。
针对改进的N次方谱频偏估计算法,通过设置不同采样频率Fs、接收符号长度Ns和根升余弦滤波器滚降系数α等参数,进一步分析改进算法的频偏估计性能。
从图3可以看出,改进的频偏估计算法具有较好的鲁棒性,频偏估计性能与采样频率无关;受滚降系数影响较小,滚降系数为0.3时,频偏估计性能比0.15时的性能优约1 dB;频偏估计性能受接收处理的符号长度影响较大,随着符号数的增加,频偏估计性能明显更优。类似于前面的分析,16QAM信号下的估计性能趋势与QPSK类似,但需要更高的信噪比才能达到与QPSK相同的估计性能。
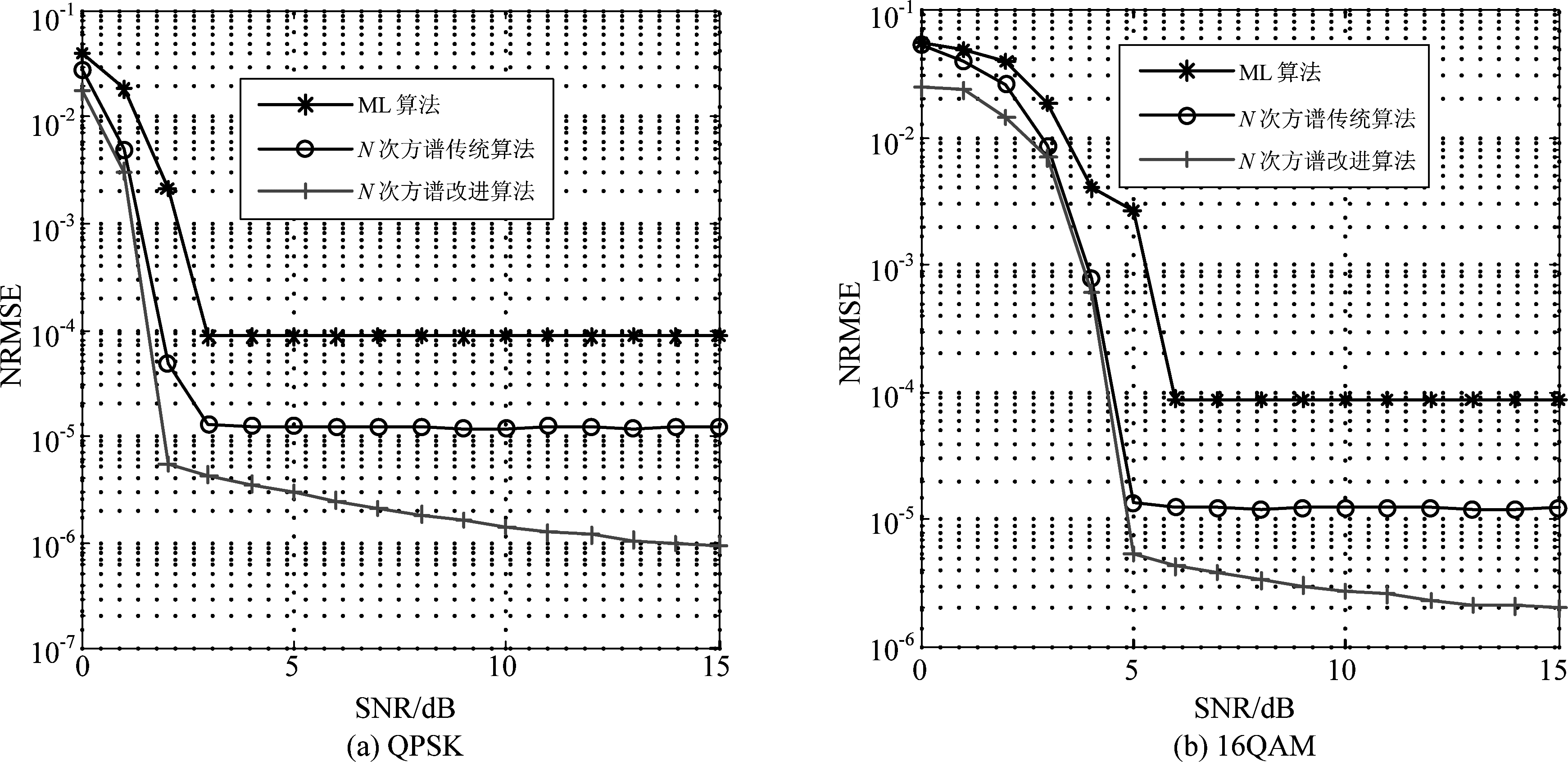
图2 不同频偏估计算法性能
Fig.2 Frequency offset estimation performance of different algorithms
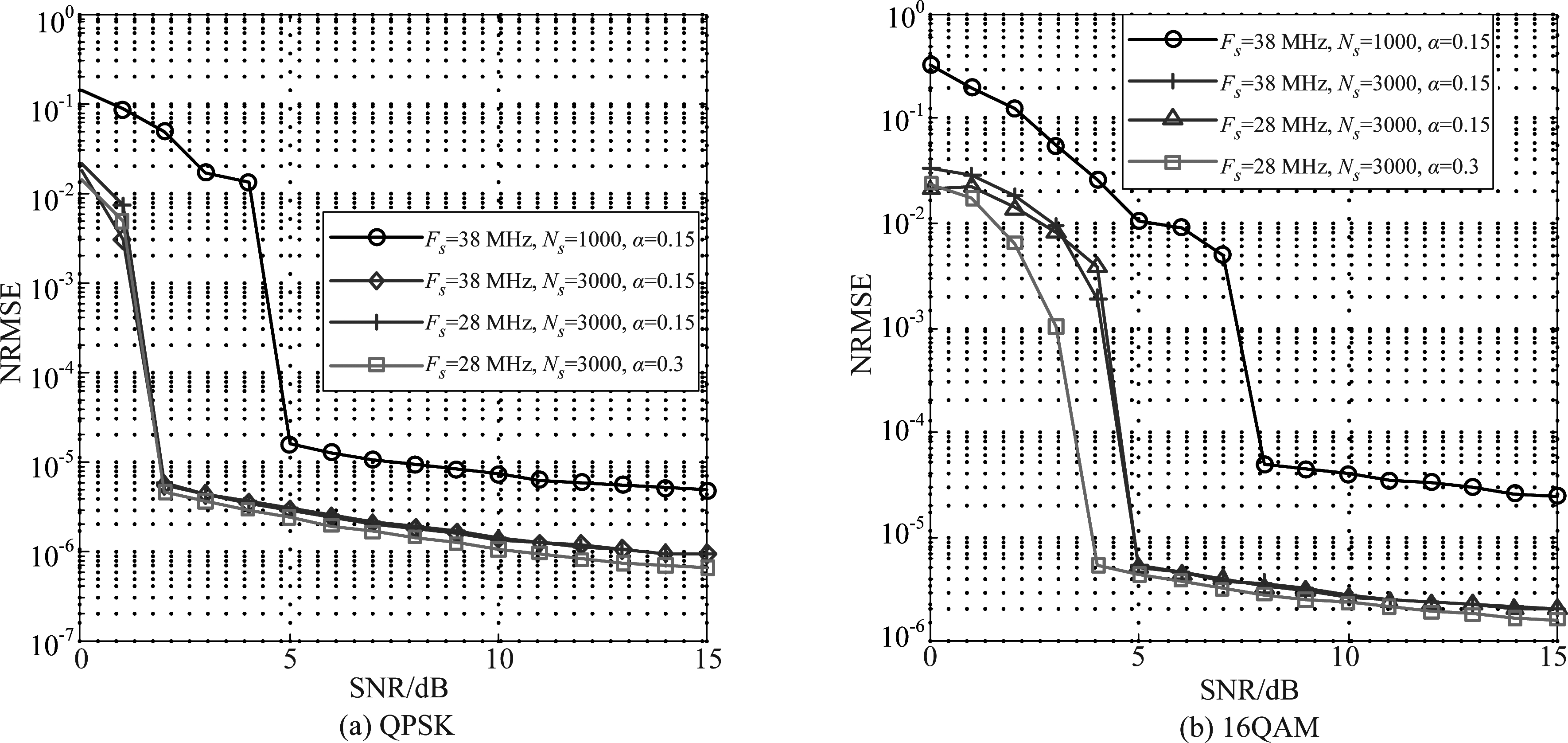
图3 改进算法在不同参数下的频偏估计性能
Fig.3 Performance of improved algorithm for frequency offset estimation under different parameters
4.2 符号速率估计性能
图4为三种符号速率估计算法的性能,从图4可以看出,由于基于IFFT的符号速率估计的分辨率低,加上小数采样的影响,造成IFFT算法的符号速率估计的NRMSE约为10-1;传统二次小波符号速率估计算法分辨率与DFT长度相关,分辨率高,在信噪比大于2 dB时其NRMSE约为10-4,但是由于DFT栅栏效应的影响出现性能平层;改进算法克服了栅栏效应的制约,相比于传统二次小波估计算法误差降低了一个数量级,符号速率估计的NRMSE低于10-6,性能优异并且克服了二次小波传统算法因DFT所导致的性能平层。16QAM信号的分析与前面的类似。
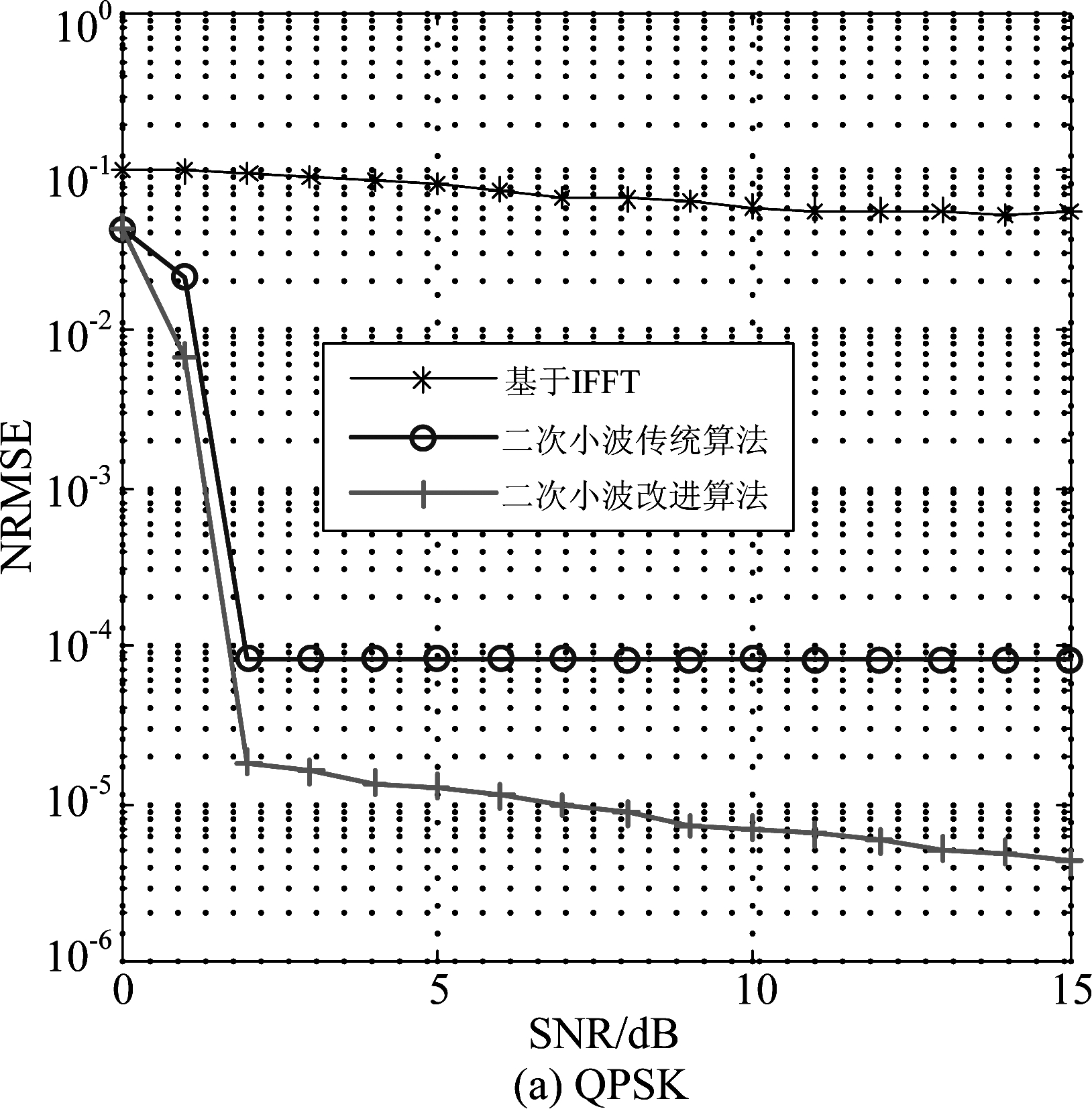
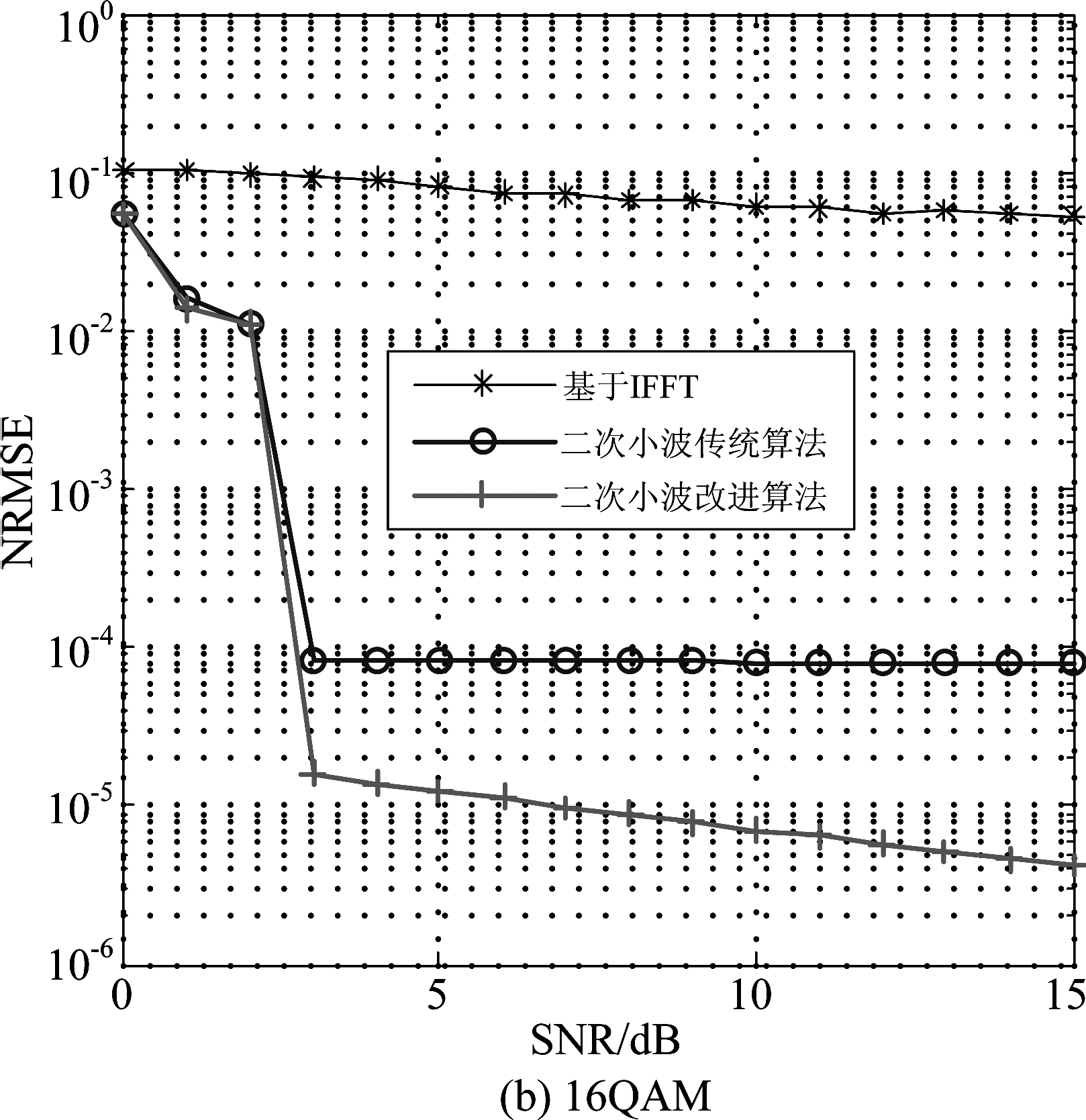
图4 不同符号速率估计算法的性能
Fig.4 Performance of different symbol rate estimation algorithms
设置不同的采样频率、符号长度和滚降系数等参数,进一步分析改进算法的符号速率估计性能,仿真结果如图5所示。
从图5可以看出,改进的符号速率估计算法具有较好的鲁棒性,符号速率估计性能与采样频率无关;滚降系数的增大使得码元交界处相位突变特性更明显,利于二次小波变换正确提取信号的瞬时特性,符号速率的估计性能有所提升;而且符号速率估计性能受接收符号长度影响较大,随着符号数的增加,估计性能更优。

图5 符号速率估计改进算法在不同参数下的性能
Fig.5 Performance of improved symbolic rate estimation algorithm under different parameters
4.3 算法复杂度分析
迭代的小数频偏估计,提高了频偏估计精度,又加入了结合信噪比的谱峰指数置信度准则,提高了低信噪比频偏估计的可靠性。在相同的频偏估计范围内,改进算法比传统算法略复杂度高,但估计精度更优。传统与改进算法复杂度、估计精度和估计范围的对比分析如表3所示。
表3 传统与改进算法对比表
Tab.3 Traditional and improved algorithm comparison table

多次方谱频偏估计算法二次小波变换符号速率估计算法传统改进传统改进复杂度乘法次数7L+3+2L∗log4L11L+2∗Δk+2L∗log4L+12(T+1)+511L+2L∗log4L+2α∗Δτ+2L∗αα∗Δτ+515L+2L∗log4L+2∗Δk+12(T+1)+2α∗Δτ+2L∗αα∗Δτ+7加法次数2L+L∗log4L6L+T+2+L∗log4L2∗αα∗Δτ∗ αα∗Δτ-1()∗L+2L+L∗log4L+122∗αα∗Δτ∗ αα∗Δτ-1()∗L+6L+L∗log4L+T+14复杂度增量乘法4L+2∗Δk+12(T+1)+2加法4L+T+2估计精度1/(2fs)受L限制<1/(2fs)不受L限制1/(2fs)受L限制<1/(2fs)不受L限制估计范围(0,fs)(0,fs)
其中L为接收信号长度,Δk为邻域参数,T为迭代次数,α为小波尺度,Δτ为离散小波基的步长,⎣·」为向下取整, fs为采样频率。
5 结论
对于MPSK/MQAM调制信号,传统基于多次方谱的频偏估计算法和基于二次小波变换的符号速率估计算法由于FFT变换的栅栏效应,估计精度有限,并有估计误差平层,而且在低信噪比情况下频偏估计误差较大。因此本文在传统估计算法基础上,提出了频偏估计和符号速率估计的改进算法,采用2L-DFT迭代校正的正弦信号频率估计算法和结合信噪比的突出谱峰指数,提高了频偏和符号速率估计精度,并保证估计结果的可靠性。
[1] 代翱, 张海剑, 孙洪.联合时域和时频域特征的数字调制信号自动分类[J]. 信号处理, 2016, 32(11): 1283-1292.
Dai Ao, Zhang Haijian, Sun Hong. Digital Modulations Automatic Classification Using the Combination of Several Features Extracted from Time and Time-Frequence Domain[J]. Journal of Signal Processing, 2016, 32(11): 1283-1292.(in Chinese)
[2] 胡国兵, 徐立中, 吴珊珊, 等.基于循环平稳分析的LFM信号盲处理结果可靠性评估[J]. 电子学报, 2016, 44(4): 788-794.
Hu Guobing, Xu Lizhong, Wu Shanshan, et al. Reliability Evaluation for Blind Processing Results of LFM Signal Based on Cyclostationarity[J]. Acta Electronica Sinica, 2016, 44(4): 788-794.(in Chinese)
[3] Proakis J G, Salehi M. Digital Communications[M]. McGraw-Hill, 2009.
[4] 赵强, 杨建波, 刘鹏, 等.一种新的联合特征调制识别算法[J]. 通信技术, 2013, 46(3): 4- 6, 9.
Zhao Qiang, Yang Jianbo, Liu Peng, et al. A New Automatic Recognition Algorithm based on Combined Feature Parameters[J]. Communications Technology, 2013, 46(3): 4- 6, 9.(in Chinese)
[5] 孙锦华, 余忠洋, 段学敏. 基于相位解模糊的简化对角互相关频偏估计算法[J]. 电子学报, 2016, 44(8): 1974-1980.
Sun Jinhua, Yu Zhongyang, Duan Xuemin. Simplified Diagonal Cross Correlation Frequency Estimation Algorithm Based on Phase Un-wrapping Method[J]. Acta Electronica Sinica, 2016, 44(8): 1974-1980.(in Chinese)
[6] 金艳, 田田, 姬红兵. 基于稀疏贝叶斯学习的码元速率估计[J]. 电子与信息学报, 2018, 40(7): 79- 84.
Jin Yan, Tian Tian, Ji Hongbing. Symbol Rate Estimation Based on Sparse Bayesian Learning[J]. Journal of Electronics and Information Technology, 2018, 40(7): 79- 84.(in Chinese)
[7] Azzouz E E, Nandi A K. Automatic Modulation Recognition of Communication Signals[J]. IEEE Transactions on Communications, 1997, 46(4): 431- 436.
[8] 徐毅琼. 数字通信信号自动调制识别技术研究[D]. 解放军信息工程大学, 2011.
Xu Yiqiong. Research on Automatic Modulation Recognition of Digital Communication Signals[D]. Information Engineering University, 2011.(in Chinese)
[9] 赵颖.基于改进算法的调制信号的载波频率估计[J]. 电子设计工程, 2016, 24(6): 29-31.
Zhao Ying.Estimation of carrier frequency of modulation signal based on improved alogorithm[J]. Electronic Design Engineering, 2016, 24(6): 29-31.(in Chinese)
[10] 柏果, 程郁凡, 唐万斌, 等. 利用DFT和迭代校正的正弦信号频率估计算法[J]. 信号处理, 2017, 33(12): 1536-1541.
Bai Guo, Cheng Yufan, Tang Wanbin, et al. A Frequency Estimation Algorithm of Sinusoidal Signal Capable of DFT and Iterative Correction[J]. Journal of Signal Processing, 2017, 33(12): 1536-1541.(in Chinese)
[11] Yang J L, Yang W J, Xu G Q. Blind Estimation of Carrier Frequency and Symbol Rate Based on Cyclic Spectrum Density[J]. Procedia Engineering, 2012, 29(4): 514-519.
[12] Flohberger M, Kogler W, Gappmair W. Symbol Rate Estimation with Inverse Fourier Transforms[C]∥2006 International Workshop on Satellite and Space Communications, 2006, 110(113): 14-15.
[13] 纪勇, 徐佩霞. 基于小波变换的数字信号符号率估计[J]. 电路与系统学报, 2003, 8(1):12-15.
Ji Yong, Xu Peixia. Symbol Rate Estimation of Digital Signal Based on Wavelet Transform [J]. Journal of Circuits and Systems. 2003, 8(1):12-15.(in Chinese)
[14] 张涛. 基于N谱峰突出指数的典型数字调制信号盲识别研究与实现[D]. 成都: 电子科技大学, 2012.
Zhang Tao. Research and Implementation of Blind Identification of Typical Digital Modulation Signals Based on N Spectral Peak Outburst Index[D]. Chengdu: University of Electronic Science and Technology of China, 2012.(in Chinese)
[15] Luise M, Reggiannini R. Carrier recovery in all-digital modems for burst-mode transmissions[J]. IEEE Trans. Comm., 1995, 43(2/3/4): 1169-1178.



