1 引言
随着移动通信的快速发展，频谱效率和系统容量等方面的需求日益增长。传统的多址方式已经不能满足发展需要，于是业内提出了一种新的多址方式，即非正交多址接入(non-orthogonal multiple access, NOMA)。作为面向第五代移动通信(fifth-generation mobile communication, 5G)的关键技术之一，NOMA通过对同时同频上的用户分配不同的功率，实现功率域的多用户共享，使无线接入总量提高了50%[1-2]。相比于第四代移动通信(fourth-generation mobile communication, 4G)，5G的NOMA对接收端的信号检测提出了更高的要求。在NOMA系统接收端，由于同时同频上叠加的各个用户之间非正交，导致接收端信号检测的复杂度增加[3- 4]。尤其在大规模天线的情况下，其检测的高复杂度会进一步增大系统的时延[5]。因此研究NOMA系统中低复杂度信号检测算法是很有必要的。
现有的接收端用户信号检测方法主要为迫零串行干扰消除(zero forcing successive interference cancellation, ZF-SIC)和最小均方误差串行干扰消除(minimum mean square error successive interference cancellation,MMSE-SIC)[6]。Neng Ye等人[7]利用星座图旋转提高了NOMA信号检测性能，但其仅适用于天线数较少的场景并且进一步增加了复杂度。Ling Binjian[8]等人针对误码传播问题，提出了一种多决策串行干扰消除(multiple decision successive interference cancellation, MD-SIC)方案，提高性能的同时增大了复杂度。Ali Cagatay Ciri等人[9]提出了一种基于自适应交替方向乘法器的低复杂度多用户检测方案，但其需要较多先验知识并且仅适用于用户数较少的场景。为了实现大规模天线下的多用户检测，本文利用诺伊曼级数近似和对角矩阵分解对ZF-SIC和MMSE-SIC进行改进，实现了检测性能相近的同时降低了复杂度。
2 基本串行检测算法
假设有N个移动用户同时向基站发送消息，发射总功率为1 dBm，则基站侧的接收信号可以表示为[10-11]：
(1)
其中，βn为用户n的功率，βn∈(0,1)。hn为用户n的M×K维信道矩阵，M是基站的接收天线数，K是用户n的发射天线数。xn为用户n调制后的发射信号，u为均值为0、方差为1的高斯白噪声。在基站侧希望分别检测出各用户信号xn，检测xn时，其他用户信号就是干扰，希望尽可能消除。
2.1 ZF-SIC检测算法
ZF算法是通过求解其他干扰用户的零空间矩阵，从而消除用户间的多址干扰。对于信道矩阵hn，假设发射信号xn的估计值为
接收信号为Y，ZF算法即使J(X)=
达到最小。对J(X)求导可得使函数J(X)最小的估计值
应满足下式:
(2)
由上式可知，当
为非奇异矩阵时，ZF检测算法所得的估计值为：
(3)
NOMA的ZF-SIC检测算法思想是按照功率从大到小的顺序对用户进行排序和检测。令第n个用户的权值向量为：
(4)
则可得第n个用户信号的初步估计值：
(5)
消除功率影响即可得第n个用户的信号估计值
进一步消除的干扰，即可检测第n+1个用户的信号
重复上述过程，直到所有用户检测完成。
2.2 MMSE-SIC检测算法
MMSE算法在选取滤波矩阵时，将噪声因素考虑进去，均衡噪声与符号间干扰，使得检测方法在统计意义下达到最优。其目标函数是使检测出的信号与真实信号的均方误差最小化，数学表达式为：
minJ=E[
]
(6)
推导可得MMSE算法的权值向量为
(7)
MMSE-SIC检测算法的步骤与ZF-SIC算法的检测步骤基本一致，只需要将ZF-SIC算法的权值向量计算式(4)更换为式(7)即可。
3 低复杂度的串行检测算法
3.1 诺伊曼级数近似
由式(4)和式(7)可见，ZF和MMSE检测算法都涉及直接矩阵求逆，对于M×K维矩阵hn，其广义逆矩阵的计算复杂度是O(K3)。随着K值的增加，计算复杂度将呈指数式增长。因此，寻求一种低复杂度的求逆方法是非常迫切的。对于矩阵Z-1，可将其写为诺伊曼级数展开形式[12]：
(8)
其中，
或者
为可逆矩阵。
用前L项近似Z-1，即：
(9)
其中αi为优化因子，作用是提高近似的精度。通常取α0=1，αi(i≥1)随着i的增加，数值逐渐减小[13-14]。矩阵Z可以分解为仅在对角线上有值的对角矩阵D和对角线上值均为0的空心矩阵E，即Z=D+E。当A=D时，代入式(9)可得：
(10)
L=2时有：
(11)
式(11)通过诺伊曼级数近似将大矩阵Z的直接求逆运算转化为D-1的乘积之和，且对角矩阵的求逆运算只需求对角线上元素的倒数。因此对于M×K维矩阵，式(11)只需要O(K2)的计算复杂度，相比于传统直接求逆矩阵O(K3)的复杂度，诺伊曼级数近似求逆算法复杂度大幅度降低。
3.2 低复杂度的ZF-SIC检测算法
对于ZF-SIC检测算法，令
当基站天线数大于用户发射天线数即M>K时，矩阵RZF成为对角占优矩阵。可将RZF分解为对角矩阵DZF和空心矩阵EZF：
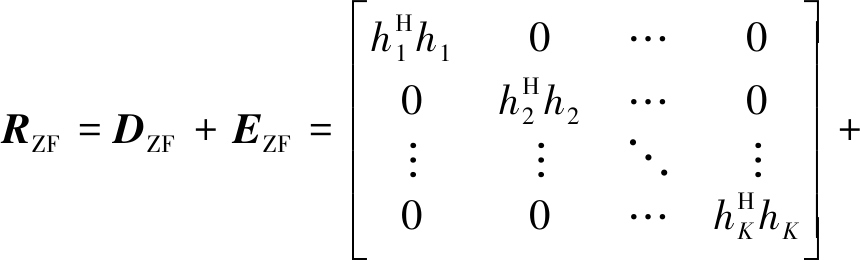
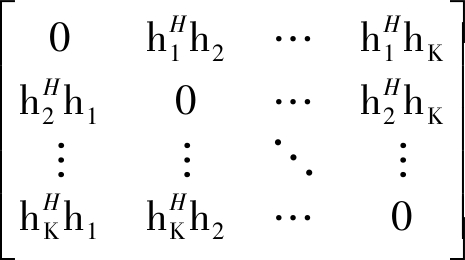
(12)
利用式(11)可得：
(13)
将式(13)代入式(4)可得：
(14)
因此得到本文提出的低复杂度的迫零串行干扰消除检测(简记为ND-ZF-SIC)算法主要步骤如下：
(1)按照功率从大到小的顺序对用户进行排序，选择功率最大的用户作为检测的初始用户, 初始化n=1。
(2)将矩阵RZF分解为对角矩阵DZF和空心矩阵EZF。
(3)利用式(14)计算权值向量wn。
(4)利用权值向量wn由式(5)计算得到
(5)消除
中功率的影响并判决，即可得第n个用户信号的估计值
(15)
(16)
(6)消除第n个用户信号的干扰，即:
(17)
更新n=n+1。
(7)重复进行(2)～(6)的检测过程，直到所有用户检测完成，迭代结束。
3.3 低复杂度的MMSE-SIC检测算法
对于MMSE-SIC检测算法，令：
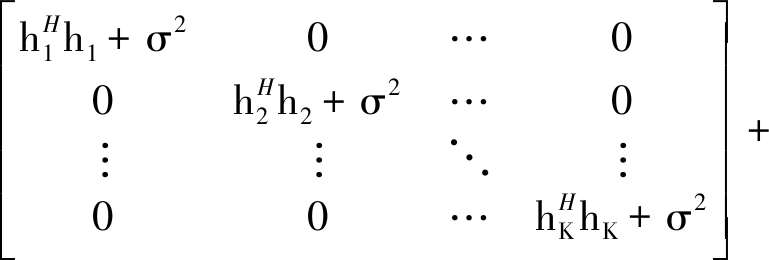
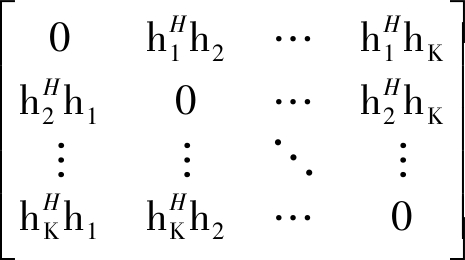
(18)
利用式(11)可得：
(19)
因此得到本文提出的低复杂度的最小均方误差串行干扰消除检测(简记为ND-MMSE-SIC)算法，其主要步骤仅需将ND-ZF-SIC算法的步骤(2)和(3)分别更换为如下：
(2) 将矩阵RMMSE分解为对角矩阵DMMSE和空心矩阵EMMSE。
(3) 利用式(19)计算权值向量wn。
4 复杂度分析与性能仿真
4.1 复杂度分析
算法的复杂度通常可以由乘法次数和加法次数的数量来衡量。表1给出了基于Cholesky分解的精确矩阵求逆运算[15]的ZF-SIC和MMSE-SIC算法与本文提出的低复杂度检测的ND-ZF-SIC和ND-MMSE-SIC算法的乘法次数与加法次数。瑞利衰落信道中，用户数为3，信源采用BPSK调制，K=4，M=32，信源长度为2×104比特时，四种算法的运行时间也在表1给出。由表1可知，传统直接求逆矩阵的复杂度为O(K3)，本文经过矩阵分解和诺伊曼级数近似将复杂度降到了O(K2)，本文算法的运行时间比传统算法快8秒多。
表1 四种算法复杂度对比
Tab.1 Complexity comparison of four algorithms
算法乘法次数加法次数运行时间/sZF-SIC16K3+4K2+K8K2+3K2+2K24.77ND-ZF-SIC8K2-4K8K2-5K16.68MMSE-SIC16K3+4K2+K8K2+3K2+3K25.12ND-MMSE-SIC8K2-4K8K2-4K16.99
4.2 算法仿真与性能分析
假设用户数为3，每个用户的发射天线数K为4，莱斯衰落信道的莱斯衰落因子为-30 dB。当信源采用BPSK调制，基站侧的接收天数M为32和64时，瑞利衰落信道中ZF-SIC、ND-ZF-SIC、MMSE-SIC和ND-MMSE-SIC的平均误码率如图1所示；当M为64，莱斯衰落信道和瑞利衰落信道中四种算法的平均误码率如图2所示。瑞利衰落信道中，信源分别采用QPSK调制和16QAM调制时，四种算法的平均误码率分别如图3所示。
由图1～3可得：(1)MMSE-SIC算法性能略优于ZF-SIC。这是因为ZF-SIC算法没有对噪声进行处理，导致了噪声的放大，而MMSE-SIC算法对此进行了改进。(2)随着接收天线数量的增加，四种算法的误码率都会降低。(3)与ZF-SIC和MMSE-SIC算法相比，在降低复杂度的情况下，ND-ZF-SIC和ND-MMSE-SIC算法性能下降不大。(4)莱斯衰落信道中四种算法的性能均优于瑞利衰落信道中的性能。(5)信源采用BPSK和QPSK时，四种算法性能分别基本相近，且性能均好于采用16QAM调制。
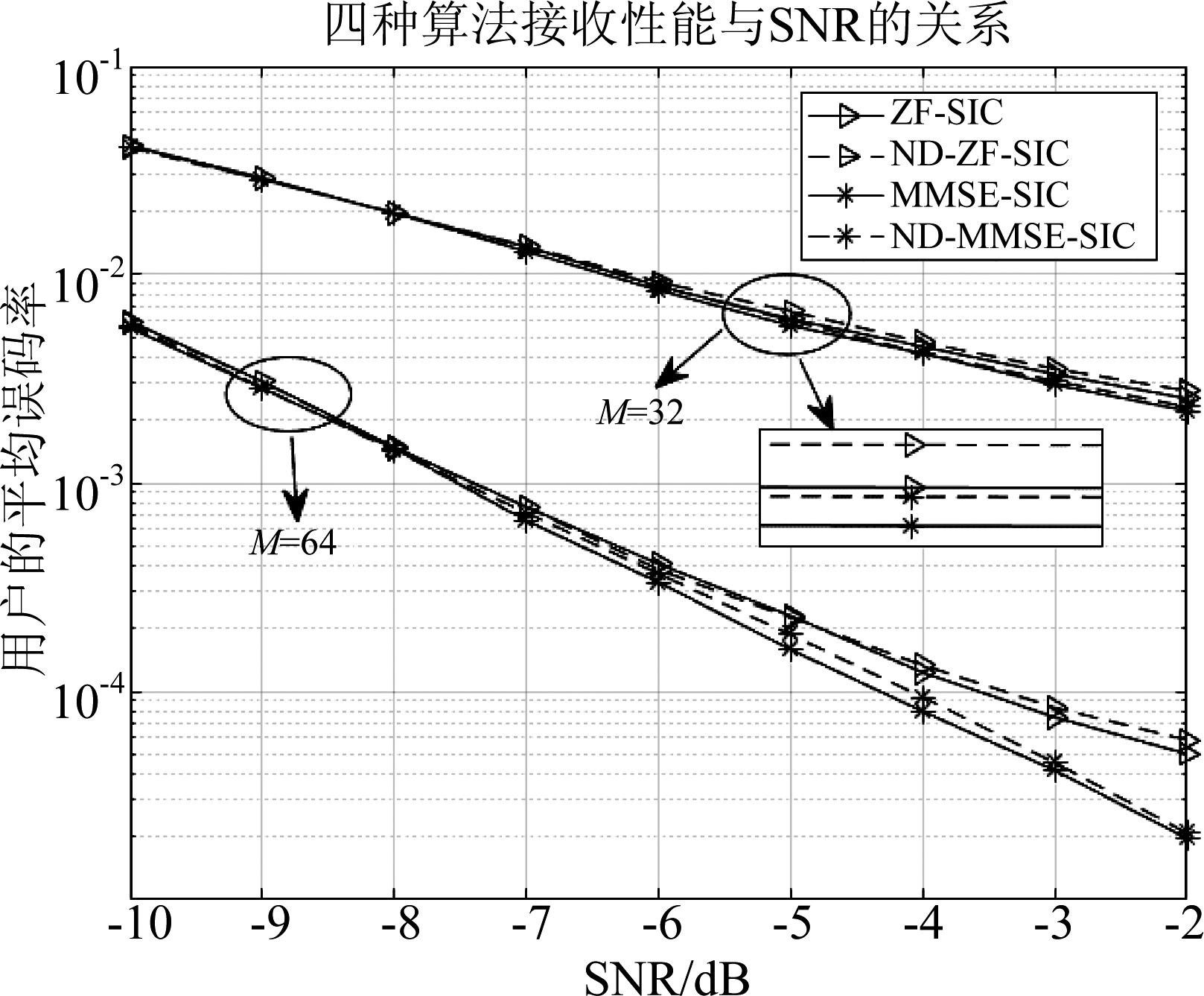
图1 接收天线数对算法误码性能的影响
Fig.1 The influence of the number of receiving antennas on BER performance
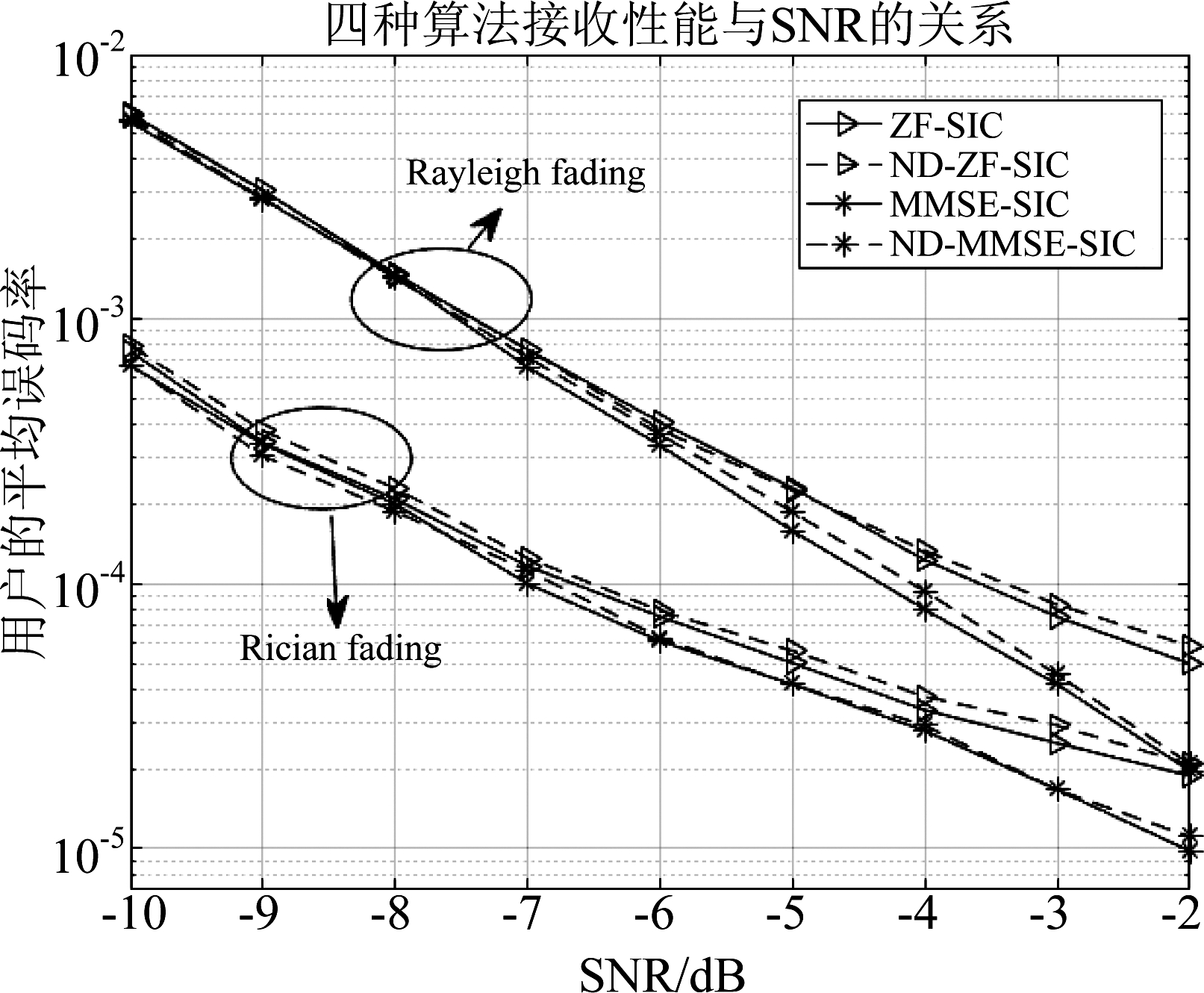
图2 瑞利衰落和莱斯衰落信道中算法误码性能比较
Fig.2 Comparison of BER in Rayleigh fading channel and Rician fading channel
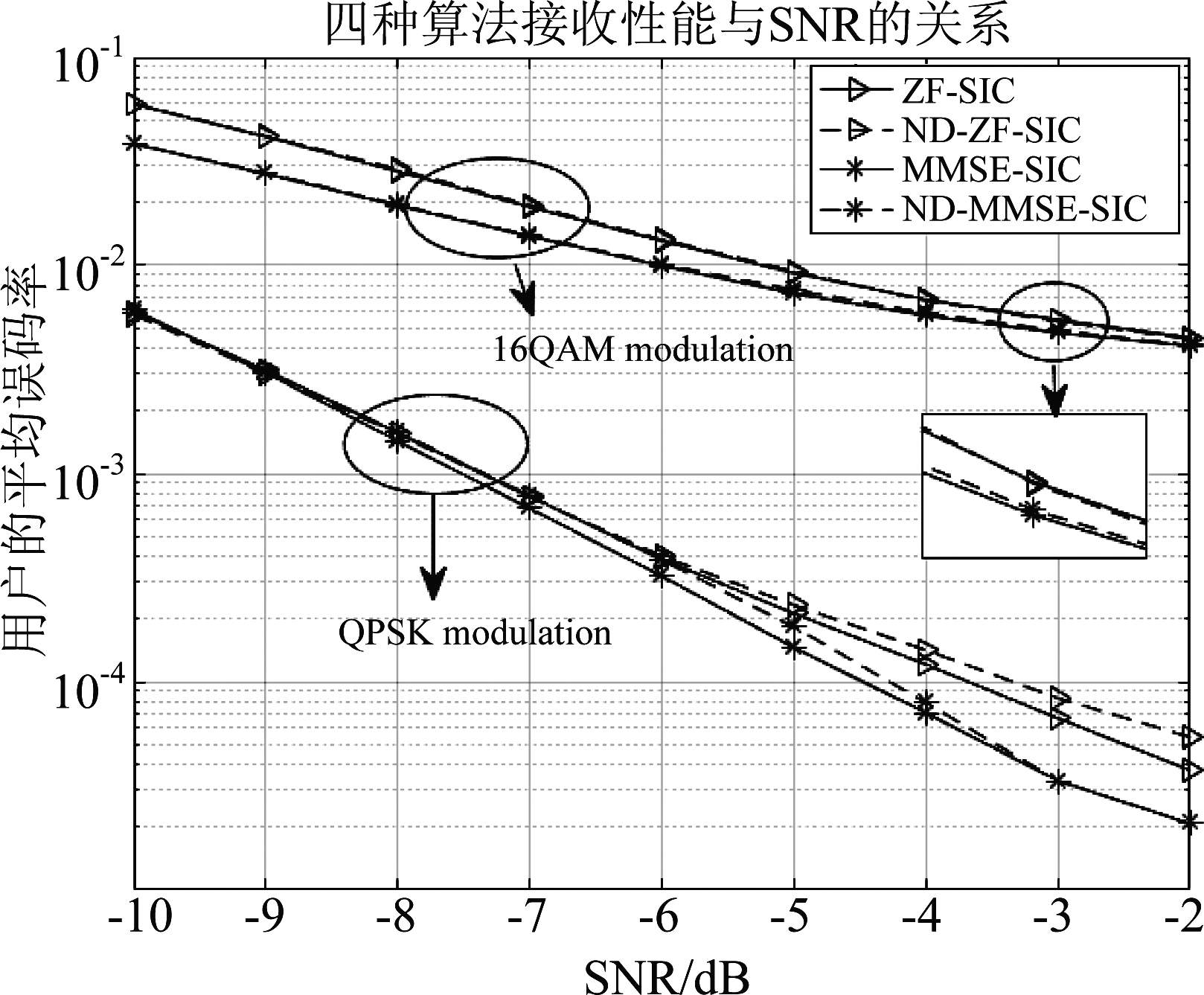
图3 不同信源调制方式时算法误码性能比较
Fig.3 Comparison of BER in different source modulation modes
当信噪比为-2 dB, K=4，M=64，信源采用BPSK调制和QPSK调制时，ZF-SIC、ND-ZF-SIC、MMSE-SIC和ND-MMSE-SIC的平均误码率随用户数的变化曲线分别如图4和图5所示。由图可知， 随着用户数的增加，四种算法的误码率都有所上升，但ND-ZF-SIC和ND-MMSE-SIC算法的性能始终非常接近ZF-SIC和MMSE-SIC算法的性能。
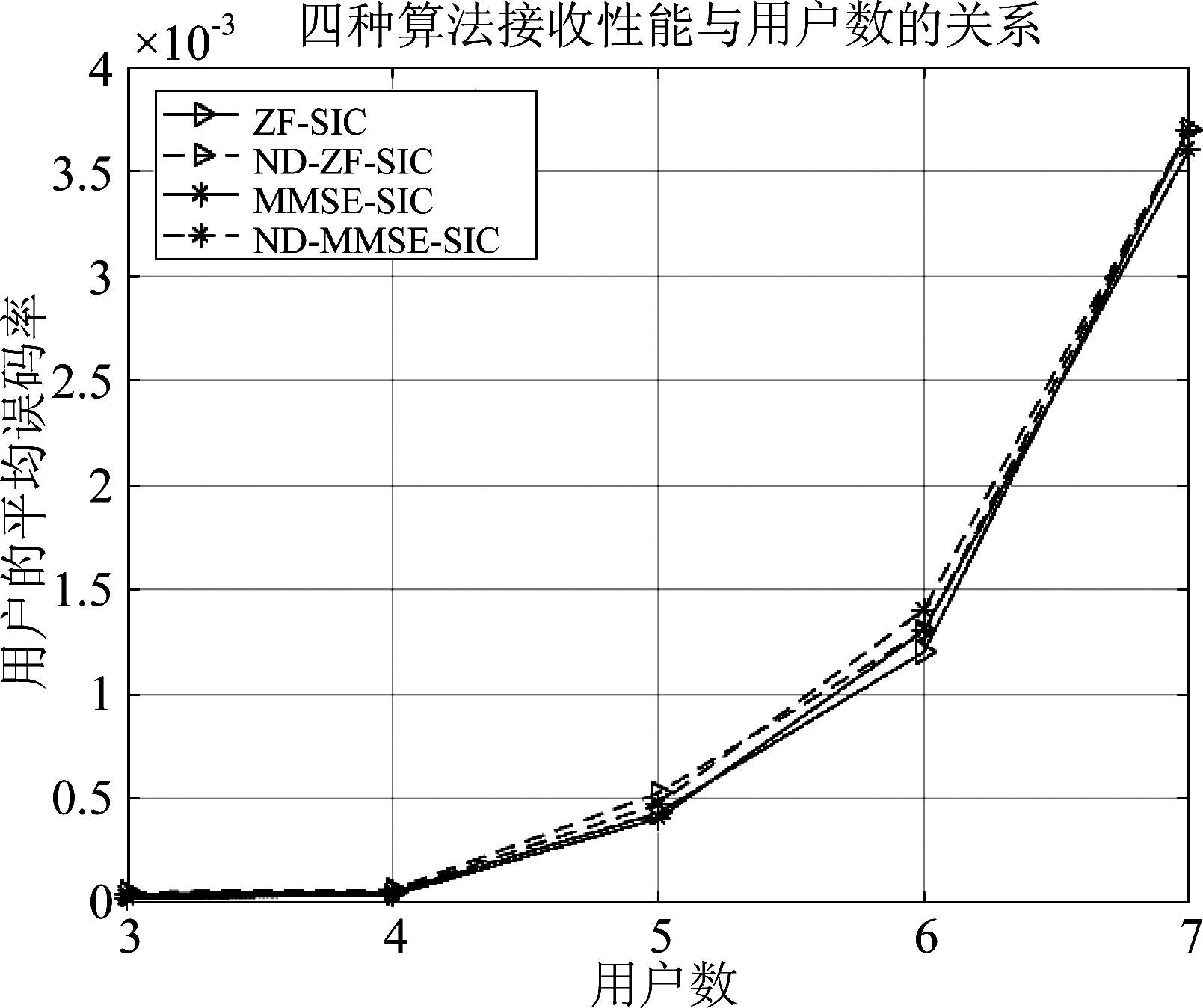
图4 算法误码性能与用户数的关系
Fig.4 The relationship between BER and user number
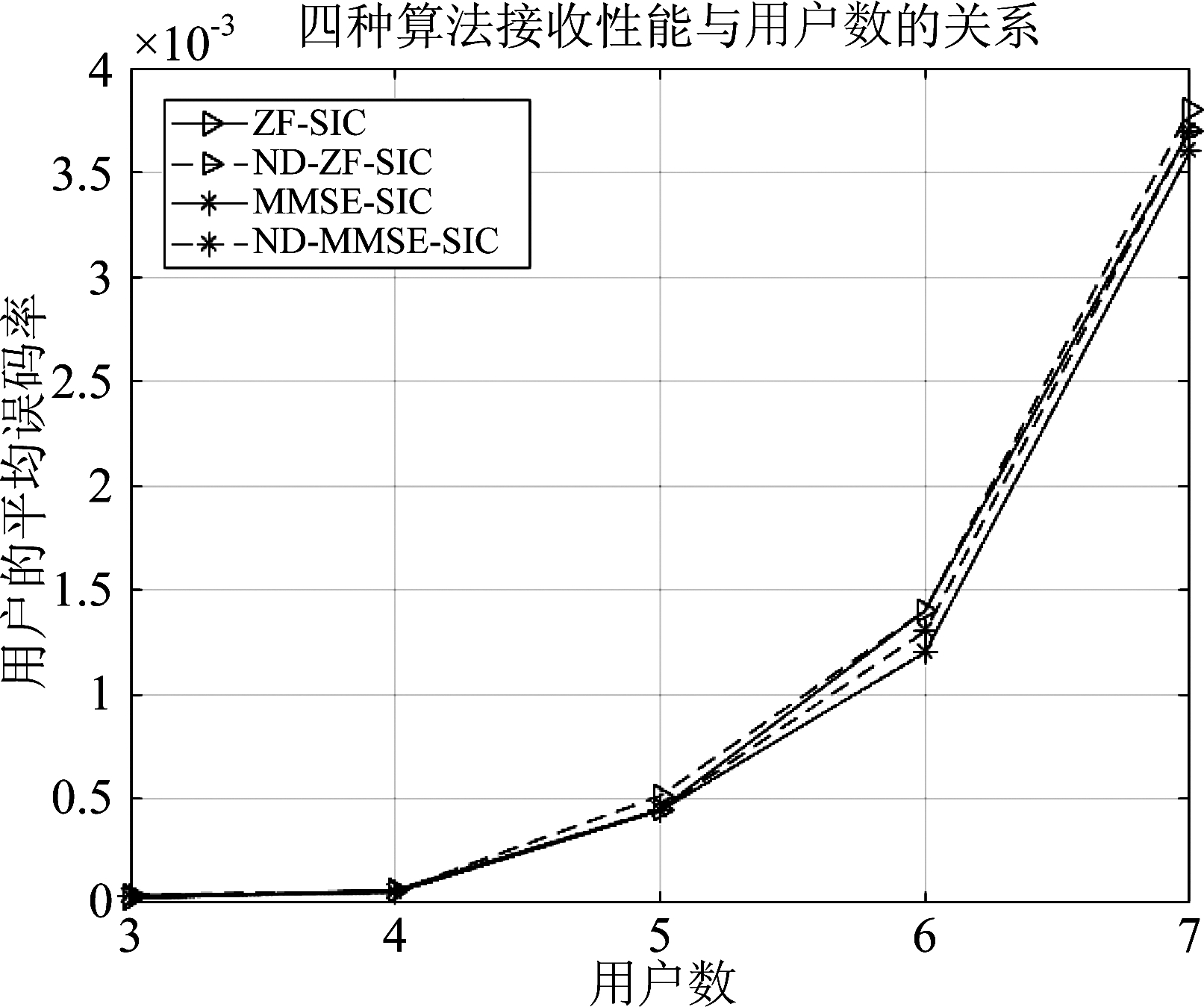
图5 算法误码性能与用户数的关系
Fig.5 The relationship between BER and user number
5 结论
针对大规模天线下，NOMA系统的ZF-SIC算法和MMSE-SIC算法高复杂度问题，利用对角矩阵分解和诺伊曼级数近似,提出了低复杂度的ND-ZF-SIC和ND-MMSE-SIC算法。仿真结果表明，ND-ZF-SIC和ND-MMSE-SIC在保持与ZF-SIC算法和MMSE-SIC算法性能相近的基础上，降低了复杂度。
[1] 张长青.面向5G的非正交多址接入技术(NOMA)浅析[J]. 邮电设计技术, 2015, 11: 49-53.
Zhang Changqing. Initial analysis of NOMA for 5G mobile networks[J]. Designing Techniques of Posts and Telecommunications, 2015, 11: 49-53.(in Chinese)
[2] 徐鑫, 金梁.NOMA系统中基于协作干扰的物理层安全方案[J]. 信号处理, 2017, 33(6): 836- 844.
Xu Xin, Jin Liang. Physical Layer Security Schemes Based on Cooperative Jamming for Non-Orthogonal Multiple Access System[J]. Journal of Signal Processing, 2017, 33(6): 836- 844.(in Chinese)
[3] Wang Hong, Zhang Zhaoyang, Chen Xiaoming. Energy-efficient power allocation for non-orthogonal multiple access with imperfect successive interference cancellation[C]∥2017 9th International Conference on Wireless Communications and Signal Processing. IEEE, 2017: 1- 6.
[4] Choi J. On generalized downlink beamforming with NOMA[J]. Journal of Communications and Networks, 2017, 19(4): 319-328.
[5] 沈哲贤, 许魁, 王雨榕, 等.全双工大规模MIMO异构网络频谱效率分析及优化[J]. 信号处理, 2018, 34(4): 379-390.
Shen Zhexian, Xu Kui, Wang Yurong, et al. Spectral Efficiency Analysis and Optimization for Full Duplex Heterogeneous Network with Massive MIMO[J]. Journal of Signal Processing, 2018, 34(4): 379-390.(in Chinese)
[6] 张德坤.非正交多址系统功率分配及干扰消除算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
Zhang Dekun. Research on power allocation and interference elimination algorithms for non-orthogonal multiple access system[D]. Harbin: Harbin Institute of Technology, 2015.(in Chinese)
[7] Ye Neng, Wang Aihua, Li Xiangming, et al. On constellation rotation of NOMA with SIC receiver[J]. IEEE Communications Letters, 2018, 22(3): 514-517.
[8] Ling Binjian, Dong Chao, Dai Jincheng, et al. Multiple decision aided successive interference cancellation receiver for NOMA systems[J]. IEEE Wireless Communications Letters, 2017, 6(4): 498-501.
[9] Cirik A C, Balasubramanya N M, Lampe L. Multi-user detection using ADMM-based compressive sensing for uplink grant-free NOMA[J]. IEEE Wireless Communications Letters, 2018, 7(1): 46- 49.
[10] Song Guanghui, Wang Xianbin, Cheng Jun. A low-complexity multiuser coding scheme with near-capacity performance[J]. IEEE Transactions On Vehicular Technology, 2017, 66(8): 6775- 6786.
[11] Zhu Ye, Zhang Zhaoyang, Wang Xianbin, et al. A low-complexity non-orthogonal multiple access system based on rate splitting[C]∥2017 9th International Conference on Wireless Communications and Signal Processing. IEEE, 2017: 1- 6.
[12] Stewart G W. Matrix algorithms: basic decompositions[M]. United States of America: Society For Industrial And Applied Mathematics, 1998: 67- 82.
[13] Müller A, Kammoun A, Björnson E, et al. Linear precoding based on truncated polynomial expansion-part I: large-scale single-cell systems[J]. Flexible, 2013, 8(5): 861- 875.
[14] Kammoun A, Müller A, Björnson E, et al. Linear precoding based on truncated polynomial expansion-part II: large-scale multi-cell systems[J]. Flexible, 2013, 8(6):
853- 867.
[15] Krishnamoorthy A, Menon D. Matrix inversion using cholesky decomposition[C]∥2013 IEEE Signal Processing: Algorithms, Architectures, Arrangements, And Applications (SPA). IEEE, 2013: 70-72.
