1 引言
太空是未来战争的主战场, 未来战争的焦点是对制天权的争夺。天基预警雷达由于平台高度的特殊性，可以不受时间、气候和地域的限制，能连续对全球进行大范围观测，因此, 天基预警雷达是全面获取空间、空中以及地面有关目标信息资源的重要手段, 是夺取制信息权的重要保障[1-2]。
天基预警雷达核心技术是实现空中动目标显示AMTI[3]。天基体制下，卫星平台和空中目标间的高速径向运动，会导致回波脉间包络距离徙动和多普勒域多普勒扩散现象[4]。为了提高相参积累增益，必须对相对运动参数进行估计，进而对回波信号进行运动补偿。由于星载雷达功率孔径积受限，且雷达和空中目标距离较远，因此回波信号的信噪比较低，常用的距离徙动补偿方法(例如互相关法、最小熵法、谱峰跟踪法等)在低信噪比情况下并不适用[5]。此外，补偿多普勒扩散需要准确估计方位时域Chirp信号的多普勒调频率，但在低信噪比下，基于传统的FFT估计方法(例如DPT法、延迟自相关法、Chirp-Z等)的估计精度会严重降低[6- 8]。
本文首先利用Keystone变换校正回波包络的距离徙动，得到目标所在距离单元内的方位时域信号；然后利用Gabor变换得到方位时域信号的时频分布；最后利用标准Hough变换将方位时域信号的时频分布变换到参数域，通过参数域内的峰值搜索，得到运动参数的估计值。仿真结果表明，本文方法在低信噪比下具有良好的估计性能，并且估计精度对信噪比变化不敏感，算法鲁棒性较好。
2 空中目标回波模型及信噪比分析
2.1 回波模型
天基预警雷达卫星平台和空中目标的几何关系如图1所示。
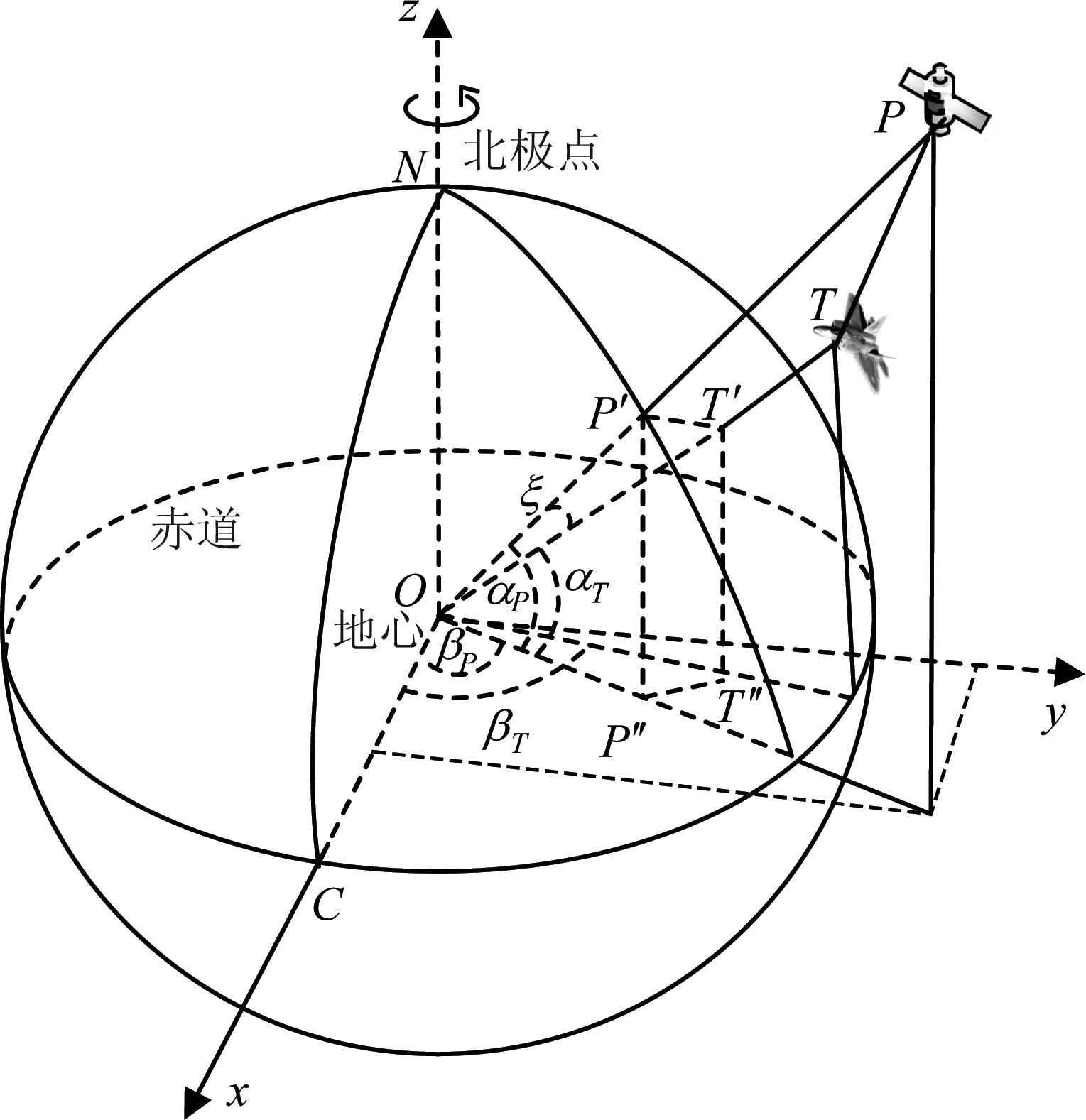
图1 卫星平台和空中目标的几何关系
Fig.1 Geometrical relationship between satellite platform and air target
图中P和T分别表示卫星平台和空中目标，∠POT=ξ表示球心角，线段PT的长度为卫星和目标的径向距离R。此外，P′和T′分别为卫星和目标的地表投影点，P″和T″分别为地表投影点在赤道面上的垂足。设投影点的经纬度坐标分别为(αP, βP)和(αT, βT)，根据图中的几何关系，利用余弦定理可以得到径向距离R为
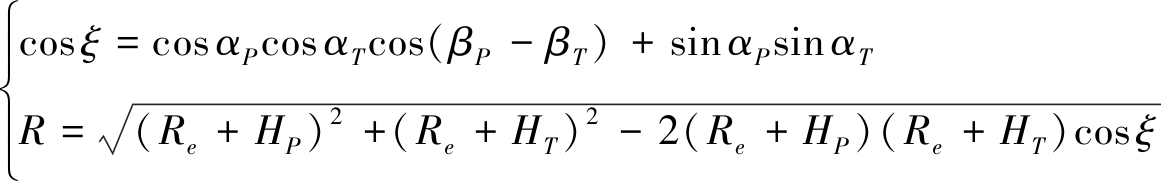
(1)
式中Re、HP、HT分别为地球半径、卫星轨道高度、空中目标飞行高度。
在一个CPI内，卫星平台和空中目标的径向距离可以表示为
(2)
式中R0为初始径向距离，νr为径向速度，ar为径向加速度，径向速度和加速度以目标与雷达接近方向为正方向，tm为慢时间，且tm=mTr，m=0,1,…,M，Tr为脉冲重复周期，M为相参脉冲数。
天基预警雷达一般采用线性调频脉冲信号，其表达式为
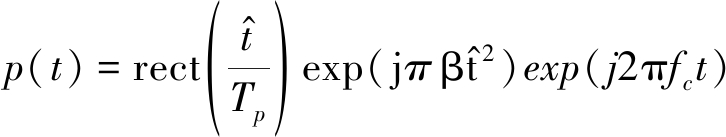
(3)
式中
为快时间，Tp为脉冲宽度，β为调频率， fc为雷达工作频率，t为总时间，且
根据式(2)～(3)，在停-跳模型下，基带回波信号为
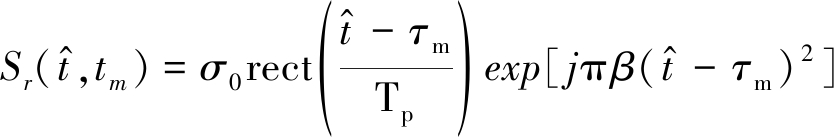
(4)
式中σ0为目标反射系数，τm为第m个脉冲的回波时延，R(tm)为第m个脉冲时刻卫星平台和空中目标间的径向距离，λ为波长。
由驻相定理，基带回波信号在距离时域脉冲压缩后为
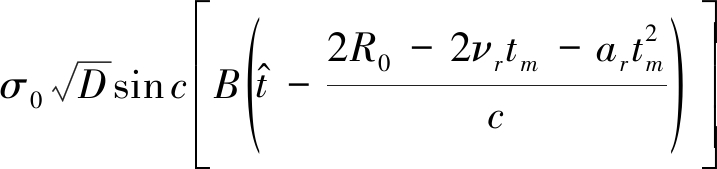
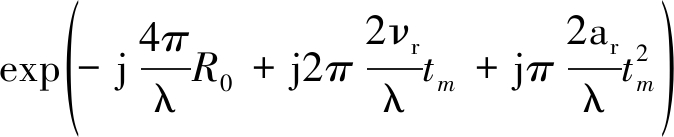
(5)
式中B为信号带宽，D=BTp为信号时宽带宽积，c为光速。
由于地杂波和噪声的影响，雷达接收机实际接收的回波信号为
(6)
式中
为脉压后的杂波，
为脉压后的噪声。本文在杂波抑制后对运动参数进行估计，因此只考虑噪声对估计性能的影响。
从式(5)可以看出，回波包络距离徙动包括径向速度νr引起距离走动，和径向加速度ar引起距离弯曲。此外，目标所在距离单元内地方位时域信号为线性调频信号，多普勒频率为fd=2νr/λ，多普勒调频率为μd=2ar/λ，多普勒调频率引起多普勒频率扩散。
2.2 回波信噪比分析
脉冲多普勒雷达接收机输出信噪比为[9]
(7)
式中Pt为峰值发射功率，Tp为脉冲宽度， fr为脉冲重复频率，Ae为天线有效孔径面积，σ为目标雷达反射截面积，K为玻尔兹曼常数，Te为等效噪声温度，B为信号带宽，F为噪声系数，L为系统损耗，R为目标散射点和天线相位中心的径向距离。
由式(7)可以看出，当天线和雷达参数确定后，接收机输出信噪比主要由卫星平台和空中目标的斜距决定。设星载雷达下视波束最小俯仰角为θEL1，最大俯仰角为θEL2，波束宽度为θ dB，雷达波束覆盖范围如图2中阴影部分所示。
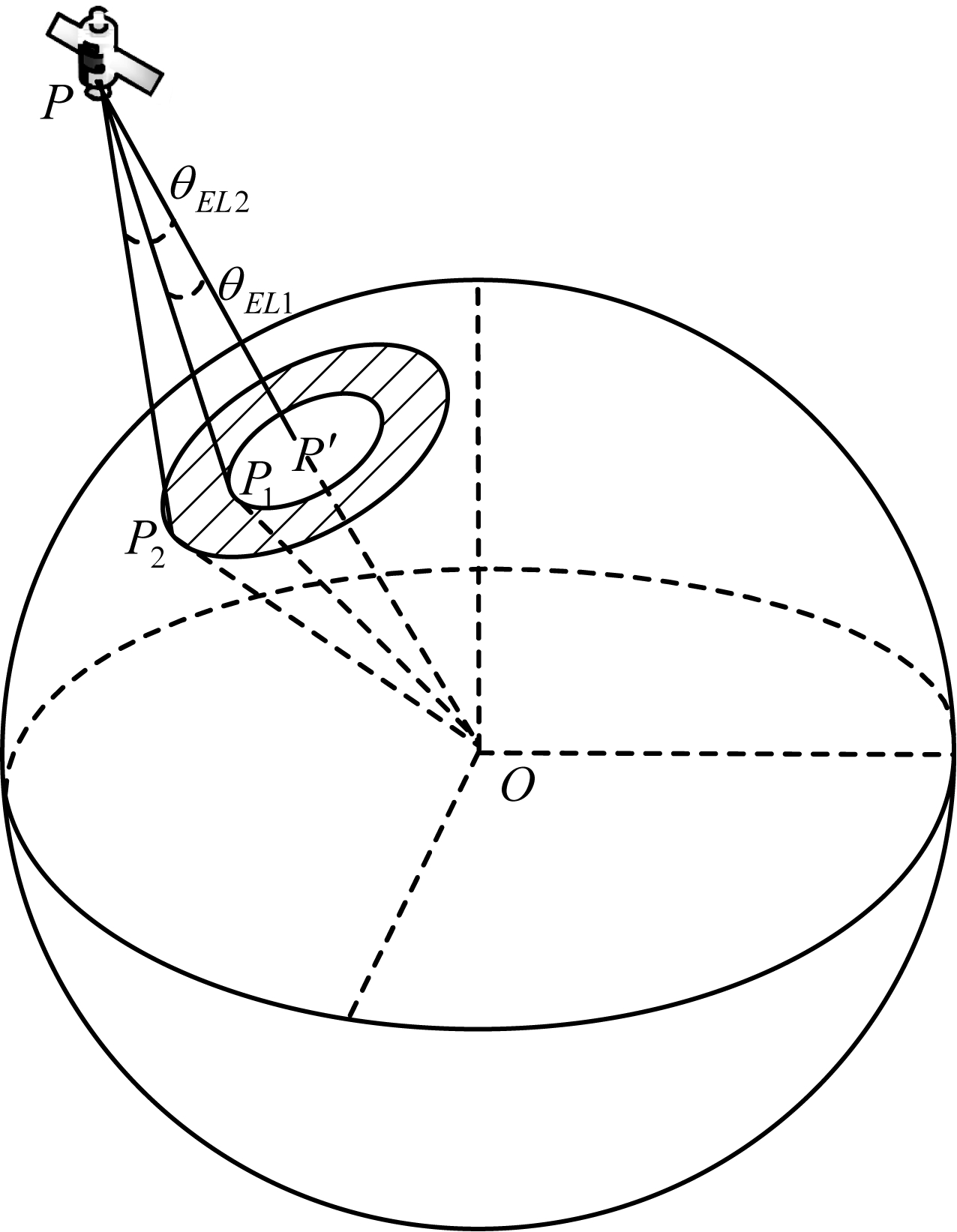
图2 雷达波束覆盖范围
Fig.2 Radar beam coverage
由余弦定理求得雷达观测斜距为
R=(Re+HP)cos θEL-
(8)
式(8)中波束俯仰角θEL的变化范围决定了雷达观测斜距R的范围。
参考文献[11]中L波段天基预警雷达参数指标[10]，设置轨道、天线和雷达参数如表1所示。
表1 轨道、天线和雷达参数
Tab.1 Parameters of orbit, antenna, and radar
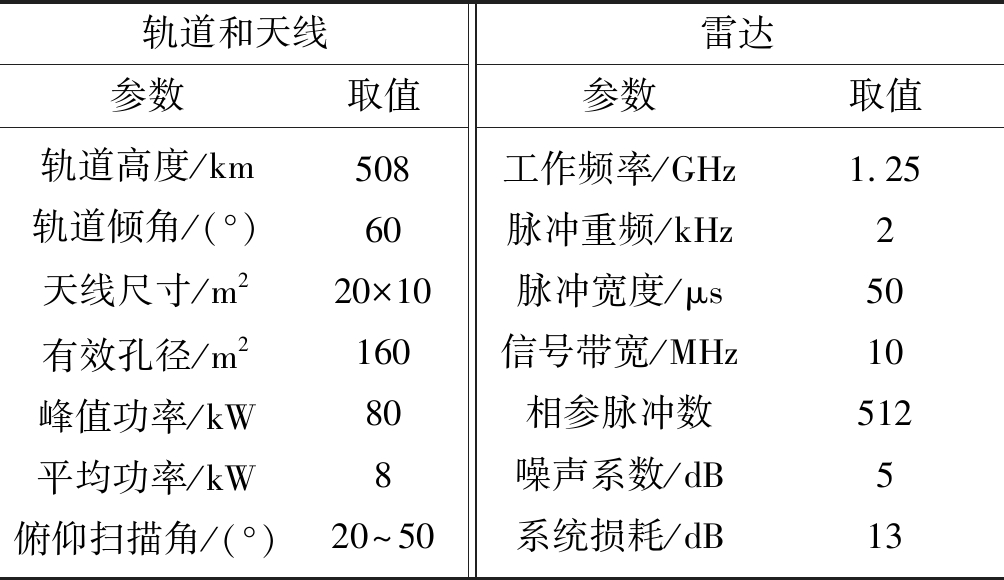
轨道和天线雷达参数取值参数取值轨道高度/km轨道倾角/(°)天线尺寸/m2有效孔径/m2峰值功率/kW平均功率/kW俯仰扫描角/(°)5086020×1016080820～50工作频率/GHz脉冲重频/kHz脉冲宽度/μs信号带宽/MHz相参脉冲数噪声系数/dB系统损耗/dB1.2525010512513
根据表1中参数，由式(7)～(8)求得接收机输出信噪范围如图3所示。
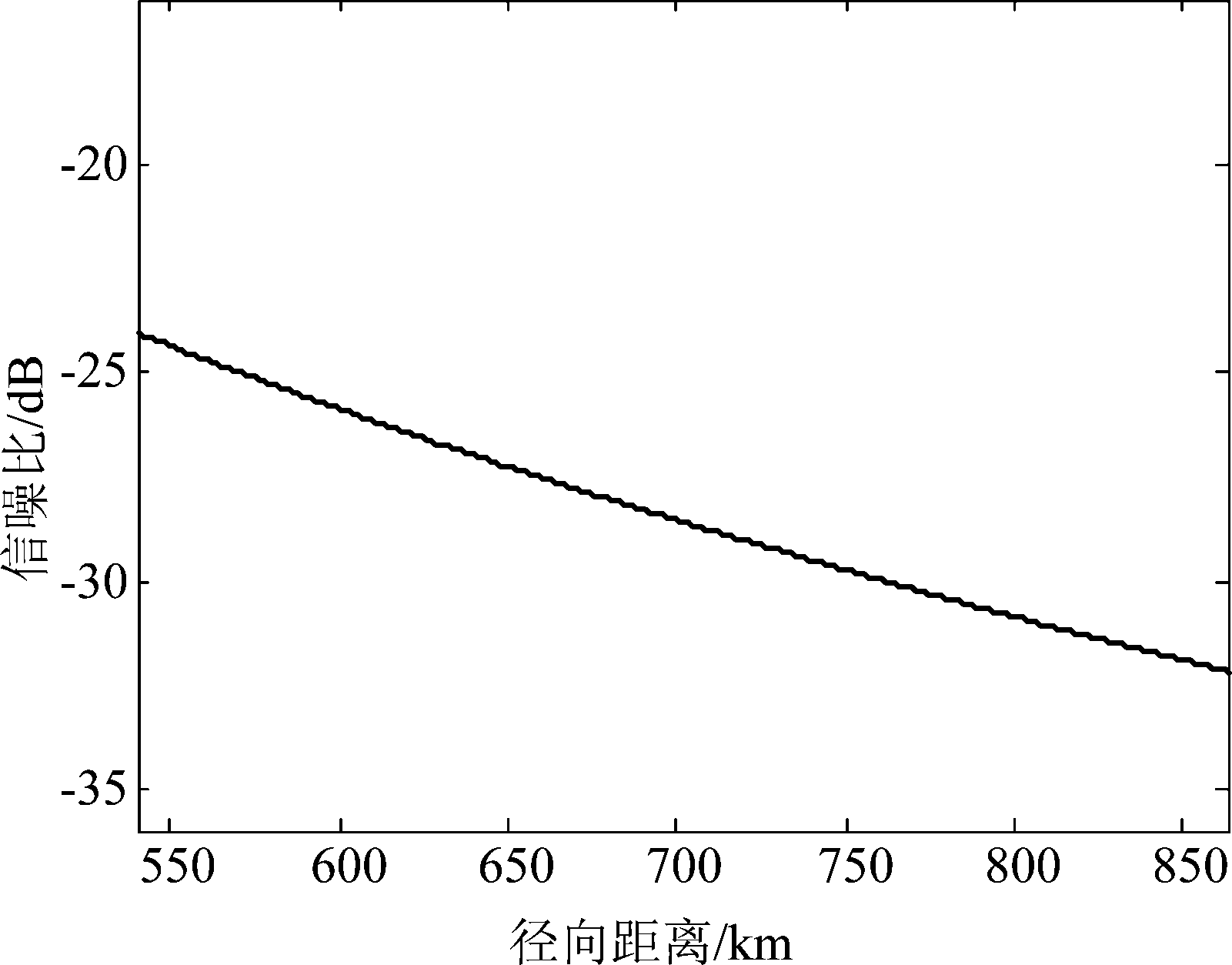
图3 信噪比随观测距离变化关系
Fig.3 Relationship between SNR and observation distance
由图3可知，在卫星轨道高度为hp=508 km，波束俯仰范围为20°～50°时，雷达探测距离范围为550 km～850 km，信噪比变化范围为-24 dB～-32 dB。
3 距离徙动校正及回波时频分析
3.1 Keystone变换校正距离徙动
对式(5)在距离时域作FFT，得到距离频域-方位时域信号
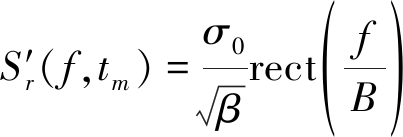
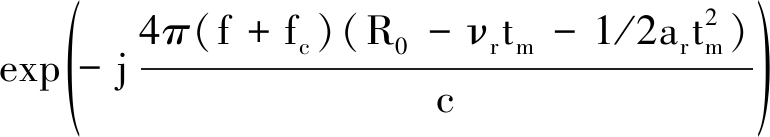
(9)
从式(9)可以看出，距离频率f和慢时间tm的一次耦合项导致包络距离走动，二次耦合项导致包络距离弯曲。为了校正包络距离徙动，在不知道运动参数先验信息的情况下，可以采用Keystone变换[11]。作变量替换
代入式(9)得
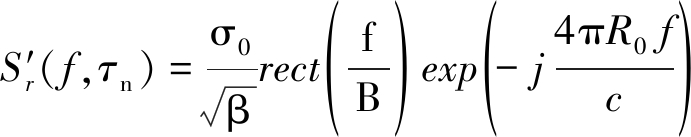
(10)
由式(10)可以看出，距离频率f和虚拟慢时间τn仍然存在二次耦合项，但在窄带条件下， f≪fc，有
式(10)可近似为
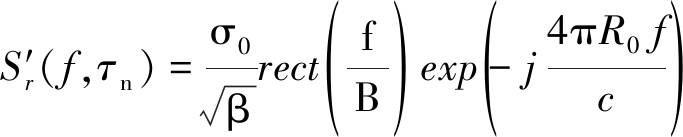
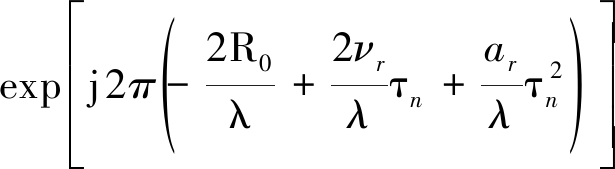
(11)
对式(11)在距离频域作IFFT，得到Keystone变换后的距离时域-方位时域信号为
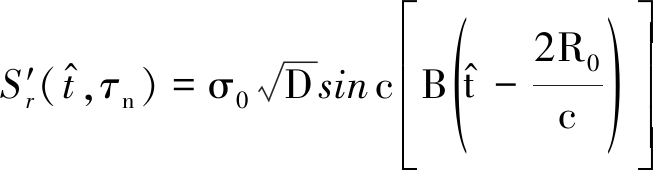
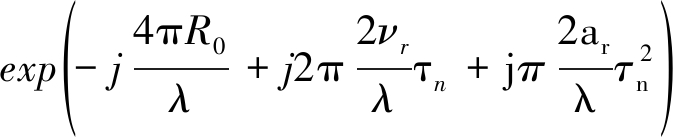
(12)
从式(12)可以看出，经过Keystone变换，所有脉冲包络都被校正到初始距离单元内，不妨记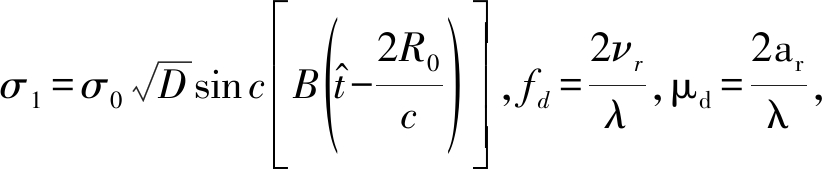
初始距离单元内的方位时域信号可表示为
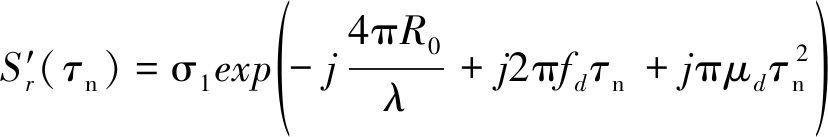
(13)
式中fd为回波信号的初始多普勒频率，μd为多普勒调频率，τn为变换后的虚拟慢时间，且有τn=nTr, (n=0,1,…,M-1)。
从式(13)可以看出，目标回波所在距离单元内的方位时域信号为Chirp信号。根据经典的Chirp信号参数方法，可以得到多普勒频率fd和调频率μd，进而得到径向速度νr和加速度ar的估计。
3.2 Keystone实现方法
将
和
分别表示为离散形式
和
变换SINC内插法的表达式为[12]
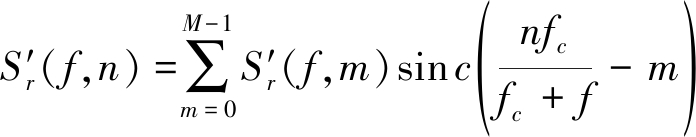
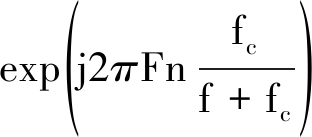
(14)
式中F为多普勒模糊数。
在天基体制下，卫星平台和空中目标的径向速度很大，多普勒模糊难以避免，因此首先需要对多普勒模糊数F进行估计。本文采用广义最大似然估计方法估计多普勒模糊数F，其表达式为
(15)
式中KT(·)表示Keystone变换，FFT(·)表示快速傅里叶变换，
表示脉压后的距离频域-方位时域信号。
3.3 离散Gabor变换进行时频分析
将τn=nTr代入式
可以表示为离散形式
其离散Gabor变换为[13]
(16)
其中WN=e-j2π/N，h(n)为窗函数，且有ωk=2πk/N(k=0,1,…,N-1)，为频率ω的N点离散化。
离散Gabor变换可以得到Chirp信号
的时频分布，理论上该分布在时频面上为一条直线，直线斜率对应多普勒调频率μd，直线截距对应多普勒频率fd。
4 Hough变换估计径向速度和加速度
4.1 Hough变换原理
Hough变换可以用来检测图像中的直线，其原理是将图像空间中的一条直线映射为参数空间的一个点，将图像空间中的直线检测转换为参数空间中的峰值检测。Hough变换对局部缺失不敏感，具有较强的鲁棒性，并且在低信噪比下具有良好的检测和估计性能[14]。
设时频分布图在笛卡尔坐标系下任意一点的坐标为(x,y)，其Hough变换为[15]
ρ=xcos θ+ysin θ
(17)
其中ρ为参数空间的纵坐标，θ为参数空间的横坐标，取值范围为0～π。
式(17)的三角函数表达形式为
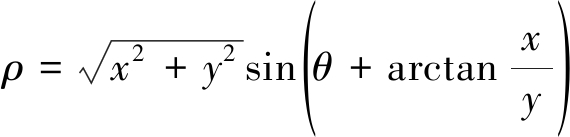
(18)
由式(18)可知，图像空间中的一点对应于参数空间中的一条正弦曲线，而参数空间中的一点对应于图像空间中的一条直线。Hough变换将图像空间的点映射为参数空间的正弦曲线，通过搜索参数域是否存在峰值，来检测图像空间中是否存在直线并得到直线斜率和截距。
4.2 Hough变换计算方法
(a)设时频面内任意一点对应的值为d(x,y)，搜索时频面上所有离散点，得到最大峰值dmax。
(b)设定阈值dth=p·dmax，其中p的取值范围为0到1。
(c)若d≥dth，则保留该点；若d<dth，则舍弃该点。记所有过门限的点的坐标为数据矩阵
其中K为过门限点的个数。
(d)设参数空间中θ的分辨率为Δθ，在0～π范围内的取值点个数为Nθ，记变换矩阵
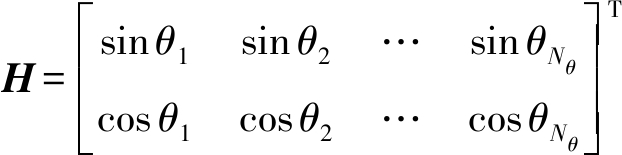
(e)将变换矩阵H和数据矩阵D相乘，得到
其中每一列对应参数空间中正弦曲线的ρ值。
( f )将R中所有的ρ值以Δρ进行量化分区，得到Nρ个量化区间，区间间隔为(ρ1,ρ2,…,ρNρ)。
(g)生成并初始化一个Nρ×Nθ的积累矩阵A， 然后对R中的每一行按量化区间进行投票，每次投票单元值加1。
(h)对积累矩阵进行峰值搜索，最大峰值点坐标(ρmax,θmax)即为待检测直线的参数估值。
4.3 相对运动参数估计
时频图像空间的点经Hough变换得到参数空间最大峰值点坐标(ρmax,θmax)，代入式(17)得
y=-cot θmaxx+ρmaxcsc θmax
(19)
其中，-cot θmax和ρmaxcsc θmax分别为时频图像空间中直线的斜率和截距。由于慢时间信号的采样频率为脉冲重复频率fr，采样间隔为脉冲重复周期Tr，相参脉冲数为 M，时频图上频率轴的分辨率为fr/M，时间轴的分辨率为Tr，再根据式(13)得到径向速度和加速度的估计表达式为
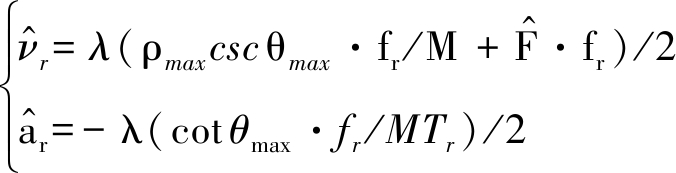
(20)
5 仿真分析
5.1 仿真场景
假设空中目标的运动参数如表2所示。
表2 空中目标运动参数
Tab.2 Motion parameters of air targets
参数参数值初始纬度/(°)26.36初始经度/(°)127.77航向/(°)-30高度/km20航速/(km/s)1
根据表1中卫星轨道参数，和表2中空中目标运动参数，由式(1)得到卫星平台和空中目标的相对运动情况及相对运动参数如图4所示。
图4为观测时间为10分钟，空中目标和卫星平台轨迹、径向距离、速度和加速度随时间的变化情况。由于星载雷达的波束观测范围为550 km～850 km，由图4(b)可知空中目标落入波束范围内的时间为181 s～389 s。以第328 s为例，由图4(c)～(d)可知，这一时刻卫星平台和空中目标的相对运动参数如表3所示。
表3 相对运动参数
Tab.3 Relative motion parameters of air targets
运动参数参数值径向速度/(km/s)-3.3788径向加速度/(m/s2)-56.3079
5.2 相对运动参数估计仿真
5.2.1 多普勒模糊数估计
由径向速度计算得到真实多普勒模糊数F=14，在信噪比SNR=-30 dB时，由式(15)得到不同多普勒模糊数下的相参积累结果如图5所示。
从图5可以看出，
时相参积累结果取得最大值，多普勒模糊数估计值等于真实值，说明在低信噪比下，基于广义最大似然估计方法仍然具有良好的估计精度。
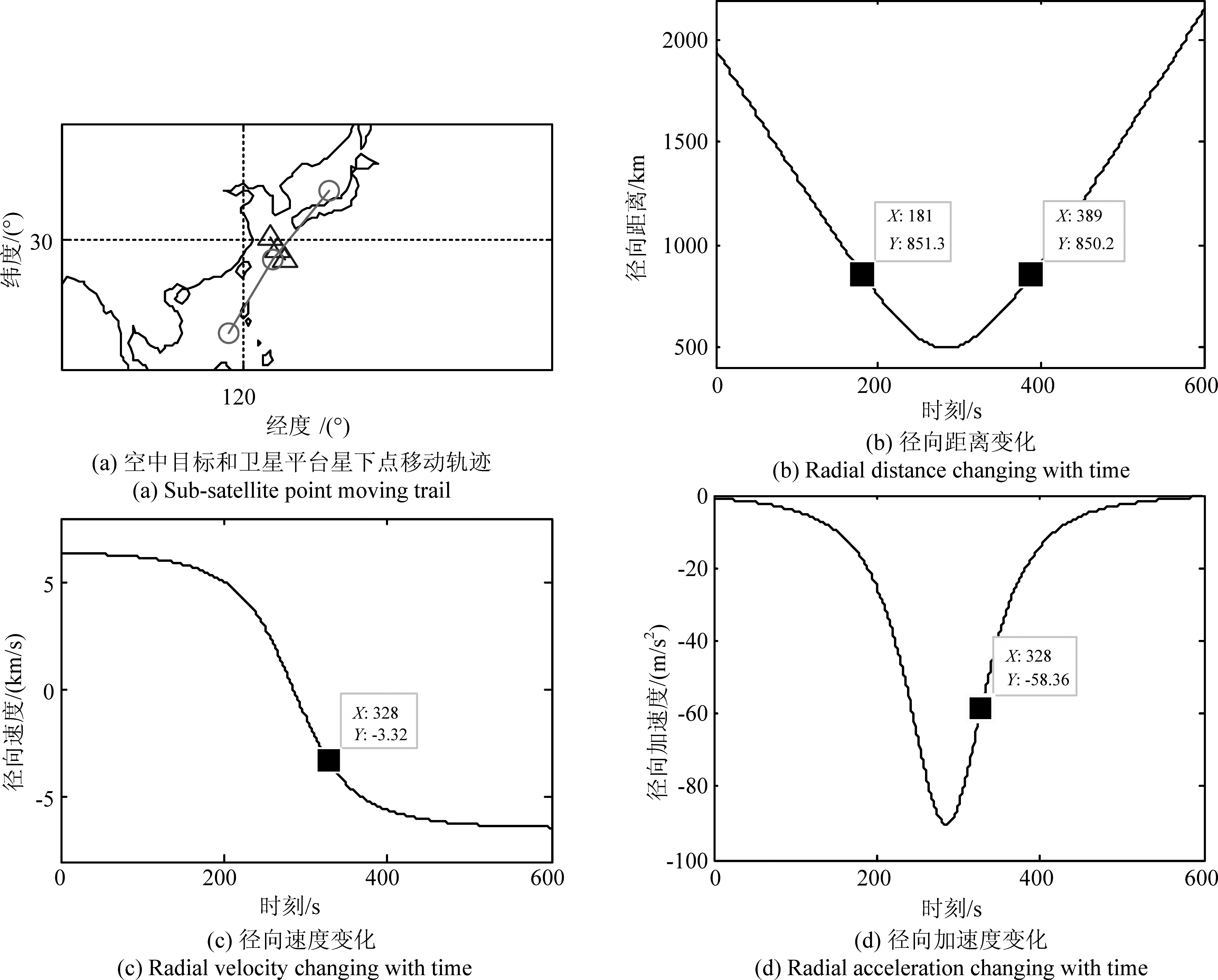
图4 星下点、径向距离、速度和加速度随时间变化情况
Fig.4 Sub-satellite point track，radial distance，velocity and acceleration changing with time
进一步根据多普勒模糊数估计值，由式(14)校正回波包络的距离徙动，其结果如图6所示。
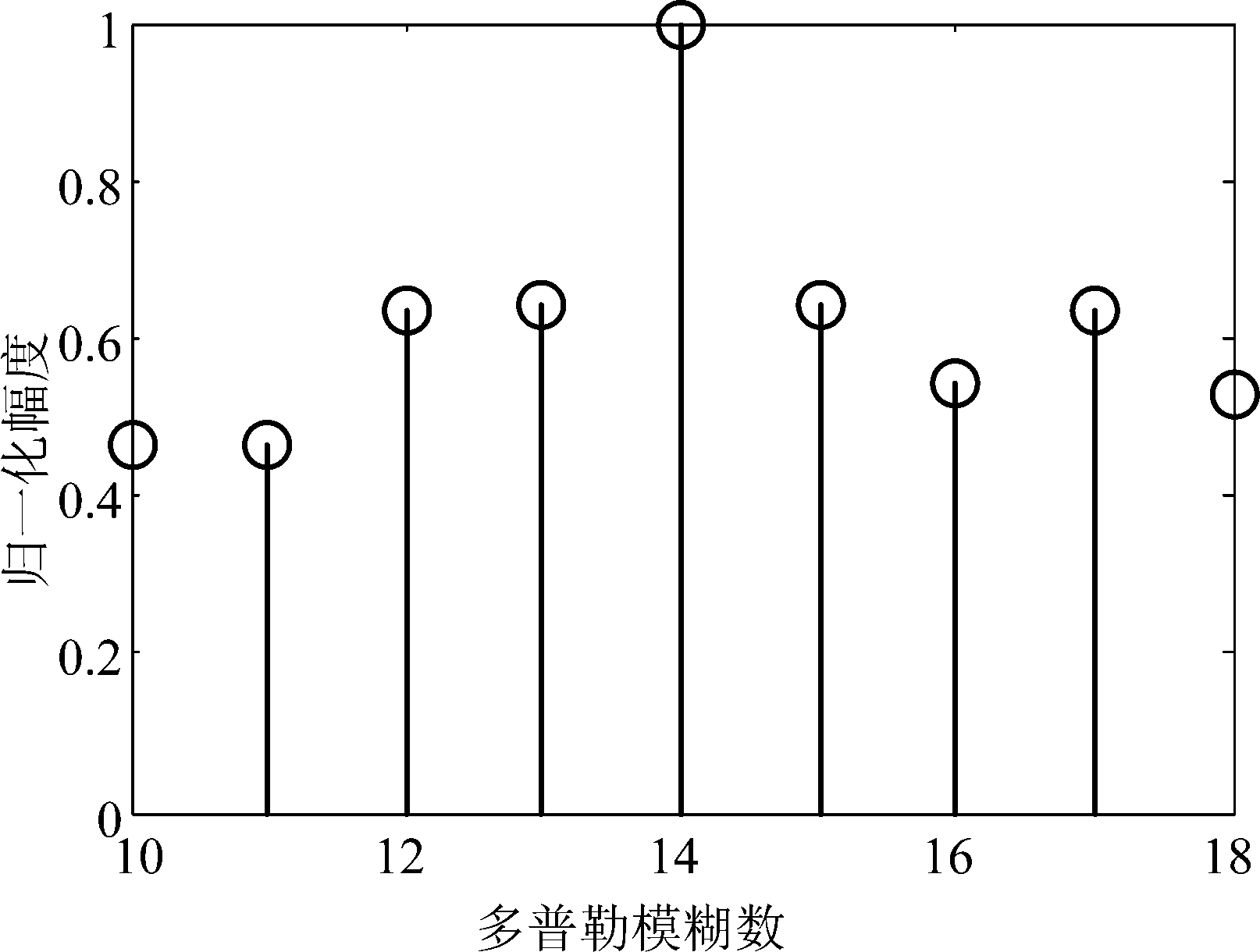
图5 SNR=-30 dB时不同多普勒模糊数相参积累结果
Fig.5 Result of coherent accumulation of different Doppler fuzzy numbers in -30 dB
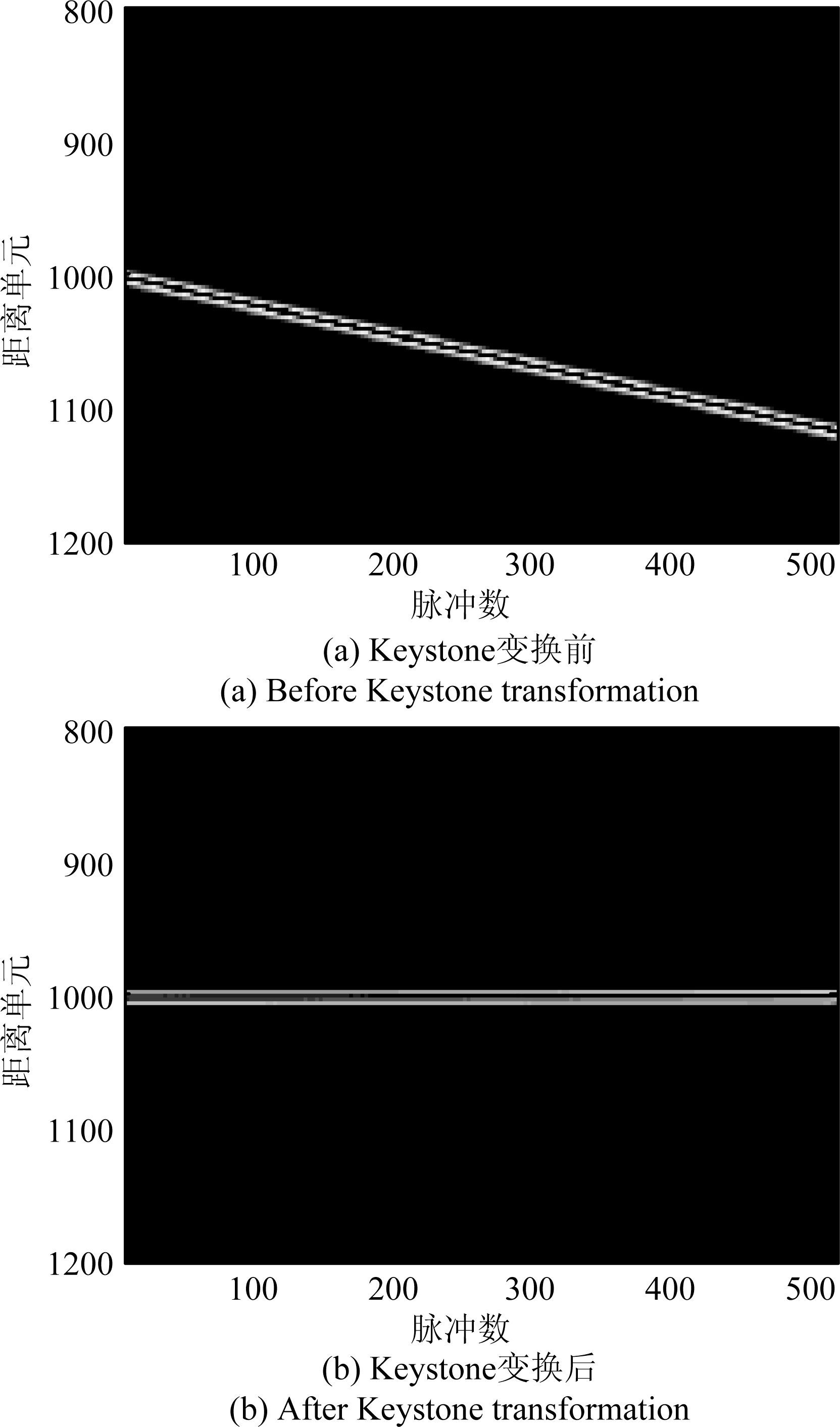
图6 回波信号距离时域-方位时域图
Fig.6 Echo signal distance-time and azimuth-time domain diagram
由图6可以看出，包络距离徙动主要表现为距离走动，距离弯曲不明显，说明由径向加速度引起的距离徙动量很小。回波信号经过Keystone变换，脉冲包络均被校正到目标所在初始距离单元内。
下一步提取目标所在距离单元内的方位时域Chirp信号，利用离散Gabor变换得到Chirp信号的时频分布，再采用高门限将时频分布二值化处理，其结果如图7所示。
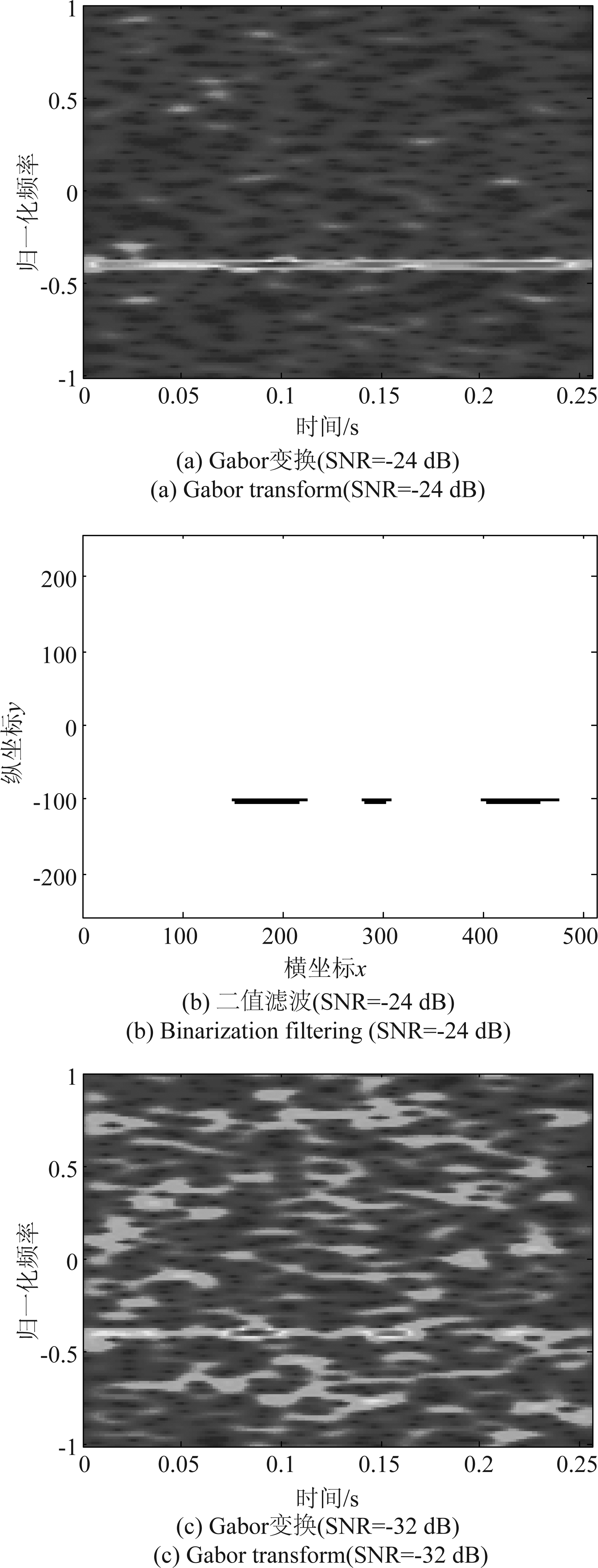
图7 离散Gabor变换和二值化结果
Fig.7 Results of discrete Gabor transform and binarization filtering
如图7所示，随着信噪比降低，时频分布分辨率变差，二值化后过门限点数越少。由于Hough变换对图像空间中直线局部缺失不敏感，即便信噪比较低， Hough变换仍适用于检测时频分布中的直线。进一步对图7(b)和图(d)进行Hough变换，结果如图8所示。
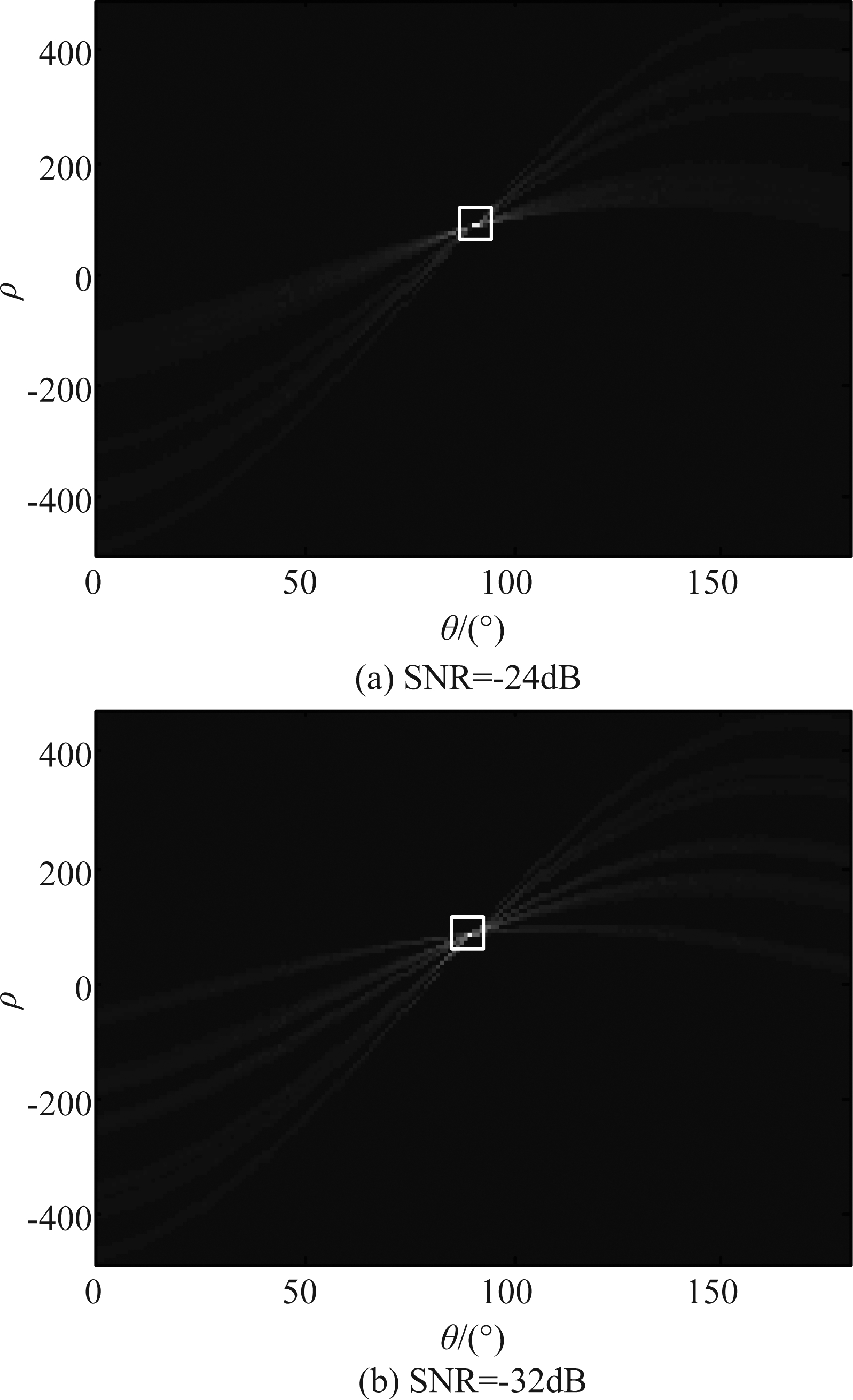
图8 Hough变换结果
Fig.8 Results of Hough transformation
从图8可以看出，在低信噪比下，参数域中仍能检测出峰值，也即存在Chirp信号。根据参数域中的峰值点坐标(θmax,ρmax)，由式(20)即可估计径向速度和加速度。
5.3 估计性能分析
设参数域中，横坐标分辨率为Δθ，纵坐标分辨率Δρ，峰值点对应坐标为(θmax,ρmax)。当Δθ=0.5°，Δρ=1时，100次蒙特卡洛仿真下的参数域坐标为:
表4 参数域峰值坐标
Tab.4 Peak coordinates in parameter domain
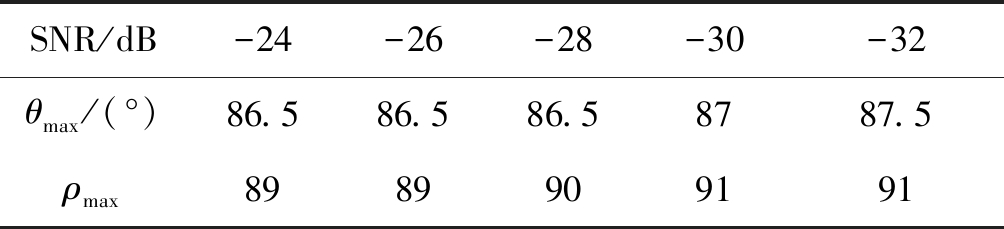
SNR/dB-24-26-28-30-32θmax/(°)86.586.586.58787.5ρmax8989909191
根据表4峰值坐标，由式(20)得到相对运动参数的估计结果如表5所示。
表5 相对运动参数估计结果
Tab.5 Estimation of relative motion parameters
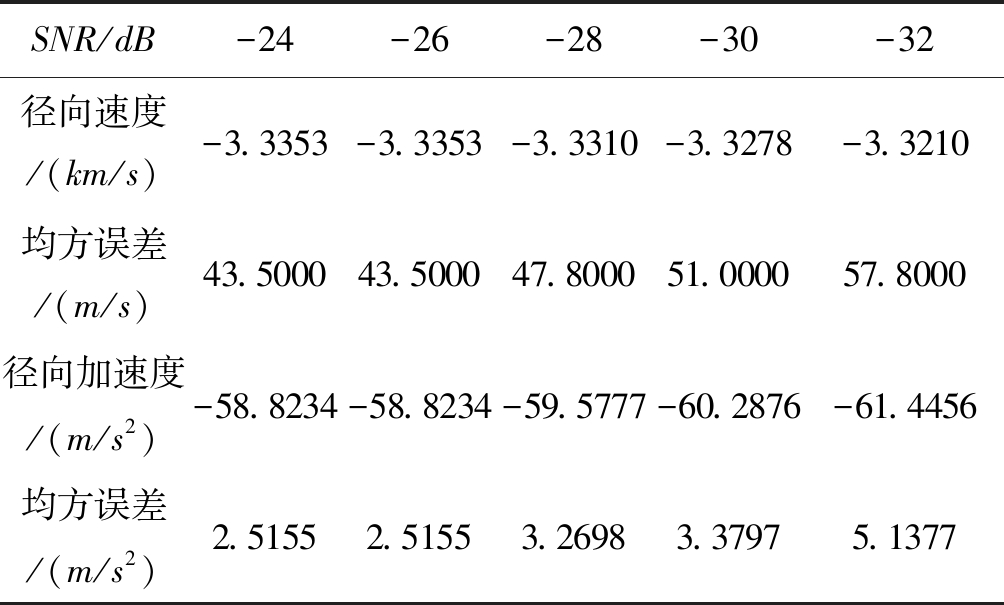
SNR/dB-24-26-28-30-32径向速度/(km/s)-3.3353-3.3353-3.3310-3.3278-3.3210均方误差/(m/s)43.500043.500047.800051.000057.8000径向加速度/(m/s2)-58.8234-58.8234-59.5777-60.2876-61.4456均方误差/(m/s2)2.51552.51553.26983.37975.1377
从表4和表5可以看出，参数域中峰值点坐标对信噪比变化不敏感，且横纵坐标分辨率决定了峰值坐标的离散取值，因此径向速度和加速度的估计值是离散值。径向速度和加速度的估计均方误差随信噪比的变化如图9所示。
从图9可以看出，本文方法在低信噪比下，能有效估计空中目标的相对运动参数。估计精度随信噪比增大而逐步逼近克拉美罗界[16]，且对信噪比的变化不敏感。这是因为在Gabor变换后，采用高门限对时频分布进行二值化处理，低信噪比下的强频率干扰点能够有效被滤除，且Hough变换对直线的局部缺失不敏感。参数估计精度主要由参数域坐标分辨率决定，分辨率越高，估计精度越高，但Hough变换的运算量也会越大，因此在选取参数域坐标分辨率时需要权衡估计精度和运算量。
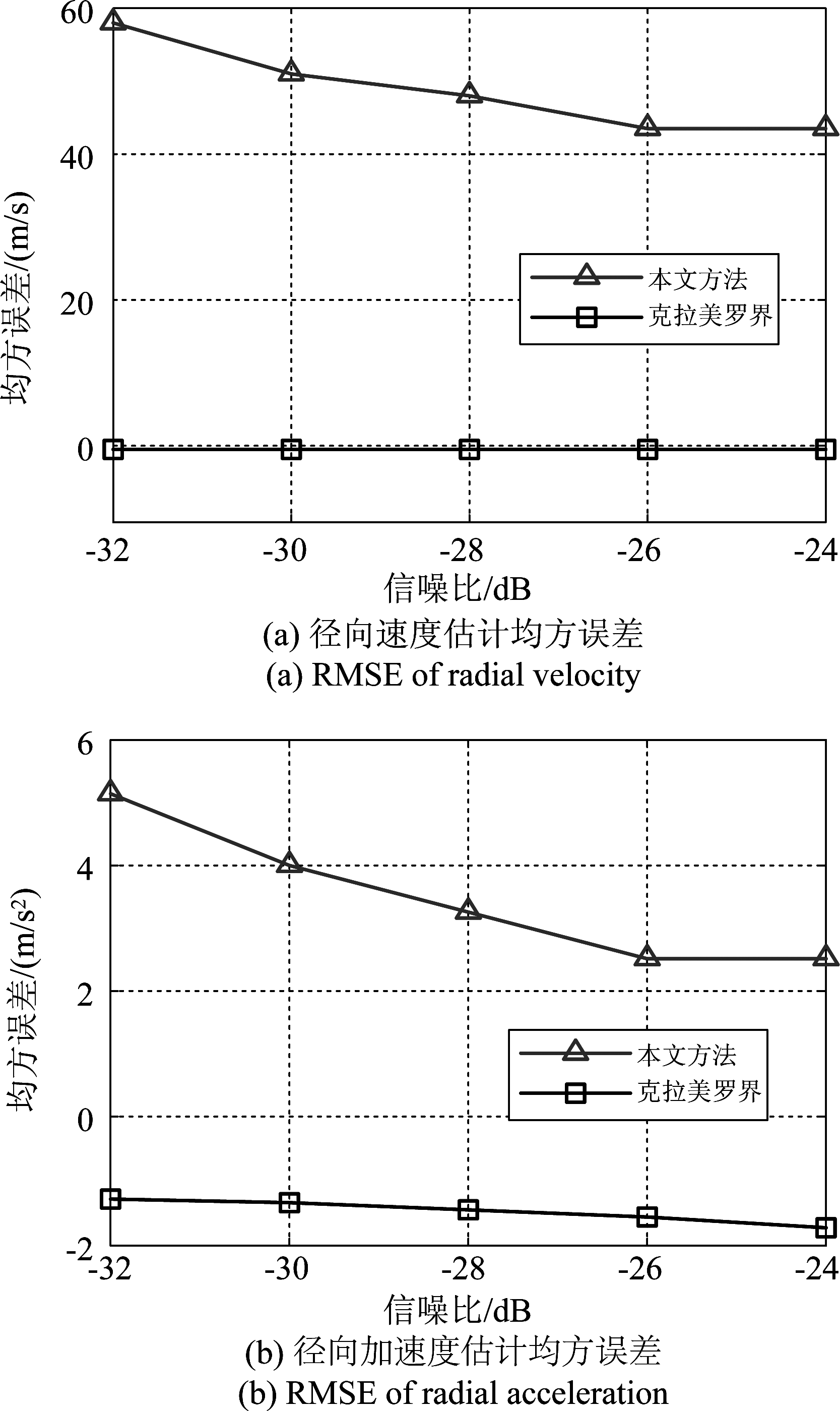
图9 径向速度和加速度估计均方误差
Fig.9 RMSE of radial velocity and accleration
6 结论
天基预警雷达卫星平台和目标间的高速径向运动导致相干处理时间内目标回波发生距离徙动和多普勒走动。通过估计相对运动参数估计，并对回波信号进行运动补偿，可以提高相参积累增益。由于星载雷达和空中目标径向距离较远，因此回波信噪比较低，严重影响了相对运动参数的估计精度。本文提出了一种低信噪比下相对运动参数的估计方法，首先利用Keystone变换校正回波包络的距离徙动；其次通过Gabor变换得到方位时域Chirp信号的时频分布；然后利用Hough变换将时频分布从时频域变换到参数域，并通过检测参数域峰值，得到峰值点坐标，进而估计出相对运动参数；最后通过仿真实验验证了本文算法的有效性。
[1] 朱庆明, 金术玲, 孟祥玲. 国外天基预警雷达系统发展现状及关键技术[J]. 电讯技术, 2012, 52(6): 1054-1058.
Zhu Qingming, Jin Shuling, Meng Xiangling. Current Developments and Key Technologies of Foreign Space-based Warning Radars[J]. Telecommunication Engineering, 2012, 52(6): 1054-1058.(in Chinese)
[2] 刘国情, 袁俊泉, 马晓岩, 等.天基预警雷达自适应转换测量卡尔曼滤波[J]. 信号处理, 2018, 34(2): 155-163.
Liu Guoqing, Yuan Junquan, Ma Xiaoyan, et al. An Adaptive Converted Measurement Kalman Filtering Algorithm for Space-based Early Warning Radar[J]. Journal of Signal Processing, 2018, 34(2): 155-163.(in Chinese)
[3] 贲德, 林幼权. 天基监视雷达[J]. 现代雷达, 2005, 27(4): 1- 4.
Ben De, Ling Youquan. Space-based Surveillance Radar[J]. Modern Radar, 2005, 27(4): 1- 4.(in Chinese)
[4] Huang Penghui, Liao Guisheng, Yang Zhiwei, et al. Approach for space-based radar manoeuvring target detection and high-order motion parameter estimation[J]. IET Radar, Sonar and Navigation, 2015, 9(6): 732-741.
[5] 杨志伟, 贺顺, 吴孙勇. 天基雷达高速微弱目标的积累检测[J]. 宇航学报, 2011, 32(1): 109-114.
Yang Zhiwei, He Shun, Wu Sunyong. A Long-Term Accumulated Detection Approach to High Speed Weak Target from Space-Borne Radars[J]. Journal of Astronautics, 2011, 32(1): 109-114.(in Chinese)
[6] 李英祥, 肖先赐. 低信噪比下线性调频信号检测与参数估计[J]. 系统工程与电子技术, 2002, 24(8): 43- 45.
Li Yingxiang, Xiao Xianci. Linear Frequency-Modulated Signal Detection and Parameter Estimation in Low Signal-to-Noise Ratio Condition[J]. Systems Engineering and Electronics, 2002, 24(8): 43- 45.(in Chinese)
[7] 胥嘉佳, 刘渝, 邓振淼. LFM 信号参数估计的牛顿迭代方法初始值研究[J]. 电子学报, 2009, 37(3): 598-602.
Xu Jiajia, Liu Yu, Deng Zhenmiao. The Starting Point Problem of Parameters Estimation for LFM Signal Based on Newton’s Method[J]. Acta Electronica Sinica, 2009, 37(3): 598- 602.(in Chinese)
[8] Peleg S, Porat B. Linear FM signal parameter estimation from discrete-time observations[J]. IEEE Trans on Aerospace and Electronic Systems, 1991, 27(7): 607-615.
[9] 贲德, 龙伟军. 天基雷达的关键技术[J]. 数据采集与处理, 2013, 28(4): 391-396.
Ben De, Long Weijun. Key Technology of Space-Based Radar[J]. Data Acquisition and Processing, 2013, 28(4): 391-396.(in Chinese)
[10] Fischman M A, Le C. Digital beamforming developments for the joint NASA/Air force space based radar[C]∥IEEE International Geoscience and Romote Sensing. Anchorage, AK: IEEE Press, 2004: 687- 690.
[11] 战立晓, 汤子跃, 朱振波. 米波双基地雷达长时间相参积累算法[J]. 信号处理, 2013, 29(3): 351-359.
Zhan Lixiao, Tang Ziyue, Zhu Zhenbo. Long Term coherent Integration Algorithm for Metric Band Bistatic Radar[J]. Journal of Signal Processing, 2013, 29(3): 351-359.(in Chinese)
[12] 张顺生, 曾涛. 基于keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 1675-1678.
Zhang Shunsheng, Zeng Tao. Weak Target Detection Based on Keystone Transform[J]. Acta Electronica Sinica, 2005, 33(9): 1675-1678.(in Chinese)
[13] 张辉, 范雪林, 李东风. 一种改进的短时傅里叶算法实现[J]. 通信技术, 2017, 50(5): 1066-1068.
Zhang Hui, Fan Xuelin, Li Dongfeng. Implementation of Modified Short-time Fourier Transform[J]. Communications Technology, 2017, 50(5): 1066-1068.(in Chinese)
[14] Carlson B D, Evans E D, Wilson S L. Search radar detection and track with the Hough transform, part I: System concept[J]. IEEE Transaction on Aerospace and Electronic Systems, 1994, 30(1): 102-108.
[15] 刘健庄. 一种高效的Hough变换实现方法[J]. 信号处理, 1992, 8(1): 43- 48.
Liu Jianzhuang. An Efficient Implementation of the Hough Transform[J]. Signal Processing, 1992, 8(1): 43- 48.(in Chinese)
[16] Peleg S, Porat B. The Cramer-Rao Lower Bound for Signals with Constant Amplitutude and Polynomial Phase[J]. IEEE Trans. Signal Processing, 1991, 39(3): 749-752.
