1 引言
近年来，临空高超声速飞行器相关研究已经成为一大热点[1-2]，但对于其探测防御尚没有明确有效的手段。雷达探测作为一种基本的探测手段，在地基雷达针对临近空间目标的探测方法上已经取得很多研究进展，但是目标距离远[1]、回波强度弱[3- 4]、存在探测盲区以及工作环境干扰大[1]等始终是地基雷达探测无法回避的问题。
平流层飞艇是一种高空平台，可以做为多种探测器的载体。其工作环境的电磁背景良好[5]，并且工作位置与临空目标距离较近，不仅可以为雷达探测临空目标提供良好的平台基础，还可使雷达兼顾低空目标探测。但与地基雷达相比较，使用平流层飞艇搭载雷达工作也存在载荷有限，发射功率受限制、高空能源传输困难[5]以及平台复杂运动影响雷达探测等问题。
平流层飞艇依靠填充的气体提供升力，依靠控制和推进系统控制飞行，它体积质量比大，具有明显的惯性特征[6]，运动复杂多变，受环境影响较大。文献[6-12]采用了多种方法对飞艇的运动模态进行了分析。
目前，对于艇载雷达信号处理的研究主要集中在对下视地海杂波的研究，而忽视飞艇运动对雷达信号的影响，这是由于当前飞艇的体量小，艇载雷达孔径有限，主要探测近程目标，飞艇运动造成的影响十分微弱，但是随着技术的进步飞艇必然向着大型化发展，探测目标也更加多样，大孔径的艇载雷达天线受飞艇运动的影响将变得明显。
本文在综合借鉴了平流层飞艇的运动特性相关研究文献的基础上，提出了一种飞艇运动状态下艇载雷达回波信号的计算模型，从信号层面分析了艇载雷达运动对雷达探测的影响，为设计可以使艇载雷达更好的发现和探测目标的信号处理算法奠定了基础。
2 飞艇运动对艇载雷达探测影响的计算模型
因本文只关注飞艇的运动特点，不关注飞艇的运动原理，故将文献[6-7]中讨论飞艇的运动特性简化为飞艇的平动和三个方向的旋转，如图1。
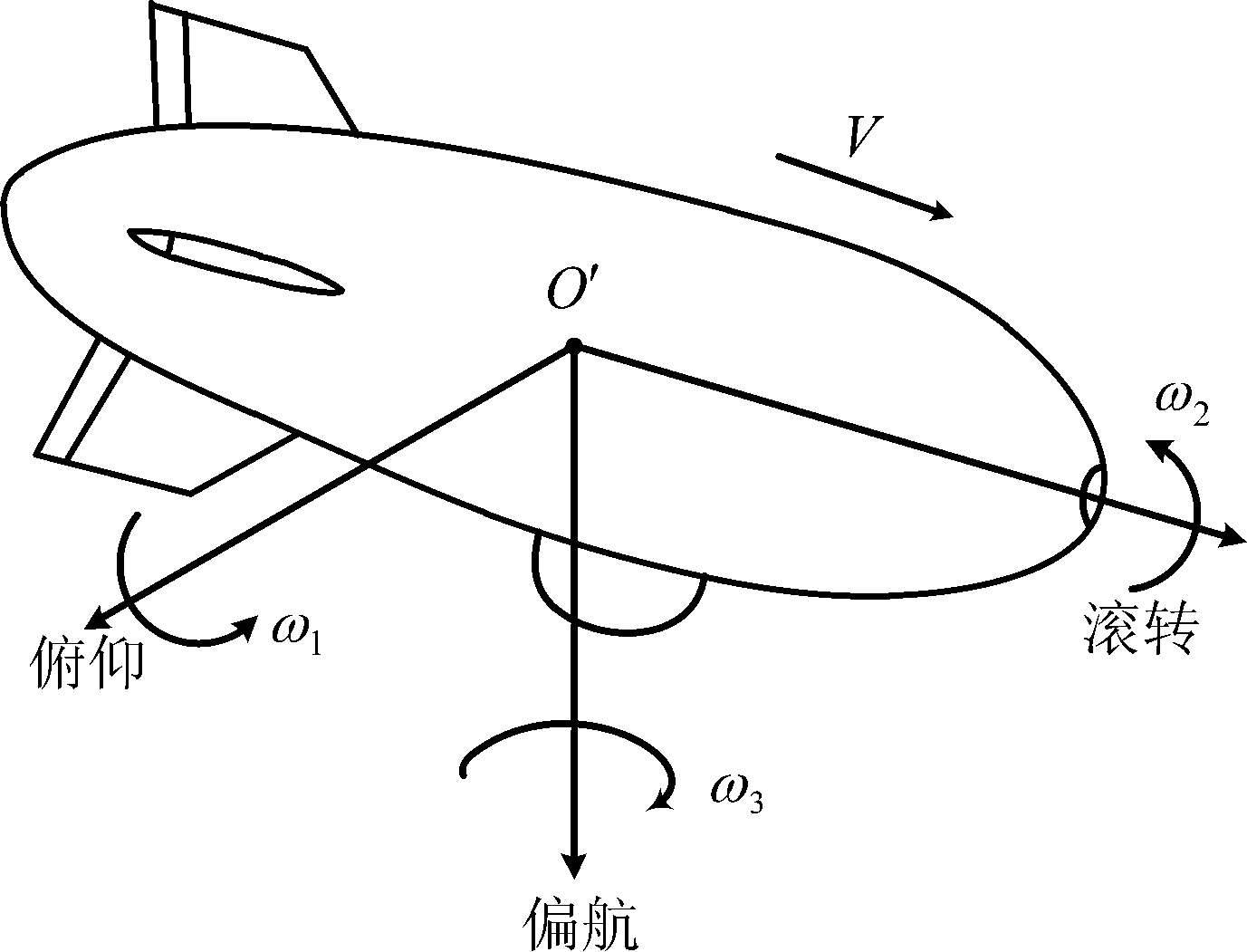
图1 飞艇运动特性示意图
Fig.1 Schematic diagram of airship movement
图中，O′为飞艇的浮心，ω1、ω2和ω3分别是俯仰、滚转和偏航三个方向的角速度，将飞艇在三个方向的旋转运动定义为飞艇的微动，V为飞艇平动速度。
飞艇的平动是飞艇整体性运动，速度通常不大，对雷达探测不会造成明显的影响，在本文中不做讨论，本文主要分析飞艇微动对雷达探测的影响。
2.1 天线运动计算模型
飞艇搭载雷达工作时，雷达通常采用相控阵体制[5]，天线多为布置在飞艇表面的共形相控阵天线，因此艇载雷达会出现探测时天线随飞艇运动的现象。为了分析飞艇的微动对艇载雷达的探测造成的影响，本文在将共形阵天线简化为平面阵天线的基础上，建立了一种在飞艇运动的状态下计算艇载雷达相控阵天线各阵元运动的模型，如图2。
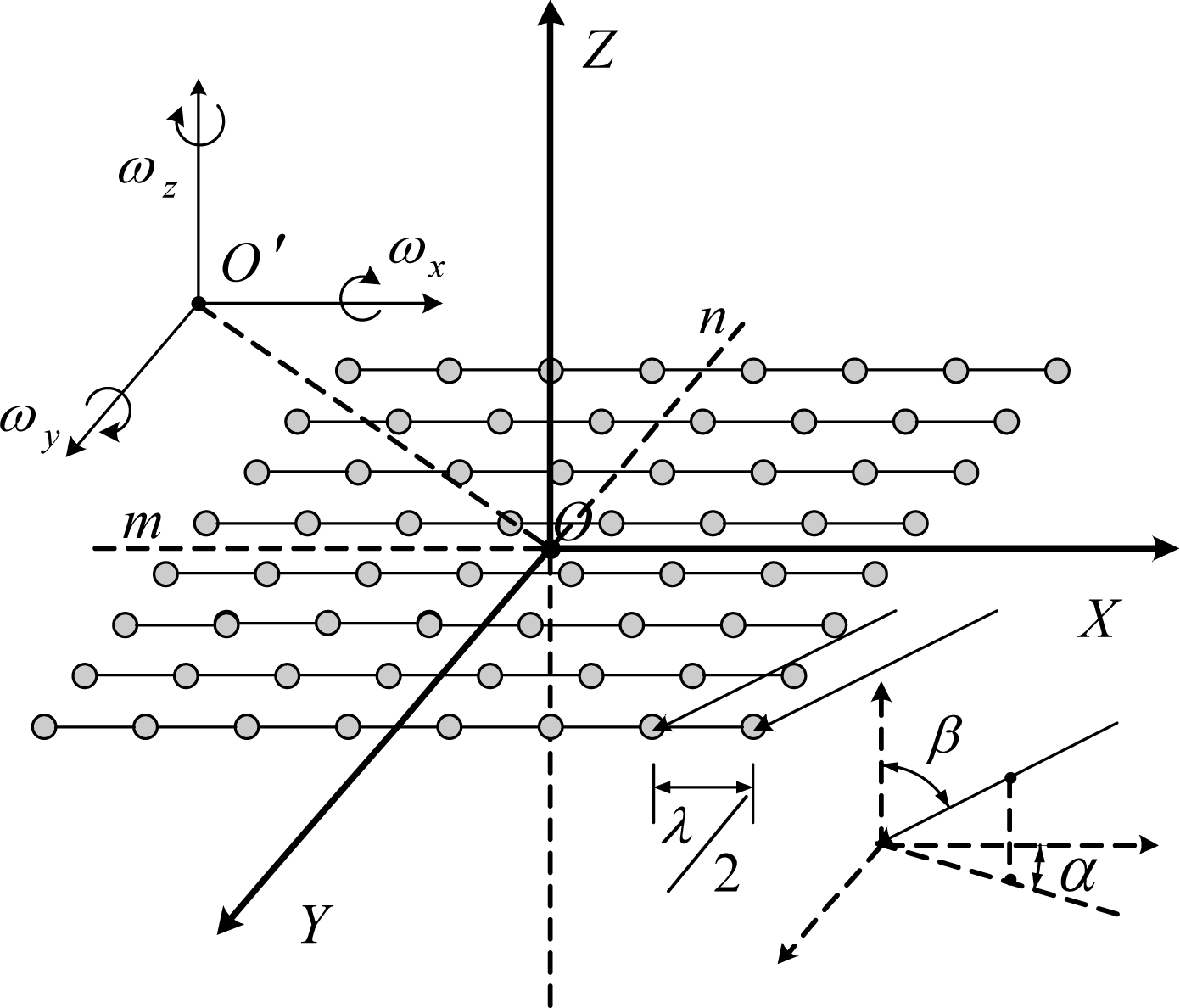
图2 飞行相控阵天线运动计算模型
Fig.2 Flight phased array antenna motion calculation model
图中，以阵面中心O建立坐标系，m、n分别为X、Y方向上的阵元数量，ωx、ωy、ωz分别为飞艇在三轴方向上的转动角速度分量，可由天线布置位置以及ω1、ω2和ω3间接得到。α为回波方向在XOY平面内投影与X轴正方向夹角，以XOY平面内顺时针方向为正； β为回波方向与Z轴正方向的夹角，以YOZ平面为界偏向X轴正方向为正。定义(α, β)为回波方向，本文分析目标回波方向均以天线中心为参考点，不引入雷达方位角和俯仰角的概念，实际中俯仰角和方位角可由天线布置位置和α、 β导出。回波的方向向量为
e=(sin(β)cos(α),sin(β)sin(α),cos(β))
(1)
设图2中X方向阵元间的距离为dx，Y方向阵元间的距离为dy，当天线为平面阵时，通常dx与dy相等且为雷达发射信号半波长。假设m、n均为偶数，设阵元坐标为aij(x(i),y(j),0)，可得
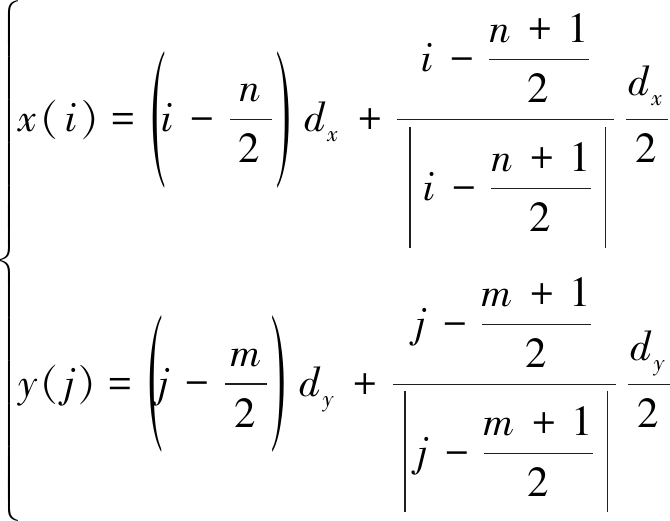
i=1,2,…,n; j=1,2,…,m
(2)
飞艇转动时，阵面以O′为旋转中心，以X、Y、Z三个方向为轴，进行角速度分别为ωx、ωy、ωz的转动，规定角速度对三个坐标轴满足左手螺旋的方向为正方向。设O′坐标为(x,y,z)，飞艇晃动时认为天线阵面为刚体，则各个阵元的在三个方向旋转的线速度大小和方向向量分别为
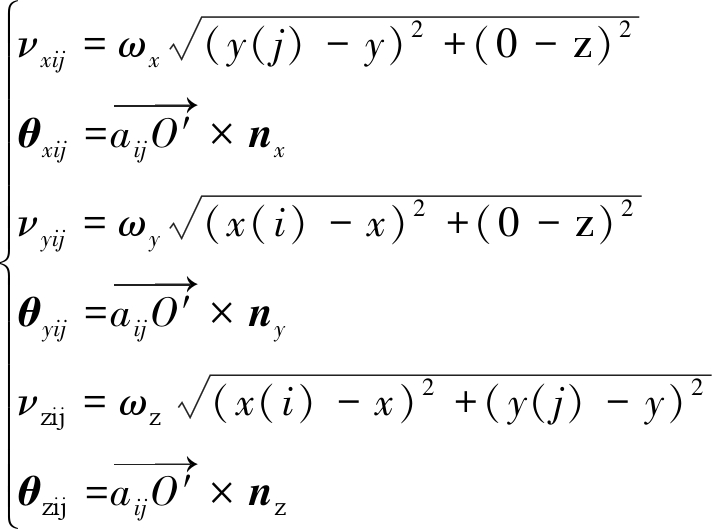
(3)
式中nx、ny、nz分别为X、Y、Z三轴方向的单位向量，进一步可得各阵元在回波方向上的投影速度为
(4)
通过式(4)可以看出，各阵元在回波方向上的速度与回波所在的方向以及飞艇晃动的角速度有关。
此模型可通过控制浮心O′的位置来描述雷达天线与飞艇的任意位置关系。
2.2 回波信号计算模型
通常雷达发射信号为线性调频信号，可表示为[13]
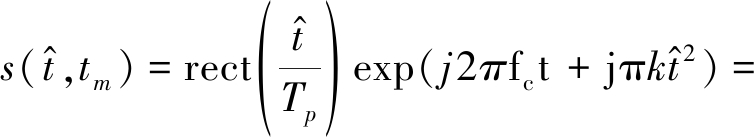
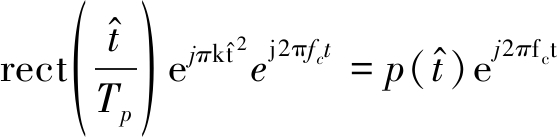
(5)
式中，
表示雷达快时间，tm是以雷达重复周期Tr为步长的信号脉间时间，又称为慢时间，Tp为脉冲宽度，k为线性调频斜率， fc为信号载频。
相控阵雷达回波是经过移相器将各阵元接收的目标回波相位对齐后叠加得到的，如图3。
图3 相控阵接收回波示意图
Fig.3 Schematic diagram of phased array receiving echo
图中，N为阵元数目，ΔφB为相邻阵元的距离引起的回波相位差。理想情况下，各阵元接收到的回波可经移相器将阵元间距产生的相位完全对齐。
假设目标为点目标，那么经过理想移相器的各阵元回波信号叠加并经下变频消去基带后应有如下形式
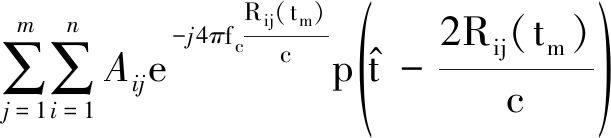
(6)
式中，Aij为各阵元回波的幅度调制信息， c为光速，Rij(tm)为各阵元接收回波的目标信息，当阵面固定时各阵元接收的回波移相后的目标信息相同，通常认为具有如下形式[13]
(7)
式中，R0为目标初始距离，ν为目标的径向速度，a为目标径向加速度，J为目标径向加加速度，对于常规目标通常J为0。
当艇载雷达天线随飞艇微动时，各阵元在回波方向上具有不同的速度分量，这会导致信号收发的时间间隔内各阵元存在一个不一致的微小位移，如图4。
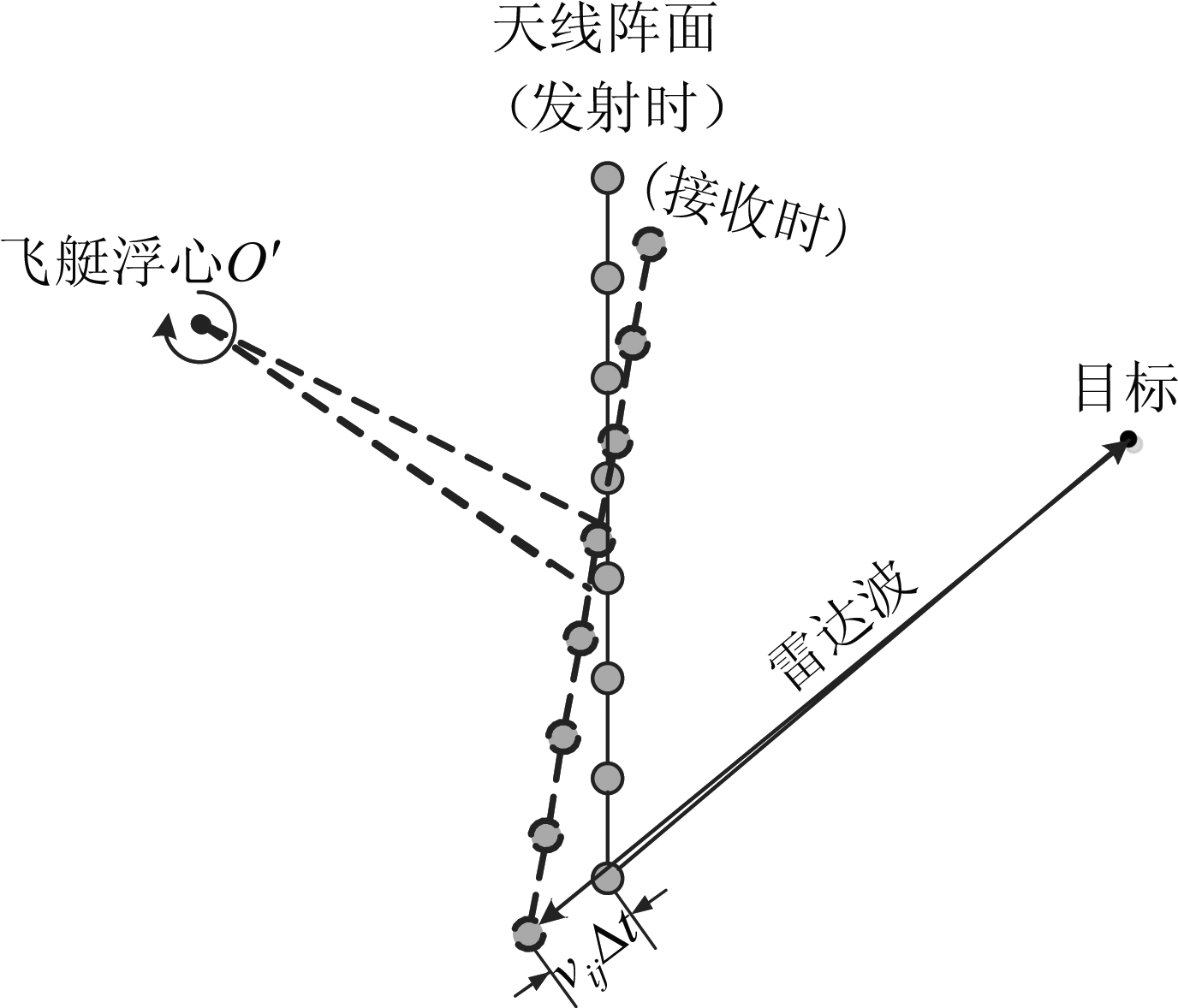
图4 飞艇晃动时艇载雷达天线收发情况示意图
Fig.4 Schematic diagram of a shipborne radar antenna reception and launch when the airship is shaking
图中，忽略天线运动带来的目标与阵元间的角度变化，假设信号收发的时间内飞艇运动没有发生变化，则信号收发期间天线转动导致的阵元位移为νijΔt，Δt为雷达信号从发射到接收经过的时间，具体意义如图5。
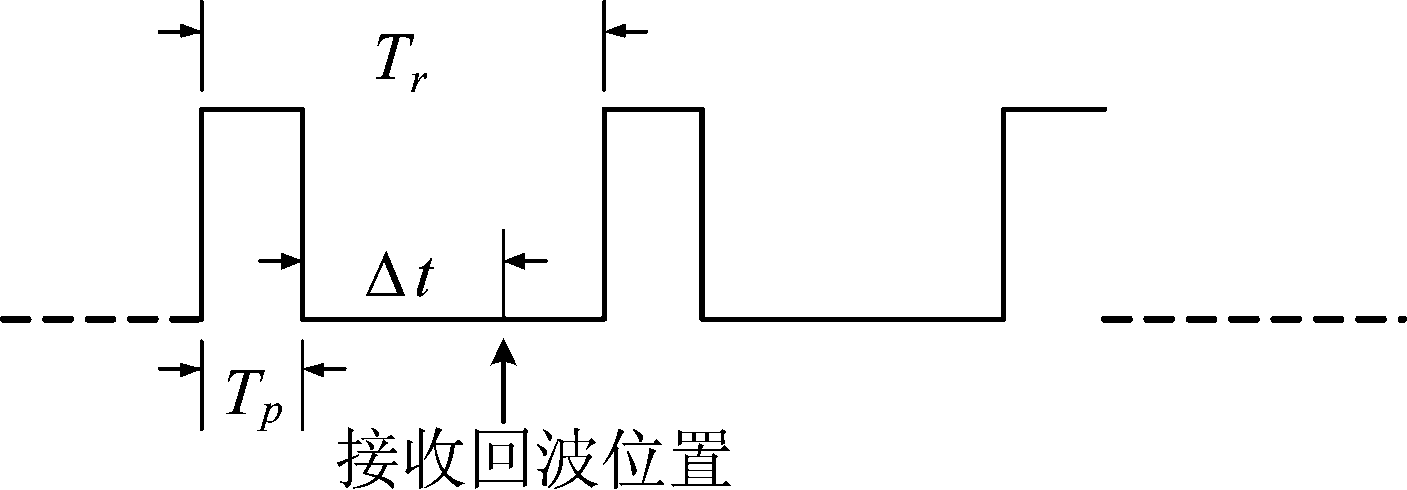
图5 雷达信号收发时序图
Fig.5 Radar signal transceiver timing diagram
在不考虑雷达距离模糊的情况下，忽略发射期间的阵元移动，可近似认为收发时间间隔为目标时间延迟。将阵元位移等效在目标信息上，Rij(tm)可改写为
(8)
对于目标速度引起的多普勒频移，可表示为
(9)
式中，νc表示目标的真实速度，φ表示目标速度与雷达波束之间的夹角，λ为雷达信号波长。当飞艇晃动时，理论上各阵元发射波束与目标之间的位置关系发生变化，则波束与目标速度之间的夹角也相应发生变化，但由于雷达发射时间极短且目标处于远场区，因此夹角变化极小，晃动对目标多普勒频率影响不大。
另外，假设艇载雷达天线为刚性天线，飞艇晃动时天线形状不发生变化，故晃动不会引起天线方向图变化。因此，本文主要分析晃动对艇载雷达回波强度的影响。
3 飞艇微动对雷达信号的影响
雷达重复周期长度Tr的选取与雷达探测不模糊距离的需求相关，若按照雷达不模糊距离1000 km计算，周期长度Tr为0.0033 s，综合文献[6-7]中对飞艇运动的仿真结果来看，飞艇的运动是连续的，不会出现跳变，周期长度在飞艇运动变化的时间粒度之内，因此可以近似认为在一个雷达重复周期内飞艇运动状态没有发生变化。故本文在分析飞艇微动对雷达信号影响时，假设一个重复周期的时间内飞艇运动状态恒定，且忽略晃动引起的波束方向改变。
3.1 对回波强度的影响
分析式(6)可知，当阵面固定时，各阵元接收的回波目标时延完全相同，可完全对齐叠加，而当阵面随飞艇微动时，各阵元的速度差异会导致回波的时延不一致，回波无法完全对齐，叠加后回波展宽并且强度下降。在阵面尺寸较小或飞艇晃动不剧烈时，回波受其影响十分微弱可以忽略不计，但在阵面较大且飞艇晃动剧烈的条件下，晃动会对回波造成一定的影响。
3.2 对信号脉冲压缩的影响
根据卷积的分配率，式(6)经脉压后的回波信号为
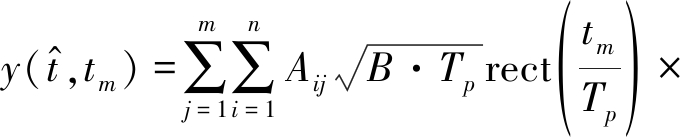
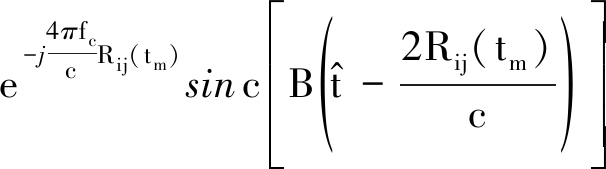
(10)
虽然式(10)为阵面全部阵元和回波的脉压结果，但观察其形式，可以将其等效看做阵面各阵元回波脉压结果之和，并可以看出各阵元等效的回波脉压的峰值出现在
处。所以当阵面固定时，各阵元在回波方向相对静止，Rij(tm)由式(7)表示，各阵元脉压分量的峰值出现在同一位置，叠加后脉压有十分明显的效果，但由于飞艇的微动，各阵元在回波方向的速度分量存在差异，Rij(tm)由式(8)表示，各阵元脉压分量的峰值不在同一位置，这会导致各分量峰值无法在同一位置叠加，脉压效果下降。
显然，回波强度和回波脉压效果的下降程度与阵元间速度相差程度和阵元的数目以及目标与雷达间的距离相关，各阵元的速度相差越大，阵元的数目越多，目标距飞艇越远对脉压效果的影响也越大。
4 仿真分析
经过以上的分析，可以得出飞艇晃动时对艇载雷达探测造成影响的因素主要是：天线阵元回波方向上的速度差异和目标与飞艇之间的距离。因此，若要分析飞艇晃动时信号的变化，首先要分析飞艇晃动时天线阵元的速度情况。
4.1 阵元在回波方向上的速度仿真
根据本文所建立的模型分析可知，影响阵元回波方向速度的因素有：浮心和阵面的相对位置、回波方向、飞艇微动角速度大小以及天线阵元的数目。
其中，微动角速度对阵元速度的影响是显而易见的：转速越大阵元速度越大，同等条件下阵元间速度差异也越大。为了方便讨论其他因素对阵元速度的影响，突出影响结果，根据文献[6]中对于飞艇运动特性的分析结果，选取旋转速度ωx=ωy=ωz=1.5 rad/s。
浮心和阵面的相对位置描述的是阵面布置在飞艇表面的位置以及飞艇的大小。由于飞艇形状为椭球形，故当阵面布置在飞艇表面时浮心总是位于阵面中心轴线附近，飞艇形状越接近球体，浮心距中心轴线也越近。
根据文献[5]中飞艇体积的数据得知，飞艇的长在50 m至150 m。假设O′落在Z轴上，则设置浮心Z坐标的范围为[-50,-25]，取值的正负是由设置的回波方向决定的。
根据假设浮心始终落在阵面中心轴线上，因此对于不同的浮心位置，阵元速度在各个回波方向上的起伏特性是相同的。为了分析不同回波方向上浮心位置对阵元速度的影响，首先应分析各回波方向上阵元速度差异的起伏性质。
4.1.1 回波方向对阵元速度差异影响
回波方向对阵元速度差异的影响与阵元数目关系不大，因此可在小阵元数目条件下讨论阵元速度的差异性，并将其运用到回波仿真中。
设置阵元个数为8×8。根据相控阵实际能达到的探测角度，设置α的范围为[-180°,180°]，设置β的范围为[-60°,60°]，浮心Z坐标为-35，仿真结果如图4。
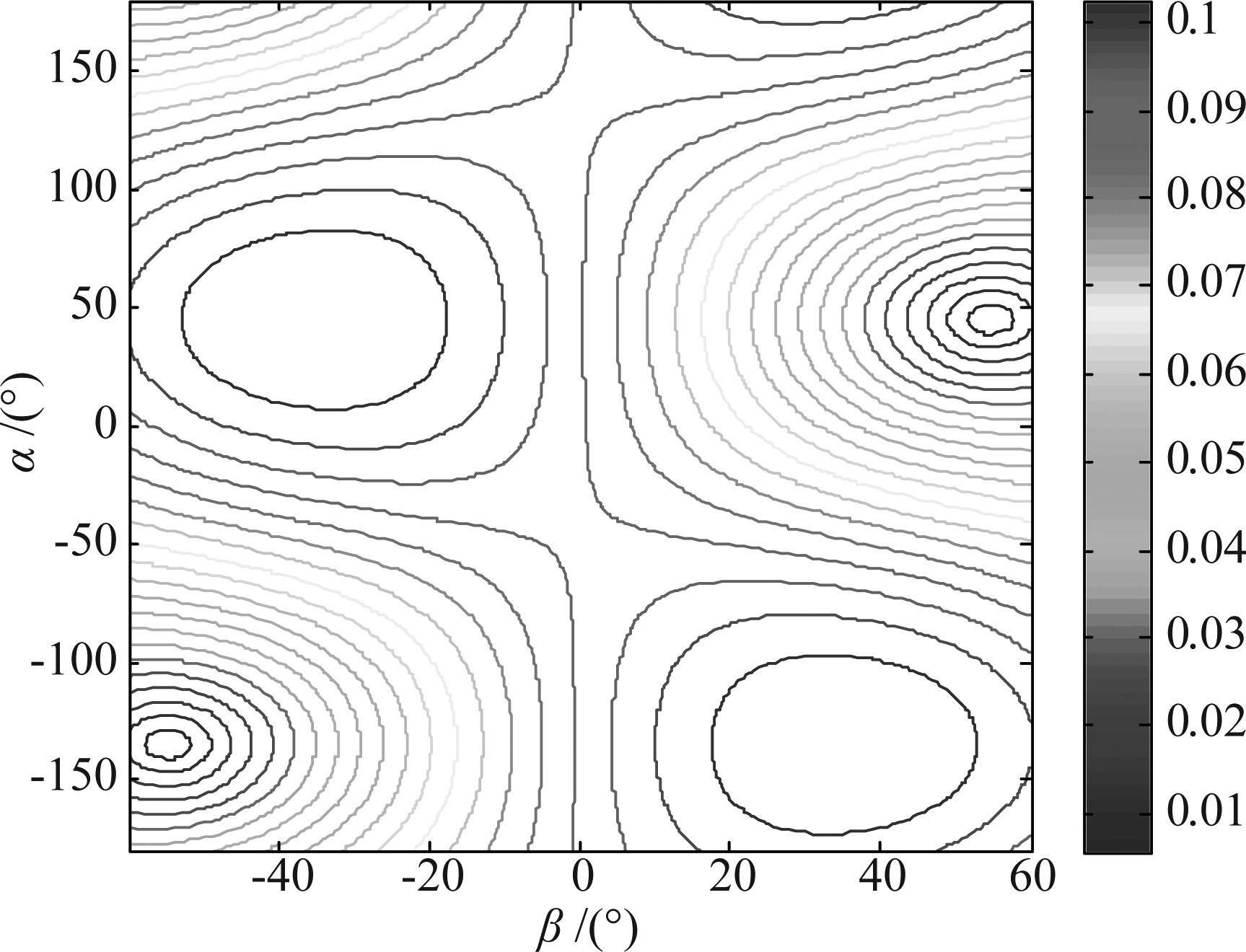
图6 各回波方向阵元速度的方差
Fig.6 Variance of array element velocity in each echo direction
图6描述的是在不同的回波方向，阵面中各阵元在回波方向上的速度相差的程度。可以看出，在回波方向为(45°,-35°)和(-135°,35°)时阵元速度相差的程度最大，回波方向为(-135°,-55°)和(45°,55°)时阵元速度相差的程度最小。
各回波方向阵元速度相差的程度反应的不仅是各回波方向阵元速度相差的大小，也说明了各回波方向阵元位置对阵元速度的影响程度。显然，在阵元速度相差程度大的回波方向，阵元位置对阵元速度的影响也较大，在阵元速度相差程度小的回波方向，阵元位置对阵元速度的影响也较小。
4.1.2 天线与飞艇浮心的位置关系影响
分别在阵元速度相差程度最大和最小的回波方向上分析浮心位置对阵元速度的影响。
根据假设，阵面始终沿中心轴线转动，阵元速度平均值恒为0，所以在分析不同条件阵元速度变化情况时以最大阵元速度为依据。
设置阵元个数为6400，即式(2)中m=n=80，设置浮心Z坐标的范围为[-50,-25]，回波方向分别为(45°,-35°)和(-135°,-55°)，仿真结果如图7。
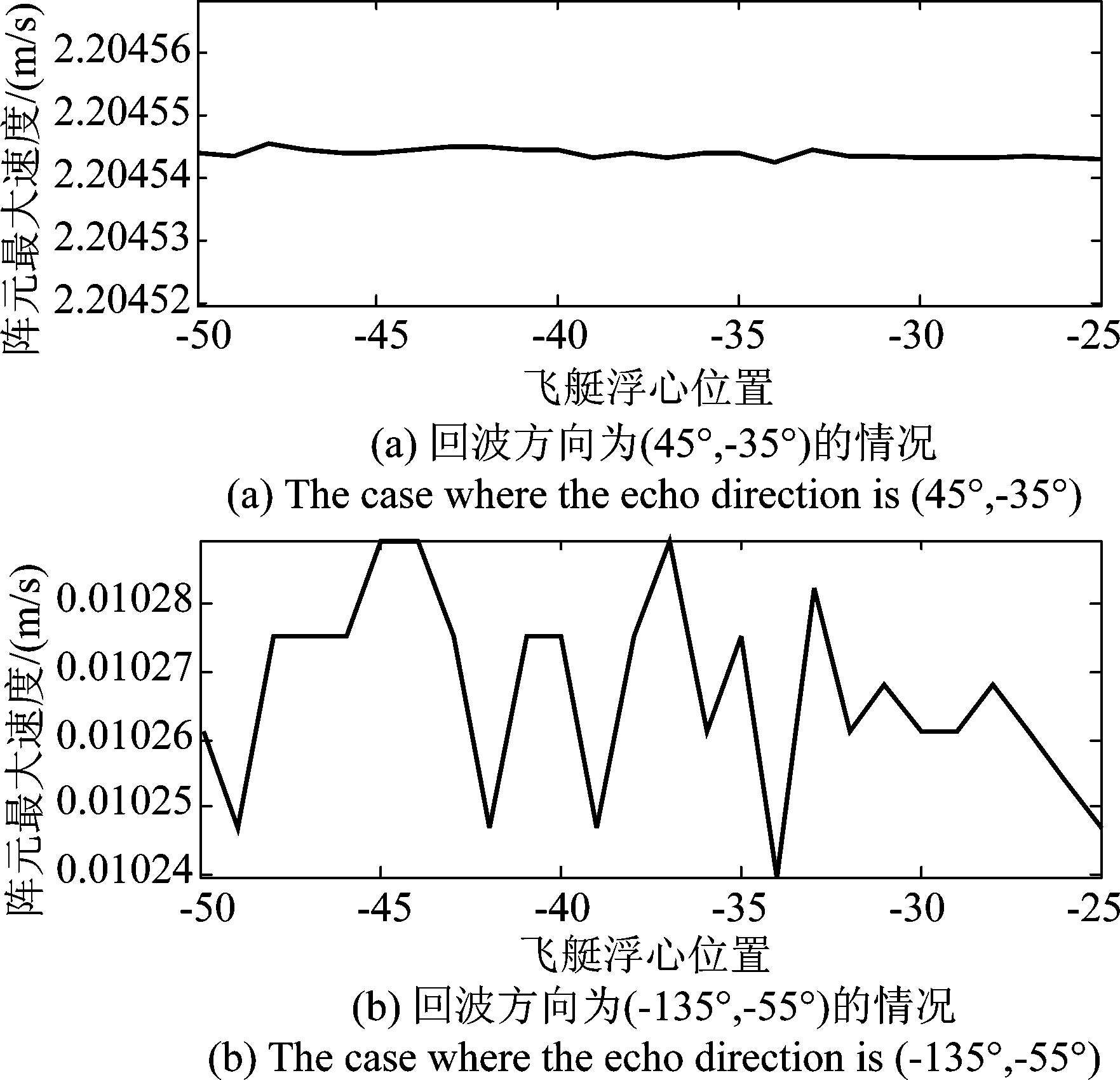
图7 阵元速度随浮心位置的变化
Fig.7 The speed of the array element varies with the position of the buoyancy center
通过图7的(a)和(b)可以看出无论是阵元速度相差程度大的回波方向还是相差程度小的回波方向，阵元在回波方向速度的数值随浮心坐标的变化均不大，这说明阵面大小不变时，飞艇体积的大小对雷达探测的影响不大。
4.1.3 阵面大小的影响
设X和Y方向的阵元数相同，则以某一方向上的阵元的数目描述阵面大小。设置阵元个数为50×50至100×100，浮心Z坐标为-35，回波方向为(45°,-35°)，仿真结果如图8。
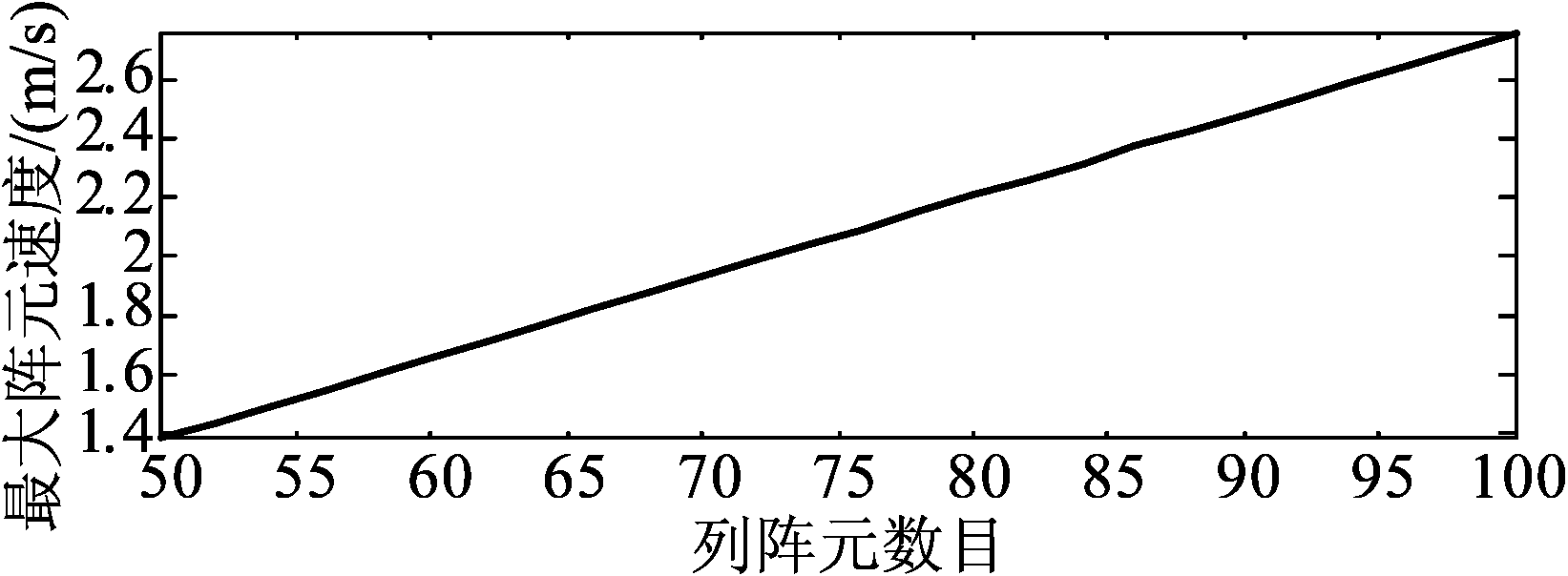
图8 阵元速度随阵面大小的变化
Fig.8 Variation of antenna element speed with antenna size
从图8中可以看出，阵元速度的最大项随阵面变大而增大，由此可推断阵元速度相差程度也随阵面变大而增大，并且随阵面增大，探测所用的阵元数目也随之增多，更多的阵元速度项叠加会使回波强度和脉压效果更加分散，因此艇载相控阵雷达的天线阵面越大探测效果受飞艇微动的影响也越大。
4.2 艇载相控阵雷达的回波仿真及对比
引起固定天线雷达与飞艇微动状态下的艇载雷达探测差异的因素除了阵元速度的相差程度还有目标距离。前面的仿真分析了一些因素对阵元速度差异影响，间接分析了它们对于信号的影响程度，因此，不在信号层面对这些因素进行进一步仿真。下面为定量分析针对不同距离目标探测时，飞艇微动对艇载雷达探测的影响程度，本文分别在阵元速度相差程度最大与最小的情况下，对比同等参数条件下，艇载雷达与固定天线雷达针对不同距离的目标的回波差异。
4.2.1 阵元速度相差程度最大的回波方向
设置雷达参数：载频fc为10 GHz，带宽B为1 MHz，时宽Tp为300 μs，重频fr为200 Hz，采样频率1 MHz，阵元接收的回波信号幅度调制信息Aij=1，目标参数：分别设置初始距离R0为100 km和500 km，径向速度ν为3 Ma，径向加速度a为100 m/s2，飞艇参数：旋转速度ωx=ωy=ωz=1.5 rad/s，阵元数目n=m=80，浮心坐标O′(0,0-35)，回波方向为(45°,-35°)，仿真结果如图9。
图9 回波方向为(45°,-35°)时各阵元回波方向速度
Fig.9 Echo direction velocity of each element when the echo direction is (45°,-35°)
图9描述的是仿真条件下各阵元回波方向速度。可以看出，在阵元速度相差程度最大的回波方向上，在所设置的参数条件下阵元速度相差范围为5 m/s左右。
图10的(a)和(b)对比的是艇载雷达与固定天线雷达在阵元速度相差最大的回波方向上对于100 km目标的回波以及回波脉压的情况，对于100 km目标来说艇载雷达晃动对于回波强度和回波脉压的影响并不明显，但可以看出脉压效果较之固定天线雷达还是略有下降。
图11的(a)和(b)对比的是艇载雷达与固定天线雷达对于500 km目标的回波以及回波脉压的情况，对于500 km目标来说艇载雷达回波强度和回波脉压效果均有明显的下降，飞艇晃动对于雷达探测的影响已经凸显出来。
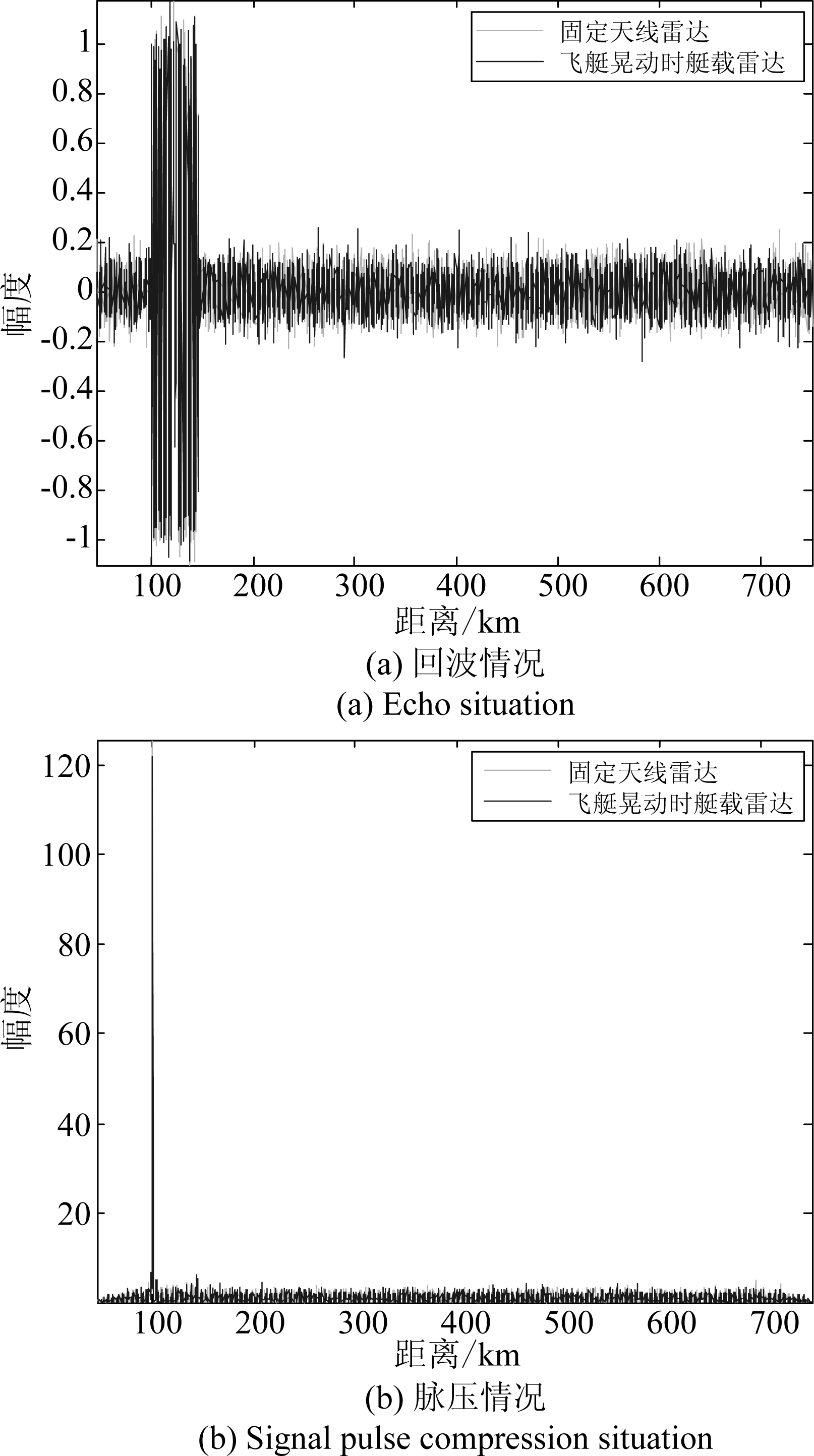
图10 方向为(45°,-35°)距离100 km时的目标回波
Fig.10 Target Echo at (45°,-35°)Distance 100 km
图11 方向为(45°,-35°)距离500 km时的目标回波
Fig.11 Target Echo at (45°,-35°) Distance 500 km
4.2.2 阵元速度相差程度最小的回波方向
设置回波方向为(-135°,-55°)，其余参数保持不变，仿真结果如图12。
图12 回波方向为(-135°,-55°)时各阵元回波方向速度
Fig.12 Echo direction velocity of each element when the echo direction is(-135°,-55°)
从图12中可以看出，在阵元速度相差程度最小的回波方向上阵元速度相差范围为0.02 m/s左右。
在阵元速度相差程度最大的回波方向上，目标距离100 km时飞艇的晃动对艇载雷达的影响很小，那么在阵元速度相差程度最小的回波方向上，对于距离100 km的目标，艇载雷达与固定天线雷达自然也不会有大的区别，因此，在阵元速度相差程度最小的回波方向上，直接给出了目标距离500 km时艇载雷达与固定天线的回波仿真，如图13。
从图13的(a)和(b)对比情况来看，在阵元速度相差程度最小的回波方向上，即使对于距离500 km的目标，艇载雷达回波的脉压情况仅有略微下降，飞艇晃动对于艇载雷达探测也没有造成明显的影响。
图13 回波方向为(-135°,-55°)距离500 km时的目标回波
Fig.13 Target Echo at (-135°,-55°) Distance 500 km
5 结论
本文依据飞艇的运动特点，建立了飞艇微动时阵面的运动模型以及回波信号的计算模型，在建立的模型基础上，进一步从信号的角度分别分析了飞艇微动对雷达回波信号和回波脉压，并进行了仿真计算，综合理论分析和仿真结果可以得出：
(1)飞艇晃动会造成艇载雷达回波减弱及其脉压效果下降；
(2)针对越远距离的目标，减弱与下降的程度越强；
(3)在不同的探测方向回波信号受飞艇晃动的影响程度不同。
本文分析结果可以为艇载雷达天线的设计和布置提供参考，也可为研究艇载雷达信号处理算法提供依据，此外，本文所建立的模型还可拓展到其他不固定载体搭载相控阵雷达的应用场景中。
[1] 梁晓庚, 田宏亮. 临近空间高超声速飞行器发展现状及其防御问题分析[J]. 航空兵器, 2016(4): 3-10.
Liang Xiaogeng, Tian Hongliang. Analysis of the Development Status and the Defense Problem of Near Space Hypersonic Vehicle[J]. Aero Weaponry, 2016(4): 3-10.(in Chinese)
[2] Huang W, Ma L, Wang Z G, et al. A Parametric Study on the Aerodynamic Characteristics of a Hypersonic Wave Rider Vehicle[J]. Acta Astronautica, 2011, 69(3- 4): 135-140．
[3] 李江挺, 郭立新, 方全杰, 等. 高超声速飞行器等离子鞘套中的电磁波传播[J]. 系统工程与电子技术, 2011, 33(5): 969-973.
Li Jiangting, Guo Lixin, Fang Quanjie, et al. Electromagnetic Wave Propagation in Hypersonic Aircraft Plasma Sheath[J]. Systems Engineering and Electronics, 2011, 33(5): 969-973.(in Chinese)
[4] 于哲峰, 刘佳琪, 刘连元, 等. 临近空间高超声速飞行器RCS特性研究[J]. 宇航学报, 2014, 35(6): 713-719.
Yu Zhefeng, Liu Jiaqi, Liu Lianyuan, et al. Research on the RCS Characteristics of Hypersonic Near Space Vehicle[J]. Journal of Astronautics, 2014, 35(6): 713-719.(in Chinese)
[5] 沈杰. 平流层飞艇载雷达系统研究[D]. 成都: 电子科技大学, 2009: 18-20.
Shen Jie. Research on Stratospheric Airshipborne Radar System[D]. Chengdu: University of Electronic Science and Technology of China, 2009: 18-20.(in Chinese)
[6] 杨跃能, 郑伟, 闫野, 等. 平流层飞艇飞行模态分析[J]. 国防科技大学学报, 2015, 37(4): 57- 64.
Yang Yueneng, Zheng Wei, Yan Ye, et al. Flight mode analysis for stratospheric airships[J]. Journal of National University of Defense Techonlogy, 2015, 37(4): 57- 64.(in Chinese)
[7] 陈丽, 周革, 段登平. 平流层飞艇变质心姿态运动仿真[J]. 系统仿真学报, 2012, 24(12): 2434-2438.
Chen Li, Zhou Ge, Duan Dengping. Simulation of Moving-mass Control of Stratospheric Airship[J]. Journal of System Simulation, 2012, 24(12): 2434-2438.(in Chinese)
[8] White J E, Robinett R D. Principal Axis Misalignment Control for Deconing of Spinning Spacecraft[J]. Journal of Guidance, Control and Dynamics (S1533-3884), 1994, 17(4): 823- 830.
[9] Khoury G A, Gillett J D. Airship technology[M]． USA: Cambridge University Press, 1999．
[10] Kulczycki E A, Johnson J R, Bayard D S, et al. On the development of parameterized linear analytical longitudinal airship models[C]∥Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii, 2008．
[11] Eric A, Kulczycki S M, Koehler A E, et al. Development of an analytical parameterized linear lateral dynamic model for an aerobot airship[C]∥Proceedings of AIAA Guidance, Navigation, and Control Conference, Oregon, USA, 2011．
[12] Etkin B, Reid L D. Dynamics of flight: stability and control[M]. 3rd ed. USA: Wiley, 1996．
[13] 商哲然, 谭贤四, 曲智国, 等. 高超声速目标雷达检测方法综述[J]. 现代雷达, 2017, 39(1): 1- 8, 40.
Shang Zheran, Tan Xiansi, Qu Zhiguo, et al. Review on Radar Detection Technology of Hypersonic Targets[J]. Modern Radar, 2017, 39(1): 1- 8, 40.(in Chinese)
