1 引言
现如今导航定位系统的应用越来越广泛，但由于导航信号及其微弱，导航接收机接收到的干扰信号相对于有用信号高出大概20～30 dB，因此导航接收机抗干扰技术一直是重点研究问题。传统的抗干扰技术有很多，文献[1-2]提出了基于盲信号处理的波束形成算法，通过建立信号模型，然后采用子空间剔除去除干扰信号后进行波束形成。文献[3]提出了基于单孔径双极化天线的卫星导航信号抗干扰方法,推导了三维空间极化信号模型进行抗干扰处理。文献[4]提出了两级结构的卫星导航压制式和欺骗式干扰联合抑制算法，通过PI算法对压制式干扰进行抑制，利用CLEAN算法估计出欺骗式干扰的波达方向进而对干扰信号子空间估计，并对干扰信号进行抑制。文献[5- 6]提出了线性约束最小方差(LCMV)算法，在保证加权矢量w在一定值时，对输出信号功率进行约束达到对干扰信号的抑制目的。文献[7]提出了一种自适应波束形成抗干扰技术，文献[8-10]提出了Gram-Schmidt(G-S)正交化算法，在已知干扰信号波达角(DOA)的情况下，构建干扰信号的正交基，并通过该正交基与原始权矢量相乘得到最佳权矢量从而对干扰信号进行抑制。文献[11]提出了一种基于小波包变换的自适应预测器用于GNSS接收机的新型抗干扰算法。文献[12]提出了基于均匀圆阵Capon-Laplace的导航接收机抗干扰算法，适用于高动态下导航接收机抗干扰。文献[13]提出了利用周期重复的CLEAN的GNSS欺骗式干扰抑制算法。文献[14]提出了利用子空间投影和波束形成的GNSS接收机抗干扰算法性能分析，通过构造干扰信号子空间的正交补空间，再将接收到的导航信号向其投影，最后在进行波束形成，进而达到抑制干扰信号保留期望信号的目的。目前干扰抑制算法虽然很多，但大都是针对窄带干扰而言，所以宽带抗干扰技术已经成为现如今的热门话题。文献[15]提出了宽波束形成器，通过对空间响应的波动程度描述定义了空间响应偏差(SRV)因子，在凸优化设计思想的基础上设计宽波束形成器，大大降低了计算量。文献[16]提出了基于四元天线阵列GPS抗干扰射频前端设计，文献[17]结合最小二乘法及空间响应偏差(SRV)约束条件提出了更为稳健的宽带波束形成算法。文献[18-19]分别提出了基于不同结构的宽带自适应波束形成。但上述算法还依旧存在计算量大，对干扰抑制不够充分等一些问题。基于上述分析，本文采用基于TDL结构的空间响应偏差(SRV)算法，通过Frost迭代算法求取权矢量，可以在保留期望信号的同时对干扰信号进行有效抑制，并对输出信号稳健性进行考虑，输出信号信噪比有所降低，降低计算量。
2 基于TDL结构的阵列信号处理模型
本文采用等间距的线性天线阵列接收频率范围为Ω的远场信号，假设有L个信号源，M个阵元，各阵元间距为d，波长为λ，一般情况下取d=λ /2，且振幅相等，相位超前或滞后相同的角度。输入信号以角度θ入射到由M个阵元组成的线性天线阵，则第m个阵元在t时刻接收到的信号可表示为：
(1)
其中nm(t)是0均值，方差为1的高斯白噪声。将式(1)用频域模型表述为：
(2)
其中J为宽带信号频域分解窄带信号数，s(fj)=[s1(fj),s2(fj),…,sk(fj)]T；N(fj)=[N1(fj),N2(fj),…,NM(fj)]T；A(fj)=[a(fj,θ1),a(fj,θ2),…,a(fj,θk)]；a(fj,θk)=[a1(fj,θ1),a2(fj,θ2),…,aM(fj,θk)]T，将上式简化为：
X(fj)=A(fj,θ)S(fj)+N(fj)
(3)
将M个阵元组成的阵列后接N阶FIR滤波器，每级FIR滤波器延时Td，加权矢量wi, j，如图1所示。
输入信号xMN×1(n)为x(t)第n次采样得到的复数据向量x(n)=[x0(t),...,xM-1(t),...,x0(n-N+1),...,xM-1(n-N+1)]T，由于天线位置的差异，传输距离差为dsin θ，则每个阵元相对于上一个阵元的时间延迟为τ=dsin θ/c，其中c为光速，令TDL结构的导向矢量为：
aMN×1(f,θ)=a(ft,θ)⊗a(fi,θ)
(4)
式中：
a(ft,θ)=[1,exp(-j 2πTd),...,
exp(-j 2π(N-1)Td)]T
(5)
a(fi,θ)=[1,exp(-j 2πτ),...,
exp(-j 2π(M-1)τ)]T
(6)
则输出信号y(n)为输入信号x(n)乘以信号的加权矢量w，即y(n)=wHx(n)，其中w=[w0,0,...,wM-1,0,...,w0,N-1,...,wM-1,N-1]。
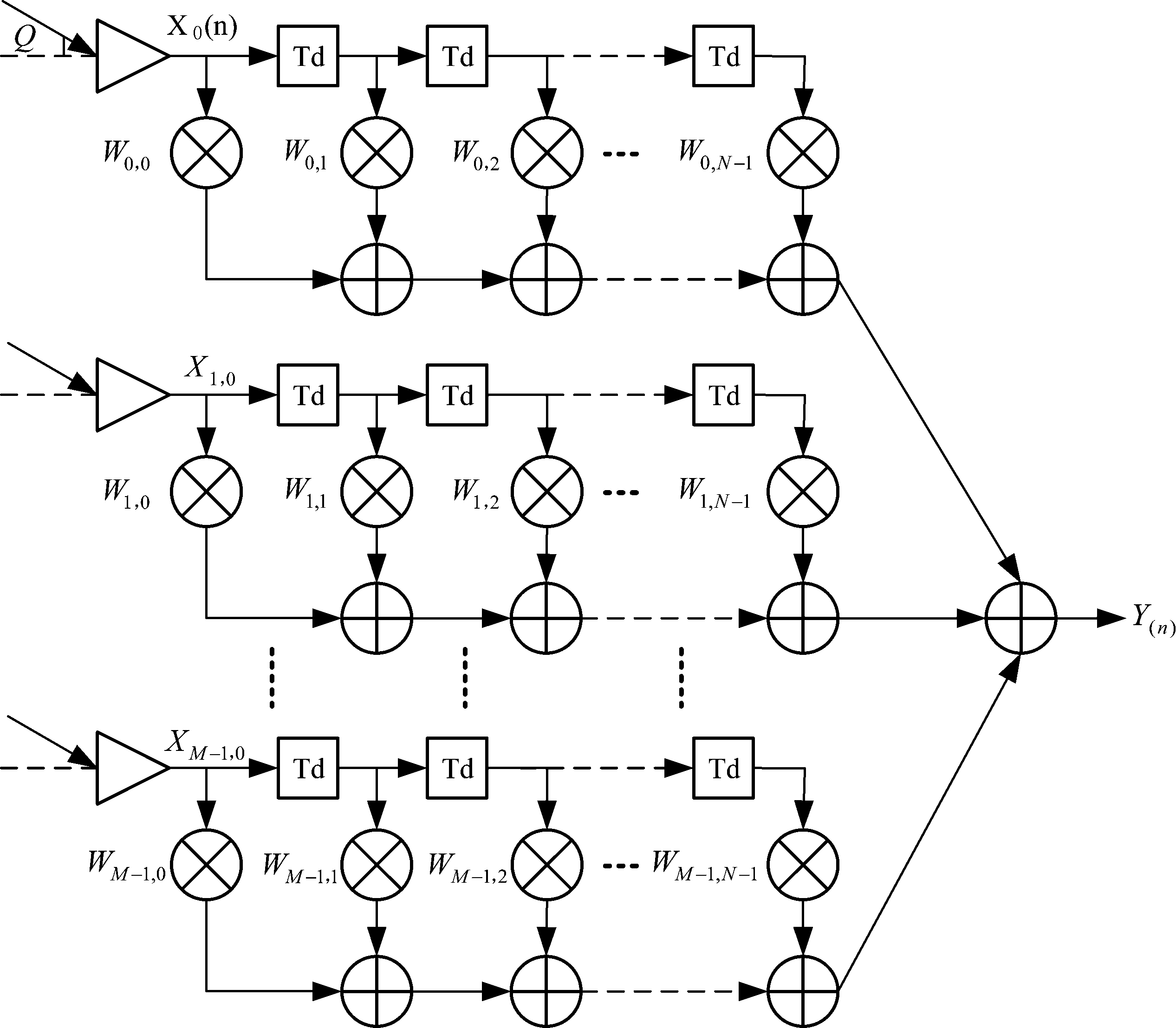
图1 TDL结构
Fig.1 TDL structure
3 优化的SRV算法
3.1 LCMV准则
LCMV准则又称线性约束最小方差准则，通过线性约束条件使输出信号功率最小。LCMV准则通常用于导航接收机抗压制式干扰中，即当干扰信号功率较大，期望信号功率较小时，可在干扰信号方向产生零陷，期望信号方向保留有用信号。通常表示为：
(7)
其中
利用拉格朗日数乘法可求得权矢量w为：
(8)
3.2 SRV算法
SRV算法又称为空间响应偏差算法，在一定的频率Ωi，角度θi范围内的波动程度被描述为空间响应偏差，连续信号的SRV因子可表示为：
(9)
其中：
将SRV离散化，即在频率Ωi，角度θi范围内对其进行均匀采样，可改写为离散形式：
WHa(fD,θk)|2=WHUW
(10)
其中U的离散形式为：
为导向矢量a(f,θ)在频率、角度范围内的均匀采样值。
3.3 本文算法
通过调整加权矢量w使得空间响应偏差波动最小，并结合LCMV算法，以得到输出最优频率不变性。基于LCMV约束条件可得表达式为：
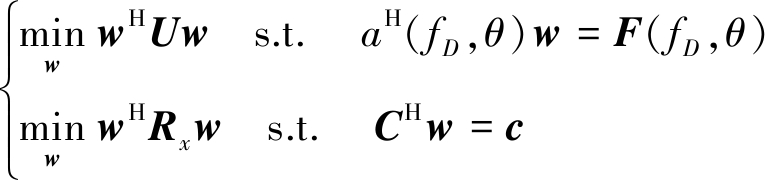
(11)
其中F(fD,θ)为约束的期望信号输出，Rx=E[x(n)xH(n)]为输入信号协方差矩阵，C为约束矩阵，c为约束向量。
综合考虑式(11)约束条件，将其简化为(其中令aH(fD,θ)w=F(fD,θ)包含于CHw=1)：
(12)
其中β为平衡因子，控制Rx、U所占比例进而控制抗干扰性能。
利用拉格朗日数乘法可得目标函数为：
L(w)=WH(Rx+βU)W+λ(CHW-1)
(13)
对式(13)求导，可求得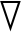
L(w)：
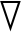L(w)=2(Rx+βU)W(n)+λC
(14)
一般的求解过程为，令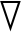L(w)=0，求解W(n)：
(15)
令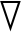L(w)=0，求解λ：
λ=-2(Rx+βU)W(n)C-1
(16)
将λ带入式(15)解得W(n)为：
w=(Rx+βU)-1C(CH(Rx+βU)-1C)-1
(17)
由上述求解过程可知传统的计算方法中出现了很多矩阵求逆过程，计算量较大，矩阵奇异性也没有考虑，适用性较低。
本文根据Frost梯度算法：
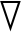L(w)]=
(18)
由于约束条件(12)可得：
CHW(n)=CHW(n+1)=1
(19)
将式(18)带入到式(19)可得：
CHW(n+1)=CHW(n)-
(20)
求得λ：
1-μCH(Rx+βU)W(n)]
(21)
将λ带回到式(18)可得：
W(n+1)=W(n)-μ(Rx+βU)W(n)-
(CHC)-1CHW(n)C+μ(CHC)-1CH(Rx+
βU)W(n)C+(CHC)-1C
(22)
令A=(CHC)-1，B=Rx+βU，D=ACH，E=AC。则加权矢量W可简化为：
(23)
4 实验仿真结果及分析
本文采用阵元数为12，抽头数为8，输入信号波长为λ=c/fl(fl为约束频段的下限频率，c=3×10Λ8 m/s为光速)，采样点数为3000，阵元间距为输入信号半波长的均匀线阵。将SRV约束结合TDL结构，设置权重因子β=0.01，假设期望信号的中心频率为75 MHz，带宽为10 MHz，其DOA为(90°,30°)，信噪比SNR=0 dB。干扰信号中心频率75 MHz，带宽为10 MHz，其DOA为(90°,-40°)，干噪比INR=10 dB。约束频段为70 MHz～80 MHz[20-21]，并在该频段均匀采样Nf=10。梯度因子μ=0.1，约束矩阵F=[1 0 0 0 0]T，采用零均值，方差为1的高斯白噪声。输出的三维方向图和在不同频点的二维方向图(在70 MHz～80 MHz范围内均匀选取十个频点绘制)如图2、图3所示。
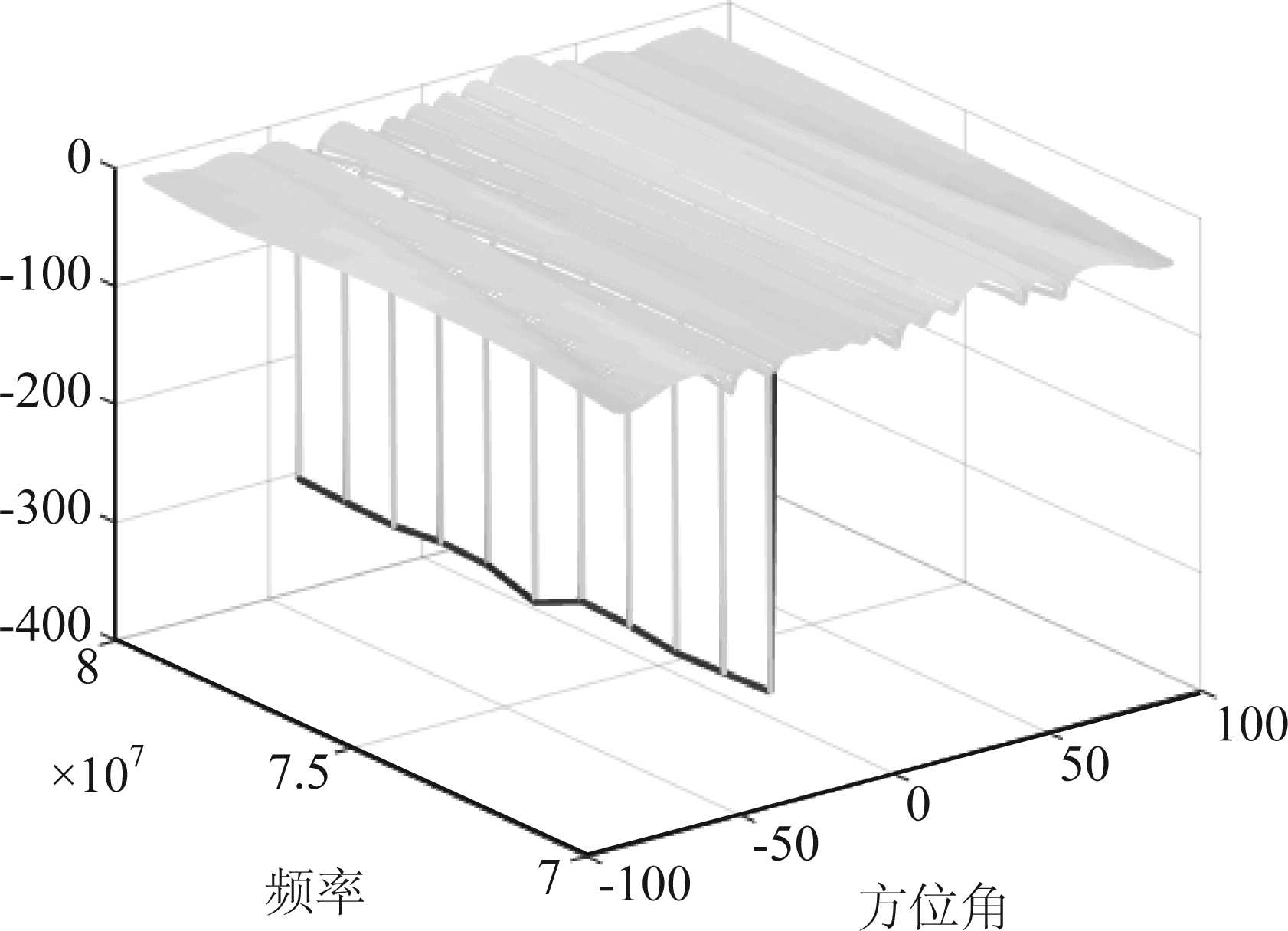
图2 本文算法三维方向图
Fig.2 3D pattern of algorithm in this paper
通过对比图3和图4可以看出，在频段70 MHz～80 MHz范围内，本文提出的改进算法在抑制干扰方向上明显优于参考算法。在图3中，干扰信号方向为-40°的方向上产生320 dB左右的衰减增益，将干扰信号有效的滤除；在图4中，干扰信号方向为-40°的方向上产生70 dB左右的衰减增益，相比于本文提出的改进算法，参考算法对干扰抑制较小，对期望信号方向的保留也不够明显。本文提出的改进算法可以在干扰信号方向产生较深零陷，收敛速度较快，对期望方向的导航信号在30°方向上也进行了保留。所以，本文提出的改进算法在主瓣及零陷方向相对比较优异。
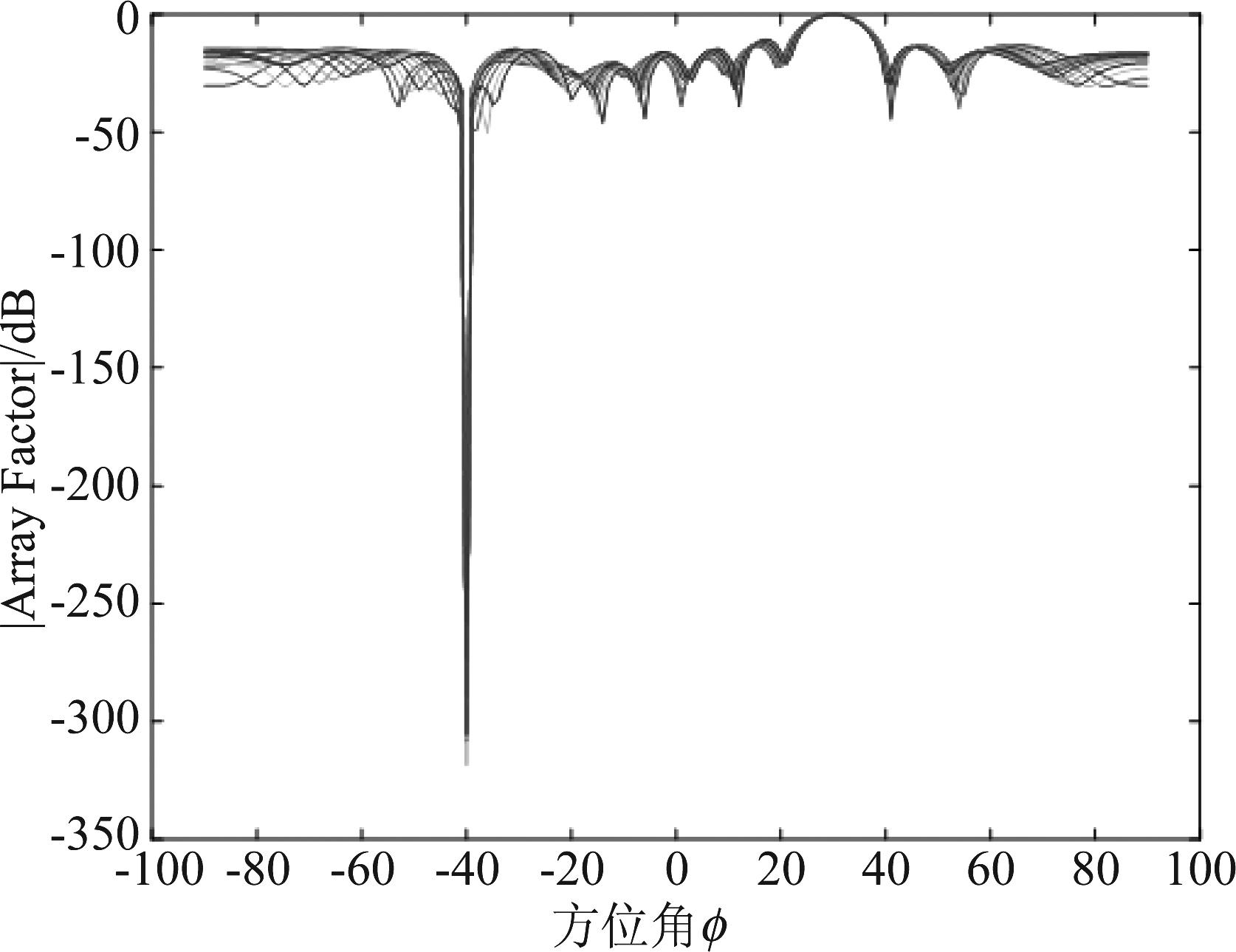
图3 本文算法二维方向图
Fig.3 Two-dimensional pattern of algorithm in this paper
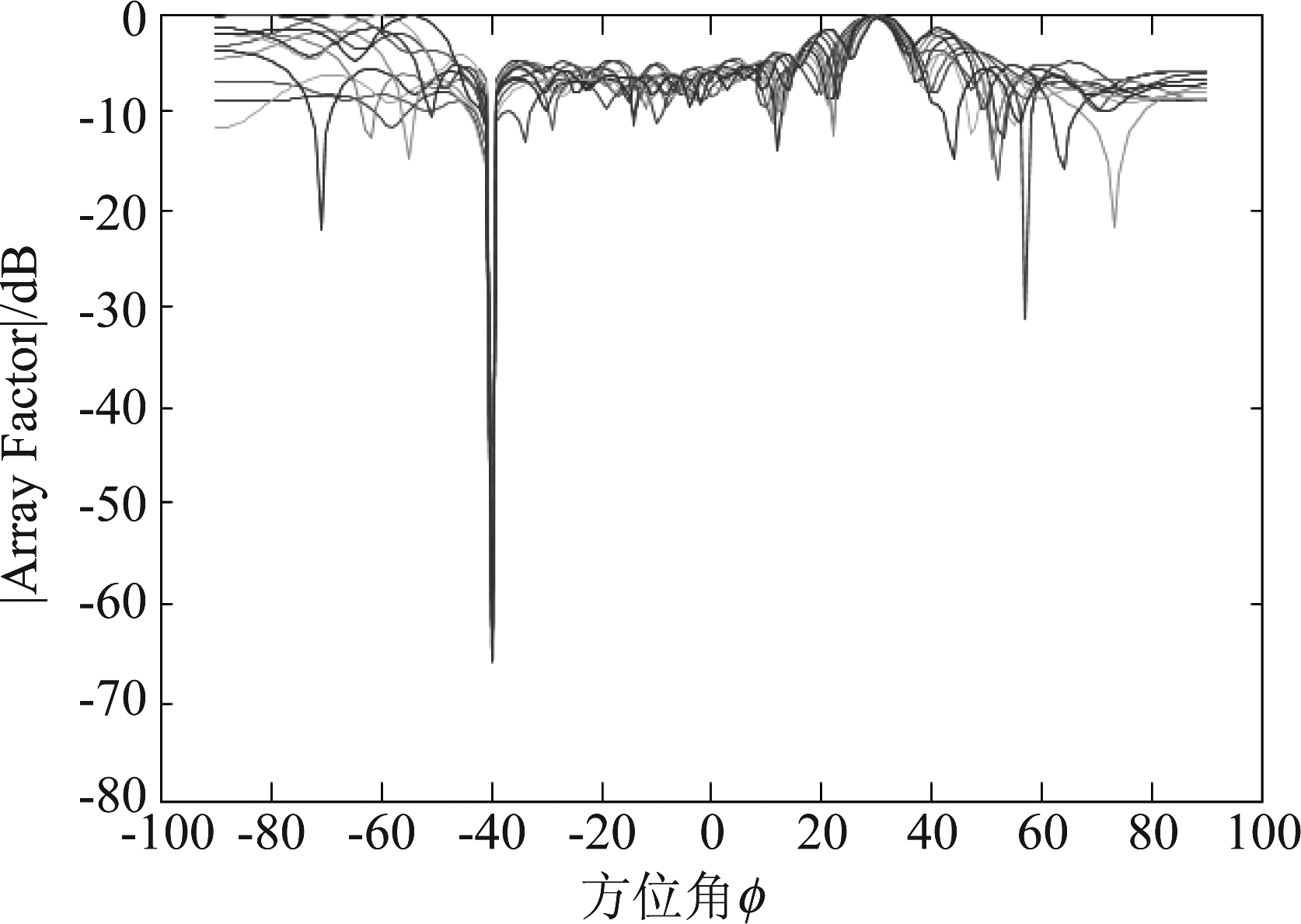
图4 SRV算法二维方向图
Fig.4 SRV algorithm two-dimensional directional diagram
为了进一步说明本文提出的改进算法的抗噪声能力强，通过改变输入信号信噪比来观察，则输入信噪比及误码率的关系图如图5所示。
通过图5可知随着输入信噪比的增加误码率逐渐减小，当信噪比(SNR)在-9 dB左右时，误码率已经达到10-4～10-5并趋于稳定，可近似看为0。干扰信号可导致GPS接收机的信噪比C/N下降，但结合图2、图3对比可以看出本文在有效抑制干扰信号的同时对噪声的抑制能力也比较突出，提高了输出信号的信噪比。
与参考算法相比，本文通过采用Frost梯度算法减少了矩阵求逆运算，降低计算量，从而使得算法复杂度降低。假设M为阵元个数，N为延时单元数，N1为时域快拍数。则不同算法的计算复杂度如表1所示。
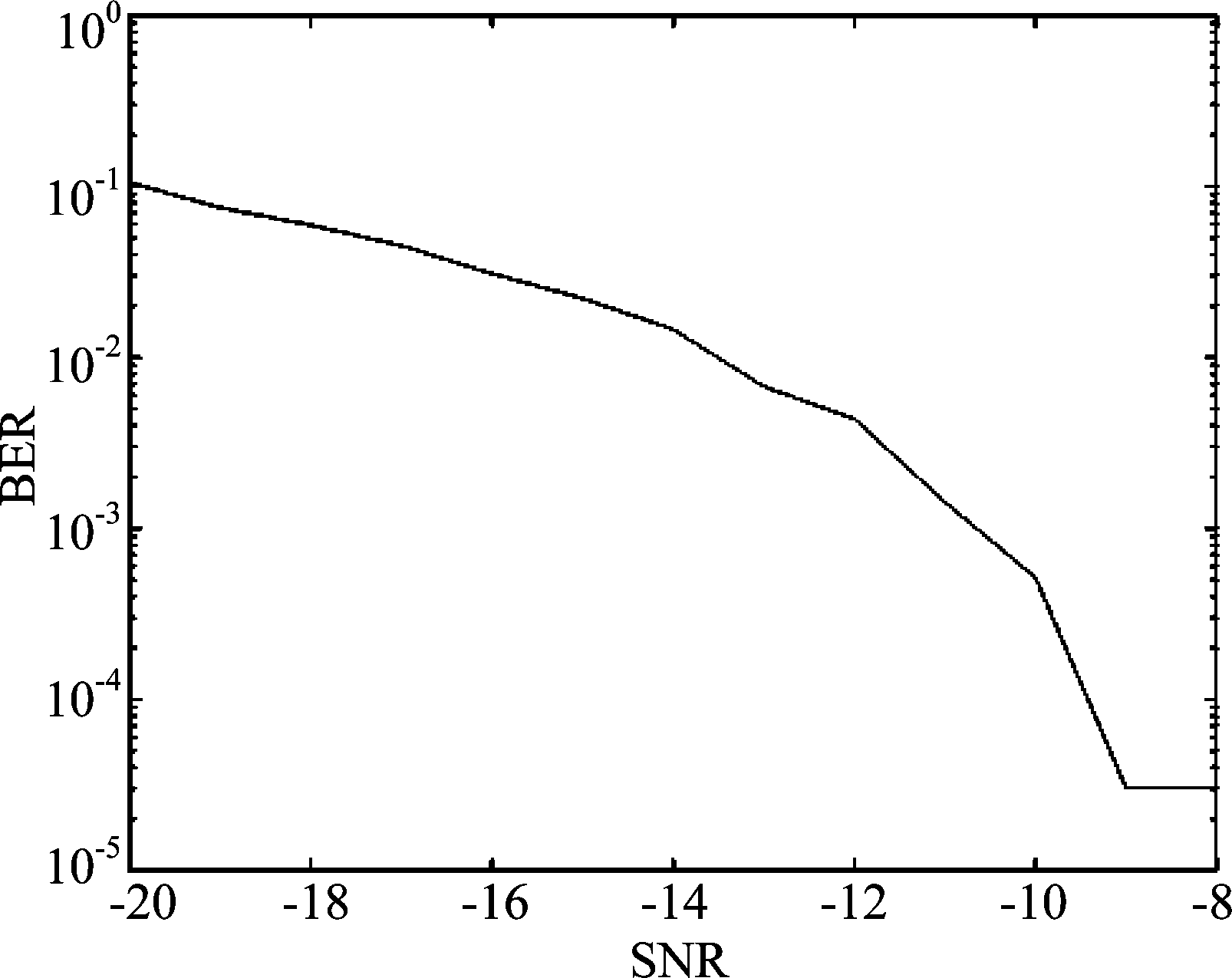
图5 输入信噪比及误码率
Fig.5 Input SNR and bit error rate
表1 算法复杂度比较
Tab.1 Algorithm complexity comparison
计算量运行时间/s本文提出的改进算法O((MN)2+(MN)2)1.562参考算法(SRV)[22]O((MN)3+(MN)2(N1+2))2.249
5 结论
本文阐述了一种改进的导航接收机宽带干扰抑制算法，基于TDL结构的SRV算法并结合LCMV算法，利用迭代技术求得加权矢量，可以对导航接收机接收到的干扰信号进行有效的抑制，在干扰信号方向产生较深零陷，收敛速度快，且频率稳定性好。利用Frost迭代技术求得加权矢量，可以降低计算量。本文提出的改进算法在保留期望信号的同时，还可以在输入信噪比较小的情况下对干扰信号进行较好的抑制，适用于导航接收机宽带干扰抑制。
[1] 刘海颖, 叶伟松, 李静. GPS天线阵列盲信号波束形成研究[J]. 遥测遥控, 2011, 32(2): 4-9.
Liu Haiying, Ye Weisong, Li Jing. Blind Beamforming Technique for GPS Antenna Array[J]. Journal of Telemetry, Tracking and Command, 2011, 32(2): 4-9.(in Chinese)
[2] Berefelt F, Boberg B, Eklöf F, et al. INS/GPS Integration with Adaptive Beamforming[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2003: 1096-1106.
[3] 王展, 李双勋, 战永红, 等.单孔径双极化天线的导航信号抗干扰[J]. 信号处理, 2009, 25(6): 990-993.
Wang Zhan, Li Shuangxun, Zhan Yonghong, et al.Navigation Signal Anti-jamming Based on Single Dual-polarized Antenna[J]. Signal Processing, 2009, 25(6): 990-993.(in Chinese)
[4] 包莉娜, 吴仁彪, 王文益, 等.两级结构的卫星导航压制式和欺骗式干扰联合抑制算法[J]. 信号处理, 2015, 31(9): 1041-1046.
Bao Lina, Wu Renbiao, Wang Wenyi, et al.Two-step GPS Interference Suppression Algorithm for Spoofing and Jamming[J]. Journal of Signal Processing, 2015, 31(9): 1041-1046.(in Chinese)
[5] Lamare R C D. Adaptive reduced-rank LCMV beamforming algorithms based on joint iterative optimization of filters[J]. Signal Processing, 2010, 90(2): 640- 652.
[6] Chen H, Zhang R, Sheng W, et al. Fast implementation of LCMV anti-jamming algorithm for GPS navigation[C]∥IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition. IEEE, 2016: 1-3.
[7] Frost O L I. An Algorithm for Linearly Constrained Adaptive Array Processing[J]. Proceedings of the IEEE, 1972, 60(8): 926-935.
[8] 魏亮, 刘琳琳, 刘洋, 等.基于G-S算法的GPS接收机抗干扰技术研究[J]. 无线电工程, 2013, 43(4): 35-36.
Wei Liang, Liu Linlin, Liu Yang, et al.Research of Anti-jamming Using G-S Algorithm in GPS Receiver[J]. Radio Engineering, 2013, 43(4): 35-36.(in Chinese)
[9] 黄丽嫦, 黄润.基于Gram-Schmidt正交法的矩阵并行QR分解算法[J]. 佛山科学技术学院学报: 自然科学版, 2013, 31(3): 44- 47.
Huang Lichang, Huang run. The Gram-Schmidt based orthogonal method for matrixes parallel QR decomposition algorithm[J]. Journal of Foshan University: Natural Science Edition, 2013, 31(3): 44- 47.(in Chinese)
[10] 李成全, 孙维忠, 张雄.基于RLS算法与G-S算法的抗干扰分析[J]. 舰船电子工程, 2015(8): 45- 49.
Li Chengquan, Sun Weizhong, Zhang Xiong.Analysis of Anti-jamming Based on RLS Algorithm and G-S Algorithm[J]. Ship Electronic Engineering, 2015(8): 45- 49.(in Chinese)
[11] Chien Y R, Chen P Y, Fang S H. Novel Anti-Jamming Algorithm for GNSS Receivers Using Wavelet-Packet-Transform-Based Adaptive Predictors[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2017, 100(2): 602- 610.
[12] Li S, Lu D, Wu R. Anti-jamming Algorithm Analysis Based on UCA for Attitude High-Dynamic GNSS[M]. China Satellite Navigation Conference (CSNC) 2016 Proceedings: Volume I. Springer Singapore, 2016.
[13] 王璐, 李素姣, 张耀天, 等.利用周期重复CLEAN的GNSS欺骗式干扰抑制算法[J]. 信号处理, 2015, 31(12): 1636-1641.
Wang Lu, Li Sujiao, Zhang Yaotian, et al. Spoofing Interference Suppression in GNSS Using Repeated CLEAN[J]. Journal of Signal Processing, 2015, 31(12): 1636-1641.(in Chinese)
[14] Guan G, Nie J, Huang Y, et al. Performance analysis of anti-jamming algorithm in GNSS receiver utilizing subspace projection and beamforming[J]. Journal of National University of Defense Technology, 2016, 6(3).50-54.
[15] Duan H, Ng B P, See C M S, et al. Broadband Beamforming Using TDL-FORM IIR Filters[J]. IEEE Transactions on Signal Processing, 2007, 55(3): 990-1002.
[16] 魏涛, 杨祖芳, 潘伟, 等. GPS天线阵抗干扰射频前端设计[J]. 电子技术应用, 2018(5): 119-123.
Wei Tao, Yang Zufang, Pan Wei, et al. Design of GPS Antenna Array Anti-jamming RF Front-end[J]. Application of Electronic Technology, 2018(5): 119-123.(in Chinese)
[17] Zhao Y, Liu W, Langley R. Application of the least squares approach to fixed beamformer design with frequency-invariant constraints[J]. Iet Signal Processing, 2011, 5(3): 281-291.
[18] 陈晖, 刘成城, 李冬海, 等.基于子带SDL的宽带自适应波束形成[J]. 信号处理, 2012, 28(12): 1685-1691.
Chen Hui, Liu Chengcheng, Li Donghai, et al.Wideband Adaptive Beamforming with Sensor Delay Lines in Subbands[J]. Signal Processing, 2012, 28(12): 1685-1691.(in Chinese)
[19] Huang L Y, Shen B, Li M X. An Efficeient Subband Method for Wideband Adaptive Beamforming[A]. 2008: 1489-1492.
[20] 汪婉秋, 刘成城, 赵拥军, 等.一种低复杂度的稳健宽带SDL波束形成算法[J]. 信息工程大学学报, 2013, 14(1): 72-77.
Wang Wanqiu, Liu Chengcheng, Zhao Yongjun, et al. Low Complexity Robust Wideband Beamforming Algorithm for Sensor Delay Lines[J]. Journal of Information Engineering University, 2013, 14(1): 72-77.(in Chinese)
[21] 郭志亮, 陈辉, 祝转民.一种宽带零陷展宽恒定束宽波束形成算法[J]. 空间电子技术, 2016, 13(3): 26-31.
Guo Zhiliang, Chen Hui, Zhu Zhuanmin. A Wideband Null Broadening and Constant Beam Width Beam Forming Method[J]. Space Electronic Technology, 2016, 13(3): 26-31.(in Chinese)
[22] 李毓铃.宽带自适应波束形成技术的研究和实现[D]. 南京: 南京理工大学, 2017.
Li Yuling.Research and Implementation of Wideband Adaptive Beamforming Technology[D]. Nanjing: Nanjing University of Science and Technology, 2017.(in Chinese)
