1 引言
水声通信信号的调制识别是海战场目标信息获取与态势分析的重要环节，也是实现信号检测、解调的关键步骤和基础。近几年，基于传统模式识别方法的水声通信信号调制识别技术取得了较大的进展，比如：基于瞬时特征参数[1]、循环谱相关[2]、循环统计量[3]、小波变换[4]等方法，但是传统方法往往需要设计复杂的算法提取调制特征量，而这些调制特征量往往在特定环境下有效，对环境变化不稳健。深度学习技术能够通过深层次网络自动提取输入信号的特征，而且当训练数据集足够丰富时，能够提高对环境的适应性。鉴于深度学习技术在信号分类中的上述优势，本文以水声通信信号的功率谱作为识别对象，选择对一维数据具有良好表征能力而且结构简单的稀疏自动编码网络作为特征提取的神经网络，对稀疏自动编码网络结构和参数调整优化，设计了基于该网络的调制识别方法，大量实验结果验证了该方法的有效性。
2 基于稀疏自动编码网络的水声通信信号识别方法
2.1 稀疏自动编码网络概述[5-7]
稀疏自动编码网络(Sparse Audoencoding Network, SAE)是一种特殊的自编码网络，通过学习过程引入稀疏惩罚项，使网络节点随机处于激活状态，防止编码器在每一点处都具有低的重构误差而无法工作，对信号噪声等影响也具有较好的鲁棒性[5]。如图1是一个稀疏自动编码网络结构示意图，“Input”为网络输入层，“layer”表示网络隐层，为完成分类任务，需要在网络顶层设计分类器，其输出为网络的最终识别结果。“x(i)”表示第i个节点的输入数据，“
”表示第l个隐层的第i个节点输出值，网络中的箭头表示相邻两层节点之间的连接权重，“+1”为偏置项。稀疏自动编码网络在结构设计上，隐层节点数通常小于输入层或前一隐层节点数，这使得提取数据特征的同时，对数据维数进行强制压缩，网络输出往往是低维表征，其作用类似于PCA降维，对后续分类器的设计大有裨益。
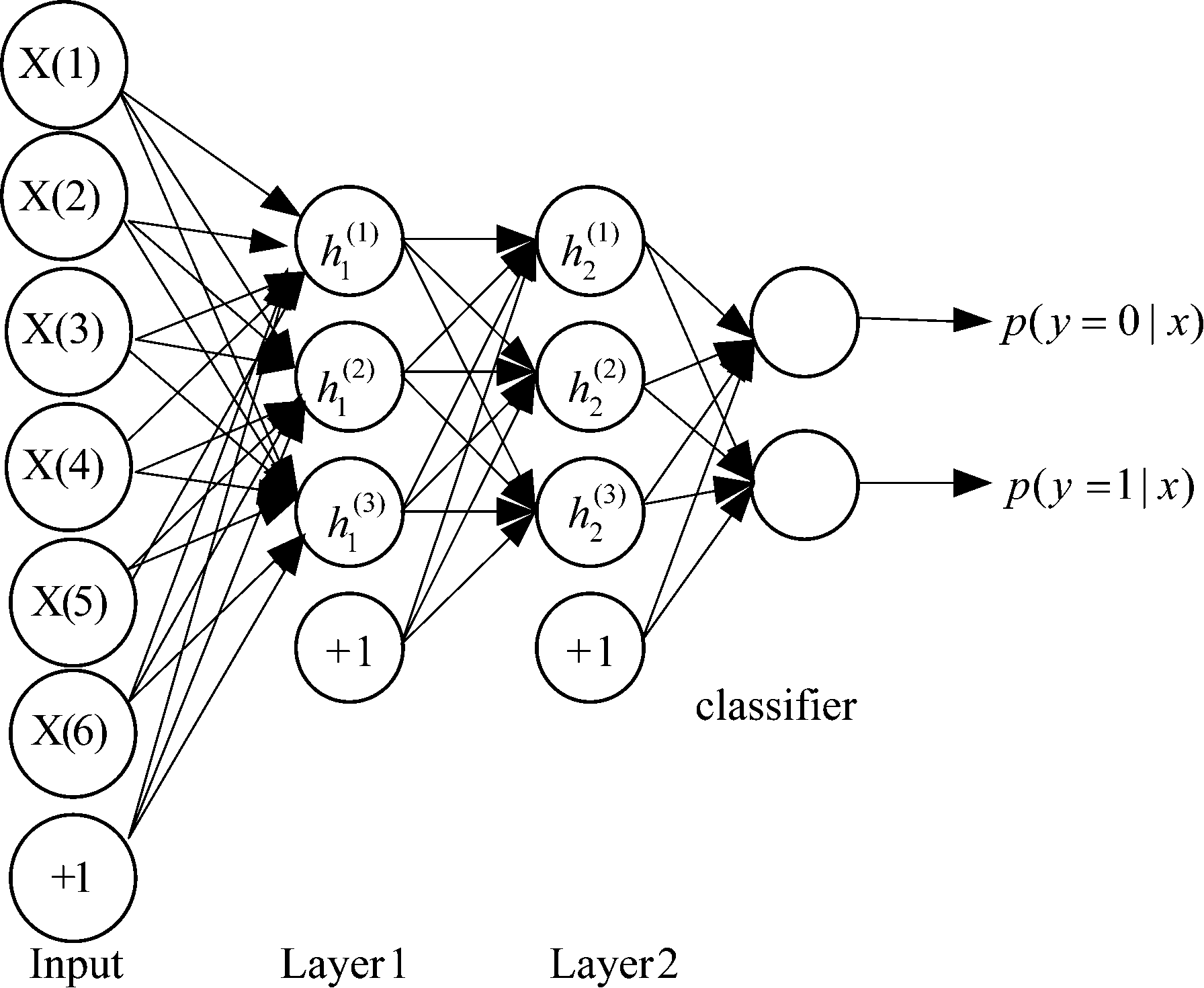
图1 双隐层稀疏自动编码网络结构
Fig.1 Structure of SAE with two hidden layers
图1中网络整体代价函数定义为[6-7]：
(1)
式中第一项是方差代价函数，第二项是规则化项，第三项为稀疏惩罚项。W为连接权值矩阵，b为偏置矩阵；y(x(i))表示第i个神经元的重构值，n表示输入层的节点个数，‖·‖k表示k范数；γ为权重衰减系数，防止权值过大引起的过拟合，sl代表第l个隐层的节点数， j表示该隐层的神经元，i表示前一隐层的神经元，Wij(l)即为第l隐层的第j个神经元和第(l-1)层的第i个神经元的连接权重； β为稀疏惩罚项的权重，KL(ρ‖ρi)表示KL散度，也叫相对熵，表示为：
(2)
其中， ρi是网络超参数，表示隐层第i个神经元的平均激活量，当稀疏参数ρ=ρi时，惩罚项为0， ρi偏离ρ的程度越大，惩罚项的值越大，当ρi靠近0或1时，相对熵趋近于
。
整个网络学习过程的目标就是最小化代价函数Jsparse(W,b)，定义好代价函数，就可以求出其偏导数：
(3)
(4)
式中，
表示第l隐层第i个神经元的误差值，表示第l隐层的第i个神经元输出值。
利用梯度下降法求解网络最优化的参数流程如下：
(1)对于每一隐层l，设置权值和偏置的更新初始值ΔW(l)=0,Δb(l)=0；
(2)使用反向传播计算代价函数关于权值和偏置的偏导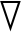
WJ(W,b)和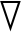bJ(W,b)，式中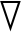为偏导算子；
(3)令ΔW(l)=ΔW(l)+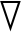WJ(W,b)，Δb(l)=Δb(l)+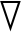bJ(W,b)；
(4)更新参数：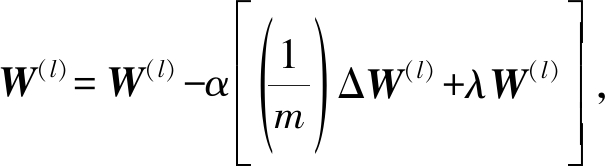
其中α为学习率，λ为权重系数。每层通过上述流程求解出的权重和偏置即为整个网络的模型参数。SAE的训练过程便是通过梯度下降法，使代价函数的偏导值达到最小。
2.2 水声通信信号调制识别方法
2.2.1 水声通信信号模型
接收信号模型为：
r(n)=h(n)*s(n)+w(n)
(5)
其中，s(n)为发射信号，r(n)为接收信号，h(n)为水声信道的冲激响应，*为卷积运算，w(n)为高斯白噪声。FSK、PSK、OFDM和LFM调制方式是目前国内外水声数字通信常用的调制方式[8-9]，本文识别的调制类型包括：2FSK、4FSK、8FSK、QPSK、8PSK、OFDM和LFM。
对于MFSK信号，其数学表达式为[10]：
(6)
式中，g1(t)为矩形脉冲成型滤波器，Ts为符号周期， fc为载波频率，an为幅度值，
为频率偏移量，θ为初始相位。
对于MPSK信号，其数学表达式为[11]：
(7)
式中，bn是信号调制相位，
，(k=0,…,m-1)，g2(t)为成型滤波器，Ts为符号周期， fc为载波频率，φn为初始相位。
对于OFDM信号，其数学表达式为[12]：
kΔfk)n+θk]
(8)
式中，k表示子载波，ak,n是第k个子载波上的第n个符号，其调制方式为PSK或QAM，g3(t)为成型滤波器，Ts为符号周期， fc为载波频率，Δfk是相邻子载波间隔，θk为第k个子载波的相位。
对于LFM信号，其数学表达式为[13]：
s(n)LFM=Aexp(jπkn2+2jπfdn)
(9)
式中，A表示LFM幅度，k为LFM信号的调频斜率， fd是初始频率。
2.2.2 基于稀疏自动编码网络的水声通信信号识别方法
接收信号功率谱在一定程度上能够反映出信号的调制特征，基于模式识别的识别方法需要提取出信号功率谱的调制特征量，再对调制特征量进行识别分类。如何提取和构造调制识别特征量是一个比较复杂的过程，而且调制识别特征量大多对环境因素不稳健，在不同环境下对调制识别特征量的取值会有不同变化，这些因素都会对调制识别的过程产生影响。本文以接收信号功率谱为识别对象，利用稀疏自动编码网络对一维数据有很好的特征提取能力的特性，通过调整稀疏自动编码网络参数，达到对接收信号功率谱提取识别特征的目的，最后通过Softmax分类器进行分类识别。算法原理如图2所示。
接收信号的谱估计采用经典谱估计方法，Welch法是加窗的周期图法，将接收信号x(n)分为L段，每段长度为N，第i段信号的功率谱估计记为
则[14]
(10)
式中，
是归一化因子，d(n)是窗函数。对L段分段周期图平均，得到整个信号的功率谱估计：
(11)
图2 算法原理框图
Fig.2 Algorithm block diagram
对于窗函数的选取，由文献[15]可知，矩形窗的频谱泄露严重，Kaiser窗在信号频率附近噪声功率提高，而Hanning窗的噪声水平较低且平稳，因此本文选用Hanning窗进行谱估计。
每个信号Welch法谱估计后的功率谱作为稀疏自动编码网络的一个训练样本，稀疏自动编码网络1的训练样本包括不同信噪比条件下的2FSK、4FSK、8FSK、QPSK、8PSK、OFDM和LFM通信信号的功率谱以及环境噪声的功率谱，稀疏自动编码网络2的训练样本包括不同信噪比条件下的QPSK和8PSK的四次方谱，其表达式如下所示：
P( f )=|F[s4(n)]|
(12)
式中，F[·]表示傅里叶变换。
通过实验分析，对不同网络结构进行性能对比，最终两个网络均采用双隐层结构设计，节点数目为2048- 800-200，训练过程采用逐层无监督式训练，即上一层的输出作为下一层的输入，稀疏自动编码网络利用其自身的无监督性，通过每层自编码不断从功率谱中提取深层特征信息，将最后一层输出的特征向量作为分类器的输入。由于稀疏自动编码网络最后一层节点数为200，所以分类器的输入数据维度为200维。
本文使用Softmax分类器通过计算概率值找到最有可能的分类结果实现最终分类，对于多分类问题，训练集{(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))}，x(m)代表多维训练数据，y(m)是其对应的类别标签，共有k个不同取值，即y(m)∈{1,2,…,k}。对于测试数据x，Softmax针对每个类别计算出概率值p(y=j|x)，即计算出每一类别出现的概率，具体函数形式如下[16]：
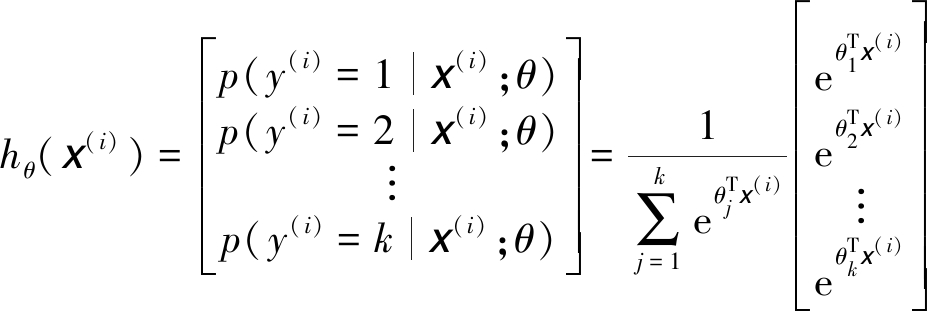
(13)
其中，{θ1,θ2,…,θk}是模型的参数，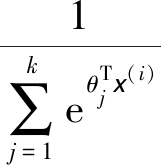
是归一化项，使所有概率值之和为1。得到的hθ(x(i))最大概率所对应的类别即为分类类别。
定义Softmax的代价函数如下[17]：
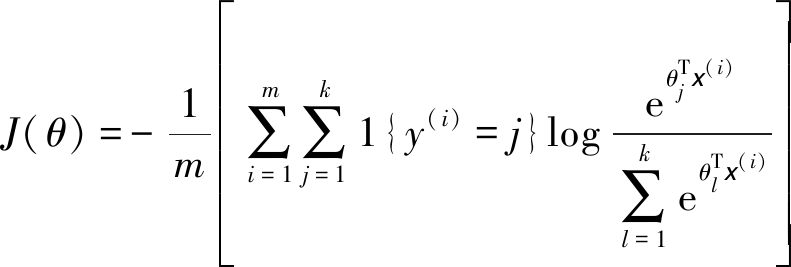
(14)
其中1{·}为指示性函数，即1{true}=1，1{false}=0。利用梯度下降法求解函数中的θ，对上式求导可得梯度公式：
p(y(i)=j|x(i);θ))]
(15)
最小化代价函数，通过梯度下降法求解模型参数{θ1,θ2,…,θk}即得到可用于测试的Softmax分类器。通过Softmax分类器1完成对2FSK、4FSK、8FSK、OFDM和LFM信号的分类，通过Softmax分类器2完成对QPSK和8PSK信号的分类。
3 仿真实验及性能分析
设计仿真实验，并对本文提出的方法进行性能分析。仿真条件如下：信号集包括2FSK、4FSK、8FSK、QPSK、8PSK、OFDM和LFM，信号采样频率为96 kHz，观测时间1 s，信号其他参数设置如表1所示，载频(或起始频率)、符号速率、频率间隔(或调频斜率)以及升余弦滚降系数在某一范围内或若干个固定值中随机取值，以保证训练集和测试集样本的多样性，其中，稀疏自动编码网络1的训练集由不过信道的7类通信信号在符号信噪比分别为0 dB、5 dB、10 dB、15 dB下产生，每个符号信噪比下产生100组信号，因此共有400×7=2800组，测试集为经过上述水声信道后的7类信号，每类信号100组，共有100×7=700组。 稀疏自动编码网络2的训练集由不过信道的QPSK和8PSK信号在符号信噪比分别为0 dB、5 dB、10 dB、15 dB下产生，每个信噪比下产生100组信号，因此共有400×2=800组，测试集为经过上述水声信道后的QPSK和8PSK信号，每类信号100组，共有100×2=200组。Welch谱估计分段点长度为2048，段间不重叠，稀疏自动编码网络输入层维数为2048。
表1 信号参数
Tab.1 Parameters of signals
信号载频(或起始频率)/kHz符号速率/B频率间隔/Hz(调频斜率/Hz/s)升余弦滚降系数2FSK5～10400～600300～600/4FSK5～10400～600300～600/8FSK5～10400～600300～600/QPSK5～10600, 800, 1000/0.2, 0.25, 0.38PSK5～10600, 800, 1000/0.2, 0.25, 0.3OFDM5～102000, 2400, 3000//LFM5～10/4000～6000/
本文主要研究水声信道环境下的信号识别，读取海洋Argo数据库中位于北纬10.5°，西经40.5°，大西洋中部的海洋信息，该海域的声速剖面图如图3所示。
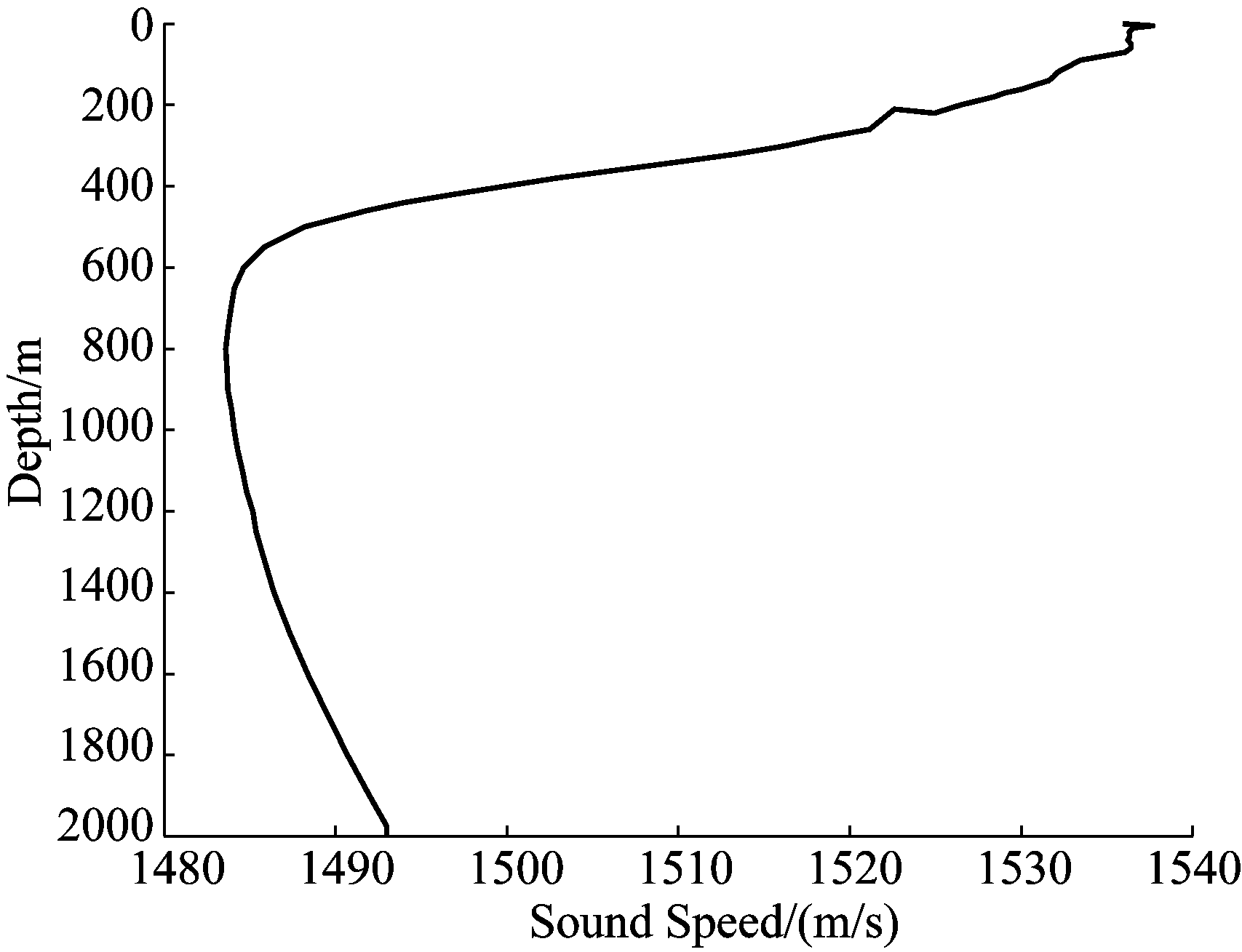
图3 声速剖面图
Fig.3 Sound speed profile
基于图3的声速剖面图，利用Bellhop仿真软件，仿真给出水平通信距离2 km，声源深度350 m，接收器深度300 m水声信道声线图如图4所示，从图4中可以看出有三条声线。其中两条沿近似的直线传播，另一条经海面反射后到达接收端。从声线传播途径可以看出该信道为多径时延信道。
图5给出了多径时延信道的冲激响应，从图中可以看出有3根非零抽头，最大多径时延为51 ms，反映出水声信道具有一定的稀疏性。图6给出了该信道以96 kHz频率采样后的冲激响应，其Z域表达式为：
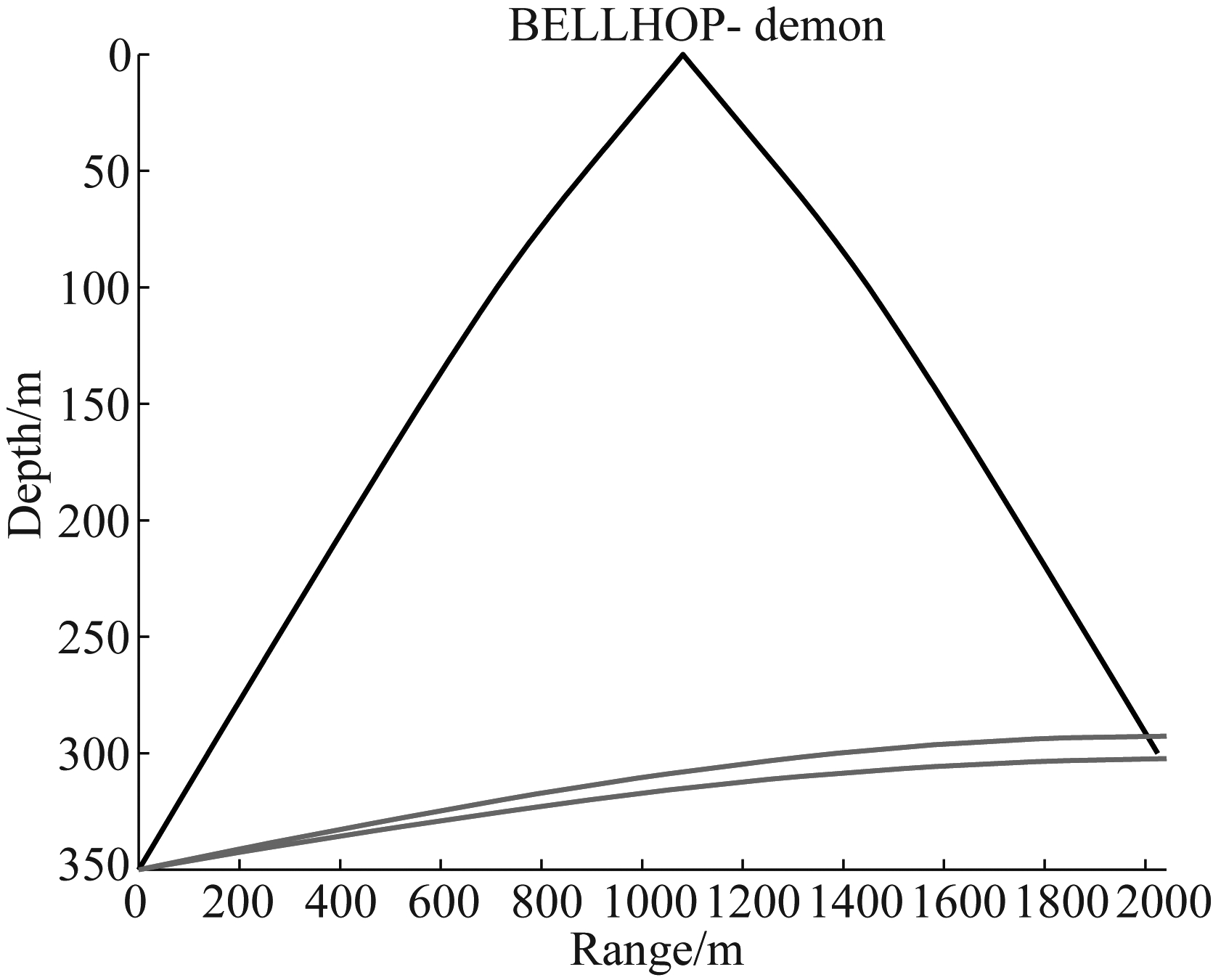
图4 信道声线图
Fig.4 Sound ray of the channel
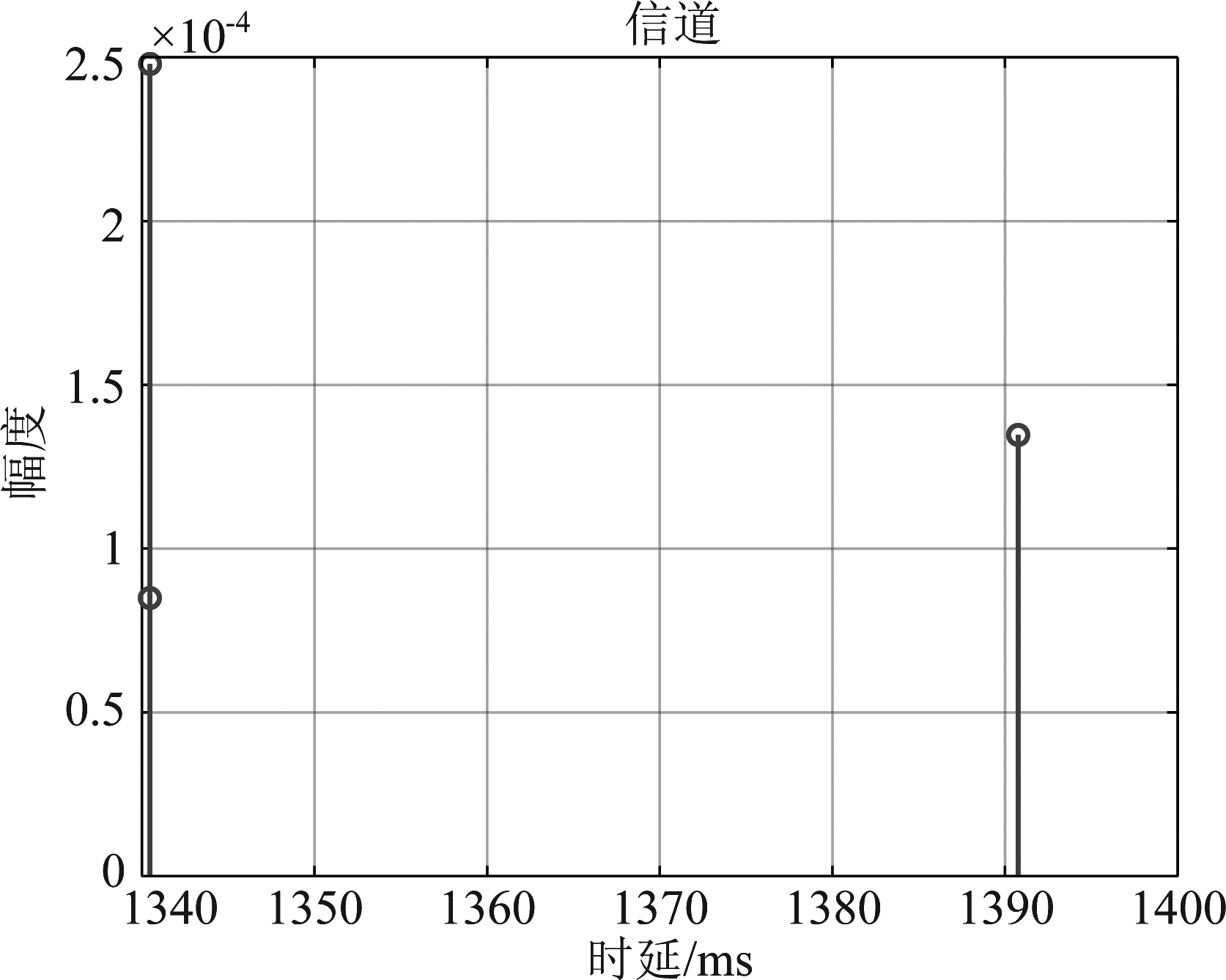
图5 信道冲激响应
Fig.5 Impulse response of the channel
H(z)=0.3425+z-1+0.5433z-4829
(16)
如图7是仿真中发送端的2FSK信号部分时域波形图，经过该信道后接收端的部分时域波形图如图8所示，波形因水声信道的稀疏多径效应发生了畸变，导致包络的起伏。
图6 信道采样后的冲激响应
Fig.6 Impulse response of the channel after sampling
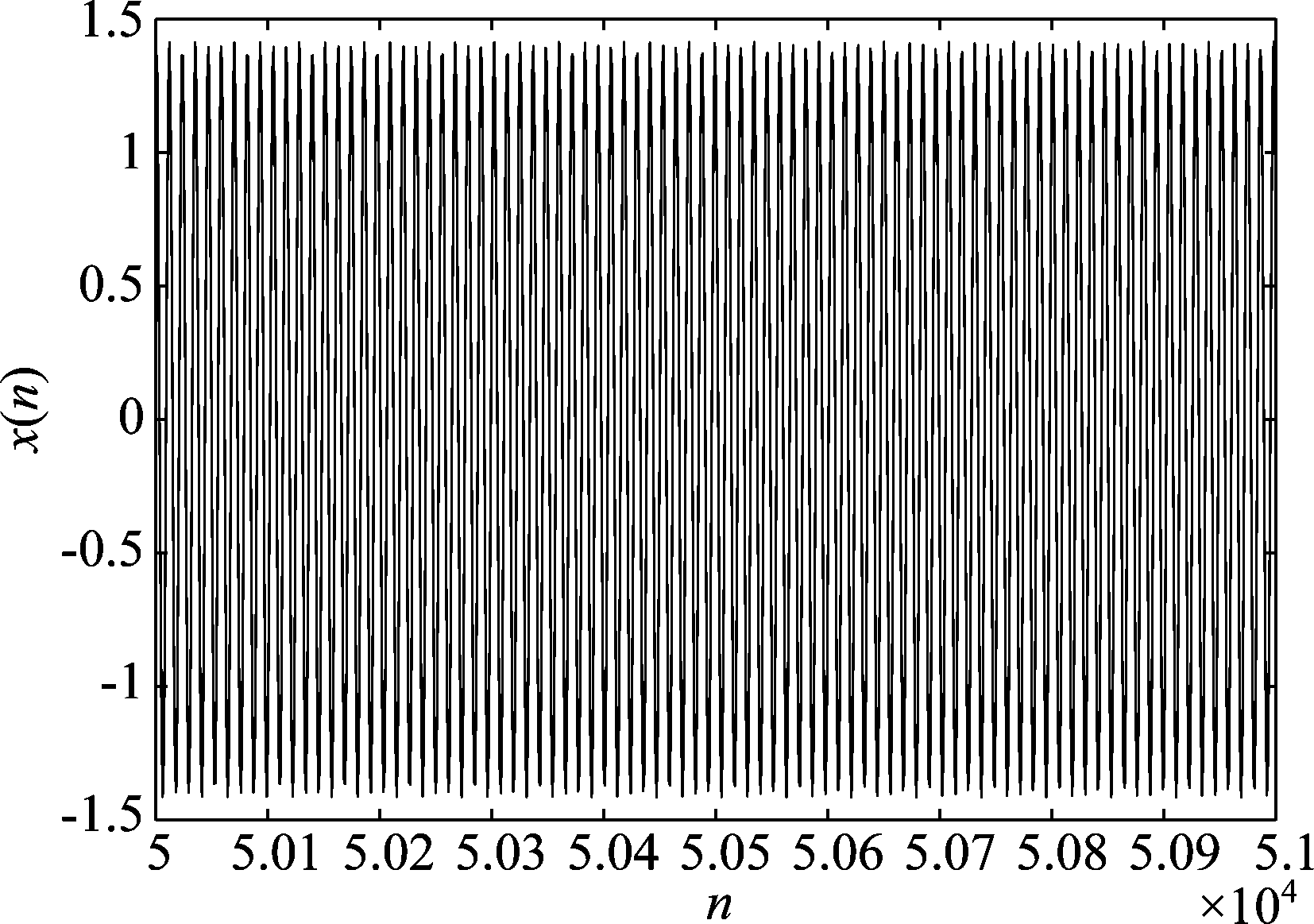
图7 发送2FSK时域波形图
Fig.7 Time domain waveform of send 2FSK signal
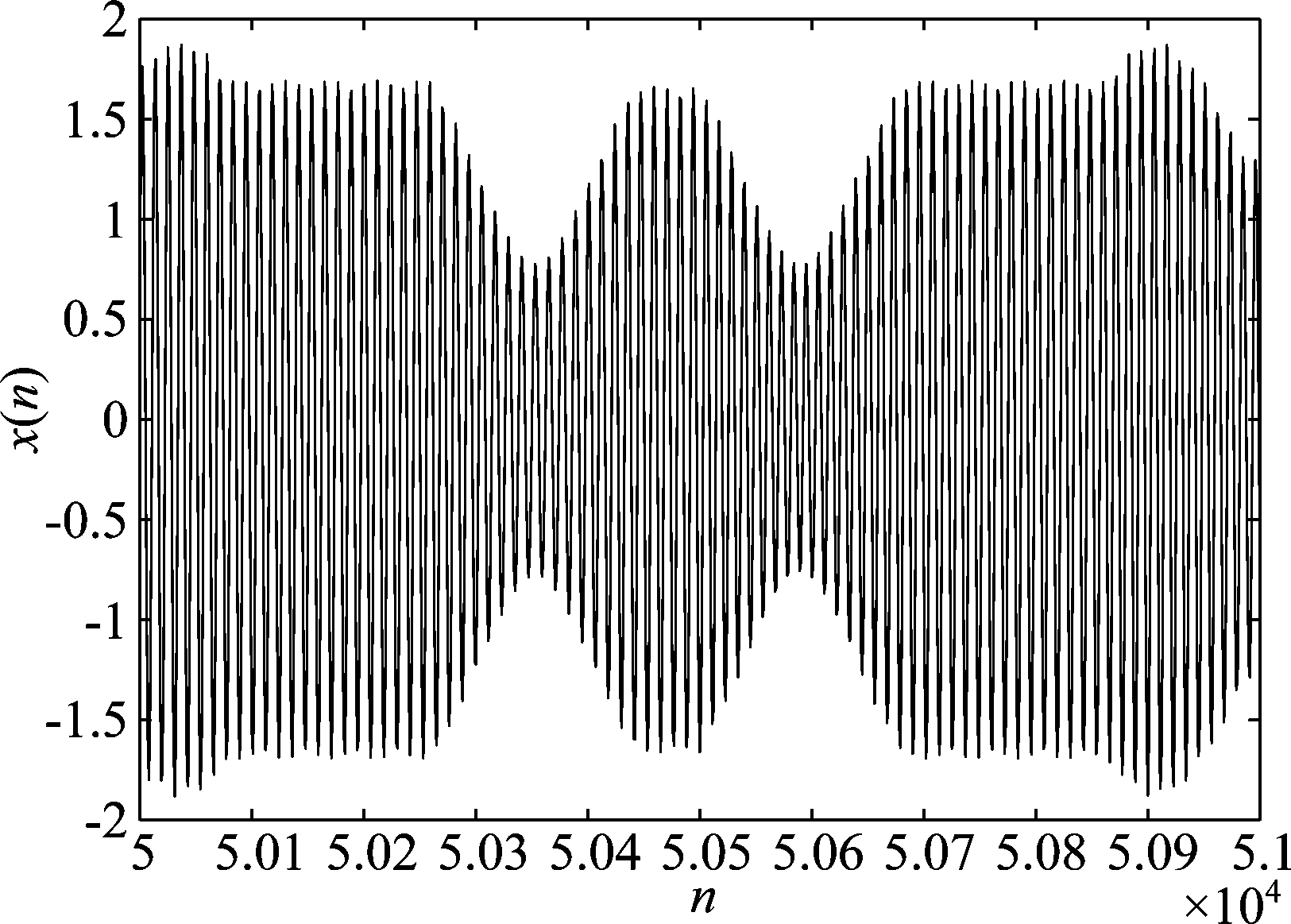
图8 接收2FSK时域波形图
Fig.8 Time domain waveform of received 2FSK signal
信号经过该信道后的功率谱如图9所示。
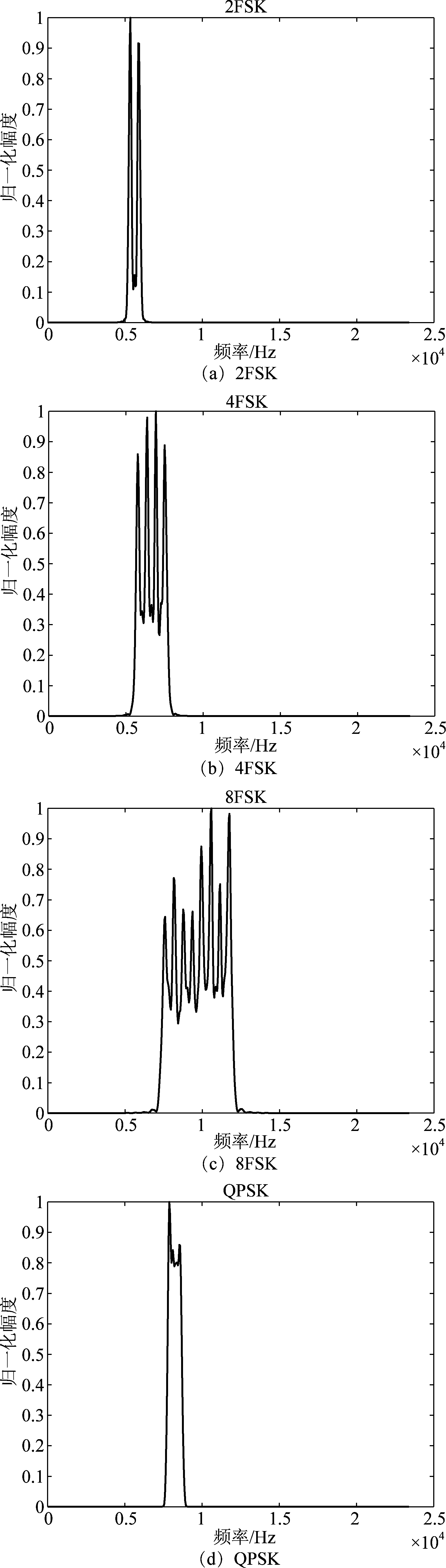
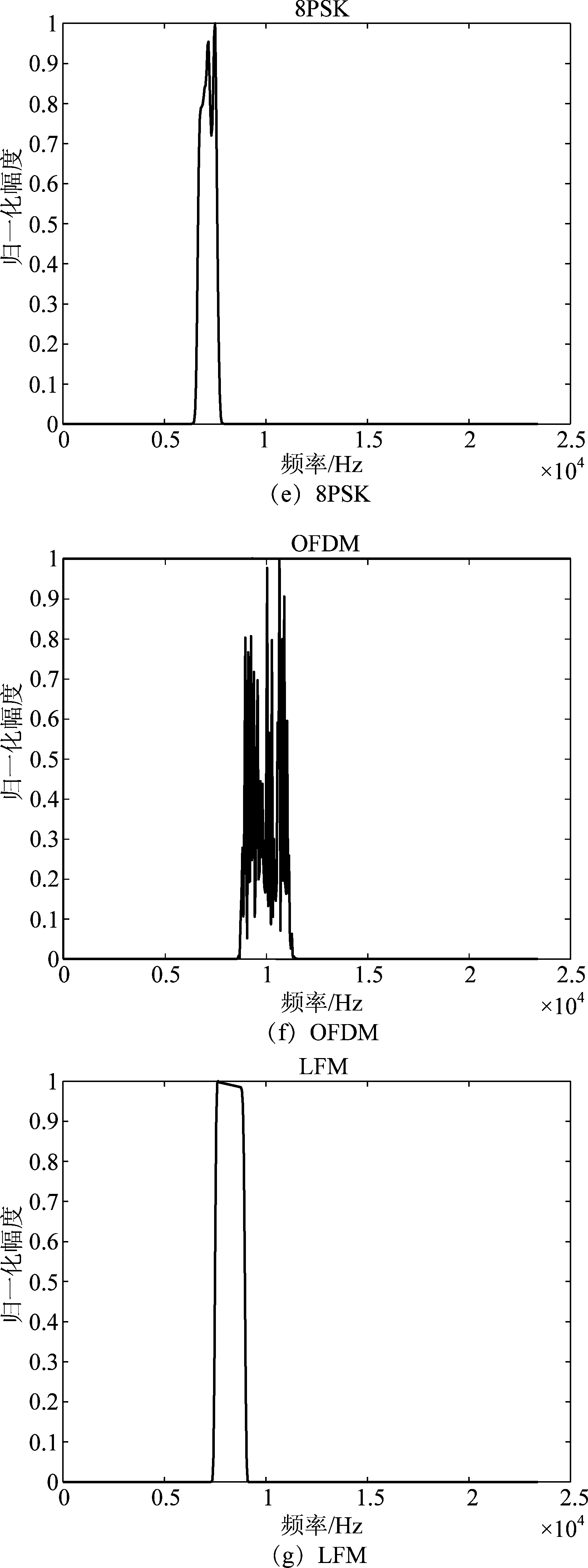
图9 水声信号的功率谱
Fig.9 Power spectrum of underwater signals
从图9中可以看出，在该水声信道模型下，不同调制方式的功率谱在谱峰数量、谱峰大小和形状上有明显不同。图10(a)所示是QPSK的四次方谱，图10(b)所示是8PSK的四次方谱。从图中可以看出，QPSK的四次方谱在四倍载频处有一根明显的离散谱线，而8PSK的四次方谱在四倍载频处是一个谱包络。
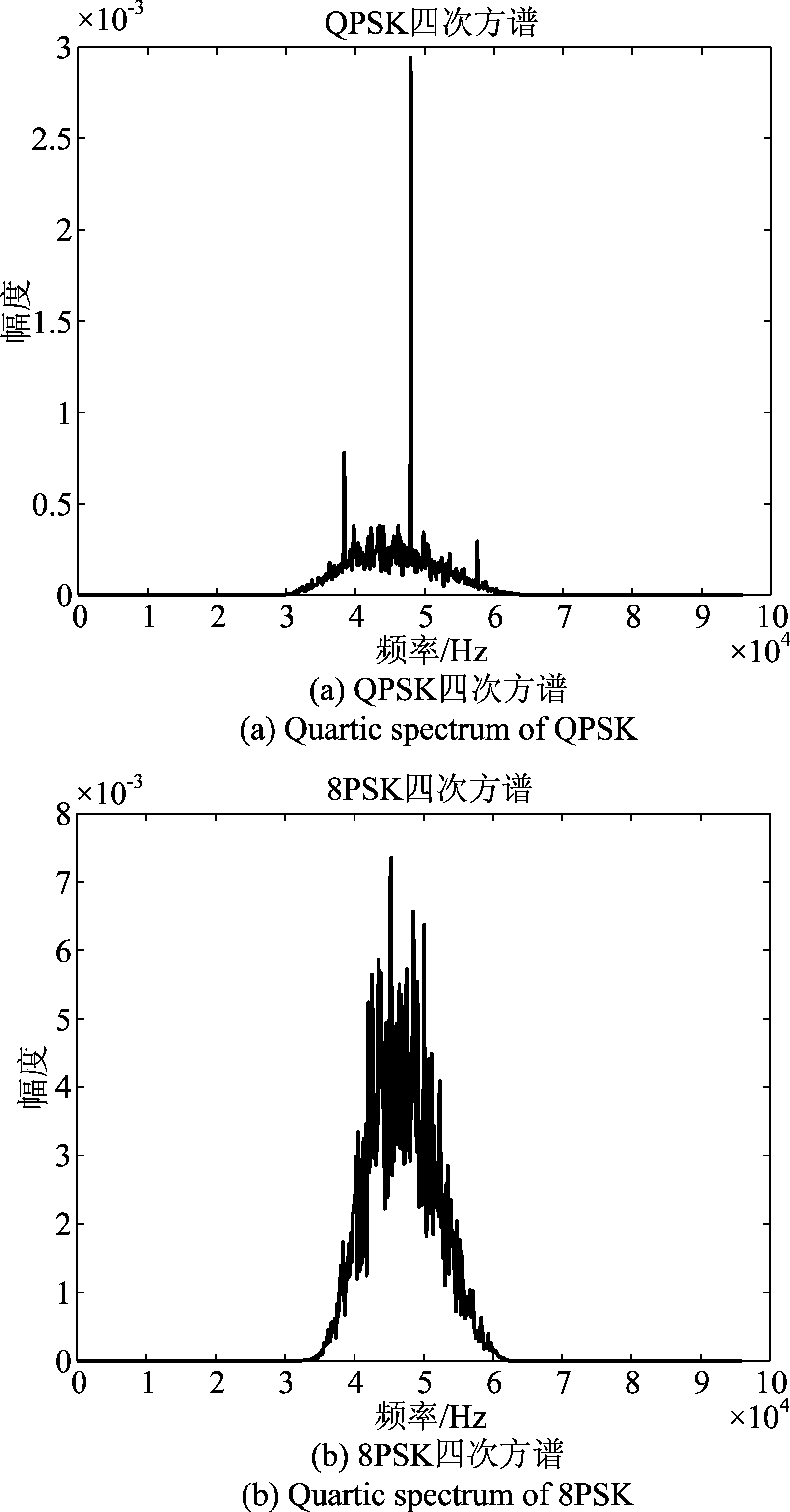
图10 PSK四次方谱
Fig.10 Quartic spectrum of PSK
实验1 在分析算法性能前，首先需要考察神经网络超参数对于识别性能的影响。选取性能最优的网络结构进行分类测试，使得到的分析结果更加可靠。因此，在符号信噪比Es/N0=10 dB的条件下，神经网络隐层层数以及隐层节点数与识别率的关系如图11所示。
从图11可以看出，稀疏自动编码网络的隐层层数、隐层节点数与识别率的关系都呈“钟”形，即识别率随着隐层节点数和隐层层数的增加先上升后下降，超参数过小则训练数据相对冗余，特征提取不充分，丢失部分有效特征；参数过大，训练数据相对不足，提取到的特征相对冗余，对有效特征提取不够充分。从图中可以得出，网络在双隐层下识别性能最优，因此，稀疏自动编码的网络参数设置如表2所示。
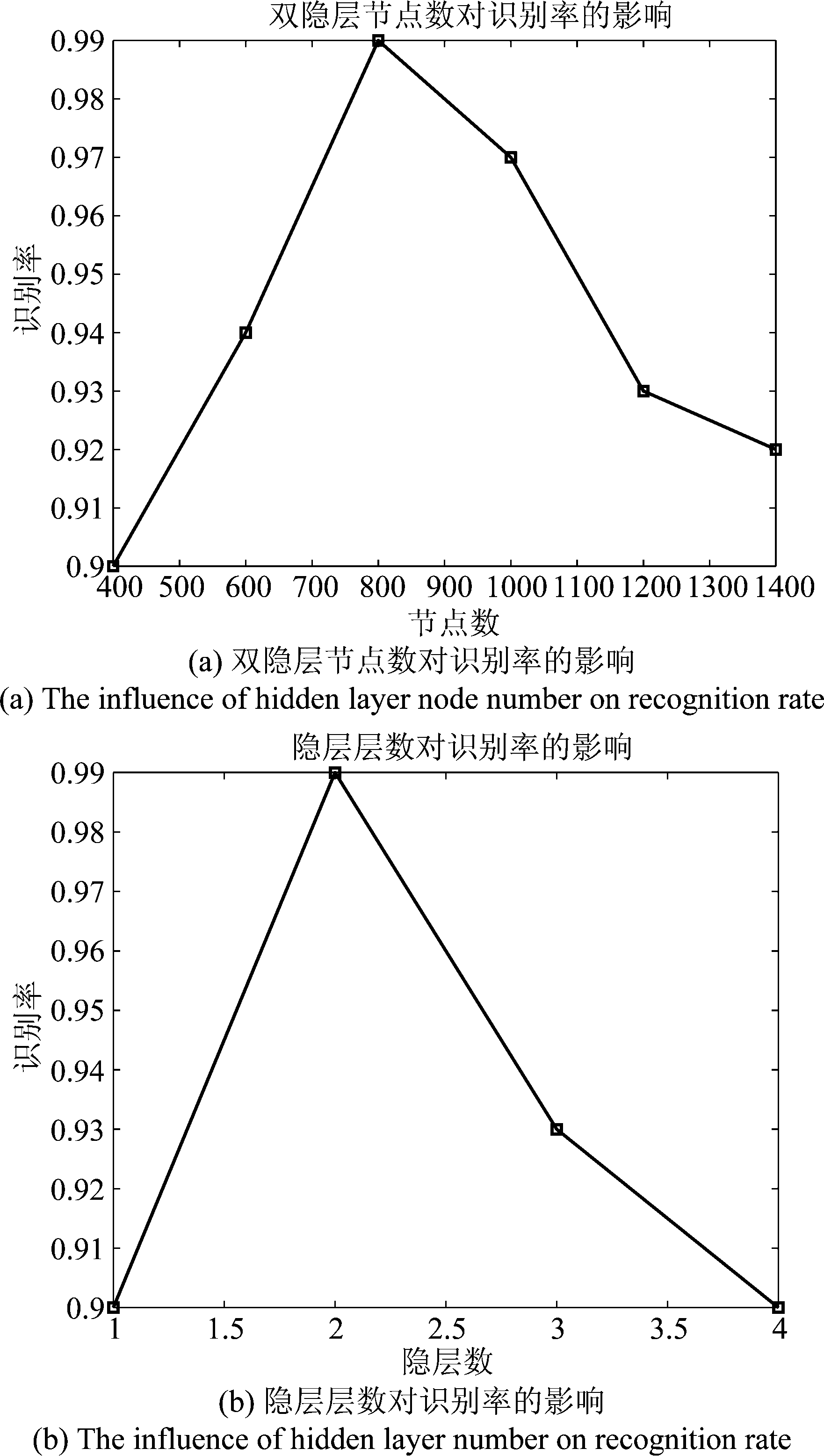
图11 神经网络超参数对识别率的影响
Fig.11 The influence of neural network hyperparameters on recognition rate
表2 稀疏自动编码网络参数
Tab.2 Parameters of SAE
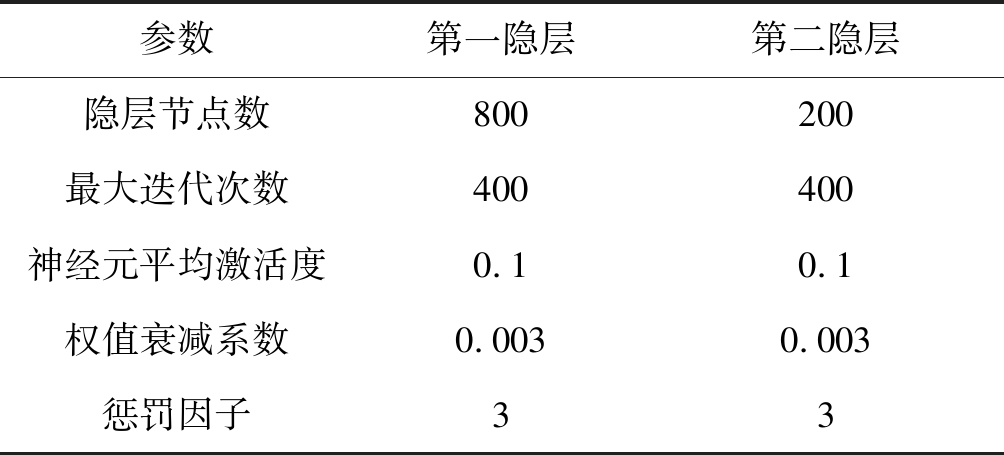
参数第一隐层第二隐层隐层节点数800200最大迭代次数400400神经元平均激活度0.10.1权值衰减系数0.0030.003惩罚因子33
实验2 信号经过上述信道后加入高斯白噪声，考察不同Es/N0下的信号识别率。Es/N0为-10 dB～15 dB，间隔5 dB取值，观测时间1 s，其他仿真条件不变。图12(a)是不同Es/N0下的类间识别结果，从图12(a)可以看出，随着Es/N0的提高，类间的识别率逐渐提升，当Es/N0低于-5 dB时，识别性能较差，当Es/N0大于10 dB时，四类信号已经可以完全识别，识别率达到100%。图12(b)是不同Es/N0下的各类信号识别结果，从图12(b)可以看出，当Es/N0较低时，利用功率谱对FSK信号的识别性能较差，但当Es/N0大于0 dB后，谱峰特征明显，识别率迅速提升。当Es/N0达到10 dB时，QPSK和8PSK信号的识别仍有混淆，当Es/N0大于15 dB时，所有信号的识别率达到100%。 仿真结果说明，本文提出的方法在较高Es/N0下是有效的。
图12 不同Es/N0下识别性能曲线
Fig.12 Recognition performance curve under different symbol SNR
实验3 本文方法与文献[14]方法进行性能对比实验。文献[14]提出了一种基于功率谱特征参数的调制识别方法，选用经典特征参数的零中心归一化瞬时幅度绝对值标准偏差σaa和零中心归一化非弱信号段瞬时频率绝对值的标准差σaf，功率谱谱峰集中度Fgan和功率谱宽度比Wd组成特征参数向量，通过BP神经网络识别分类。其中，
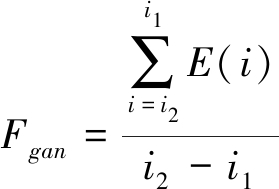
(17)
式中，i2是功率谱峰起始位置坐标，i1是功率谱峰截止位置坐标，E(i)为功率谱序列。
(18)
式中，Ep是信号零中心归一化后的功率谱，E2p是信号二倍频后的功率谱。
仿真信号参数设置相同，Es/N0为0～20 dB间隔5 dB取值，观测时间为1 s，其他仿真条件不变。BP神经网络的训练集为不过信道的7类通信信号在符号信噪比分别为0 dB、5 dB、10 dB、15 dB下产生，每个信噪比下产生100组信号，因此共有400×7=2800组，测试集为经过上述水声信道后的7类通信信号，每类信号100组，共有100×7=700组。两种方法对每类信号的识别结果如表3、表4所示。
在低符号信噪比下，信号特征辨识度较低，低于5 dB时，基于特征参数方法的识别结果很差，受噪声影响更加严重。在相同信噪比下，本文提出的算法都有更高的识别性能，对噪声有更强的鲁棒性。每类信号的识别率相加后取均值得到该符号信噪比下的总体识别率，识别结果如图13所示。
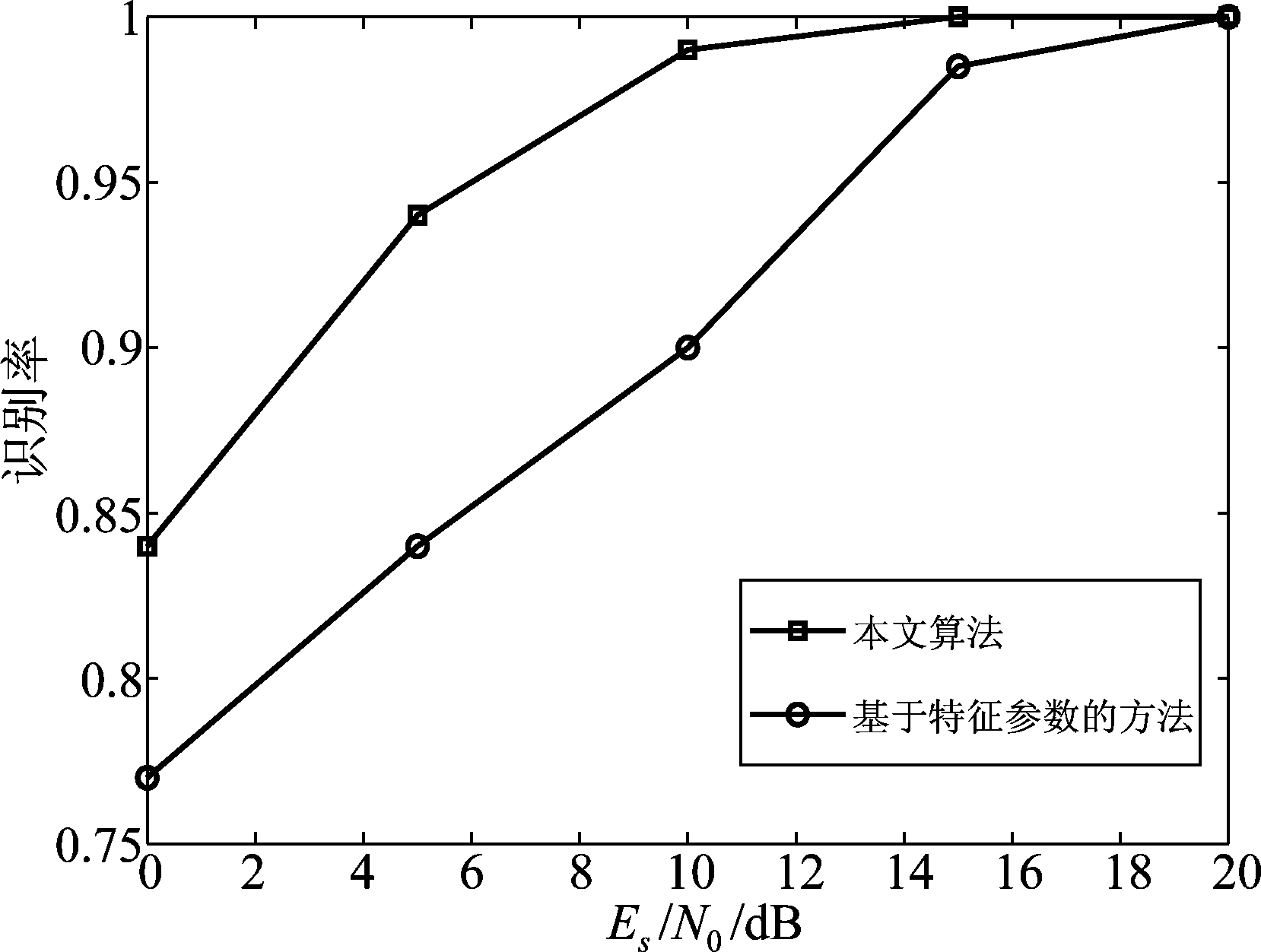
图13 不同方法下信号识别率曲线
Fig.13 Recognition rate curve under different methods
表3 本文算法识别结果
Tab.3 Recognition rate of this paper’s method
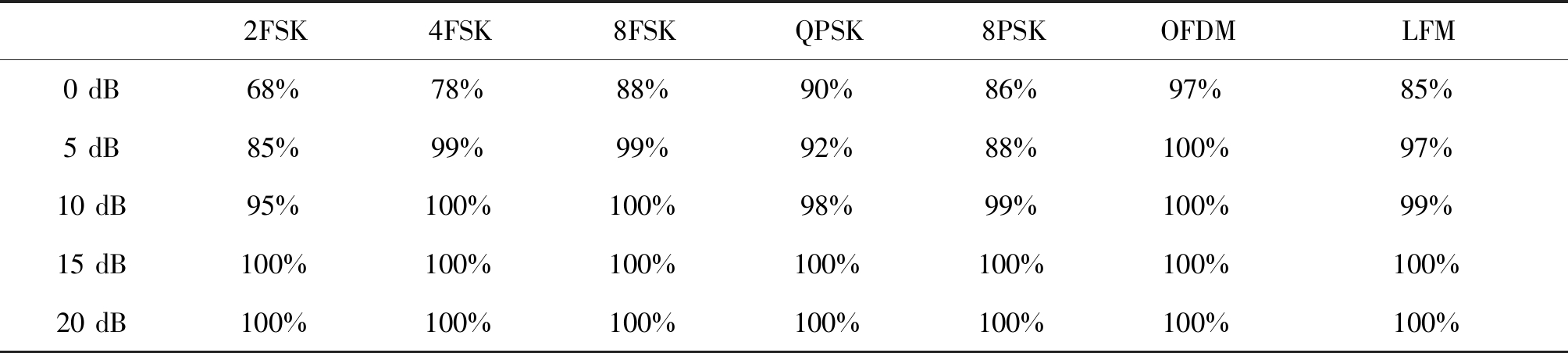
2FSK4FSK8FSKQPSK8PSKOFDMLFM0 dB68%78%88%90%86%97%85%5 dB85%99%99%92%88%100%97%10 dB95%100%100%98%99%100%99%15 dB100%100%100%100%100%100%100%20 dB100%100%100%100%100%100%100%
表4 基于特征参数方法的识别结果
Tab.4 Recognition rate of method based on feature parameters
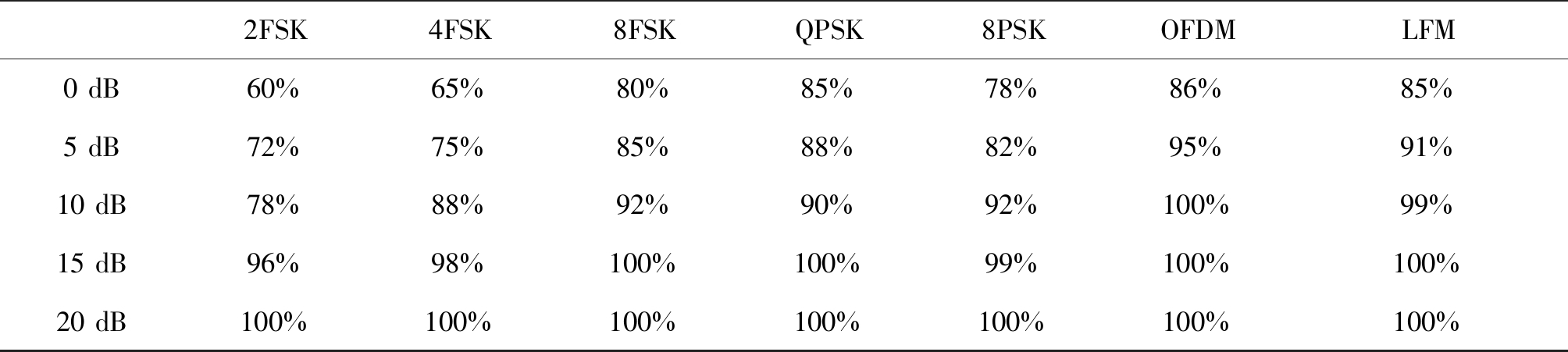
2FSK4FSK8FSKQPSK8PSKOFDMLFM0 dB60%65%80%85%78%86%85%5 dB72%75%85%88%82%95%91%10 dB78%88%92%90%92%100%99%15 dB96%98%100%100%99%100%100%20 dB100%100%100%100%100%100%100%
从图13可以看出，本文算法与文献[14]提出的算法在Es/N0较高时都获得了较好的识别性能，并且本文算法在不同Es/N0下识别率均高于文献[14]的算法。相比于基于神经网络从信号功率谱中提取特征的方法，文献[14]的方法对噪声敏感，稳健性相对较差，因此在低信噪比下，识别性能严重退化。由此可以说明，本文提出的方法在较高信噪比下有效，省去了复杂的特征参数提取的算法设计，提取到的特征对噪声等影响有较强的鲁棒性。
实验4 本文方法对于水声信道的适用性研究。为了说明本文方法对于不同水声信道环境下的泛化性能，通过Argo数据库读取三个不同位置海域的海洋信息，利用Bellhop仿真给出三种不同条件下的信道参数，信道的地理位置和仿真参数如表5所示。
三个信道的冲激响应如图14所示。
信道1的最大多径时延为1.15 s，经96 kHz采样后其Z域表达式为：
H(z)=0.1156+z-29+0.2215z-88315+0.6605z-88319+
0.029z-95430+0.8097z-95434+0.3078z-102974+
0.4957z-102979+0.1664z-110663+0.6049z-110667
(19)
信道2的最大多径时延为1.09 s，经96 kHz采样后其Z域表达式为：
H(z)=0.4623+0.1454z-81+0.3318z-531+
0.1287z-623+0.0124z-88080+0.6312z-88084+
0.1549z-104306+0.4333z-104329
(20)
信道3的最大多径时延为2.49 s，经96 kHz采样后其Z域表达式为：
H(z)=0.3264+0.4774z-69940+0.7323z-69949+
z-72189+0.1488z-72197+0.1197z-79701+0.9025z-79709+
0.6590z-82268+0.3271z-82275+0.1012z-217796+
0.1079z-217802+0.1964z-221998+0.0097z-222004+
0.1695z-234979+0.0287z-234985+0.1835z-239307
(21)
通信信号参数如表1所示，稀疏自动编码网络1的训练集由不过信道的7类通信信号在符号信噪比分别为0 dB、5 dB、10 dB、15 dB下产生，每个信噪比下产生100组信号，因此共有400×7=2800组，测试集为经过上述水声信道后加入符号信噪比为10 dB高斯白噪声的7类信号，每类信号100组，共有100×7=700组。 稀疏自动编码网络2的训练集由不过信道的QPSK和8PSK信号在符号信噪比分别为0 dB、5 dB、10 dB、15 dB下产生，每个符号信噪比下产生100组信号，因此共有400×2=800组，测试集为经过上述水声信道后加入符号信噪比为10 dB高斯白噪声的QPSK和8PSK信号，每类信号100组，共有100×2=200组。测试结果如表6所示。
表5 信道参数
Tab.5 Parameters of channels
信道地理位置/(°)声源深度/m水听器深度/m水平传播距离/km信道1西经179.5 北纬20.51002005信道2西经179.5 南纬20.53502004信道3西经129.5 南纬50.5200508
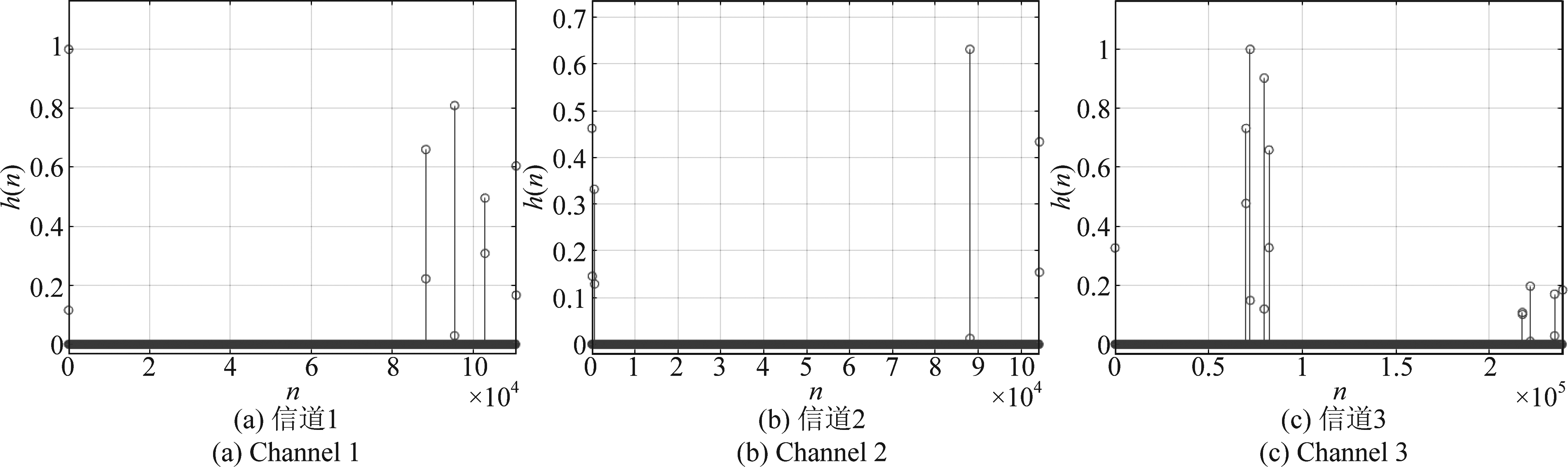
图14 信道的冲激响应
Fig.14 Impulse response of the channels
表6 三条信道下的识别率
Tab.6 Recognition rate of three channels
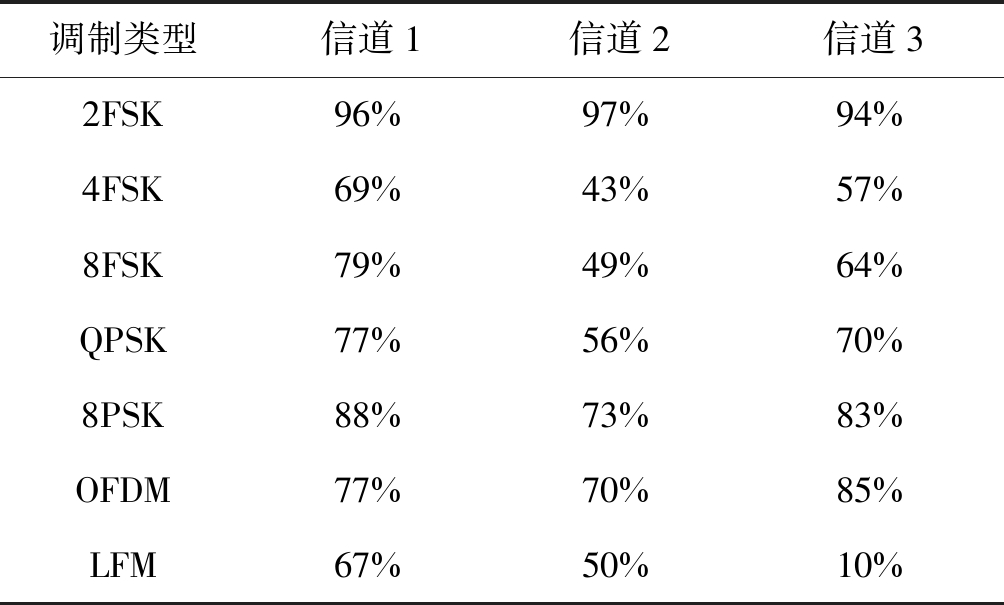
调制类型信道1信道2信道32FSK96%97%94%4FSK69%43%57%8FSK79%49%64%QPSK77%56%70%8PSK88%73%83%OFDM77%70%85%LFM67%50%10%
从表6中的识别率可以看出，3种信道对功率谱和四次方谱的识别有严重影响，由于多径信道对信号的频率选择性衰落，信号经过信道后谱特征发生畸变，导致网络识别结果很差，无法实际应用，因此，本文所提方法适用于水声信道较为理想，对通信信号功率谱、四次方谱畸变较小的情况。对于复杂水声信道环境，功率谱和四次方谱畸变较为严重的情况，本文方法失效。
4 结论
针对传统水声通信信号调制识别方法中，特征参数提取算法复杂并且对环境参数及信号参数敏感的问题，本文提出了一种基于稀疏自动编码网络的水声通信信号调制识别方法。首先对接收信号进行频域变换，将信号功率谱作为“稀疏自动编码网络1”的特征提取对象，然后，利用“Softmax分类器1”完成识别分类，其次，将PSK信号的四次方谱作为“稀疏自动编码网络2”的特征提取对象，最后，利用“Softmax分类器2”完成QPSK和8PSK的识别分类。仿真实验结果表明，稀疏自动编码网络对频域一维谱特征的谱峰个数、大小和形状等信息有较好的特征提取能力，并且网络的识别性能不受信号载频、符号速率、频率间隔、升余弦成型滤波器滚降系数的影响，网络提取的特征向量对噪声同样具有一定的鲁棒性，当Es/N0高于10 dB时，能完全识别信号集。该算法不依赖于接收信号的先验知识，且可以对中频信号直接处理，算法步骤简单，易于实现。但是本文算法在浅海复杂环境以及水声多途影响严重的条件下识别性能不佳，主要原因是接收信号功率谱对于信道影响比较敏感。但是，借助本文的基于稀疏自动编码网络识别的思想，利用对信道影响更加稳健的信号表征形式，能够提高复杂水声环境下的信号识别性能。
[1] Zhang Conghui, Wang Yiyin, Guan Xinping. Chaotic Modulation Detection for Underwater Acoustic Communications Via Instantaneous Features[C]∥Oceans. IEEE, 2016: 1-5.
[2] 赵春晖, 杨伟超, 杜宇. 采用分数低阶循环谱相干系数的调制识别[J]. 应用科学学报, 2011, 29(6): 565-570.
Zhao Chunhui, Yang Weichao, Du Yu. Modulation Recognition Using Fractional Low-Order Cyclic Spectrum Coherence Coefficient[J]. Journal of Applied Sciences, 2011, 29(6): 565-570.(in Chinese)
[3] 赵春晖, 杨伟超, 马爽. 基于广义二阶循环统计量的通信信号调制识别研究[J]. 通信学报, 2011, 32(1): 144-150.
Zhao Chunhui, Yang Weichao, Ma Shuang. Research on Communication Signal Modulation Recognition Based on Generalized Second-Order Cyclic Statistics[J]. Journal of Communications, 2011, 32(1): 144-150.(in Chinese)
[4] 周青, 孙海信, 周明章. 一种水声通信信号调制模式识别方法[J]. 通信对抗, 2017, 1(2): 12-17.
Zhou Qing, Sun Haixin, Zhou Mingzhang. One Method of Standard Recognition of Underwater Acoustic Signal[J]. Communications Countermeasures, 2017, 1(2): 12-17.(in Chinese)
[5] Goodfellow I, Bengio Y, Courville A. 深度学习[M]. 赵申剑, 黎彧君, 符天凡, 等, 译. 北京：人民邮电出版社, 2017: 306-310.
Goodfellow I, Bengio Y, Courville A. Deep Learning[M]. Zhao Shenjian, Li Yujun, Fu Tianfan, et al, Trans. Beijing: People Posts and Telecom Press, 2017: 306-310.(in Chinese)
[6] 孙文珺, 邵思羽, 严如强. 基于稀疏自动编码深度神经网络的感应电动机故障诊断[J]. 机械工程学报, 2016, 52(9): 65-71.
Sun Wenjun, Shao Siyu, Yan Ruqiang. Introduction Motor Fault Diagnosis Based on Deep Neural Network of Sparse Auto-encoder[J]. Journal of Mechanical Engineering, 2016, 52(9): 65-71.(in Chinese)
[7] Schölkopf B, Platt J, Hofmann T. Greedy Layer-Wise Training of Deep Networks[J]. Advances in Neural Information Processing Systems, 2007, 19(1): 153-160.
[8] 张歆, 张小蓟. 水声通信理论与应用[M]. 西安: 西北工业大学出版社, 2012.
Zhang Xin, Zhang Xiaoji. Theory and Application of Underwater Acoustic Communication[M]. Xi’an: Northwestern Polytechnical University Press, 2012.(in Chinese)
[9] 殷敬伟. 水声通信原理及信号处理技术[M]. 北京: 国防工业出版社, 2011.
Yin Jingwei. Underwater Acoustic Communication Principle and Signal Processing Technology[M]. Beijing: National Defense Industry Pess, 2011.(in Chinese)
[10] Zhou Y, Qaraqe K, Serpedin E, et al. FSK-signal Detection in Cognitive Radios Using First-order Cyclostationarity[C]∥Telecommunications (ICT), 2010 IEEE 17th International Conference on. IEEE, 2010: 110-115.
[11] Theodore S R. 无线通信原理与应用[M]. 周文安, 付秀花, 王志辉, 等, 译. 第2版. 北京：电子工业出版社, 2007.
Theodore S R.Wireless Communications: Principles and Practice[M]. Zhou Wen’an, Fu Xiuhua, Wang Zhihui, et al. Trans. Sencond Edition. Beijing: Pubilishing House of Electronics Industry, 2007.(in Chinese)
[12] Punchiewa A, Dobre O A, Rajan S, et al. Cyclostationarity-based Algorithm for Blind Recognition of OFDM and Single Carrier Liner Digital Modulations[C]∥IEEE PIMRC, 2007: 1-5.
[13] 刘勇, 张国毅, 张旭洲. 线性调频连续波雷达信号的参数估计[J]. 信号处理, 2014, 30(7): 848- 855.
Liu Yong, Zhang Guoyi, Zhang Xuzhou. Parameter Estimation of LFMCW Radar Signal[J]. Journal of Signal Processing, 2014, 30(7): 848- 855.(in Chinese)
[14] 史甜姝. 数字通信信号调制方式自动识别方法的研究与应用[D]. 天津: 天津大学, 2016.
Shi Tianshu. Research and Application of Automatic Modulation Recognition of Digital Communication Signals[D]. Tianjin: Tianjin University, 2016.(in Chinese)
[15] 邢晓晴, 朱根民. Welch功率谱估计中窗函数的选择与算法分析[J]. 计算机时代, 2018, 1(2): 1- 4.
Xing Xiaoqing, Zhu Genmin. Window Function Selection and Algorithm analysis in Welch Power Spectrum Estimation[J]. Computer Age, 2018, 1(2): 1- 4.(in Chinese)
[16] 刘亚冲, 唐智灵. 基于Softmax回归的通信辐射源特征分类识别方法[J]. 计算机工程, 2018, 44(2): 98-102.
Liu Yachong, Tang Zhiling. Classification and Identification Method of Communication Radiation Source Feature Based on Softmax Regression[J]. Computer Engineering, 2018, 44(2): 98-102.(in Chinese)
[17] 汪海波, 陈雁翔, 李艳秋.基于主成分分析和Softmax回归模型的人脸识别方法[J]. 合肥工业大学学报: 自然科学版, 2015, 38(6): 759-763.
Wang Haibo, Chen Yanxiang, Li Yanqiu. Face Recognition Method Based on Principal Component Analysis and Softmax Regression Model[J]. Journal of Hefei University of Technology: Natural Science, 2015, 38(6): 759-763.(in Chinese)
