1 引言
无人机作为超低空飞行的小型飞行器,具有高度低、RCS小、速度慢等典型的“低、小、慢”特征[1],目前仍无很好的探测方法。虽然国内外提出了用红外、声学、激光等传感器对无人机进行探测,但使用条件多受气象和距离等条件限制。基于检测前跟踪(TBD)算法计算量较大,不利于工程实现。目前主流的无人机探测雷达主要采用线性调频连续波体制。这种体制的典型优点是:作为一种全天候检测传感器,具有简单的收发系统以及高精度测量能力,近年来它已成为无人机探测领域的研究热点[2-3]。但无人机作为典型的低、小、慢目标,一般在与结合郊区的复杂环境下使用,具有很强的杂波背景(建筑物、车辆等),所以LFMCW雷达探测无人机性能[4-5],还面临以下问题:
(1)LFMCW雷达通过对差频信号进行2D-FFT处理获得目标的距离和速度信息[6-7],但无人机本身属于低小慢目标(广泛采用工程塑料导致 RCS非常小,旋翼无人机速度一般低于30 m/s左右),即使在干净噪声背景下,由于信噪比过低,自身检测仍面临较大问题。
(2)无人机的使用一般位于复杂的城郊结合地带,地物建筑、慢速移动车辆等强块状分布杂波必然影响目标在速度维的检测性能。一方面,雷达需要过滤掉静止地物杂波,另一方面区分和识别慢速移动车辆。因此,对速度维检测的影响机理还需要进行深入分析[8]。
本文以LFMCW雷达为研究对象,重点研究地物杂波对低小慢无人机测距、测速的影响机制。通过改变雷达相关参数(调频率、带宽、是否MTI[9]等),目标相关参数(速度、RCS等)和杂波相关参数(强度、谱宽、分布等),从理论和仿真的角度分析了相关参数的影响机理,得出了一些有意义的结论,可为无人机探测和识别提供一定的借鉴参考意义。
2 LFMCW雷达差频信号分析
2.1 差频信号时域频域分析
目标回波信号与发射信号混频之后会得到一个差频信号,差频信号本身包含了目标无人机的距离,速度和角度等信息。本文选取线性调频连续波作为雷达发射信号:
st(t)=cos[2π(f0t+Kt2/2)+φ0], 0≤t≤T
(1)
其中f0、K、φ0、T分别为中心频率、调频斜率、发射初相和扫频周期。调频斜率K=B/T,B为调频带宽。
先考虑单个目标回波的情况,则雷达接收信号:
sr(t)=Acos{2π[f0(t-τ)+K(t-τ)2/2]+
φ0+φ+φr}
(2)
其中A、τ、φ分别为接收信号幅度、目标延迟时间和目标相位,φr为接收机相移。
式(2)中目标幅度与雷达的发射功率,天线增益、目标RCS和目标距离都有关,即
(3)
其中Pt为发射功率,Gt为发射天线增益,Gr为接收天线增益,λ为雷达波长,σ为目标RCS,R为目标距离,L为综合损耗。
在接收机中,将发射信号和接收信号进行混频并滤除高频分量,得到差频信号为:
0.5Kτ2]-φ-φr}
(4)
假定目标以速度ν进行匀速运动,初时距离为R0,则目标距离为R(t)=R0-νt,时延为:
(5)
其中c为光速。将式(5)带入式(4)并整理得到差频信号为:
(6)
其中
(7)
(8)
(9)
在多目标情况下,每个目标差频信号的多项式系数a0,a1,a2是不同的。由式(6)可以看出,差频信号本质上是多分量的LFM信号,目标的瞬时频率为:
f(t)=a1+2a2t, 0≤t≤T
(10)
本质上,差频信号为线性调频信号,目标的距离和速度等信息均蕴含于各系数当中。但由于目标速度目标ν≪c,因此a2项实际上接近于零,工程中一般将差频信号近似当成单频信号来估计,估计出a1后,通过单个脉冲或多个脉冲进行组合处理,即可获取目标的距离信息和速度信息。目标距离维带来的频谱搬移项为
而目标速度维(多普勒)频移为
一般来说,测距的话只需单个重复周期即可,而测速需要多个重复周期积累才能保证精度。
注意式(10)给出的只是差频信号的时频图,工程上是较难实现的,一般只分析幅度谱。仿照LFM信号的推导方式,经过一系列变换[10],并利用菲涅尔公式的性质,可得到差频信号的近似幅度谱为:
a1-a2T/2
(11)
由式(11)可知,目标幅度谱的宽度约为a2T,由于a2项非常小,因此我们通常近似认为差频信号为单频信号,但实际上是宽度极窄的线性调频信号。幅度谱的位置虽然由式(10)决定,但幅度谱大小却由式(11)决定。幅度谱大小与目标的RCS(σ)和目标距离R以及雷达参数都是有关系的。如果目标RCS过小,又能导致幅度谱峰值不够,淹没在噪声中难以检测。
2.2 测距测速公式分析
对差频信号的频谱进行估计可得到目标距离计算公式为:
(12)
在距离维进行M采样,假设采样率为fs,则距离计算公式为:
...,M
(13)
可见,距离维的分辨率与采样率fs、调频率K和采样点个数M均有关系。一般来说,采样率fs越小,采样点个数M越多,调频率K越小(带宽越大),则距离分辨率越高。单个差频信号即可获取目标的距离信息,速度测量需要多个差频信号的长时间积累。在LFMCW雷达系统中,发射波形主要采用多周期LFMCW信号,信号处理采用2D-FFT来获得目标的速度谱。重复频率PRF重复N个周期后,速度的计算公式为:
...,N
(14)
最大测量速度为:
(15)
速度分辨率为:
(16)
由式(15)可知,最大测量速度与PRF有关,PRF越大,不模糊速度越大。但相同调频带宽下,PRF越大意味着调频周期T的减少,与上面距离维的分辨是矛盾的。对于近距离无人机而言,由于只进行近距离观测,目标速度也较小,因此距离和速度模糊问题并不是很突出。核心在于提高测速精度,而速度分辨率与PRF和积累个数N有关。PRF越小,积累时间越长,则速度分辨率越高。
3 杂波条件下LFMCW雷达检测性能分析
不管是距离维还是速度维,由于目标的RCS小,导致其信噪比(SNR)较小,如果杂波在距离维和速度维与目标差别不大时,通过2D-FFT变换后的差频信号峰值将会淹没在强地物杂波的峰值中,有必要进行理论和仿真分析,并提出改善措施。
3.1 杂波的频域分析
杂波的类型有很多种。为了简化分析,假设杂波的范围是瑞利分布,速度有一定的谱宽。在这种情况下,我们主要考虑的是速度在零频附近的分布式块结构杂波,但是RCS比所涉及的无人机要强大得多。假设杂波占据了数个距离分辨率单元。在本质上,单个距离单元的杂波可以作为单一目标进行分析。如果杂波占据L个单元,距离是Ri,平均速度是νi,RCS是σi(瑞利分布),对应的多项式系数是ai0,ai1,ai2,则杂波差频信号的频谱近似为:
(17)
此时,块状杂波的频谱会占用数个距离单位,每个频率点的峰值与该单元杂波振幅成正比。
3.2 目标二维CFAR检测概率分析
工程中为了进一步减小噪声或者杂波的影响,实用的FMCW雷达一般采用恒虚警平均(CA-CFAR)检测方法[11]。与传统的脉冲雷达不同,LFMCW雷达的CFAR检测是在距离维和速度维进行二维CFAR检测。实际操作时,可以先进行速度维的CFAR,再进行距离维的CFAR。为了充分减轻检测器的运算负担,部分雷达还可以采用动目标指示(MTI)或动目标检测(MTD)算法进一步滤除零频附近杂波的影响。
对多帧差频信号进行2D-FFT变换后,差频频谱信息转为目标的距离测量,而差频信号多普勒域信息转为目标的速度测量,本质上目标经过2D-FFT变换后的信号可简记为A(r,ν),当存在目标杂波和噪声时,总信号是他们三者的叠加。
A(R,ν)=AT(R,ν)+AC(R,ν)+AN(r,ν)
(18)
理论上式(18)可以包含多个目标和多个杂波的情况,对距离和速度维进行采样量化,则二维CFAR就是要从|A(R,ν)|,R∈[Rmin,Rmax],ν∈[νmin,νmax]中检测出超过预门限的多个目标。显然,当两个目标距离或速度相近时,大目标(如杂波)会影响小目标的检测性能。
下面以速度维的检测为例分析目标检测概率影响因素。假设目标位于二维检测平面的(Ri,νj)处,在距离单元Ri处同时存在零频杂波,则该位置回波是目标、杂波和噪声的叠加。假设有N个参考单元,检测单元记|A(Ri,νj)|,则噪声功率水平估计为:
(19)
标称化因子记为
则检测判识为:
(20)
一般与允许的虚警概率有关和参考单元个数N有关。检测概率一般和信噪比SNR和门限
有关,传统意义上当周边仅存在热噪声时目标的检测概率为:
(21)
一般来说,Pd反比于门限
当强杂波的速度和目标较为接近时,可能会占据好几个速度单元时,此时会造成门限急剧抬高,从而导致关注目标的检测概率Pd急剧下降。距离维的检测也有类似结论这里不分析。总的来说,杂波情况下,差频信号频谱的分布较为复杂,不便于理论推导,下面通过仿真的方法进行验证。
4 仿真实验
4.1 场景描述
基本的仿真参数设置如下:雷达基本频率调制带宽B=20 MHz,脉冲宽度T=80 μs,中心频率f0=10 GHz,CFAR检测单元N=32, MTI为前后两回波差分处理。目标参数为:V=20 m/s,R=10 km,SNR=30 dB;杂波参数是:平均谱宽5 m/s,均值为0,幅度为瑞利分布,SNR=30 dB,距离维呈块状分布,假设杂波距离维跨度为 2.08 km。
为了比较相互之间的作用性能,目标参数、杂波参数和雷达参数均可浮动。
4.2 仿真结果
根据上述仿真参数,进行了仿真实验。
首先,假设目标正好处于强杂波环境(如无人机背后正好有一块状建筑杂波),仿真结果见图1(a)、(b)所示。其中图1(a)是原始差频信号的频谱分析,目标淹没在分布式块状杂波中,仅露出少量峰值。图1(b)采用距离维CFAR进行检测,由于目标RCS过小,杂波的RCS过大且占据多个单元,整体检测门限得以提高,导致目标漏检。 当目标离开分布式固定杂波时(仿真干净背景,如草地上空的无人机检测),仿真结果如图1(c)、(d)所示。由图1(c)可知,此时目标仅处于噪声背景,差频峰值较为明显。图1(d)运用同样的距离维CFAR进行检测,可以检测出目标的距离值。图1(e)说明通过速度维的检测可以解决距离维检测时,目标位于杂波背景下难以检测的问题。
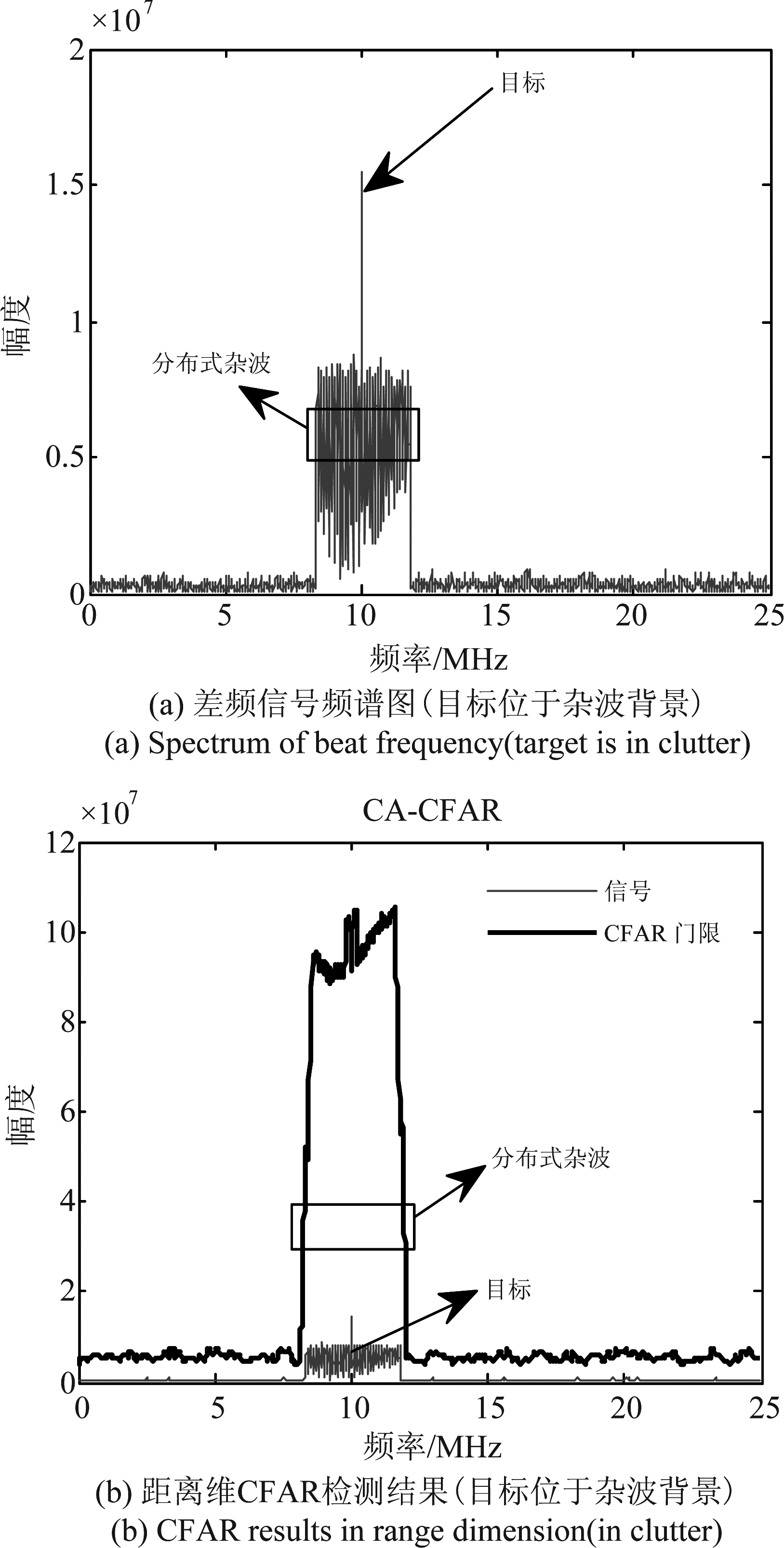
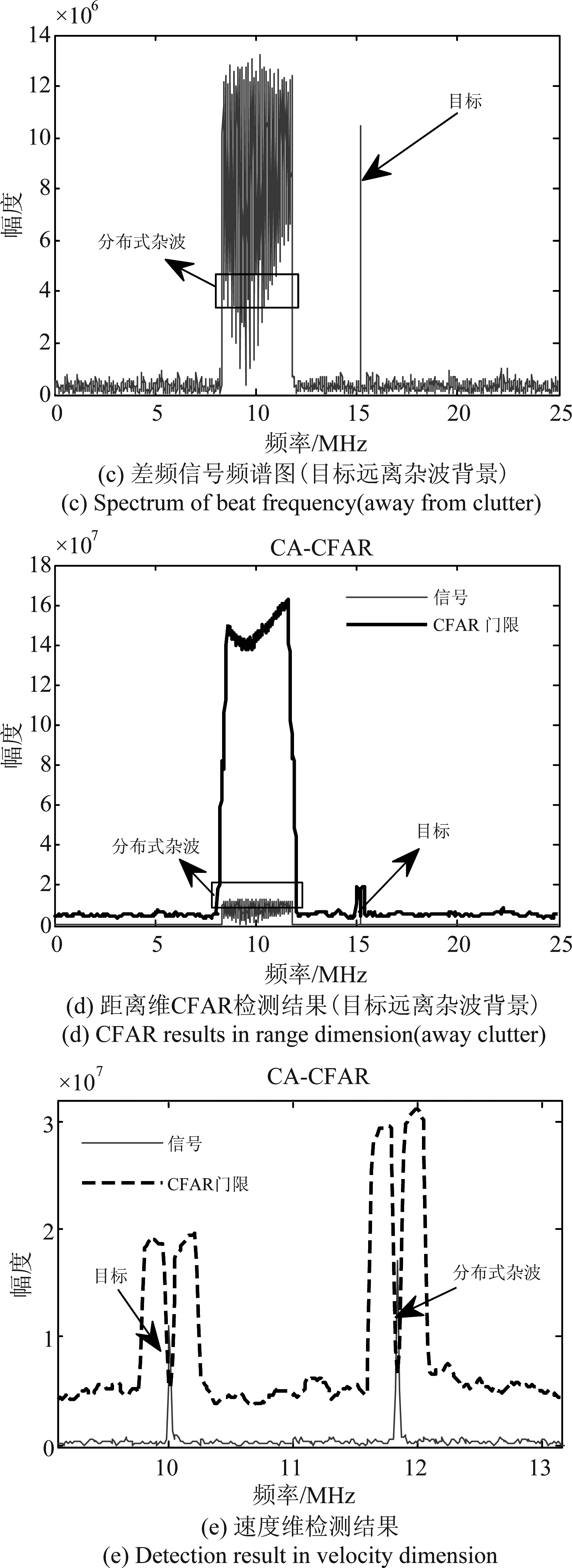
图1 差频频谱及CFAR检测结果
Fig.1 Beat signal frequency spectrum and CFAR results
图1的仿真说明仅在距离维对无人机检测是不够的,因为很多情况下无人机都是在城郊结合带使用的,存在较强的地物杂波。下面对速度维的检测进行分析。在速度维上,可见两个峰值,幅度较弱的是目标,另一个幅度较强的是多个杂波。
图2是对差频信号进行2D-FFT变换的结果。其中图2(a)是原始结果,图2(b)MTI对消处理结果。由图可知,未作MTI时,目标频谱和杂波频谱均凸显出来,仅有噪声得到抑制,目标在距离-速度二维平面上是单个峰值,而分布式块状杂波在二维平面上是一条线,速度均聚集在零速附近,而距离维呈线状。通过MTI对消后,杂波得到抑制,剩余信号仅存目标信号,有利于目标进行检测。
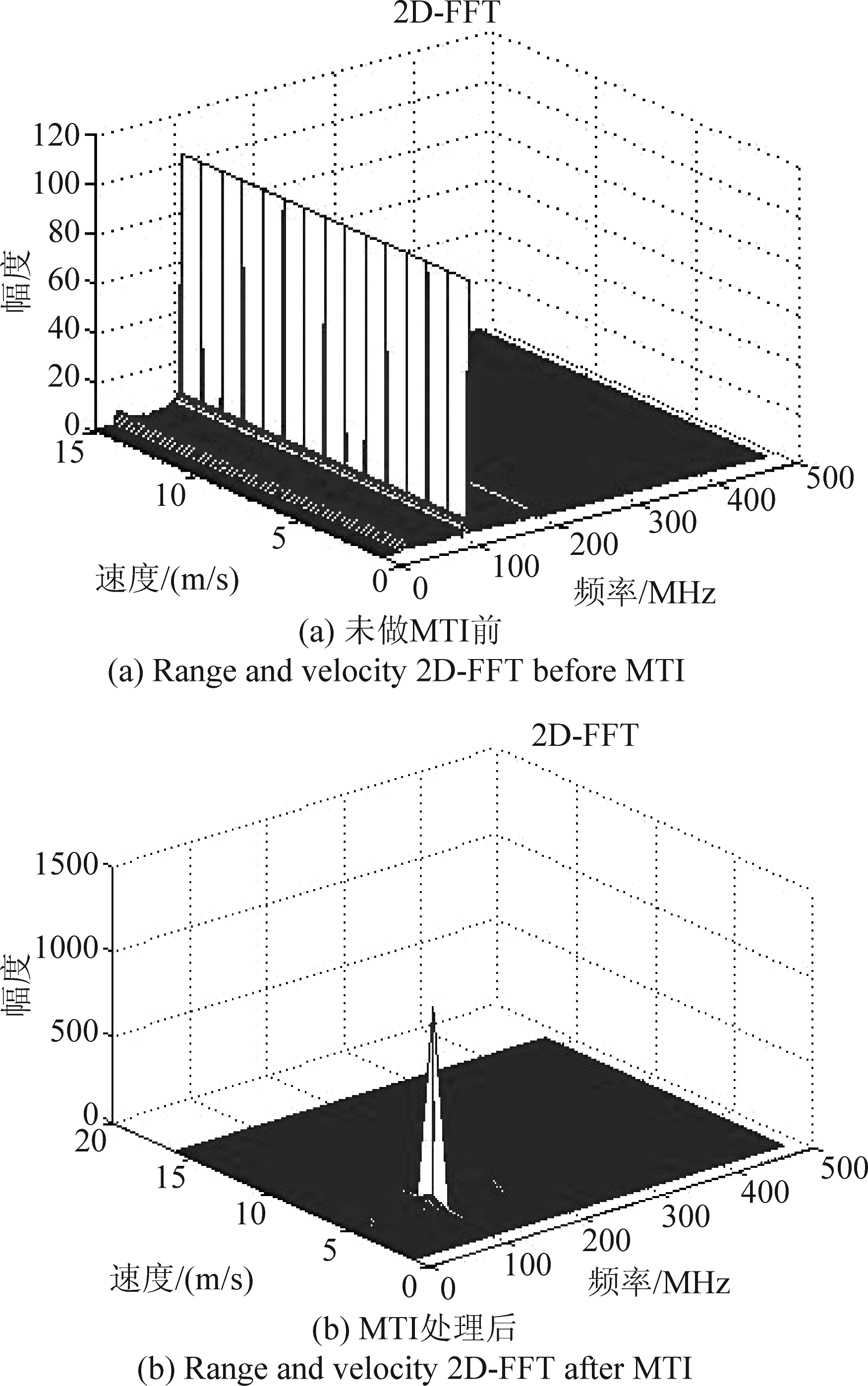
图2 差频信号2D-FFT变换结果
Fig.2 Range and velocity processing with 2D-FFT
图3 目标检测性能分析
Fig.3 Detection probability with different parameters
下面对影响检测性能的关键因素进行对比分析。
图3对影响测试性能的关键因素进行了以下100次蒙特卡罗模拟。图3(a)是脉冲积累数(NCPI=64、NCPI=512、NCPI=1024)时对检测性能的影响,图3(b)是频率调制带宽(B=6 MHz、B=8 MHz、B=12 MHz)对检测性能的影响,图3(c)是目标自身速度(ν=30 m/s、ν=3 m/s、ν=0.3 m/s)对检测的影响,图3(d)是调频周期(T=65 μs、T=60 μs、T=55 μs )对检测的影响。横坐标均为杂波的幅度(杂噪比)。
由图3(a)可知,杂波的幅度越小,目标的相干积累时间越长,则目标的检测概率越高。图3(b)固定其他参数,改变了频率调制带宽。从图中可以看出,相同情况下,雷达调频带宽越大,目标检测概率越高。事实上,带宽决定了分辨率。带宽越大,频率调制的斜率越大,距离分辨率越高,两个目标之间的差异更容易被放大,有利于检测。图3(c)是目标自身速度对检测性能的影响。从图中可以看出,目标速度对检测有很大的影响。目标速度越大才有利于和杂波进行区分。当目标速度过小时,无论是否进行MTI处理,雷达都难以将无人机和杂波进行区分。图3(d)是扫描频率周期对检测的影响。扫描周期越小,越有利于无人机检测。图3所示的横坐标均为杂波的信噪比,所有的图都表明,杂波的幅度越小越有利于目标检测。但实际情况是杂波的强度往往都高于目标强度,因此为了提高检测性能,必须在速度维和距离维同时进行高分辨处理。
5 结论
本文提出了一种运用2D-FFT技术,在强杂波背景下基于LFMCW雷达对低小慢目标检测及性能分析的新方法。在速度维和距离维上用二维傅里叶变换对无人机进行了检测,同时基于多次蒙特卡罗仿真研究了不同参数对检测性能的影响。研究表明,对于强杂波背景下的低小慢无人机检测,速度维的检测至关重要,雷达宜采用大带宽、长时间积累技术,才能有效区分杂波和目标,保证目标顺利检测。
[1] 罗宏伟.试论大型活动安保工作中“低慢小”目标的防范与处置[J]. 武警学院学报, 2015, 31(9): 27-30.
Luo Hongwei. On the prevention and disposal of “low, low and small” goals in the security work of large-scale activities[J]. Journal of Armed Police Academy, 2015, 31(9): 27-30.(in Chinese)
[2] Light hart L P, Nieuwkerk L R. System aspects of a solid-state FMCW weather surveillance radar[C]∥Conference Proceeding, 1987: 19-21, 112-115.
[3] 张宏宇, 王冬华, 李云飞, 等.一种提高LFMCW体制雷达测距精度的方法[J].雷达与对抗, 2017, 37(1): 9-12, 47.
Zhang Hongyu, Wang Donghua, Li Yunfei, et al. A method to improve the ranging accuracy of LFMCW system radar[J]. Radar and Countermeasures, 2017, 37(1): 9-12, 47.(in Chinese)
[4] Hui Zing A G, Otten M P G, Rossum W L V. Compact scalable multifunction RF payload for UAVs with FMCW radar and ESM functionality[C]∥International Radar Conference, 2009: 1- 6.
[5] 李明明.国外低慢小航空器防控装备发展现状分析[J].飞航导弹, 2017: 62-70.
Li Mingming. Analysis on the development status of low-speed small aircraft prevention and control equipment abroad[J]. Flight Missiles, 2017: 62-70.(in Chinese)
[6] Du Yuming, Yang Jianyu. Novel Method for Ambiguity Elimination in the Linear FMCW Radar[C]∥ICSP’04 Proceedings: 2066-2069.
[7] Minki Song, Jinsoo Lim, Dong-Joon Shin. The velocity and range detection using the 2D-FFT scheme for automotive radars[C]∥2014 4th IEEE International Conference on Network Infrastructure and Digital Content，2014: 507-510.
[8] Qu Y, Song Z, Shi L, et al. Moving Target Detection for FMCW Radar[C]∥in 2017 IEEE, 2017: 1756-1759.
[9] Clive Alabaster. Pulse Doppler Radar: Principles, Technology, Applications[J]. Publishing House of Electronics Industry, 2016: 102-105.
[10] 林茂庸, 柯有安. 雷达信号理论[M].北京: 国防工业出版社, 1984: 128-130.
Lin Maoyong, Ke Youan. Radar signal theory[M]. Beijing: National Defense Industry Press, 1984: 128-130.(in Chinese)
[11] 何友.雷达自动检测与恒虚警处理[M]. 第二版. 北京: 清华大学出版社, 2011: 36.
He You. Radar automatic detection and constant false alarm processing[M]. Second edition. Beijing: Tsinghua University Press, 2011: 36.(in Chinese)
