1 引言
聚类分割算法实质是利用图像各像素光谱测度在特征空间自然聚类的性质,将表征不同地物的像素进行归并,保证其分割结果中同一地物类别内像素光谱测度相似性尽可能大,不同地物类别间像素光谱测度相似性尽可能小[1]。该方法原理简单、可拓展性强、计算速度快,因此广泛应用于遥感图像分割中。目前,较为常用的聚类分割算法主要包含以下几种类型:K-means聚类[2-3]、层次聚类[4-5]、模糊聚类[6-7]、谱聚类[8-9]等分割算法。
K-means聚类分割算法是基于距离的动态聚类硬划分方法。以数据点到聚类中心距离平方和最小为准则,迭代更新聚类中心直至满足约束条件。该算法简单高效,但对初始聚类中心敏感,随机选取其初值易导致聚类结果不稳定。文献[10]在HLS颜色空间提取图像目标分类区域颜色的统计值作为初始聚类中心,同时通过加权数据点到聚类中心的距离提高像素划分的准确性,进而得到较传统K-means聚类分割算法更加理想的分割结果。然而,表征不同地物的像素光谱测度在特征空间存在一定程度的重叠,采用距离预测像素类别只能将具有相同测度值的像素划分到同一类别中,因此,基于K-means的硬划分算法不适合特征空间中具有不同尺度、非球形分布的数据处理。
层次聚类分割方法可分为凝聚和分裂两种层次聚类,亦属于硬划分算法。前者视每一数据点为一聚类,计算聚类间邻近度,并合并最接近聚类,直至满足终止条件;后者视所有原始数据为同一聚类,并按照一定准则迭代细分前次聚类,直至满足约束条件。该类算法简单直观、适合任意分布的数据处理,但对噪声敏感,同时该过程不可逆,即分裂或合并后无法回到原始状态,因此无法修正前次错误。对此研究人员将层次聚类与其他聚类算法结合提出改进层次聚类算法。如,文献[11]定义全局目标函数作为聚类合并的准则,实现合并过程的可逆性。然而,过度的分裂或合并过程,极大地增加了算法的冗余度,进而限制了其对大数据处理的能力。
模糊聚类分割算法允许每个像素点隶属于所有类别,并用隶属度函数表征其隶属程度,在一定程度上解决像素类属不确定性问题,是一种软划分算法。该类算法使用隶属度函数、非相似性测度及带有约束条件的惩罚项构建目标函数,形式灵活且易于引入约束条件。目前,主要通过添加相似度量惩罚项和模糊隶属度惩罚项作为约束条件调整图像像素归属。文献[12]通过定义包含空间信息和邻域信息的模糊要素增强对噪声和异常值的鲁棒性,进而提出模糊局部信息C均值聚类(Fuzzy Local Information C-Means clustering, FLICM)算法。文献[13]将KL(Kullback-Lerbler)信息引入模糊目标函数中,提出KL信息FCM(KL information FCM,KLFCM)算法,进而有效约束算法的聚类尺度,提高分割精度。但该算法采用欧氏距离衡量像素光谱测度与聚类的差异程度,对聚类尺度、形状、噪声和异常值均较为敏感。为了准确衡量特征空间中像素光谱测度与聚类的差异,文献[14]在KLFCM算法基础上以高斯分布的负对数定义非相似性测度,提出HMRF-FCM算法,有效提高了算法对聚类的识别能力以及对噪声和异常值的鲁棒性。文献[15]在HMRF-FCM算法基础上,引入特征场邻域模型,结合特征场和标号场邻域构建包含双邻域的模糊聚类模型,进一步提高了算法对噪声和异常值的鲁棒性。该类算法通过添加惩罚项作为约束条件,利用迭代最优化方法寻求最优解,但往往陷入局部最优,无法保证收敛到全局最优解。
谱聚类分割算法将聚类问题转化为无向图的最优划分问题。首先,通过建立图模型表达原始数据,构建无向图;而后,定义并优化划分准则,获取全局最优解。文献[16]采用不同尺度参数及随机采样的基于Nystrom逼近的谱聚类算法获得多种分割结果,并利用非负矩阵分解方法合并多种分割结果,获得较理想的分割结果。文献[17]引入Levin’s Affinity的权函数建立相似矩阵构造无向图,在此基础上采用线性映射实现数据降维,而后采用传统聚类分割算法实现图像分割。该类算法首先将高维数据降维,而后通过传统聚类分割算法分割低维数据,其分割过程本质仍为传统聚类分割算法,且图模型建立及分解过程增加了该类算法时间成本。
仿生模式识别依据同类样本在特征空间连续性分布的特性,利用多个同一几何形体覆盖每一类学习样本,以样本最佳覆盖为准则,实现监督分类[18]。为了充分利用图像各目标像素光谱测度在RGB特征空间中呈现椭球形分布的性质,提高算法对地物目标的识别能力,在RGB特征空间中将相似度较大的像素划分到同一聚类中。
本文类比仿生模式识别方法中“香肠模型”[19],采用椭球体包裹图像各类别目标主体,无需训练样本,实现图像自动化聚类分割。寻找包裹各类目标主体的最优椭球实质是确定椭球球心、三主轴方向及对应长度的过程。鉴于椭球体内特征点集各主成分方向与椭球主轴方向一致,利用主成分分析计算样本数据各主成分方向作为椭球体三主轴方向,并以样本数据均值作为椭球球心构建椭球体,而后扩充样本数据并不断更新椭球位置、姿态和形状,以寻找最优椭球。而后利用“交叉覆盖法”[20],即删除当前椭球内特征点,对余下特征点寻求下一目标主体最优椭球,如此交叉覆盖,直至各目标主体特征点全部被删除为止,最终实现图像粗分割。进一步利用图像空间的邻域关系,填充粗分割结果中未被椭球包裹的表征噪声和异常值的空洞区域,得到最终分割结果。
2 算法描述
假定X={x1, …, xi, …, xN}是一幅待分割彩色图像,其中i为像素索引,N为像素总数,xi=(xiR, xiG, xiB)T为第i个像素光谱测度矢量,xiR、xiG、xiB分别表示R、G、B三个波段的光谱反射强度,T表示转置。假设同一地物的像素具有相似的光谱测度,在RGB特征空间中则表征为具有明显聚集性的特征点集,且各类别特征点集大体呈椭球形分布[21]。为了更加清晰地表达提出算法识别目标主体的过程,生成如图1(a)所示合成图像,其大小为6![]() 64像素,分辨率为1 m。图1(b)中不同颜色散点表征各目标类别像素光谱测度均值矢量,不难看出,其在RGB特征空间的性质基本满足上述假设。表征相同地物的特征点具有明显的聚集性,表征不同类型地物的特征点之间差异较显著,且可用椭球包裹表征同一地物的目标主体(如图1(c))。椭球体外的特征点以及远离聚类的离散点与对应聚类的光谱特征差异较为明显,可视为噪声或异常值。
64像素,分辨率为1 m。图1(b)中不同颜色散点表征各目标类别像素光谱测度均值矢量,不难看出,其在RGB特征空间的性质基本满足上述假设。表征相同地物的特征点具有明显的聚集性,表征不同类型地物的特征点之间差异较显著,且可用椭球包裹表征同一地物的目标主体(如图1(c))。椭球体外的特征点以及远离聚类的离散点与对应聚类的光谱特征差异较为明显,可视为噪声或异常值。
假设各类别目标主体在RGB特征空间呈椭球形分布,为了有效区别不同地物,采用椭球体包裹各目标主体。已知椭球球心及三个主轴的方向和长度即可确定椭球位置和姿态,因此包裹各目标主体实际上是寻找椭球体球心、三个主轴最优方向及对应长度的过程。对椭球而言,球内变化最大的方向为其最长的主轴方向,其次为与最长主轴垂直的次长主轴方向,再次为与上述两主轴垂直的第三主轴方向。对特征点集而言,其第一主成分为特征点集方差变化最大的方向,第二主成分为特征点集方差变化次大的方向,第三主成分为特征点集方差变化第三大的方向。为了更好的包裹目标主体,椭球内特征点集的变化方向应与椭球各主轴的方向一致,即第一主成分方向对应椭球最长主轴方向,第二主成分方向对应椭球次长主轴方向,第三主成分方向对应椭球第三主轴方向。因此,可利用主成分分析计算样本数据第一到第三主成分方向,将其视为椭球体的三个主轴方向,并以样本数据均值作为椭球球心构建椭球体。随着样本数据逐渐增加,其各主成分方向逐渐逼近目标主体主成分方向,当样本数据趋于稳定,此时确定的椭球体即为最优椭球(如图1(d)所示)。具体操作如下:
为了准确定位并包裹目标主体,首先随机选取一个特征点作为代表点,并计算RGB特征空间中与该代表点最近的m个特征点作为初始样本数据(本文m=100)。由于RGB特征空间中,目标主体具有显著的聚集性,而噪声和异常值分布较为稀疏。为了保证样本数据为某一类别主体的子集而非噪声或异常值,当其方差小于给定阈值时,则接受样本数据,否则需重新初始化该代表点。而后,以样本数据几何中心为球心,以样本数据在各主成分方向投影的最短距离为直径,初始化球体。并在此基础上沿样本主成分方向将初始球体拓展为椭球体,并将椭球内特征点视为新的样本数据,直至包裹该类目标主体。假设当前椭球内有n个样本数据,该样本数据可表示为,
(1)
其中,xjl(τ)为第j类第l个像素的测度,j为聚类索引,τ为椭球拓展次数索引,l为当前椭球下隶属于第j类的像素索引。则样本数据均值矢量可计算为,
(2)
其协方差矩阵为,
(3)
基于样本数据协方差矩阵,进一步求解其特征值,并降序排列为:![]() 其中各特征值所对应的单位特征向量分别为
其中各特征值所对应的单位特征向量分别为![]() 和
和![]() 相应地,主成分分析变换矩阵可表达为,
相应地,主成分分析变换矩阵可表达为,
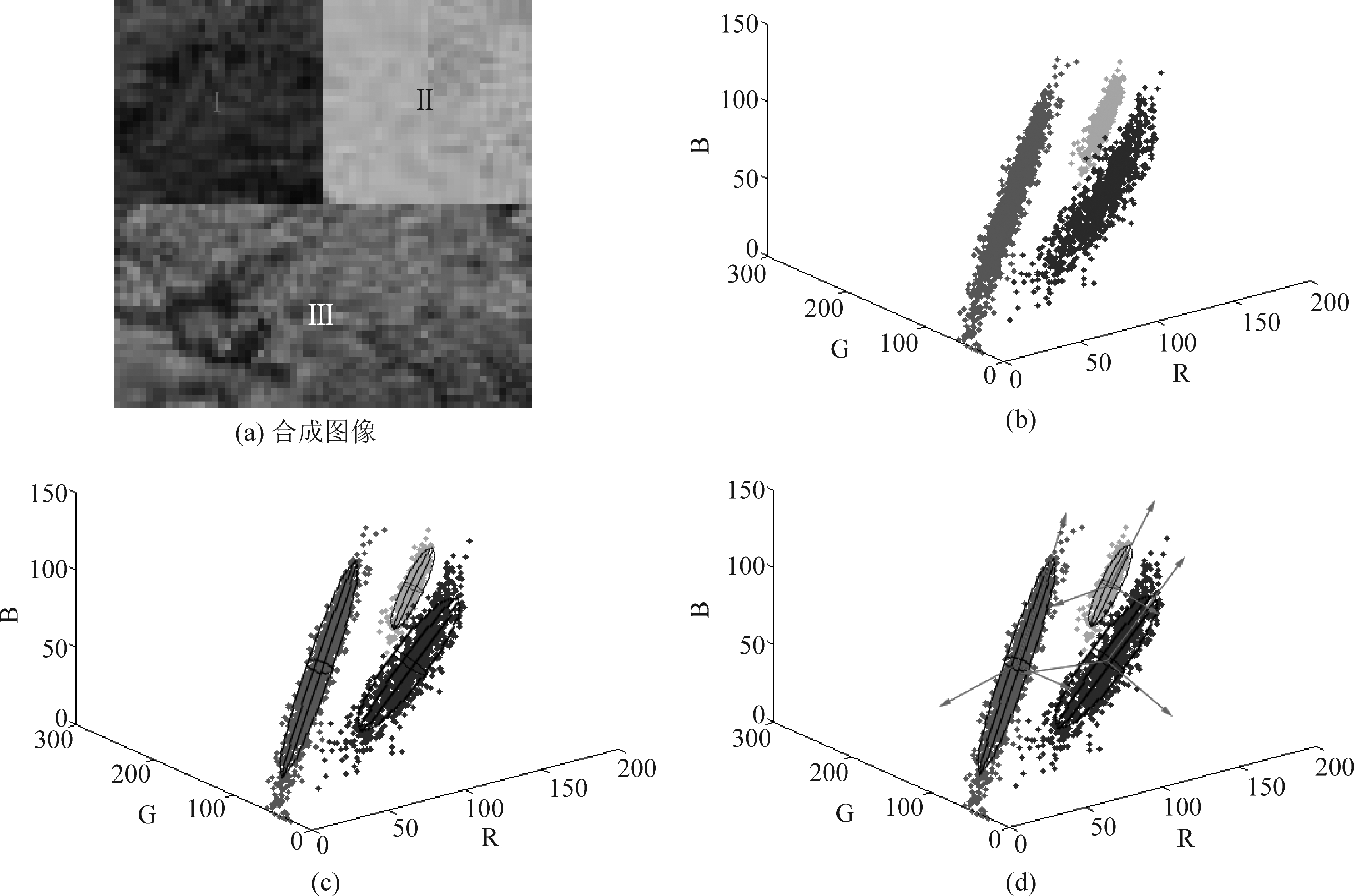
图1 合成图像及像素颜色在RGB特征空间的分布图
Fig.1 Synthetic image and distribution diagram of pixels in the RGB color feature space
(4)
其中,![]() 中各列为该样本数据的前三个主成分方向矢量,将其作为椭球主轴方向。为使扫描过程具有可行性,每次拓展椭球前需进行坐标系的旋转和平移,将坐标系原点平移至样本数据几何中心,各坐标轴方向旋转为样本数据主成分方向,即
中各列为该样本数据的前三个主成分方向矢量,将其作为椭球主轴方向。为使扫描过程具有可行性,每次拓展椭球前需进行坐标系的旋转和平移,将坐标系原点平移至样本数据几何中心,各坐标轴方向旋转为样本数据主成分方向,即
(5)
此时,椭球可表示为,
(6)
其中,u、 ν和![]() 分别为
分别为![]() 和
和![]() 方向(新坐标轴方向)上的变量,
方向(新坐标轴方向)上的变量,![]() 和
和![]() 分别为椭球三个轴的半长度。
分别为椭球三个轴的半长度。
沿![]() 的正负方向,以Δr个灰度级(本文定义为2)为步长,拓展当前椭球,则拓展后的椭球表达式为,
的正负方向,以Δr个灰度级(本文定义为2)为步长,拓展当前椭球,则拓展后的椭球表达式为,
(7)
分别统计公式(6)和(7)确定的椭球在![]() 轴正负方向半椭球内新增特征点的个数,若一侧方向半椭球内新增特征点的个数大于给定阈值(经验阈值为5~20,本文定义为5,普遍适用于中、小场景图像),则该方向新增特征点密集度较大,认定新增特征点和样本数据类属同一类别,接受该方向椭球半轴的延长,且将新增特征点转换为样本数据;否则该方向椭球半轴长度不变,无新增样本数据。当
轴正负方向半椭球内新增特征点的个数,若一侧方向半椭球内新增特征点的个数大于给定阈值(经验阈值为5~20,本文定义为5,普遍适用于中、小场景图像),则该方向新增特征点密集度较大,认定新增特征点和样本数据类属同一类别,接受该方向椭球半轴的延长,且将新增特征点转换为样本数据;否则该方向椭球半轴长度不变,无新增样本数据。当![]() 轴正负方向拓展均被接受时,该方向椭球轴长为
轴正负方向拓展均被接受时,该方向椭球轴长为![]() 当
当![]() 轴一侧方向拓展被接受时,该方向椭球轴长为
轴一侧方向拓展被接受时,该方向椭球轴长为![]() 否则,轴长
否则,轴长![]() 不变。而后以公式(6)所示椭球为基准,分别沿
不变。而后以公式(6)所示椭球为基准,分别沿![]() 方向拓展该椭球。
方向拓展该椭球。
沿椭球三个主轴方向拓展后,重新计算样本数据几何中心作为椭球球心,三个主成分方向作为椭球体三个主轴方向,并将延长后的主轴长度作为新的主轴长度,构建新的椭球体。因新椭球体球心位置及各主轴方向和长度的变化,使得部分特征点转换为样本数据、部分样本数据转换为未被包裹的特征点。在步长较小的前提下,新椭球所包裹的特征点与样本数据中特征点差异较小,这种差异可以忽略不计。扫描过程中通过不断重新计算样本数据主成分方向,逐渐调整椭球方向及大小,使其逼近目标主体。当椭球体各主轴方向及长度不再改变时,停止扫描,此时,样本数据即为目标主体。完成一类目标主体的扫描后,在不考虑该类目标主体的情况下,重新扫描下一类目标主体,设图像聚类数为C,直至所有C个目标主体均被识别出来。此时,特征空间中表示不同类别的特征点被有效区分开来,只余下一部分噪声和异常值。
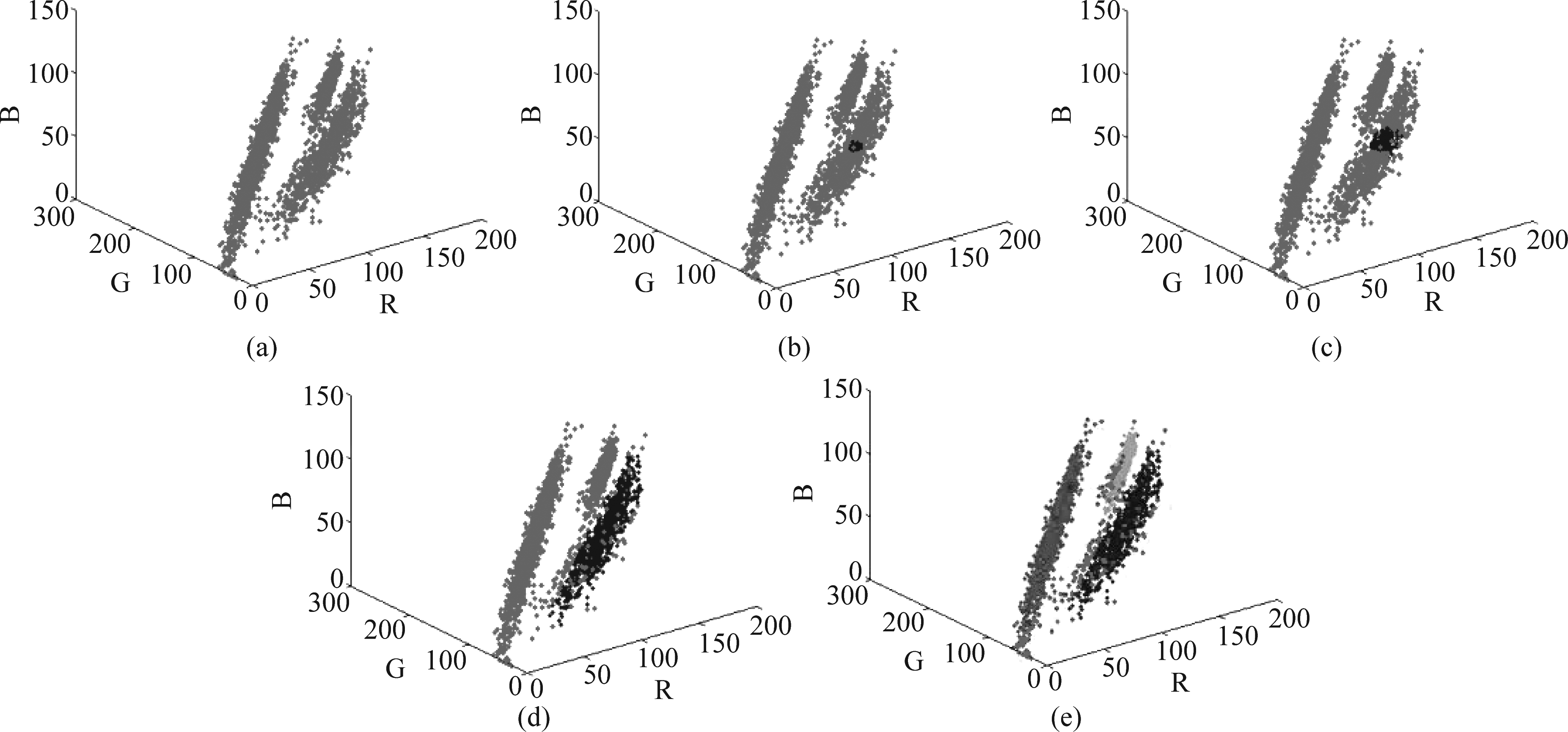
图2 扫描过程示意图
Fig.2 Scanning process diagram
为了清晰地表现算法扫描数据过程,选取部分具有代表性的扫描结果列于图2。其中,图2(a)为RGB空间特征点分布图,图2(b)~(d)为扫描过程中区域Ⅰ目标主体的识别情况,图2(b)中紫色点为初始化椭球体内包裹的特征点,大致位于该目标主体中间位置;图2(c)为209个特征点的扫描聚类结果;图2(d)为该类目标扫描结束后得到的目标主体(包含902个特征点),图2(e)为各类目标主体的扫描结果(包含3867个特征点)。不难发现,各类别目标主体在特征空间中可区分性较强,即使对于方差较大的目标主体,也能对其进行有效包裹。
将RGB特征空间各目标主体的扫描结果表达在图像空间,如图3(a)所示,不同类别目标主体能够被有效区分,而未被椭球包裹的噪声和异常值则表现为空洞(红色区域)。空洞区域表现为单像素或多像素构成的连通体,对粗分割结果进行二值化,应用连通区域标记算法检测空洞区域。图像空间中,相邻像素隶属于同一类别的可能性较大,故将空洞邻域区域的类别属性赋予空洞区域。假设Hk表示图像空间每个空洞的像素集合,其中k为空洞索引,则空洞区域标号表示为,
Lk=max{len(Hk∩Hk′)|k′为Hk邻接区域索引}
(8)
其中,Lk为空洞区域标号,len(Hk∩Hk′)表示空洞与其邻接区域相邻边界长度。遍历所有空洞区域,当其邻域区域只包含一类地物时,将该类别属性赋予空洞;当其邻域区域邻接多类地物时,将邻接边界最长的邻域区域类别属性赋予空洞。图3(b)为去除空洞区域后最终分割结果,虽然个别边界位置分割结果不甚理想,区域Ⅱ中像素误分为区域Ⅰ,但整体上看,跨越边界的空洞位置较少,不影响算法整体精度。

图3 分割结果
Fig.3 Segmentation results
3 实验结果
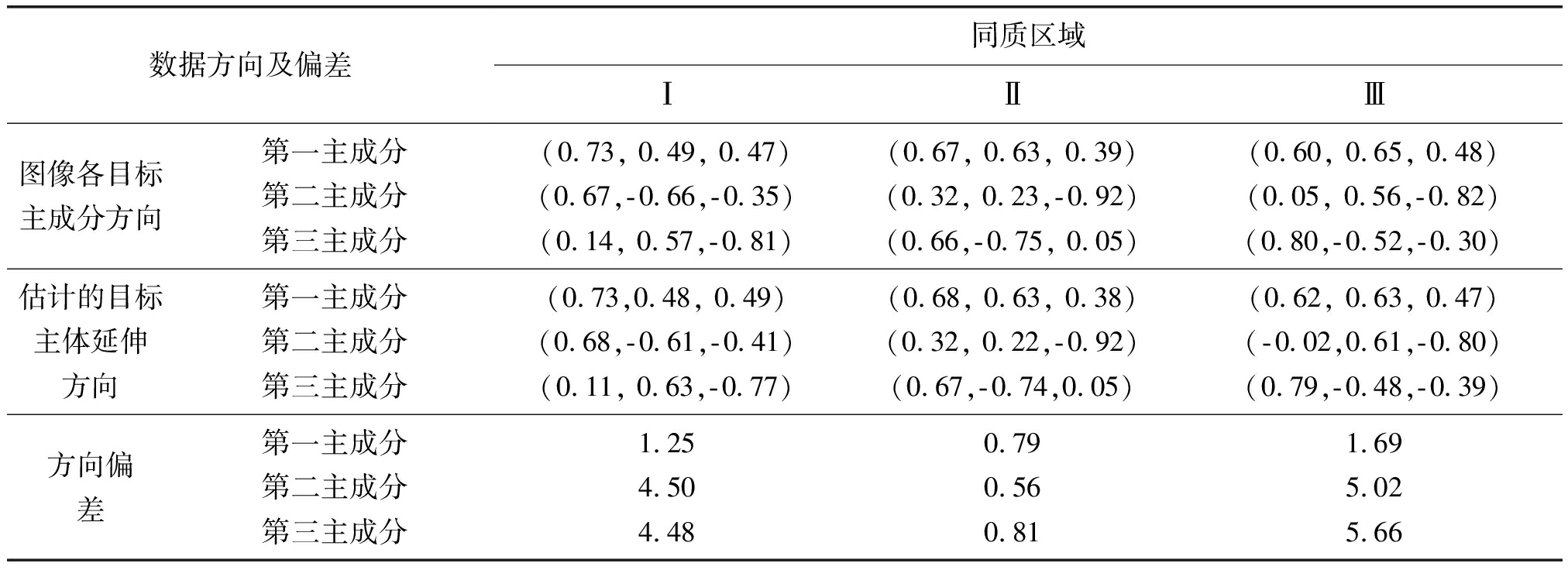
为了验证提出算法估计的目标主体主成分方向与该类目标真实主成分方向的差异,以图1(a)对应模板图像为标准,分别计算图像各目标主成分方向、估计的目标主体延伸方向及偏差(见表1)。不难发现,图像各目标真实主成分方向与估计主成分方向偏差较小,最大偏差不超过5.66°。其真实主成分方向与估计的目标主体主成分方向的差异主要受离散分布在目标主体周围的噪声以及随机分布在整个空间的异常值影响。而提出算法利用椭球只包裹目标主体,忽略RGB特征空间噪声和异常值。实验表明,利用上述方法估计的目标主体延伸方向能够趋近于目标主体的真实方向,进而利用椭球能够较为准确地包裹目标主体。
为了验证本文算法的有效性,根据图4(a)模板图像合成一幅高分辨率遥感图像(如图4(b)),该图像由2.5 m分辨率SPOT图像拼接而成,包含森林、水田、裸地、草地四种常见地物类别,对应图中区域Ⅰ-Ⅳ。

图4 模板图像与合成图像
Fig.4 Template image and synthetic image
K-means聚类算法作为最常用的动态聚类硬划分方法,先指定聚类数目并随机生成初始聚类中心,而后以像素到聚类中心欧式距离最小作为相似性准则进行逐像素聚类,并以各聚类均值矢量作为新的聚类中心,重新聚类,直至收敛。本文算法亦属于硬划分方法,指定聚类数目,并随机生成初始代表点,而后以特征点密集度作为相似性准则,进行像素聚类;模糊C均值(Fuzzy C-means Algorithm, FCM)算法[22]作为经典的模糊聚类分割算法,具有较为完备的理论基础,在图像分割领域应用广泛。该算法基于类内加权误差平方和构建目标函数,最小化目标函数准则下,进行像素聚类。本文算法在类内像素相似度大准则下识别目标主体,使各目标主体方差最小;结合马尔可夫高斯模型的双邻域模糊聚类分割算法(DNS-MGM)[15]为改进FCM算法的彩色图像分割算法,引入像素特征场和标号场的邻域关系,对噪声和异常值具有较强的鲁棒性。本文算法在特征场中识别各聚类目标主体,标号场中完善图像分割;改进的谱聚类彩色图像分割算法将无向图映射至低维空间,而后执行距离测度学习方法进行聚类。本文方法亦属于距离测度学习。分别使用K-means聚类算法、FCM算法、DNS-MGM算法、谱聚类算法及本文算法对合成图像进行分割实验,分割结果如图5所示。实验环境是Inter(R).Core(TM).i5- 4590.3.3GHz/4G内存/Matlab2013a。
传统的K-means聚类算法用像素到聚类中心的欧氏距离作为划分准则将像素划分到距离最近的聚类中心;FCM算法用欧氏距离定义像素与聚类的相似性测度,但欧氏距离只适用于RGB特征空间中聚类呈球形分布的图像,对噪声和异常值敏感。因此,对于方差较大的森林、水田及草地区域,图5(a)和(b)分割结果中包含大量误分像素。DNS-MGM算法同时考虑特征场和标号场邻域作用,改进的谱聚类彩色图像分割算法在构造无向图时考虑邻域像素相关性,二种算法都能够在一定程度上提高算法对噪声和异常值的鲁棒性,故图5(c)和图5(d)分割结果略优于K-means算法和FCM算法。而原始图像(如图4(b))中森林、水田及草地区域,噪声和异常值在图像中呈现聚集性(即区域性),采用邻域关系无法有效削弱其影响,因而森林区域分割结果中误分明显,本文算法依据图像不同地物类别在RGB特征空间自然聚类,而噪声表现为远离聚类的孤立点或孤立点集的特性,采用椭球体包裹表征不同类型地物的目标主体,获取包含空洞的图像粗分割结果。并在粗分割结果的基础上,结合区域邻域关系填补空洞,进而实现图像分割。算法粗分割过程能够忽略噪声影响,并通过填补空洞操作获得最终分割结果,对噪声和异常值不敏感,故图5(e)分割结果明显优于上述算法。
表1 主成分方向及偏差(°)
Tab.1 Principal component directions and deviation(°)
数据方向及偏差同质区域ⅠⅡⅢ图像各目标主成分方向第一主成分第二主成分第三主成分(0.73, 0.49, 0.47)(0.67,-0.66,-0.35)(0.14, 0.57,-0.81)(0.67, 0.63, 0.39)(0.32, 0.23,-0.92)(0.66,-0.75, 0.05)(0.60, 0.65, 0.48)(0.05, 0.56,-0.82)(0.80,-0.52,-0.30)估计的目标主体延伸方向第一主成分第二主成分第三主成分(0.73,0.48, 0.49)(0.68,-0.61,-0.41)(0.11, 0.63,-0.77)(0.68, 0.63, 0.38)(0.32, 0.22,-0.92)(0.67,-0.74,0.05)(0.62, 0.63, 0.47)(-0.02,0.61,-0.80)(0.79,-0.48,-0.39)方向偏差第一主成分第二主成分第三主成分1.254.504.480.790.560.811.695.025.66
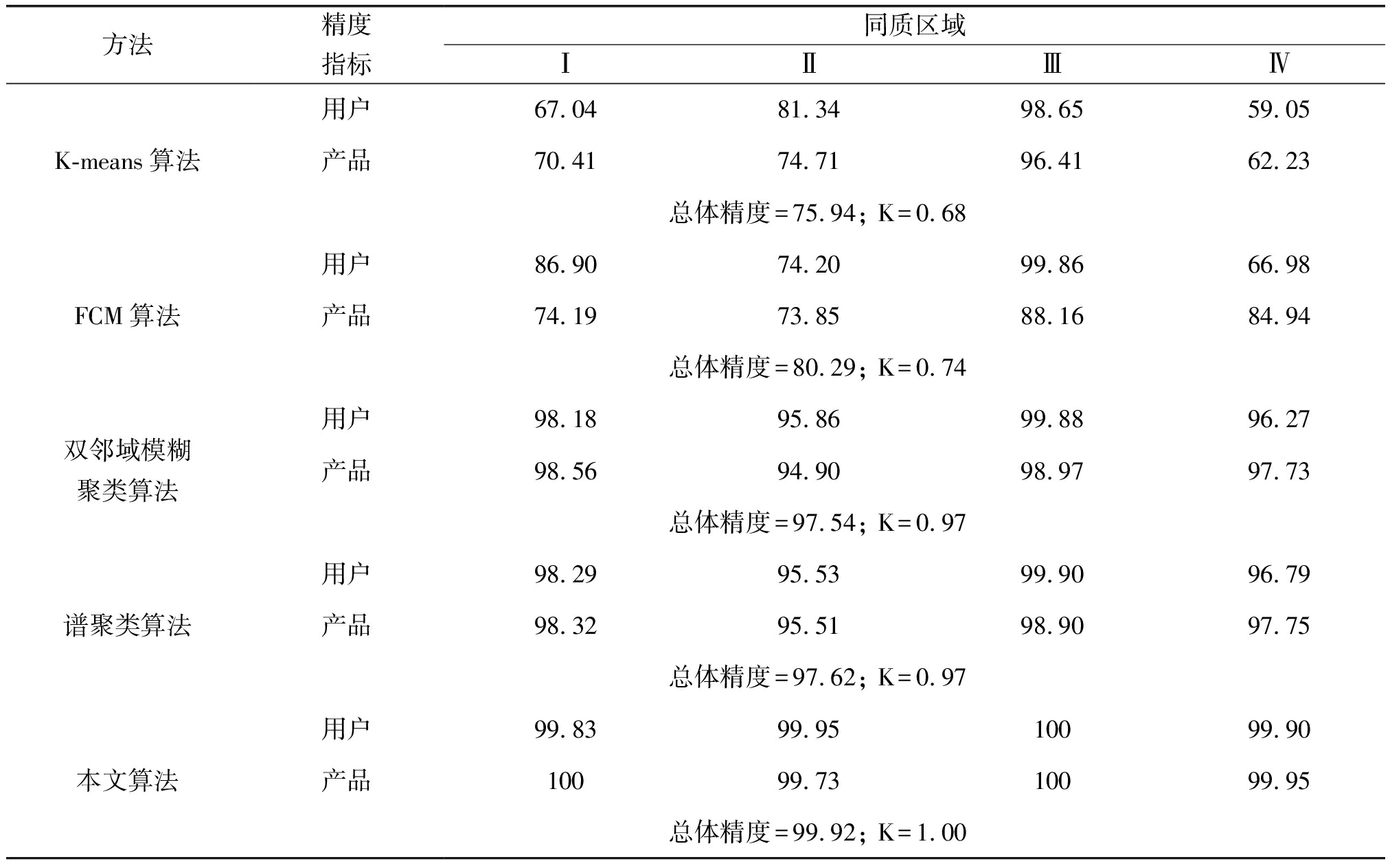
以图4(b)对应模板图像(如图4(a))为标准,分别计算上述分割结果的产品精度,用户精度、总精度和Kappa(K)系数(见表2),其中,用户精度为正确分类与所有分为该类的像素数的比值;产品精度为正确分类与参考数据中该类像素数的比值;总体精度为被正确分类的像素数总和除以总像素数;Kappa(K)系数表征实验分割结果与标准分割结果一致性。从表2不难看出,K-means算法和FCM算法无论用户精度、产品精度、总精度以及Kappa系数均低于后三种算法,在类内方差较小的裸地区域,用户精度及产品精度较高,能达到88%以上。而对于类内方差较大的森林、水田及草地区域误分现象明显,产品精度和用户精度偏低,无法满足实际生产需求。DNS-MGM算法和谱聚类算法引入邻域像素关系,算法精度及Kappa系数均高于K-means和FCM算法。但对于类内方差较大的地物类别,基于像素邻域关系无法有效削弱噪声和异常值影响,导致森林、水田、裸地及草地区域均包含不同程度的误分像素。本文算法依据图像在RGB特征空间自然聚类特性,采用椭球体包裹各类别特征点,且在标号场中实现噪声和异常值的分类,因此本文算法精度更高,总体精度可达99.92%,Kappa系数甚至为1。
为进一步验证本文算法有效性,选取五幅彩色高分辨率WORLDVIWE-2、IKONOS图像,如图6所示,同质区域个数为3、3、4、4、4,包含农田、草地、道路、裸地、森林等地物类别。分别用K-means聚类算法、FCM算法、DNS-MGM算法、谱聚类算法及本文算法进行分割实验。

图5 K-means算法、FCM算法、DNS-MGM算法、谱聚类算法和本文算法分割结果
Fig.5 K-means, FCM, DNS-MGM, spectral clustering and proposed algorithm segmentation results

图6 真实高分辨率彩色图像
Fig.6 Real high resolution images
表2 算法精度(%)及Kappa(K)系数
Tab.2 Algorithm accuracy and Kappa coefficient
方法精度指标同质区域ⅠⅡⅢⅣK-means算法用户67.0481.3498.6559.05产品70.4174.7196.4162.23总体精度=75.94; K=0.68FCM算法用户86.9074.2099.8666.98产品74.1973.8588.1684.94总体精度=80.29; K=0.74双邻域模糊聚类算法用户98.1895.8699.8896.27产品98.5694.9098.9797.73总体精度=97.54; K=0.97谱聚类算法用户98.2995.5399.9096.79产品98.3295.5198.9097.75总体精度=97.62; K=0.97本文算法用户99.8399.9510099.90产品10099.7310099.95总体精度=99.92; K=1.00
图8(a1)~(a5)、(b1)~(b5)、(c1)~(c5)、(d1)~(d5)和(e1)~(e5)分别为K-means聚类算法、FCM算法、DNS-MGM算法、谱聚类算法和本文算法分割结果。不难发现,图6(e)中各地物类内方差较小,因此,各算法均能较完整地分割该图像(如图8(a5)~(e5))。但K-means聚类算法、FCM算法、DNS-MGM算法和谱聚类算法分割结果中均含有少量误分像素,结果不及本文算法。K-means聚类算法和FCM算法仅利用像素强度信息分割图像,不考虑邻域像素相关性,对于类内方差较大的地物类别,其分割结果中误分现象明显(如图8(a1)~(a4)、(b1)~(b4))。DNS-MGM算法和谱聚类算法考虑邻域像素相关性,一定程度地增强了对噪声和异常值的鲁棒性,但误分现象仍然明显,图8(c1)分割结果中,各类地物均存在误分现象;图8(d1)分割结果中,大量草地区域误分为裸地;图8(c2)、(d2)、(c3)和(d3)分割结果中,误分现象较为明显;图8(c4)分割结果中,部分森林区域误分为草地,不同种类草地区域间误分现象明显;图8(d4)分割结果中,包含有区域性噪声,将部分裸地区域和草地区域误分为森林。本文算法能够有效消除噪声和异常值影响,分割结果较为理想。图8(e1)中利用区域邻域像素相关性填补空洞,使得森林及裸地区域几乎无误分像素,图8(e2)和图8(e3)分割结果中,各地物类别分割结果均较为完整。图8(e4)分割结果中,少量森林区域误分为草地区域。整体看来,本文算法优于其他各类算法。
以图6对应的模板图像(如图7)为标准,分别计算图8中各算法分割结果的总体精度、Kappa系数及平均精度(见表3)。不难看出,K-means算法和FCM算法总体精度及Kappa系数偏低,总体精度均值低于84%,Kappa系数均值不高于0.75;DNS-MGM算法和谱聚类算法分割精度较K-means算法和FCM算法有所提高,总体精度均值达到92%,Kappa系数均值达到0.88。相比之下,本文算法无论总体精度还是Kappa系数均高于其他算法,其总体精度可达95%,Kappa系数甚至为0.93。
图9(a1)~(a5)为本文算法粗分割结果,不难发现本文算法能够识别不同类别目标主体,进一步结合图像空间邻域关系填补空洞区域,能够得到理想分割结果。

图7 标准分割结果
Fig.7 Standard segmentation results

图8 K-means算法、FCM算法、DNS-MGM算法、谱聚类算法和本文算法分割结果
Fig.8 K-means, FCM, DNS-MGM, spectral clustering and proposed algorithm segmentation results
表3 总精度(%)及Kappa(K)系数
Tab.3 Total accuracy and Kappa coefficient
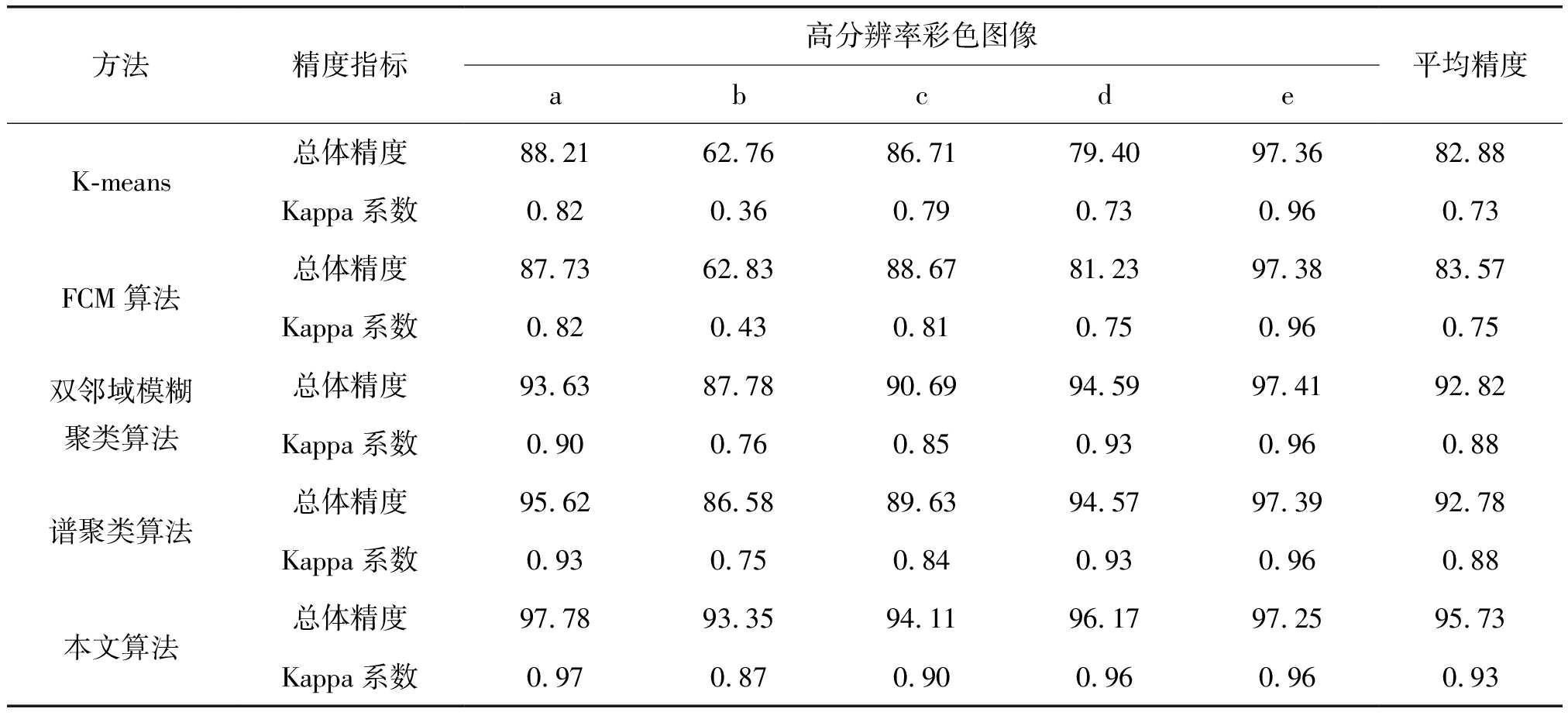
方法精度指标高分辨率彩色图像abcde平均精度K-means总体精度88.2162.7686.7179.4097.3682.88Kappa系数0.820.360.790.730.960.73FCM算法总体精度87.7362.8388.6781.2397.3883.57Kappa系数0.820.430.810.750.960.75双邻域模糊聚类算法总体精度93.6387.7890.6994.5997.4192.82Kappa系数0.900.760.850.930.960.88谱聚类算法总体精度95.6286.5889.6394.5797.3992.78Kappa系数0.930.750.840.930.960.88本文算法总体精度97.7893.3594.1196.1797.2595.73Kappa系数0.970.870.900.960.960.93

图9 粗分割结果
Fig.9 Coarse segmentation results
4 结论
本文基于图像各目标在RGB特征空间自然聚类,噪声和异常值随机分布在整个空间的特性,利用主成分分析估计目标主体延伸方向,并沿该方向扫描特征点,从而将目标主体包裹在椭球体内部,而后在图像空间结合邻域相关性填补空洞,进而提出基于扫描聚类的遥感图像分割算法。该算法忽略RGB特征空间噪声和异常值的影响,通过邻域相关性填补图像上未被RGB特征空间椭球体包裹而产生的空洞,能够得到较为理想的分割结果。实验表明,文本算法对RGB特征空间中较复杂的聚类,尤其对于方差较大的地物类别也能够准确的估计其目标主体延伸方向,实现各类别特征点聚类划,且算法对噪声和异常值具有较强的鲁棒性。此外,算法通过初始样本数据特征判断代表点的有效性,其分割结果不受代表点选取的影响。
[1] 孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48- 61.
Sun J G, Liu J, Zhao L Y. Clustering algorithms research[J]. Journal of Image Software, 2008, 19(1): 48- 61. (in Chinese)
[2] 王慧贤, 靳惠佳, 王娇龙,等. K均值聚类引导的遥感影像多尺度分割优化方法[J]. 测绘学报, 2015, 44(5): 526-532.
Wang H X, Jin H J, Wang J L, et al. Optimization approach for multi-scale segmentation of remotely sensed imagery under k-means clustering guidance[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 526-532. (in Chinese)
[3] Likas A. The global k-means clustering algorithm[J]. Pattern Recognition, 2003, 36(2): 451- 461.
[4] Jarvis R A, Patrick E A. Clustering using a similarity measure based on shared nearest neighbors[J]. IEEE Transactions on Computers, 1973, 22(11): 1025-1034.
[5] Guha S, Rastoga R Shim K. An efficient clustering algorithm for large databases[J]. Information Systems, 2001, 26(1): 35-58.
[6] 赵泉华, 李晓丽, 赵雪梅, 等. 结合Voronoi划分HMRF模型的模糊ISODATA图像分割[J]. 信号处理, 2016, 32(10): 1233-1243.
Zhao Q H, Li X L, Zhao X M, et al. Fuzzy ISODATA image segmentation integration Voronoi tessellation HMRF model[J]. Journal of Signal Processing, 2016, 32(10):1233-1243. (in Chinese)
[7] 湛西羊, 李良群, 张富有. 融入局部信息的直觉模糊核聚类图像分割算法[J]. 信号处理, 2017, 33(3): 397- 405.
Zhan X Y, Li L Q, Zhang F Y.An intuitionistic kernel-based fuzzy C-means clustering algorithm with local information for image segmentation[J]. Journal of Signal Processing, 2017, 33(3): 397- 405. (in Chinese)
[8] Kong W, Hu S, Zhang J, et al. Robust and smart spectral clustering from normalized cut[J]. Neural Computing and Applications, 2013, 23(5): 1503-1512.
[9] 徐海霞, 田铮, 丁明涛. 基于谱聚类与混合模型的SAR图像多尺度分割[J]. 中国图像图形学报, 2010, 15(3): 450- 454.
Xu H X, Tian Z, Ding M T. Multiscale segmentation for SAR image based on spectral clustering and mixture model[J]. Journal of Image and Graphics, 2010, 15(3): 450- 454. (in Chinese)
[10] 李翠, 冯冬青. 基于改进K-均值聚类的图像分割算法研究[J]. 郑州大学学报, 2011, 43(1): 109-114.
Li C, Feng D Q. A Distributed data mining system based on mobile agent and data mining standards[J]. Journal of Zhengzhou University, 2011, 43(1): 109-114. (in Chinese)
[11] Ward J H. Hierarchical grouping to optimize an objective function[J]. Journal of the American Statistical Association, 1963, 58(301): 236-244.
[12] Krinidis S M, Chatzis V. A robust fuzzy local information c-means clustering algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328-1337.
[13] Ichihashi H, Miyagishi K, Honda K. Fuzzy c-means clustering with regularization by K-L information[C]∥Proceedings of the 10th IEEE International Conference on Fuzzy System, 2001: 924-927.
[14] Chatzis S P, Varvarigou T A. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation[J]. IEEE Transactions on Fuzzy System, 2008, 16(5): 1351-1361.
[15] 赵雪梅, 李玉, 赵泉华. 结合马尔可夫高斯模型的双邻域模糊聚类分割算法[J]. 计算机辅助设计与图形学学报, 2016, 28(4): 614- 622.
Zhao X M, Li Y, Zhao Q H. A fuzzy clustering image segmentation algorithm with double neighborhood system combined with Markov Gaussian model[J]. Journal of Computer Aided Design & Computer Graphics, 2016, 28(4): 614- 622. (in Chinese)
[16] 邓晓政, 焦李成, 卢山. 基于非负矩阵分解的谱聚类集成SAR图像分割[J]. 电子学报, 2011, 39(12): 2905-2909.
Deng X Z, Jiao L C, Lu S. Spectral clustering ensemble applied to SAR image segmentation using nonnegative matrix factorization[J]. Acta Electronica Sinica, 2011, 39(12): 2905-2909. (in Chinese)
[17] 钱素静, 彭宏京, 刘越. 一种改进的谱聚类彩色图像分割方法[J]. 小型微型计算机系统, 2013, 34(6): 1413-1416.
Qian S J, Peng H J, Liu Y. A color image segmentation approach based on improved spectral clustering[J]. Journal of Chinese Computer Systems, 2013, 34(6): 1413-1416. (in Chinese)
[18] 王守觉. 仿生模式识别(拓扑模式识别)——一种模式识别新模型的理论与应用[J]. 电子学报, 2002, 30(10): 1417-1420.
Wang S J. Bionic(Topological) pattern recognition—a new model of pattern recognition theory and its applications[J]. Acta Electronica Sinica, 2002, 30(10): 1417-1420. (in Chinese)
[19] 王守觉, 曹宇, 赵星涛. 仿生模式识别[J]. 中国人工智能学会第10届全国学术年会, 2009.
Wang S J, Cao Y, Zhao X T. Biomimetics pattern recognition[J]. Chinese Association for Artificial Intelligence, 2009. (in Chinese)
[20] 张玲,张钹, 殷海风. 多层前向网络的交叉覆盖设计算法[J]. 软件学报, 1999, 10(7): 737-742.
Zhang L, Zhang B, Yin H F. An alternative covering design algorithm of multi-layer neural networks[J]. Journal of Software, 1999, 10(7): 737-742. (in Chinese)
[21] 欧春江. 实例分析遥感图像处理中的主成分分析[J]. 测绘与空间地理信息, 2006, 29(5): 56-59.
Ou C J. Research on principal component analysis of remote sensing images processing through example[J]. Geomatics & Spatial Information Technology, 2006, 29(5): 56-59. (in Chinese)
[22] Bezdek J. Pattern recognition with fuzzy objective function algorithm[M]. New York: Plenum, 1981: 79- 88.



