1 引言
随着移动通信的快速发展，频谱效率和系统容量等方面的需求日益增长。传统的多址方式已经不能满足发展需要，于是业内提出了一种新的多址方式，即NOMA(non-orthogonal multiple access，非正交多址接入)。作为面向5G的关键技术之一，NOMA通过对同时同频上的用户分配不同的功率，实现功率域的多用户共享，使无线接入总量提高了50%[1]。现有研究表明NOMA 可以比 OMA(orthogonal multiple access，正交多址接入)获得更高的系统容量和更高的频谱效率[2]，因此NOMA系统中的功率分配问题近年来引起学术界的广泛关注。
针对NOMA系统中的功率分配算法的研究，目标函数主要集中在总发射功率最小化[3-5]、中断概率最小化[6-9]、和系统吞吐量最大化[10-13]等方面。现有算法主要FSPA(full search power allocation，全空间搜索算法)[14]、FPA(fixed power allocation，固定功率分配算法)[14]、 IWPA(iterative water-filling power allocation，迭代注水功率分配算法)[15]以及FTPA(fractional transmit power allocation，分数阶发射功率分配算法)[16]。张德坤[14]在非正交多址系统功率分配及干扰消除算法研究中指出，FSPA通过搜索所有的用户对功率分配组合，能够实现非正交多址系统的最佳性能，但FSPA存在高复杂度的问题并且系统开销比较大，故实际系统中一般不予采用；FPA虽然复杂度较低，但是系统性能受功率分配因子的影响较大，且通常不能达到系统的最佳性能。赵蕊[15]在非正交多址系统的研究中指出，IWPA可以实现较好功率分配性能，但其存在局部最优及高复杂度的问题。Satio Y[16]等人提出了FTPA算法，FTPA平衡了低信噪比用户的公平性并且降低了接收端译码的复杂度，但是FTPA是局部最优化方案，并且系统性能同样受到所选功率分配因子的影响，因此FTPA方案还有待进一步完善。
由于共轭梯度法计算复杂度与最速下降法相当，但是收敛速度优于最速下降法[17]，所以本文提出一种基于共轭梯度法的快速功率分配方案，其复杂度低于FSPA，系统性能优于FPA和FTPA，实现了复杂度与系统性能折中。
2 NOMA系统功率分配优化模型
2.1 NOMA系统性能
假设系统发送端采用单天线发射模式，同时同频资源块上，系统调度N个用户，基站将发送给N个用户的信号经过功率分配后，在功率域进行线性叠加，则发送的等价复基带信号可以表示为：
(1)
其中，s1、s2、…和sN分别是发送给用户1、用户2、…用户N的能量归一化信号(Es1=1,Es2=1,…,EsN=1)； β1、 β2、…和βN是功率分配因子，满足
通常距离基站越远的用户会被分配更大的功率。
经过无线信道，用户n(1≤n≤N)的接收信号为：
yn=hnx+wn
(2)
其中，hn是信道系数，wn是包含小区干扰的高斯白噪声，服从均值为0，方差为
的复高斯分布。
在NOMA下行链路的接收端，用户采用干扰消除接收机进行检测。当其他用户解码之后，就可以对本用户的干扰进行消除，从而实现正确译码。以两个用户为例，假设用户1远离基站端，则会对用户1分配更大的功率，在接收端，对用户1可以直接解码出所需信号x1。对于用户2，需要先解码出用户1的信号x1，再通过接收到的信号y2减去x1的相关成分。因此用户2解码信号x2时就已经去除了x1的干扰，从而可以实现信号的正确解码。
基于以上分析，对基于SIC接收机的NOMA系统，假设有N个用户，从用户1到用户N，用户与基站的距离逐渐减小。利用香农公式，可以分别得到每个用户的可达容量，假设分配给用户n的功率分配因子为βn，则用户n的可达容量为：
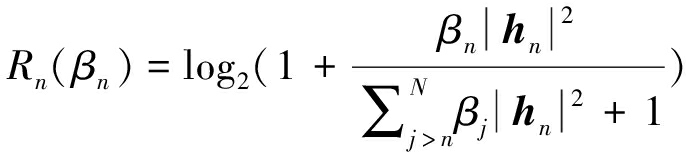
(3)
为保证用户调度的公平性，采用加权和速率Rsum最大化为用户功率分配的准则[18]：
(4)
以上问题可以总结为如下优化函数：
(5)
s.t. 0≤βN≤βN-1≤…≤β1≤1
对上式求极值即可得到最优功率分配因子。为了解决此有约束优化问题，本文先采用内点惩罚函数法[19]将其转化为无约束最优化问题，后采用共轭梯度下降法求最优解。令β=[β1β2…βN]T。
2.2 无约束最优化的目标函数
惩罚函数法中的内点罚函数法是将新目标函数定义于可行域内，这样它的初始点以及后面产生的迭代点序列也必定在可行域内，对可能脱离可行域的点给予惩罚，相当于在可行域的边界上设置一道障碍，阻止迭代点穿越到可行域之外，因此内点罚函数法也称为障碍函数法。将式(5)中改写为如下形式：
(6)
s.t. βn-1≤0,n=1,…,N
βn+1-βn≤0,n=1,…,N-1
-βn≤0,n=1,…,N
则可以构造如下目标函数：
(7)
其中，um是惩罚因子，是递减的正数序列，即：
(8)
通常取um=1.0，0.1，0.01…。内点惩罚函数法收敛的终止准则如下：
(9)
(10)
其中
为惩罚因子为um时，无约束优化的最优点。
3 共轭梯度下降法
共轭梯度法是求解优化问题的一类有效算法，它的迭代公式可以写为：
βk+1=βk+αkdk
(11)
其中，αk由某种线性搜索决定，已有的搜索算法包括精确线性搜索[20]和近似线性搜索方法如：Wolfe线性搜索[20]、Armijo线性搜索[20]和Goldstein线性搜索[20]等。L Grippo等人[21]证明了采用Armijo线性搜索时共轭梯度法中的PRP算法[22]的全局收敛性。故本文采用Armijo线性搜索算法，求最小的非负整数h，使得步长因子αk=ρh满足下列条件：
(12)
其中ρ∈(0,1)，δ>0。dk为第k次的搜索方向，由以下计算公式得出：
(13)
其中gk=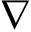
f(βk)是函数f在点βk处的梯度。参数γk的选取满足共轭性，现有的共轭梯度法包括：FR算法[22]、PRP算法、HS算法[22]、CD算法[22]和DY算法[22]。本文中选取PRP算法计算γk值，γk的定义如下：
(14)
其中
是欧式范数。
综上所述，基于共轭梯度法的无约束功率分配方案的步骤如下：
(1)给定可行域内初始点β0，ε>0；计算g0=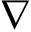f(β0)，令k=0。
(2)若
停止迭代；否则，令d0=-g0。
(3)按照精确线性搜索求步长因子αk；
更新βk+1=βk+αkdk，k=k+1。
(4)计算gk=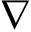f(βk)，若
停止迭代；否则转步骤(5)。
(5)利用式(9)计算γk，dk=-gk+γkdk-1。
(6)若
则令β0=βk，并转向步骤(1)；否则转向步骤(3)。
增加约束条件后，基于共轭梯度法的有约束功率分配方案的步骤如下：
(1)给定可行域内初始点β0，以及u0、c、计算精度ε1、ε2，令m=0。
(2)调用以上无约束优化方法，求f的最优解
和
(3)运用终止准则判断是否收敛，若收敛，停止迭代，有约束功率分配方案最优点为
若不收敛，则令
并转入第(2)步继续计算。
4 算法仿真与性能分析
假设信道服从瑞利衰落，仿真两用户模型的系统性能。当用户1的发射功率SNR1=10 dB，用户1和用户2的信噪比差SNR2-SNR1分别为10 dB、20 dB、30 dB和40 dB时，本文算法的加权和速率Rsum随功率分配因子的变化情况如图1所示。由图可见，(1)功率分配因子的选取直接影响加权和速率的大小；(2)在用户1的信噪比固定时，随着两用户信噪比差值的增大，最佳功率分配因子逐渐减小，这也表明远端用户会被分配更多的功率，这是因为本文采用的准则是用户调度公平性原则；(3)用户间信噪比的差值越大，系统的加权和速率越大。
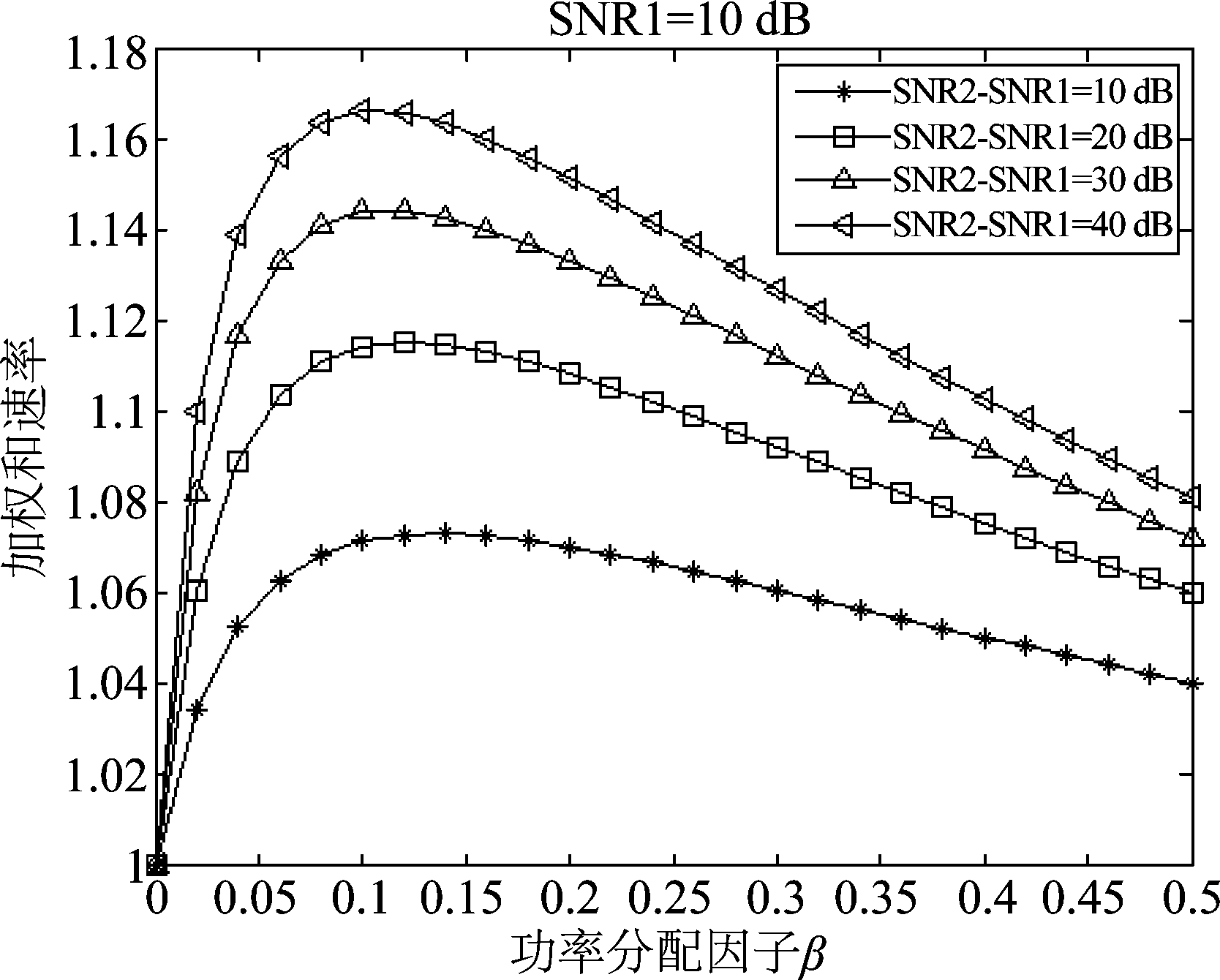
图1 加权和速率与功率分配因子β及用户信噪比的关系(SNR1=10 dB)
Fig.1 The relationship between weighted sum rate and power allocation factor β and user signal-to-noise ratio (SNR1=10 dB)
当用户间信噪比差值固定(SNR2-SNR1=20 dB)，改变用户1信噪比，SNR1分别为2 dB、4 dB、6 dB、8 dB和10 dB时，本文算法的加权和速率随功率分配因子的变化曲线如图2所示。由图可以看出，当用户间信噪比差值固定时，加权和速率随用户1信噪比的增大而增大。这是因为用户间信噪比差值固定、用户1信噪比的增大时，对应的用户2信噪比也增大，因此二个用户的等效信道条件都变好，因此加权和速率就增大。
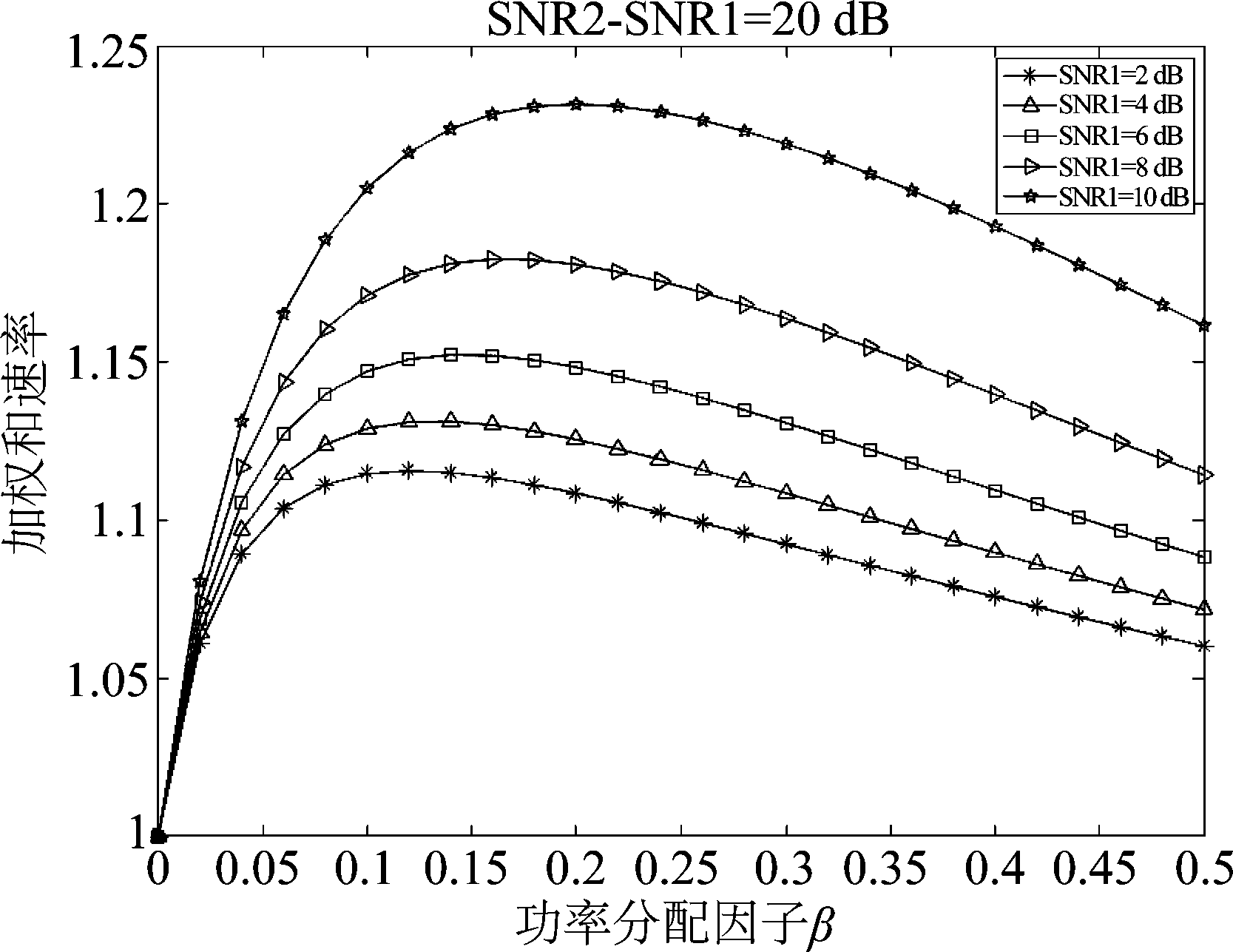
图2 加权和速率与功率分配因子β及用户信噪比的关系(SNR2-SNR1=20 dB)
Fig. 2 The relationship between weighted sum rate and power allocation factor β and user signal-to-noise ratio (SNR2-SNR1=20 dB)
当用户数为2并且SNR1=5 dB，应用本文算法、FPA算法[11]以及FTPA算法[13]的NOMA系统的加权和速率随SNR2的变化曲线如图3所示。当用户数为3、4、5、6、7时，应用本文算法、FPA算法以及FTPA算法的NOMA系统的加权和速率随用户数的变化曲线如图4所示。由图3、图4可得，随着用户2信噪比的增加，等效信道条件变好，三种算法的系统加权和速率都会增加。由于本文算法寻优能力更强，所以本文算法性能明显优于FPA算法和FTPA算法，并且随着用户数的增多，本文算法性能略有提高，而FPA和FTPA算法由于没有充分考虑边缘用户的影响，其系统加权和速率会逐渐下降，所以本文算法的优势会更加明显。
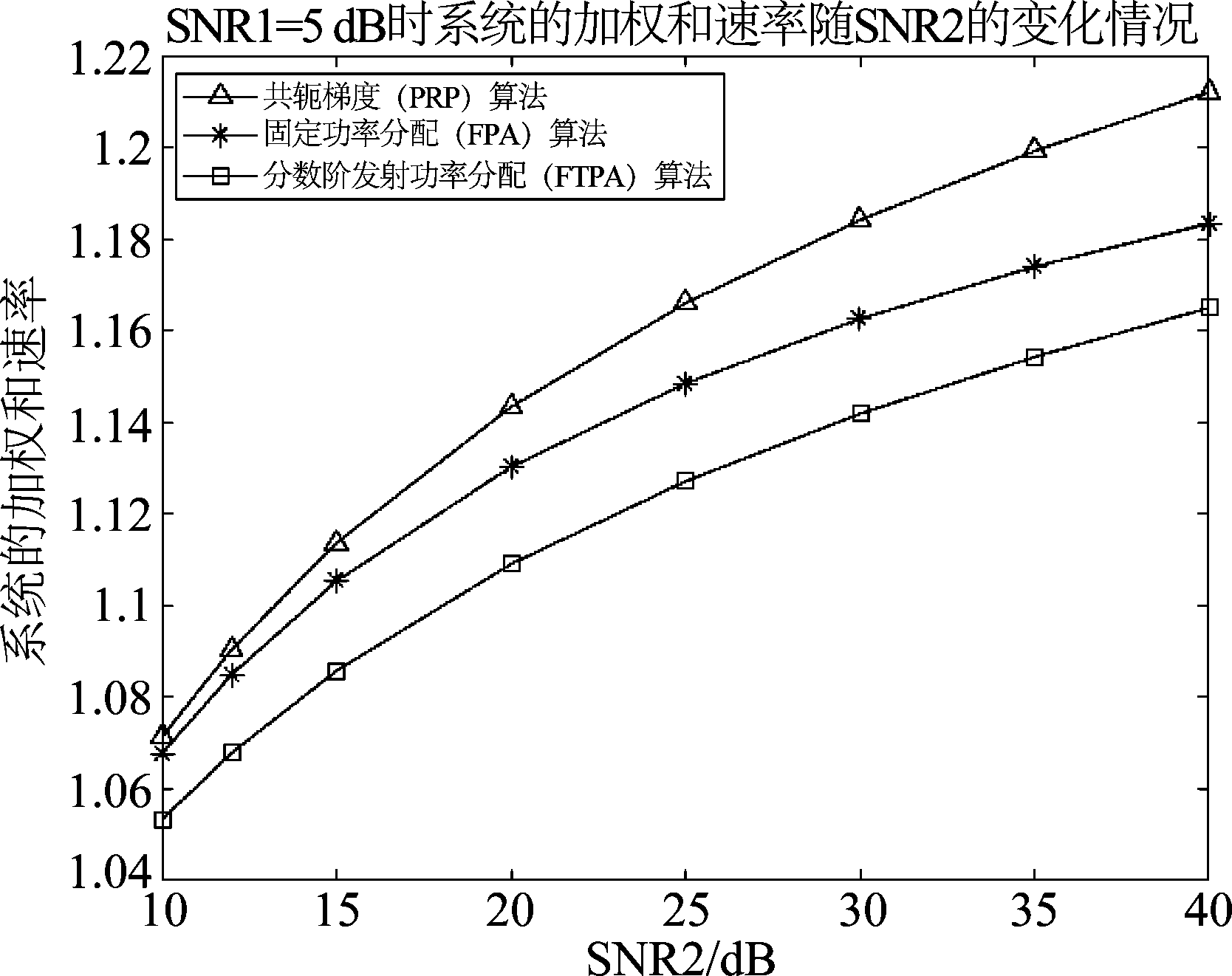
图3 SNR1=5 dB时三种算法的加权和速率随SNR2的变化情况
Fig.3 The weighted sum rate of the three algorithms varies with SNR2 when SNR1=5 dB
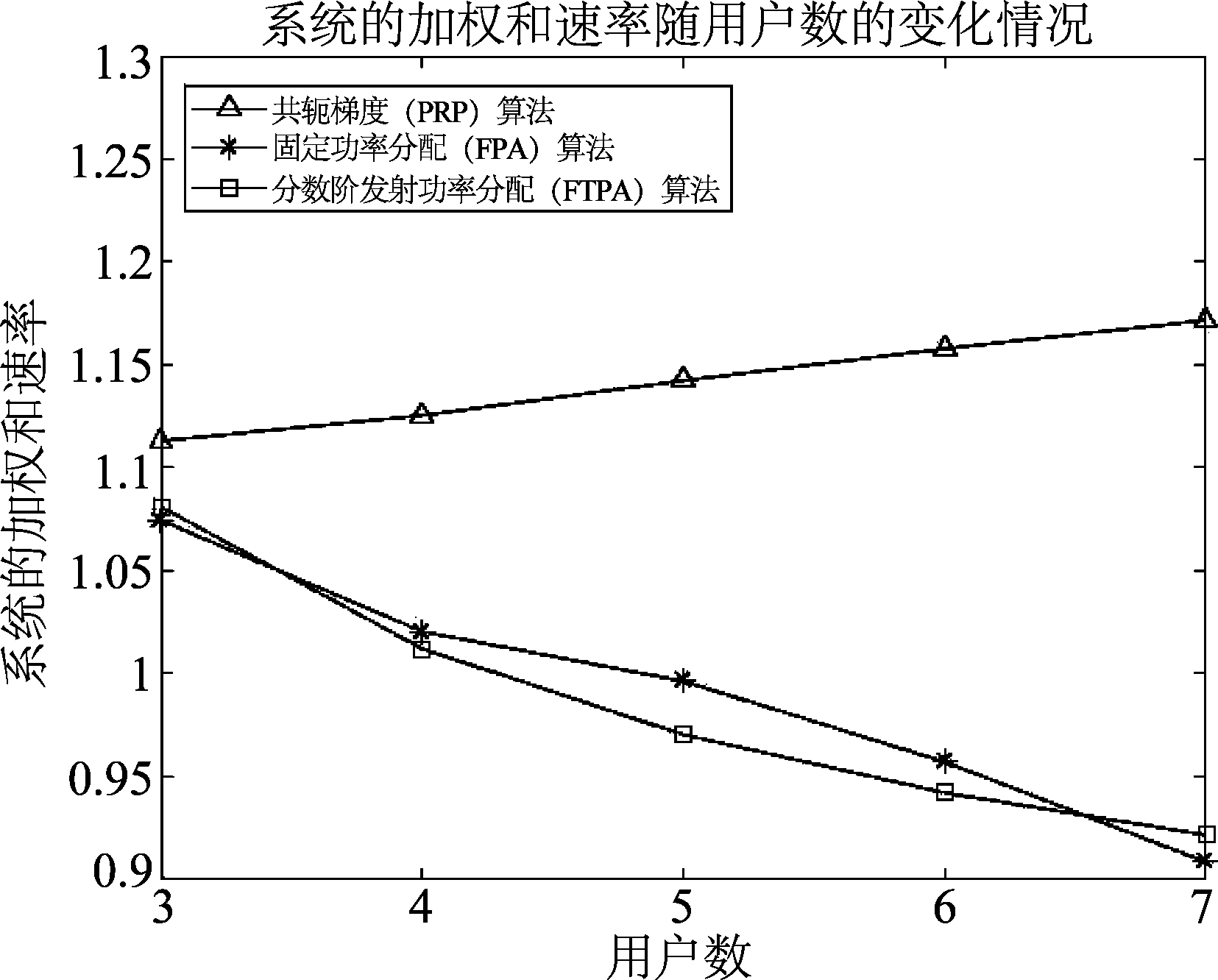
图4 三种算法的加权和速率随用户数的变化情况
Fig.4 The weighted sum rate of the three algorithms varies with the number of users
当用户数为2并且SNR1=5 dB，应用本文算法的NOMA系统及OMA系统的和速率随SNR2的变化曲线如图5所示。当用户数为3、4、5、6、7时，应用本文算法的NOMA系统及OMA系统的和速率随用户数的变化曲线如图6所示。由图5、图6可得，相比于正交多址系统，非正交多址系统性能得到了明显提升。
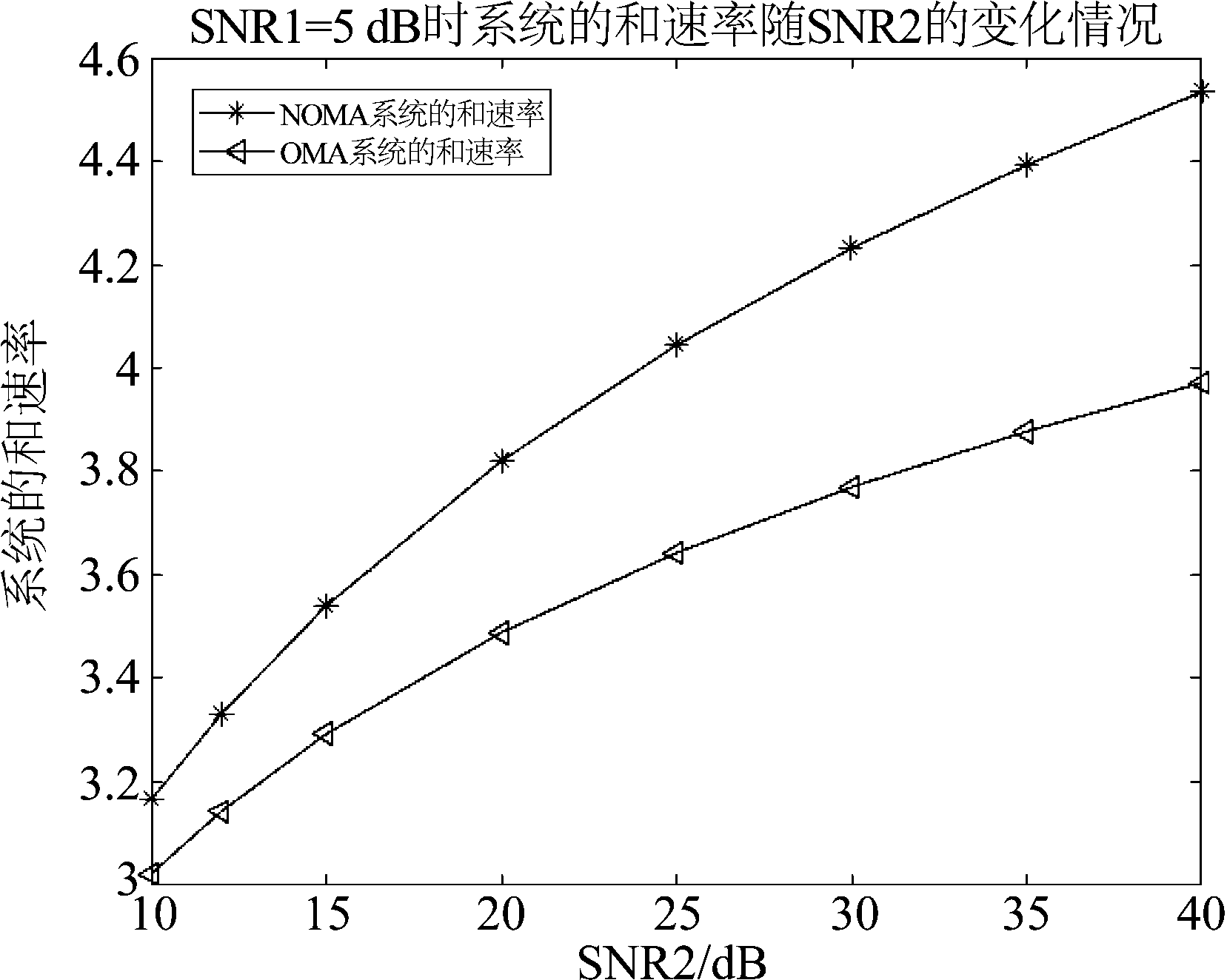
图5 SNR1=5 dB时NOMA系统及OMA系统的和速率随SNR2的变化情况
Fig.5 The change of the sum rate of NOMA system and OMA system with SNR2 when SNR1=5 dB
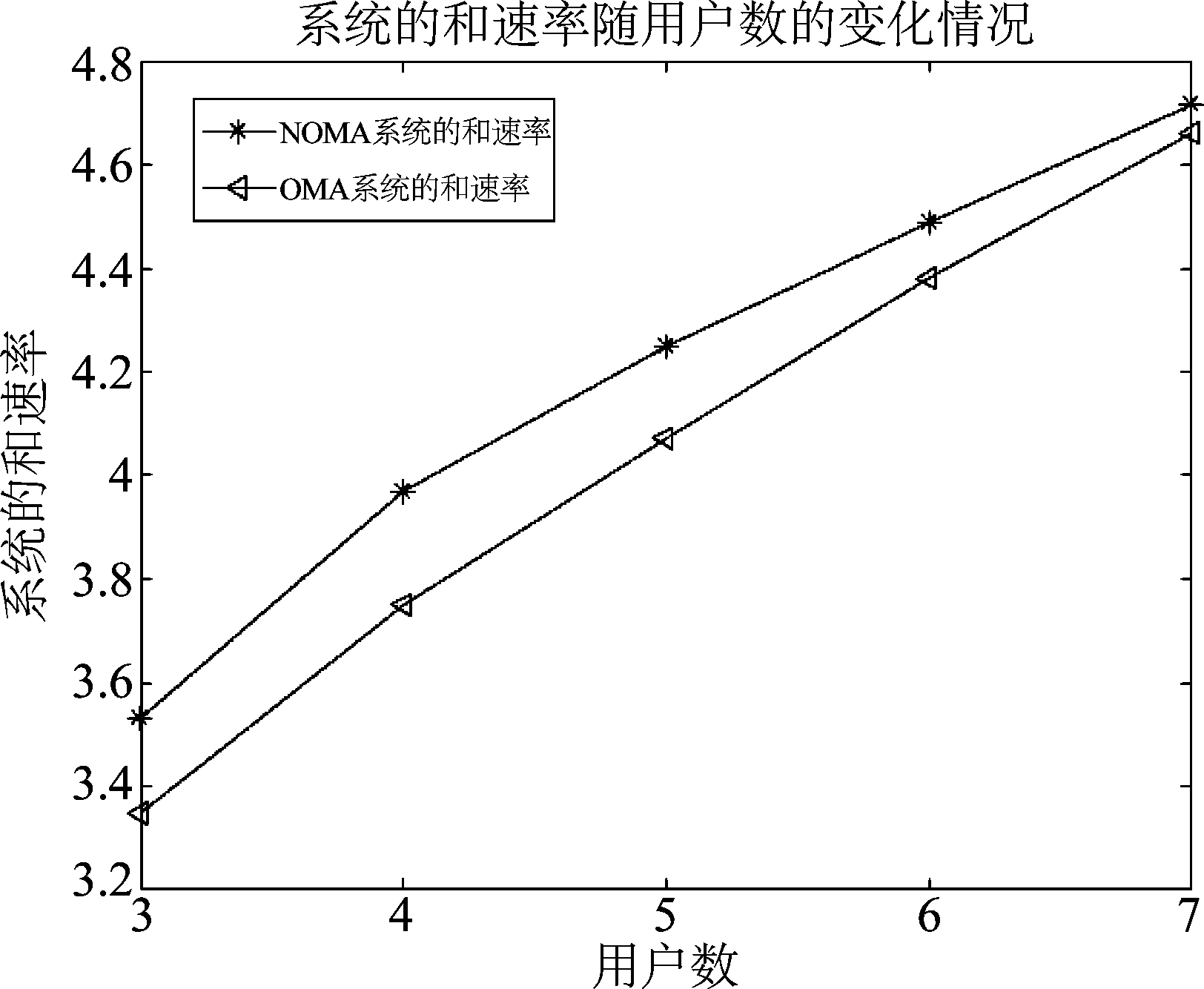
图6 NOMA系统及OMA系统的和速率随用户数的变化情况
Fig.6 The change of the sum rate of NOMA system and OMA system with the number of users
5 结论
针对5G的NOMA系统中的功率分配问题，本文提出了一种基于共轭梯度法的功率分配方案，在保证收敛速度的同时，可以使加权和速率达到最大化。仿真结果证明了本方法性能的优越性。
[1] 张长青.面向5G的非正交多址接入技术(NOMA)浅析[J].邮电设计技术，2015，11：49-53.
Zhang Changqing. Initial analysis of NOMA for 5G mobile networks[J]. Designing Techniques of Posts and Telecommunications, 2015,11:49-53. (in Chinese)
[2] 徐鑫,金梁.NOMA系统中基于协作干扰的物理层安全方案[J].信号处理,2017,33(6): 836- 844.
Xu Xin, Jing Liang. Physical layer security schemes based on cooperative jamming for non-orthogonal multiple access system[J]. Journal of Signal Processing, 2017,33(6):836- 844. (in Chinese)
[3] Dawadi R, Parsaeefard S, Derakhshani M, et al. Power-efficient resource allocation in NOMA virtualized wireless networks[C]∥2016 IEEE Global Communications Conference. IEEE, 2016:1- 6.
[4] Wei Zhiqiang, Ng D W K, Yuan Jinhong. Power-efficient resource allocation for MC-NOMA with statistical channel state information[C]∥2016 IEEE Global Communications Conference. IEEE,2016: 1-7.
[5] Li Xunan, Li Chong, Jin Ye. Dynamic resource allocation for transmit power minimization in OFDM-based NOMA systems[J]. IEEE Communications Letters, 2016, 20(12): 2558-2561.
[6] Cai Wenbo, Chen Chen, Bai Lin, et al. User selection and power allocation schemes for downlink NOMA systems with imperfect CSI[C]∥2016 IEEE 84th Vehicular Technology Conference. IEEE, 2016: 1-5.
[7] Liu Xin, Wang Xianbin, Liu Yanan. Power allocation and performance analysis of the collaborative NOMA assisted relaying systems in 5G[J]. China Communications, 2017, 14(1): 50- 60.
[8] Yang Zheng, Ding Zhiguo, Fan Pingzhi, et al. A general power allocation scheme to guarantee quality of service in downlink and uplink NOMA systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7244-7257.
[9] 李小娅,谢显中,雷维嘉,等.具有功率分配因子的不可信中继系统的中断性能和遍历保密容量[J].信号处理, 2014,30(11): 1349-1356.
Li Xiaoya, Xie Xianzhong, Lei Weijia, et al. Outage performance and ergodic secrecy capacity for untrusted relay networks with power allocation factor[J]. Journal of Signal Processing, 2014,30(11): 1349-1356. (in Chinese)
[10] Yang Zhaohui, Xu Wei, Pan Cunhua, et al. On the optimality of power allocation for NOMA downlinks with individual QoS constraints[J]. IEEE Communications Letters, 2017, 21(7): 1649-1652.
[11] Sun Yan, Ng D W K, Ding Zhiguo, et al. Optimal joint power and subcarrier allocation for MC-NOMA systems[C]∥2016 IEEE Global Communications Conference. IEEE, 2016: 1- 6.
[12] Chen Zhiyong, Ding Zhiguo, Dai Xuchun, et al. An optimization perspective of the superiority of NOMA compared to conventional OMA[J]. IEEE Transactions on Signal Processing, 2017, 65(19):5191-5202.
[13] 谭锴,朱琦.基于能量采集的译码转发中继系统功率分配算法[J].信号处理, 2017,33(6):887- 893.
Tan Kai, Zhu Qi. The algorithm of power allocation in decode-and-forward relaying system with energy harvesting[J]. Journal of Signal Processing, 2017,33(6): 887- 893. (in Chinese)
[14] 张德坤.非正交多址系统功率分配及干扰消除算法研究[D].哈尔滨：哈尔滨工业大学,2015.
Zhang Dekun. Research on power allocation and interference elimination algorithms for non-orthogonal multiple access system[D]. Harbin: Harbin Institute of Technology, 2015. (in Chinese)
[15] 赵蕊.非正交多址技术中功分多址的研究[D].北京：北京邮电大学，2015.
Zhao Rui. Research on power allocation in non-orthogonal multiple access[D]. Beijing: Beijing University of Posts and Telecommunications, 2015. (in Chinese)
[16] Saito Y, Benjebbour A, Kishiyama Y, et al. System-level performance evaluation of downlink non-orthogonal multiple access(NOMA)[C]∥IEEE International Symposium on Personal Indoor & Mobile Radio Communications. IEEE,2013:611- 615.
[17] 孙峰，龚晓玲，张炳杰,等.一种基于共轭梯度法的广义单隐层神经网络[J].郑州大学学报:工学版,2018(2):28-32.
Sun Feng, Gong Xiaoling, Zhang Bingjie, et al. An efficient generalized single-hidden layer neural networks based on conjugate gradient method[J]. Journal of Zhengzhou University: Engineering Science, 2018(2):28-32. (in Chinese)
[18] Schaepperle J, Ruegg A. Enhancement of Throughput and Fairness in 4G Wireless Access System by Non-Orthogonal Signaling[J]. Journal of Bell Labs Technical, 2009,13(4):59-77.
[19] Zhu Zhibin. A feasible interior-point algorithm for nonconvex nonlinear programming[J]. Applied Mathematics & Computation, 2005, 163(2):745-753.
[20] 张立卫.最优化方法[M].北京：科学出版社，2010：51-72.
Zhang Liwei. Optimization method[M]. Beijing: Science Press, 2010:51-72. (in Chinese)
[21] Grippo L, Lucidi S. A globally convergent version of the Polak-Ribière conjugate gradient method[J]. Mathematical Programming, 1997, 78(3):375-391.
[22] Antoniou A, Lu Wusheng. Practical Optimization, Algorithms and Engineering Applications[M]. New York: Springer, 2007:187-210.
