1 引言
正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)[1]技术由于频谱利用率高、抗多径能力强、实现方便等优点，已成为水声通信、移动通信、短波通信等领域的关键技术之一。在非合作通信条件下，对接收OFDM信号的子载波数进行估计，是准确恢复信息的重要前提，因此，有效估计实际使用子载波数一直是研究人员关注的问题，目前已取得了一些重要成果：Liedtke. F[2]利用倒谱法估计，但仅适用于信号质量较高的情况；付哥佳[3]引入小波函数对倒谱法进行改进，提高了一定的输出峰值与估计精度；郑文秀[4]则引入了高阶循环累积量的方法，但不适用于子载波数较多和子载波间隔较小的情况；李国汉[5]基于KS距离进行估计，低信噪比下误差较大。总体看来，在信号变弱的情况下，上述方法均会出现不同程度的性能下降，如何在低信噪比条件下实现微弱OFDM信号子载波数的有效估计，已成为本领域亟待探索的研究课题。
近年来，随着非线性动力学和统计物理理论的发展，随机共振(Stochastic Resonance，SR)理论及相关技术引起通信领域的日益关注。随机共振能够将噪声的部分能量转化为有用信号的能量，使得系统输出的局部信噪比有了较高的提升[6]，在微弱信号检测等领域取得了不少丰硕成果，为精准、高效提取强噪声背景中的目标信号提供了新的思路。本文以高斯白噪声信道为例，研究了低信噪比下微弱OFDM信号的子载波数检测问题，提出了一种基于随机共振的改进方法。该方法在倒谱法及其小波改进法的基础上，利用随机共振方法对微弱OFDM信号进行带内能量的增强和带外噪声的抑制，从而进一步增强频谱的等波纹周期性，不仅增大了检测的峰值和精度，而且降低了检测的信噪比门限，较大程度地提升了对OFDM信号子载波数估计的算法性能，在低信噪比的情况下凸显了一定的优势。
2 基本理论
2.1 OFDM子载波数估计方法
OFDM采用重叠子载波调制技术[7]，在频域把信道分成多路正交子信道，其基本思想是把高速数据流由串行变为N路低速的子数据流，用它们调制N个子载波，并分别在N路子信道上进行并行传输。其具体实现可以利用离散傅里叶变换进行[8]，后来诞生了离散傅里叶变换的快速算法，便采用IFFT/FFT进行调制与解调。在信号的调制过程中，可以产生与IFFT点数N相同数目的正交并行子载波，而在实际应用中，只是选择部分子载波传输信号，其原理如图1所示，第三方接收则需要对实际使用子载波的个数进行估计[9]。
图1 OFDM信号子载波分配示意
Fig.1 OFDM signal subcarrier distribution
2.1.1 倒谱法
倒谱法是对频谱的一种二次分析方法，它将卷积变为求和，从而达到分离特征的目的，可以用来分析语音信号中的基音周期等参数，由于OFDM信号具有等波纹的特殊频谱形状，因此可以利用倒谱法对其实际子载波数进行估计。基本思路如下：
设接收信号为x(n)，其Z变换为
对
取对数log，再进行逆Z变换，得到其倒谱为：
(1)
实际应用中，计算倒谱则是利用FFT/IFFT实现的，FFT实际上是对Z变换在单位圆上的取样，因此有如下公式：
C(q)=IFFT(log(|FFT(x(n))|))
(2)
其中，q被称为倒频率。利用式(3)和(4)即可计算子载波数M：
(3)
(4)
其中，η为信号采样率与带宽的比值。
倒谱法估计子载波数的过程如图2：首先，利用Welch谱估计[10]方法对接收到的OFDM信号进行预处理，这是对数据分段交叠并加窗作FFT的一种功率谱估计方法，相比对信号直接作FFT而言，可有效降低估计方差；然后取对数，进行IFFT；最后对输出的倒谱进行谱峰检测，从而估计出实际的子载波数。
图2 倒谱法
Fig.2 Method of cepstrum
2.1.2 小波改进倒谱法
一般情况下，利用Welch法得到的功率谱中往往会存在很多有干扰谐波，求倒谱后，峰值的阈值并不是很高，因此可以使用小波函数进行改进，将与子载波带宽不一致的分量滤除，尽可能减少干扰，突出IFFT之后的峰值。
利用Haar小波，其离散的表示为WTha(a,k)，将其与Welch功率谱取对数之后的结果进行卷积，得到Z(k)，表示为下式：
Z(k)=log(X(k))*WTha(a,k)
(5)
小波改进倒谱法的具体流程如图3所示，Haar小波处理环节增加在IFFT之前，其余环节与倒谱法一致。
图3 小波改进倒谱法
Fig.3 Improved method of cepstrum based on wavelet transform
小波改进法虽然是对倒谱法的提升，但由于Haar系数必须要由预估的子载波带宽来确定(具体参考文献[3])，增加了一定的复杂度，而倒谱法算法简单，容易实现，两种方法各有优势，因此，本文对这两种传统方法都进行了基于随机共振的改进，实际应用时视具体情况选择合适的方法即可。
2.2 随机共振理论2.2.1 朗之万方程
双稳态系统是一类典型的非线性系统，其可由Langevin方程[5]表示：
(6)
式中a和b为双稳态系统的参数，s(t)=Acos(2πf0t+φ)为被检测信号，A为信号幅值， f0为信号频率，Γ(t)为均值为0、噪声强度为D高斯白噪声，〈Γ(t)〉=0，〈Γ(t)Γ(0)〉=2Dδ(t)，其中〈·〉为时间平均。
随机变量x的概率分布函数ρ(x,t)遵循Fokker-Planck方程[11]：
(7)
式中初始条件为ρ(x,t0|x0,t0)=δ(x-x0)。由式(7)分析知，系统的输出状态受输入Acos(2πft)影响，势垒ΔU=a2/4b越高，系统在势阱中暂留的时间越多。当噪声促使微弱输入信号在两个势阱中不断改变时，系统的切换速度与输入同频，因此存在系统与信号的周期量程匹配问题。
在Fokker-Planck方程中，存在时变项
解析方法无法得到定态解，也不能得到任何解的表达式，因此需要近似手段来处理这一方程，主要便是绝热近似理论[12]和采用微扰展开方法的线性响应理论[13]。
2.2.2 绝热近似理论
对于双稳态系统，定义n±(t)为时刻t系统处于稳态±xm的概率。当系统的平衡在输入信号周期驱动力的作用下被破坏，导致势阱间跃迁行为的出现，定义W±(t)为时刻t系统从稳态±xm跃迁的概率，可得关于n±(t)的方程：
n'/±(t)=-W±(t)n±(t)+W∓(t)n∓(t)
(8)
处于两个势阱的概率n±(t)满足：
n±(t)+n∓(t)=1
(9)
当信号的频率f很小时，可认为系统在势阱中到达平衡状态所用的时间远远小于势阱之间概率整体平衡所用的时间，也远远小于系统随着输入信号的变化所用的时间，这就是绝热近似。在绝热近似条件下，Fokker-Planck方程(7)在长时间后将演进为n+(t)和n-(t)之间的概率交换。
在绝热近似条件下，即输入信号频率远小于rK，同时输入信号幅值A和噪声强度D≪1，即f≪rK，A≪1,D≪1。式中rk为Kramers跃迁率：
(10)
经过相关理论(参考文献[11]、[12])推导，可得系统输出功率谱：
[δ(ω-ω0)+δ(ω+ω0)]
(11)
其中
由式(11)，输出功率的能量由噪声能量GN(ω)和信号能量GS(ω)两部分组成。因此双稳态随机共振系统输出信号功率谱与系统参数a,b，噪声强度D，输入信号频率f，幅值A等均有关系，但是系统输出总功率为
没有因为随机共振过程改变。也说明了随机共振过程中，噪声能量和信号能量发生了相互转化，功率谱的信号部分出现峰值。
2.2.3 归一化处理
为了突破绝热近似理论对输入必须满足小参数的限制，引入以下变量对其进行归一化[14]处理：
(12)
带入式(6)得：
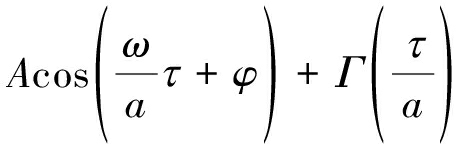
(13)
其中Γ(t)变换为Γ(τ/a)即为Γ(t)在时域上进行a倍拉伸，也相当于在频域上进行1/a倍的压缩，但白噪声拉伸或压缩，并不影响其功率值，因为它在所有频率上都为定值。噪声Γ(τ/a)满足〈Γ(τ/a)Γ(0)〉=2Dδ(τ)，因此有
其中ξ(τ)满足〈ξ(τ)〉=0，〈ξ(τ)ξ(0)〉=δ(τ)，即均值为0，方差为1的白噪声。式(13)可进一步化简：
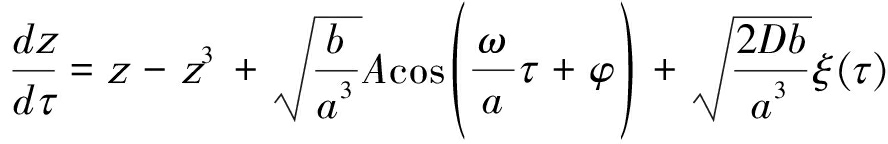
(14)
归一化处理对信号频率进行压缩，对信号与噪声的幅度进行同比例缩放，即突破了小参数的制约，可处理大参数信号，使随机共振能够被广泛应用于更多的实际信号。
3 随机共振在微弱OFDM信号子载波数估计中的算法实现
由于随机共振能够有效地将噪声能量转移到信号中，且对单频周期信号的频率谱线具有较好的增强作用，而在OFDM信号子载波数的倒谱估计方法中，正是利用了其等波纹频谱的周期性，因此设想利用随机共振来加强其频谱中的周期成分，再利用倒谱法及小波改进法进行检测，提高检测性能。
改进算法的处理流程如图4所示，首先，设置高采样率接收OFDM信号，高采样率是为了避免随机共振输出发散，一般至少高于50倍的信号最高频率[6]。其次，利用随机共振对信号处理，由于随机共振产生的条件较为苛刻，只有选取了合适的系统参数，才可以产生最佳随机共振，本文利用孔德阳提出的ASRASN算法[15-16]来确定系统参数，此算法是根据信号载波频率的数量级确定出系统参数的大致范围，并在此范围内根据人工鱼群算法，结合归一化原理选取最佳参数。最后，利用倒谱法及其小波改进法计算参数。
在实际处理中，利用四阶Runge-Kutta方程[12]将连续的差分方程转变为离散的数值求解，迭代步长h取采样率Fs的倒数，即h=1/Fs。
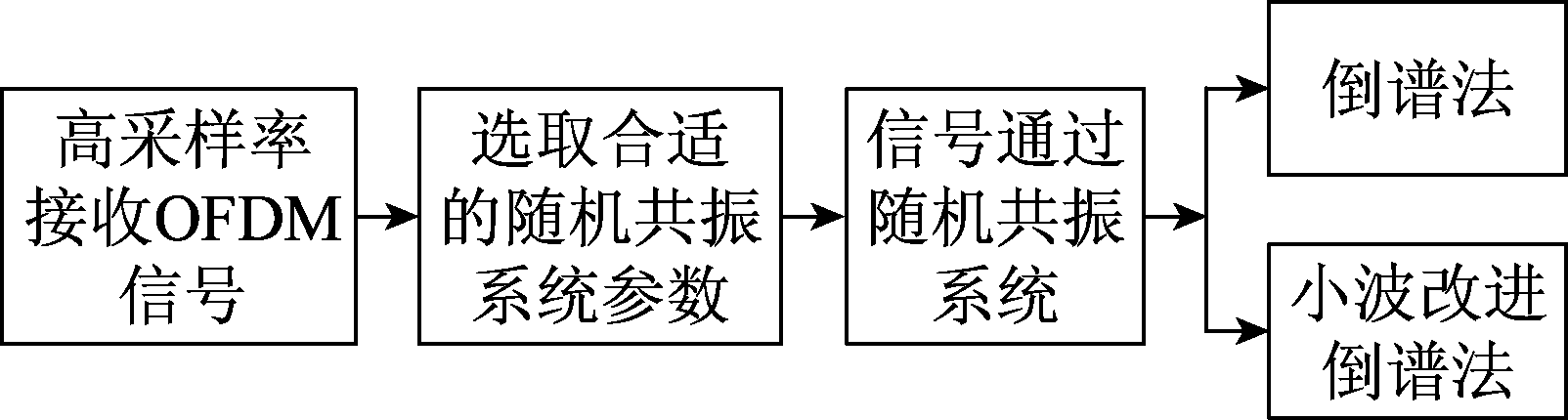
图4 OFDM实际子载波数的估计流程
Fig.4 Estimation process of the actual number of subcarriers in OFDM
(1)定义局部信噪比(Local SNR，LSNR)为
(15)
其中，S(q)为信号功率谱密度，SN(q)为噪声在信号频率附近的强度大小，需要注意的是，这里的频率实际指的是倒谱域上的倒频率。LSNR衡量的是倒谱域上峰值的突显程度和尖锐程度，其值越大，则代表谱峰越明显，越易观测。
(2)定义局部信噪比增益(Local SNR Improvement， LSNRI)为
LSNRI=LSNRsr/LSNRori
(16)
其中，LSNRsr与LSNRori分别指通过随机共振方法改进后和未改进原始方法获得的局部信噪比，LSNRI的大小代表了随机共振方法相比于原始方法获得的增益大小，以dB为单位，其值若大于0则证明随机共振方法输出的谱峰得到改善，其值越大，改善程度也越大。
(3)定义平均误差(Average Error，AE)为
(17)
其中，n为观测次数，M为实际子载波个数，
为估计出的子载波个数。AE衡量了估计的精度，其值越接近0，则估计的精度越高。
4 仿真实验与结果分析
4.1 实验1：有效性验证
OFDM信号仿真参数如下：码元个数为100，IFFT点数N为128，循环前缀NG长度为1/4×N，并行子载波个数M为25，载波频率间隔Δf为40 Hz，子载波调制方式采用QPSK，采样率Fs为5.12 kHz，由于随机共振要求信号有较高的采样率，将采样率扩大100倍，即Fs为512 kHz，在高斯白噪声信道条件下设定SNR为-15 dB。利用上节方法，使信号通过随机共振系统(经过ASRASN确定出a=5100，b=114)，然后分别经过倒谱法和小波改进法，并与经典方法对比，结果分别如图5、图6所示。为方便对比，所有输出都进行了最大幅值为1的归一化处理。
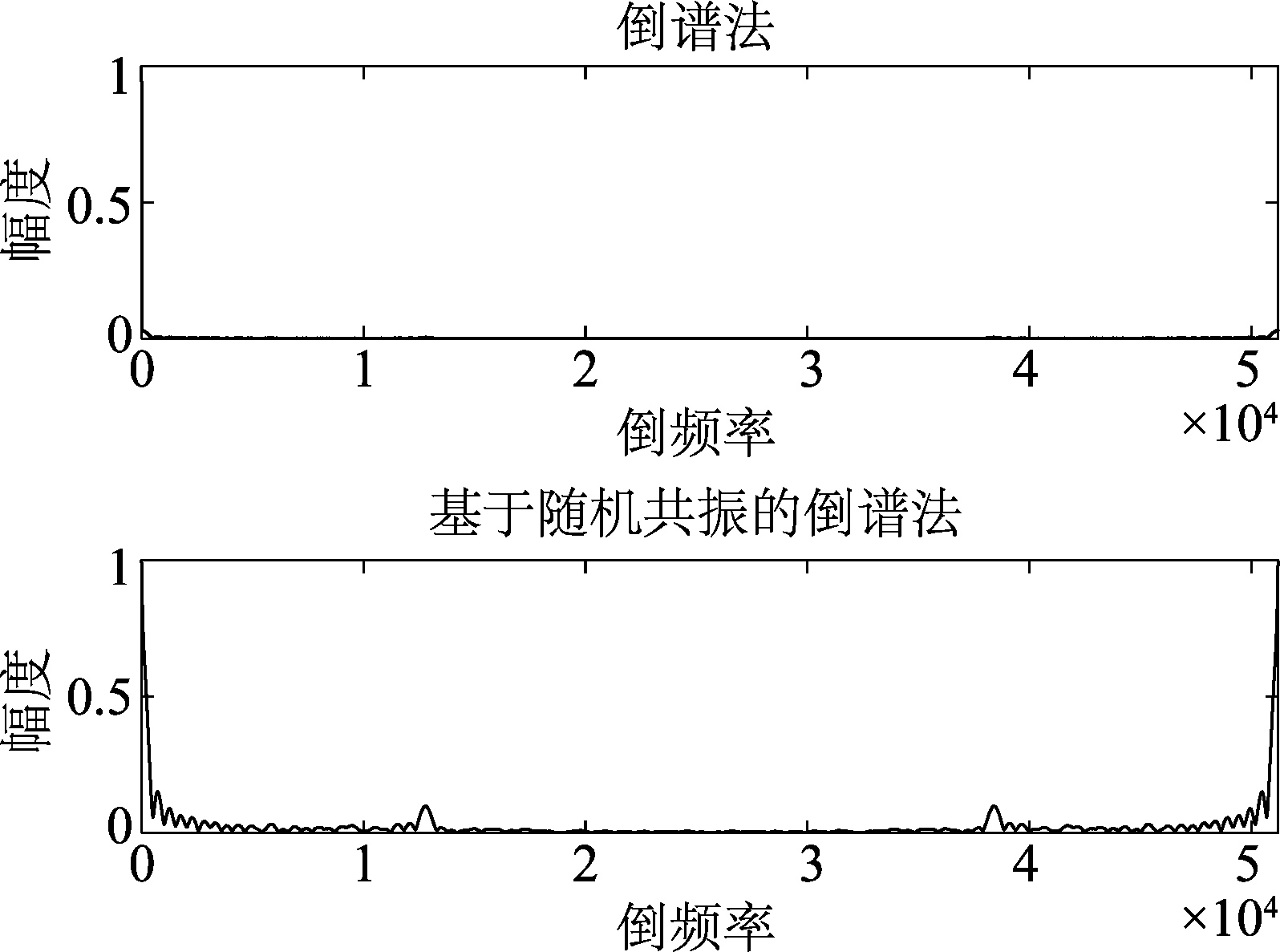
图5 基于随机共振的倒谱法对比
Fig.5 Comparison of the cepstrum method based on stochastic resonance
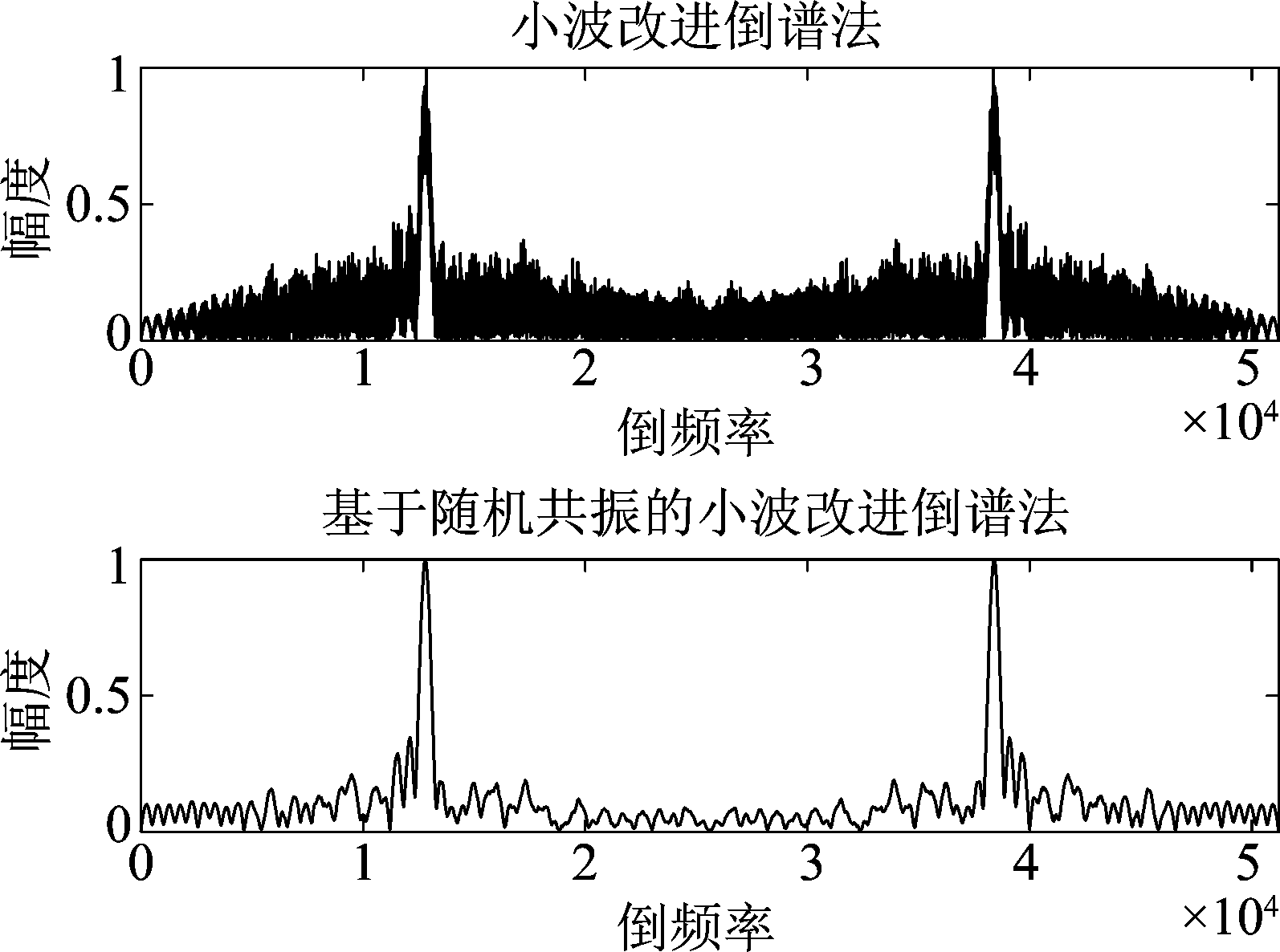
图6 基于随机共振的小波改进倒谱法对比
Fig.6 Comparison of the wavelet improved cepstrum method based on stochastic resonance
(1)与倒谱法对比。当信道中白噪声强度较高的情况下，直接利用倒谱法得到的输出，谱峰用肉眼基本无法辨识，而使用随机共振方法改进后，峰值凸显，易于测量(如图5所示)。
(2)与小波改进倒谱法对比。在同样的条件下，小波改进倒谱法相比于倒谱法而言，谱峰更加凸显，但同时噪底提高，且谱峰不够尖锐，而使用随机共振方法对其改进后，噪声被大幅度抑制，谱峰尖锐且高耸，测量结果更加明晰(如图6所示)。
(3)估计信号的实际子载波个数。以基于随机共振的倒谱法为例，利用式(3)和式(4)，得：
其中，12780为倒谱中的峰值坐标，即倒频率，512000是采样率，1005为估计的信号带宽，经过四舍五入取整即可正确估计出子载波的个数为25。
4.2 不同条件下算法性能对比与分析
本节将在不同的信号条件下检验算法性能，所有实验均采用蒙特卡罗仿真方法，实验次数为200次。
4.2.1 实验2：不同信噪比下算法性能
仿真参数如下：根据美军标(MIL-STD-188-110B)产生39音OFDM信号，码元个数设置为100，IFFT点数N为128，循环前缀NG长度为1/4×N，并行子载波个数M为39，子载波调制方式采用QPSK，载波频率间隔Δf为56.25 Hz，采样率Fs由7.2 kHz提高至720 kHz。信道为高斯白噪声信道，SNR由-30 dB增加到10 dB。经过ASRASN确定出a=5025，b=103。
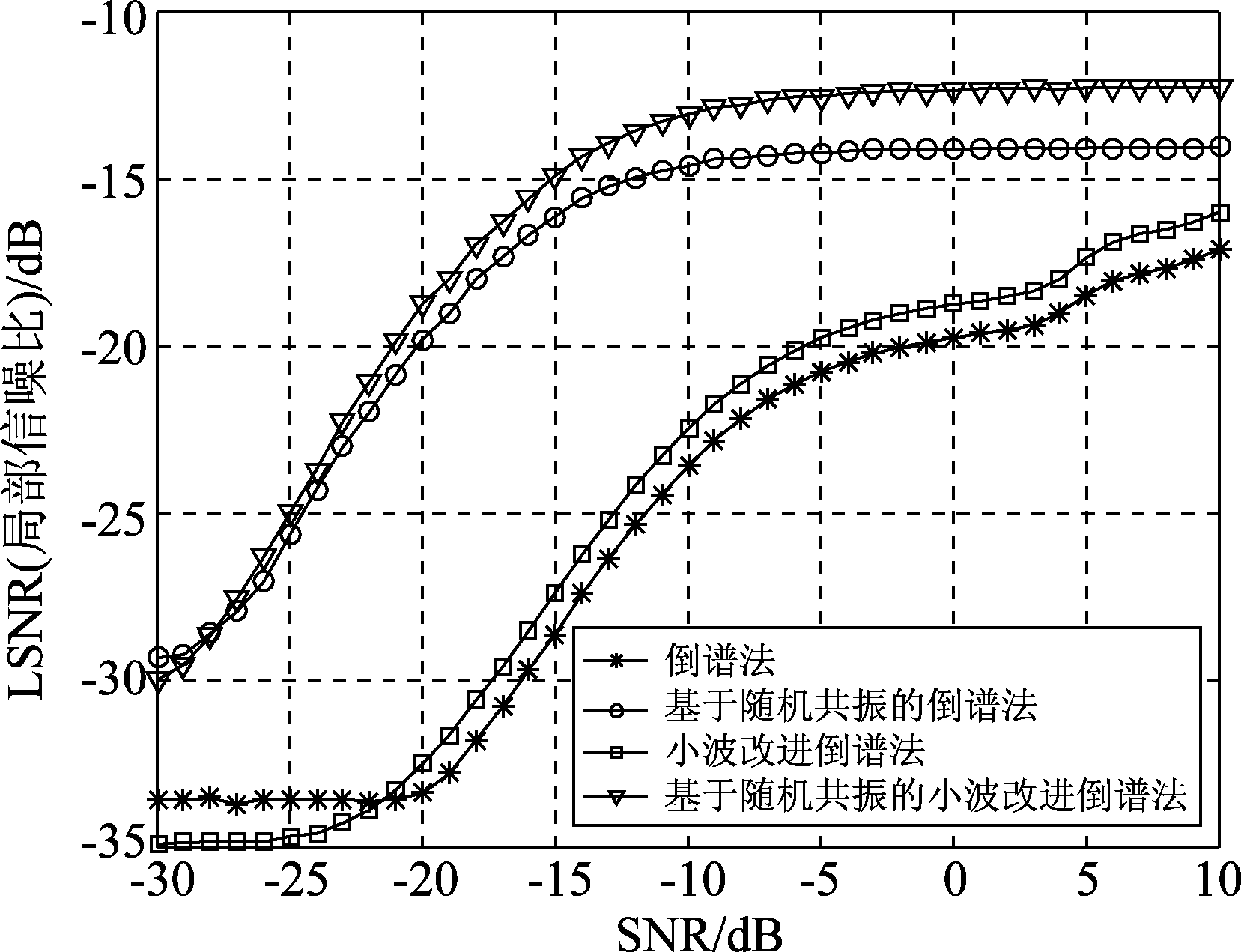
图7 LSNR随SNR的变化
Fig.7 The change diagram of LSNR with SNR
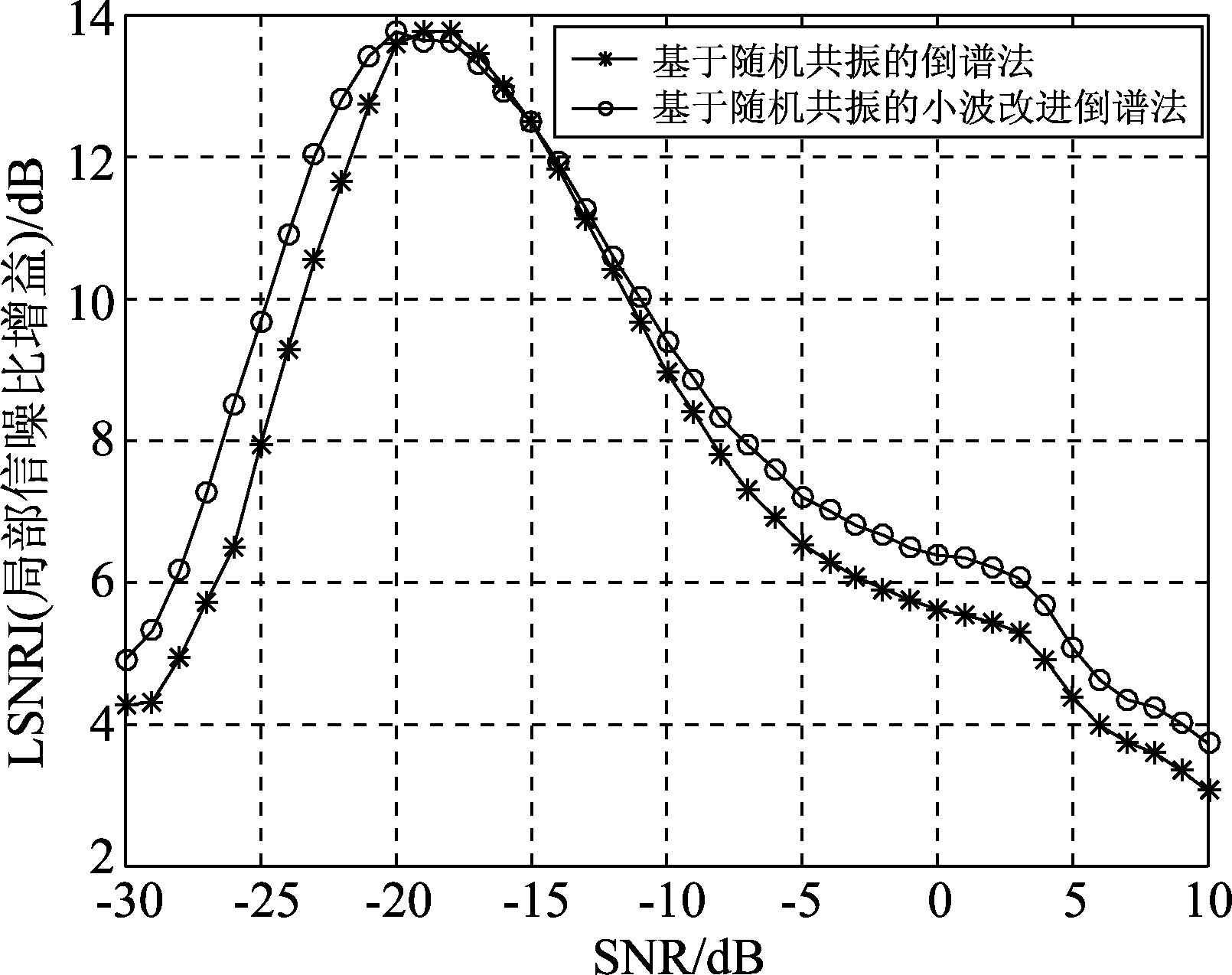
图8 LSNRI随SNR变化
Fig.8 The change diagram of LSNRI with SNR
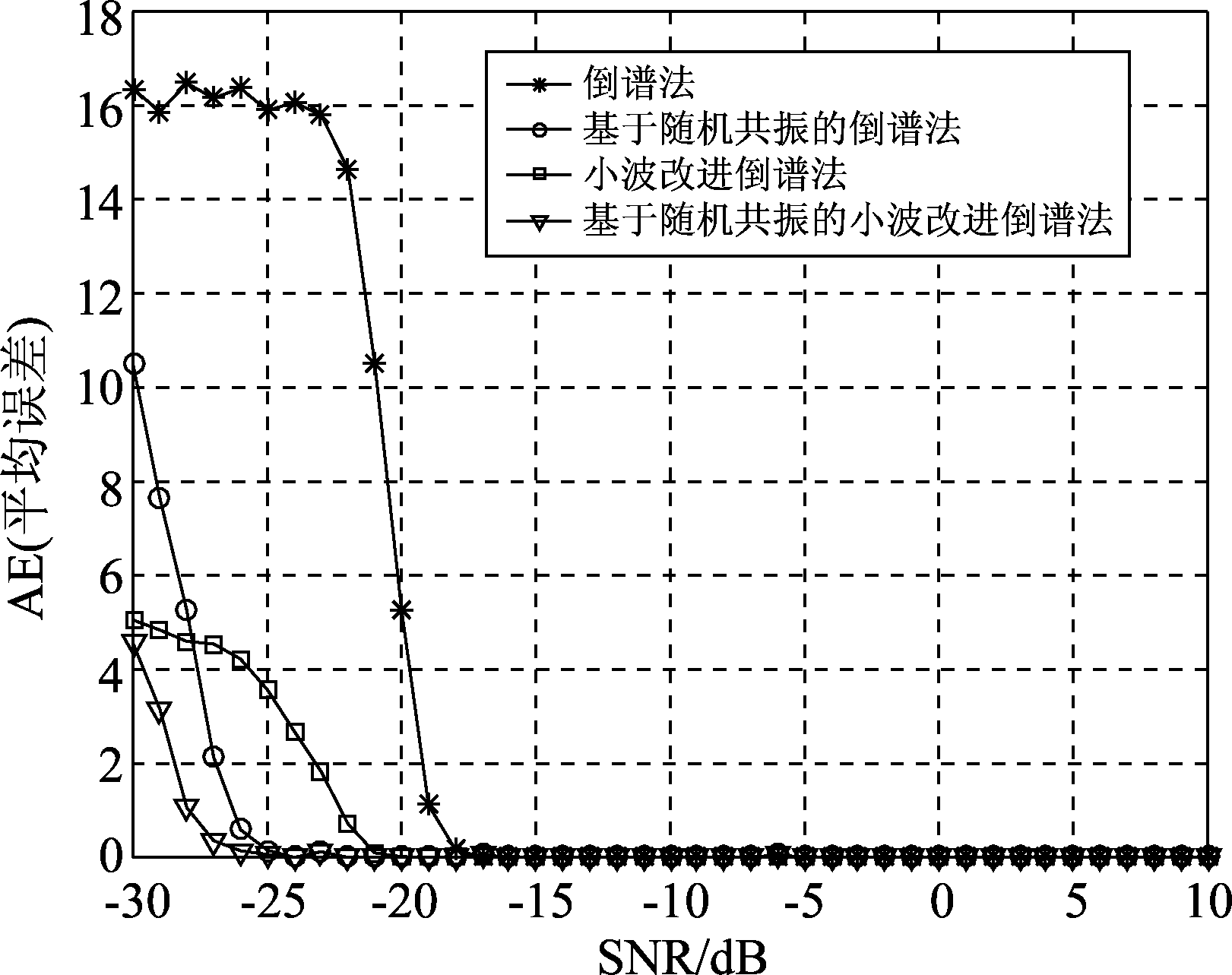
图9 AE随SNR的变化
Fig.9 The change diagram of AE with SNR
由图7所示，随着输入信噪比的不断增大，四种方法输出的局部信噪比均呈现不断上升的趋势。倒谱法及其小波改进法在分别进行随机共振改进之后，均获得了较高的增益提升。
图8描述了随机共振方法改进后的局部信噪比增益的变化规律，与图7相比，更加清晰地体现了采用随机共振方法带来的局部信噪比增益。随着SNR的提高，两种方法的LSNRI变化趋势相同，先增大后减小，且均在-20 dB左右达到最高增益14 dB，此时应为噪声、信号、系统三者达到最佳匹配状态，符合随机共振理论。
图9则呈现了四种方法的平均误差变化规律，在低信噪比条件下，倒谱法估计精度最低，小波改进法在一定程度上降低了误差和信噪比门限，而基于随机共振的两种方法相比原始方法而言，在-25 dB处平均误差几乎为零，进一步降低了信噪比门限, 较倒谱法降低约7 dB, 较小波改进法降低约5 dB。而且在更恶劣的信道条件下，误差也得到一定程度的降低。
4.2.2 实验3：不同调制方式下算法性能
将子载波调制方式改为16QAM，随机共振参数不变，按照实验2的方法对比LSNR、LSNRI及AE随SNR的变化情况。
图10、11、12分别画出了子载波调制方式为16QAM与QPSK时的局部信噪比、局部信噪比增益以及平均误差，虚线代表16QAM，实线代表QPSK，可以看出，两种调制方式下的曲线仅有微小差异，基本保持一致，可见改进算法并不受子载波调制方式的影响，具有很好的鲁棒性。
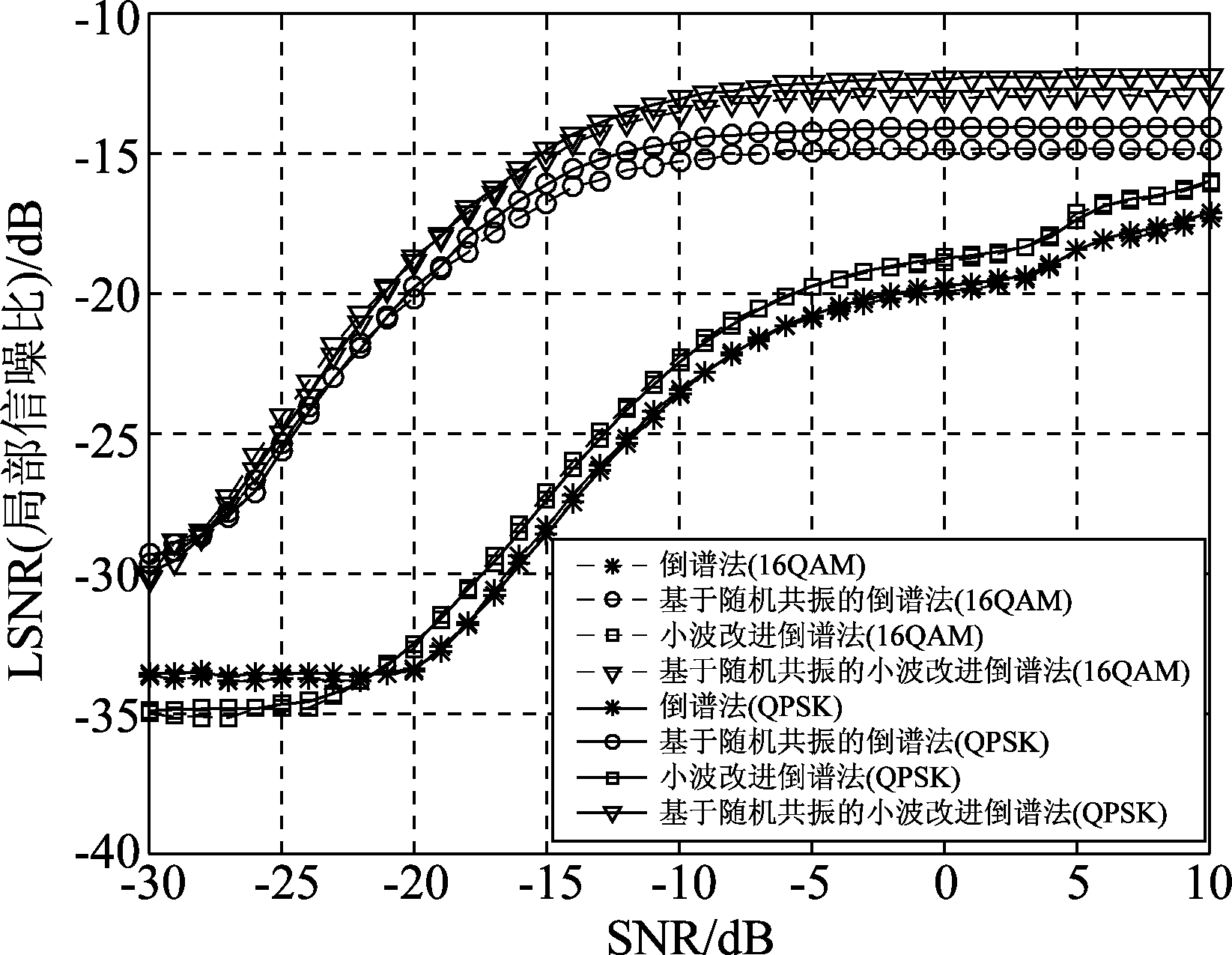
图10 LSNR随SNR的变化
Fig.10 The change diagram of LSNR with SNR
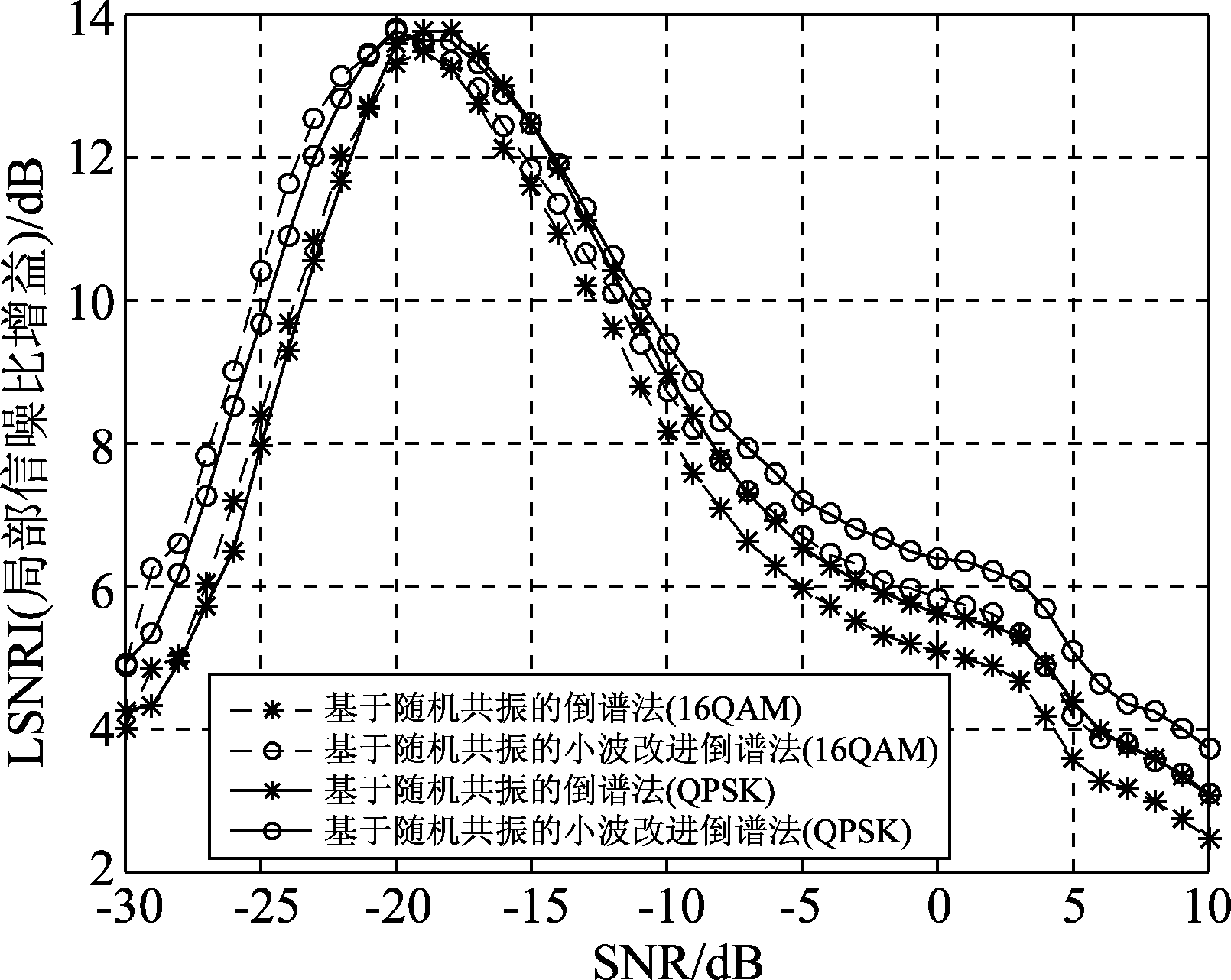
图11 LSNRI随SNR的变化
Fig.11 The change diagram of LSNRI with SNR
图12 AE随SNR的变化
Fig.12 The change diagram of AE with SNR
4.2.3 实验4：不同子载波数目下算法性能
子载波数设置为20到50，以2为间隔递增。SNR为-23 dB，其余参数同实验2。
如图13，随着子载波数的增加，输出的局部信噪比增益波动不大，图14则说明了由随机共振带来的增益也不会随着子载波数的变化而出现较大改变。由图15可知，倒谱法及其小波改进法的平均误差随着子载波数的增加而上升，而随机共振改进算法的平均误差一直为零。
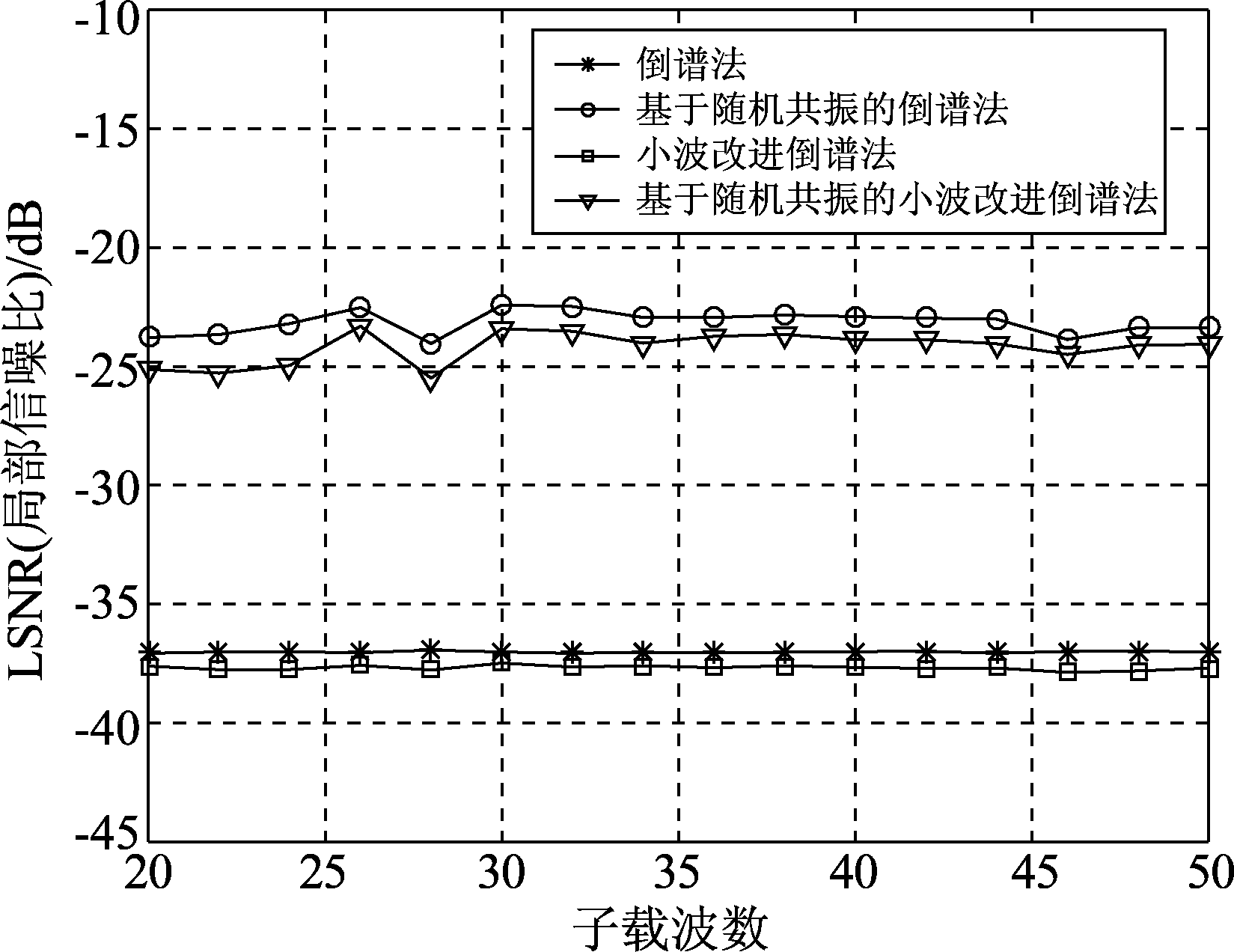
图13 LSNR随子载波数的变化
Fig.13 The change diagram of LSNR with number of subcarriers
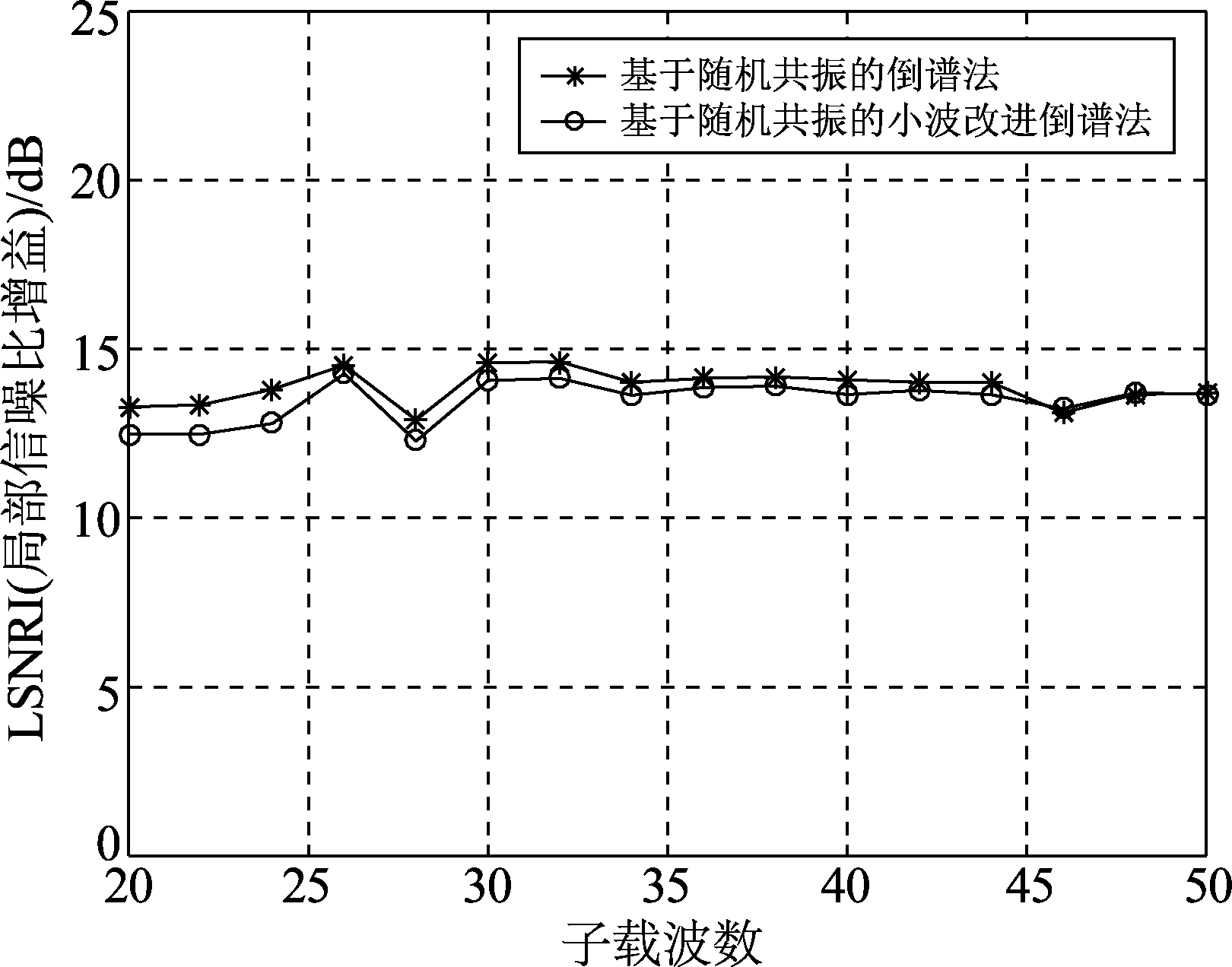
图14 LSNRI随子载波数的变化
Fig.14 The change diagram of LSNRI with number of subcarriers
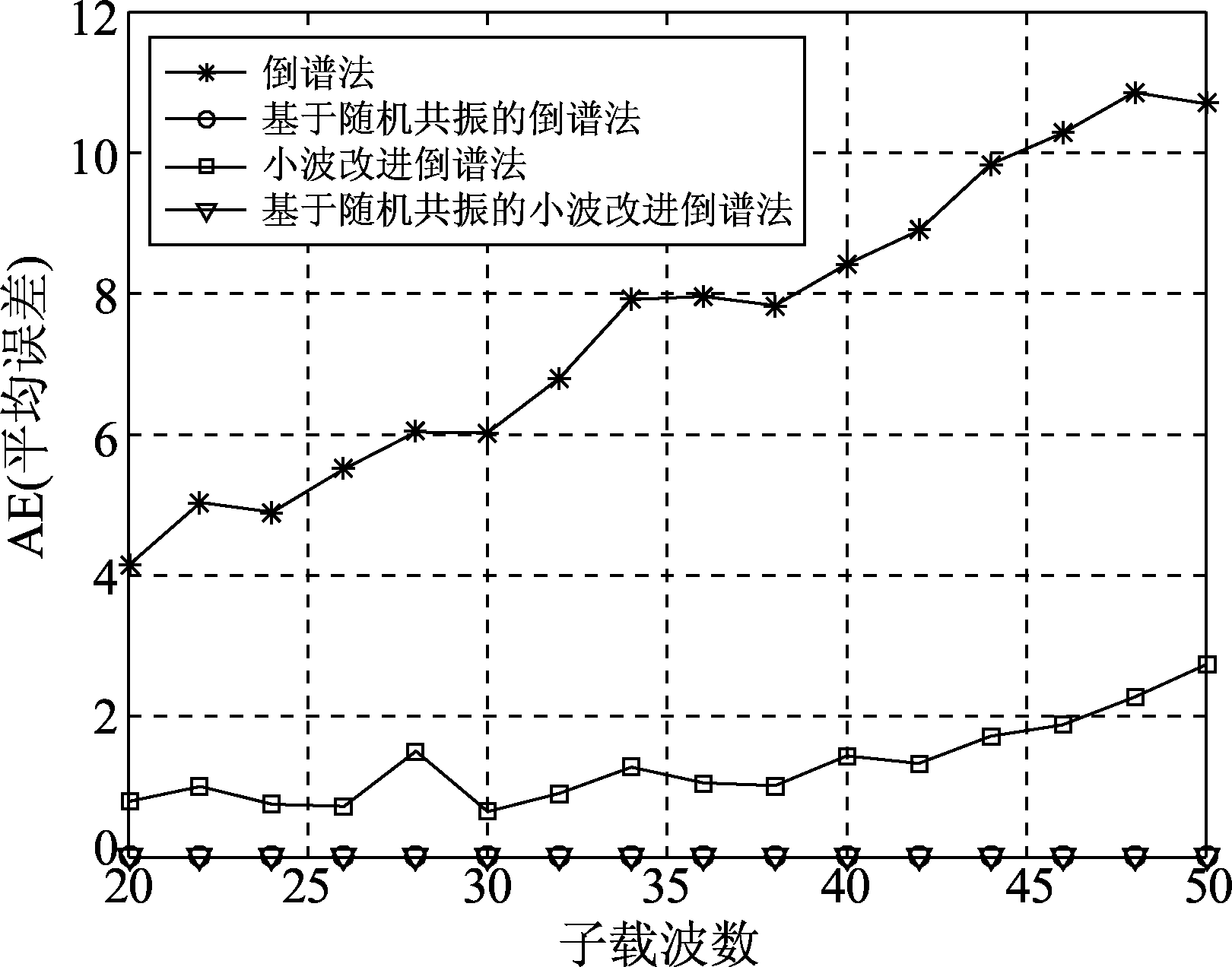
图15 AE随子载波数的变化
Fig.15 The change diagram of AE with number of subcarriers
由此可以看出，本文提出的算法在不同子载波数条件下，均显示出比原有倒谱法及其小波改进法更好的估计性能。
5 结论
本文利用了随机共振中噪声对于微弱信号的增强作用，探索和发掘了随机共振对于高斯白噪声信道下的OFDM信号子载波个数估计中的谱线提升能力，并在仿真实验条件下做了有效性和鲁棒性的分析。算法是在倒谱法和小波改进法的基础上完成的，综合了这些方法的优点，为整体的估计性能带来了如下好处：第一，增大输出的峰值，提升检测性能；第二，降低信噪比门限，在信道环境恶劣的情况下发挥优势；第三，提高估计精度。结果表明，应用随机共振的改进算法较原有的两种算法在有效性和鲁棒性上都具有更好的性能，为低信噪比条件下OFDM信号的后续解调以及信息恢复等起到了重要作用。同时，也拓展了随机共振在通信信号中的应用范围。
[1] Boroujeny B F. OFDM versus filter bank multicarrier[J]. IEEE Signal Processing Magazine, 2011, 28(3):92-112.
[2] Liedtke F, Albers U. Evaluation of features for the automatic recognition of OFDM signals in monitoring or cognitive receivers[J]. Journal of Telecommunications and Information Technology, 2008, 34(37):135-136.
[3] 付哥佳, 段田东, 刘瑞东,等. 短波OFDM信号调制参数估计算法研究[J]. 解放军信息工程大学学报, 2012, 13(6): 688- 694.
Fu Gejia, Duan Tiandong, Liu Ruidong, et al. Modulation Parameter Estimation Algorithm for HF OFDM Signal[J]. Journal of Information Engineering University, 2012,13(6): 688- 694. (in Chinese)
[4] 郑文秀, 赵国庆, 罗明. 基于高阶循环累积量的OFDM子载波盲估计[J]. 电子与信息学报, 2008, 30(2): 346-349.
Zheng Wenxiu, Zhao Guoqing, Luo Ming. Blind Estimation of OFDM Sub-carrier Frequencies Based on the High-Order Cyclic Cumulants[J]. Journal of Electronics and Information Technology, 2008, 30(2): 346-349. (in Chinese)
[5] 李国汉, 王可人, 金虎. 一种基于KS距离的OFDM子载波数估计法[J]. 计算机工程, 2012, 38(21): 100-102.
Li Guohan, Wang Keren, Jin Hu. An OFDM Sub-carrier Number Estimation Method Based on KS Distance[J]. Computer Engineering, 2012, 38(21): 100-102. (in Chinese)
[6] 胡茑庆. 随机共振微弱特征信号检测理论与方法[M]. 北京: 国防工业出版社, 2012:2-25.
Hu Niaoqing. Theory and Method of Stochastic Resonance Weak Characteristic Signal Detection[M].Beijing: National Defense Industry Press, 2012:2-25. (in Chinese)
[7] 张歆, 张小蓟. 水声通信系统[M]. 西安: 西北工业大学出版社, 2012: 291-293.
Zhang Xin, Zhang Xiaoji. Underwater Acoustic Communication System[M]. Xi’an: Northwestern Polytechnical University Press, 2012: 291-293. (in Chinese)
[8] Weinstein S B. Ebert P M. Data transmission by frequency division multiplexing using the discrete Fourier transform[J]. IEEE Trans on Communication, 1971, 19(5): 628- 634.
[9] 曹鹏. 短波多载波信号识别与参数估计[D]. 郑州: 解放军信息工程大学, 2010.
Cao Peng. Signal Recognition and Parameter Estimation for Multi-carrier Systems in Shortwave Communications[D]. Zhengzhou: PLA Information Engineering University, 2010. (in Chinese)
[10] 宋宁, 关华. 经典功率谱估计及其仿真[J]. 现代电子技术, 2008, 31(11): 159-161.
Song Ning, Guan Hua. Classical Power Spectrum Density Estimation and Its Simulation[J]. Modern Electronics Technique, 2008, 31(11): 159-161. (in Chinese)
[11] Mcnamara B，Wiesenfeld K. Theory of stochastic resonance[J]．Phys Rev A Gen Phys, 1989, 39(9): 4854- 4869.
[12] Namara Mc, Wiesenfeld K, Roy R．Observation of stochastic resonance in a ring laser[J]．Physical Review Letters, 1988, 60(25):2626.
[13] Gammaitoni L, Marchesoni F, Saetta E, et al．Stochastic resonance in bistable systems[J]．Physical Review Letters, 1989, 62(62): 349-352.
[14] 杨定新, 胡政, 杨拥民. 大参数周期信号随机共振解析[J]. 物理学报, 2012, 61(8): 50-59.
Yang Dingxin, Hu Zheng, Yang Yongmin. The Analysis of Stochastic Resonance of Periodic Signal with Large Parameters[J].Acta Physica Sinica, 2012, 61(8): 50-59. (in Chinese)
[15] 孔德阳,彭华,马金全. 基于人工鱼群算法的自适应随机共振方法研究[J]. 电子学报,2017,45(8):1864-1872.
Kong Deyang, Peng Hua, Ma Jinquan. Adaptive Stochastic Resonance Method Based on Artificial-Fish Swarm Optimization[J]. Acta Electronica Sinica, 2017, 45(8): 1864-1870. (in Chinese)
[16] 孔德阳, 彭华, 马金全. 随机共振应用于窄带PSK信号处理的研究[J]. 信号处理, 2017, 33(5): 721-731.
Kong Deyang, Peng Hua, Ma Jinquan. Application of Stochastic Resonance in Narrow-band PSK Signal Processing[J].Journal of Signal Processing, 2017, 33(5): 721-731. (in Chinese)
