1 引言
在电子侦察和信息对抗领域,如何高效可靠地对通信辐射源进行识别,有着非常重要的意义。由于辐射源个体之间存在差异,导致通信信号携带设备个体差异特征,所以只要能够提取通信信号中携带的个体特征便可以进行分类识别[1]。基于暂态信号特征和稳态信号特征的个体识别[2]是目前主流的两大方法。其中稳态信号获取容易、稳定、实用性强,获得了广泛的研究,目前主要基于稳态信号特征提取的方法识别性能较好,主要有基于频率源特性[3]、噪声特性[4]、调制参数[5]和杂散特性[6]的4种方法。其中基于杂散特性的特征提取方法性能较好,获得了广泛的研究[7]。目前针对杂散成分的识别主要有基于高阶统计量[8]、谱相关[9]、小波变换[10]等方法,在高斯信道下均有一定的识别效果。
功率放大器作为重要的通信器件存在于所有辐射源系统中,由于制造工艺的限制,功率放大器的输入-输出幅度呈现出非线性特性,该特性对信号的个体差异影响较大,可以作为识别特征。目前基于功率放大器杂散特性特征提取识别的方法主要有:基于高阶统计量特性[8]、频谱再生特性[9]以及多重分形维数[7]的方法。
小波变换(wavelet transform,WT)通过变换能够充分突出信号某些方面的特征,能对时间(空间)频率的局部化分析。在个体识别领域,通过小波变换可以提取分析出信号特征的差异,从而达到识别的目的。文献[10]利用Daubechies小波基,对信号进行特征提取用以识别,在信噪比为10 dB的情况下识别率达到了80%。但是小波基类型众多,适用环境各不相同,上述研究中,只选用了一种小波基,并没有能够选择到分类性能最优,识别效果最好的小波基,同时小波特征对噪声比较敏感,不同信噪比条件下,小波特征往往有着较大的变化,在已有的研究中普遍采用的是同一信噪比下的样本训练和识别,在信噪比发生变化时,类间特征参数将发生交叠,以致无法识别。
为解决上述问题,进一步研究小波变换在个体识别领域的应用,本文通过类间距离最远准则,在8类小波基共54种不同的小波变换中筛选出分类性能最好的小波基用于通信辐射源的个体特征提取,并根据特征分布选取特定小波基下的小波系数复杂度作为信噪比参考值辅助个体识别。
2 功率放大器非线性模型
在无线通信设备中,功率放大器作为其中最重要的器件之一,起着放大信号功率的作用。在理想情况下,功率放大器的增益倍数恒定不变,如图1(a)虚线所示。然而由于制造工艺的限制和器件的随机性,功率放大器的理想线性增益特性往往变成了非线性,甚至即使是同型号、同批次的功率放大器的增益也不可能完全相同,非理想功率放大器的增益倍数随输入功率的变化如图1(a)实线所示。
图中实际增益倍数并非恒定,且因工艺限制实际增益G1、G2间也存在增益差△g,于是输入和输出的幅度关系如图1(b)所示,不同的非线性特性就为信号添加了“指纹特征”,即通过不同非线性器件后信号所呈现出的细微差异,由于其差异细微且能够作为身份识别的依据,所以在现有的大部分研究中称之为“指纹特征”。为研究此类“指纹特征”,需要对功率放大器进行建模来表征其工作特性。目前针对功率放大器的建模方式主要有Taylor级数模型、Saleh模型、Rapp模型等[11],各种模型应用场合各不相同,其中Taylor级数模型是应用较为广泛的一种。当功放的非线性较弱,用泰勒级数模型可较好地描述功放的非线性特性[12]。其模型如式(1)所示。
(1)
其中an表示功率放大器Taylor模型的第n阶参数,x(t)为输入信号,y(t)为输出信号。an的不同将导致功率放大器的增益效果的不同,如图1所示,各实线即为不同参数导致的功率放大器的非线性差异。
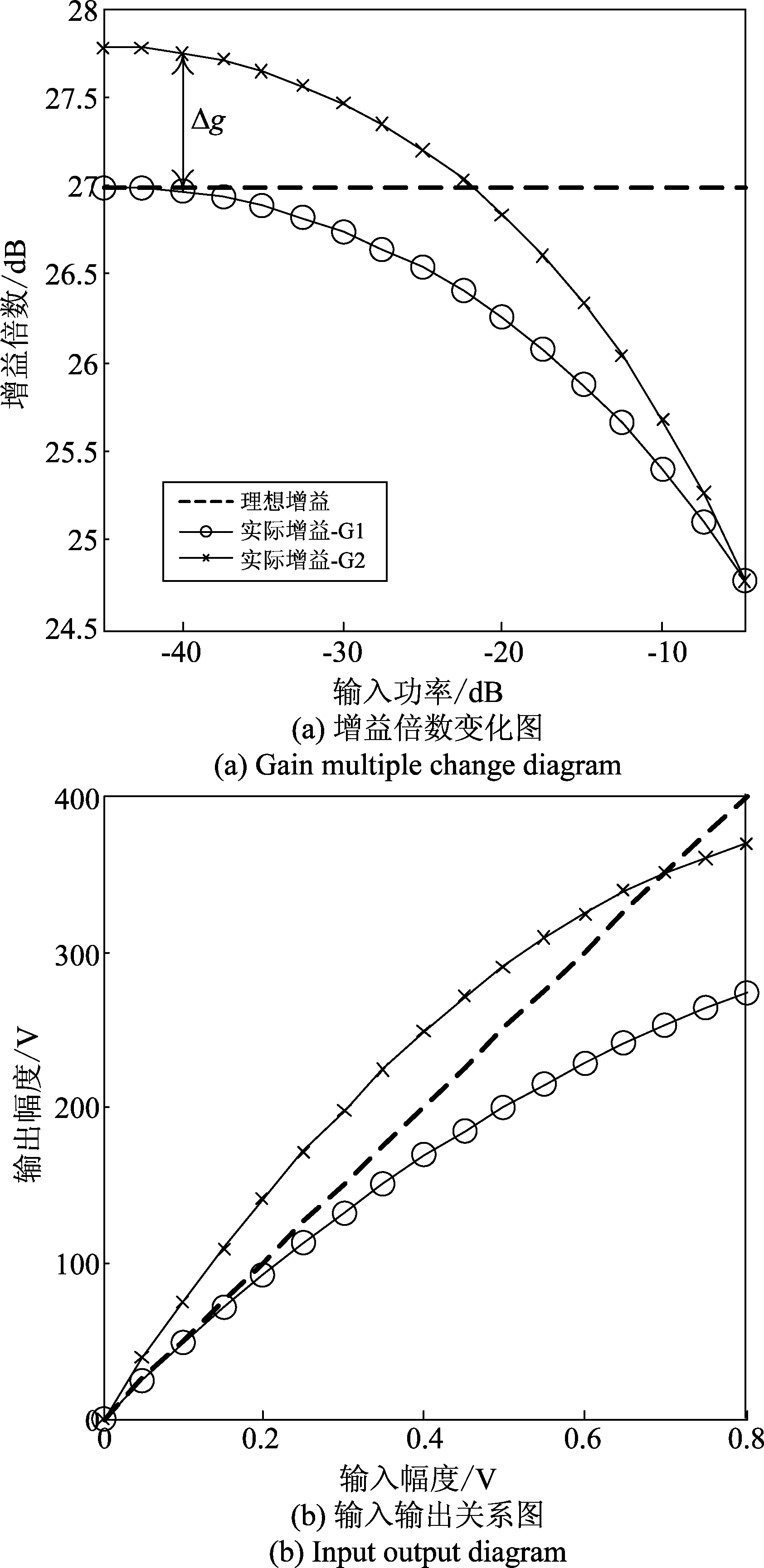
图1 功率放大器增益曲线
Fig.1 Gain curve of power amplifier
为证明模型选择的合理性和适用性,本文同时选取了Saleh模型、Rapp模型与Taylor模型进行横向对比,通过计算三种模型互相拟合的误差来判断模型拟合的适用性和精度。
首先确定需要拟合模型的参数分别为:
Taylor级数模型:
(1)y(t)=450.8x(t)-540.0x2(t)+230.0x3(t)-0.07006x4(t)+0.2501x5(t)-0.5267x6(t)+0.6486x7(t);
(2)y(t)=412.1x(t)-485.6x2(t)+198.7x3(t)-0.05827x4(t)+0.208x5(t)-0.4388x6(t)+0.535x7(t);
(3)y(t)=503.7x(t)-593.6x2(t)+242.9x3(t)-0.07121x4(t)+0.2542x5(t)-0.5364x6(t)+0.6538x7(t);
(4)y(t)=448.7x(t)-528.8x2(t)+216.4x3(t)-0.06345x4(t)+0.2265x5(t)-0.4778x6(t)+0.5825x7(t);
(5)y(t)=457.9x(t)-539.6x2(t)+220.8x3(t)-0.06474x4(t)+0.2311x5(t)-0.4876x6(t)+0.5944x7(t);
Saleh模型:
Rapp模型:
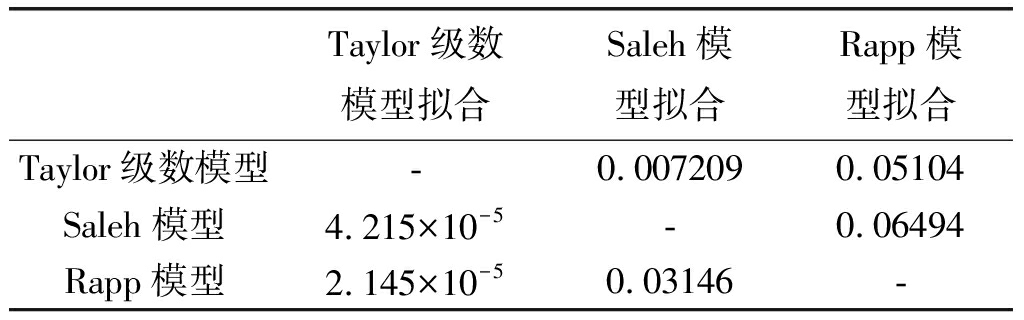
在选取好待拟合模型的基础上,用其他模型进行拟合并计算均方根误差,具体数据如下:
表1 各模型拟合的均方根误差
Tab.1 Root mean square error of each model fitted
Taylor级数模型拟合Saleh模型拟合Rapp模型拟合Taylor级数模型-0.0072090.05104Saleh模型4.215×10-5-0.06494Rapp模型2.145×10-50.03146-
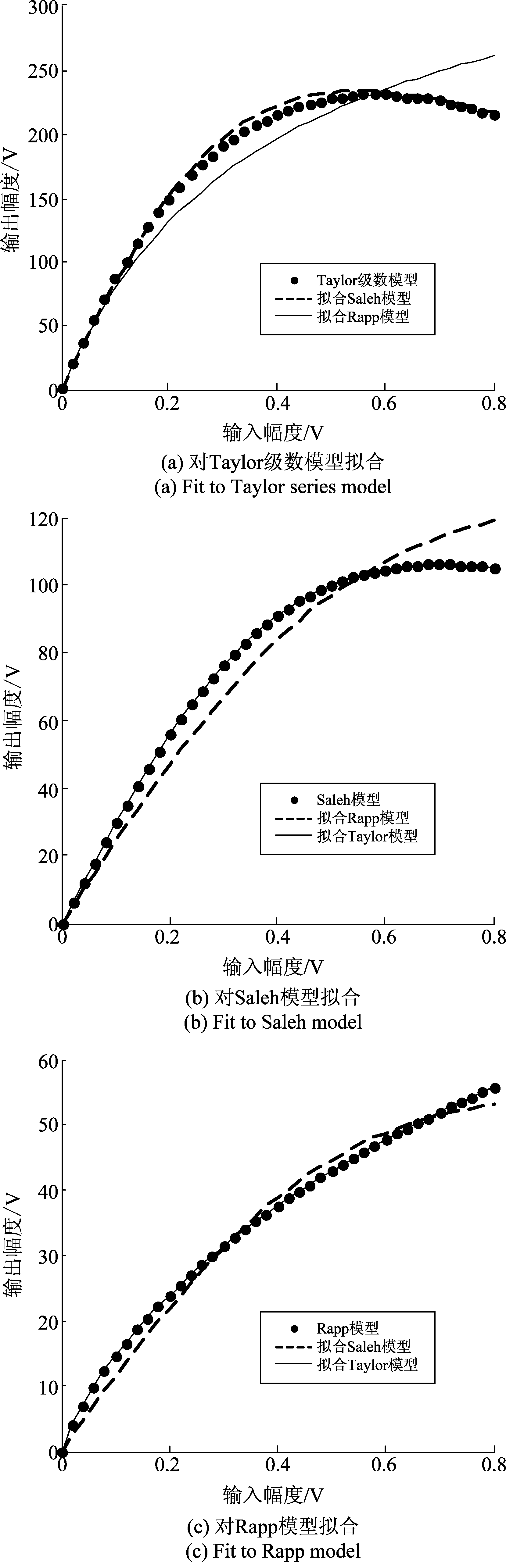
图2 对各模型拟合结果
Fig.2 Fit results for each model
从上述拟合分析可以得出以下结论:
(1)Taylor级数模型的拟合能力最强,Saleh模型次之,Rapp模型的拟合能力最差。
(2)Saleh模型和Rapp模型是针对特定功率放大器的建模方法,应用范围比较局限。
(3)现行功放技术发展迅速,功放非线性较弱。由于本文分析的对象为同型号电台,其个体差异较小,而Taylor级数模型表征精度高,更能有效的体现电台的个体差异。
综上所述,最终确定Taylor级数模型为本文研究对象的建模方法。
3 小波变换特征提取算法原理
傅里叶变化是通过无限长的周期性正弦波和余弦波构造而成,所以该方法适合去表征那些具有周期性波动的平稳信号,而对于非周期或非平稳的信号,正弦波和余弦波的表征能力就有所下降,因此对于非周期非平稳过程,傅里叶变换存在局限性。而小波变换将无限长的三角函数基换成了有限长且会衰减的小波基,小波可以按比例缩小或放大尺度获取频率信息,也可以延时间轴前后平移获取时间信息,从而成为了分析非平稳过程的有效方法。
3.1 小波变换
设ψ(t)∈L2(R),其傅里叶变换为![]() 当
当![]() 满足允许条件(完全重构条件或恒等分辨条件)时称ψ(t)为一个小波基。将小波基ψ(t)经伸缩平移后可得[13]:
满足允许条件(完全重构条件或恒等分辨条件)时称ψ(t)为一个小波基。将小波基ψ(t)经伸缩平移后可得[13]:
(2)
称其为一个小波序列。其中:a为尺度因子,b为平移因子。对于时间序列信号f(t)∈L2(R)的小波变换为:
(3)
其中<f,ψa,b>表示f与ψa,b的数量积
其重构公式(逆变换)为:
(4)
3.2 基于LZ复杂度的特征参数提取方法
时间序列经过小波变换后得到小波系数还需进一步地特征提取才能构成特征向量,此处考虑到Lempel-Ziv复杂度[14](简称LZ复杂度)是一种能够刻画序列波形变换规律的方法,能够较好的反映系统内在结构的变换过程,文献[10]采用LZ复杂度对小波系数进行进一步特征提取。
对于上一步所得到的小波系数![]() 提取其LZ复杂度的主要步骤如下:
提取其LZ复杂度的主要步骤如下:
(1)对小波系数![]() 进行变换
进行变换
(5)
(2)对变换序列![]() 进行量化
进行量化
(6)
![]() 表示变换序列
表示变换序列![]() 的均值,得到量化后的由符号“0”和“1”构成的信号序列
的均值,得到量化后的由符号“0”和“1”构成的信号序列![]()
(3)将信号序列![]() 转化为符号序列
转化为符号序列![]()
(4)设初始生成池为空,初始添加操作次数A=0,将![]() 添加进生成池,操作次数加1,A=1。
添加进生成池,操作次数加1,A=1。
将Q中的其他符号依次添加进生成池。假定生成池已有符号串![]() 将下一个符号串定义为
将下一个符号串定义为![]() 尝试将符号串Y添加进生成池X得到XY,并删除符号串XY右边最后一个符号后所得到的符号表示为XYπ(当符号串Y中只包含一个符号时XYπ=X);此时判断符号串Y是否可从符号串XYπ中截取获得,如果可以,符号串X保持不变,而符号串Y添加下一个小波系数组成新的符号串
尝试将符号串Y添加进生成池X得到XY,并删除符号串XY右边最后一个符号后所得到的符号表示为XYπ(当符号串Y中只包含一个符号时XYπ=X);此时判断符号串Y是否可从符号串XYπ中截取获得,如果可以,符号串X保持不变,而符号串Y添加下一个小波系数组成新的符号串![]() 如果符号串Y不能从符号串XYπ中截取获得,则将Y添加到生成池中,且操作次数A加1,然后改变符号串X和Y为
如果符号串Y不能从符号串XYπ中截取获得,则将Y添加到生成池中,且操作次数A加1,然后改变符号串X和Y为![]()
(5)重复步骤(4),直到生成池中包含序列![]() 中的所有符号。
中的所有符号。
(6)计算![]() 的LZ复杂度:
的LZ复杂度:
(7)
文献[10]采用辐射源信号f(t)经Danubechies小波变换后得到的小波系数![]() 计算其LZ复杂度值作为该辐射源的特征参数进行识别。但是文献[10]仅针对信噪比固定情况下的个体识别,在信噪比区间增大时,特征参数的可分性不明显,识别率降低。本文考虑通过小波基选择来提升可分性,增大信噪比适用区间,以提高识别率。
计算其LZ复杂度值作为该辐射源的特征参数进行识别。但是文献[10]仅针对信噪比固定情况下的个体识别,在信噪比区间增大时,特征参数的可分性不明显,识别率降低。本文考虑通过小波基选择来提升可分性,增大信噪比适用区间,以提高识别率。
4 基于小波基选择的特征提取方法
由小波变换的计算过程可以看出,不同的小波基得到的小波系数是不同的,所以根据小波系数计算得到的LZ复杂度也将不同,特征参数的类间可分效果也将不同。因此并不是每一种小波都适用于个体识别领域,小波基丰富多样的同时也使得小波基的选择变得困难,恰当地选择小波基获取有效的特征参数用于通信辐射源个体识别是关键技术难点。
目前对于小波基特性的描述都比较模糊,通常情况下需要实验选择多种小波基直至达到所需的工程效果。因此本文针对通信辐射源的个体识别设计了一种基于类间分离度的准则用以衡量小波基在该情况下的适用程度。该方法主要分为以下几步:一维小波分离度粗评、二维小波拟合类中心、计算类宽度、计算类间分离度。
(1)一维小波分离度粗评估
通过式(7)可以计算出一组小波系数的复杂度,通过计算同一辐射源个体在多种信噪比条件下的N组小波系数样本可以得到复杂度序列LZC(i),(i=1,2,…,N)。计算LZC(i)的重心![]() (本文研究3组辐射源个体,故取q=1,2,3),再计算三组辐射源个体重心的方差
(本文研究3组辐射源个体,故取q=1,2,3),再计算三组辐射源个体重心的方差![]() 其中μ 表示{Eq}的均值)用以表征一维小波的分离度,从而为构建二维小波复杂度值特征向量提供数值参考,选取两种(此处记为a、b)小波基构成特征向量s(i)=[LZCa(i) LZCb(i)]。
其中μ 表示{Eq}的均值)用以表征一维小波的分离度,从而为构建二维小波复杂度值特征向量提供数值参考,选取两种(此处记为a、b)小波基构成特征向量s(i)=[LZCa(i) LZCb(i)]。
(2)二维小波拟合类中心
此时对各辐射源个体的特征向量s(i)=[LZCa(i) LZCb(i)],(i=1,2,…,N)进行曲线拟合,目的在于拟合出类的“骨架”。此处采用最小二乘法对样本点进行3次多项式拟合。此处记xi=LZCa(i),yi=LZCb(i)。
设拟合多项式为:
y=a0+a1x+a2x2+a3x3
(8)
各点(xi,yi)到这条曲线的距离之和:
(9)
对式(9)求ai,i=1,2,3,4 偏导数,得到:
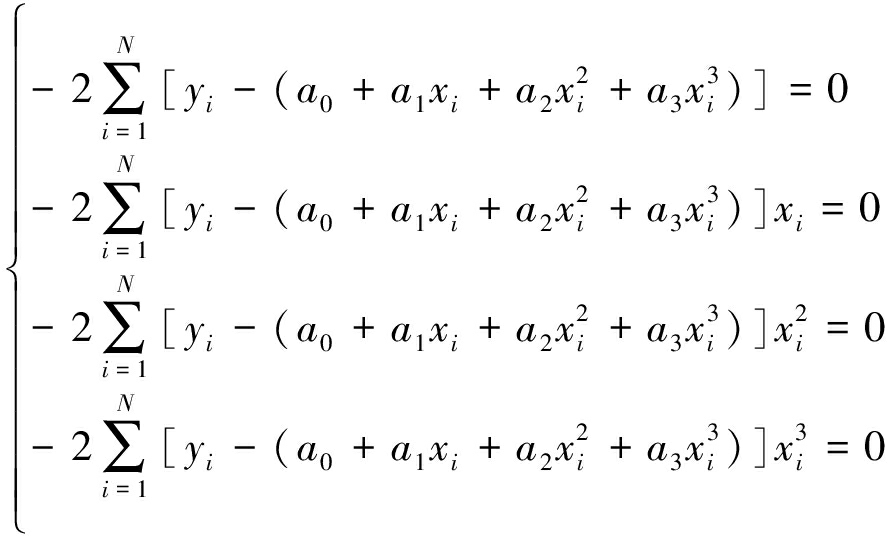
(10)
将式(10)展开:
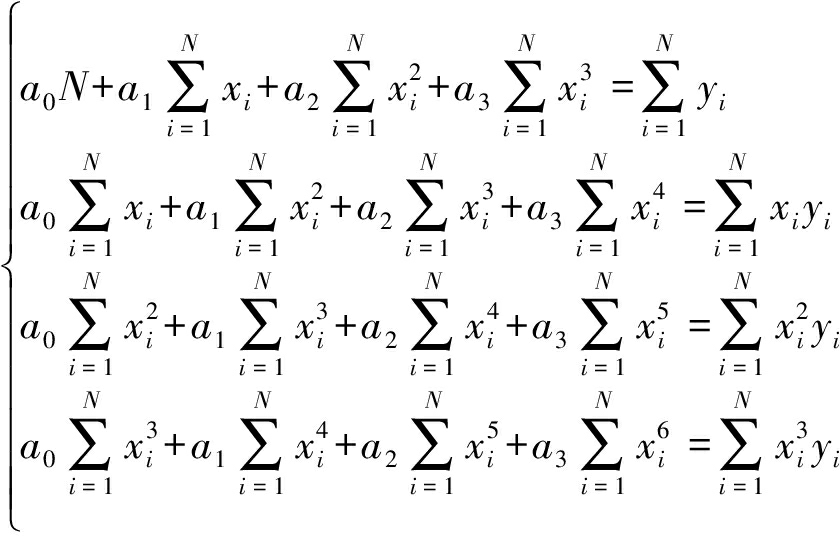
(11)
表示为矩阵形式:
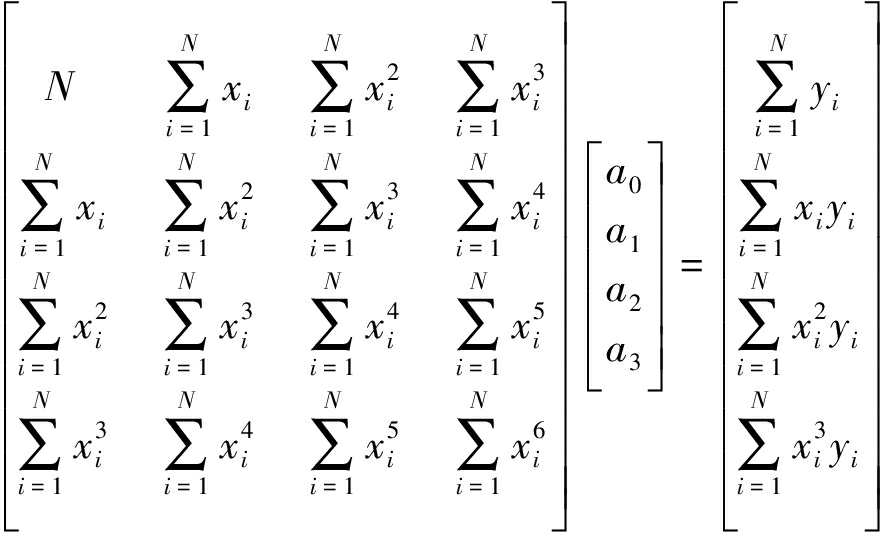
(12)
式(12)中的系数矩阵是一个对称正定矩阵,故该矩阵满足范德蒙特矩阵化简条件,化简后得到:
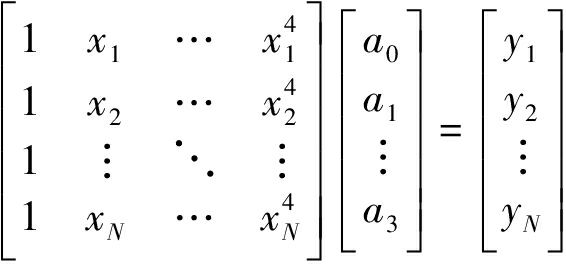
(13)
即:XA=Y故:A=X-1Y,即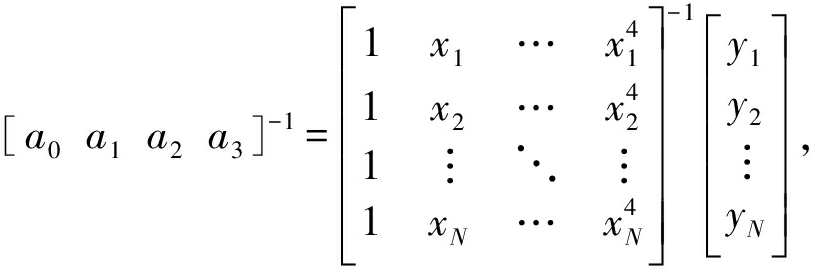 解得a0,a1,a2,a3的具体值,从而拟合出3次多项式y=a0+a1x+a2x2+a3x3作为类中心。
解得a0,a1,a2,a3的具体值,从而拟合出3次多项式y=a0+a1x+a2x2+a3x3作为类中心。
(3)计算类宽度
步骤(1)计算出了类中心,如图3实线所示,下面计算类边界,本文考虑采用一种计算简单的方法均方根误差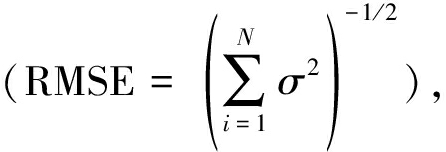 其中σ2表示样本点到曲线y=a0+a1x+a2x2+a3x3的最近距离)来定量描述类的宽度,均方根误差能够较好的反映数据的离散程度,同时对数据中特大或特小的误差反映非常敏感,所以,均方根误差能够很好地反映出测量的精密度。根据这样的属性,本文考虑将均方根误差作为类宽度参数进行类区域划分,其区域在y+RMSE/2和y-RMSE/2之间,如图3两条虚线所包围区域所示。
其中σ2表示样本点到曲线y=a0+a1x+a2x2+a3x3的最近距离)来定量描述类的宽度,均方根误差能够较好的反映数据的离散程度,同时对数据中特大或特小的误差反映非常敏感,所以,均方根误差能够很好地反映出测量的精密度。根据这样的属性,本文考虑将均方根误差作为类宽度参数进行类区域划分,其区域在y+RMSE/2和y-RMSE/2之间,如图3两条虚线所包围区域所示。

图3 类区域示意图
Fig.3 Class area sketch map
即类区域:
(14)
(4)加权计算类间分离度
本文定义类间分离度为平均类总面积减去交叠区域面积,即类间分离度:
(15)
其中RMSEavg表示两类区域的平均均方根误差RMSEavg=(RMSE1+RMSE2)/2,R表示定义域,R2表示交叠区域,r 表示定义域宽度,yq、yp分别表示区域的上界和下界。对于三个个体区域的计算,取相邻两个区域的个体分别计算得d1、d2,再定义d=d1+d2。
由式(15)定义可以看出,类间分离度越高,可分性越强。因此选取类间分离度d最大的一组特征向量,进行训练识别。
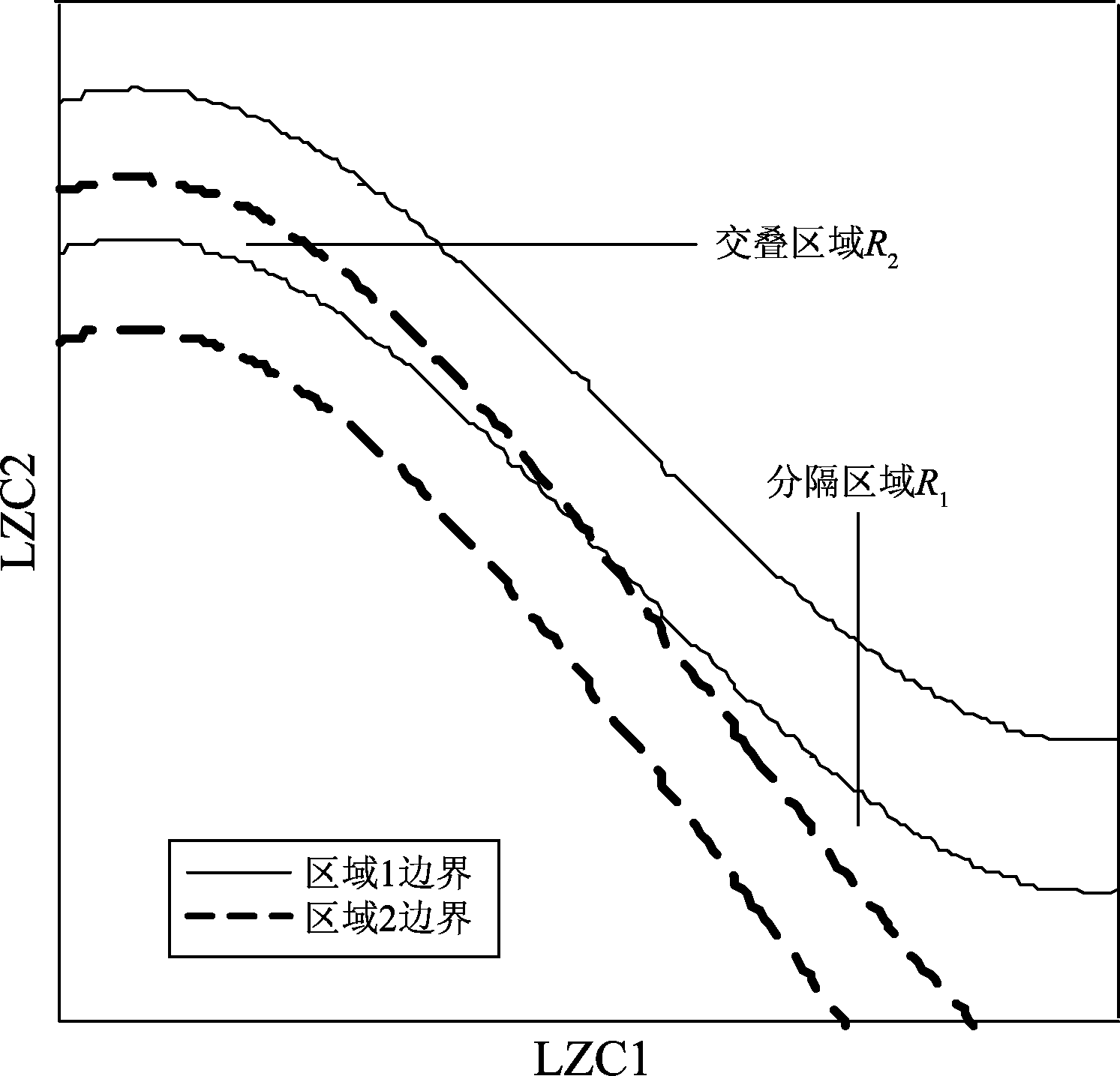
图4 分离度计算示意图
Fig.4 Sketch map of separation degree calculation
综上所述,基于最优小波基选择的特征提取识别方法流程如下:
1)选择多种小波基分别对接收信号f(t)进行小波变换,计算得到小波系数![]()
2)计算小波系数![]() 的LZ复杂度值LZC;
的LZ复杂度值LZC;
3)对多组各信噪比条件下的小波系数进行复杂度计算得到复杂度序列LZC(i);
4)对复杂度值LZC(i)进行一维小波分离度粗评估,得到一维小波分离度σ2;
5)利用一维小波分离度σ2,选择分离度合适的小波基构造特征向量s(i)=[LZCa(i)LZCb(i)];
6)用三次多项式拟合特征向量s(i)=[LZCa(i)LZCb(i)]的类中心y=a0+a1x+a2x2+a3x3;
7)计算特征相对于类中心的均方根误差RMSE作为类宽,从而构建类区域;
8)加权计算类间分离度d,并选取d最大的小波组作为特征向量组;
9)运用支持向量机对已知样本的特征向量组进行训练,最后运用训练结果对未知样本进行识别。
支持向量机(Support Vector Machine,SVM),是常见的一种判别方法,在机器学习领域,是一个有监督的学习模型,通常用来进行模式识别、分类以及回归分析,该方法的核心思想是权衡学习能力和训练模型的复杂度。本文考虑到该分类方法的发展较为成熟,分类效果较为稳定,且在个体识别领域的研究大多采用该方法对提取到的特征向量进行分类,故本文选取该方法对特征向量组进行训练,并运用训练结果对未知样本进行识别。
5 仿真实验与分析
5.1 实验条件
本文选取了8类小波基共54种不同的小波变换,如表2所示。
本文选择的功率放大器模型为Taylor级数模型,本文研究的对象是同型号的功率放大器的细微特征,为了体现其“细微”的程度,选择了9阶系数进行建模,表达式如下:
(16)
其中Von表示第n个功率放大器的输出电压,Vin表示输入电压。
上式建立了三个差异细微的功率放大器的模型,由图5可见其差异较为细微。
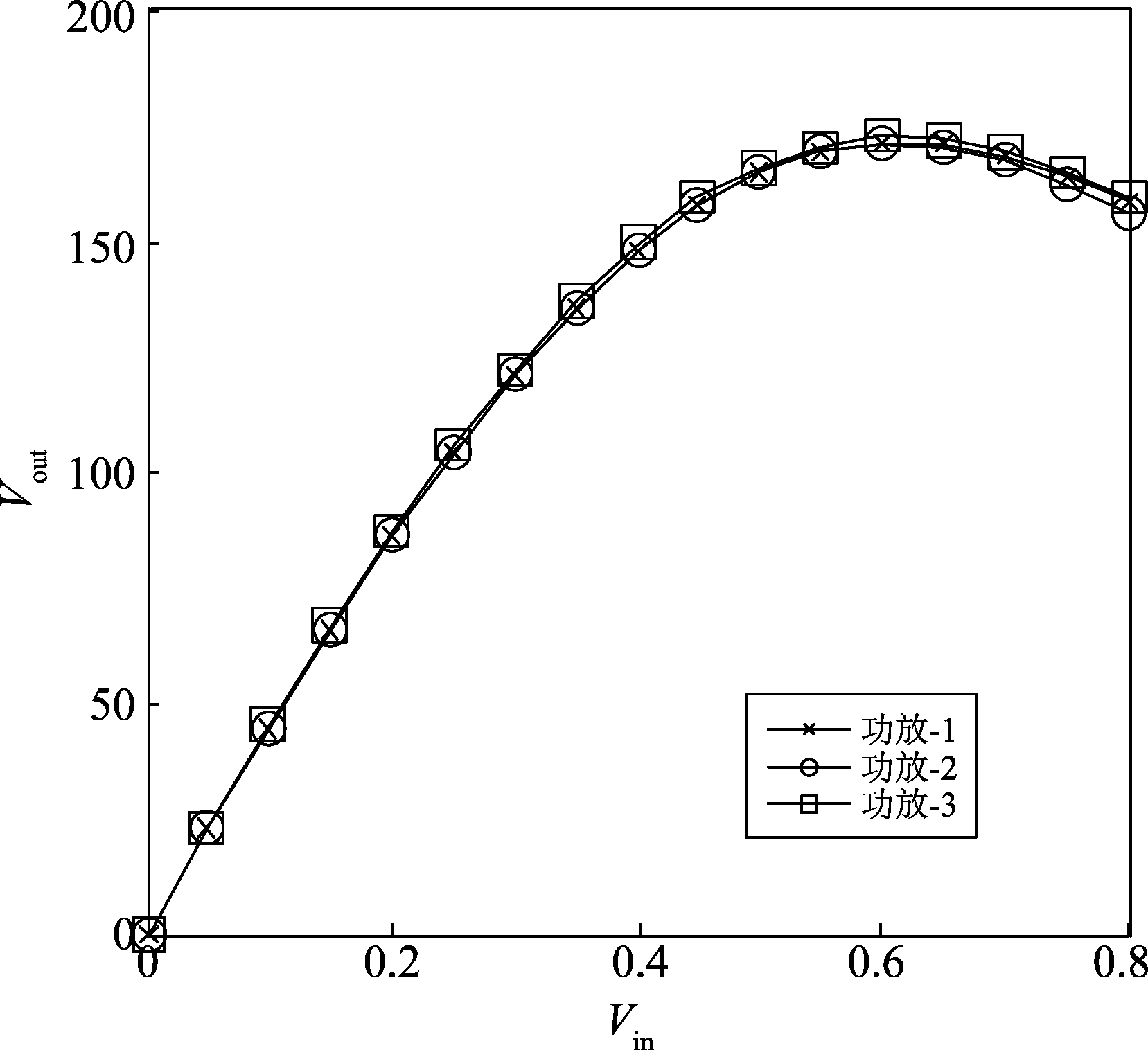
图5 功率放大器增益差异对比
Fig.5 Comparison of gain difference of power amplifier
表2 小波基及其参数设置
Tab.2 Wavelet basis and its parameter settings

小波基参数设置Haar小波-Meyer小波-Morlet小波-Daubechies小波db1、db2、db3、db4、db5、db6、db7、db8、db9、db10Symlets小波sym2、sym3、sym4、sym5、sym6、sym7、sym8Coiflets小波coif1、coif2、coif3、coif4、coif5BiorSplines小波bior1.1、bior1.3、bior1.5、bior2.2、bior2.4、bior2.6、bior2.8、bior3.1、bior3.3、bior3.5、bior3.7、bior3.9、bior4.4、bior5.5、bior6.8ReverseBior小波rbio1.1、rbio1.3、rbio1.5、rbio2.2、rbio2.4、rbio2.6、rbio2.8、rbio3.1、rbio3.3、rbio3.5、rbio3.7、rbio3.9、rbio4.4、rbio5.5、rbio6.8
本文在高斯信道下,选择了码元速率为75 Baud的2FSK(f1=1550 Hz, f2=1800 Hz)信号作为输入信号,同一信噪比条件下针对三台功率放大器每次截获40个随机生成的码元序列,每台生成300个样本,共生成900个样本,其中每一台默认随机选取20%的样本作为训练样本,剩余80%作为识别样本,本文在0~20 dB信噪比条件下,取整数信噪比进行了21次样本仿真,共得到了21×900个样本,从中每个信噪比下随机选取10个训练样本,剩余21×890个样本作为待识别样本。
5.2 仿真与分析
首先进行步骤(1)~(3)得到一维小波各重心方差σ2的降序排名如表3所示。
由图6(a)可以看出sym5小波的分离度十分理想,但是小波的复杂度值LZC对信噪比十分敏感,在实际应用时,对信噪比估计的精度要求比较高。在本文功放非线性的实验条件下,多种信噪比估计方法的误差通常都达到了±5 dB,因此一维sym5、coif4小波良好的分离性就不能被很好地利用。也正是该信噪比敏感的特性,也使得类似于文献[10]单一信噪比下的研究实际应用价值大幅度降低,如图6(b),在10 dB下的训练识别效果将非常好,但是却难以适用于信噪比发生变化时的情况。基于这样的情况,本文提出了一种利用分离度极差的小波,作为信噪比相对参考值的方法,如图6(c)所示,rbio3.3小波在面对信噪比变化时呈现出了较为线性的变换且三个个体间的平均差异在±1 dB,可以观察到图6(a)sym3小波在信噪比≥5 dB时,就已经可以克服1 dB以内的信噪比估计误差了。
因此在上文所述“二维小波构建”时,选取sym5和rbio3.3小波基构成特征向量s1(i)=[LZCrbio3.3(i)LZCsym5(i)]。同时选取(sym5-coif4)、(sym5-db4)2组小波基作为对比构成特征向量s2(i)=[LZCsym5(i)LZCcoif4(i)]和s3(i)=[LZCsym5(i)LZCdb4(i)]。
下面以s1(i)=[LZCrbio3.3(i)LZCsym5(i)]为例,介绍步骤(5)~(7)的实验过程。
表3 一维小波分离度
Tab.3 The separation degree of one-dimensional wavelet
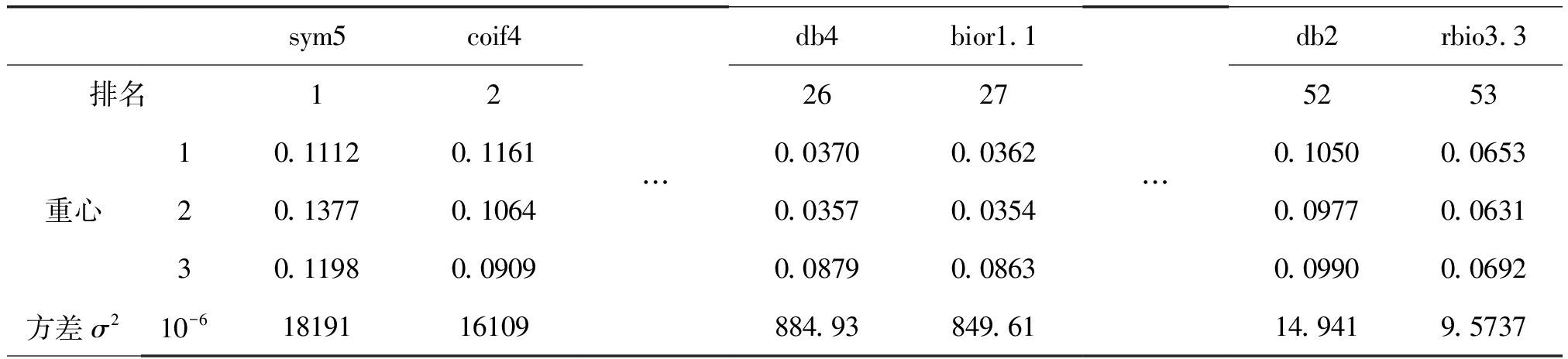
sym5coif4排名12重心方差σ210.11120.116120.13770.106430.11980.090910-61819116109…db4bior1.126270.03700.03620.03570.03540.08790.0863884.93849.61…db2rbio3.352530.10500.06530.09770.06310.09900.069214.9419.5737
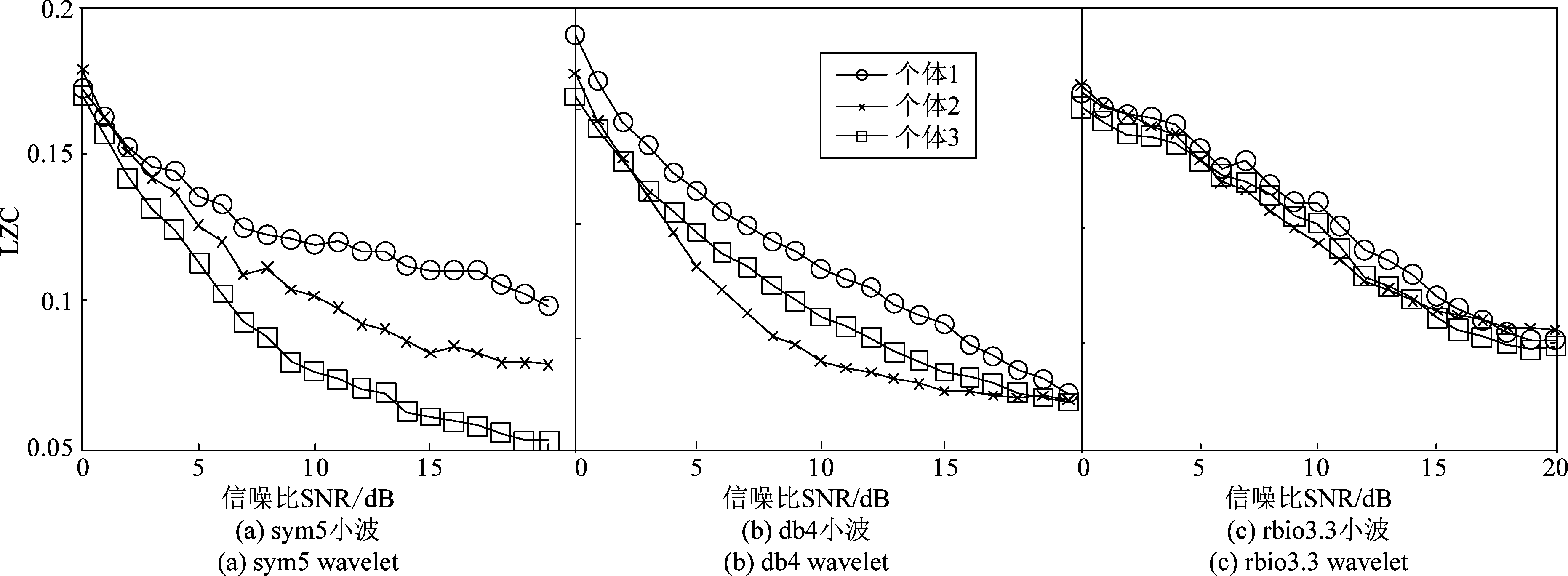
图6 一维小波特征参数分离度
Fig.6 The separation of characteristic parameters of one-dimensional wavelet
由式(8)~(13)三次多项式拟合类中心:
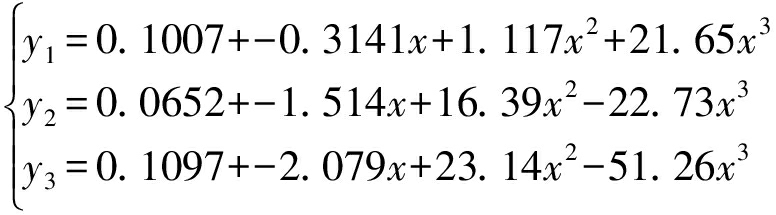
再计算类内均方根误差得到类宽度:
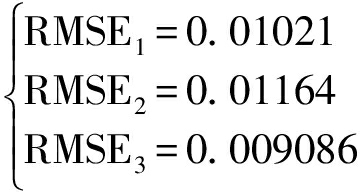
由此可以构造类区域如图7所示。
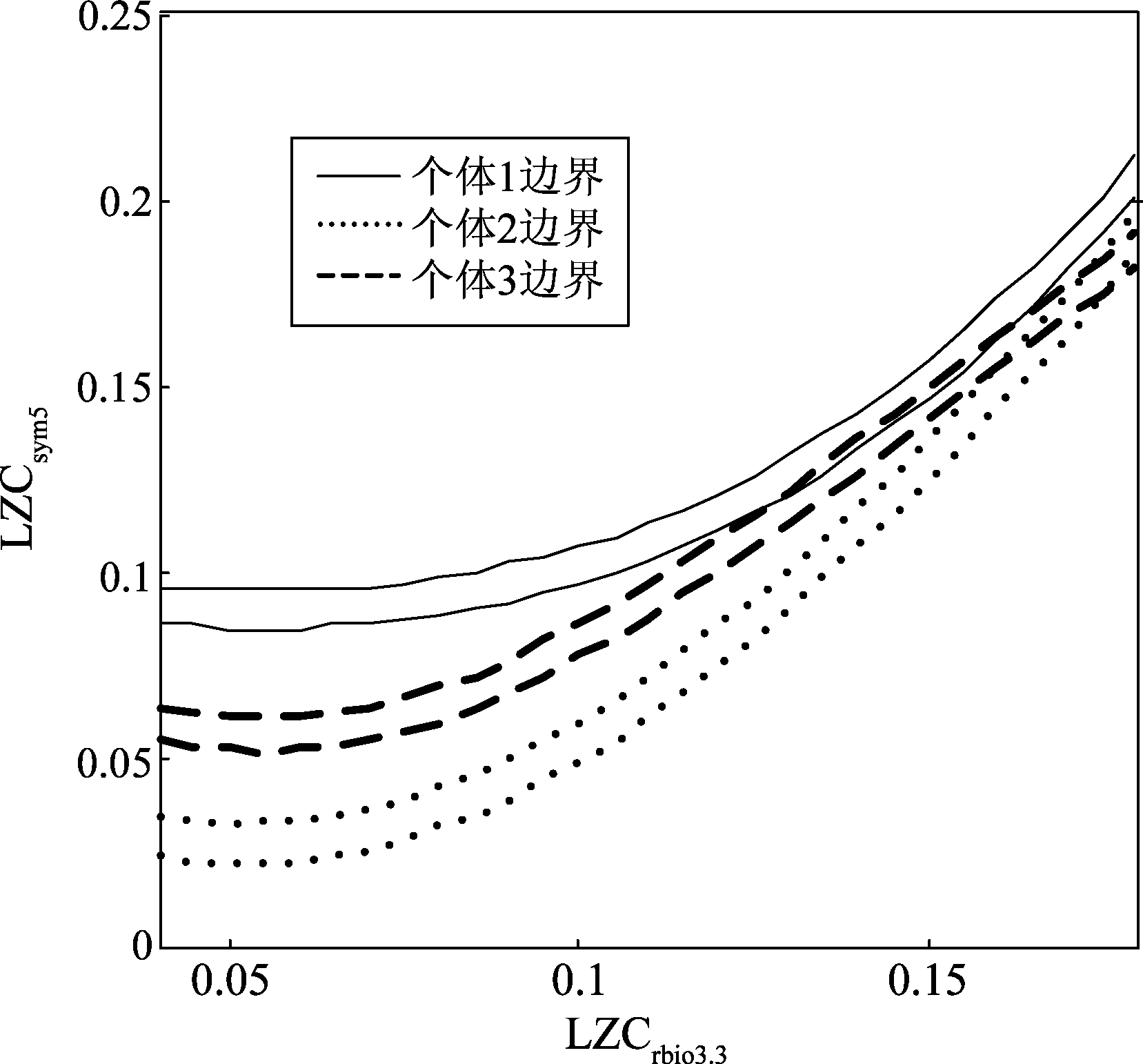
图7 s1类区域图
Fig.7 s1Class area sketch map
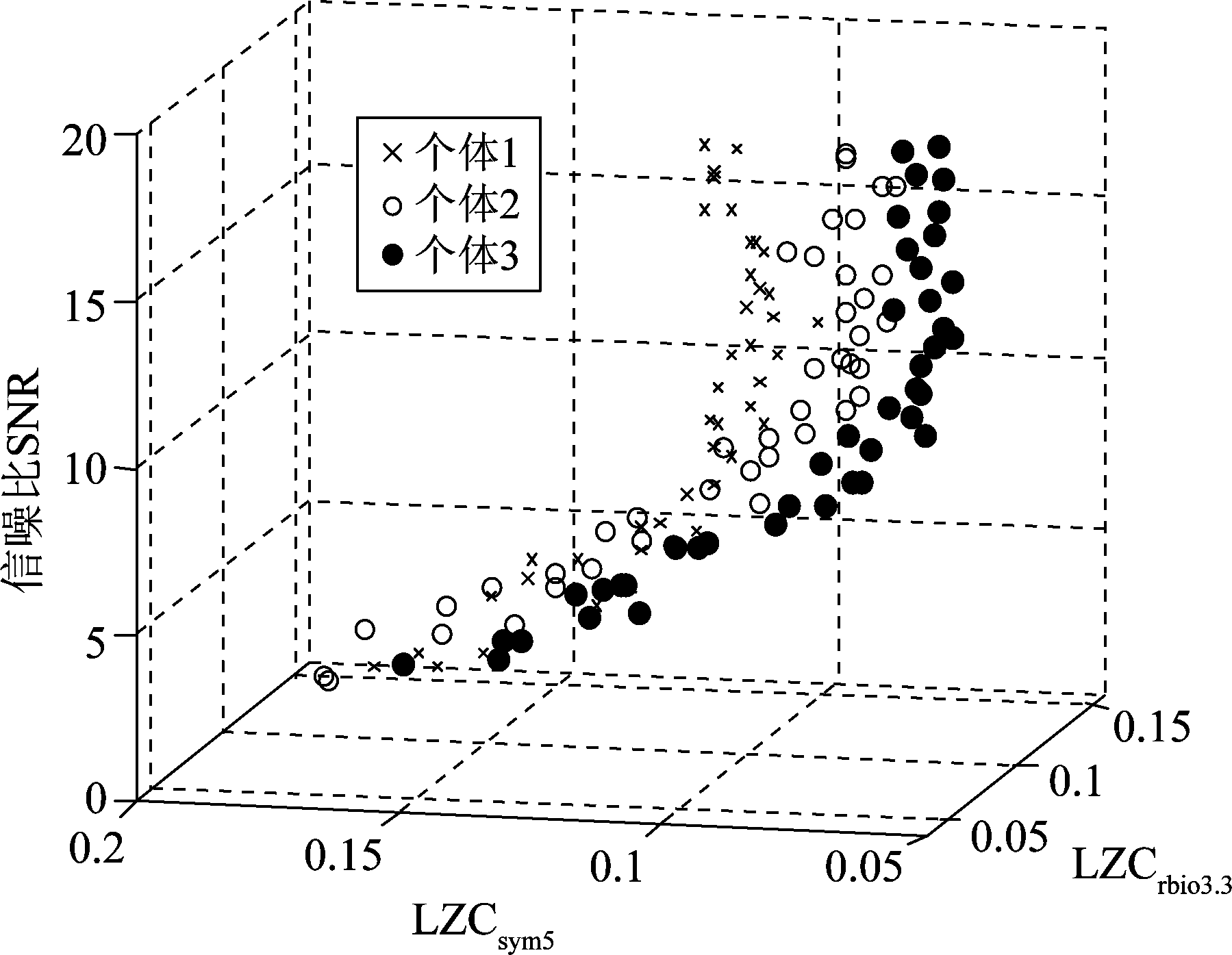
图8 特征分布图
Fig.8 Characteristic distribution diagram
由图7、图8可以看出,在高信噪比的情况下,个体间的分离度很高。根据式(15)计算出类间分离度d1=0.0164。同理可以计算得到d2=0.0132,d3=0.00975。由此看来特征向量s1(i)=[LZCrbio3.3(i)LZCsym5(i)]的识别效果应该是最好的。其特征分布如图8所示,可以看出类间可分性比较明显。下面进行仿真试验验证,识别效果如图9所示。
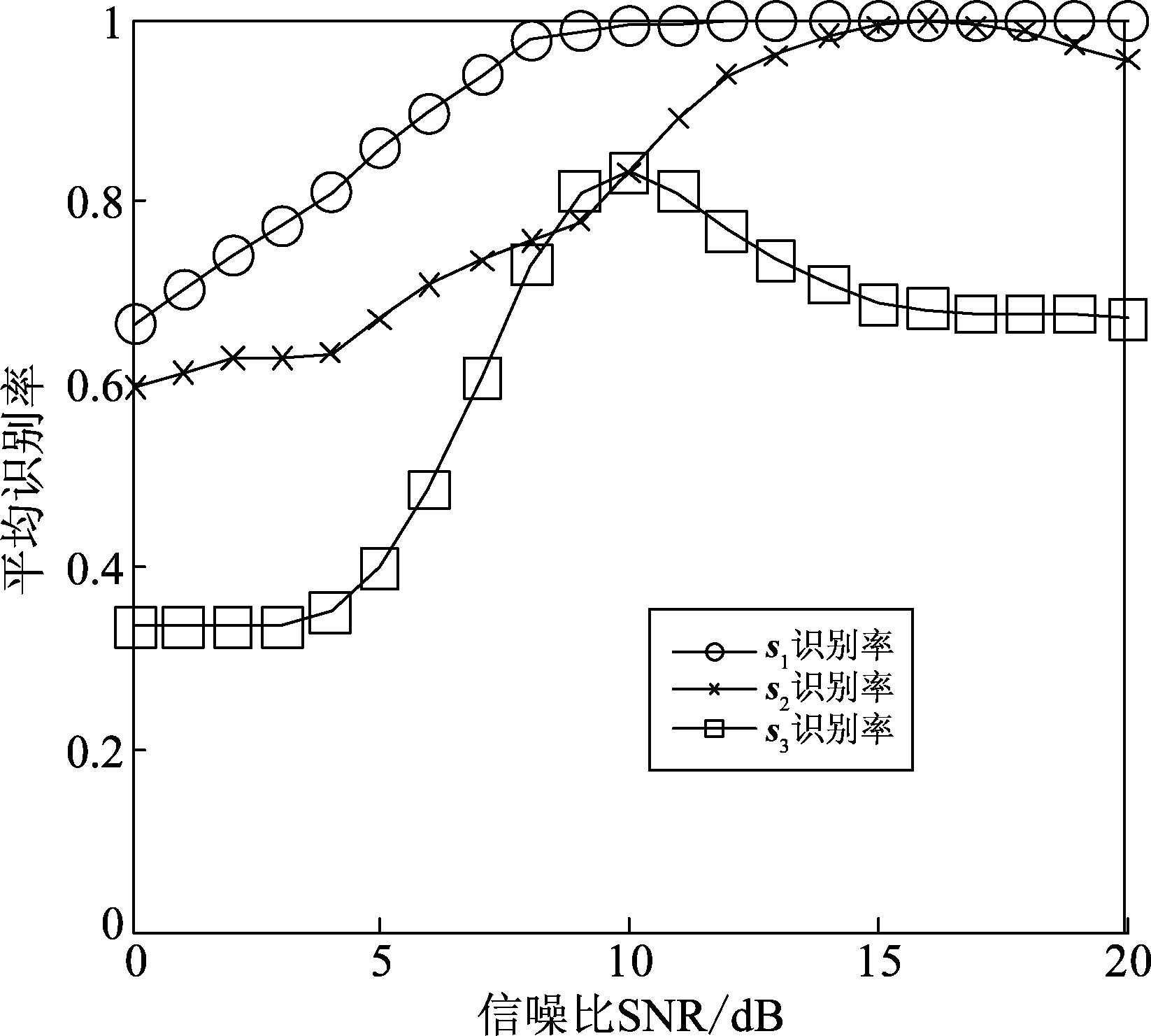
图9 各特征向量平均识别率
Fig.9 Average recognition rate of each feature vector
由图9可见,在本文实验条件下,类间分离度最低的特征向量s3(i)=[LZCsym5(i)LZCdb4(i)]仅在信噪比为10 dB时获得了约80%的识别,其他情况下识别效果并不理想,类间分离度居中的特征向量s2(i)=[LZCsym5(i)LZCcoif4(i)]在信噪比大于13 dB时,识别率超过90%,识别效果较好。类间分离度最高的特征向量s1(i)=[LZCrbio3.3(i)LZCsym5(i)]在信噪比大于6 dB时,方法的识别率超过90%,取得了较好的识别效果,证明了方法的有效性。
6 结论
本文针对通信辐射源的个体识别问题,研究了基于功率放大器非线性特性的特征提取方法,提出了一种基于小波变换的通信辐射源识别方法,针对小波基多样性的现状,提出了一种能够筛选出最优小波基的方法,针对FSK信号,进行了基于SVM支持向量机的训练及分类,并进行了计算机仿真。结果表明在噪声环境中模型间差异较小的情况下,通过计算类间分离度筛选出了最优小波组构成特征向量,收到了较好的识别效果,解决了信噪比变化环境中功率放大器个体差异较小情况下文献[10]方法失效的问题。下一步应针对含多径、衰落等实际信道环境展开通信个体识别研究,使方法更具实际应用价值。
[1] Dudczyk J, Kawalec A, Owczarek R. An application of iterated function system attractor for specific radar source identification[C]∥International Conference on Microwaves, Radar and Wireless Communications. IEEE Xplore, 2008:1- 4.
[2] Chan Y T, Gadbois L, Yansouni P. Identification of the modulation type of a signal[C]∥Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP. IEEE, 1985:838- 841.
[3] 张旻, 王若冰, 钟子发,等. 通信电台个体识别中的载波稳定度特征提取技术研究[J]. 电子与信息学报, 2008, 30(10):2529-2532.
Zhang Min, Wang Ruobing, Zhong Zifa, et al. Study on the Techniques on Extracting Carrier Frequency Stability of Individual Communication Transmitter Identification[J]. Journal of Electronics and Information Technology, 2008, 30(10):2529-2532.(in Chinese)
[4] 张泽君, 程伟, 杨瑞娟. 基于噪声功率估计的通信电台个体识别性能仿真研究[J]. 空军预警学院学报, 2015(4):266-270.
Zhang Zejun, Cheng Wei, Yang Ruijuan. Simulation study on individual identification performance of communication station based on noise power estimation[J]. Journal of Air Force Early Warning Academy, 2015(4): 266-270. (in Chinese)
[5] 王伦文, 钟子发. 2FSK信号"指纹"特征的研究[J]. 电讯技术, 2003, 43(3):45- 48.
Wang Lunwen, Zhong Zifa. Fingerprint characters of 2FSK signal of[J]. Telecommunication Engineering, 2003, 43(3): 45- 48. (in Chinese)
[6] Huang G, Yuan Y, Wang X, et al. Specific Emitter Identification for Communications Transmitter Using Multi-measurements[J]. Wireless Personal Communications, 2016:1-20.
[7] 唐智灵. 通信辐射源非线性个体识别方法研究[D]. 西安:西安电子科技大学, 2013.
Tang Zhiling. Research on nonlinear identification method of communication emitter[D]. Xi’an: Xi’an Electronic and Science University, 2013.(in Chinese)
[8] Talbot K I, Duley P R, Hyatt M H, et al. Specific emitter identification and verification[J]. Technology Review, 2003,32(1): 27-33.
[9] Liu M W, Doherty J F. Specific Emitter Identification using Nonlinear Device Estimation[C]∥Sarnoff Symposium. IEEE, 2008:1-5.
[10] 梁颖. 基于跳频信号的指纹识别研究[D]. 北京:北京邮电大学, 2014:29-33.
Liang Ying. Research on fingerprint identification based on frequency hopping signal[D]. Beijing: Beijing University of Posts and Telecommunications, 2014:29-33.(in Chinese)
[11] Loyka S L. On the use of Cann's model for nonlinear behavioral-level simulation[J]. IEEE Transactions on Vehicular Technology, 2000, 49(5):1982-1985.
[12] 许丹, 柳征, 姜文利,等. 窄带信号中的放大器“指纹”特征提取原理分析及FM广播实测实验[J]. 电子学报, 2008, 36(5): 927-932.
Xu Dan, Liu Zheng, Jiang Wenli, et al. Analysis of the principle of fingerprint feature extraction in narrowband signals and experiment of FM broadcast measurement[J]. Acta Electronica Sinica, 2008, 36(5): 927-932. (in Chinese)
[13] Daubechies I. The Wavelet Transform. Time-Frequency Localisation and Signal Analysis[J]. IEEE Transactions on Information Theory, 2015, 36(5):961-1005.
[14] Allouche J P. On the complexity of infinite sequences. (Sur la complexité des suites infinies.)[J]. Bulletin of the Belgian Mathematical Society Simon Stevin, 1994(2).


