1 引言
随着现代无线通信技术的发展，绿色通信已经引起了人们广泛关注，而能量采集这项技术已经有了一些研究，并且开始应用于无线传输网络，比如传感网中的传感器使用能量采集技术可以延长节点的使用寿命。而无线能量传输这项技术已经有了许多研究[1-3]，且开始应用于无线通信中。无线能量传输技术的应用可以让系统更灵活的调动资源，提高系统的性能。
在能量采集通信系统中的最优功率分配方面，已经有了一些文献对其进行研究。在文献[4]中，针对单用户的能量采集通信系统离线场景，以最小化传输完成时间为目标，作者研究了两种数据到达情况下的最优分组调度问题。文献[5]考虑了电池容量受限这一条件，首先证明了传输时间最小化与系统吞吐量最大化问题具有一致性，然后提出了吞吐量最大化的功率分配方法。文献[6]讨论了信道时变情况下吞吐量最大化的问题，在离线场景中提出了定向注水算法，然后运用动态规划知识研究了在线情况下的功率分配问题。文献[7]放宽限制条件，只考虑总能量约束提出了几何注水算法，然后在此基础上加入能量因果约束提出了递归几何注水算法。
对于能量采集中继系统中的优化问题也有许多文献进行了讨论。文献[8]研究了传统的三节点通信问题，其中中继节点能量采集供电，而源节点为总能量限制，作者同时考虑全双工和半双工两种中继工作模式对系统吞吐量最大化问题进行了研究，提出了最优的功率分配方案。文献[9]针对中继蜂窝异构网络，利用最优条件以及次梯度算法，提出了系统容量最大化的功率分配算法。文献[10]研究了放大转发中继网络，讨论了时间切换和功率分割两种传输方案，针对有无时延要求对系统吞吐量进行了性能分析。在文献[11]中，源节点为能量采集，中继节点有总能量限制和平均功率限制且是半双工模式，作者考虑源节点采取定向注水算法对传输过程进行时间划分，然后再根据能量和数据因果性对功率进行优化调整。文献[12]针对中继系统配置大规模天线的场景，提出了三种天线选择方案，并通过理论和仿真分析了三种方案各自的优缺点。文献[13]中源和中继节点都具有能量采集功能，信道为时变衰落信道，针对数据可存储和不可存储两种中继，同时讨论了离线和在线功率分配算法。文献[14]将重点放在了对放大转发中继网络的在线功率分配算法的研究，将联合优化问题转化为李雅普诺夫优化问题进行求解，并仿真验证了算法性能。
无线能量传递技术的出现引发了新的无线网络中的功率优化问题。文献[15]将无线能量传递引入中继信道、双向信道以及多址信道中，且假设能量单向传递，对场景进行建模和优化，并且提出了二维注水算法来分配功率。文献[16]相较[15]变成了能量可双向传递，且将优化问题分为功率优化和传递能量优化两个子优化问题进行求解，在中继场景中提出了“双流水”注水算法。
本文所研究的是中继节点和源节点都为能量采集供电的无线传输场景，信道为时变衰落信道，能量可双向传递，中继是全双工工作，且数据不可存储，即中继在一个时隙中需要转发源发来的所有数据，在优化前已知所有的信道信息和能量到达，即在离线场景下进行全局优化。具体步骤为：首先对优化问题进行简化，然后使用拉格朗日乘子法和KKT条件解优化，假设能量传递无损耗，即传递效率为100%，提出理想的最优功率分配方案，然后以此方案为基础，在满足能量因果性、数据因果性和实际传递效率的条件下，针对出现能量传递的时隙进行传递能量和发射功率的优化。
2 系统模型
考虑一个三节点的无线传输中继系统，源节点先将数据发送给中继节点，中继节点再将数据转发给目的节点，系统模型与文献[16]相似，如图1所示。在此场景中，假设数据传输时长为N个时隙，源节点和中继节点都具有能量采集功能，在时隙i开始采集的能量分别为Esi和Eri。源节点和中继节点之间可以能量传递，传递效率分别为αs和αr，源节点和中继节点在时隙i传递的能量分别为δsi和δri。假设电池容量足够大，采集的能量不会溢出，且采集的能量全部用于数据传输和协作，中继节点采用全双工的工作模式，并且采用译码转发模式，数据不可存储，即在一个时隙内需要转发源节点当前时隙发送过来的所有数据。
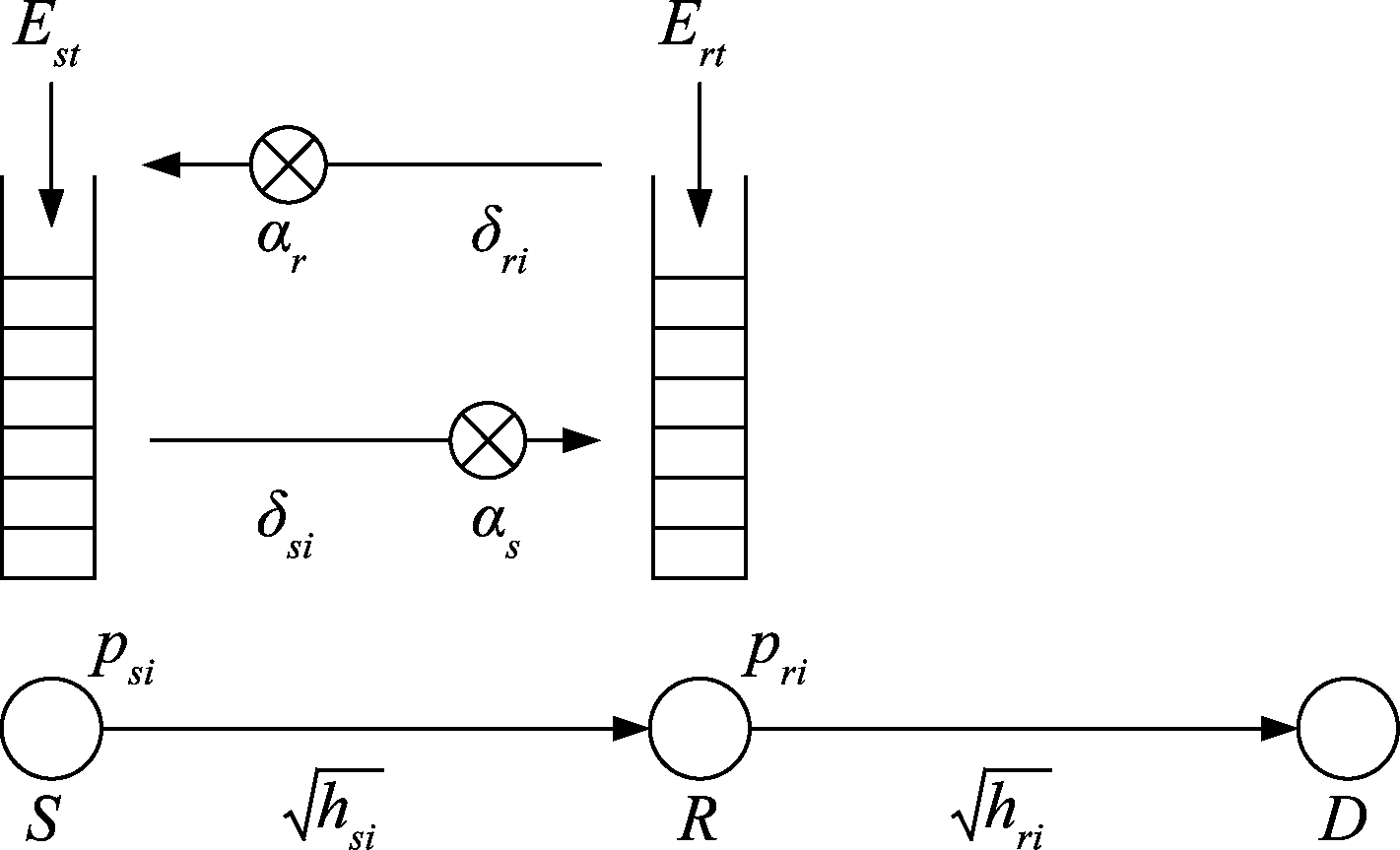
图1 系统模型
Fig.1 System model
中继节点和目的节点接收到的信号可以表示为：
(1)
(2)
其中，xsi和xri分别为具有单位功率的源和中继在i时刻发送的信号，psi和pri分别为源和中继在i时刻的发射功率，
和
分别为源-中继和中继-目的信道增益，两个参数相互独立且都服从瑞利分布。nri和ndi分别为中继和目的处的噪声，本文假设都为均值为0方差为1的加性高斯白噪声。根据香农公式，源和中继的瞬时传输速率可以分别表示为：
Rsi=log2(1+hsipsi)
(3)
Rri=log2(1+hripri)
(4)
则系统吞吐量表达式为
Ri=min(Rsi,Rri)
(5)
本文假设系统在功率分配前已知全部的信道信息和能量达到情况，即在离线场景下讨论系统吞吐量最大化的问题[16]。
3 能量协作中继系统的功率优化分配
根据能量因果性和数据因果性，以最大化系统吞吐量为目标，优化问题P1可以描述为：
(6)
(7)
(8)
log2(1+hripri)≤log2(1+hsipsi),∀i
(9)
pri,psi,δri,δsi≥0,∀i
(10)
其中，条件(7)、(8)分别表示中继节点和源节点处的能量因果性，(9)表示数据因果性，即中继转发的数据量不会超过源发给中继的数据量，(10)表示功率和传递能量的非负性。
由于中继节点数据不可存储，而源和中继可以相互传递能量，所以考虑最优情况，源和中继的功率应该满足：
hsipsi=hripri
(11)
证明：假设最优解的情况下存在某个时隙满足hsipsi>hripri，则该时隙的吞吐量为log2(1+hripri)，而由于中继和源之间可以能量传递，一定存在ΔE>0(ΔE为该时隙源向中继传递的能量值)，使得等式log2(1+hri(pri+αsΔE))=log2(1+hsi(psi-ΔE))成立，那么该时隙的吞吐量log2(1+hri(pri+αsΔE))>log2(1+hripri)，与最优矛盾。
根据式(11)得到了源和中继功率之间关系的等式，因此，源的功率可以由中继功率来表示，原问题可以消去一个变量，简化后的问题P2为：
(12)
(13)
(14)
pri,δri,δsi≥0, ∀i
(15)
采用文献[15]的方法，通过将变量pri转化为Rri=log2(1+hripri)， P2等价于一个凸优化问题，因此可以运用凸优化知识，则P2的拉格朗日方程为：
(16)
为了简化运算，且pri>0在大多数情况下都满足，在这里设拉格朗日乘子ηi=0。将拉式方程分别对变量求导，得到的KKT条件为：
(17)
(18)
(19)
剩余的KKT条件为：
(20)
(21)
ρkδrk=0,ψkδsk=0, ∀k
(22)
观察以上所有的KKT条件，发现变量数量较多，不能够直接求解获得最优解。为了能够继续求解，假设能量传递无损耗，即传递效率αs和αr都为100%，则(17)、(18)和(19)可以简化为：
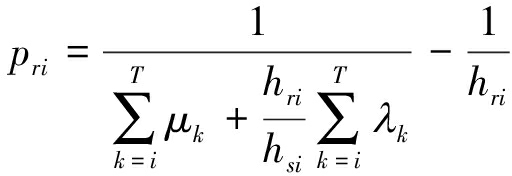
(23)
ρi+ψi=0
(24)
其中ρi和ψi都是非负拉格朗日乘子，所以结合(24)，可得ρi=ψi=0，则
式(23)可以简化成：
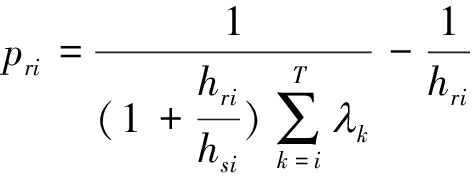
(25)
式(25)表达式类似于注水的形式，其中注水值为
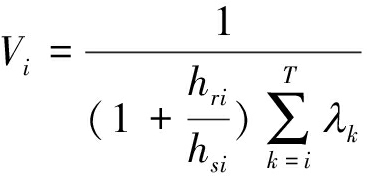
(26)
式(25)中的hri值是已知的量，因此只要求得注水值Vi即可求出最优功率。
接下来讨论最优解需要满足的几个条件：
(1)当某个时隙存在能量传递时，即δri>0或δsi>0，该时隙结束时，源节点中的电池能量为0或者中继节点中的电池能量为0，这个条件参考了文献[15]中的引理3。
(2)从出现能量传递的时隙的下一个时隙开始，到下一次出现能量传递的时刻为止，因为电池中的能量不为0，所以这些时隙的拉格朗日乘子λ或μ为0，根据式(26)可以算出这些时隙的注水等级满足比例关系，例如某一符合条件的时间段为从j时刻到k时刻，在这一时间段中的注水值满足：
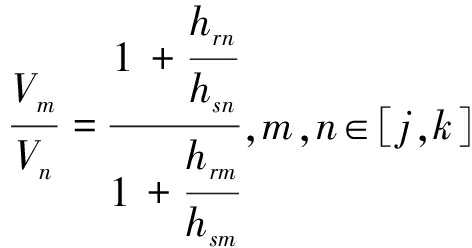
(27)
(3)由于在这里讨论最优解的前提是能量传递无损耗，可能存在多种最优解的情况，这时候应该选取能量传递次数最少的最优解，这是由于后面需要讨论能量传递效率小于100%的情况，能量传递次数越多，说明浪费的能量越多。
(4)当传输结束时，源和中继用完所有采集的能量和接收的能量。
根据以上总结的条件，分配功率的第一步需要将整个传输过程进行分段。首先假设只有一个时隙，则最优注水值V1可以通过下面的方程计算出：
(28)
判断出现能量传递的条件是pr1>Er1或者ps1>Es1。以此类推，当时隙数大于等于2时，设
和
分别表示源和中继从初始时刻开始到i时隙采集的总能量，
和
分别表示源和中继从初始时刻开始到i时隙所消耗的总功率，得到以下方程组：
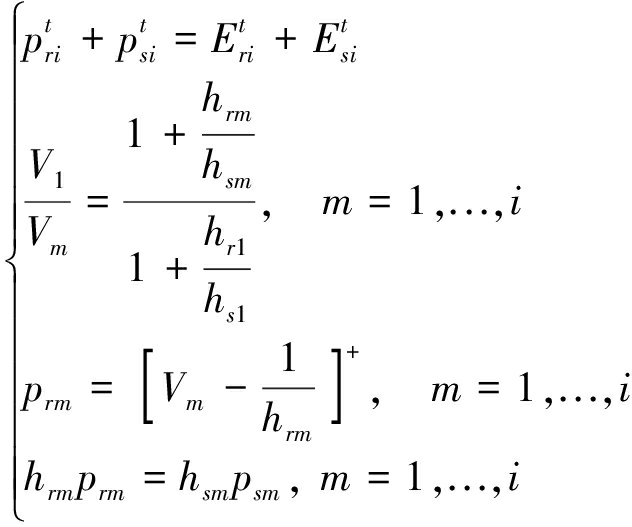
(29)
以上方程组计算的是到i时隙为止，源和中继用光所有能量时的功率分配，如果存在1≤j≤i，使得
说明此功率分配方案违反能量因果性，此方案需要被舍弃。如果满足能量因果性，则根据出现能量传递的判断条件，找出此方案中最早出现能量传递的时隙并记录为iM。从第一个时隙开始到最后一个时隙，计算出所有的功率分配方案，去掉不满足能量因果性的方案，从剩余的方案中找出最大的iM所对应的方案，即找出能量传递出现最晚的功率分配方案，选取第一个时隙到iM时隙这一段时间的功率分配作为整个传输过程的第一段。第一段选取完成后，剩余时隙重复同样的方法进行分段，完成所有时隙的功率分配。
具体的功率分配算法步骤如表1所示。
表1 能量传递效率为100%时中继系统功率分配算法
Tab.1 Power allocation algorithm with 100% energy transfer efficiency for relay systems
算法1: 能量传递效率为100%时中继系统功率分配算法1.初始化:psi=pri=0,δri=δsi=0,ii=1,k=1;2.while ii≤N3. iM(k)=0, ∀k;4. k=0;5. for i=ii:N6. k=k+1;7. 根据方程组(22)计算出prj,psj,Vj,j=ii,...,i;8. for j=ii:i9. if ptrj+ptsj>Etrj+Etsj10. break;
续表1
11. end if12. if ptrj>Etrjor ptsj>Etsj13. iM(k)=j;14. break;15. end if16. if j==i17. iM(k)=i;18. end if19. end for20. end for21. for j=ii:maxk(iM(k))22. 按照maxk(iM(k))所对应的方案分配prj和psj,计算δrj和δsj;23. end for24. ii=maxk(iM(k))+1;25.end while
现在讨论能量传递效率不为100%的情况。通过以上步骤已经得到了能量传递效率为100%时的最优功率分配方法，且此功率分配方案的原则是能量传递尽量少出现，则能量传递效率为αs和αr时的分配方案可以在此基础上进行修改，且只需要在出现能量传递时的时隙进行功率调整即可。在算法1的功率分配方案中，当i时隙出现能量传递，假设
和
分别表示能量传递未发生前中继和源节点中可使用的所有能量， 如果是源传能量给中继，则
而
一定存在Ex>δsi使得：
(30)
则该时隙的功率调整为
相对应的，如果是中继传能量给源节点，则
而Ex满足：
(31)
调整后的功率为
按照此方法调整所有出现能量传递时隙的功率，其他时隙的功率分配保持不变，则能量传递效率为αs和αr时的中继系统功率分配具体步骤如表2所示。
表2 能量传递效率为αs和αr时中继系统功率分配算法
Tab.2 Power allocation algorithm with αs and αr energy transfer efficiency for relay systems
算法2: 能量传递效率为αs和αr时中继系统功率分配算法1. 初始化:得到算法1中的所有pri,psi,δri和δsi;2. for i=1:N3. if ptri>Etri4. Ecri=pri-δsi,Ecsi=psi+(pri-Ecri);5. Solvelog2(1+hsi(Ecsi-Ex))=log2(1+hri(Ecri+αsEx));6. psi=Ecsi-Ex,pri=Ecri+αsEx;7. end if8. if ptsi>Etsi9. Ecsi=Etsi-pts(i-1),Ecri=pri+(psi-Ecsi);10. Solvelog2(1+hri(Ecri-Ex))=log2(1+hsi(Ecsi+αrEx));11. psi=Ecsi+αrEx,pri=Ecri-Ex;12. end if13. end for
4 仿真结果与分析
本文仿真场景采用瑞利衰落信道，且源到中继信道和中继到目的节点的信道相互独立，信道增益期望为
图2和图3对应的能量到达服从[0,2]J的均匀分布，且假设电池容量足够大，传输时隙个数为N，每个时隙的时长为1 s。参考文献[1]和[2]，能量传递效率设为40%。为了对比本文能量可双向传递的算法，本文同时仿真了文献[13]的无能量协作的最优算法、能量仅能单向传递的算法以及每个时隙用完所有能量的能量不存储算法，而能量传递效率为100%时的功率分配算法仅作为上界值来参考。其中仅单向能量传递指的是只允许源传给中继能量或者中继传给源能量，经仿真发现，两种情况下的算法性能差距很小，所以这里仅使用源传给中继能量这种情况下的算法来与其他算法进行比较。
图2所示的是不同算法在不同时隙数下的系统平均吞吐量。其中双向能量传递以及单向能量传递的传递效率都为40%，且能量到达服从均值为1 J的均匀分布。可以看出，当时隙数增加，各算法的吞吐量有所提高，最终趋于平缓，这是由于时隙数多了，可以调动的资源相对变多，功率分配算法能更好的体现价值。纵向比较发现，能量不存储的分配功率方法效果最差，而本文提出的算法优于仅单向能量传递的算法和无能量协作的分配方法，说明具有能量传递功能的中继系统能有效地提高系统的平均吞吐量。而本文的双向能量传递的功率分配算法比较接近理想的上界值，说明算法的修改与推导较为合理。
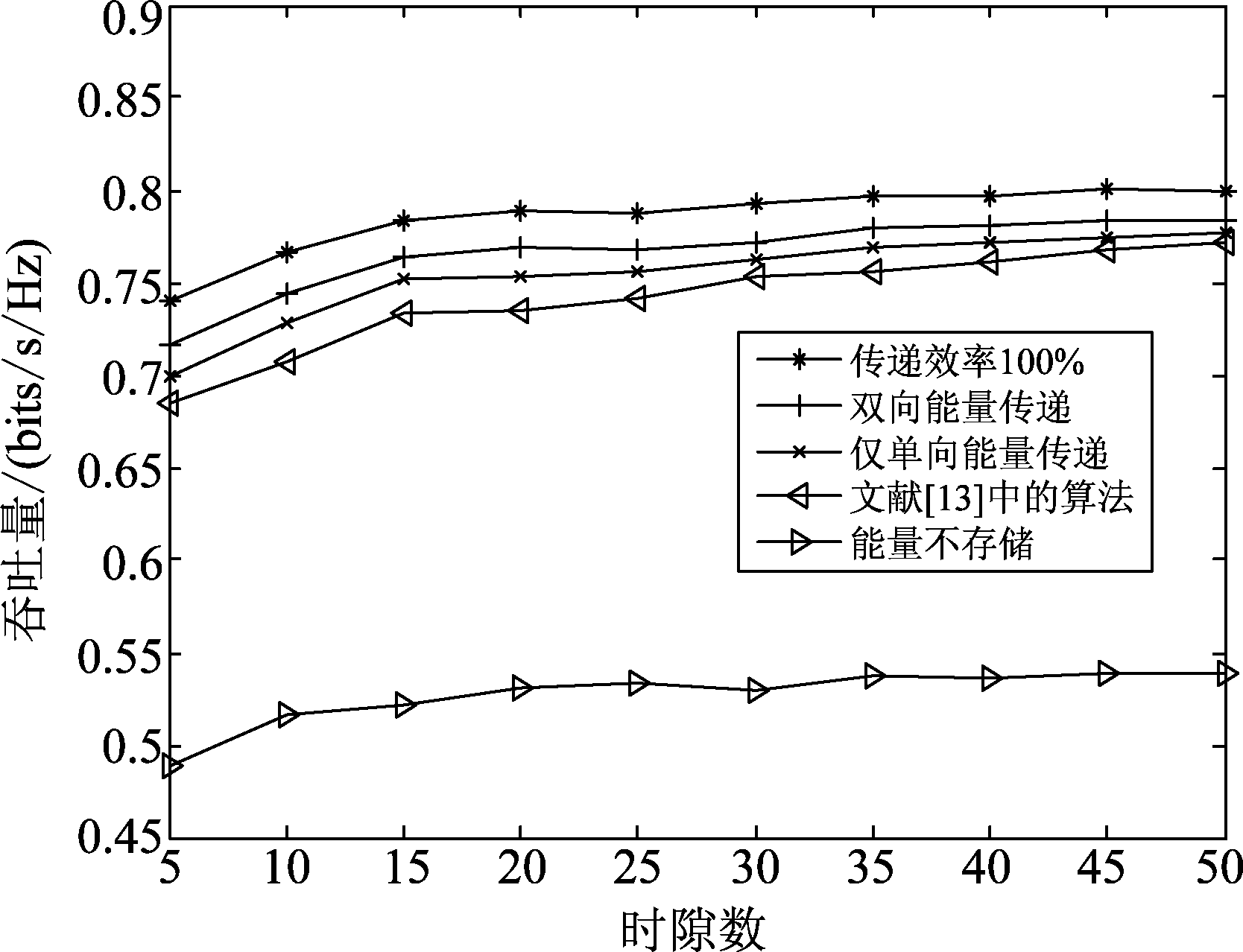
图2 不同时隙数下系统平均吞吐量比较，能量传递效率为40%
Fig.2 The comparison of average system throughput under different time slots with 40% energy transfer efficiency
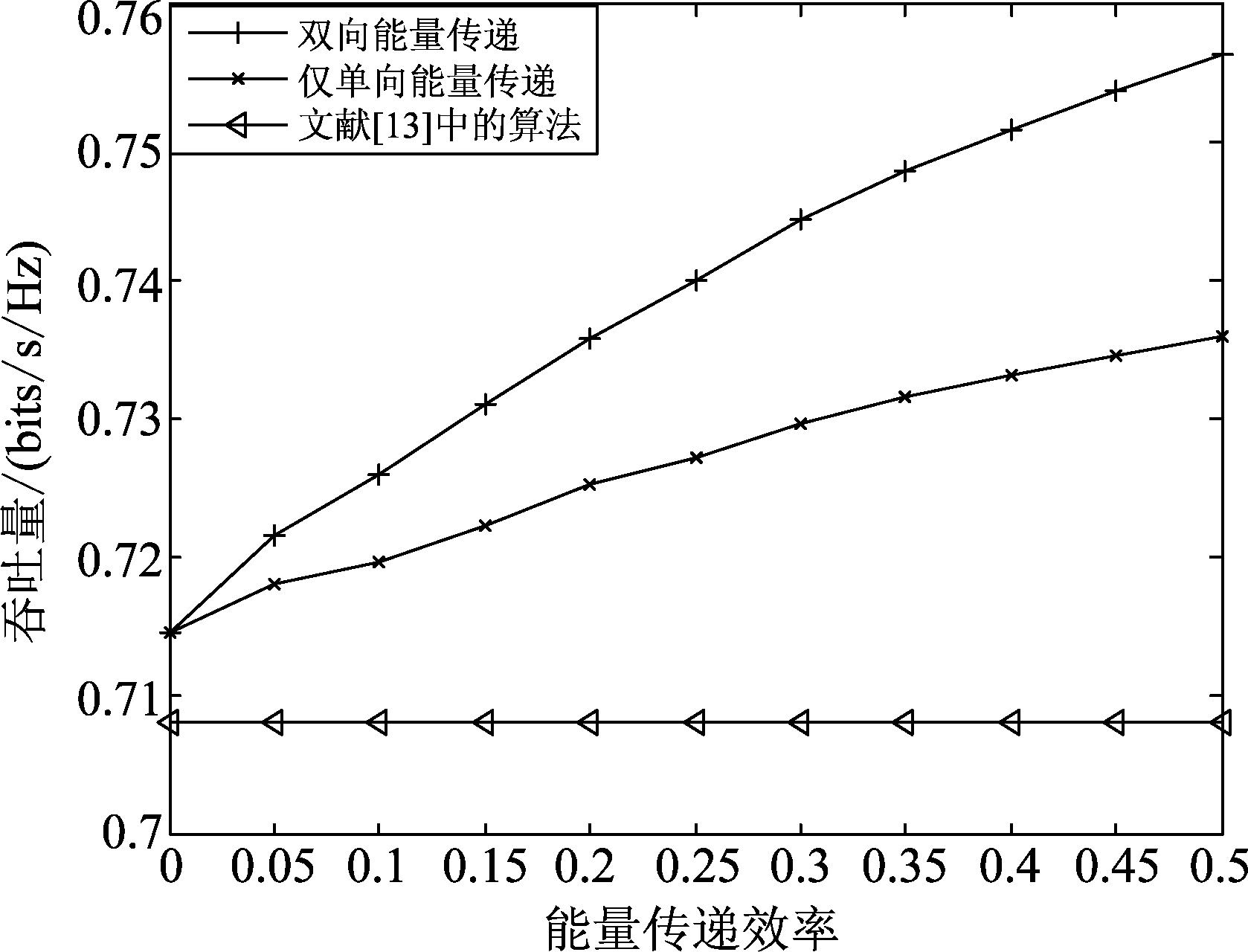
图3 不同能量传递效率下系统平均吞吐量对比，时隙数为10
Fig.3 The comparison of average system throughput under different energy transfer efficiency within 10 time slots
图3所示的是在不同能量传递效率下各个算法的性能，时隙数为固定的N=10，且能量到达服从[0,2]J的均匀分布。从图中可以看出，随着能量传递效率的不断提高，双向能量传递的算法与仅单向能量传递的算法的系统吞吐量都有明显提升，而文献[13]的算法因为与能量传递效率无关，所以性能曲线为一条直线，且算法性能随着能量传递效率的不断提高与可能量传递的算法相比逐渐落后，再一次验证了能量协作的重要性。
图4展示的是各个算法在不同能量到达均值下的系统平均吞吐量图，能量传递效率固定为40%，且时隙数为10。随着能量到达均值的提高，各个算法的系统平均吞吐量都有所提升。从图中还可以发现，当能量到达均值较低时，能量到达随机性较小，可调动的资源较少，几种优化算法性能相近，能量协作的优势不是很明显。而随着能量到达均值提高，能量到达的随机性变大，且可调动的能量资源变多，能量协作的优势逐渐变大，体现了能量协作的重要性。
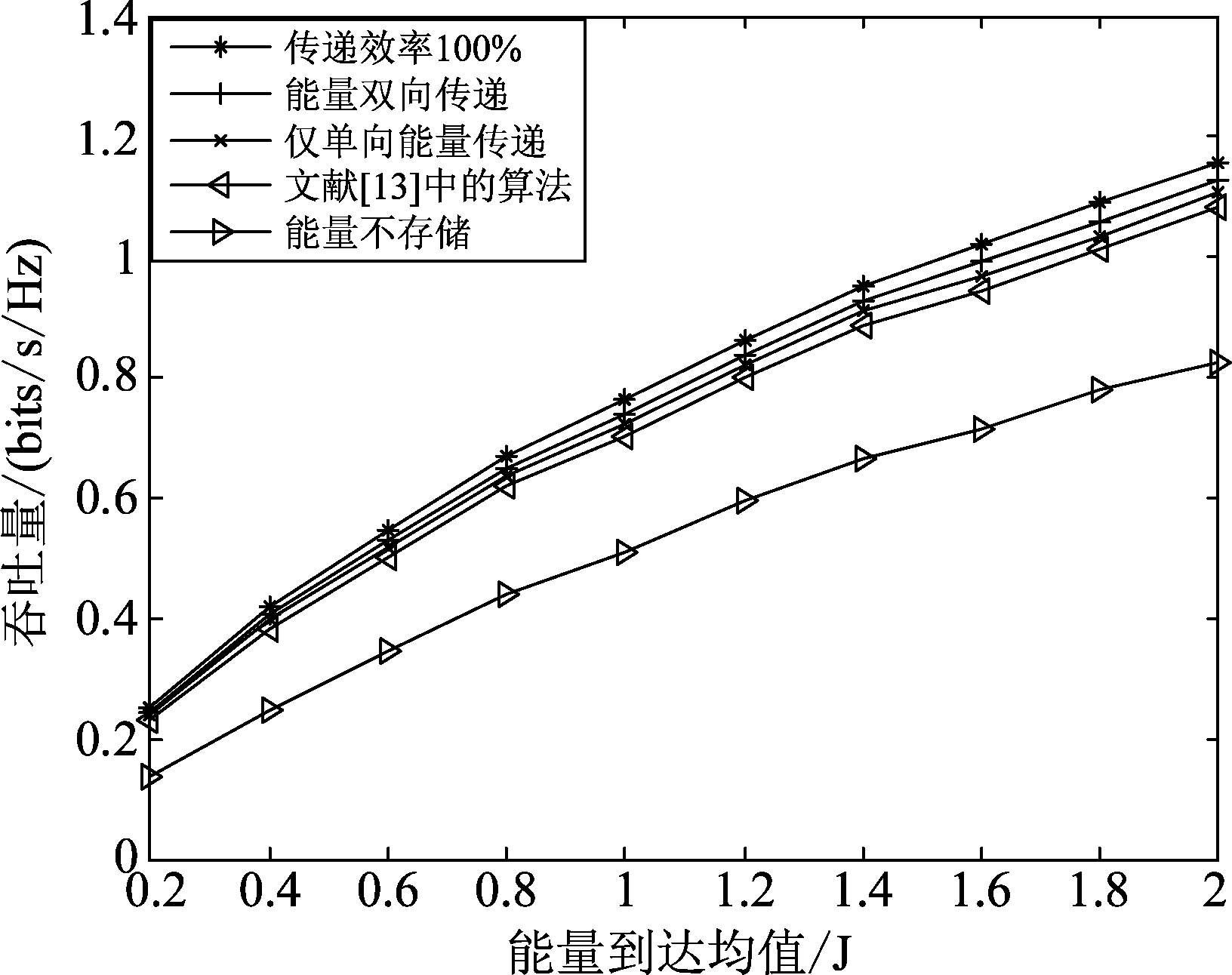
图4 不同能量到达均值下系统平均吞吐量对比，能量传递效率为40%，时隙数为10
Fig.4 The comparison of average system throughput under different average value of energy-arrival with 40% transfer efficiency in 10 time slots
图5所示的是不同平均SNR下各个算法的性能对比图，可以发现与图4趋势基本一致，各算法的性能差距在信道环境变好的情况下有逐渐拉大的趋势，同样体现了能量协作的重要性与本文所提算法的合理性。
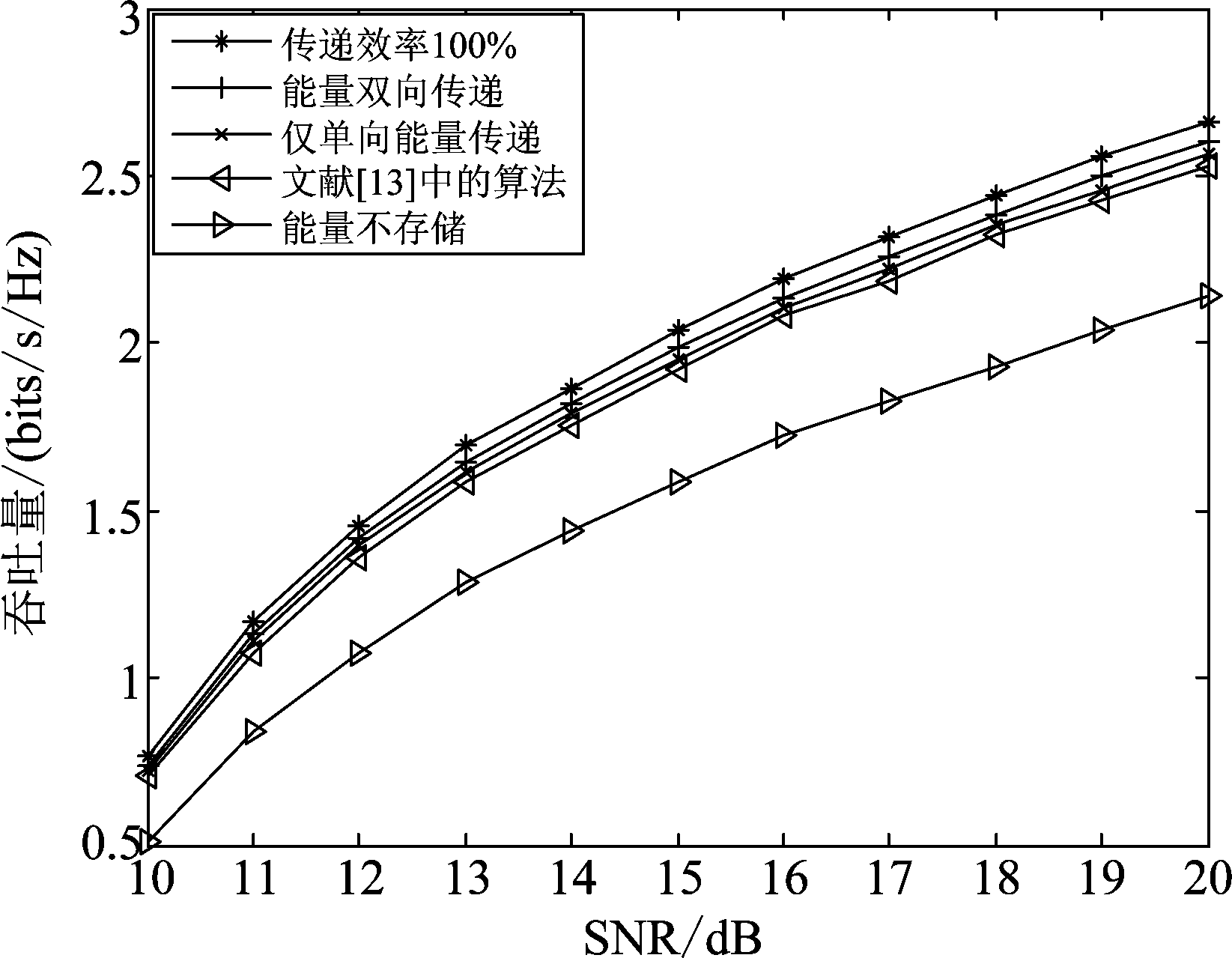
图5 不同SNR下系统平均吞吐量对比，能量传递效率为40%，时隙数为10
Fig.5 The comparison of average system throughput under different SNR with 40% transfer efficiency in 10 time slots
5 结论
本文针对可能量协作的中继系统无线传输数据场景，以最大化系统吞吐量为目标提出了功率分配方案。首先对场景进行建模，提出优化问题，用凸优化知识进行求解，先放宽条件假设能量传递效率为100%，以KKT条件得出的表达式为基础，提出了理想功率分配方法，然后在此算法基础上提出了能量传递效率不为100%时的功率分配算法。仿真结果表明，本文提出的可双向传递能量的功率分配算法优于其他的算法，证明了能量协作能有效提高系统性能。
[1] Jawad A M, Nordin R, Gharghan S K, et al. Opportunities and Challenges for Near-Field Wireless Power Transfer: A Review[J]. Energies, 2017, 10(7):1022.
[2] Giuseppina M, Che W, Wang Q, et al. Wireless power transfer between one transmitter and two receivers: optimal analytical solution[J]. Wireless Power Transfer, 2016, 3(1):63-73.
[3] Rabie K M, Adebisi B, Alouini M S. Wireless Power Transfer in Cooperative DF Relaying Networks with Log-Normal Fading[C]∥Global Communications Conference. IEEE, 2017:1- 6.
[4] Jing Y, Ulukus S. Optimal Packet Scheduling in an Energy Harvesting Communication System[J]. IEEE Transactions on Communications, 2012, 60(1):220-230.
[5] Tutuncuoglu K, Yener A. Optimum Transmission Policies for Battery Limited Energy Harvesting Nodes[J]. IEEE Transactions on Wireless Communications, 2012, 11(3):1180-1189.
[6] Ozel O, Tutuncuoglu K, Yang J, et al. Transmission with Energy Harvesting Nodes in Fading Wireless Channels: Optimal Policies[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(8):1732-1743.
[7] He P, Zhao L, Zhou S, et al. Recursive Waterfilling for Wireless Links With Energy Harvesting Transmitters[J]. IEEE Transactions on Vehicular Technology, 2014, 63(3):1232-1241.
[8] Gunduz D, Devillers B. Two-hop communication with energy harvesting[C]∥IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing. IEEE, 2011:201-204.
[9] 谭锴, 朱琦. 基于能量采集的译码转发中继系统功率分配算法[J]. 信号处理, 2017, 33(6):887- 893.
Tan Kai, Zhu Qi. The Algorithm of Power Allocation in Decode-and-Forward Relaying System with Energy Harvesting[J]. Journal of Signal Processing, 2017, 33(6):887- 893.(in Chinese)
[10] Nasir A A, Zhou X, Durrani S, et al. Relaying Protocols for Wireless Energy Harvesting and Information Processing[J]. IEEE Transactions on Wireless Communications, 2013, 12(7):3622-3636.
[11] Luo Y, Zhang J, Letaief K B. Optimal Scheduling and Power Allocation for Two-Hop Energy Harvesting Communication Systems[J]. IEEE Transactions on Wireless Communications, 2013, 12(9):4729- 4741.
[12] 聂志巧, 赵睿, 方嘉佳,等. 基于功率分配能量采集的全双工放大转发中继系统[J]. 信号处理, 2017, 33(4):641- 648.
Nie Zhiqiao, Zhao Rui, Fang Jiajia, et al. Amplify-and-Forward Full-Duplex Relaying Systems with Power Splitting-Based Energy Harvesting[J]. Journal of Signal Processing, 2017, 33(4):641- 648.(in Chinese)
[13] Ahmed I, Ikhlef A, Schober R, et al. Power Allocation for Conventional and Buffer-Aided Link Adaptive Relaying Systems with Energy Harvesting Nodes[J]. IEEE Transactions on Wireless Communications, 2014,13(3):1182-1195.
[14] Dong M, Li W, Amirnavaei F. Online Joint Power Control for Two-Hop Wireless Relay Networks with Energy Harvesting[J]. IEEE Transactions on Signal Processing, 2017, PP(99):1-1.
[15] Gurakan B, Ozel O, Yang J, et al. Energy Cooperation in Energy Harvesting Communications[J]. IEEE Transactions on Communications, 2013, 61(12):4884- 4898.
[16] Tutuncuoglu K, Yener A. Energy Harvesting Networks with Energy Cooperation: Procrastinating Policies[J]. IEEE Transactions on Communications, 2015, 63(11):4525- 4538.
