1 引言
ADS-B系统由多个地面站和机载站构成,机载ADS-B通信设备依靠全球定位系统(Global Position System,GPS)定位,并将飞机的识别号、经纬度、高度等信息以广播式发出,使周围飞机和地面站能都对其实时监测。目前ADS-B 监视系统有三种工作架构:S模式1090ES数据链、UAT数据链和VDL- 4数据链。其中基于S模式1090ES数据链的ADS-B系统由二次雷达S模式发展而来,与二次雷达监视手段相比,其精度更高,成本更低,广泛地应用于各大机场。随着越来越多的飞行器开始配备ADS-B收发设备,使用ADS-B的空域流量逐渐增多,且ADS-B信号以随机接入方式广播,难免会出现信号交织问题。其中,两条信号交织问题最常发生[1-2]。
由于二次雷达与ADS-B信号体制相近,国内外一些解决二次雷达信号交织的方法可以应用于ADS-B交织问题,这些方法可以分为时域解交织和空域解交织。时域解交织利用的信息有限,通常需要附加特定条件[3- 4]。而空域解交织具有空间分辨能力,成为国内外研究热点。其中一类是基于空间信号波达方向(Direction of Arrival,DOA)估计的方法,例如文献[5]应用最大似然估计法解交织,但需要阵列校准或信号重构;另一类则应用盲源分离算法,如快速独立主成分分析(Fast Independent Component Analysis,FastICA)[6-7]、曼彻斯特解码(Manchester Decoding Algorithm,MDA)算法[8]、PA算法[9]等。FastICA算法通过矩阵迭代求出分离权矢量的过程中,若初值选取不当会直接影响算法收敛性;MDA算法求解较繁杂,且低信噪比下解交织的性能有待提高。而PA有较强的稳健性,且不需要阵列校准或矩阵迭代。但PA算法是利用投影技术抑制其中一条源信号,从而获得另一条源信号,对目标信号无增强能力。本文将PA算法与Capon算法[10]相结合,使其在一条信号方向上形成零陷,同时在目标信号的方向上形成主瓣,利用天线阵增益提高目标信号的输出信噪比,同时应用RCB算法,减小导向矢量的估计误差,进一步提高了算法的稳健性。
2 信号模型
1090ES数据链的ADS-B消息格式采用脉冲位置调制(Pulse Position Modulation,PPM)编码,其消息时序特征如图1所示,ADS-B信号发射信息的脉冲宽度为0.5 μs,帧总长度为120 μs,包含8 μs前导脉冲和112 μs的数据块脉冲,来自飞机或地面的监视系统提供的飞机高度、经纬度、航班号、飞机状态等信息存储在112 μs数据块中[11]。
考虑一个间距为半波长的M阵元等距线阵,当L个ADS-B信号交织时,阵列天线收到的信号为:
(1)
式(1)中:x(t)表示阵列接收数据,n(t)为高斯白噪声,a(θl)为第l个ADS-B信号的导向矢量,且a(θl)=[1,e-jπsin θl,...,e-j(M-1)πsin θl],sl(t)表示第l个ADS-B源信号。由于两条信号交织的现象最为常见,所以本文以L=2为例,进行算法的推导和验证。
3 高增益的稳健PA算法
3.1 PA算法原理
假设接收到的信号x(t)由两条ADS-B信号交织组成,时域波形如图2所示。
由图2可以看出,从t1到t2时刻,只有信号1的信息,t2到t3时刻两条ADS-B信号交织,从t3到t4时刻,只有信号2的信息。这里可以通过对接收到的数据进行分段奇异值分解,将特征值重组成关于时间的函数,由特征值的分布情况即可检测信号的交织时刻,具体交织检测方法在文献[9]中给出了详细介绍,这里不再赘述。分别令[t1,t2]和[t3,t4]时间段内接收的信号为x1(t)和x2(t),可以写成如下形式:
x1(t)=a(θ1)·s1(t)+n1(t)
(2)
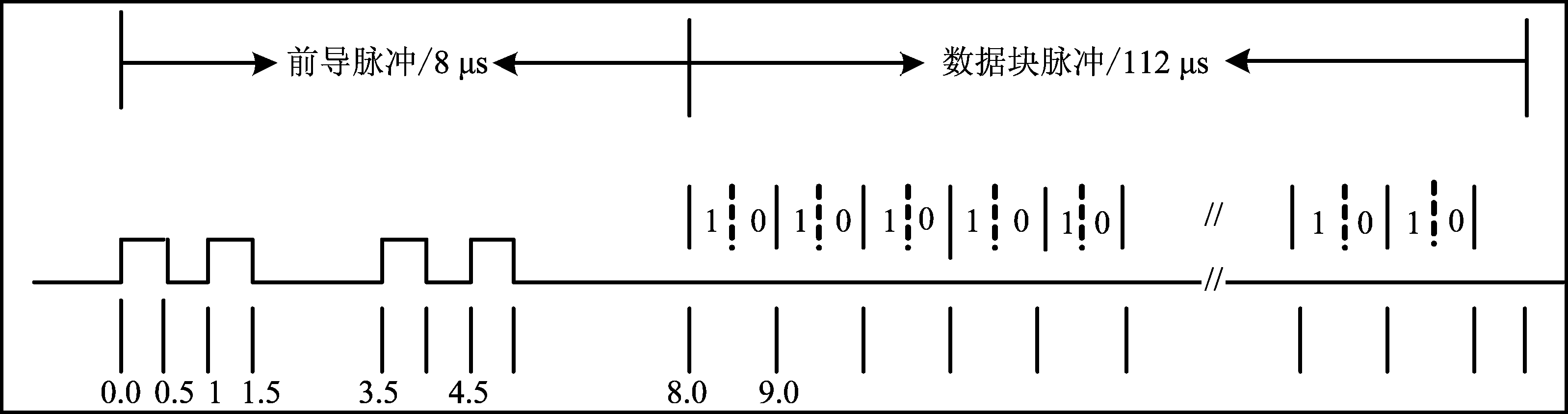
图1 ADS-B时序特征图
Fig.1 Characteristics of ADS-B time series
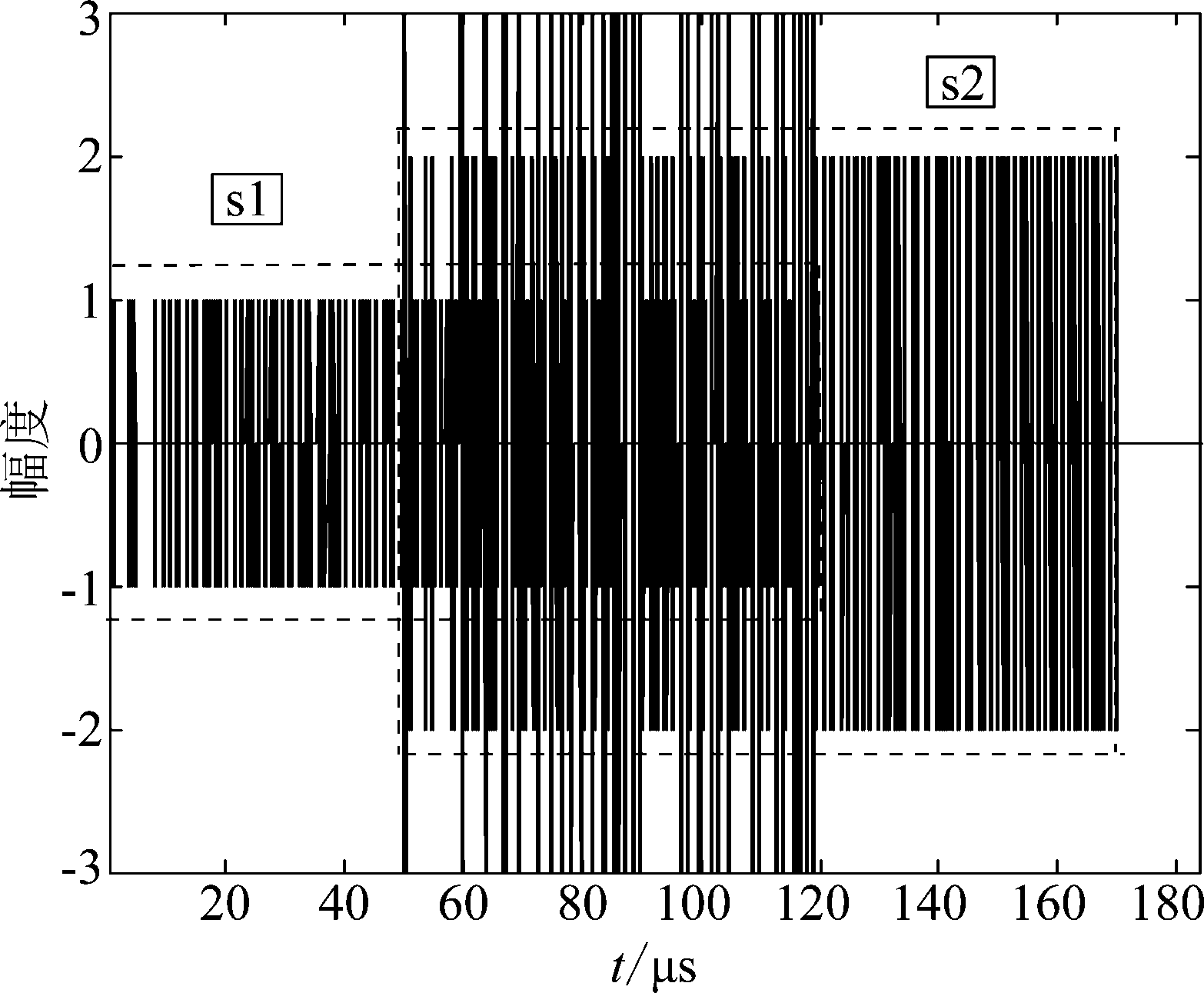
图2 两条ADS-B信号交织时域波形图
Fig.2 Two overlapped ADS-B signals in time domain
x2(t)=a(θ2)·s2(t)+n2(t)
(3)
由于式(2)中仅包含一个信号,对其进行奇异值分解时,大奇异值对应的奇异矢量可作为导向矢量的估计值,记为u1,即![]() 由此可知信号1的投影为p1,则:
由此可知信号1的投影为p1,则:
(4)
p1是信号1在交织信号上的投影,应用投影除去交织信号中的信号1,可获得信号2的信息。则解交织后的ADS-B信号2可以表示成如下形式:
s2(t)=(I-p1)*x(t)
(5)
同理可获得解交织信号1。
3.2 高增益稳健的解交织算法
PA算法是将一条信号投影到目标信号的零空间上,从而分离出目标信号,但对目标信号无增强作用。考虑到PA算法可以得到目标信号导向矢量的估计,将其与Capon算法相结合,可以提高目标信号的输出功率,进而提高输出信噪比,为了方便,将此方法称为Capon-PA算法,Capon算法的推导过程可参考文献[10],这里不做赘述。则Capon-PA解交织的信号1权矢量w1可表示为:
(6)
其中,Rx为交织信号x(t)的协方差矩阵。
由于PA算法采用大奇异值对应的奇异矢量作为信号导向矢量的估计值,可能会存在指向误差,使算法的性能下降[12]。对此,本文依据RCB算法[13]精确估计实际的导向矢量来改善Capon-PA算法的稳健性,提出了高增益的稳健PA算法,简称RCB-PA。为了推导RCB算法,有下面的优化函数:
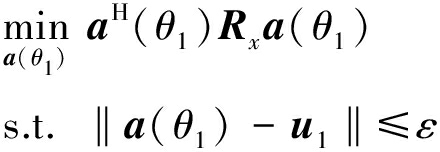
(7)
这里用a(θ1)表示信号1实际的导向矢量,ε为导向矢量的误差限,利用拉格朗日乘数法,对a(θ1)求导可获得信号1的导向矢量估计值![]()
(8)
其中,k是拉格朗日乘数因子,且k≥0。对Rx进行特征值分解,U的列向量对应于Rx的特征向量;Λ的对角线元素(Λ1≥Λ2≥…≥ΛM)对应于其相应的特征值。令:
(9)
把式(8)代入约束条件中,定义:
(10)
令![]() 表示向量z的第m个元素,将式(9)代入式(10)有:
表示向量z的第m个元素,将式(9)代入式(10)有:
(11)
利用牛顿迭代法可以求解式(11)中的拉格朗日乘数因子k,代入式(8)就可以得到信号1实际导向矢量的估计值,信号2同理。
至此,基于PA的高增益稳健解交织算法具体步骤如下:
(1)对仅存在信号1的数据x1(t)进行奇异值分解,大奇异值对应的奇异矢量u1为信号1导向矢量的估计值;
(2)利用牛顿迭代法求解式(11)中的拉格朗日乘数因子k;
(3)把k代入式(8)中精确估计导向矢量:![]()
(4)利用Capon方法计算权矢量有:w1=
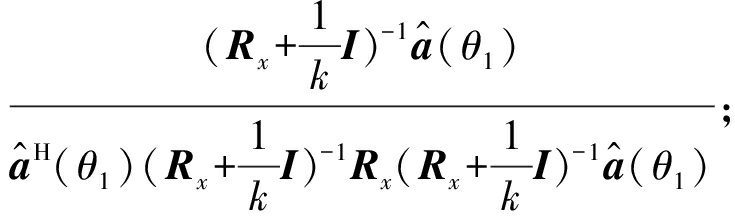
(5)求得解交织后的信号![]() 信号2同理:
信号2同理:![]()
(6)利用ADS-B接收机对解交织信号s1(t)和s2(t)进行解码。
本文算法流程图如图3所示。
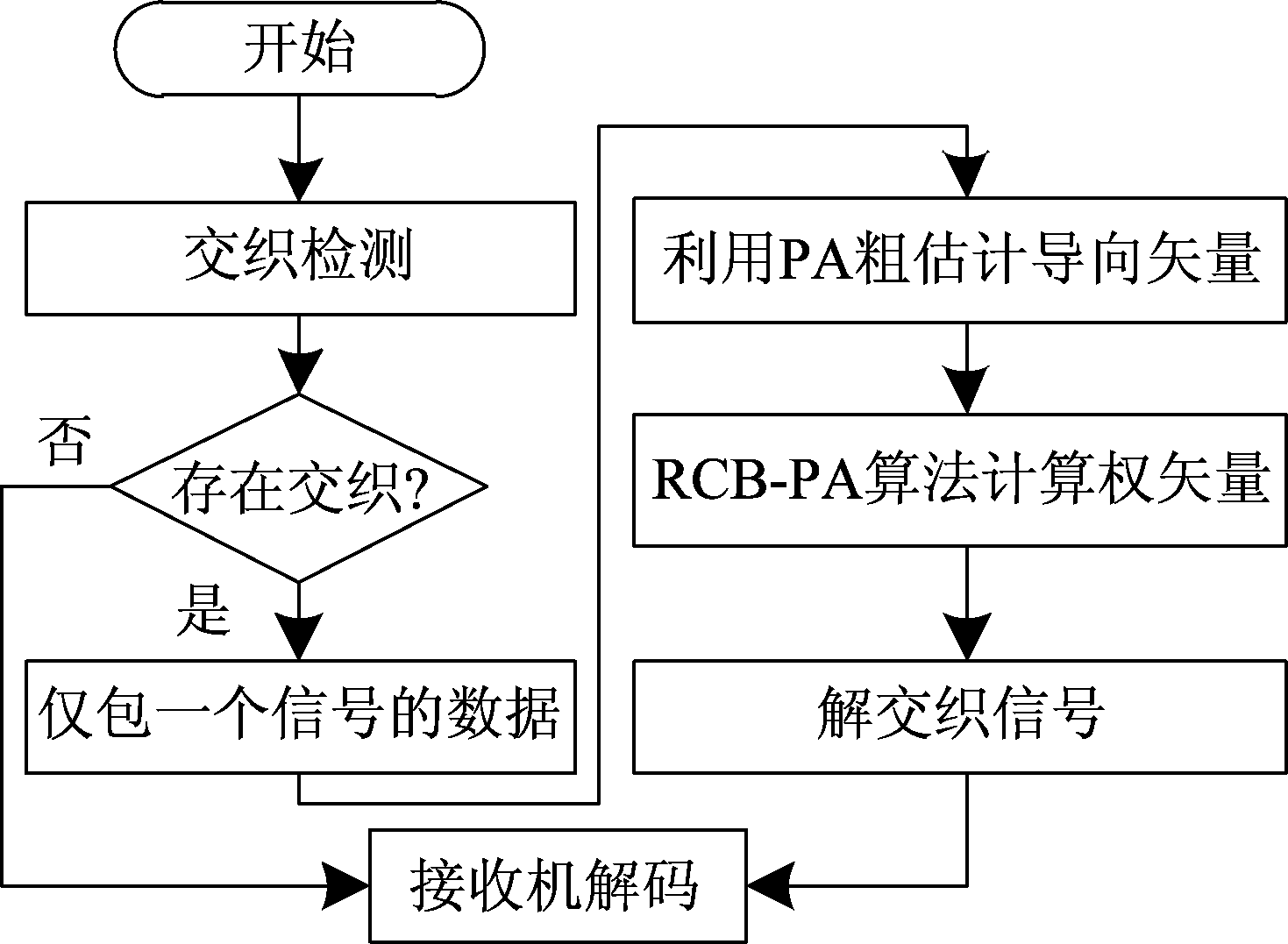
图3 算法流程图
Fig.3 The flow diagram of algorithm
表1给出了PA与RCB-PA算法的运算量及运行时间比较,其中仅有信号1存在的数据长度为N1。可以看出,RCB-PA与PA的运算时间和运算量相当,改进的算法几乎没有提高复杂度。
表1 运算量比较
Tab.1 Comparison of computation

复乘次数复加次数运行时间/sPA2M3+M2N1+3M2L2M3+M2N1+3M2L-3M2-MN1-2LM0.448449RCB-PA3M3+M2N1+M2L3M3+M2N1+M2L-3M2-MN1-LM0.469640
4 仿真实验结果
仿真实验采用间距为半波长的4阵元等距线阵处理两条ADS-B信号交织,采样频率为40 MHz。其中一条信号的来向为-20°,信噪比为19 dB,数据位信息:飞机号780123,高度34100 ft,经度117.5,纬度37.5;另一条信号的来向为30°,信噪比为20 dB,数据位信息:飞机号780ABC,高度32100 ft,经度117.8,纬度37.4。两条信号的相对时延为50 μs。
图4是交织信号时域波形图,将交织信号以4 μs为一个区间做奇异值分解进行交织检测,根据噪声信号特征值服从卡方分布,选择合适的检测门限。特征值1、特征值2及检测门限的分布情况如图5所示,从图4和图5可以看出:0~50 μs和120~170 μs仅有一个特征值超过检测门限,由于ADS-B信号固定120 μs的信号长度,则可判断0~50 μs仅包含信号1的信息,120~170 μs仅包含信号2的信息。然后利用检测到的仅有一个信号的数据区间估计导向矢量。

图4 交织信号时域波形图
Fig.4 Overlapping signal in time domain
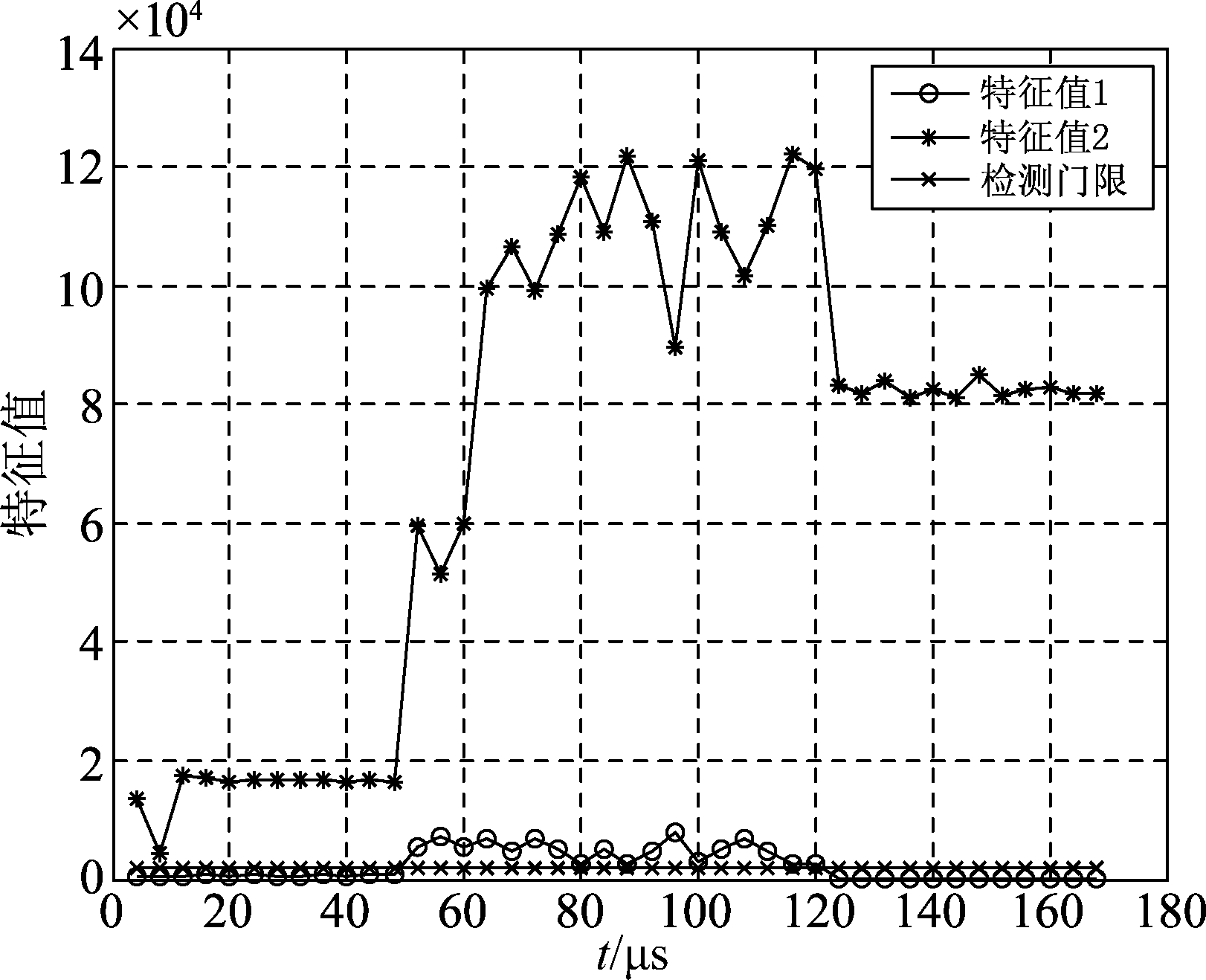
图5 特征值分布曲线
Fig.5 Eigenvalue distribution curve
图6比较了PA、Capon-PA和RCB-PA算法解交织的信号1阵列方向图,由图6可以看出:PA算法仅在信号2来向30°处形成零陷,抑制了信号2,在信号1来向无增益;Capon-PA算法在抑制信号2的同时在信号1来向-20°处形成较宽主瓣,但存在指向误差;RCB-PA算法在Capon-PA算法的基础上可以较精确的在信号1来向上形成主瓣,说明应用RCB改进的PA算法能够抑制其中一条信号,同时较准确地在另一条信号来向上获得主瓣增益。
图7将RCB-PA算法解交织的两条信号与源信号的时域波形进行对比,从波形幅度看,经本文算法处理后的信号输出功率高于源信号,所以输出信噪比也会提高。
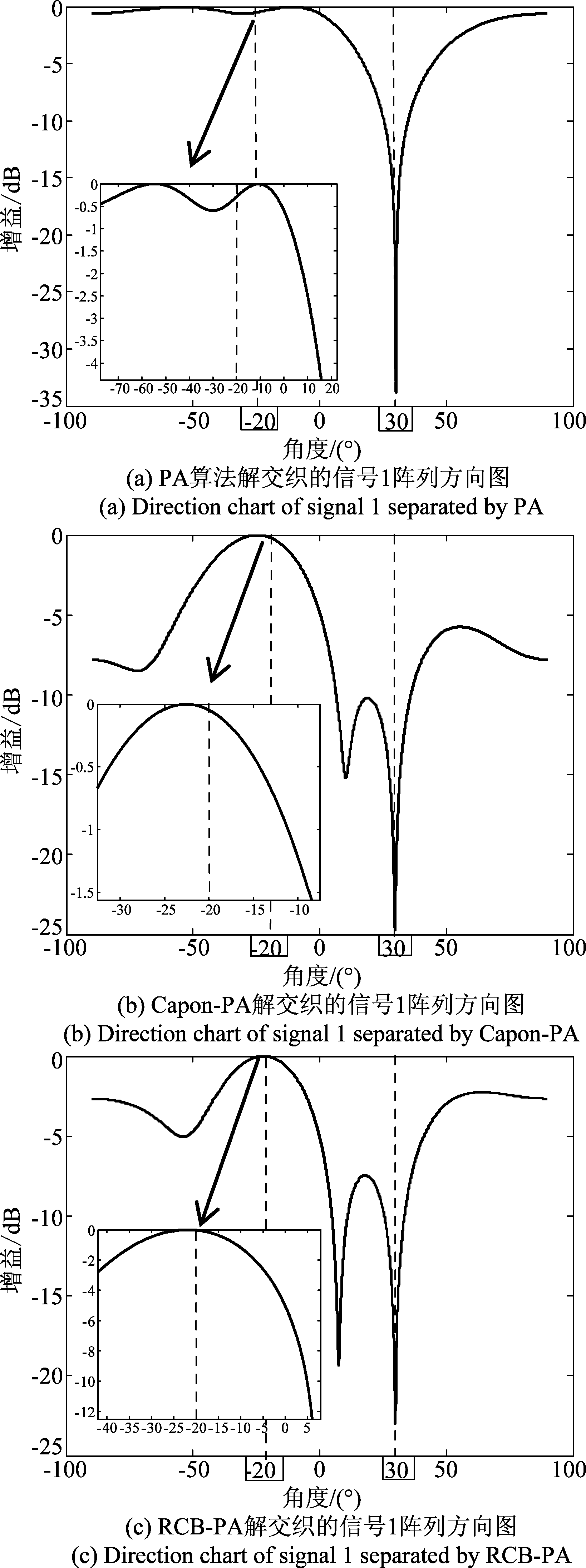
图6 PA、Capon-PA 和 RCB-PA解交织信号1阵列方向图
Fig.6 Direction chart of separated signals of PA、Capon-PA and RCB-PA
为了进一步验证RCB-PA算法的分离结果,将解交织的两条信号在接收机中解码,结果如表2所示:表中数据与仿真的ADS-B信号信息一致,可获得与仿真相同的飞机识别号、飞行高度、经纬度等信息。
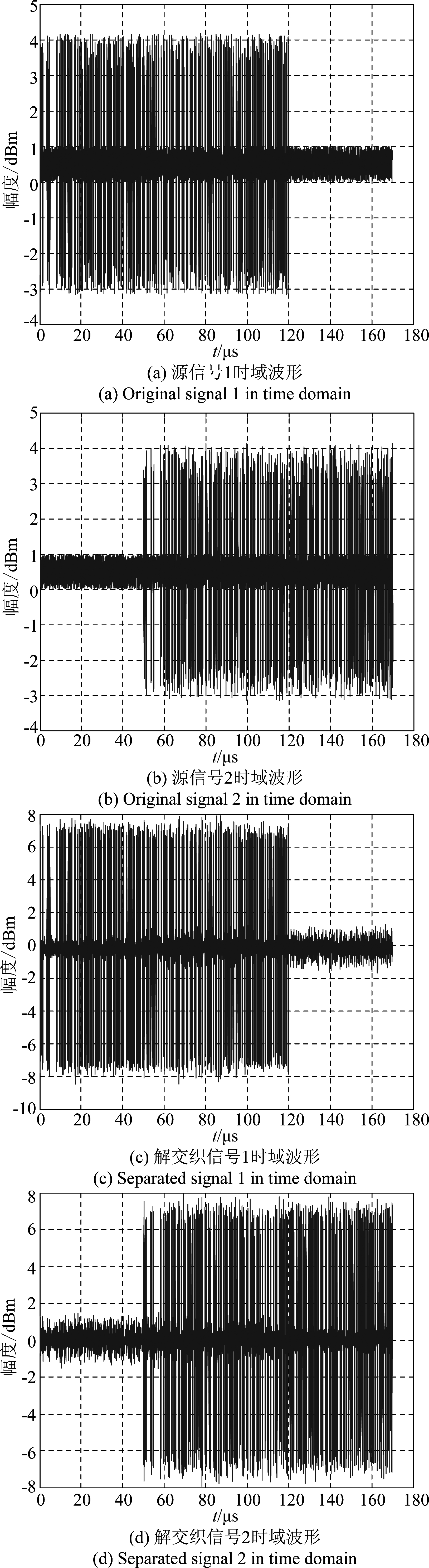
图7 源信号与解交织信号时域波形对比图
Fig.7 Contrastive figure of original signals and separated signals in time domain
表2 接收机解码结果
Tab.2 Decoding result of receiver

AADF消息类型高度/ft经度纬度信号178012317空中位置信息34100117.537.5信号2780ABC17空中位置信息32100117.837.4
为验证RCB-PA算法的准确性,图8比较了输入信噪比对ICA、MDA、PA和RCB-PA解码正确率的影响(所用接收机可以解码信噪比9 dB以上的ADS-B信号)。可以看出,在输入信噪比大于10 dB时,四种算法的解码正确率都呈上升趋势。ICA算法对初值选取敏感影响算法稳健性,使得解码正确率出现波动;MDA算法对信噪比要求较高,在14 dB以上才能保证解交织正确率,不适用于低信噪比的交织信号;PA在输入信噪比12 dB以上时解交织正确率大于95%;而RCB-PA算法在7 dB的输入信噪比时,其解码正确率就已超过95%,说明RCB-PA算法提高了低信噪比交织信号的解码正确率。

图8 解码正确率与输入信噪比关系曲线
Fig.8 The relation curve between the decoding accuracy and the input signal to noise ratio
为了更清晰说明RCB-PA算法对信号输出信噪比的影响,图9将其与ICA、MDA和PA算法的输出信噪比进行比较。由图9可知,在相同输入信噪比时,PA算法的输出信噪比高于MDA算法和ICA算法,而RCB-PA要比PA算法的输出信噪比高约6 dB,因此RCB-PA解交织算法能够获得更高的输出信噪比。

图9 输出信噪比与输入信噪比关系曲线
Fig.9 The relation curve of the output signal to noise ratio and the input signal to noise ratio
5 实采数据结果
为了进一步验证算法的有效性,本小节通过实采数据验证算法的性能。阵列天线实物如图10所示,实采数据是除备用天线外的其他5个阵元在机场附近接收到的ADS-B信号,阵列间距d=0.091 m,采样频率80 MHz。将接收到的两条信号进行人为交织,交织信号时域波形如图11所示,可以看出信号1的幅度约为14 dBm,信号2的幅度约为9 dBm。

图10 阵列天线实物
Fig.10 Array antenna
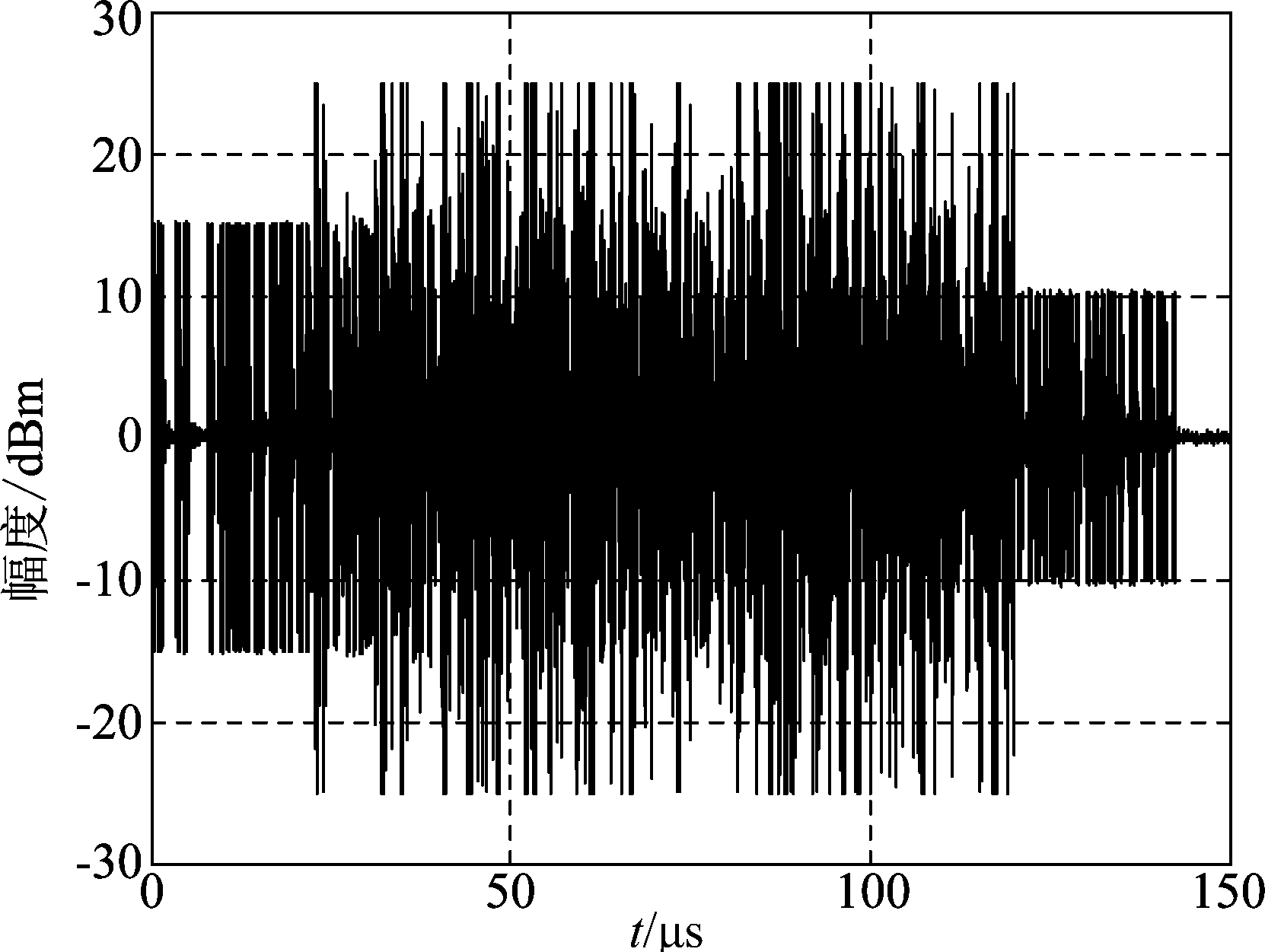
图11 实采交织信号时域波形
Fig.11 Time domain waveform of test overlapped signal
图12将RCB-PA与PA算法的实采数据解交织波形图进行比较,由图(a)和(b)可以看出,利用PA算法获得信号幅度与源信号基本相等;而图(c)和(d)利用RCB-PA算法解交织获得的信号中,信号1的幅度达到了30 dBm,信号2的幅度增加到20 dBm,所以RCB-PA算法能够有效地提高信号的输出功率。
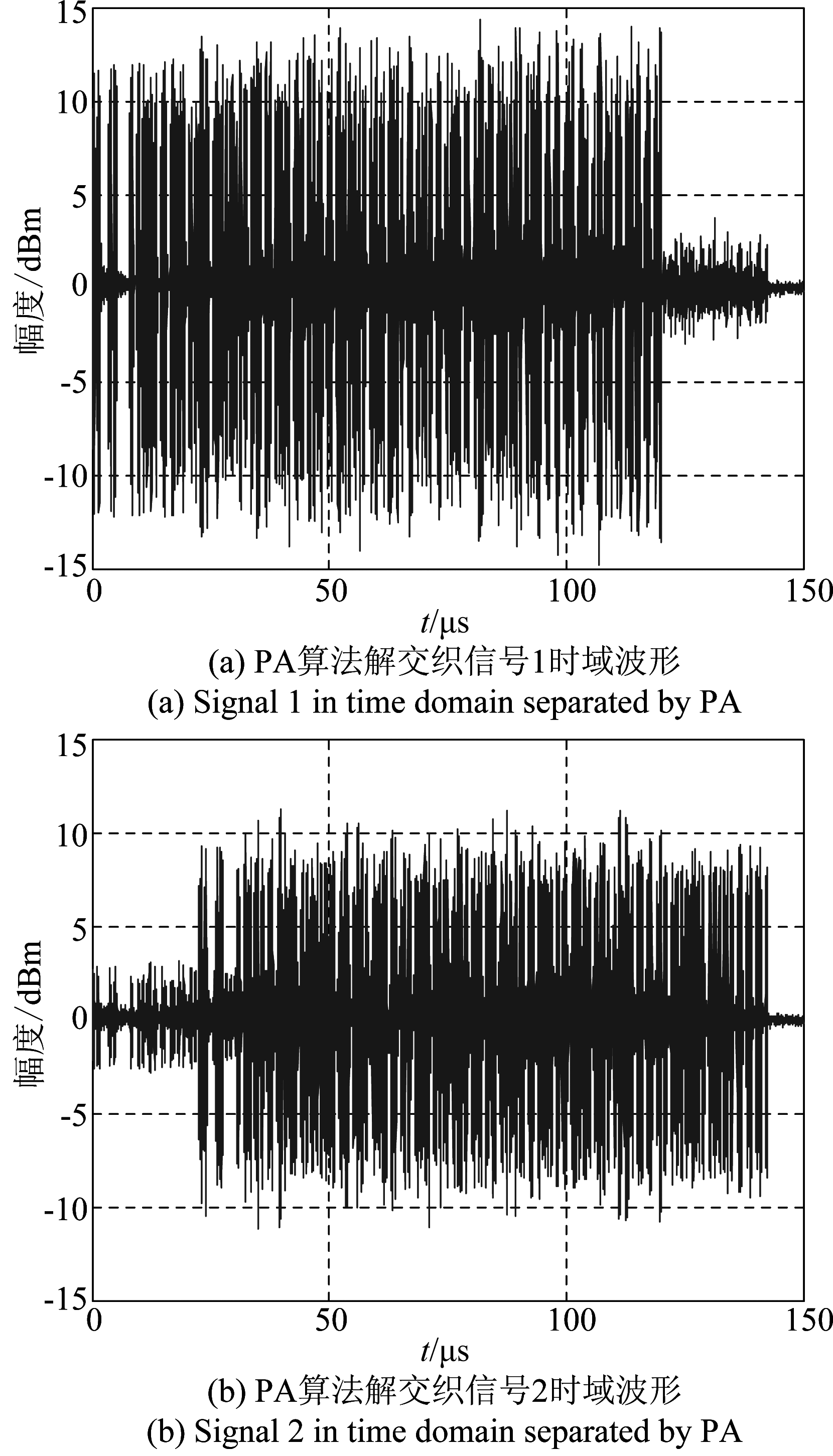
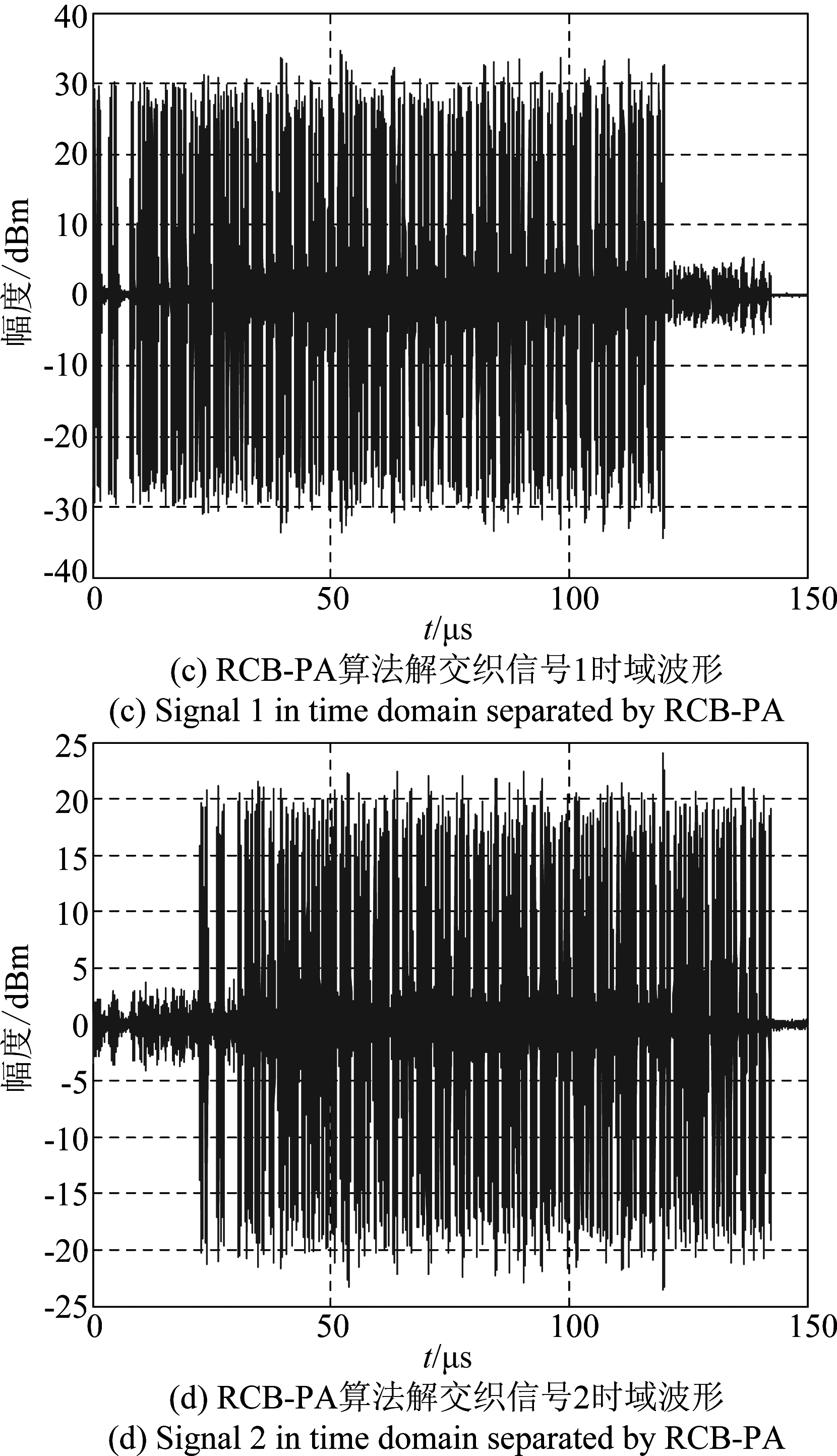
图12 实采信号解交织时域波形
Fig.12 Separated test signals in time domain
将交织实采信号和解交织后的两条ADS-B信号经接收机解码,结果如表3所示,交织信号无法通过CRC校验,而经RCB-PA算法解交织后的信号则可以通过CRC校验,能够解出正确的飞机信息。
表3 时采数据接收机解码结果
Tab.3 Receiver decoding result of test signals
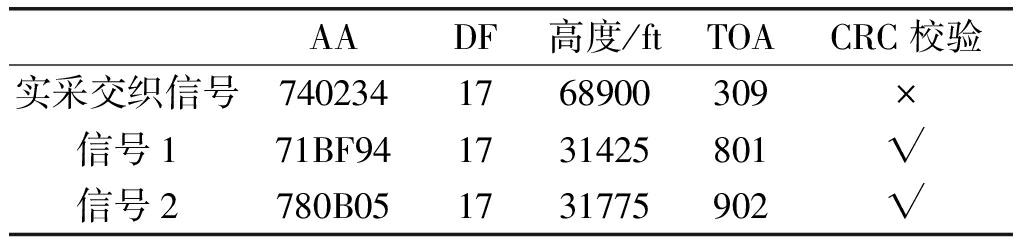
AADF高度/ftTOACRC校验实采交织信号7402341768900309×信号171BF941731425801√信号2780B051731775902√
6 结论
针对ADS-B交织问题,考虑到PA在解交织时具有不需要阵列校验、训练序列等优点,本文结合了Capon波束形成和RCB算法,提出了高增益的稳健PA算法。通过仿真和实采实验表明:高增益的稳健解交织算法不仅能较准确地分离交织信号,而且利用阵列信号处理带来的增益,在保证算法稳健性的同时提高了信号的输出信噪比,降低了算法对输入信噪比的要求,使得低信噪比交织信号处理的性能得到一定的改善。
[1] Liu Kai, Zhang Tao,Ding Yang. Blind signal separation algorithm for space-based ADS-B[C]∥International Conference on Mechatronics Engineering and Information Technology(ICMEIT):Beijing, China,2016:384-390.
[2] 吴仁彪,吴琛琛,王文益.基于累加分类的ADS-B交织信号处理方法[J].信号处理,2017,33(4):572-576.doi:10.16798/j.issn.1003- 0530.2017.04.017.
Wu Renbiao,Wu Chenchen,Wang Wenyi.A method of overlapped ADS-B signal processing based on accumulation and classification[J].Journal of Signal Processing,2017,33(4):572-576.doi:10.16798/j.issn.1003- 0530.2017.04.017.(in Chinese)
[3] Galati G, Petrochilos N, Piracci E G.Degarbling Mode S replies received in single channel stations with a digital incremental improvement[J].IET Radar Sonar and Navigation, 2015,9(6):681- 691.doi: 10.1049/iet-rsn.2014.0335.
[4] Wu Chuanlong, Liu Zheng, Wang Xiang,et al.Single-Channel blind source separation of Co-Frequency overlapped GMSK signals under Constant-Modulus constraints[J].IEEE Communications Letters, 2016,20(3):486- 489.doi: 10.1109/LCOMM.2016.2521737.
[5] 唐波,程水英,张浩. 基于多通道阵列处理的二次雷达混扰信号分选[J]. 电讯技术, 2014,54(5):534-540.doi:10.3969/j.issn.1001- 893x.2014.05.002.
Tang Bo,Cheng Shuiying, Zhang Hao.Separation of garbled secondary surveillance radar signal based on multichannel arrary processing[J]. Telecommunication Engineering, 2014,54(5):534-540.doi:10.3969/j.issn.1001- 893x.2014.05.002.(in Chinese)
[6] Kumara T N, Gamaarachchi H,Prathap G. Generalized and hybrid Fast-ICA implementation using GPU[C]∥International Conference on Advances in ICT for Emerging Regions (ICTer): Sri Lanka,2016:13-20.
[7] Novey M,Adali T.On extending the complex FastICA algorithm to noncircular sources[J].IEEE Transactions on Signal Processing, 2008,56(5):2148-2154. doi: 10.1109/TSP.2007.911278.
[8] Petrochilos N, Van der Veen A J. Algebraic algorithms to separate overlapping secondary surveillance radar replies[J].IEEE Transactions on Signal Processing, 2007,55(7):3746-3759.doi: 10.1109/TSP.2007.894248.
[9] Petrochilos N,Galati G,Piracci E.Separation of SS R signals by array processing in multilateration systems[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(3): 965-982.doi: 10.1109/TAES.2009.5259177.
[10] 张小飞,汪飞.阵列信号处理的理论与应用[M].第2版.北京:国防工业出版社,2013:18-23.
Zhang Xiaofei,Wang Fei.Theory and application of array signal processing[M]. Second edition. Beijing: National Defese Industry Press,2013:18-23.(in Chinese)
[11] Chen Weilu,Lu Qibin,Li Zhengxiang.A test platform for baseband signal processing module of ADS-B[C]∥IEEE International Conference on Software Engineering and Service Science (ICSESS):Beijing, China,2016:1005-1008.
[12] 张琦,唐斌.一种稳健自适应多波束形成算法[J].信号处理,2018,34(1):13-20.doi:10.16798/j.issn.1003- 0530.2018.01.002.
Zhang Qi,Tang Bin.A robust adaptive multi-beamforming algorithm[J].Journal of Signal Processing,2018,34(1):13-20.doi:10.16798/j.issn.1003- 0530.2018.01.002.(in Chinese)
[13] Lie J P,Ser W,See C M S.Adaptive uncertainty based iterative robust capon beamformer using steering vector mismatch estimation[J].IEEE Transaction on Signal Processing, 2011,59(4):4483- 4488.doi:10.1109/TSP.2011.2157500.
[14] 周琳,黄春琳,粟毅.基于鲁棒性Capon波束形成的探地雷达成像算法[J].电子与信息学报,2012,34(5):1024-1029.doi:10.3724/SP.J.1146.2011.01195.
Zhou Lin,Huang Chunlin,Su Yi.A ground penetrating radar imaging algorithm based on robust Capon beamforming[J].Journal of Electronics & Information Technology,
2012,34(5):1024-1029.doi:10.3724/SP.J.1146.2011.01195. (in Chinese)

