1 引言
海杂波环境下的多目标检测是舰载雷达的核心功能之一,在现代战争中具有十分重要的意义。目前常用的海面多目标检测方法主要有恒虚警检测和背景拟合等技术。单元平均恒虚警检测技术[1-3]根据海杂波先验分布信息进行参数估计从而计算检测门限,存在因分布模型与实际杂波的非高斯特性不符而导致检测效果下降的问题,同时容易因临近目标进入参考单元而造成检测困难。背景拟合技术[4]将数据映射到拟合空间,根据拟合空间的海杂波幅度产生门限曲线并根据海况进行适应性调整,能够消除临近目标的影响,但门限的局部值与复杂环境较难符合,且在多变的海况环境下适应能力有限。因此,迫切需要一种更加有效的海面多目标检测方法。
近年来,深度学习理论在模式识别领域掀起了一股研究热潮,相关的理论和研究成果不断涌现。卷积神经网络[5](CNN,Convolutional Neural Network)是深度学习的常用网络之一,最早由加拿大多伦多大学LeCun教授提出,较好地解决了网络训练过程中的梯度不稳定问题,并且具备由浅入深的层次性特征自适应学习能力,在模式识别领域取得了较多成功的应用[6]。卷积神经网络在雷达领域的应用主要集中在雷达图像识别[7- 8],即用于二维图像分类,目前针对雷达一维数据的多目标检测方面未见公开报道。
基于卷积神经网络的特点,本文尝试将其应用于海杂波环境下的多目标检测。首先采集某型对海相控阵雷达的实测数据作为网络训练输入。通过优化网络结构,使其适用于多目标检测问题,提高目标检测概率。同时提出定向惩罚方法,加速网络训练。最后采用ROC曲线和信杂比改善因子考察网络的综合性能。实验结果表明,本文的方法具有良好的海面多目标检测能力,证明了其有效性。
2 卷积神经网络概述
卷积神经网络主要由输入层、卷积层、池化层、全连接层和输出层组成,可以实现从输入到输出的任意非线性映射[9]。网络的基本结构如图1所示。
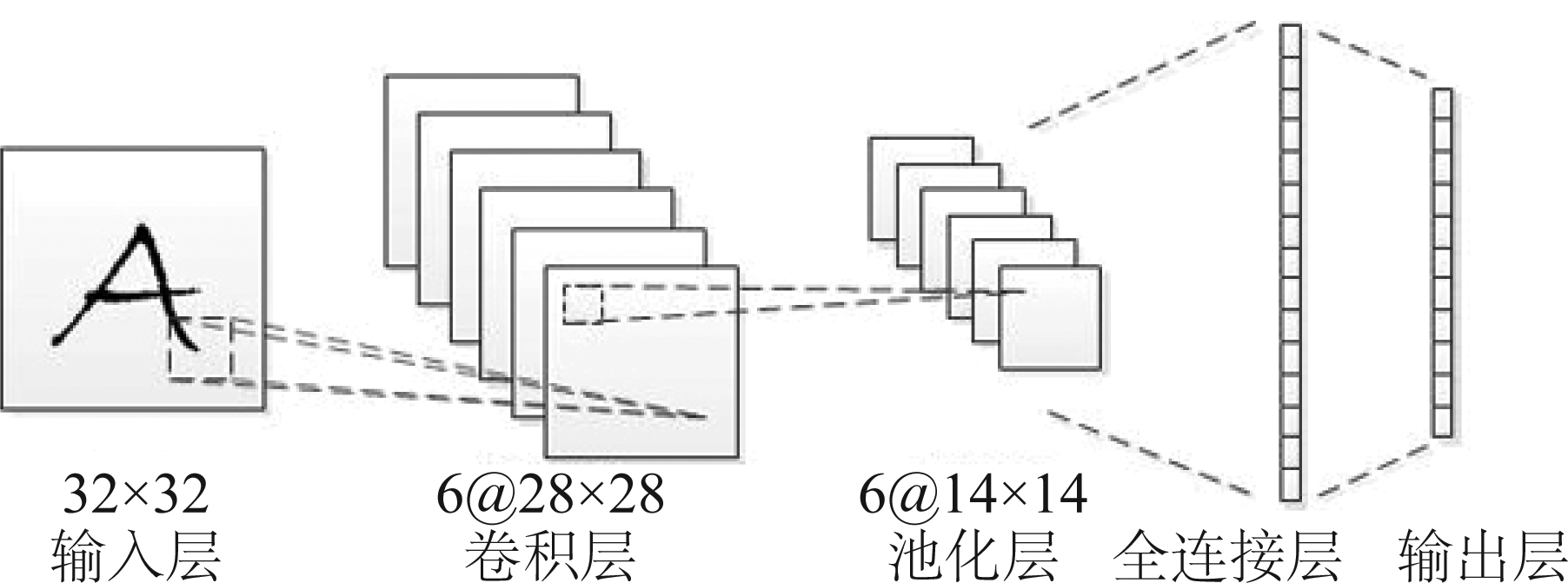
图1 卷积神经网络基本结构
Fig.1 Basic structure of convolutional neural network
输入层的作用在于接收原始输入图像,其大小与输入图像的维度一致。
卷积层通过卷积操作提取特征,若用al表示第l层特征图,wl表示该层卷积核,bl表示该层偏置,σ(x)表示其非线性激活函数,则前一层图像al-1通过该层后的输出即为第l层特征图,可表示为
al=σ(al-1*wl+bl)
(1)
其![]() 表示卷积操作。常用的非线性激活函数有sigmoid函数、ReLu函数等,其中
表示卷积操作。常用的非线性激活函数有sigmoid函数、ReLu函数等,其中
(2)
池化层通常设置在卷积层之后,用于对特征图的局部区域进行下采样操作,常用的方法有均值池化和最大值池化,分别取池化范围内数据的均值和最大值。池化范围为2×2时,池化后的图像变为原图的1/4。
全连接层位于特征提取之后,接收经过多个卷积层和池化层交替传递后的特征图,有针对性地进行高层特征的映射。用wl表示全连接层权值,则该层的输出为
al=σ(wl·al-1+bl)
(3)
输出层也是全连接层的一种,其形式面向具体任务,该层常见的激活函数包括sigmoid函数、softmax函数等。
卷积神经网络的训练目标是最小化代价函数。输入图像经过各层的前向传播后根据代价函数计算与期望值之间的差异。常见的代价函数有均方差代价函数、交叉熵代价函数等[10]。均方差代价函数按下式进行计算。
(4)
其中,y表示期望输出值,L表示总层数,aL为最后一层即输出层的输出值,n表示训练样本总数。
卷积神经网络一般采用随机梯度下降[11]算法进行训练。该方法能够进行误差的反向传播计算,通过下一层误差反向计算得到上层误差,从而计算各层权值和偏置的梯度。
最后,根据权值和偏置的梯度,按梯度下降的方向进行权值和偏置更新,更新公式为
(5)
(6)
其中,η表示学习速率,用于控制梯度下降的步长。m为随机梯度下降算法的小批量数据样本总数。
3 海面多目标检测原理
相控阵雷达每隔一定角度对海域进行搜索,每一角度称为一个波位,形成一帧一维回波数据,包含海杂波及若干目标,从中检测各目标位置。雷达一维数据与图像分类中的二维数据有很大区别,主要特点是一维数据带宽更小,分辨目标的能力较低,包含更少的目标细节。因此,本文针对一维数据的实际特点,在常用的卷积神经网络基础上,采用数据驱动的方法研究适合于多目标检测的模型,提升目标的发现概率,增强模型的泛化能力。
多目标检测网络的输出与图像分类网络有较大区别。图像分类网络输出图像类别,常用softmax输出层,将不同类别的输出值对应为各类别的概率分布[10]。对于一维回波数据,网络输出需要包含每个数据点有无目标的信息。由于每个点是否有目标的独立性,无法使用概率分布型的输出层。本文采用sigmoid输出层,网络输出值域为[0,1]。对于目标点,提升目标幅度,使其输出接近网络输出的最大值1。对于非目标点则抑制其幅度,使其输出接近网络输出的最小值0。这种输出类型的网络本质上依托于神经网络对从输入到输出的任意非线性映射的强大拟合能力[9]。
网络的代价计算采用均方差代价函数,如公式(4)所示,每个点对总代价的贡献比例相同。由于目标在整帧数据中的比例往往较小,导致达到网络收敛的速度较慢;而当虚警产生时,同样不能快速学习虚警导致的代价差异。针对该缺点,本文提出定向惩罚的方法,在两个方面影响代价计算:一是目标点的输出值偏离理想输出时,网络在该点产生一个较大的误差;二是产生虚警时,网络在该点产生较大的误差。定向惩罚将输出误差分为三部分,包含目标的误差点集Ed,包含虚警的误差点集Efa,以及剩余的误差点集Eb,用定向惩罚因子α作为调节参数,总代价的计算方法如下:
C=α·Ed+α·Efa+(1-α)·Eb
(7)
定向惩罚使目标点的误差以及虚警点的误差对总代价的贡献比例增大,能够加快训练速度,使网络更易于达到最优。
网络的池化层具有降低数据量和特征选择的作用,然而在一维回波检测中,以池化区域为2×1的最大值池化为例,池化之后数据长度变为原来的一半,且无论目标在池化区域两个点中的哪一个,均输出相同结果,因此池化过程模糊了目标位置信息,使网络无法实现准确的目标位置辨别,故上述模型在卷积层之后取消池化层,以消除池化带来的不利影响,在实际训练过程中得到了证实。
网络的卷积层数量常和输入数据的层次结构相关,而每层的卷积核数量则和数据的待检特征数目相关。对于一维回波数据,其单个目标的细节较少,而整帧的层次结构主要体现在待检目标与邻近目标及海杂波的关系。本文通过输入实测数据,并不断迭代改变网络结构,考察检测效果,从而搜寻网络的最佳结构状态。具体实施中,采用穷举式的循环搜索方法,设置具有不同网络层数、卷积核数量、卷积核长度的网络结构,针对每一种结构进行超参数优化,并以测试集上发现概率最大的网络作为最优结构。
经过实验探索,最终确定的多目标检测网络具有四层网络结构,分别是输入层、卷积层1、卷积层2、全连接输出层,如图2所示。其中输入层输入值为帧长500的一维数据;卷积层1卷积核大小为11×1,数量为5个,特征图大小为490×1,共5幅;卷积层2卷积核大小为15×1,接收上层的5幅特征图,卷积核数量为5×5个,特征图大小为476×1,共5幅;输出层为包含476个神经元的全连接层。网络从输入到输出的帧长减小24个点,为两次卷积后首尾的舍去点数。
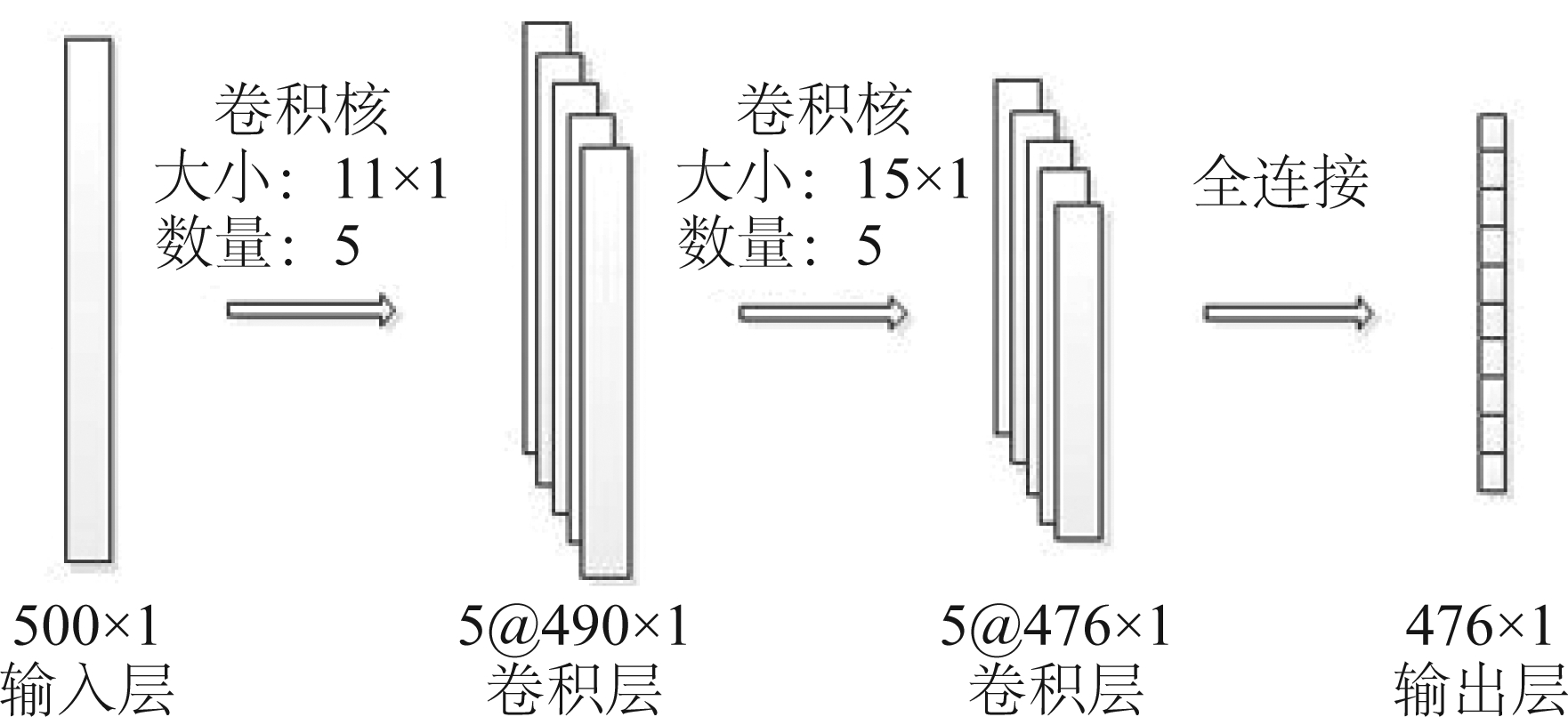
图2 多目标检测网络结构
Fig.2 Structure of multi-targets detection network
4 数据获取与网络训练
海面实测数据来源于某型相控阵雷达,采集时间为2018年6月。海面存在渔船、货轮、海岛等目标。雷达工作期间,阵面对着指定海域按一定的方位角间隔进行搜索,每个波位采集一帧数据,覆盖特定的距离段。取脉冲压缩后的数据,每帧包含500个数据点,每个点称为一个距离单元。每帧数据包含同相I和正交Q两路,按公式(8)计算对数功率值,并按公式(9)进行归一化后用于网络输入。
D=10·log10(I2+Q2)
(8)
Dnormalize=(D-Dmin)/(Dmax-Dmin)
(9)
在不同时段搜索该海域,采集有船只目标的数据,得到100帧基础数据集。为了实现海杂波下的多目标检测,本文采用数据驱动的方法提升网络性能,使训练样本具备较大的容量,并且尽可能多地涵盖不同目标及目标相邻的情景。因此按以下步骤对基础数据集进行扩展[10]:
(1)标记并提取基础数据集中的目标数据,建立目标库;
(2)将不含目标或去除目标的数据作为海杂波背景,建立背景库;
(3)随机选取多个目标和一个背景,并将目标置于随机位置以生成新的帧,其中一半的帧限制目标间距,使目标随机间隔1至10个距离单元。
同时,扩展过程中需要使测试集与训练集、验证集完全分离,确保网络泛化能力的测试不受训练集影响。因此,基础数据集的前90帧用于产生训练集和验证集,扩展后共计3000帧。后10帧用于产生测试集,扩展后共计100帧,如图3所示。
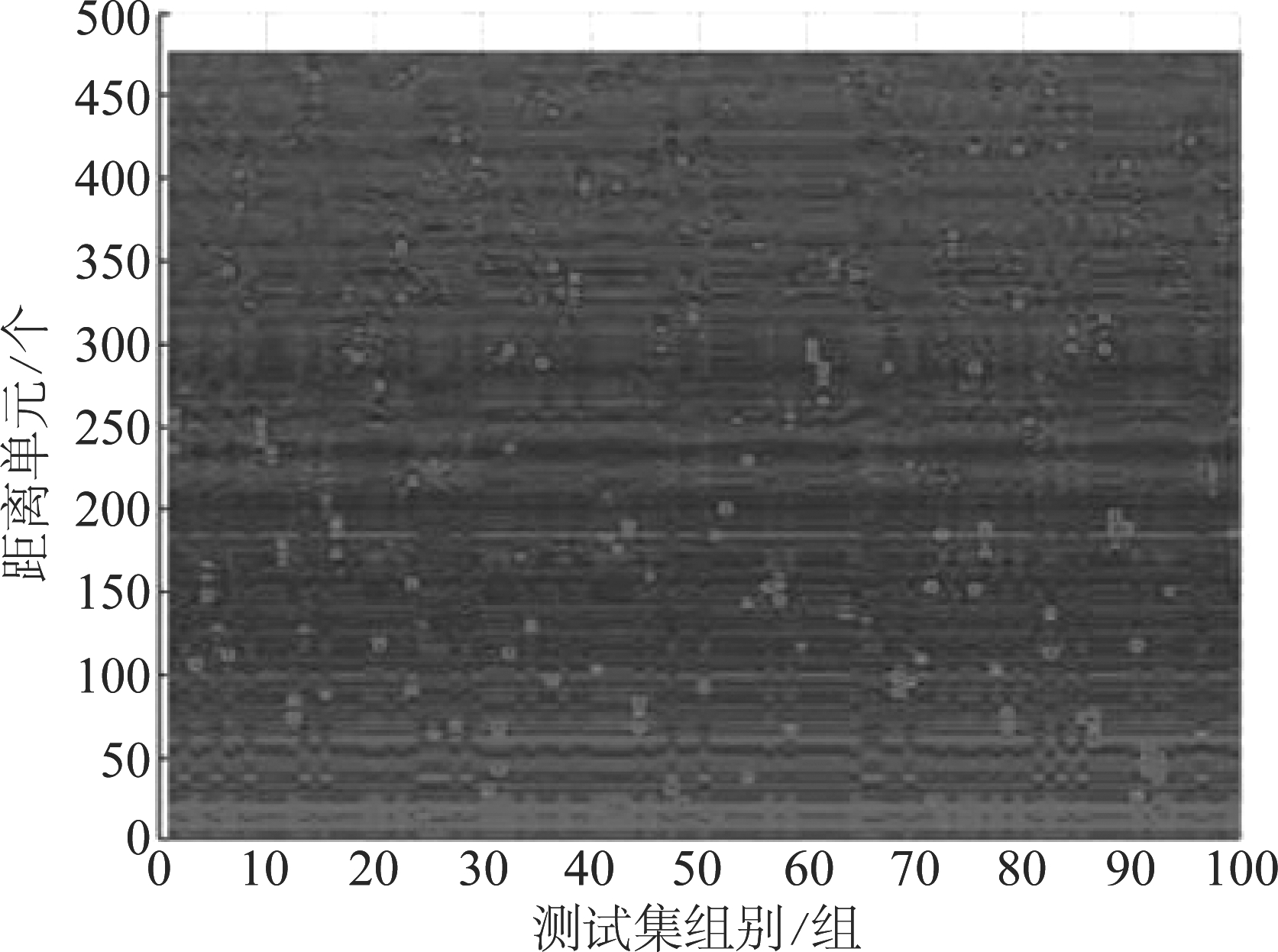
图3 测试集数据
Fig.3 Test data set
网络训练时,取3000帧数据中的100帧作为验证集,余下的2900帧作为训练集。采用附加动量[12]的随机梯度下降算法用于训练,并用正则化[13]技术减轻过拟合影响。每次输入20帧作为一个小批量数据,进行权值和偏置的一次更新。使用完整个训练集为一个迭代周期,并计算验证集上的发现概率。当代价函数值在一定迭代周期内不再下降或验证集上的发现概率不再上升时,网络达到收敛状态,结束训练。训练结束后计算测试集上的发现概率和虚警概率,并考察网络的综合性能。
网络的超参数包括学习速率、附加动量系数、正则化系数、定向惩罚因子、输出层检测门限等。采用超参数搜索方法设置最优值,本文使用随机搜索[10]算法,在超参数具有不同耦合情况时均能达到较好效果。最终设置学习速率为0.615,附加动量系数为0.337,正则化系数为0.003,定向惩罚因子为0.7,输出层检测门限为0.5。
多目标检测网络的一次训练按以下步骤进行:
(1)初始化权值和偏置。采用基于高斯分布的初始化方法[14],该方法按本层输入输出维度对参数范围进行限制,是一种有效的初始化方法。
(2)输入训练样本集合。由于网络输入定义域为[0,1],需要首先对训练集、验证集和测试集进行归一化,采用每帧单独归一化的方式进行。
(3)网络前向传播计算。按公式(1)至(3)进行输入数据的前向传播计算,得到网络输出。
(4)反向误差和梯度计算。采用随机梯度下降算法进行误差的反向传播计算,得出各层权值和偏置的梯度。
(5)权值和偏置更新。按公式(5)至(6)进行各层的权值和偏置更新。
5 结果分析与模型评价
多目标检测网络经过100次迭代训练过程,达到收敛状态。训练过程中的代价函数变化如图4所示。当训练完成时,网络在训练集上的发现概率达到98.5%,在验证集上的发现概率为94.6%。采用测试集进行测试,发现概率达到91.7%,虚警概率为7.8e-3。
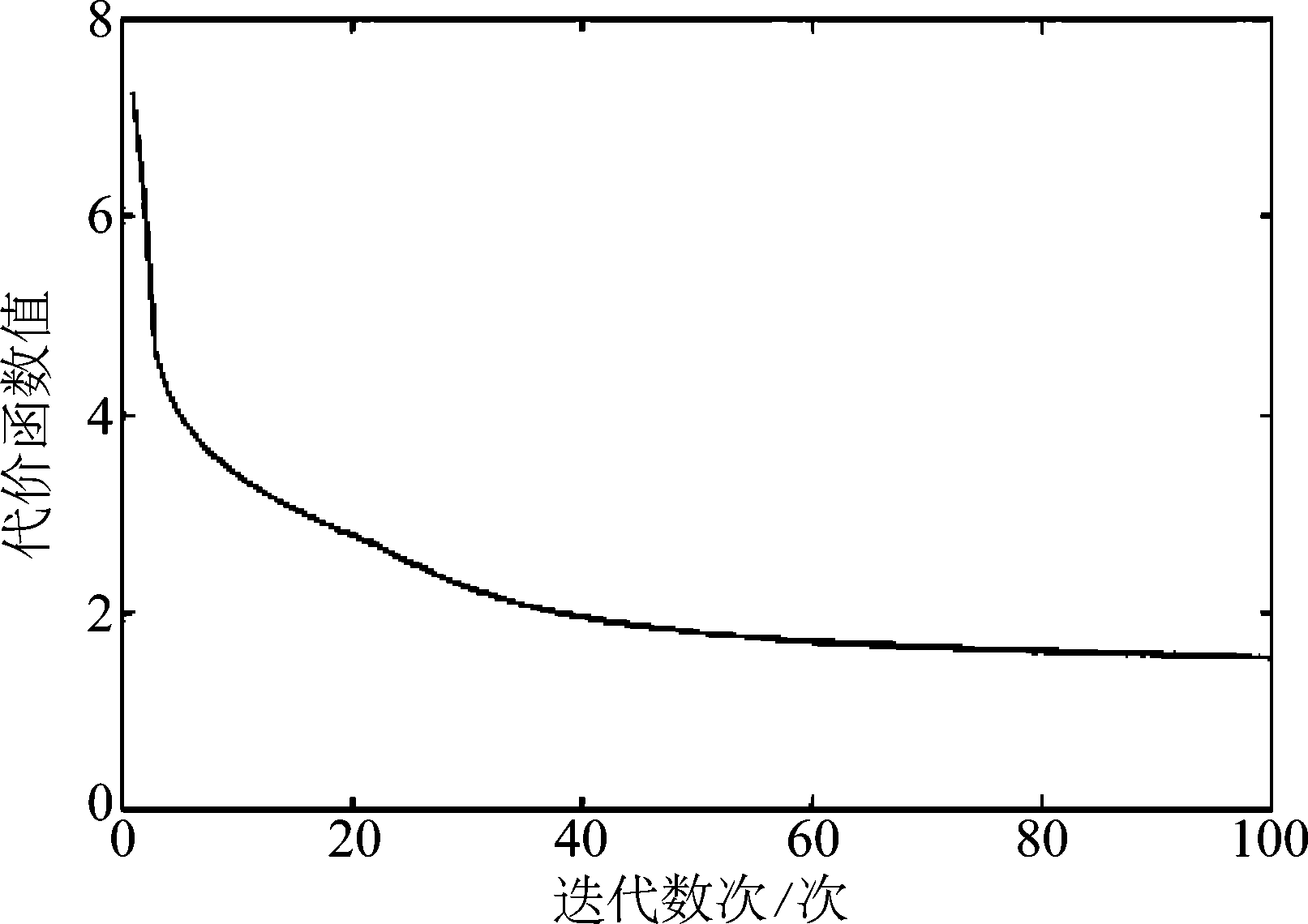
图4 代价函数变化曲线
Fig.4 Curve of the cost function
为了评价神经网络的检测性能,考察系统在一定性杂比下的工作特性,即ROC(Receiver Operating Characteristic)曲线。ROC曲线是发现概率和虚警概率的关系曲线,当改变检测门限时可得不同的Pd和Pfa,从而绘制出该曲线。对于本网络而言,改变输出层的检测门限,绘制出ROC曲线如图5所示。
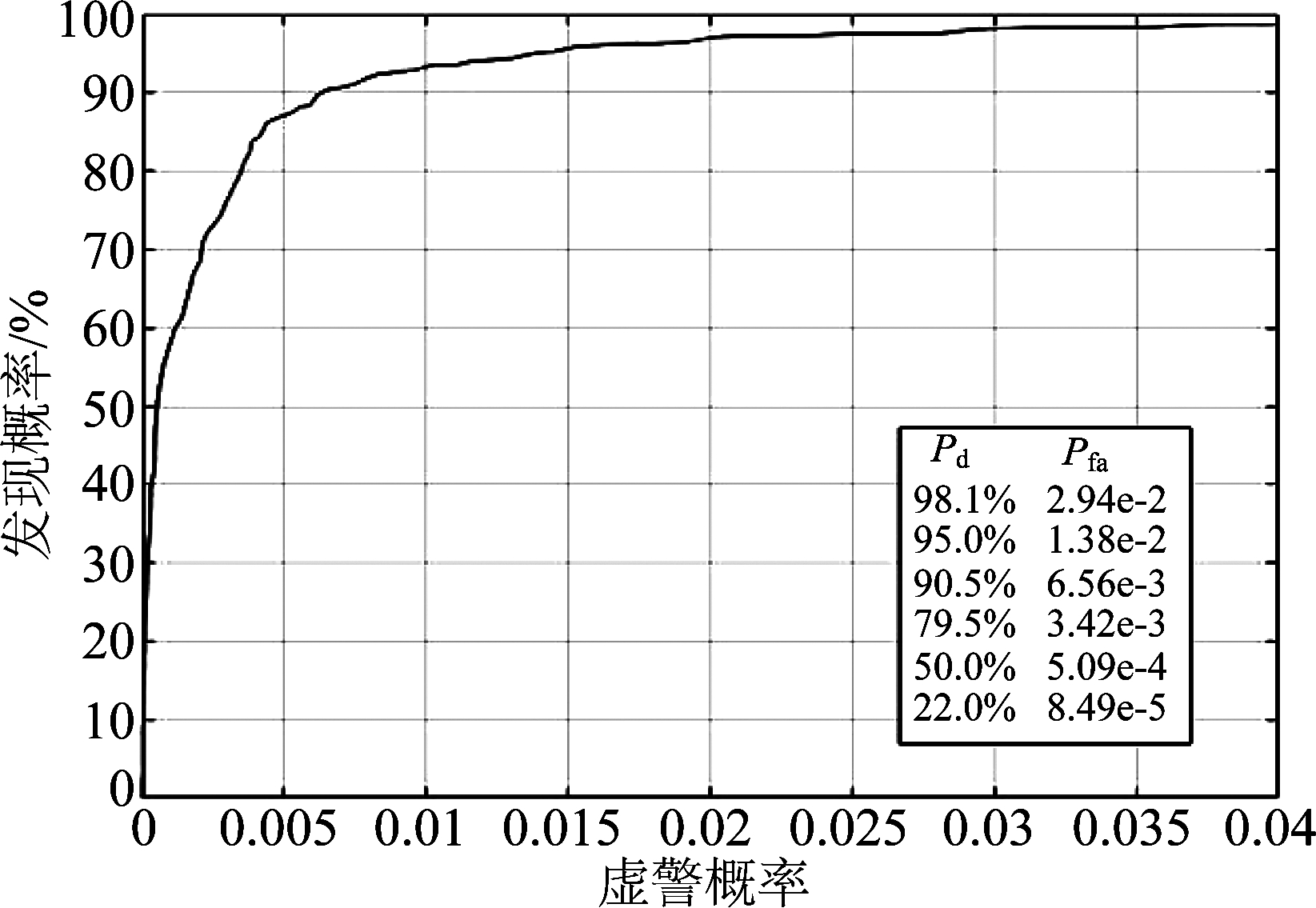
图5 ROC曲线
Fig.5 Receiver operating characteristic curve
同时,引入信杂比改善因子,并提出背景抑制因子的概念,从而进行神经网络检测性能的进一步分析。信杂比改善因子ISCR定义如下:
(10)
提出背景抑制因子IC,其定义如下:
(11)
由于神经网络的输出值域为0至1,首先采用公式(9)的逆运算对神经网络的输出值进行逆归一化,之后对每一帧测试集数据进行信杂比改善因子和背景抑制因子的计算。测试集数据的信杂比如图6所示,均值为24.0 dB,分布于10至42 dB范围内。信杂比改善因子如图7所示,均值为18.1 dB,其中95%的数据在一定程度上改善了信杂比。背景抑制因子如图8所示,均值为25.0 dB,所有数据在一定程度上抑制了海杂波。可见多目标检测网络能够优化检测环境,具备良好的目标检测能力。
对信杂比改善因子最高的第99组进行分析,如图9、10所示,平均信杂比改善为29.0 dB,平均背景抑制为25.6 dB。虚线为原始输入数据,实线为输出数据,点划线为输出数据检测门限,下同。距离单元185~186、251~255、379的不同长度的目标均过检测门限。可见神经网络在一定程度上提升了目标强度,并有效抑制海杂波,能够较好地改善信杂比,以提高检测性能。
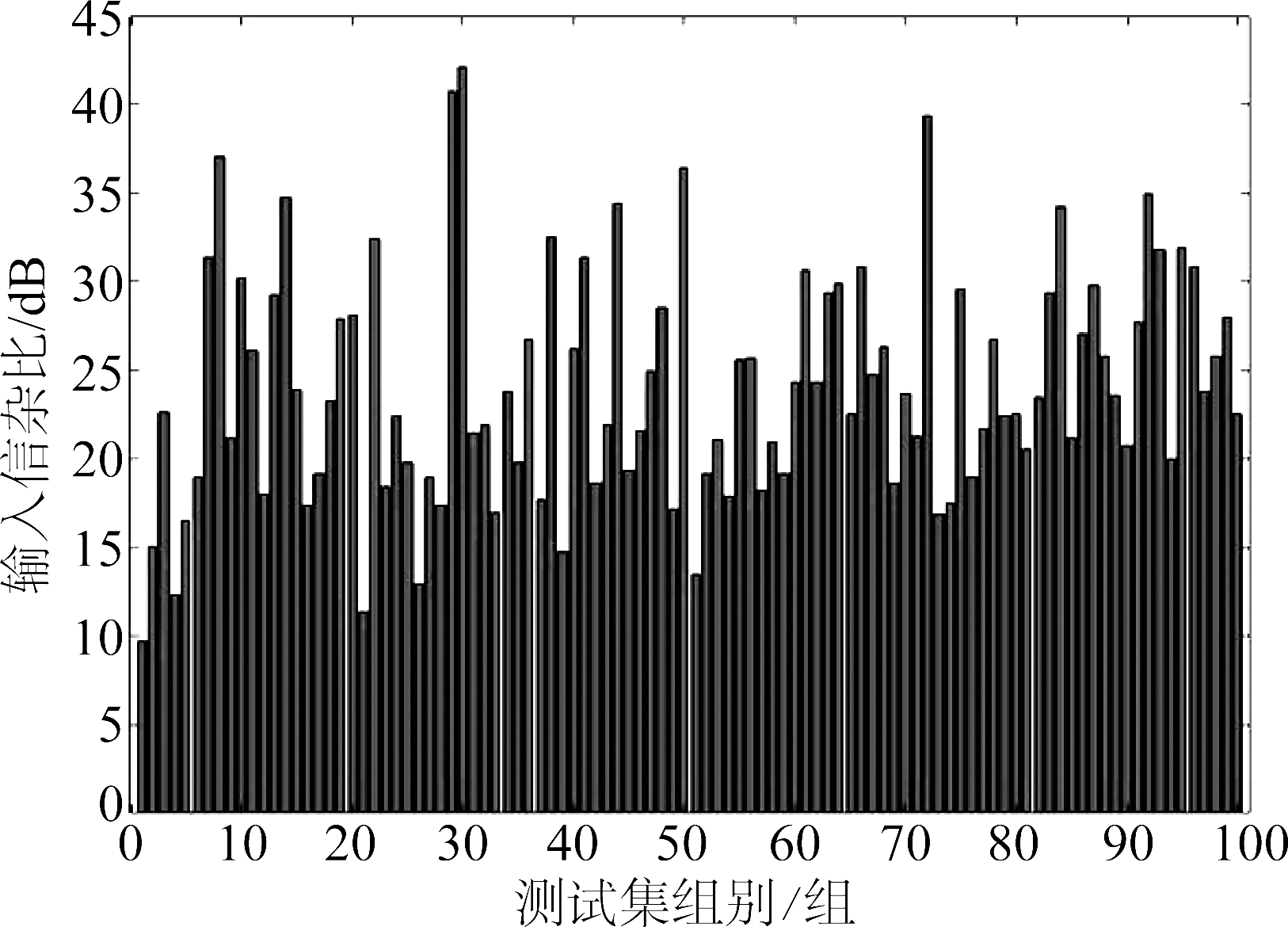
图6 测试集信杂比
Fig.6 SCR of the test data
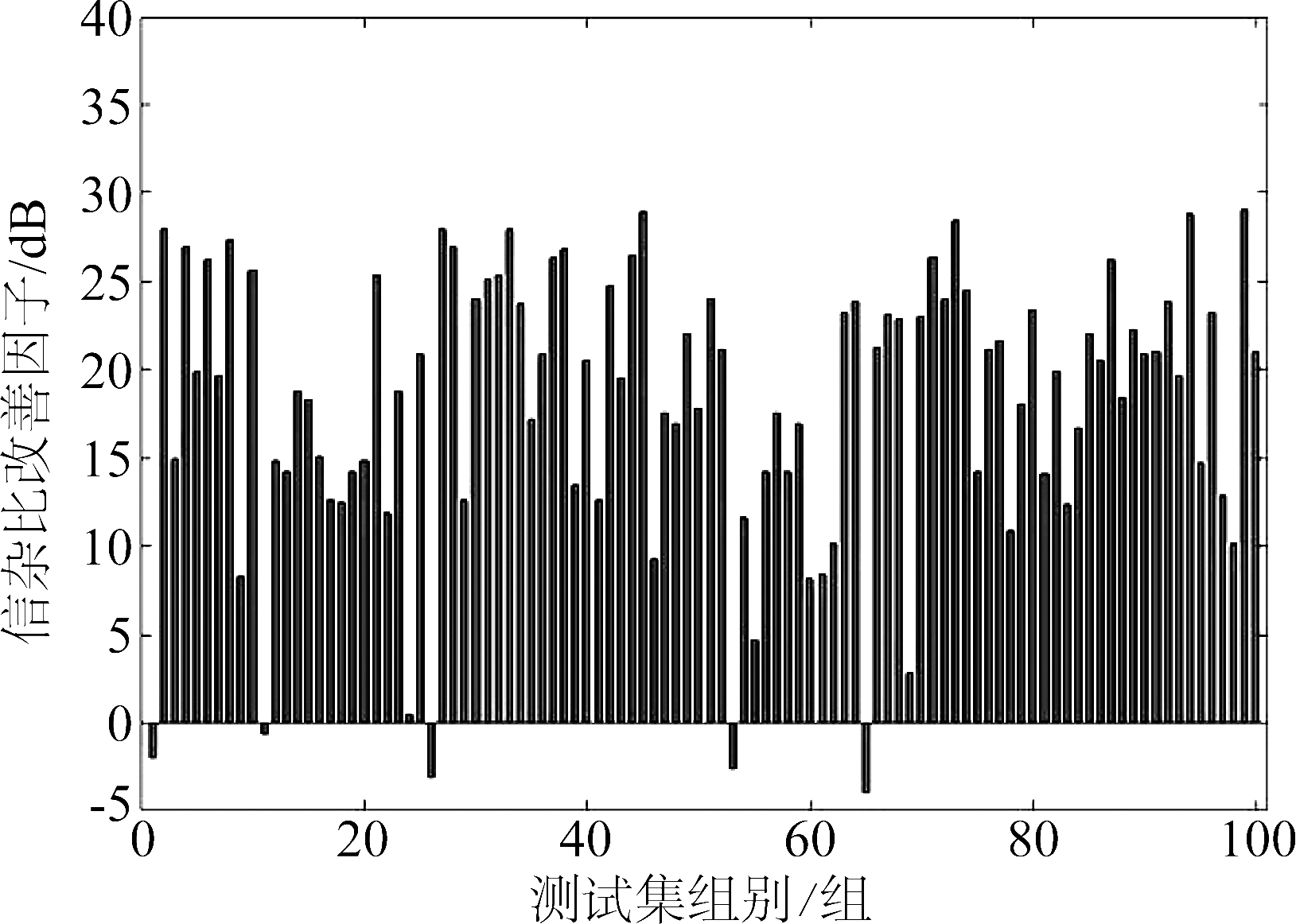
图7 测试集信杂比改善因子
Fig.7 SCR improvement factor of the test data
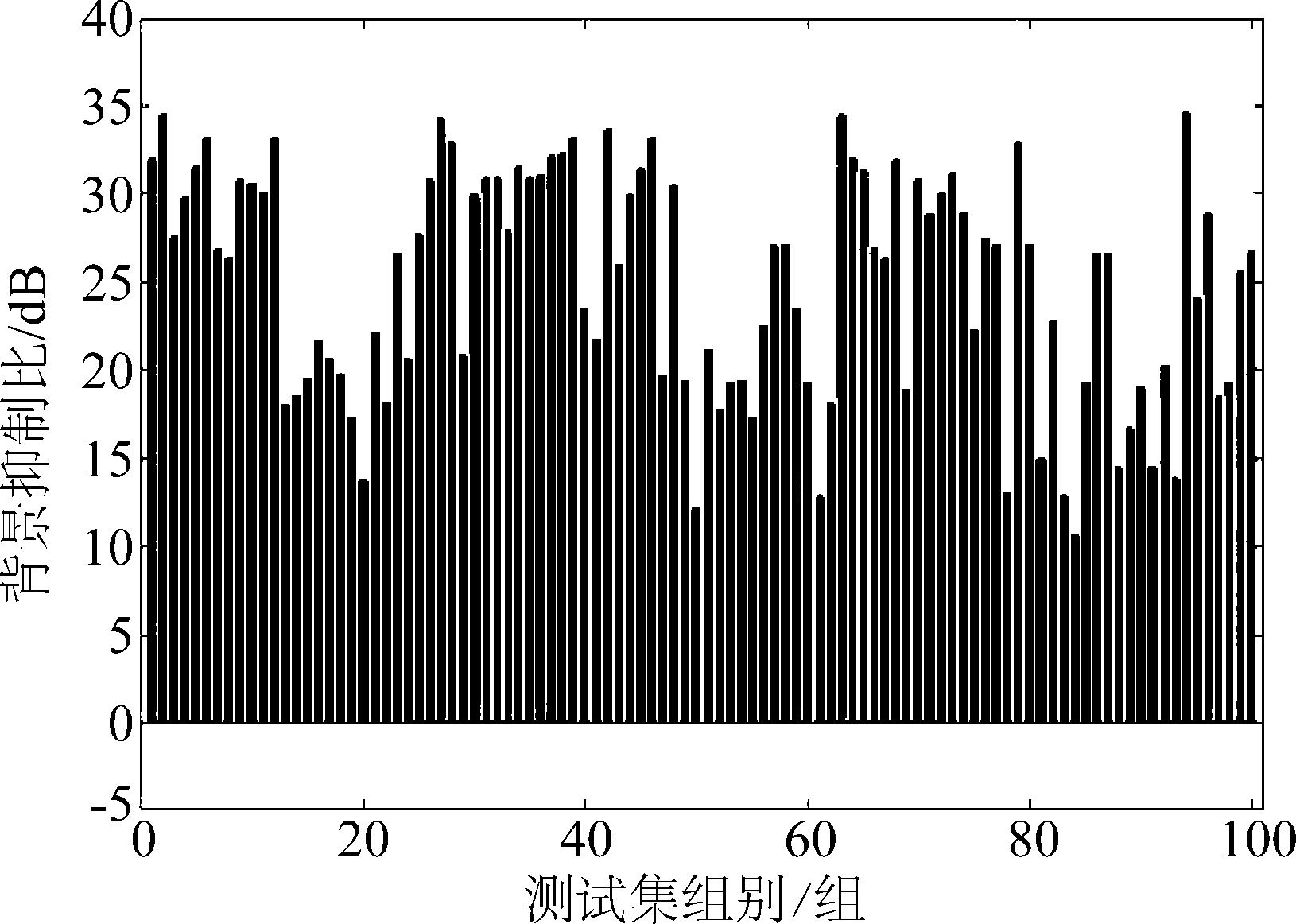
图8 测试集上的背景抑制因子
Fig.8 Background suppression ratio in the test data
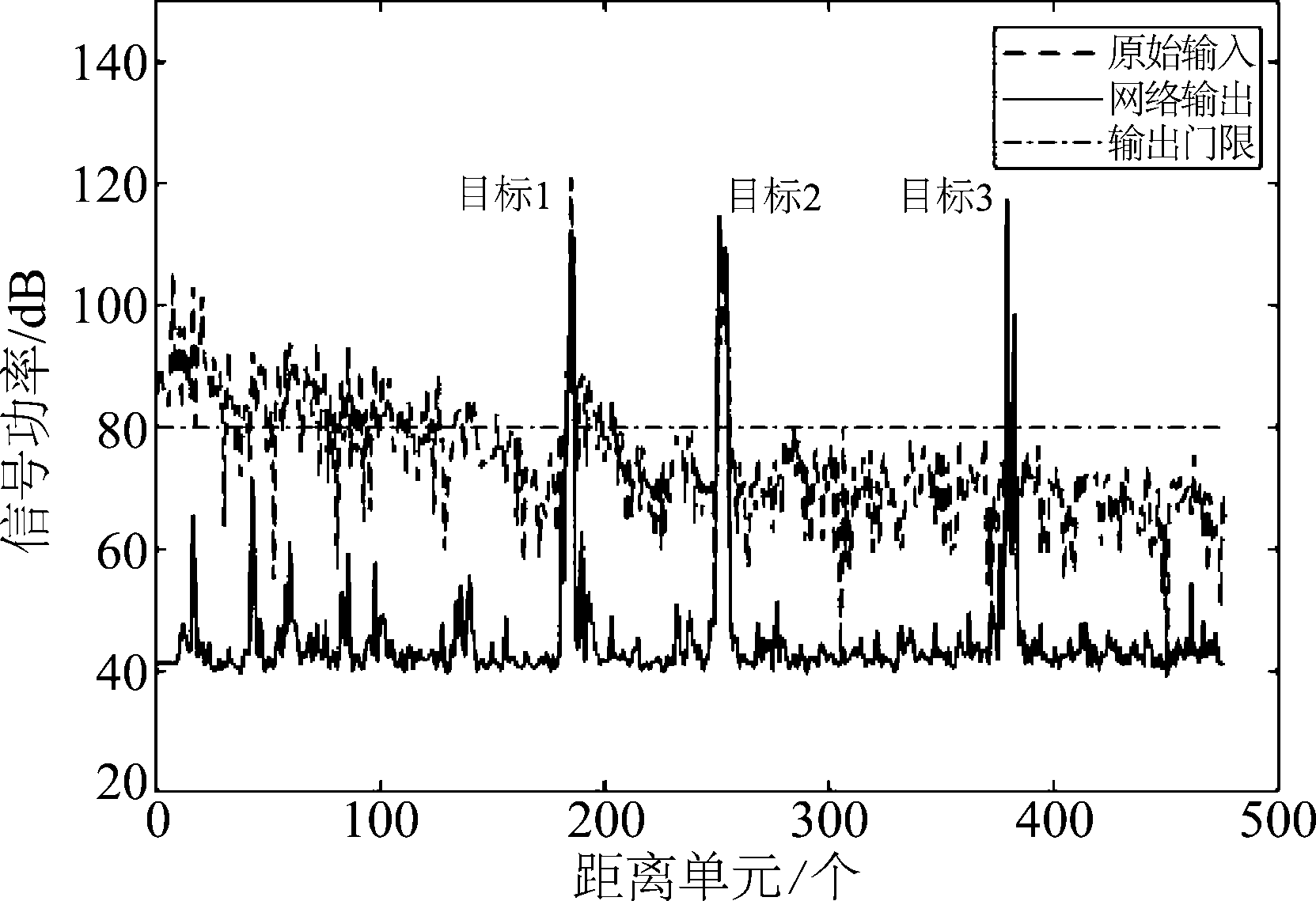
图9 第99组数据
Fig.9 The 99th data set

图10 第99组局部放大图
Fig.10 Partial enlarged images of the 99th data set
对包含距离较近目标的第7组数据进行分析,如图11、12所示,平均信杂比改善为19.3 dB。目标1位于距离单元381~385,目标2位于392~393,目标3在400~405,间隔均为6个距离单元,从网络输出可知上述目标均过检测门限。而采用单元平均CFAR时,若单侧保护单元少于目标覆盖范围,此处为25个,则目标点落入参考单元将引起检测门限抬高,从而造成检测困难。可见多目标检测网络能够降低临近目标对检测的不利影响,是一种更加通用的检测技术。
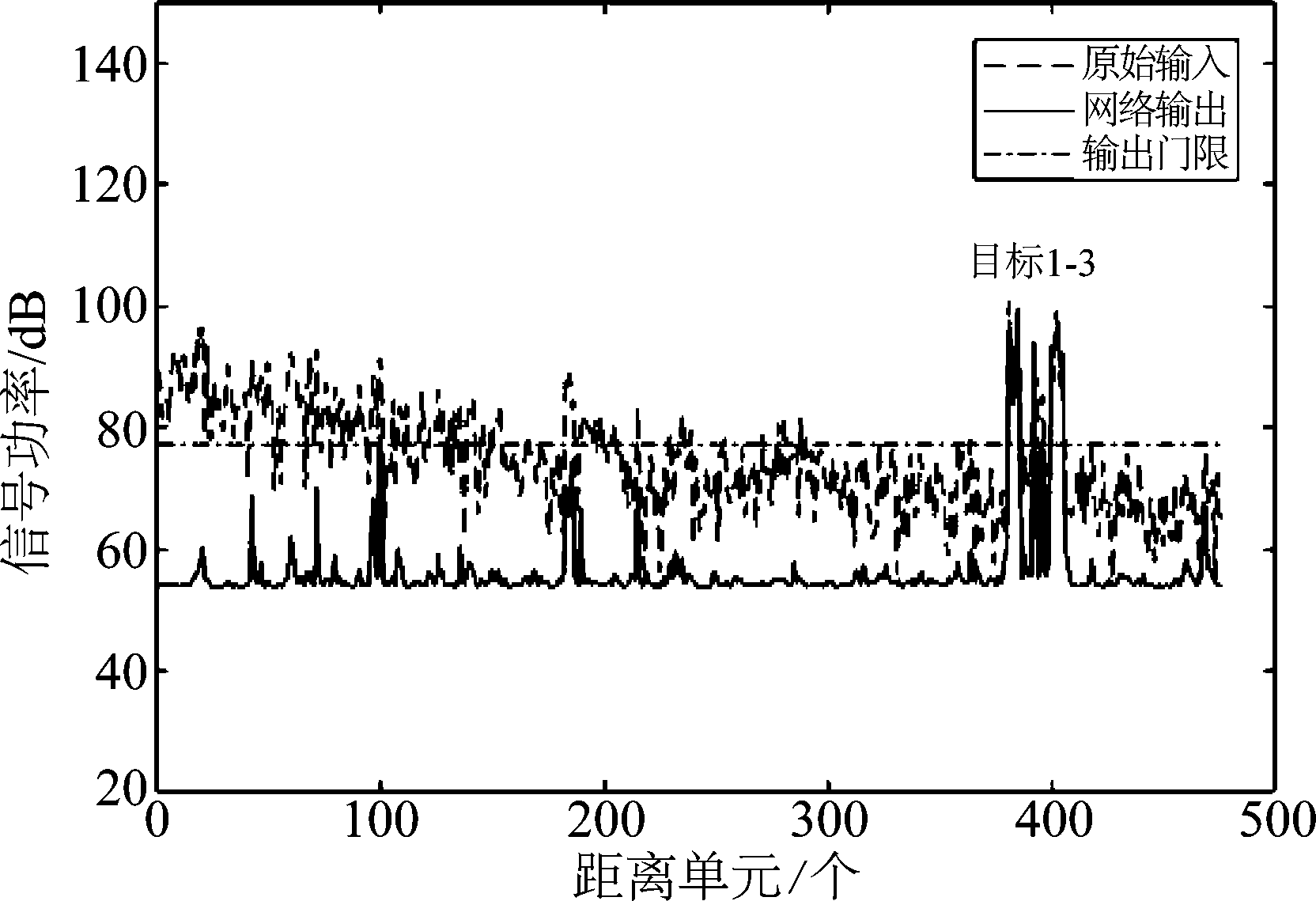
图11 第7组数据
Fig.11 The 7th data set
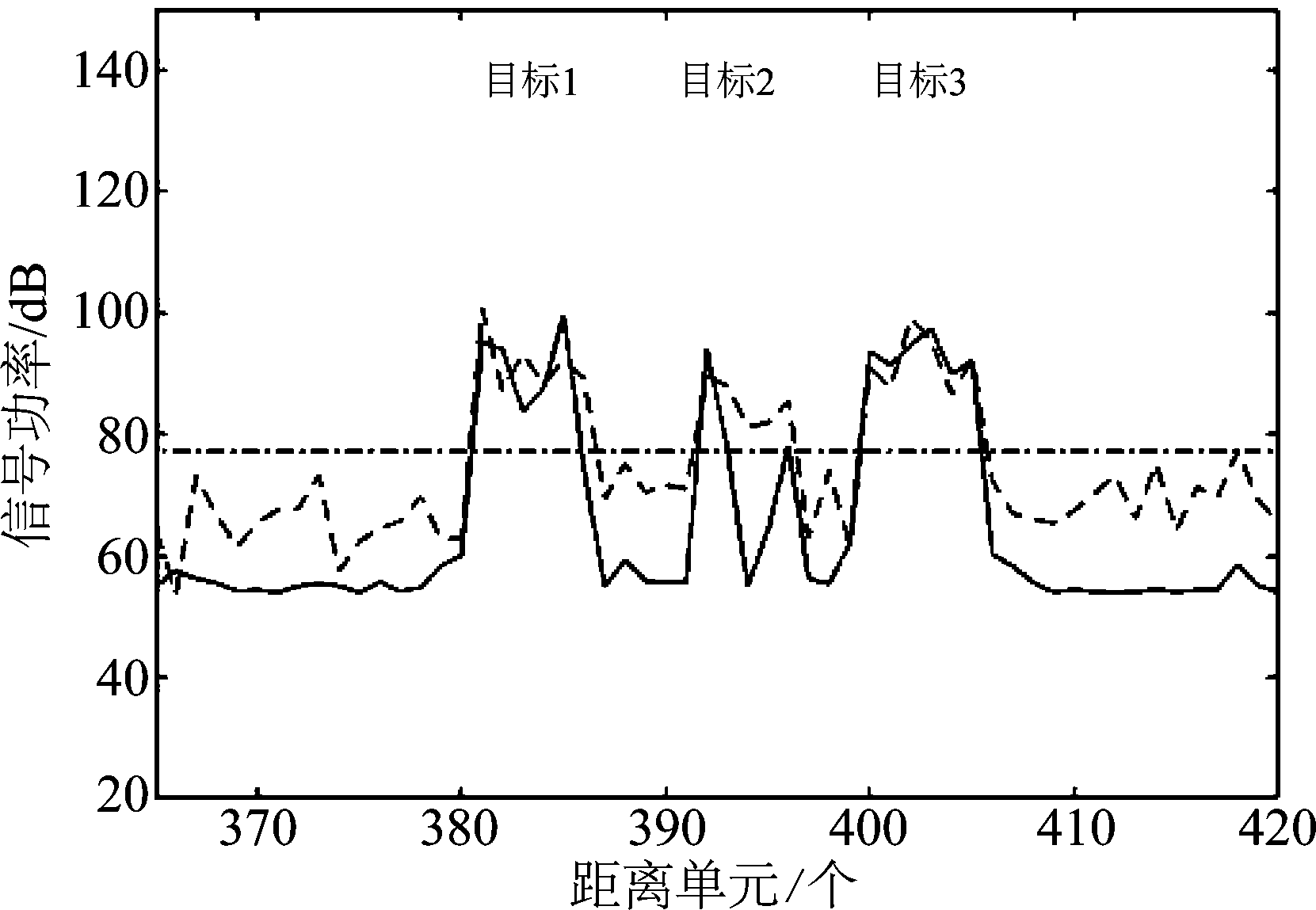
图12 第7组局部放大图
Fig.12 Partial enlarged images of the 7th data set
对改善因子最低的第65组进行分析,如图13、14所示,平均信杂比改善为-3.97 dB。距离单元133的目标1未过检测门限,而134产生虚警,等效为检测结果错位1个单元。355处的目标2提升幅度不明显,产生漏检,而418处的杂波产生虚警。由于目标点数较少,漏检使目标信号平均幅度大幅降低,使改善因子成为负值。可见在特定的测试数据下,虽然网络有效抑制了海杂波,但对个别目标的强度提升效果不足,或将幅度偏大的杂波识别为目标,从而产生漏检或虚警。
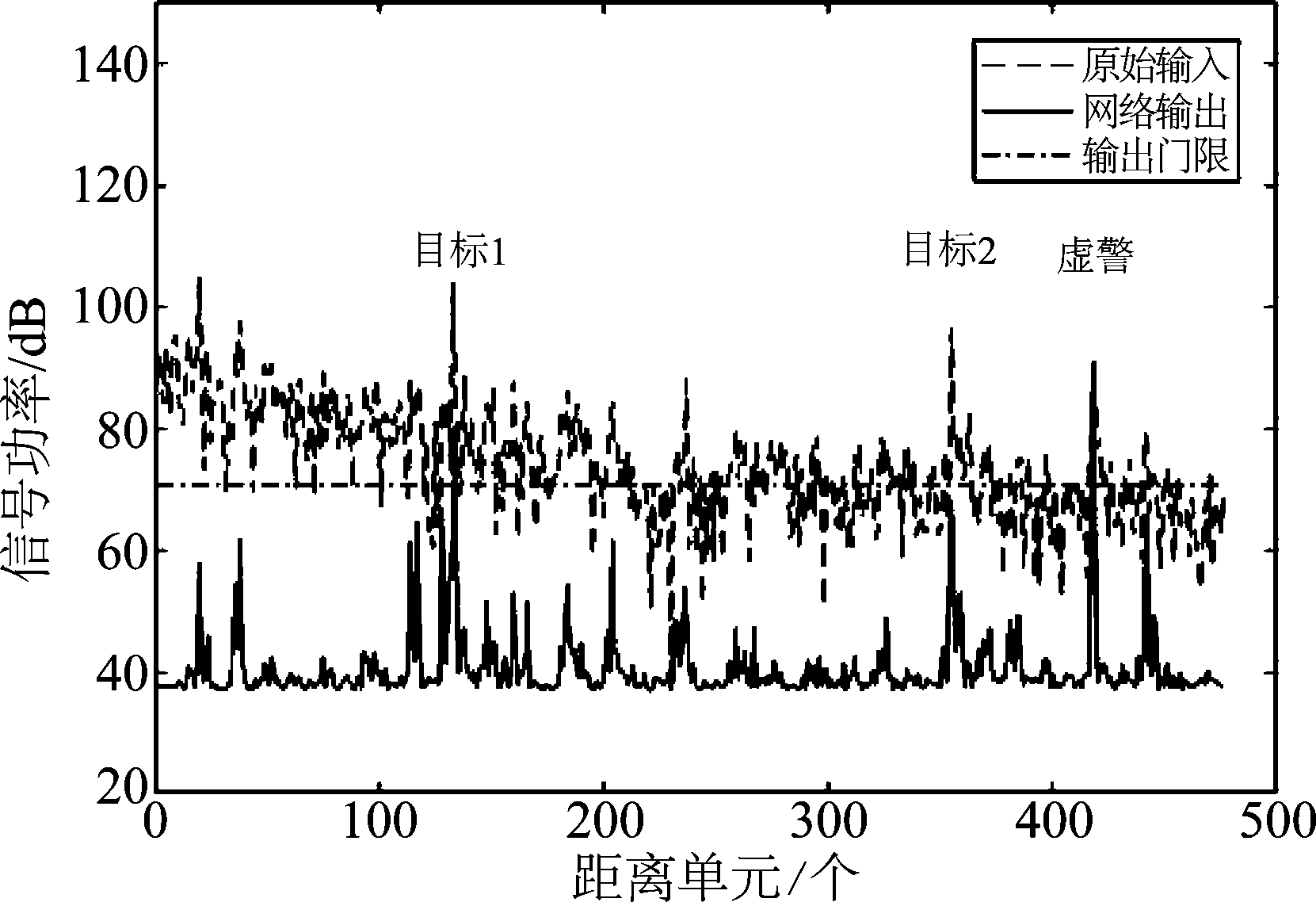
图13 第65组数据
Fig.13 The 65th data set
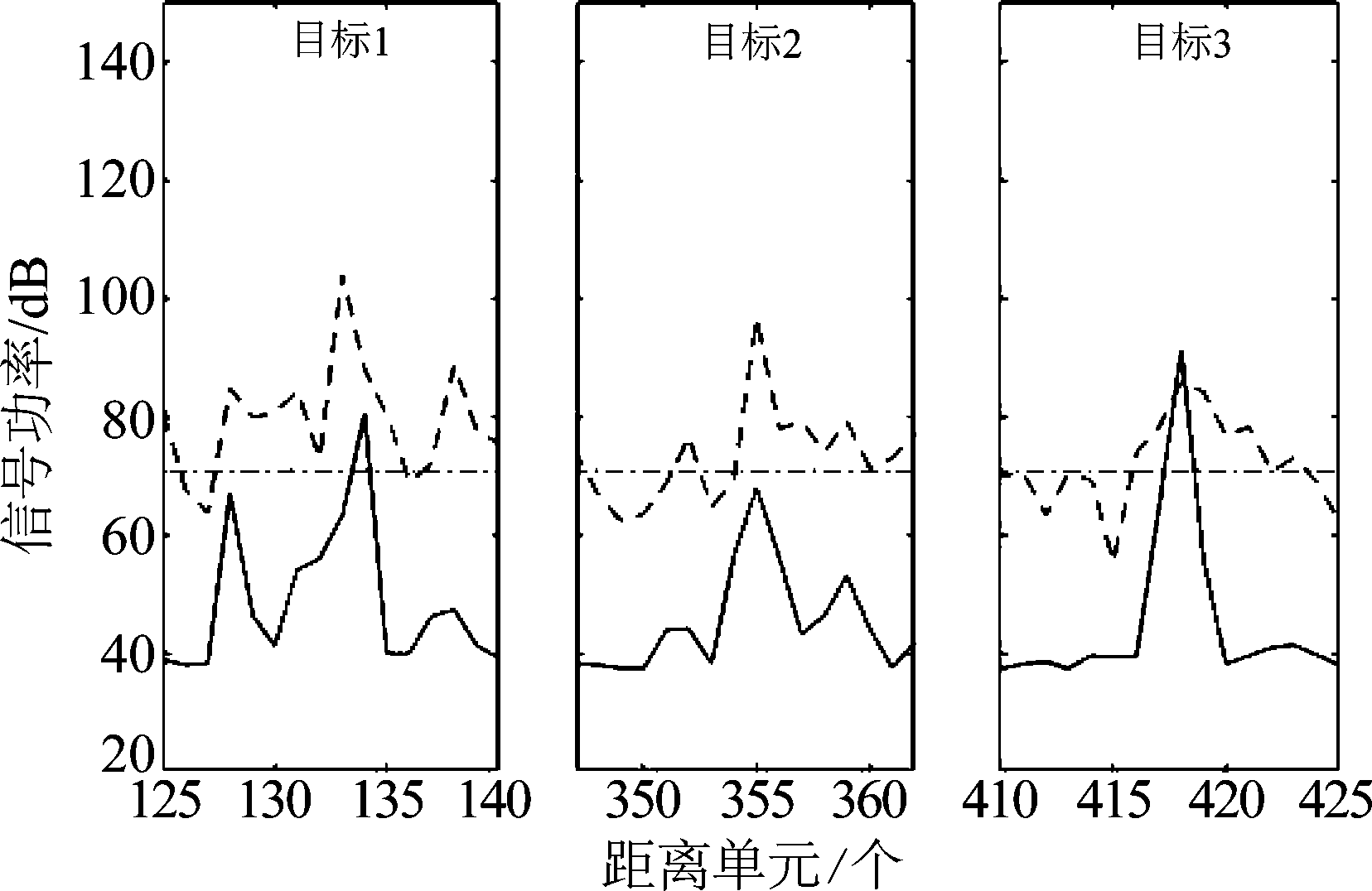
图14 第65组局部放大图
Fig.14 Partial enlarged images of the 65th data set
6 结论
针对海杂波环境下的多目标检测问题,本文提出了一种采用卷积神经网络的目标检测方法。通过研究适用于多目标检测的网络结构,优化代价函数,基于实测数据对该方法进行了验证。实验结果表明,该方法达到了较高的发现概率,具有良好的泛化能力,能够有效改善海面目标信杂比,提升多目标检测性能。针对虚警和漏检现象,从信号处理全过程而言,结合背景估计、MTI、时间去相关等技术能够消除输入数据中部分海杂波的影响;从网络检测而言,使用更完善的训练数据库或采用集成检测方法能够提升网络性能。综上所述,卷积神经网络在海面多目标检测领域具有一定的应用价值,值得进一步深入研究。
[1] 曾浩, 李洁, 鉴福升. 强海杂波环境下目标检测方法对比分析[J]. 雷达科学与技术, 2015, 13(1): 33-36.
Zeng Hao, Li Jie, Jian Fusheng. Comparative Analysis of Target Detection Methods in Strong Sea Clutter Background[J]. Radar Science and Technology, 2015, 13(1): 33-36. (in Chinese)
[2] 李琪. 海杂波背景下的目标检测算法[D]. 西安:西安电子科技大学, 2013.
Li Qi. Methods of Target Detection in the Sea Clutter Environment[D].Xi’an:Xidian University, 2013. (in Chinese)
[3] Fernandez M, Martínez T, Vidal B. CA-CFAR Adjust-ment Factor Correction with a priori Knowledge of the Clutter Distribution Shape Parameter[J]. International Journal of Interactive Multimedia and Artificial Intelligence, 2017, 4(4): 7-13.
[4] 刘瑜. 基于自适应曲面拟合的红外图像背景估计[J]. 科技创新导报, 2012, 4: 38- 40.
Liu Yu.Infrared Image Background Estimation Based on Adaptive Surface Fitting[J]. Science and Technology Innovation Herald, 2012, 4: 38- 40. (in Chinese)
[5] Liu M, Shi J, Li Z, et al. Towards better analysis of deep convolutional neural networks[J]. IEEE Transactions on Visualization and Computer Graphics, 2017, 23(1): 91-100.
[6] 洪新海, 宋彦. 结合CNN不同层信息的全变量建模人脸特征表达学习方法[J]. 信号处理, 2017, 33(8): 1073-1081.
Hong Xinhai, Song Yan. Total Variability Modeling for Face Representation Learning with CNN Multi-Layers[J]. Journal of Signal Processing, 2017, 33(8): 1073-1081. (in Chinese)
[7] 杨予昊, 孙晶明, 虞盛康, 等. 基于卷积神经网络的高分辨距离像目标识别[J]. 现代雷达, 2017, 39(12): 24-28.
Yang Yuhao, Sun Jingming, Yu Shengkang, et al. High Resolution Range Profile Target Recognition Based on Convolutional Neural Network[J]. Modern Radar, 2017, 39(12): 24-28. (in Chinese)
[8] 邹浩, 林赟, 洪文. 采用深度学习的多方位角 SAR 图像目标识别研究[J]. 信号处理, 2018, 34(5): 513-522.
Zou Hao, Lin Yun, Hong Wen. Research on Multi-Aspect SAR Images Target Recognition Using Deep Learning[J]. Journal of Signal Processing, 2018, 34(5): 513-522. (in Chinese)
[9] Hornik K,Stinchcombe M, White H. Multilayer feedforward networks are universal approximators[J]. Neural Networks, 1989, 2(5): 359-366.
[10] Goodfellow I,Bengio Y, Courville A, et al. Deep learning[M]. Cambridge: MIT Press, 2016.
[11] Prusa J D, Khoshgoftaar T M. Improving deep neural network design with new text data representations[J]. Journal of Big Data, 2017, 4(1): 7-22.
[12] Sutskever I, Martens J, Dahl G, et al. On the importance of initialization and momentum in deep learning[C]∥International Conference on Machine Learning, 2013: 1139-1147.
[13] Scardapane S,Comminiello D, Hussain A, et al. Group sparse regularization for deep neural networks[J]. Neurocomputing, 2017, 241(12): 81-89.
[14] Glorot X,Bengio Y. Understanding the difficulty of training deep feedforward neural networks[C]∥Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 2010: 249-256.


