1 引言
当今时代，信息技术迅速发展，需要处理的信号带宽越来越宽，如果对模拟信号用奈奎斯特采样率进行采样，将需要更大的存储和传输代价，同时对硬件采样系统也有更高的要求。于是，为了解决上述难题，有学者便提出了新的理论—压缩感知理论(Compressed Sensing, CS)[1-2]。CS理论是一种新的信号获取和处理方式，它在数据采集的同时完成数据的压缩，从而节约了软硬件资源和数据处理的时间。基于压缩感知的信号采样速率远低于传统奈奎斯特采样方法。这些优点使得其在很多领域有着广阔的应用前景,如在雷达[3-5]、成像[6]、信号处理[7]、信道估计[8-9]等。CS理论利用信号的稀疏特性或者将其变换到稀疏域，通过求解优化问题实现信号的精确重建。
重建算法是CS理论的关键问题，它应该在已知测量矩阵和测量向量的前提下，高效并且精确的实现对原始信号的重建。目前主要的重建算法有：组合优化类重建算法、凸优化类算法和统计分析类算法以及贪婪迭代类算法。组合优化类算法,如傅里叶采样算法[10]的重建效果比较好，但是在实际条件下由于系统要求比较严格，存在各种约束，因此很难广泛运用；凸优化类算法，如基追踪算法(Basis Pursuit, BP)[11]等算法，其需要的采样值较少，重建精度较好，但是算法复杂度高，在压缩感知系统的实际应用中很难得以广泛运用；统计分析类算法，如贝叶斯压缩感知[12]重建算法、从稀疏到结构化稀疏: 贝叶斯方法[13]、结合自适应字典学习的稀疏贝叶斯重建算法[14]等, 其在优化上达到局部最优，误差较小，重建效果较好，具有一定的应用前景；贪婪迭代类算法运算量小，运行效率和采样效率较高，且具有一定的重建精度，因此应用最为广泛。
作为应用最为广泛的贪婪迭代算法，现在已经有一些传统的算法，如正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)[15]。除此之外,还有一些由OMP算法加以优化所形成的算法[16-17]。上述算法的前提均要求已知信号的稀疏度，这一要求在实际应用中很难实现。能否在信号稀疏度未知的情况下，通过基于贪婪迭代的算法自适应的估计信号的稀疏度，使之更加精确的重建信号？针对该问题，有学者研究并且提出了具有一定程度自适应能力的分段正交匹配追踪算法(Stagewise Orthogonal Matching Pursuit, StOMP)[18]，它能够在未知信号稀疏度的前提下重建信号，因为其预先只需要把迭代次数设定为某一固定值即可，在文献[18]中,作者建议迭代次数取10，但其重建性能不够理想。本文在StOMP重建算法的基础上提出了一种增强型自适应分段正交匹配追踪算法(Enhanced Adaptive Stagewise Orthogonal Matching Pursuit Algorithm，EAStOMP)。该算法在已有StOMP算法的基础上，引入回溯思想，在原有的阈值参数的基础上通过引入一个新的标识参数，达到有效的二次支撑集筛选，从而可以更好的进行稀疏度估计，更加准确地重建信号。仿真结果表明，本文提出的重建算法具有很好的重建性能，重建精确度高，运算量适中，具有很好的实际应用场景。
2 压缩感知理论与传统重建算法
假设x∈RN是长度为N的原始信号向量，非零值元素个数为K，即稀疏度为K，y∈RM是长度为M的测量信号向量，Φ∈RM×N是M×N维的测量矩阵(或称为观测矩阵，其满足M≪N), x与Φ相乘得到y，即
y=Φx
(1)
当满足约束等距性质[19]时，重建端通过y与Φ则能以很大概率完成信号重建，前提是式(2)成立：
M≥cK log(N/K)≪N
(2)
其中c是一个很小的常数[20]。
对于信号的重建，实际上就是由式(1)求解最小l0范数优化问题，即
min‖x‖0, s.t. y=Φx
(3)
这是一个NP难问题，但是可以在一定条件下将其转化为更简单的最小l1范数优化问题来近似求解，即
min‖x‖1, s.t. y=Φx
(4)
当有噪声时，式(1)就变为：
y=Φx+n
(5)
其中n表示噪声向量。
类似的，此时的信号重建，实际上就是由式(5)求解最小l0范数优化问题，即
min‖x‖0, s.t. y=Φx+n
(6)
式(6)同样可以在一定条件下转化为更简单的最小l1范数优化问题来近似求解，即
min‖x‖1, s.t. y=Φx+n
(7)
对于最小l1范数优化问题可以通过线性规划方法来求解，如基追踪(BP)算法，但是其计算复杂度太高。所以，便出现了一类计算复杂度较低并且易于实现的贪婪迭代类重建算法，如比较经典的OMP算法以及一些改进算法[16-17]。
传统的OMP，它在每次迭代时首先通过计算此时残差向量与观测矩阵的内积，然后选取相关性最大的一个原子，放入索引集，然后更新残差和进行迭代次数的判断。不断重复上述过程，当迭代次数增加到信号的稀疏度时，则迭代终止，并输出重建信号估计值。由于每次迭代只选取一个原子，所以当稀疏度很大时需要的步数会大幅增加，重建效率有所降低。而分段正交匹配追踪StOMP算法则是在每次迭代时根据阈值参数来选取一个原子集合，然后利用最小二乘法求得重建信号，同时更新支撑集和残差，在一定程度上改善了重建效率。
StOMP算法的主要步骤[18]如下：
输入：测量矩阵Φ，测量信号向量y。
输出：重建信号
1)初始化残差r0=y，初始支撑集F0=∅，迭代次数k=1，终止最大迭代次数P；
2)筛选原子：Jk={j:|gk(j)|>tσk}，其中：gk=ΦTrk-1，gk(j)为向量gk中第k个元素，
σk为正常噪声水平；t为阈值参数，通常的取值范围为2≤t≤3；
3)合并形成新的支撑集：
Fk=Fk-1∪Jk;
4)更新残差：
5)判断终止迭代条件：如果k<P则执行k=k+1,转步骤2)；否则停止迭代并且输出重建信号近似值
在文献[18]中,作者建议P取10；其中的ΦFk表示从Φ中取支撑集Fk里的索引所对应的列构成的矩阵；
表示ΦFk的伪逆矩阵，且伪逆矩阵
对于上述的一些传统重建算法，如OMP、ROMP算法，它们都是以信号的稀疏度作为先验条件的，然而这在实际当中是很难实现的，所以需要一种具有稀疏度认知能力的自适应重建算法。虽然StOMP算法可以通过预先设定的迭代次数，实现在未知信号稀疏度的情况下的信号重建，但重建性能并不是很好。本文在StOMP算法的基础上进行了相应的改进，提出了增强型自适应分段正交匹配追踪算法，简记为EAStOMP。
3 EAStOMP算法
3.1 算法思想
本文在StOMP算法的基础上，引入回溯思想[21-22]，在原有的阈值参数的基础上通过引入一个新的标识参数I，通过标识参数来进行每步的可变步长的操作以及残差的更新，以更好的逼近估计信号稀疏度，更加有效的进行二次支撑集筛选，达到更好的信号重建的目的。该算法的停止迭代条件也有所变化，不再是最大迭代次数而是一个阈值参数ε。该阈值参数是一个很小的值，可根据实际情况来进行设置，也可以是噪声功率。这样通过更加有效的选取原子，以及更加合理的稀疏度估计过程，逐渐逼近信号稀疏度，最后可以更加高效的完成信号重建。
3.2 算法步骤
EAStOMP的主要算法步骤如下：
输入：测量矩阵Φ，测量信号向量y，初始迭代次数s。
输出：重建信号
1)初始化残差r0=y,初始支撑集F0=∅，起始步长L=s，迭代次数k=1，阶段标识I=0;
2)初选原子形成候选集：
Jk={j:|gk(j)|>tσk};
其中：
为正常噪声水平；t为阈值参数，本文的阈值参数通常取值范围为1≤t≤3，与StOMP不同；候选集Ck=Fk-1∪Jk；
3)阶段标识值判断与更新：
如果size(Ck)>μ*M，则I=1，其中size(Ck)表示候选集中的元素个数；
4)支撑集形成：
如果size(Ck)≥L，则
否则，F=Ck；其中
表示从
中选择前L个最大的元素所对应的索引；
5)残差：
6)判断停止迭代条件：如果
则停止迭代并且输出重建信号近似值
否则，转步骤7);
7)如果
且I=0，则L=L+2*s,Fk=Fk-1,rk=rk-1;如果且I=1,则L=L+s,Fk=Fk-1,rk=rk-1；否则，Fk=F,rk=r;
8)k=k+1，转步骤2)。
该算法中的第1)步进行初始化，其中的起始步长s既不能太大也不能太小，太大会降低重建质量，太小会增加重建时间，实际中，可以根据不同的目标选取合适的值。为了获取较高的重建质量，本文选取s=1。第2)步通过阈值参数t得到候选集Ck；t的取值范围为[1,3]，其下限相比于StOMP的取值更低，本算法在进行原子初选的时候就不会因为阈值过高而导致漏选了某些有效原子，即使在第一步初选原子的时候出现非有效原子，但是通过算法的二次筛选便可以将有效的原子筛选出来，达到更好的有效支撑集筛选效果。第3)步引入了新的阶段标识参数I，通过size(Ck)>μ*M来进行阶段标识的判断与更新，μ为标识阈值参数，根据1/4原则[2]，μ取μ<1/4即可。第4)步通过回溯思想和最小二乘法获得更加有效的支撑集F；回溯思想[19-20]通过对候选集的原子进行二次筛选，剔除一些不相关的原子，最终形成真的支撑集，以达到更好的重建性能。第5)步根据第4)步的支撑集计算残差r；第6)步判断停止条件是否满足，满足则输出重建信号
否则进入第7)步；第7)步通过第5)步计算的残差的2范数与上一次迭代的2范数的比较以及阶段标识I来进行不同的步长更新以及本次迭代的最终支撑集和残差的更新。这也是与StOMP算法不同的，因为StOMP算法并没有涉及到步长操作，其仅仅是通过阈值参数来选取原子，而我们提出的算法在原子初选之后进行的二次筛选过程与步长有关，而且在第7)步也进行了变步长的更新。当I=0，表示候选集的个数较小，所以下一次迭代采取大步长，有效扩大支撑集逼近稀疏度；I=1，表示候选集个数较大，为了防止过估稀疏度，所以采用小步长来筛选原子和逼近稀疏度。这样通过标识参数来进行变步长，可以更加有效的扩充支撑集和自适应的估计稀疏度，达到更好的信号重建性能。
4 仿真结果及分析
本节将通过Matlab仿真，在测量值无噪声和有噪声两种情况下，对比本文提出的EAStOMP算法和其他现有相关算法的重建性能。本文仿真实验中，仿真时所采用的观测矩阵为高斯随机矩阵，稀疏信号为一维高斯随机信号，稀疏信号长度记为N，稀疏度记为K。对于K稀疏的信号而言，向量中有K个服从高斯分布的非零元素，其余元素为0值，不同信号非零元素的位置是随机变化的。噪声为加性高斯白噪声，测量值个数也即测量向量长度记为M。由于比较的是稀疏度未知情况下的重建性能，为了比较的公平性，仿真中所用OMP算法均为未知稀疏度，迭代停止条件为‖r‖2<ε，ε是一个很小的值。仿真中OMP算法和EAStOMP算法的ε均取10-6。
当没有噪声的时候，用信号的准确重建概率作为重建性能指标。本节仿真中，准确重建定义为：重建信号与原始信号之差的2-范数小于一个极少值(仿真中取10-6)，即满足式(8)：
(8)
当有噪声的时候采用归一化均方误差(Mean Square Error, MSE)来衡量信号的重建性能。归一化MSE定义为:
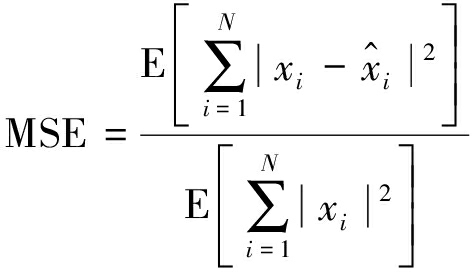
(9)
其中xi表示稀疏信号x的第i个元素，
表示重建后的信号
的第i个元素。仿真时EAStOMP算法的μ取1/8。每次仿真进行1000次，取其平均结果。
4.1 无噪声条件下准确重建概率
该仿真是在无噪声条件下，即式(4)所示模型。稀疏信号长度N取256时，M分别取128、64时，得到的不同算法的准确重建概率与稀疏度的关系。
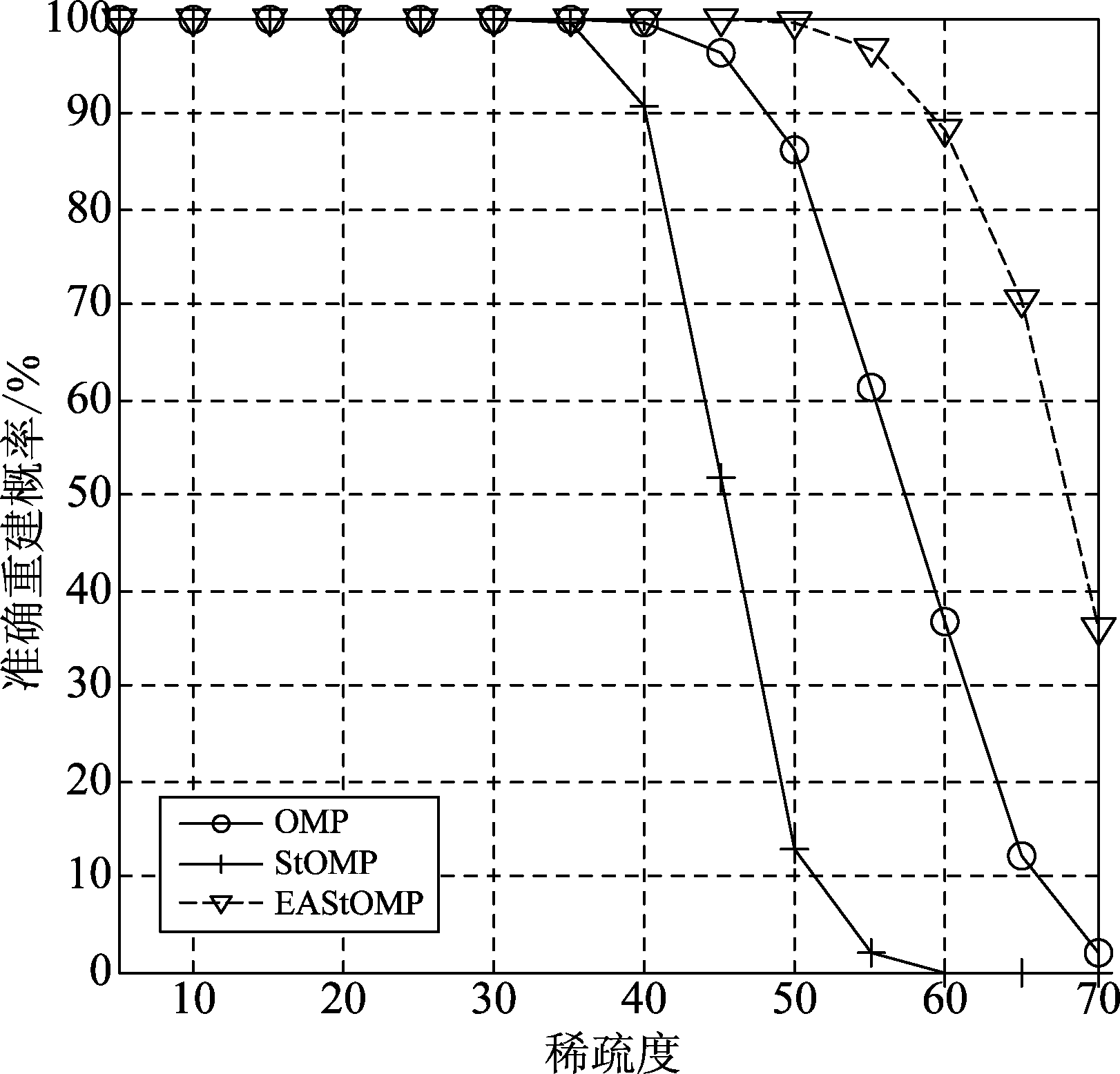
图1 不同算法的准确重建概率与稀疏度的关系(N=256, M=128)
Fig.1 The exact reconstruction probability to the sparisty of different algorithms(N=256, M=128)
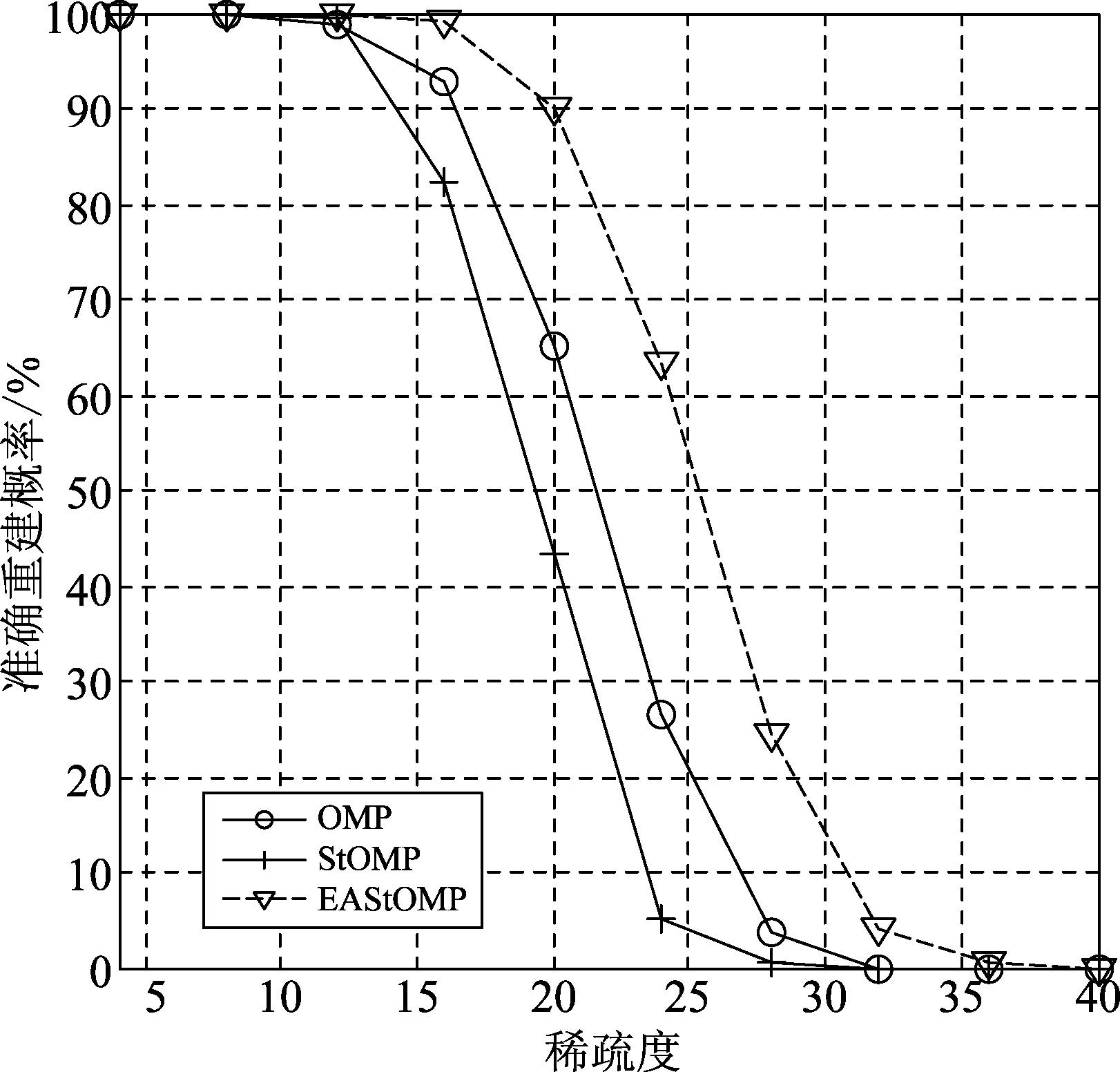
图2 不同算法的准确重建概率与稀疏度的关系(N=256, M=64)
Fig.2 The exact reconstruction probability to the sparisty of different algorithms(N=256, M=64)
从图1、图2可以看出，本文提出的EAStOMP算法在未知信号稀疏度的条件下，准确重建概率性能明显优于OMP和StOMP算法，如在M=128，K=55时，StOMP算法已经几乎无法重建信号，仅有1.8%的准确重建概率，OMP算法也仅有61.2%的准确重建概率，但是EAStOMP算法仍然有高达96.8%的准确重建概率。
4.2 有噪声条件下MSE的比较
该仿真是在测量值存在加性高斯白噪声条件下进行的，即采用式(7)所示模型。
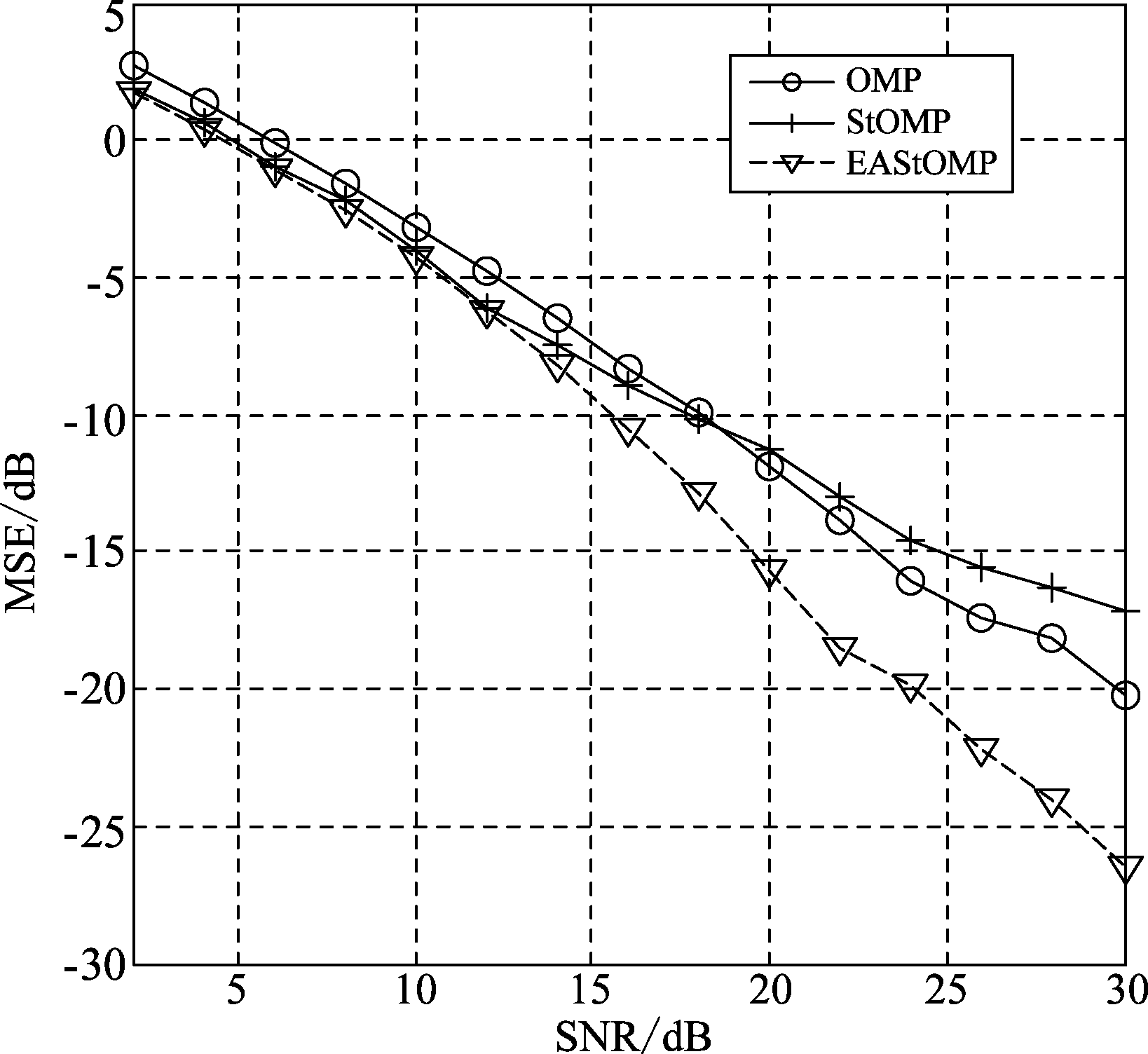
图3 不同算法信号重建性能MSE与信噪比SNR的关系(N=256,M=128,K=48)
Fig.3 The reconstruction performance MSE to SNR of different algorithms(N=256,M=128,K=48)
从图3可以看出，在加性高斯白噪声条件下，当N=256，M=128，K=48时，EAStOMP算法重建信号的MSE要优于OMP和StOMP算法。而且随着信噪比(Signal to Noise Ratio, SNR)的增大，性能优势越来越明显，当SNR=30 dB时，EAStOMP算法重建信号MSE优于StOMP算法10 dB左右。
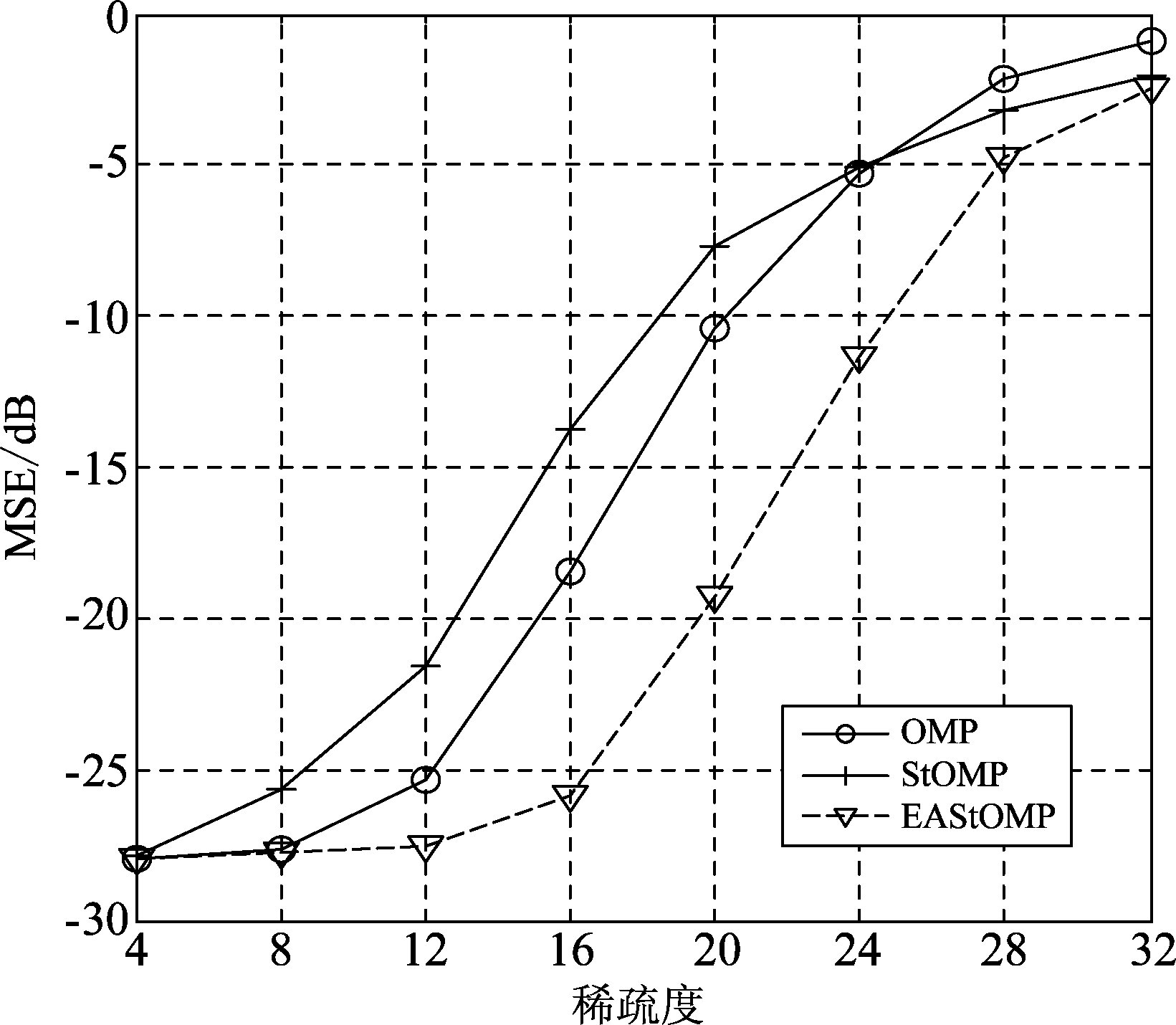
图4 不同算法信号重建MSE与稀疏度的关系(N=256, M=64, SNR=30 dB)
Fig.4 The reconstruction performance MSE to SNR of different algorithms(N=256, M=64, SNR=30 dB)
从图4可以看出，在加性高斯白噪声条件下，N=256，M=64，SNR=30 dB时，本文的EAStOMP算法信号重建MSE优于OMP算法和StOMP算法，且相对于StOMP算法MSE性能改善了很多，最大可达12 dB左右。
图5、图6是在N=256, SNR=30 dB时，K分别为20、40,得到的不同算法信号重建MSE与测量值个数的关系。从仿真结果可见，EAStOMP算法在不同测量值个数条件下的信号重建MSE都要优于图中OMP和StOMP算法，最高优于StOMP算法20 dB左右。且随着稀疏度K的增加，该算法相对于其他两种算法的性能优势越来越明显，尤其相对于StOMP算法表现的更突出。
4.3 无噪和有噪条件下的算法复杂度
4.1、4.2节的仿真结果都很好的说明了本文提出的EAStOMP算法无论在无噪条件下还是在有噪条件下，重建信号的质量性能都要优于其他算法，尤其是StOMP算法。而本节则对算法复杂度来进行比较，通过算法重建时间这一指标来衡量算法复杂度。
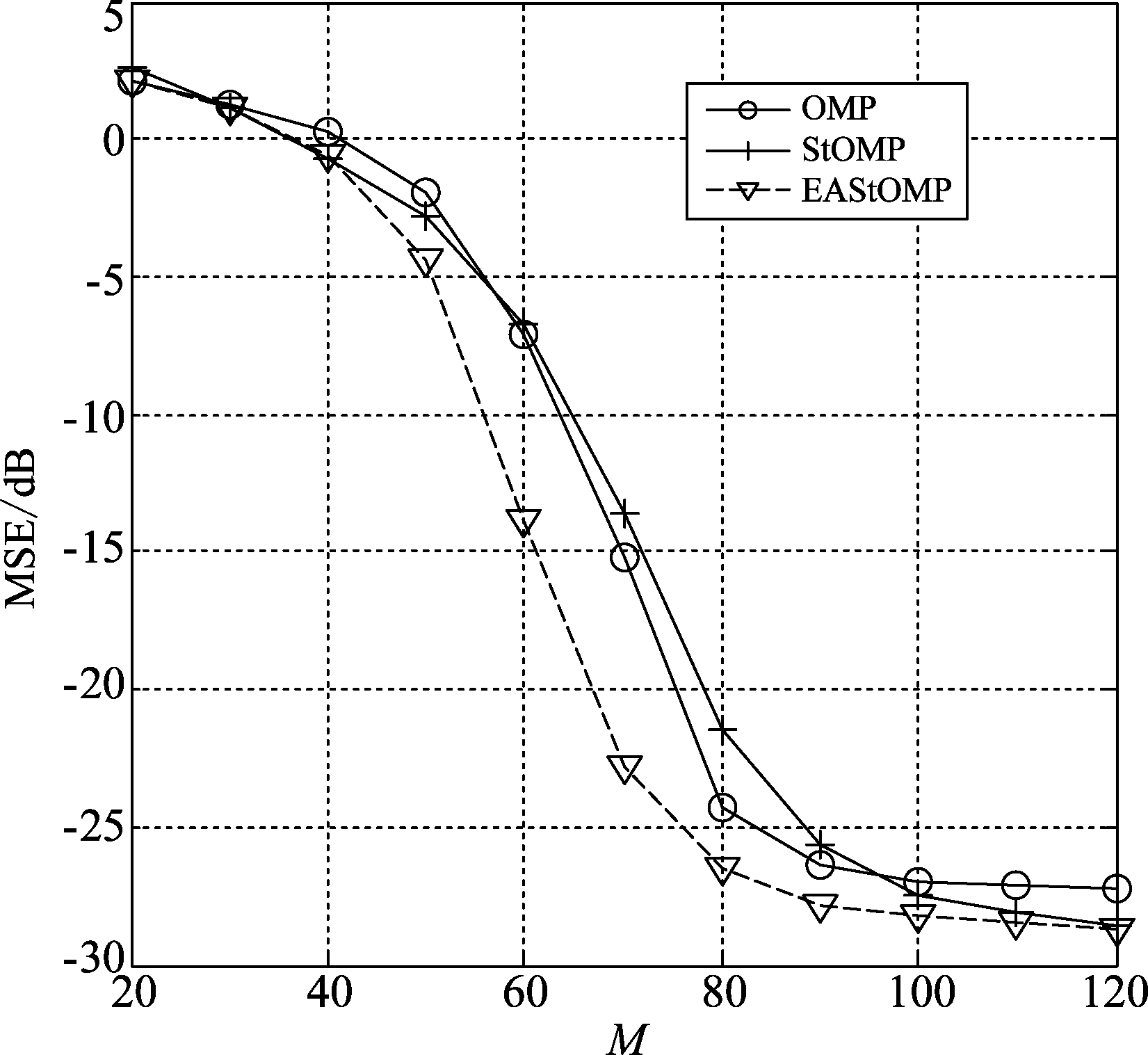
图5 不同算法信号重建MSE与测量值个数的关系(N=256, K=20,SNR=30 dB)
Fig.5 The reconstruction performance MSE to the number of measurements of different algorithms(N=256, K=20,SNR=30 dB)
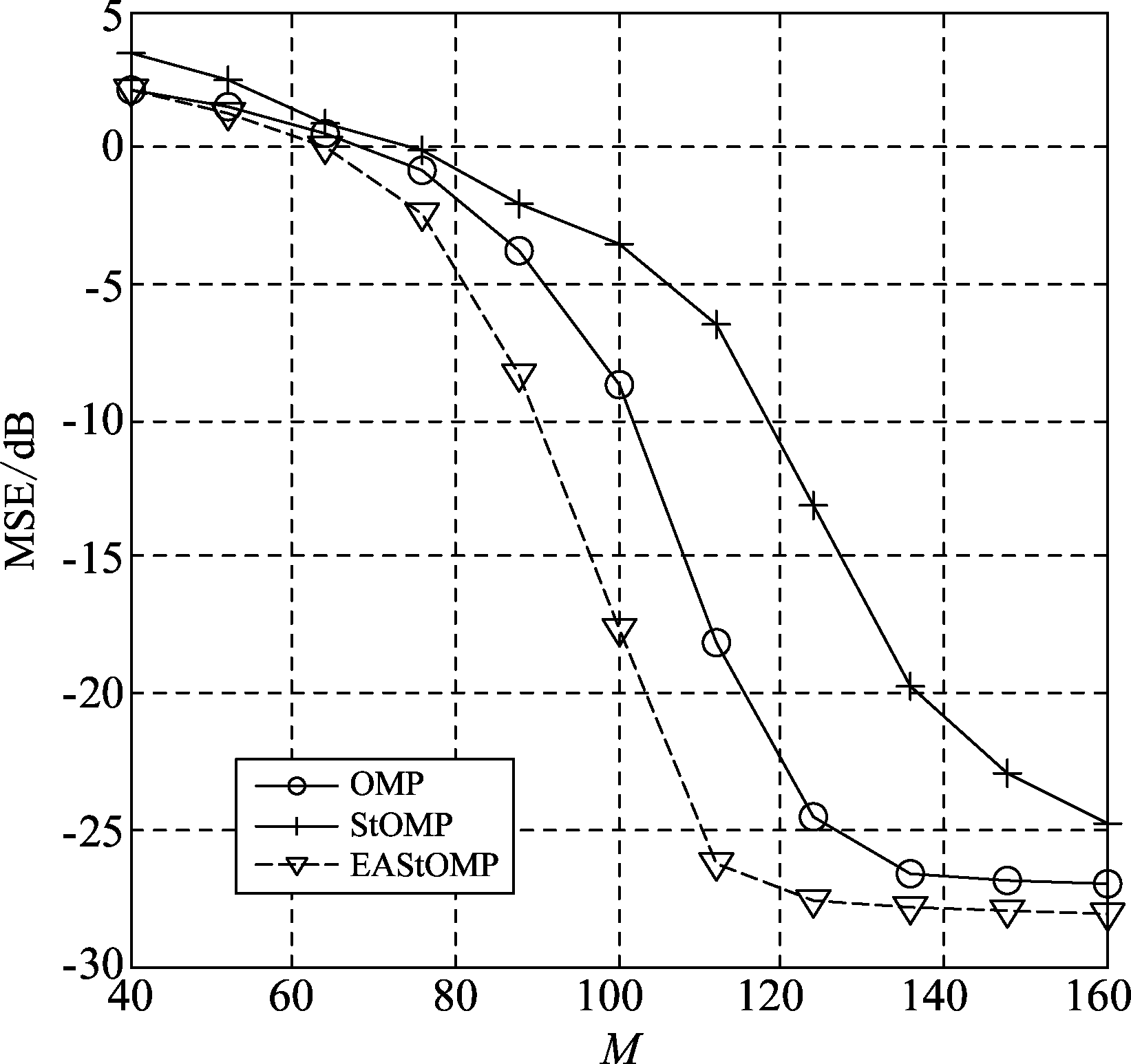
图6 不同算法信号重建MSE与测量值个数的关系(N=256, K=40,SNR=30 dB)
Fig.6 The reconstruction performance MSE to the number of measurements of different algorithms(N=256, K=40,SNR=30 dB)
在无噪声时，仿真中N=256,M=64,K依次取8、12、16、20。
从表1可以看出，EAStOMP算法重建信号的运行时间比OMP算法要小，且随着稀疏度增大优势越明显。虽然运行时间略高于StOMP算法，但是它的重建性能是优于StOMP算法，所以综合考虑EAStOMP算法重建性能还是有优势。
表1 无噪条件下不同算法重建信号运行时间(ms)
Tab.1 Different algorithms run time of signal reconstruction without noise (ms)
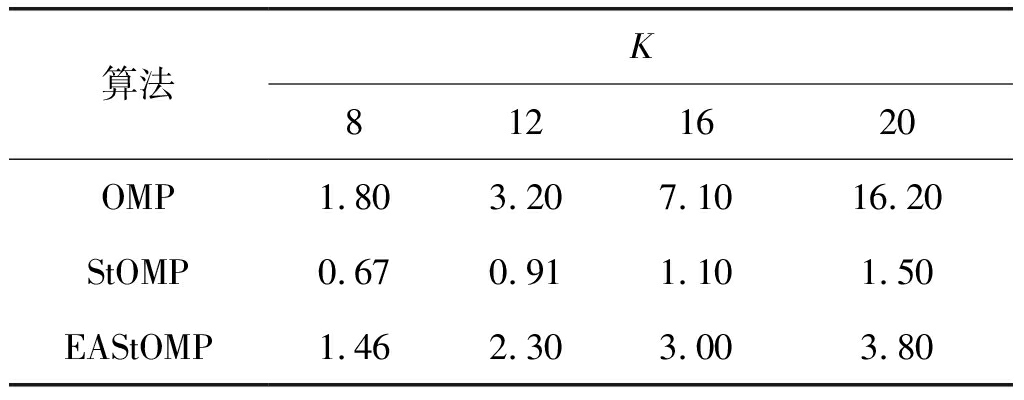
算法K8121620OMP1.803.207.1016.20StOMP0.670.911.101.50EAStOMP1.462.303.003.80
在有加性高斯白噪声时，仿真中N=256，M=64，SNR=30 dB，K依次取8、12、16、20。
表2仿真结果表明，在有噪声的条件下，EAStOMP算法重建信号的运行时间明显低于OMP算法。虽然略高于StOMP算法，但是信号重建MSE的性能优于StOMP算法2～12 dB左右。
表2 有噪条件下不同算法重建信号运行时间(ms)
Tab.2 Different algorithms run time of signal reconstruction with noise (ms)
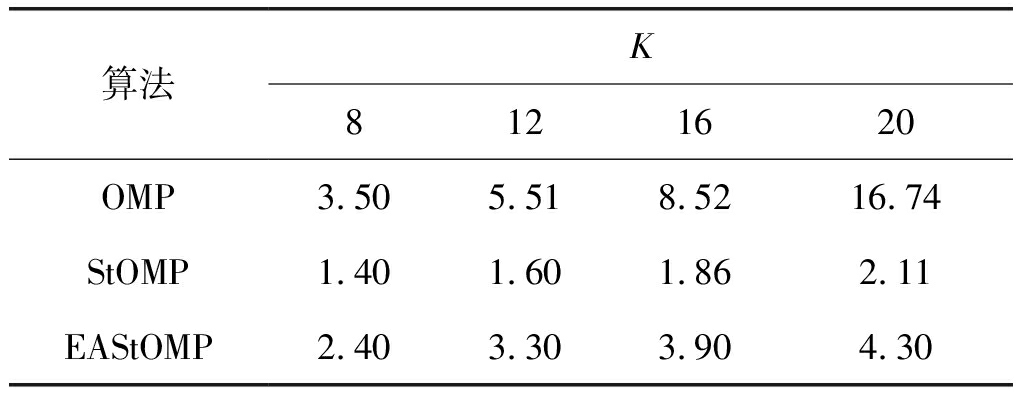
算法K8121620OMP3.505.518.5216.74StOMP1.401.601.862.11EAStOMP2.403.303.904.30
表1、表2的仿真结果表明，在无噪和有噪条件下，EAStOMP算法在未知信号稀疏度的条件下，自适应的重建信号的运行时间均优于OMP算法，OMP算法运行时间长主要是因为它无法很好的自适应估计信号的稀疏度，迭代次数过多； EAStOMP算法虽然运行时间略高于StOMP算法，为StOMP算法运行时间的2倍左右，但是信号重建质量性能优于StOMP算法很多。
综合以上仿真结果，EAStOMP算法的重建性能优于OMP算法，但会牺牲少量算法复杂度，即EAStOMP算法的重建时间略长于StOMP算法。当我们优先考虑重建质量时， EAStOMP算法将明显优于StOMP算法。
5 结论
本文在深入研究了StOMP算法以及其他传统压缩感知重建算法的基础上，通过在原有的StOMP算法中引入标识参数进行变步长和回溯思想，提出了一种增强型自适应分段正交匹配追踪算法EAStOMP。该算法在未知信号稀疏度的条件下，通过标识参数进行变步长以及回溯思想进行原子的筛选和稀疏度的估计逼近，从而有效的完成信号重建。仿真结果表明，在未知信号稀疏度的条件下，相比于StOMP算法和OMP算法，可以更加有效的自适应重建信号，且重建信号的质量很高，重建信号时间较低。在不同参数条件下，与StOMP算法相比，EAStOMP算法无噪时准确重建概率平均提高30%～40%左右，有噪时MSE提高5～10 dB左右。下一步， 还需研究如何将本文提出的EAStOMP算法应用在实际应用中，以评估其实用性能的提升水平。
[1] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.
[2] Candes E J, Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2):21-30.
[3] 王雪君, 孙进平, 张旭旺. 基于压缩感知的PD雷达序贯扩展卡尔曼滤波跟踪方法[J]. 信号处理, 2017,33(4):601- 606.
Wang Xuejun, Sun Jinping, Zhang Xuwang. New sequential extended Kalman filter for Pulse Doppler radar tracker based on compressed sensing[J]. Journal of Signal Processing, 2017, 33(4):601- 606. (in Chinese)
[4] 严韬, 陈建文, 鲍拯. 一种基于压缩感知的天波超视距雷达短时海杂波抑制方法[J].电子与信息学报, 2017, 39(4):945-952.
Yan Tao, Chen Jianwen, Bao Zheng. Sea clutter suppression method for over-the-horizon radar with short coherent integration time based on compressed sensing[J]. Journal of Electronics & Information Technology, 2017, 39(4):945-952. (in Chinese)
[5] 赵春雷, 王亚梁, 毛兴鹏, 等.基于压缩感知的高频地波雷达二维DOA估计[J].系统工程与电子技术, 2017(4):733-741.
Zhao Chunlei, Wang Yaliang, Mao Xingpeng, et al. Compressive sensing based two-dimensional DOA estimation for high frequency surface wave radar[J]. Systems Engineering and Electronics, 2017(4):733-741. (in Chinese)
[6] 卜红霞, 白霞, 赵娟,等.基于压缩感知的矩阵型联合SAR成像与自聚焦算法[J].电子学报, 2017, 45(4):874- 881.
Bian Hongxia, Bai Xia, Zhao Juan, et al. Joint matrix form SAR imaging and autofocus based on compressed sensing[J]. Acta Electronica Sinica, 2017, 45(4):874- 881. (in Chinese)
[7] Elad M. Sparse and redundant representations from theory to applications in signal and image processing[M]. New York, Springer, 2010, 2(1):1094-1097.
[8] Bajwa W U, Haupt J, Sayeed A M, et al. Compressed channel sensing: A new approach to estimating sparse multipath channels[J]. Proceedings of the IEEE, 2010, 98(6):1058-1076.
[9] 林格平, 马晓川, 鄢社锋,等. 无字典的超分辨率多径稀疏信道估计方法[J]. 信号处理, 2017, 33(9):1239-1247.
Lin Geping, Ma Xiaochuan, Yan Shefeng, et al. Super-resolution multipath sparse channel estimation with no dictionary[J]. Journal of Signal Processing, 2017, 33(9):1239-1247. (in Chinese)
[10] Gilbert A C, Muthukrishnan S, Strauss M. Improved time bounds for near-optimal sparse Fourier representations[C]∥Proceedings of SPIE, San Diego, California, United States, 2005: 5914, Wavelets XI,59141A.
[11] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159.
[12] Ji S, Xue Y, Carin L. Bayesian compressive sensing[J].IEEE Transactions on Signal Processing, 2008, 56(6):2346-2356.
[13] 孙洪, 张智林, 余磊. 从稀疏到结构化稀疏: 贝叶斯方法[J]. 信号处理, 2012, 28(6):759-773.
Sun Hong, Zhang Zhilin, Yu Lei. From Sparsity to Structured Sparsity: Bayesian Perspective[J]. Signal Processing, 2012, 28(6):759-773. (in Chinese)
[14] 王勇,乔倩倩,杨笑宇,等.结合自适应字典学习的稀疏贝叶斯重构[J].西安电子科技大学学报:自然科学版, 2016, 43(4):1- 4.
Wang Yong, Qiao Qianqian, Yang Xiaoyu, et al. Sparse bayesian reconstruction combined with self-adaptive dictionary learning[J]. Journal of Xidian University:Nature Science Edition, 2016,43(4):1- 4. (in Chinese)
[15] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655- 4666.
[16] Needell D, Vershynin R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):310-316.
[17] Wang J, Kwon S, Shim B. Generalized orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(12):6202- 6216.
[18] Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2):1094-1121.
[19] Candes E J, Tao T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12):4203- 4215.
[20] Baraniuk R G. Compressive sensing[Lecture Notes][J]. IEEE Signal Processing Magazine, 2007, 24(4):118-121.
[21] Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5):2230-2249.
[22] Needell D, Tropp J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.
