1 引言
图像超分辨率算法的目标是通过低分辨率图像来重建高分辨率图像。图像超分辨率在图像处理和计算机视觉中有着很重要且广泛的应用,在医学诊断[1]、卫星遥感[2]等领域都有着非常重要的应用。图像为人们提供了可视化的直观信息,其质量的好坏直接影响识别、检测及分类等操作[3]。图像的分辨率是评价图像质量的重要指标,主要反映了图像所含信息量的多少[4]。图像的分辨率越高,所含信息量就越多,视觉效果也越好,它对于视频监控、医学诊断等有着极其重要的作用。
图像超分辨率重建由Harris等人在1964年首次提出[5],之后有许多学者对其进行了深入研究。由于图像超分辨率重建是由低分辨率图像来重建高分辨率图像,所以超分辨率重建是图像处理中典型的病态反问题[6]。单幅图像超分辨率算法大体上可以分为两大类[7]:一类是基于插值的方法,一类是基于学习的方法。基于插值的超分辨率算法[8-9]比较简单,容易实现,但是对于重建质量较高的图像纹理和细节信息存在一定的困难。目前主流的基于学习的方法大致有三大类:基于稀疏表示的学习算法[10-11]、基于近邻嵌入的学习算法[12-14]和基于深度学习的算法[15-20]。基于稀疏表示的方法是通过学习高、低分辨率图像块的过完备字典来重建高分辨率图像。基于近邻嵌入的学习是利用图像特征空间上的结构相似性,对低分辨率图像块及其在特征空间上最近邻的图像块进行学习,以此来重建对应的高分辨率图像。近年来基于深度学习的图像超分辨率问题受到大家越来越多的关注和研究,尤其是卷积神经网络应用于图像超分辨率重建取得了很大的成功。卷积神经网络通过卷积运算能更好的利用一个像素点的周围像素来获取此像素点的信息,而且卷积神经网络可以处理比较复杂的映射关系并对数据进行并行处理。卷积神经网络的学习其本质是寻找输入与输出之间复杂的非线性映射关系;其应用于图像超分辨率重建,则是通过学习低分辨率图像块与高分辨率图像块之间端到端的映射关系来重建高分辨率的图像。
基于卷积神经网络的图像超分辨率算法发展比较迅速。最早用卷积神经网络实现图像超分辨率的是Dong Chao等人,其提出了SRCNN[15]的方法。该方法采用三层卷积网络来学习输入低分辨率图像块和输出高分辨率图像块之间的映射关系,三层卷积分别用于特征提取、非线性映射和重建。SRCNN的优点是结构简单,相比较于插值、稀疏表示以及近邻嵌入方法可以取得更好的性能,缺点是由于训练的困难即使加深网络也无法提高图像的重建质量[16]。随后,为了提高训练速度,Dong Chao等人又提出了FSRCNN[17]的方法。FSRCNN重新设计了SRCNN的结构,该网络直接输入原始的低分辨率图像,并在网络最后使用转置卷积层把图像放大到需要的大小。FSRCNN算法无需图像的插值预处理,大大减少了计算的复杂度;而且在网络的映射部分选用尺寸更小的滤波器以及更多的映射层,为了降低网络的计算量在映射前缩小输入特征维数,映射后再扩大回来,以免影响图像的重建质量。经过这样的修改不仅加快了训练速度而且提高了性能。由于深层网络模型在图像分类问题上取得很大突破,受此启发,Kim等人提出了一个深层的卷积神经网络模型VDSR[18]。VDSR采用20层卷积网络,利用残差训练,不再简单的学习低分辨率图像与高分辨率图像之间的映射,而是通过网络来学习高分辨率图像和低分辨率图像的残差图像。VDSR方法提出的残差训练和梯度裁剪方法不仅解决了深层网络容易出现的梯度消失和爆炸的问题,而且Kim的实验[18-19]也表明利用残差训练可以加快网络的收敛速度并提高图像的重建质量。虽然VDSR算法取得了较好的性能,但是其网络结构是卷积层的堆叠,网络结构越深,梯度消失现象就会越明显。
在CVPR2017中,Lai等人提出LapSRN算法来快速精确实现超分辨率重建[20],该算法采用深度拉普拉斯金字塔网络来逐级重建高分辨率图像。Tai等人提出的DRRN算法[21],用一个深度回归残差网络来重建高分辨率图像,可以有效提高算法的重建性能。U-net是一种很好地用于图像语义分割的网络结构,其结构包括一个收缩支路来提取信息和一个对称的扩展支路来重建信息[22]。受此启发,为提高超分辨率算法的性能,本文设计了一种利用多尺度卷积核的收缩--扩展残差网络。本文提出的算法有三大优点:本文算法利用多尺度卷积核的滤波器并且采用收缩--扩展的网络结构来提取不同尺度的图像信息,以此来提高重建图像的质量;利用网络结构的跳跃连接更有利地传播信息以及残差训练的方法来提高性能;损失函数不再使用l2范数损失函数,而是采用l1范数损失函数,使得性能有所提高。实验结果表明本文算法不仅可以较好的提高图像的重建质量,而且训练速度也相对较快。
2 网络结构
本文的网络结构如图1所示,该网络在整体上可以看做是一个具有收缩--扩展结构的残差网络。前一部分(左侧)是网络的收缩部分,采用两次下采样把训练图像缩放两次,即缩减为输入图像的四分之一;网络的后一部分(右侧)是与收缩部分完全对称的扩展部分,对应的使用两次上采样把缩小的图像扩大回原来的大小。
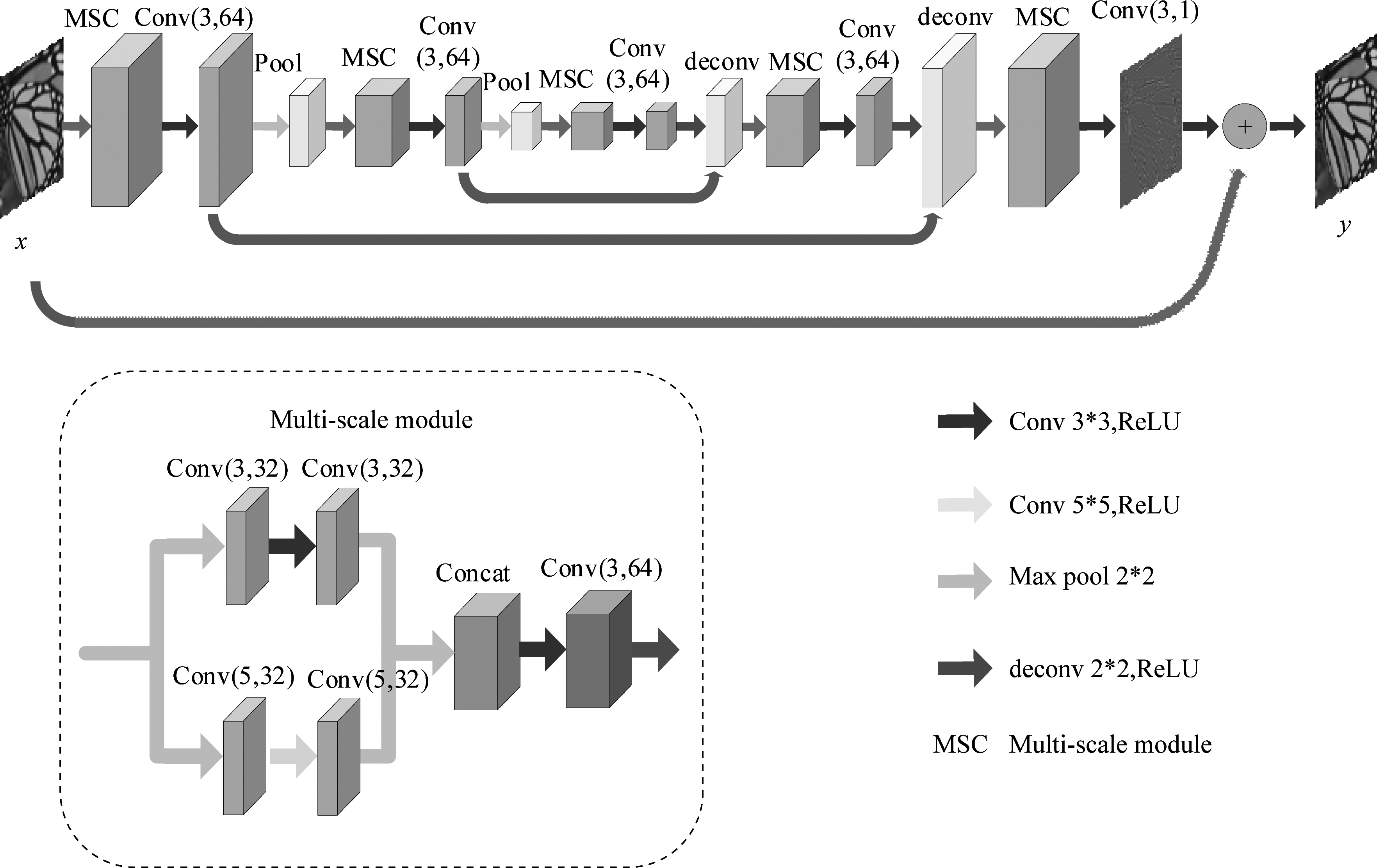
图1 多尺度卷积神经网络的网络结构图
Fig.1 Network structure of multi-scale convolution neural network
本文的网络结构包含20层卷积层、2层下采样和2层上采样。x和y分别是网络的输入和输出,conv(k,n)中k为卷积核大小,n为卷积核的个数。输入层首先连接的是一个多尺度模块,该网络结构中共包含5个多尺度模块:
(1)
其中,xm和ym分别表示第m个多尺度模块的输入和输出,且x1=x,m=1。每个多尺度模块由三个卷积层组成,每个卷积层卷积核的个数为64。Φ表示的是激活函数,本网络选用的激活函数为![]() 和
和![]() 分别是第m个多尺度模块中第三层卷积的权重和偏置。F(xm;θ)为多尺度模块中前两层多尺度卷积层对应的非线性映射,是两个尺度非线性映射的拼接(concat):
分别是第m个多尺度模块中第三层卷积的权重和偏置。F(xm;θ)为多尺度模块中前两层多尺度卷积层对应的非线性映射,是两个尺度非线性映射的拼接(concat):
F(xm;θ)=Concat(f1(xm;θ1), f2(xm;θ2))
(2)
其中,θ={θ1,θ2}表示两层多尺度卷积层的权重和偏置。fi(xm;θi),i=1,2为每个多尺度卷积层对应的非线性映射的输出,![]() 为每个尺度卷积层对应的滤波器的权重和偏置。多尺度卷积层采用两个尺度的卷积核,即64个卷积核中有32个卷积核大小为3×3,32个卷积核为5×5,每个尺度的非线性映射都有两层卷积组成:
为每个尺度卷积层对应的滤波器的权重和偏置。多尺度卷积层采用两个尺度的卷积核,即64个卷积核中有32个卷积核大小为3×3,32个卷积核为5×5,每个尺度的非线性映射都有两层卷积组成:
i=1,2
(3)
其中,![]() 和
和![]() 表示第m个多尺度模块中第i个尺度非线性映射中第j层卷积的权重和偏置。
表示第m个多尺度模块中第i个尺度非线性映射中第j层卷积的权重和偏置。
在网络的收缩部分,每个多尺度模块之后都连接一个卷积层和一个下采样层。卷积层采用的卷积核是3×3,卷积核的个数为64。下采样层采用的是最大池化,池化操作的区域为2×2,步幅为2,最大池化即找出池化区域中的最大值。
在网络的扩展部分,则是在转置卷积层之后连接一个多尺度模块和一个卷积核为3×3的卷积层,这两个多尺度模块之后连接的两个卷积层的卷积核个数分别是64和1。转置卷积层选用的卷积核为2×2、卷积核个数为64,该层的作用即为上采样。
除最后一层卷积层和下采样层之外,每一层后都使用一个ReLU层。此外,为了使网络能更高效的传递信息,在每个下采样层之前的卷积层和上采样层之间都使用跳跃连接,跳跃连接指的是这两层作和,而卷积核个数不变。本文网络结构的优点是采用多尺度的卷积核和收缩--扩展的网络结构来提取图像多尺度的信息,且采用跳跃连接和残差训练来提高图像的重建质量。
本文在网络的多尺度模块采用多尺度卷积核的滤波器,即在同一个卷积层上应用不同尺寸的滤波器。采用多尺度的卷积核有两大优点,首先,多尺度的卷积核最大的优点是不同尺寸的卷积核可以提取图像不同尺度的特征,以便滤波器提取和学习更丰富的图像信息;其次,卷积神经网络训练模型时,是通过学习滤波器的参数(权重和偏置)来实现的,即不断地学习滤波器的参数,使其达到一个最贴近标签的最优值;本文采用多尺度的卷积核,目的是让某一卷积层具有多样性的滤波器,从而使权重和偏置的学习更加多样性,近而可以充分有效的提取并学习图像的有用信息。
本文采用的是完全对称的收缩--扩展网络结构,即先把图像缩小,共缩小两次,图像大小变为输入图像的四分之一,为了便于传播信息和重建图像再对称的扩大回原来的大小。收缩--扩展的网络结构中,网络的收缩部分用于学习和提取同一图像不同尺度的特征,可学习同一图像不同分辨率下的信息;扩展部分则用来合并和重建图像信息。利用多尺度的图像信息,使得训练图像的信息更加丰富,进而促进网络更高效的学习。不仅如此,该网络结构因为有对图像的收缩处理,会降低计算的复杂度,提高训练和测试的速度。
文中下采样层和上采样层分别用于缩小和扩大图像,下采样层可采用2×2的最大池化,或是步幅为2的卷积。实验结果表明采用步幅为2的卷积层与池化效果相差不多,但由于池化运算参数较少,训练速度更快,所以本文采用最大池化来进行下采样。上采样采用转置卷积层实现,转置卷积层是通过一系列转置卷积滤波器来上采样图像到相应的大小。
网络的跳跃连接体现在收缩部分每个下采样层之前的卷积层都会与扩展部分相应的转置卷积层相连。采用跳跃连接有利于图像信息在网络结构中的传播,在深层网络结构中,由于卷积层数增多、使用池化层或转置卷积层,会损失或退化图像的细节信息[24]。本文采用对称的收缩--扩展结构,在图像的收缩(池化)和扩展(转置卷积)过程中均会损失一些细节信息。在这种情况下使用跳跃连接,连接前面的卷积层和后面对应的转置卷积层,可使更多的图像信息直接传播到后面的网络结构中,以此来弥补这些信息的损失。跳跃连接还有残差学习的作用,可以直接把前面的特征映射到后面,增加网络后层的特征输入,以此便于网络高效的学习和训练。此外,深层网络结构在实际训练过程中常常遇到的一个困难就是梯度消失的问题,而跳跃连接在网络的反向传播过程中可以使梯度更好的向底层传播,可以有效地解决这一问题,使网络训练更容易。
多数用于超分辨率重建的网络都是直接由低分辨率图像块训练高分辨率图像块,而残差训练则是训练高分辨率图像与低分辨率图像的差![]() ,
,![]() =Y-X。其中Y和X分别是高分辨率图像和低分辨率图像。如图1所示,本文网络的输出为:
=Y-X。其中Y和X分别是高分辨率图像和低分辨率图像。如图1所示,本文网络的输出为:
y=x+fres(x)
(4)
其中, fres(x)为网络的残差输出。使用残差训练不仅可以很好的避免深层网络易出现的梯度消失的问题,而且还可以加快训练的收敛速度并提高重建图像的质量。
在多数的网络结构中,训练的损失函数为l2范数损失函数:
(5)
其中,n为样本数,yi是高分辨率图像, f(xi;Θ)为网络的预测输出,Θ={w1,w2,…;b1,b2,…}。本文算法训练的损失函数选用l1范数损失函数:
(6)
3 训练和测试
本文的训练实验是通过Caffe[25]来实现,图形处理器(GPU)使用的是GTX 1080。训练图像共291张,这291张图像与VDSR算法所用的训练图像完全一致,其中91张图像源自论文Image super-resolution via sparse representation[15],其余200张源自Berkeley Segmentation Dataset[26]。实际的训练图像还进行了数据增强处理,即把这291张图像进行旋转和缩放,经过这一数据增强的处理,原来的291张图像就变为了5820张图像。测试所用数据集为‘Set5’和‘Set14’,是两个用于测试的基准数据集。
使用网络结构进行训练前,要先对输入图像做预处理,选用的处理方法是与SRCNN方法相同的双三次插值法。使用卷积神经网络训练模型时,为了能高效快速的进行训练,一般对图像进行分块处理,因为批量处理更方便计算而且分块处理可得到更多数量的样本。本文实验把图像分成40×40的图像块作为训练样本,取块步幅为30,训练阶段批量处理的大小为64,一共训练30轮,用GTX 1080训练需要270分钟。训练所采用的优化算法是Adam[27],Adam是一种自适应时刻估计,相比较于SGD,Adam优化方法更灵活,Adam利用梯度的一阶矩估计和二阶矩估计来动态的调整每个参数的学习率,每一次迭代更新后都会把学习率控制在一定范围内,使得参数的学习更加稳定。Adam有两个动量参数,本文实验采用的两个参数分别是0.9和0.999,学习率设置为0.0001,l2范数正则化的权重衰减率设为0.0001,采用l2范数正则化的作用主要是为了防止网络的过拟合。
4 实验结果
4.1 与其他算法比较
为评价本文算法的性能,本文算法分别与SRCNN[15]、FSRCNN[17]、VDSR[18]、LapSRN[20]以及DRRN[21]五种算法进行了对比实验。主要用于评价实验结果的指标为峰值信噪比(PSNR)和结构相似度(SSIM)。
实验结果如表1、表2所示。分别给出了SRCNN、FSRCNN、VDSR、LapSRN算法与本文算法在PSNR、SSIM上的实验结果对比。本文所有对比实验的数据均来自各个论文中作者给出的代码和训练模型。如表1所示,通过比较五种算法在两个不同测试集(Set5和Set14)的平均PSNR可以看出,在不同放大因子(×2、×3、×4)下,本文所提出的算法相比较于SRCNN算法和FSRCNN算法PSNR有明显的提高。尤其与性能相对较好的VDSR算法相比,在Set5数据集上,不同放大因子(×2、×3、×4)下本文算法的平均PSNR分别高出VDSR算法0.27 dB、0.27 dB和0.28 dB,而在含有较多细节信息图像的Set14数据集上优势相对较小,不同放大因子(×2、×3、×4)下分别比VDSR算法高0.15 dB、0.02 dB和0.10 dB。由表1也可以看出在放大因子为2和4时,本文算法相比较于LapSRN算法在Set5数据集上的平均PSNR分别提高0.34 dB和0.10 dB,在Set14中分别提高0.25 dB和0.04 dB。并且,从表2可以看出,本文提出的算法在结构相似度(SSIM)上也有一定程度的提高。实验结果表明,本文所提出的算法在图像超分辨率重建问题中相比较于SRCNN算法、FSRCNN算法、VDSR算法以及LapSRN算法在性能上取得了较大的提高。
如表3所示,本文算法与VDSR算法在测试时间上进行了对比,本文采用与VDSR完全相同的训练集和测试集,测试平台为GPU GTX1080 Matlab 2015b。VDSR算法采用的是20层卷积网络的残差训练,而本文的网络结构一共25层,虽然本文的网络结构层数比VDSR多,由于本文采用的是收缩--扩展的网络结构,即在测试时先对图像进行收缩,然后再扩展,在图像与卷积核进行卷积运算时映射变小,有效减小了计算量,所以在运行时间上与VDSR算法相当。如表3所示,在Set5数据集上放大因子为2和3时以及Set14数据集上放大因子为4时,本文算法比VDSR算法快0.01 s。
表1 五种超分辨率算法在Set5和Set14数据集上的PSNR(dB)对比
Tab.1 The five super-resolution algorithms are compared with PSNR(dB) on Set5 and Set14 data sets
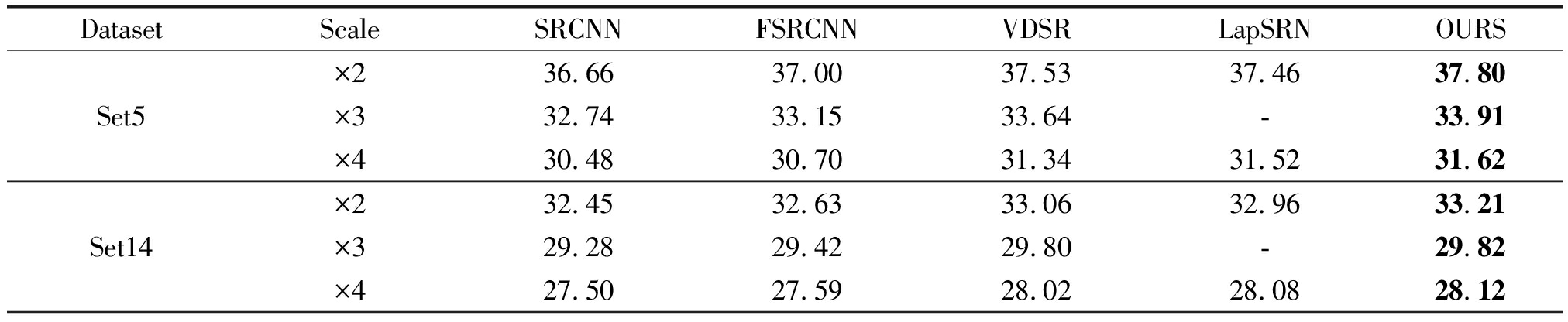
DatasetScaleSRCNNFSRCNNVDSRLapSRNOURSSet5×2×3×436.6632.7430.4837.0033.1530.7037.5333.6431.3437.46-31.5237.8033.9131.62Set14×2×3×432.4529.2827.5032.6329.4227.5933.0629.8028.0232.96-28.0833.2129.8228.12
表2 五种超分辨率算法在Set5和Set14数据集上的SSIM对比
Tab.2 The five super-resolution algorithms are compared with SSIM on Set5 and Set14 data sets
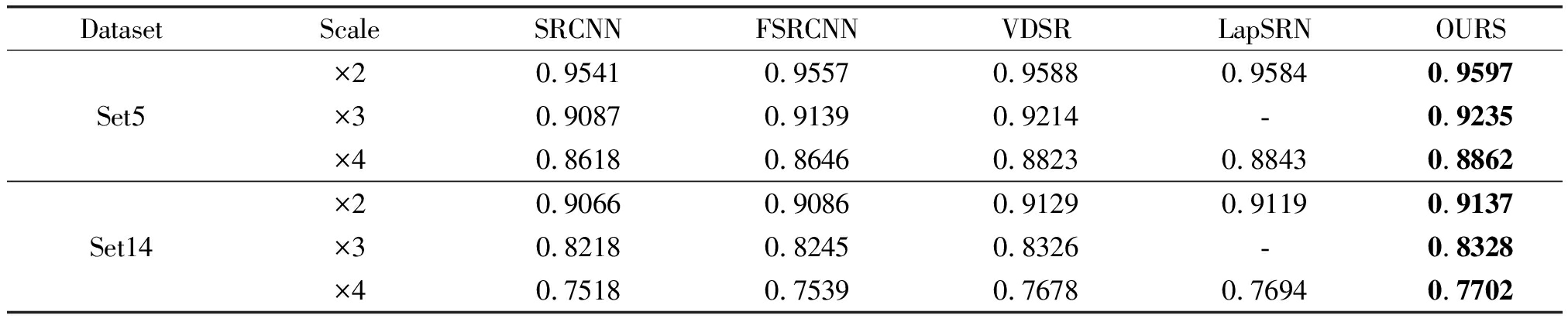
DatasetScaleSRCNNFSRCNNVDSRLapSRNOURSSet5×2×3×40.95410.90870.86180.95570.91390.86460.95880.92140.88230.9584-0.88430.95970.92350.8862Set14×2×3×40.90660.82180.75180.90860.82450.75390.91290.83260.76780.9119-0.76940.91370.83280.7702
本文实验在Intel Core i5- 4460 CPU和GTX 1080的GPU操作平台上进行,除与上述几种算法对比外,本文利用Set5数据集中的四张测试图像与DRRN算法对比了图像的重建结果。四张图像如图2所示,记为Set4数据集。本文算法与DRRN算法的对比结果如表4所示。对比实验中选用了DRRN算法在1个回归模块、9个残差单元共包含20层卷积情况下的实验结果。由表4可知,在放大因子为2和4时,本文算法的性能要高于DRRN算法,但在3倍放大因子下本文算法的性能略低于DRRN算法。DRRN算法中每一个卷积层有128个卷积核,而本文算法的卷积层采用64个卷积核,并且本文在网络中采用收缩--扩展的网络结构,网络参数大大减少,所以从运行时间上来看,本文算法速度较快。由表4可知,本文算法的运行时间是DRRN算法的四分之一。
除了PSNR、SSIM以及测试时间等评价指标外,本文还选取了Set5和Set14两个数据集中比较有代表性的三张图像,将这几张图像显示出来进行对比,结果如图3、图4和图5所示,三张图像的大小分别为:336×220,380×576,648×520。从图中可以看出,在放大因子为4时,本文算法的重建图像细节信息更丰富,相比较于其他三种算法图像明显更清晰。
表3 两种超分辨率算法在Set5和Set14数据集上的测试时间对比(s)
Tab.3 Comparison of test time between the two super-resolution algorithms on Set5 and Set14 data sets (s)
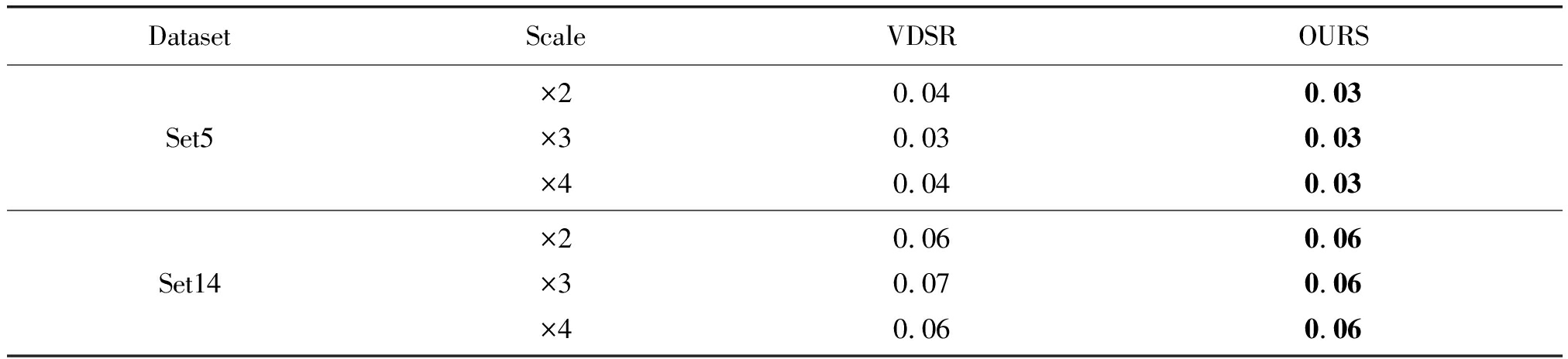
DatasetScaleVDSROURSSet5×2×3×40.040.030.040.030.030.03Set14×2×3×40.060.070.060.060.060.06

图2 Set4数据集中的四张图像
Fig.2 Four images in Set4 dataset
表4 两种超分辨率算法在Set4数据集上的PSNR(dB)/SSIM/运行时间(s)的对比
Tab.4 The two super-resolution algorithms are compared with PSNR(dB)/SSIM/test time(s) on Set4 data sets

DatasetScaleDRRN(B1U9)OURSSet4×2×3×437.39/0.9570/0.1233.56/0.9227/0.1231.06/0.8835/0.1237.53/0.9577/0.0333.52/0.9224/0.0331.14/0.8850/0.03


图3 Set5中woman_GT图像在放大因子为4时的视觉对比
Fig.3 Visual comparison of the woman_GT image in Set5 with the scale of 4
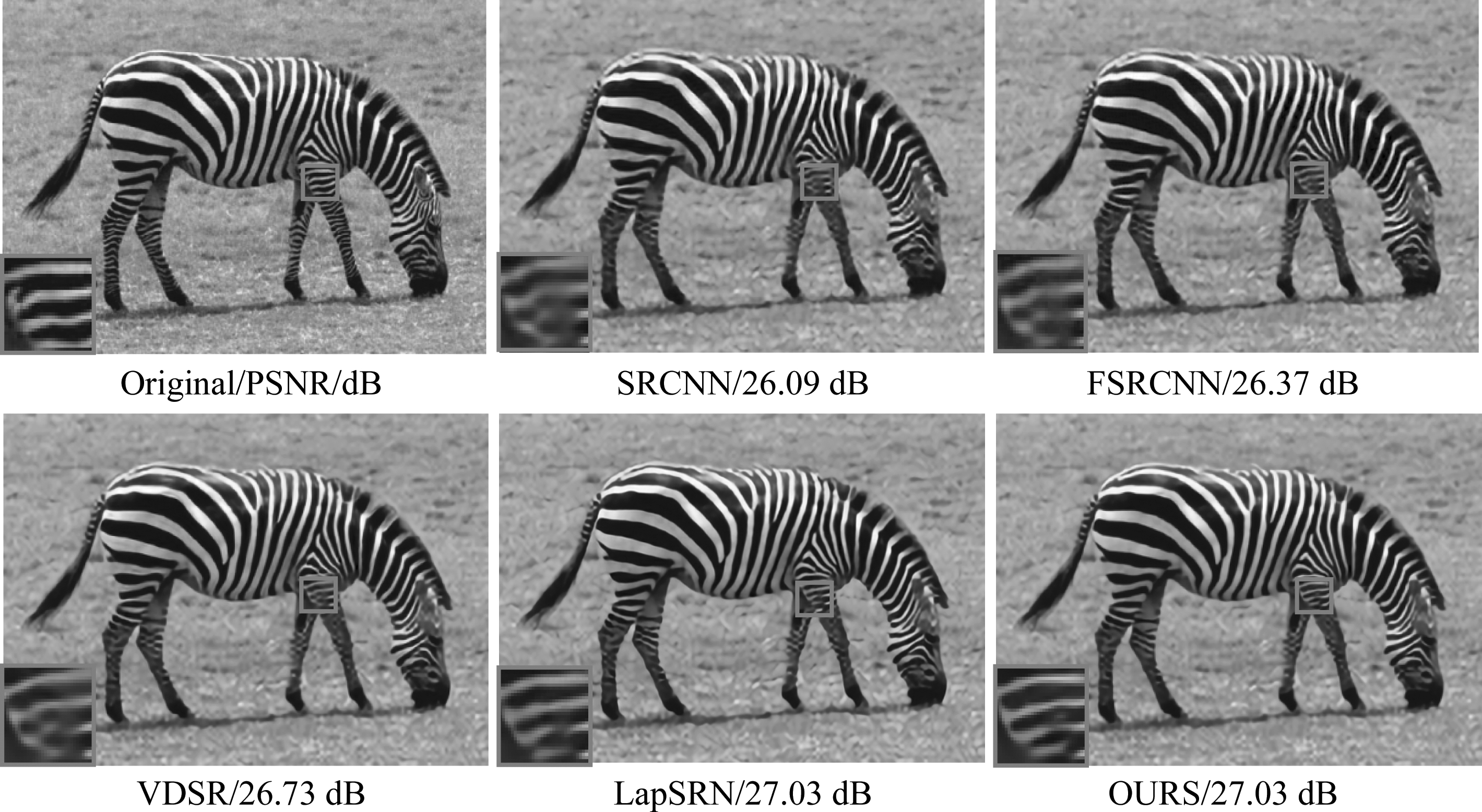
图4 Set14中zebra图像在放大因子为4时的视觉对比
Fig.4 Visual comparison of the zebra image in Set14 with the scale of 4

图5 Set14中ppt3图像在放大因子为4时的视觉对比
Fig.5 Visual comparison of the ppt3 image in Set14 with the scale of 4
除了上述标准测试图像外,本文还增加了医学图像和遥感图像进行测试,分别选取了一张医学图像和一张遥感图像进行了视觉对比,如图6、图7所示,图像大小分别是248×248,248×248。其中,图7的遥感图像选自NWPU-RESISC45数据库。从图6、图7可以看出本文算法相比较于其他三种算法重构图像的细节信息更清晰,并且相比较于SRCNN、FSRCNN及VDSR算法图6的PSNR分别提高0.98 dB、0.67 dB、0.59 dB,图7的PSNR分别提高了1.49 dB、0.94 dB和0.86 dB。
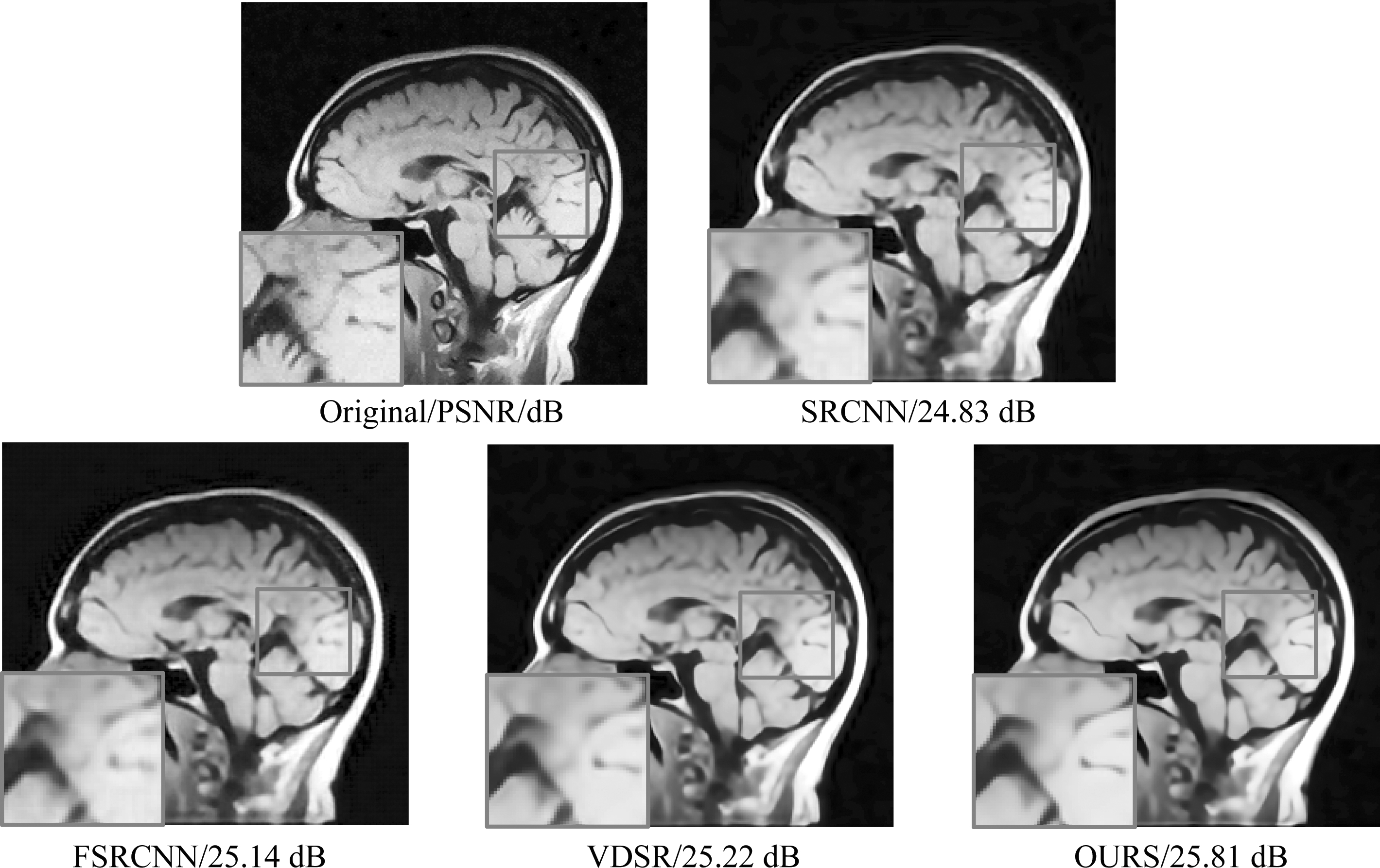
图6 Brain图像在放大因子为4时的视觉对比
Fig.6 Visual comparison of the Brain image with the scale of 4

图7 runway图像在放大因子为4时的视觉对比
Fig.7 Visual comparison of the runway image with the scale of 4
4.2 不同损失函数下性能比较
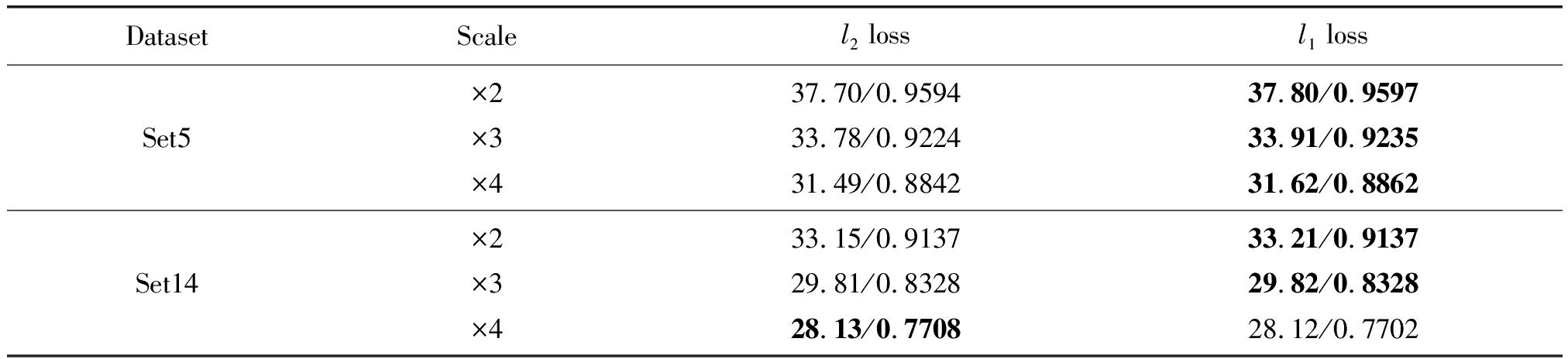
l2范数损失函数广泛应用于图像处理优化问题中,在使用时一般假设噪声与图像的局部特性是相互独立的,但是人类视觉系统对噪声的灵敏度是依赖于图像的局部特性的[28]。所以在使用l2范数时具有一定的局限性。而l1范数损失函数所得到的预测图像与清晰图像的误差是稀疏的,能更直观地反映实验结果。文献[29]指出从PSNR和SSIM的角度来说,l2范数损失函数并不能保证总能优于其他类型的损失函数,文献[29]提出的EDSR算法也使用了l1范数损失函数来代替l2范数损失函数,并取得了相对较好的性能。本文通过实验对比了两种损失函数的性能,实验结果如表5所示。
在Set5数据集上,不同放大因子(×2、×3、×4)下,采用l1范数损失函数的平均PSNR分别比l2范数损失函数的平均PSNR高0.1 dB、0.13 dB和0.13 dB,而在Set14数据集上取得提高比较小,不同放大因子(×2、×3)下分别提高0.06 dB、0.01 dB,在放大因子为4时低了0.01 dB。由表5也可以看出使用l1范数损失函数的SSIM也相对较高一些。实验结果表明在网络训练时选用l1范数损失函数比l2范数损失函数所得到的重建图像性能更高。
4.3 两种下采样方法的对比实验
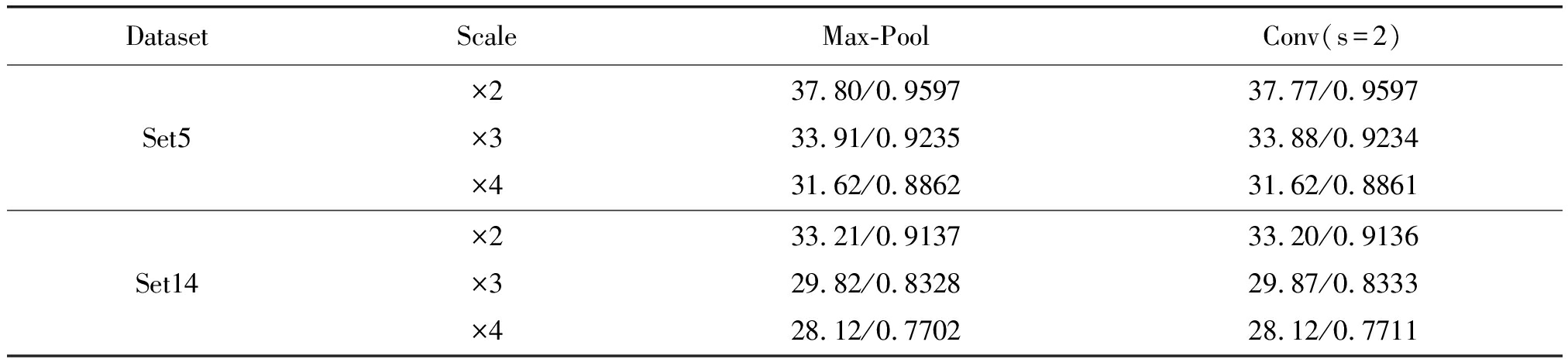
本文网络结构的下采样部分可以采用最大池化和步幅为2的卷积两种方法,如表6所示,两种方法在PSNR和SSIM上都相差不多。在Set5数据集上,放大因子为2和3时池化方法的PSNR稍稍高了0.03 dB,SSIM相差不多;但是在Set14数据集上当放大因子为3和4时最大池化方法比步幅为2的卷积方法的SSIM分别低了0.0005和0.0009。虽然在性能上两种方法相差不多,但是相比较于卷积,池化所需参数更少,训练速度较快。本文通过实验记录了两种方法在同样的数据集和训练参数下共训练30轮所需时间,在GPU GTX1080上池化方法所需训练时间比卷积方法少半个小时。所以本文实验选用池化方法进行下采样。
4.4 不同网络层数的对比实验
本文通过实验对比了不同网络层数对实验性能的影响。本文采用的网络结构共25层,在此网络基础上,在网络的每一个多尺度模块后分别减少和增加一个卷积层来进行对比实验。每个多尺度模块后减少一个卷积层后网络共20层,每个多尺度模块后增加一个卷积层后网络共30层。本次对比实验在放大因子为3的情况下进行,实验结果如表7所示。当网络层数从25层降为20层时,Set5和Set14数据集的平均PSNR分别低了0.09 dB和0.01 dB;当网络层数由25层增加为30层时,Set14数据集的平均PSNR增加了0.03 dB,但Set5数据集的平均PSNR反而下降了0.07 dB。由表7实验结果可知,当网络层数达到一定数量后,即使增加网络层数,实验性能也不会有明显改善。
表5 在Set5和Set14数据集上两种损失函数PSNR(dB)/SSIM对比
Tab.5 PSNR (dB) / SSIM comparison of two loss functions on Set5 and Set14 data sets
DatasetScalel2 lossl1 lossSet5×2×3×437.70/0.959433.78/0.922431.49/0.884237.80/0.959733.91/0.923531.62/0.8862Set14×2×3×433.15/0.913729.81/0.832828.13/0.770833.21/0.913729.82/0.832828.12/0.7702
表6 在Set5和Set14数据集上两种下采样方法PSNR(dB)/SSIM对比
Tab.6 Comparison of PSNR (dB) / SSIM for two downsampling methods on Set5 and Set14 data sets
DatasetScaleMax-PoolConv(s=2)Set5×2×3×437.80/0.959733.91/0.923531.62/0.886237.77/0.959733.88/0.923431.62/0.8861Set14×2×3×433.21/0.913729.82/0.832828.12/0.770233.20/0.913629.87/0.833328.12/0.7711
表7 Set5和Set14数据集不同网络层数时PSNR(dB)/SSIM对比
Tab.7 Comparison of PSNR(dB)/SSIM for different network layers of Set5 and Set14 data sets

Dataset25 Layers20 Layers30 LayersSet533.91/0.923533.82/0.922933.84/0.9231Set1429.82/0.832829.81/0.832829.85/0.8332
表8 Set5和Set14数据集不同卷积核个数时PSNR(dB)/SSIM对比
Tab.8 Comparison of PSNR(dB)/SSIM for different number of convolution kernel on Set5 and Set14 data sets

Dataset4864128Set533.82/0.923033.91/0.923533.92/0.9240 Set1429.81/0.832829.82/0.832829.81/0.8330
4.5 不同卷积核个数的对比实验
本文在放大因子为3的情况下对比了不同卷积核个数对网络性能的影响,如表8所示,分别对比了卷积核个数为48,64,128三种情况下的实验结果。从表8可以看出,卷积核个数为48时,与本文所选用的64个卷积核相比,Set5和Set14数据集的平均PSNR分别低了0.09 dB和0.01 dB;卷积核的个数为128时,相比较于64个卷积核,Set5数据集的平均PSNR增加了0.01 dB,Set14数据集的平均PSNR下降了0.01 dB。由表8实验结果可知,本文算法选取卷积核个数为64是比较合适的。
4.6 不同训练样本数量的对比实验
本文在291张图像的基础上增加了100张图像作为训练集,经过数据增强处理后的训练图像由5820张增加到7820张,实验结果如表9所示。增加训练样本后,在Set5数据集上性能并无明显改善,在Set14数据集的平均PSNR增加了0.05 dB。由此可知,当训练样本达到一定规模后,再增加样本,对实验性能也不会有显著提高。
表9 Set5和Set14数据集不同训练样本数量时PSNR(dB)/SSIM对比
Tab.9 Comparison of PSNR(dB)/SSIM for different number of train sample on Set5 and Set14 data sets

Dataset58207820Set533.91/0.923533.91/0.9238Set1429.82/0.832829.87/0.8346
5 结论
本文采用了一个具有多尺度卷积核的收缩--扩展残差网络,多尺度的卷积核使得训练时不仅可以提取不同尺度的特征信息还可以增加权重和偏置的多样性,以此高效的学习图像的有用信息。采用收缩--扩展的网络结构来提取多尺度的图像信息,使得训练更加高效,然而对网络进行收缩和扩展就要使用下采样和上采样层,这两层的使用会丢失图像的一些细节信息,所以本文使用跳跃连接来弥补这些损失的信息,使得信息更好的传播;并且采用残差训练的方式来提高重建图像质量。本文的实验结果表明,在相同训练集和测试集下,本文提出的网络结构用于图像的超分辨率重建,可以在不以时间为代价的前提下取得更高的性能。
[1] Shi W Z, Caballero J, Ledig C, et al. Cardiac image super-resolution with global correspondence using multi-atlas patch match[C]∥Medical Image Computing and Computer-Assisted Intervention, Nagoya, Japan, 2013: 9-16.
[2] Thornton M W, Atkinson P M, Holland D A. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping[J]. International Journal of Remote Sensing, 2006, 27(3): 473- 491.
[3] 王民, 刘可心, 刘利, 等. 基于优化卷积神经网络的图像超分辨率重建[J]. 激光与光电子学进展, 2017, 54(11): 111005.
Wang M, Liu K X, Liu L, et al. Super-resolution reconstruction of image based on optimized convolution neural network[J]. Laser & Optoelectronics Progress, 2017, 54(11): 111005. (in Chinese)
[4] 肖进胜,刘恩雨,朱力,等. 改进的基于卷积神经网络的图像超分辨率算法[J]. 光学学报,2017, 37(3): 0318011.
Xiao J S, Liu E Y, Zhu L, et al. Improved image super-resolution algorithm based on convolutional neural network[J]. Acta Optica Sinica, 2017, 37(3): 0318011. (in Chinese)
[5] Harris J L. Diffraction and resolving power[J]. Journal of the Optical Society of America, 1964, 54(7): 931-936.
[6] Zhu Y, Zhang Y, Yuille A L. Single image super-resolution using deformable patches[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 2917-2924.
[7] Qu Y, Shi C, Liu J, et al. Single Image super-resolution via convolutional neural network and total variation regularization[C]∥International Conference on Multimedia Modeling, MIAMI, USA, 2016: 28-38.
[8] Hou H, Andrews H. Cubic splines for image interpolation and digital filtering[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1978, 26(6): 508-517.
[9] Keys R. Cubic convolution interpolation for digital image processing[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153-1160.
[10] Yang J, Wright J, Huang T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11):2861-2873.
[11] Yang J, Wright J, Huang T, et al. Image super-resolution as sparse representation of raw image patches[C]∥Computer Vision and Pattern Recognition, Anchorage, AK, USA, 2008: 1- 8.
[12] 曹明明, 干宗良, 陈杰, 等. 自适应邻域选取的邻域嵌入超分辨率重建算法[J]. 信号处理, 2015,31(1): 8-16.
Cao M M, Gan Z L, Chen J, et al. Neighborhood embedding super-resolution reconstruction algorithm based on adaptive neighborhood selection[J]. Journal of Signal Processing, 2015, 31(1): 8-16. (in Chinese)
[13] Yang J, Lin Z, Cohen S. Fast image super-resolution based on in-place example regression[C]∥IEEE Conference on Computer Vision and Pattern Recognition, Portland, USA, 2013: 1059-1066.
[14] Chang H, Yeung D Y, Xiong Y M. Super-resolution through neighbor embedding[C]∥Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 2004, 1: 275-282.
[15] Dong C, Loy C C, He K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-304.
[16] Liang Y, Timofte R, Wang J, et al. Single image super resolution-when model adaptation matters[OL]. http:∥arxiv.org/abs/1703.10889, 2017.
[17] Dong C, Loy C C, Tang X. Accelerating the super-resolution convolutional neural network[C]∥European Conference on Computer Vision, Amsterdam, Netherlands, 2016: 391- 407.
[18] Kim J, Kwon Lee J, Mu Lee K. Accurate image super-resolution using very deep convolutional networks[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,Las Vegas,USA,2016:1646-1654.
[19] Kim J, Kwon Lee J, Mu Lee K. Deeply-recursive convolutional network for image super-resolution[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1637-1645.
[20] Lai W S, Huang J B, Ahuja N, et al. Deep laplacian pyramid networks for fast and accurate super-resolution[C]∥The IEEE Conference on Computer Vision and Pattern Recognition. Hawaii, USA, 2017: 624- 632.
[21] Tai Y, Yang J, Liu X. Image super-resolution via deep recursive residual network[C]∥The IEEE Conference on Computer Vision and Pattern Recognition. Hawaii, USA, 2017: 3147-3155.
[22] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]∥International Conference on Medical Image Computing and Computer-Assisted Intervention.Munich,Germany,2015: 234-241.
[23] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]∥Advances in Neural Information Processing Systems, USA, 2012: 1097-1105.
[24] Mao X J, Shen C, Yang Y B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections[C]∥Advances in Neural Information Processing Systems, Barcelona, Spain, 2016: 2802-2810.
[25] Jia Y, Shelhamer E, Donahue J, et al. Caffe: Convolutional architecture for fast feature embedding[C]∥Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, Florida, USA, 2014: 675- 678.
[26] Martin D, Fowlkes C, Tal D,et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]∥IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 2001, 2: 416- 423.
[27] Kingma D, Ba J. Adam: A method for stochastic optimization[C]∥The International Conference on Learning Representations, San Diego, USA, 2015.
[28] Zhao H, Gallo O, Frosio I, et al. Loss functions for image restoration with neural networks[J]. IEEE Transactions on Computational Imaging, 2017, 3(1): 47-57.
[29] Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, HI, USA, 2017: 136-144.



