1 引言
从目前的军事装备发展趋势来看，精确制导武器是未来现代化战争研究的一个重要方向[1]，而相控阵雷达导引头具有数据率高、体积小、多目标跟踪以及抗干扰能力强等优点[2-3]，更是世界各军事强国关注的焦点。对于采用捷联体制的相控阵雷达导引头而言，运用有效的算法隔离弹体姿态干扰对波束指向的影响以及精确地提取制导所需的弹目视线角速率成为其关键技术之一[4]。文献[5- 6]根据波束指向在惯性空间不变的原理，提出了运用相关坐标系的转换保持相控阵雷达导引头波束稳定的算法；文献[7]针对相控阵天线波束扫描离散性的特点，建立了基于波束误差角在线补偿去耦的模型，从一定程度上改善了弹目视线角速率估计值的精度；文献[8]介绍了一种抖动自适应法，通过在导弹方位轴和俯仰轴两个方向施加正弦激励的方式来调整导引头的输出，从而补偿相应的偏差，这种方法对弹体抖动频率要求比较高；文献[9-12]研究了卡尔曼滤波在捷联去耦上的运用，但是由于捷联体制导引头内部系统复杂，不能有效地掌握系统的噪声统计特性，这就导致我们所得到的系统有关模型以及噪声统计的特性总是存在误差的，进而影响滤波的估计作用，更严重地会使卡尔曼滤波算法不收敛。
对于捷联体制的相控阵雷达导引头而言，由于其捷联惯导系统中的惯性仪表直接和基座固联，在加上弹体本身的姿态干扰，使得动态环境十分恶劣[13]，导致滤波过程中对噪声模型缺乏完整的了解，所以卡尔曼滤波去耦算法容易发散。
本文提出了一种自适应卡尔曼滤波去耦算法，通过引入遗忘因子来优化滤波的性能，加强了新近的数据在滤波过程中的作用，对于陈旧的数据随着时间的延迟而逐渐遗忘，同时建立了时变噪声的递推和预测估计器，对捷联控制系统内噪声进行实时预测。最后通过实验仿真对比，表明自适应卡尔曼滤波去耦算法能够较好地对系统和量测噪声的统计特性进行估计，验证了算法在相控阵雷达导引头捷联去耦上的有效性。
2 问题的提出
2.1 相控阵雷达导引头系统模型
相控阵雷达导引头系统主要由天线阵面、射频组件、分配网络、信号发生器、接收机、微型计算机和波束控制器组成[14]。天线阵面相当于多个辐射元组成的，并且每个辐射元都和一个射频单元相连接，相当于一个发射和接收的单元组件，当它在低电平信号的激励下，会经移相、放大和倍频处理后送到辐射器；接收时会把信号变换到中频进行处理。系统的分配网络会把信号发生器所产生的信号功率分配给相应的发射单元和振荡器，同时实现中频信号的合成。微型计算机主要是完成数字信号的处理和数据处理，进而形成波束控制指令和制导所需的信号。波束控制器是为了对收发组件的相位进行调节，从而控制系统对目标的搜索与跟踪。
如图1所示为相控阵雷达导引头系统各角度之间的几何关系，其中q表示惯性参考系下的视线角，ϑ为导弹弹体的姿态角，θB表示发出的波束角，ε是实际瞄准的偏差角。
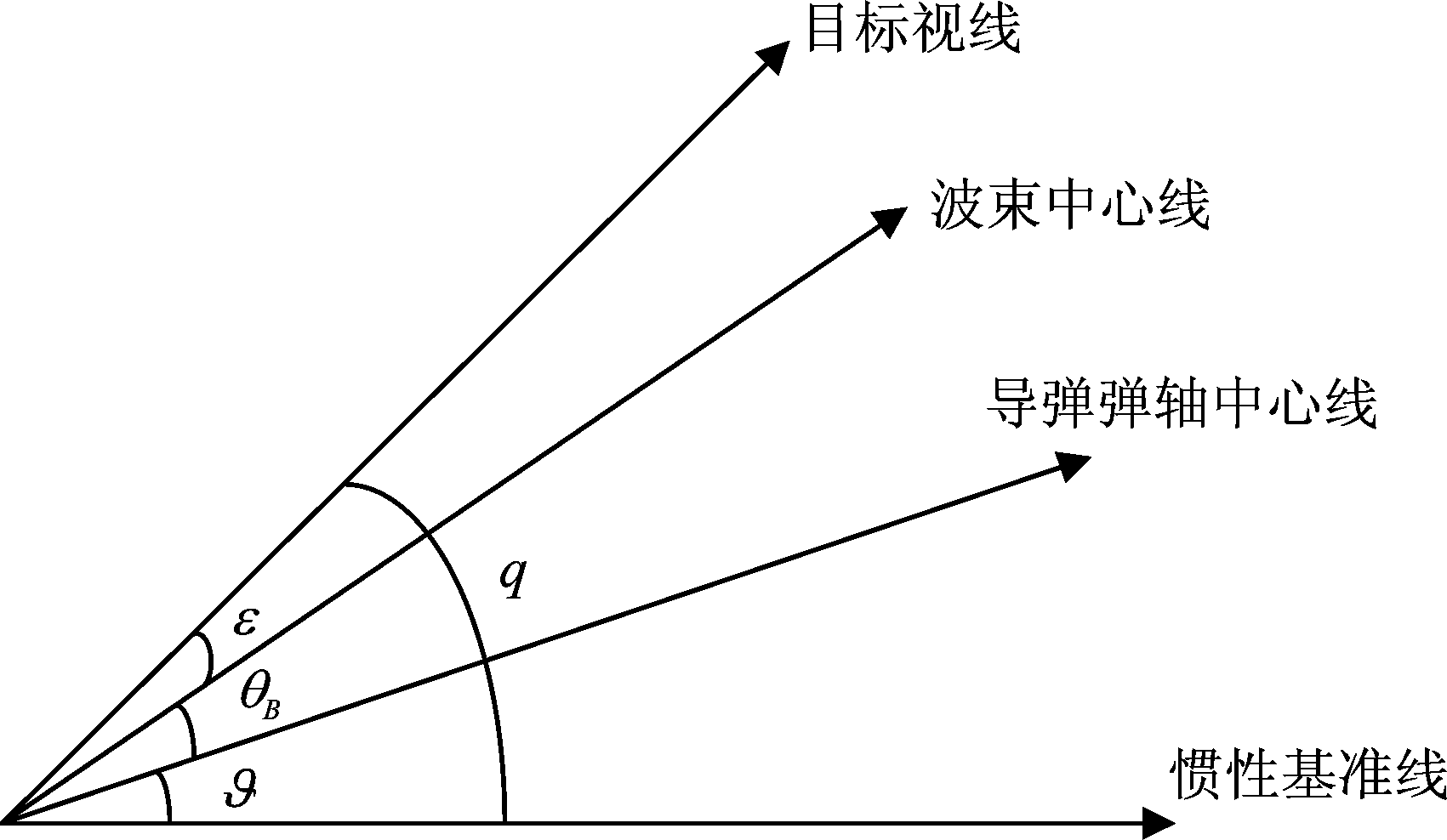
图1 相控阵雷达导引头系统角度的几何关系图
Fig.1 Geometry diagram of phased array radar seeker system angle
2.2 耦合产生的原因及解耦目的
根据图1给出的角度几何关系可知视线角q可以表示为：
q=ε+θB+ϑ
(1)
则：
ε=q-θB-ϑ
(2)
由式(2)可得，导引头的瞄准偏差角既包含了视线角的信息，也包含了导弹弹体姿态角的信息，这说明在导引头制导的敏感信息中耦合了弹体的姿态干扰。
对于采用比例导引律的导引头而言，视线角速率是制导信息中的重要成分，如果存在弹体姿态的干扰信息，会急剧增大导弹的脱靶量，降低导弹的性能，所以必须采用合适的算法对视线角速率进行估计，去除弹体的姿态干扰信息，这样输出的视线角速率才能作为导弹的制导信号。
3 自适应卡尔曼滤波算法的实现
3.1 算法的原理
首先，根据相控阵雷达导引头制导跟踪回路中的参数选择合适的量测量和状态量，通过传递函数的关系建立合适的滤波方程，对系统噪声和量测噪声的期望和方差值进行递推和预测时，在文献[15]中提到的Sage和Husa次优无偏递推MAP噪声统计的基础上，引入遗忘因子，构建相应的加权系数序列，改进估计噪声统计特性的模型，提高滤波去耦的性能。将滤波方程和噪声统计特性估计方程联立就可以完成对弹目视线角速率的预测和实时估计，实现相控阵雷达导引头捷联去耦的目的，其算法原理框图如图2所示。
图2 自适应卡尔曼滤波算法原理框图
Fig.2 Principle block diagram of adaptive Kalman filter algorithm
3.2 滤波模型的建立
由于需要通过惯导测量弹体的姿态角，必须要考虑惯导数据输出的滞后效应，这里处理的思路是把时间基准统一到主惯导数据时刻进行卡尔曼滤波，然后通过时间更新得到当前时刻子惯导的误差估计值[16]。假设tk-1时刻的估计值为
对应估计的误差为P(tk-1)，在主惯导数据到来时，计算对应时刻tk-τ的量测量
在区间[tk-1, tk-τ]将系统方程离散化处理，进行正常的卡尔曼滤波，然后在时间段[tk-τ, tk]内离散化处理系统方程，并做出时间更新，这样可以得到当前时刻对应的状态估计值
和估计的误差Pk。重复这一过程可以得到各个时间点上状态的估计值。但是需要注意的是，在计算过程中需要存储每个计算时间段的转移矩阵和tk-τ时刻量测矩阵需要的导航信息。经过上述处理之后，可以有效地解决传递对准中惯导参考信息滞后的问题，在子惯导对准主惯导参考信息后进行自适应卡尔曼滤波解决相控阵雷达导引头捷联耦合的问题。
对于自适应卡尔曼滤波而言，主要需要解决的问题是：基于量测量求噪声的统计特性以及状态估计值，这里先考虑滤波方程的构建。如图3所示为相控阵雷达导引头制导跟踪回路，图中q为真实的弹目视线角，ε是误差角，ϑ和
分别是弹体干扰角和角速率，θBC是相控阵导引头发出的波束角指令，θB是实际发出的波束角。我们可以从这些参数中选取合适的量测量和状态量建立滤波方程。
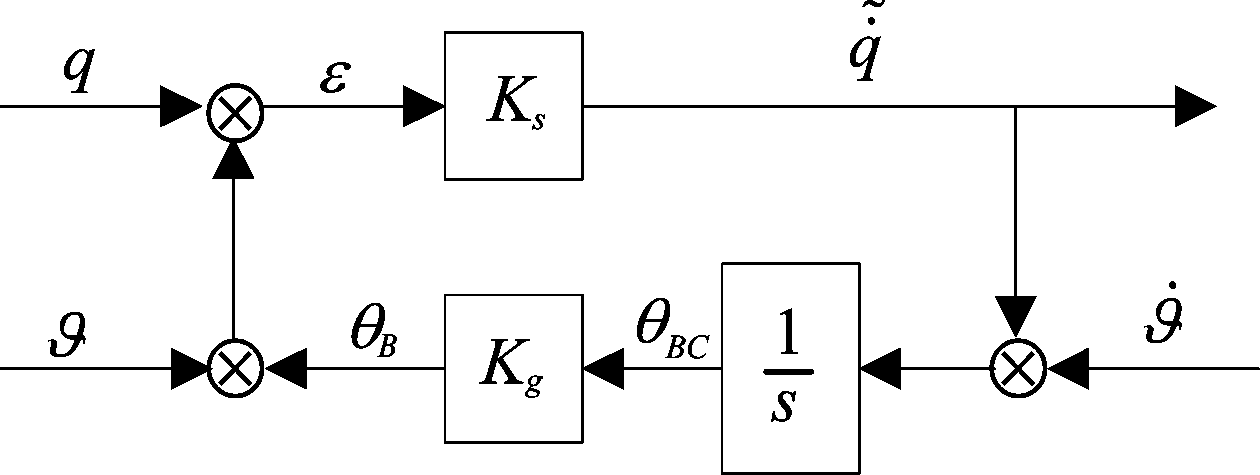
图3 相控阵雷达导引头制导跟踪回路
Fig.3 Phased array radar seeker tracking loop
由于去耦的目的是为提取制导过程中所需的弹目视线角速率，这里状态量选择为：
(3)
量测量为：
(4)
则该系统的系统方程和量测方程为：
Z(t)=H(t)X(t)+V(t)
(5)
其中：
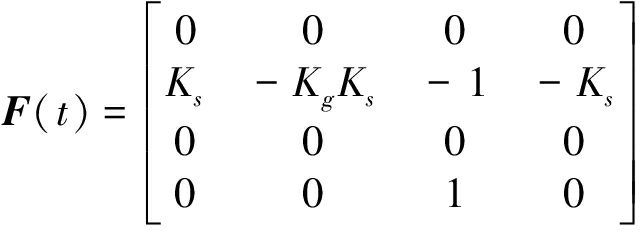
(6)
对上式进行离散化处理，这里取步长为Δt,进而得到状态转移矩阵为：
Φk/k-1=I+F(t)Δt=
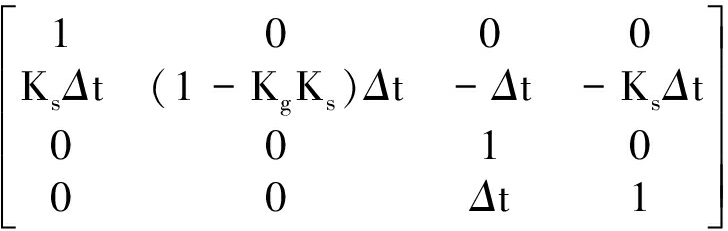
(7)
根据图3系统变量之间的关系，可以计算出：
(8)
离散化处理后量测矩阵为：
(9)
对于滤波方程而言其状态转移矩阵Φk/k-1和量测矩阵Hk定了，只需对系统噪声矩阵Wk和量测噪声矩阵Vk进行噪声特性估计就可以确定系统的滤波方程。
3.3 噪声递推预测估计数学模型
由于Wk和Vk是相互独立的白噪声，考虑噪声统计特性时主要是均值和方差[17]，设其对应的噪声统计为：
Ε{Wk}=qk
Ε{Vk}=rk
Ε{[Wk-qk][Wk-qk]T}=Qk
Ε{[Vk-rk][Vk-rk]T}=Rk
(10)
式中的qk、rk、Qk、Rk分别表示系统噪声和量测噪声的均值和方差，假设它们都是未知的，根据邓自立[15]提出的次优无偏噪声统计估值器可得：
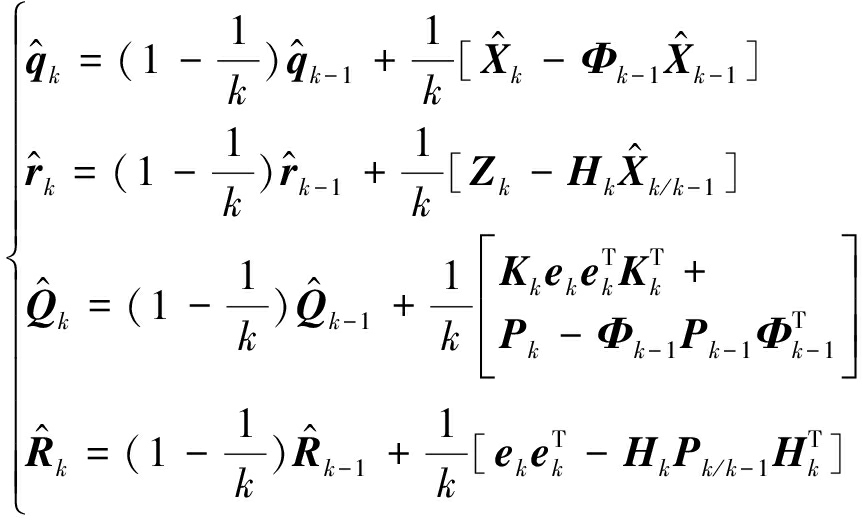
(11)
式(11)相当于在时刻k对噪声统计特性的无偏非递推，可以看出每一项的加权系数都是
相当于算数平均的效果，但是在整个滤波过程中应该强调新数据在滤波过程中的作用，对于陈旧的数据应给予遗忘，所以这里引入遗忘因子b，构建加权系数序列{βi}使之满足：
(12)
其中0<b<1，b的具体取值要通过实验来确定。
若遗忘因子b定后，则有等式：
(13)
所以有：
(14)
为了达到优化滤波性能，满足加权系数序列的要求，令：
(15)
将上式代入式(11)，可得到引入遗忘因子的噪声统计特性的估计数学模型：
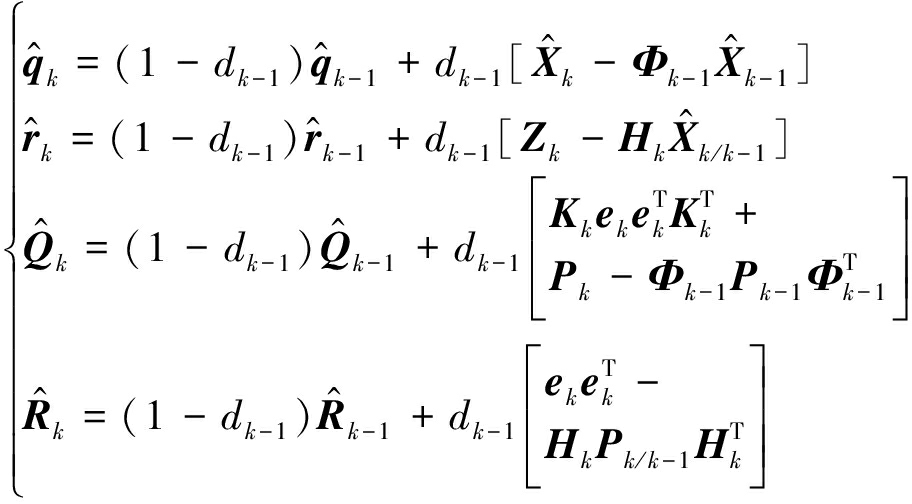
(16)
将式(7)、式(9)以及式(16)代入式(5)便能够得到完整的系统方程和量测方程，其具体的递推过程如下所示：
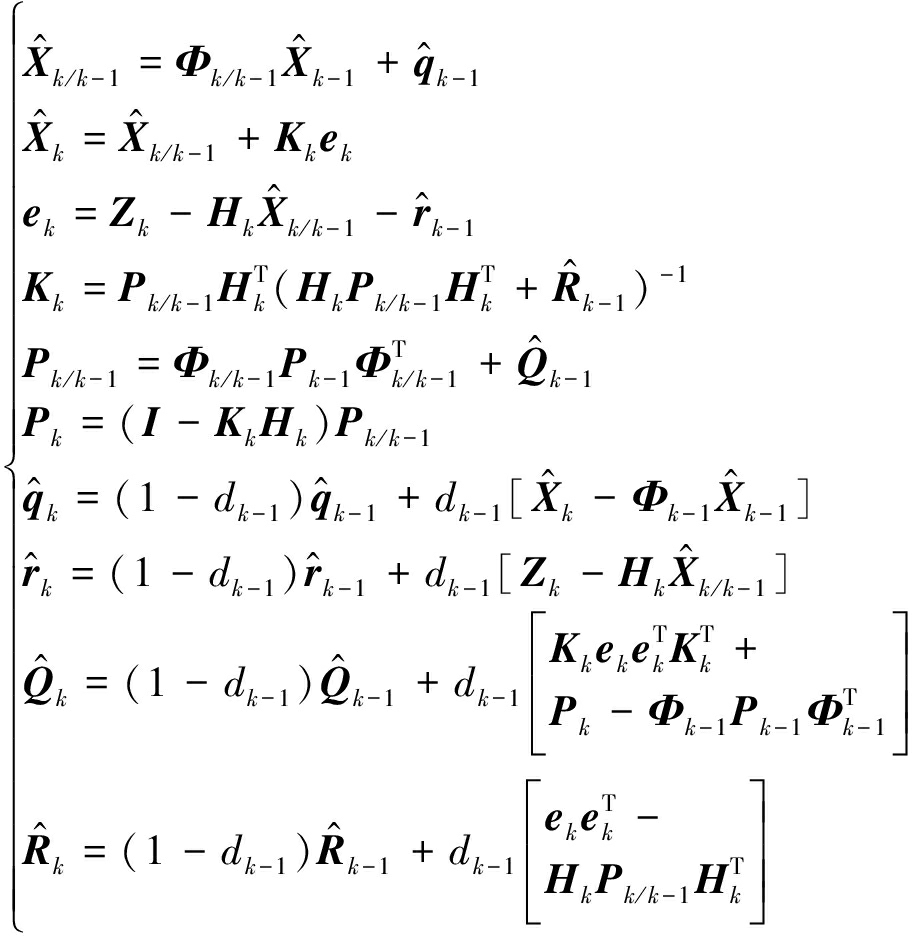
(17)
根据式(17)可知，相比于标准的卡尔曼滤波算法，所提算法增加了对噪声统计特性的估计部分，在算法的计算量上有一定的增加，但不会引起量级的增长，同时计算的复杂度并没有发生较大变化，因此所提算法有一定的可行性。
4 自适应卡尔曼滤波去耦算法验证
4.1 遗忘因子的选取
通过递推估计式(17)中引入遗忘因子，可以对噪声的统计特性不断进行修正和实时预测，使算法达到自适应的效果，但是在这种数据跟踪的算法中，如果遗忘因子b选取过小，虽然会使参数的估计值适应比较快，但会导致跟踪数据的偏差趋势越大；若遗忘因子b选取过大会大大减小估计值的适应速度，所以选取合适的遗忘因子对于本算法而言十分重要[18-19]。参考文献[20]中要求遗忘因子0.95≤b≤0.995，结合导弹制导控制系统的特点，选取b=0.96,b=0.97,b=0.98,b=0.99这四种情况，对不同迭代次数下所提取弹目视线角速率平均误差进行仿真模拟，所得到的曲线图如图4所示。
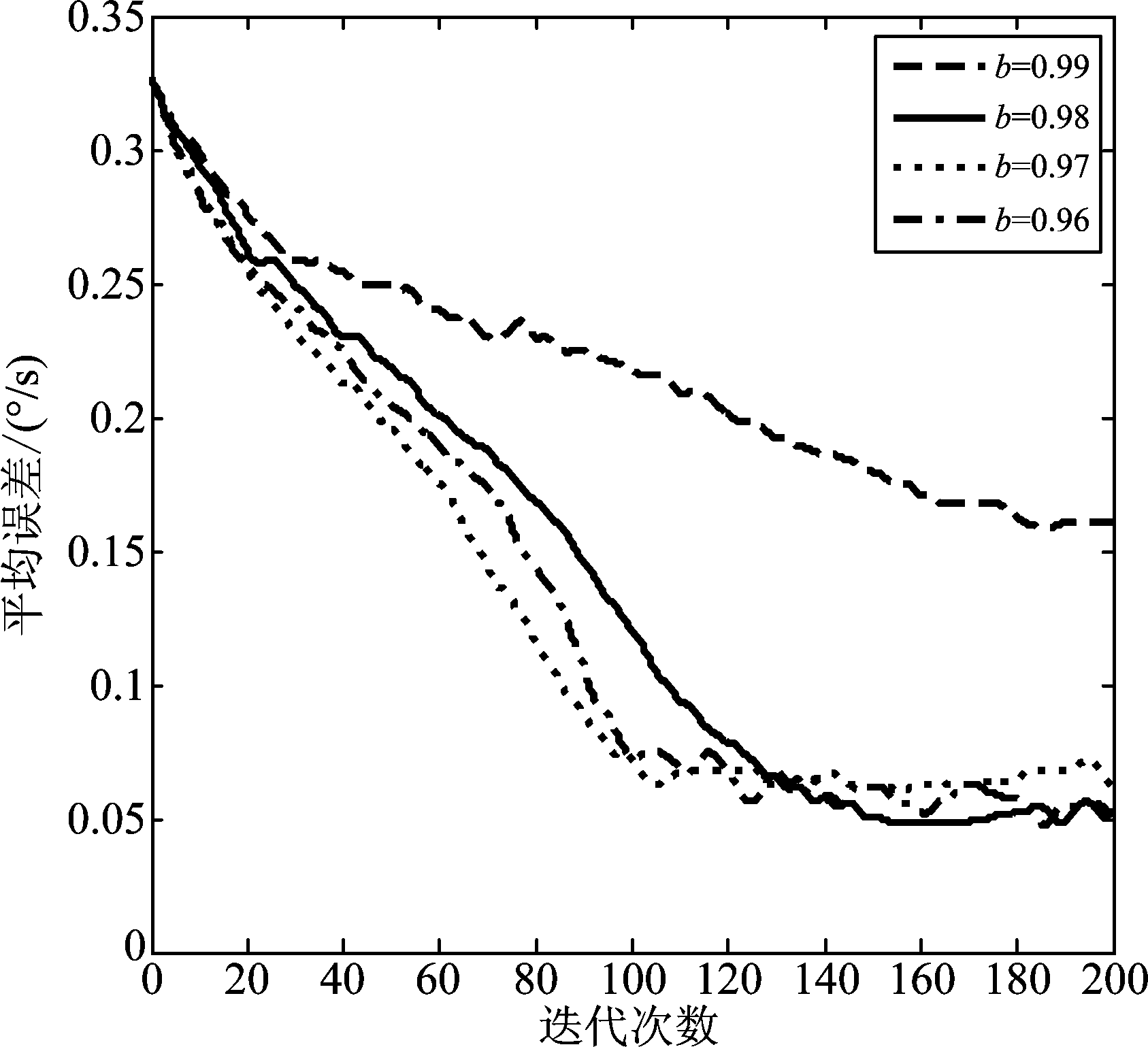
图4 不同迭代次数下提取数据平均误差曲线图
Fig.4 Average error curve of extracted data under different iterations
通过图4发现随着迭代次数的增加，平均误差不断减小，当迭代次数为200左右时误差区域平稳，其中b=0.98,0.97,0.96时，对应的平均误差下降速度比较快，并且其滤波的精度要明显优于遗忘因子b=0.99时的情况。当遗忘因子b为0.98和0.96时，平均误差的趋势变化大致相同，但是遗忘因子为0.98的平均误差曲线变化较为平滑，抖动比较小，因此在本算法中遗忘因子取0.98效果较好。为了更明显地表征遗忘因子对提取数据误差的影响，表1给出了迭代次数为200次时不同遗忘因子下对应的俯仰和方位弹目视线角速率估计误差以及对应的平均误差数据。
表1 迭代次数为200次时不同遗忘因子对应误差的大小
Tab.1 Value of error of different forgetting factors when the number of iterations is 200
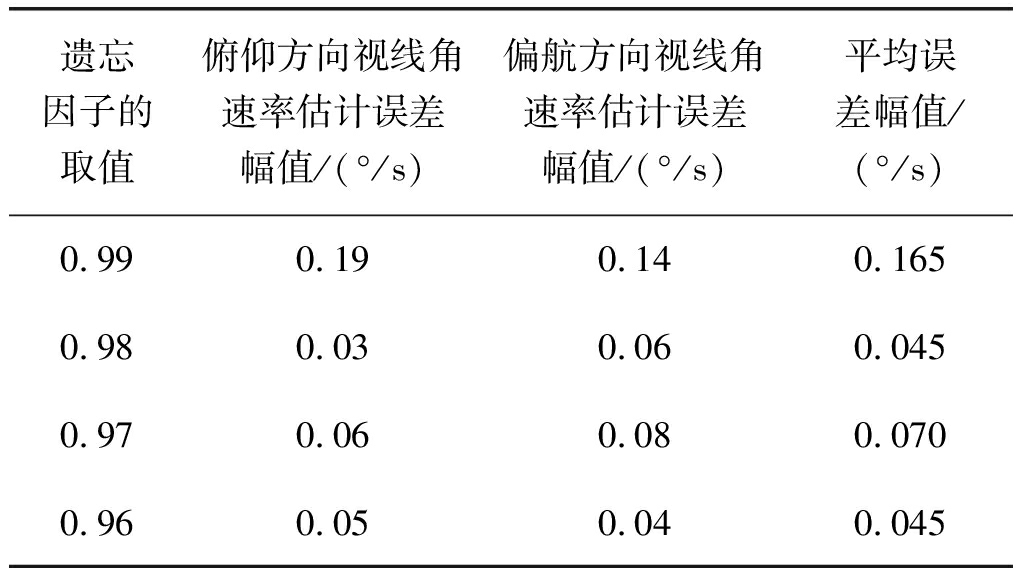
遗忘因子的取值俯仰方向视线角速率估计误差幅值/(°/s)偏航方向视线角速率估计误差幅值/(°/s)平均误差幅值/(°/s)0.990.190.140.1650.980.030.060.0450.970.060.080.0700.960.050.040.045
从表1中也可以明显地看出遗忘因子b取0.98和0.96时平均误差最小，但考虑到滤波过程中的平稳，选取0.98为遗忘因子。
4.2 去耦效果与性能分析
在4.1中确定了遗忘因子b的值，将值代入式(17)中。选取导引头的增益参数Ks=10，Kg=1，假设真实的弹目视线角速率为q=1°/s，导弹弹体作幅值大小为3°、频率为3 Hz的正弦摆动，相应的表达式为ϑ=3sin(2π×3t)°，设置状态估计的初始值为
估计协方差的初始值为P0=I4×4，噪声进行随机初始化处理，对去耦算法性能仿真得到估计的弹目视线角速率和真实的弹目视线角速率对比图，如图5所示。
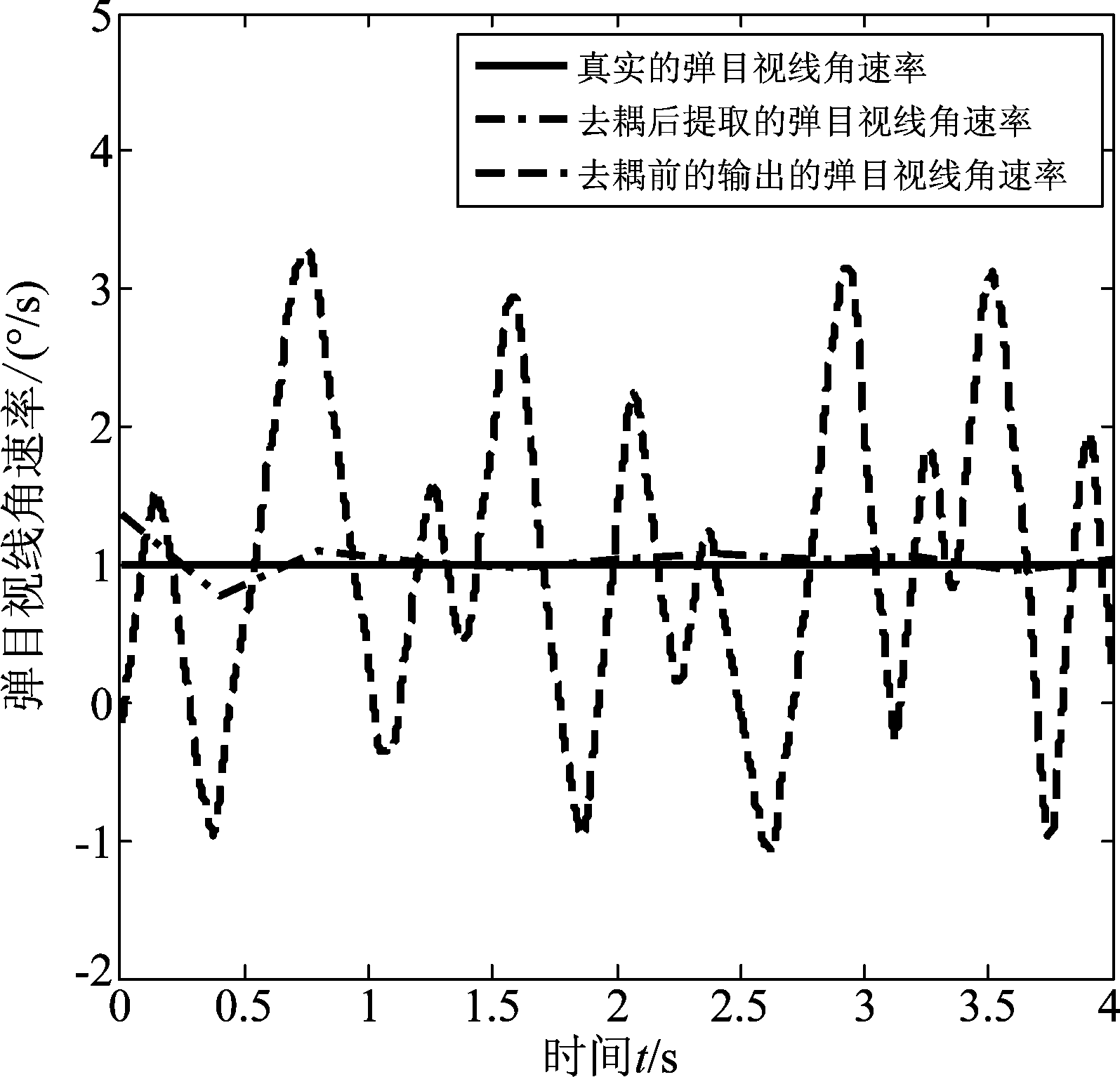
图5 弹目视线角速率对比图
Fig.5 Curve of Line of sight rate extraction
通过图5中的仿真结果表明不经过去耦算法处理时输出的弹目视线角速率受导弹姿态运动的干扰较为严重，与真实的弹目视线角速率有很大的误差。经过自适应卡尔曼滤波去耦算法对弹目视线角速率进行估计发现虽然在滤波的开始过程中有较大的抖动，不能完全地跟踪真实的弹目视线角速率，但是整体上能够完整地对弹目视线角速率进行估计，并且与真实值的误差在可允许的范围内，表明所提的去耦算法在导引头捷联去耦上的有效性。
为了突出算法的优良性，对标准卡尔曼滤波去耦和自适应卡尔曼滤波去耦两种算法的平均误差进行对比仿真，如图6所示。
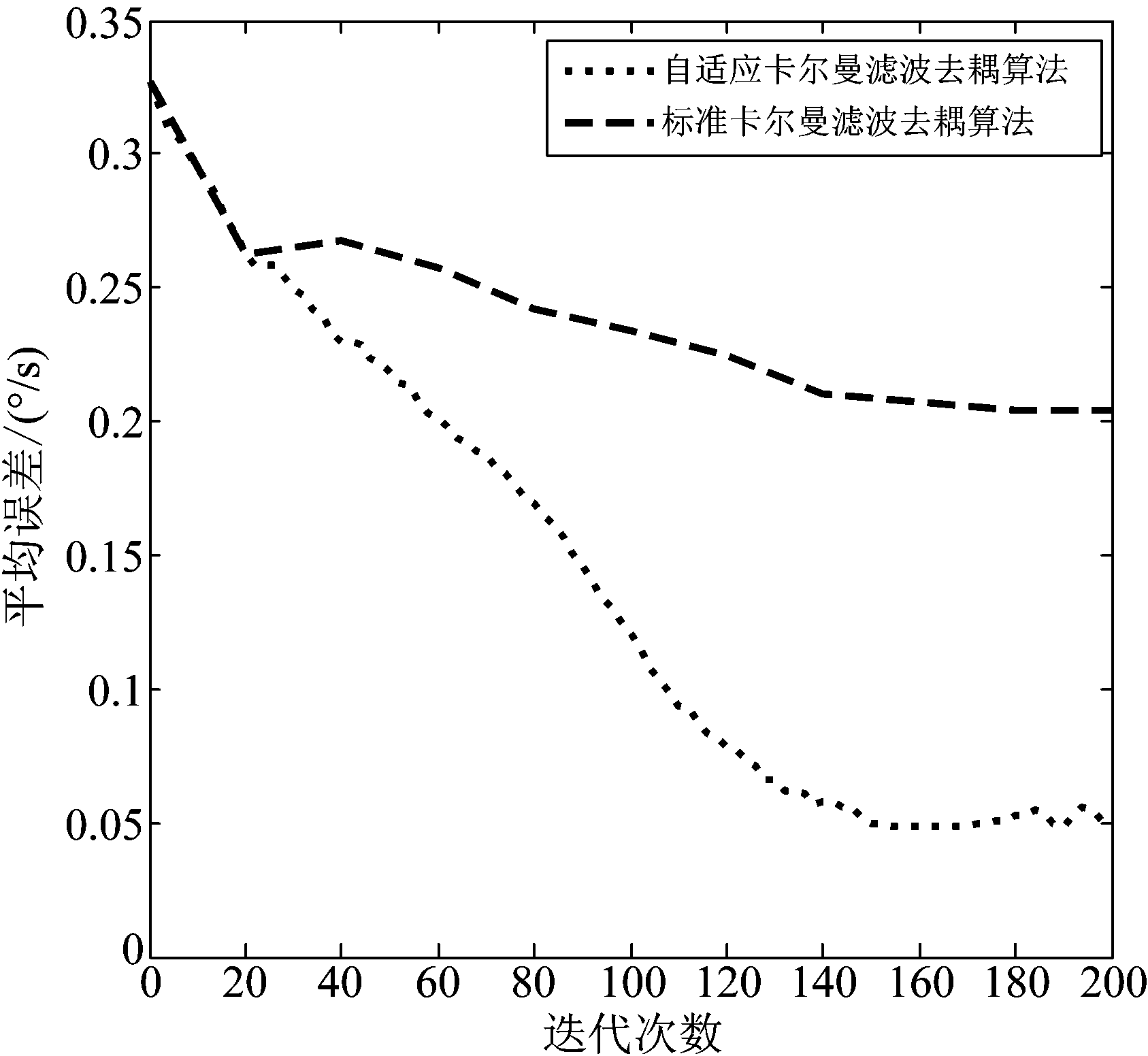
图6 两种算法平均误差对比图
Fig.6 Curve of average errors between the two algorithms
从仿真图6中可以发现，在迭代次数较少的时候两种算法的平均误差相差不大，但是随着迭代次数的增多，自适应卡尔曼去耦算法的平均误差明显比标准的卡尔曼滤波去耦算法的平均误差小，说明了算法引入噪声特性统计模型后在估计数据精度上有较大的提高，验证了算法的优良性。
5 结论
本文所提的自适应卡尔曼滤波去耦算法基于遗忘因子的加权作用，构建了噪声统计特性的估计数学模型，优化了整个滤波的性能。算法在选择遗忘因子时，以估计数据的平均误差为衡量标准，选取了合适的遗忘因子，建立了噪声递推和估计的方程式，进而联立滤波方程对制导系统中需要提取的弹目视线角速率进行估计和预测，通过仿真发现自适应滤波卡尔曼去耦算法在去耦上有一定的效果，并且其估计数据的精度要比标准的卡尔曼滤波去耦算法精度高，从而在一定的程度上提高导弹的制导性能，因此在相控阵雷达导引头捷联去耦中有较大的参考意义和运用价值。
[1] 汤永涛, 林鸿生, 陈春. 现代导弹导引头发展综述[J]. 制导与引信, 2014, 35(1): 12-17.
Tang Yongtao, Lin Hongsheng, Chen Chun. The Development and Summary of Modern Missile Seeker[J]. Guidance and Fuze, 2014, 35(1): 12-17. (in Chinese)
[2] 高烽. 相控阵雷达导引头的基本特点和关键技术[J]. 制导与引信, 2005, 26(4): 1-5.
Gao Feng. Basic Characteristics and Key Techniques of Phased Array Seeker[J]. Guidance and Fuze, 2005, 26(4): 1-5. (in Chinese)
[3] 汤晓云, 樊小景, 李朝伟. 相控阵雷达导引头综述[J]. 航空兵器, 2013(3): 25-30.
Tang Xiaoyun, Fan Xiaojing, Li Chaowei. Summarization of Phased Array Radar Seeker[J]. Aero Weaponry, 2013(3): 25-30. (in Chinese)
[4] 樊会涛, 闫俊. 相控阵制导技术发展现状及展望[J].航空学报,2015, 36(9): 2807-2814.
Fan Huitao, Yan Jun. Development and outlook of active electronically scanned array guidance technology[J].Acta Aeronautica Et Astronautica Sinica, 2015, 36(9): 2807-2814. (in Chinese)
[5] 樊会涛, 杨军, 朱学平. 相控阵雷达导引头波束稳定技术研究[J]. 航空学报, 2013, 34(2): 387-392.
Fan Huitao, Yang Jun, Zhu Xueping. Research on Beam Stable Technology of Phased Array Radar Seeker[J]. Acta Aeronautica Et Astronautica Sinica,2013,34(2): 387-392. (in Chinese)
[6] 李秋生.相控阵雷达导引头捷联去耦技术研究[J]. 制导与引信, 2005, 26(2): 19-22.
Li Qiusheng. Strapdown Decoupling Technique Research on Phased Array Radar Seeker[J]. Guidance and Fuze,2005,26(2):19-22. (in Chinese)
[7] 鲁天宇, 尹健, 夏群利, 等. 基于波束角误差补偿的相控阵导引头解耦算法[J]. 系统工程与电子技术, 2015, 37(9): 2123-2128.
Lu Tianyu, Yin Jian, Xia Qunli, et al. A Kind of Decoupling Algorithm of Phased Array Seeker Based on Beam Angle Error Compensation[J]. Systems Engineering and Electronics, 2015, 37(9): 2123-2128. (in Chinese)
[8] 贾鑫, 罗艳伟, 罗丽. 全捷联导引头解耦技术方法[J]. 战术导弹技术, 2013(1): 77- 81.
Jia Xin, Luo Yanwei, Luo Li. Research on Decoupling Methods of Strapdown Seeker[J]. Tactical Missile Technology, 2013(1): 77- 81. (in Chinese)
[9] Elgame S A, Soraghan J. Target Tracking Enhancement Using a Kalman Filter in the Presence of Interference[J]. IEEE International Geoscience and Remote Sensing Symposium, 2009(3): 681- 684.
[10] Vergez P L, McClendon J R. Optimal Control and Estimation for Strapdown Seeker Guidance of Tactical Missiles[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(3): 225-226.
[11] Chen J, Li J H, Yang S H, et al. Weighted Optimization-based Distributed Kalman Filter for Nonlinear Target Tracking in Collaborative Sensor Networks[J]. IEEE Trans. on Cybernetics, 2017, PP(99): 1-14.
[12] 宗睿. 导引头天线罩误差及相控阵导引头波束指向误差在线补偿方法研究[D]. 北京: 北京理工大学, 2016.
Zong Rui. Research on Online Compensation Methods for Radome Error of Seeker and Beam Direction Error of Phased Array Seeker[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese)
[13] 李丽锦. 基于自适应卡尔曼滤波的捷联惯导非线性对准技术研究[D]. 西安: 西北工业大学, 2006.
Li Lijin. The Nonlinear Strapdown Inertial Navigation Alignment Technique Study Based on Adaptive Kalman Filter[D]. Xi’an: Northwestern Polytechnical University, 2006. (in Chinese)
[14] 梁棠文. 导弹技术词典[M]. 北京: 宇航出版社, 1991.
Liang Tangwen.Missile Technology Dictionary[M]. Beijing: Aerospace Press, 1991. (in Chinese)
[15] 邓自立. 自校正滤波理论及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003.
Deng Zili. Self-Tuning Filtering Theory with Applications[M]. Harbin: Press of Harbin Institute of Technology, 2003. (in Chinese)
[16] 夏家和, 秦永元, 赵长山. 传递对准中主惯导参考信息滞后处理方法研究[J]. 兵工学报, 2009, 30(3): 342-345.
Xia Jiahe, Qin Yongyuan, Zhao Changshan. Study on Master Inertial System Reference Data Delay Processing Method in Transfer Alignment[J]. Acta Armamentarii, 2009, 30(3): 342-345. (in Chinese)
[17] 陈明建, 龙国庆, 黄中瑞. 非均匀噪声背景下信源数估计算法[J]. 信号处理, 2018, 34(2): 134-139.
Chen Mingjian, Long Guoqing, Huang Zhongrui. Source Number Estimation in the Presence of Nonuniform Noise[J]. Journal of Signal Processing, 2018, 34(2): 134-139. (in Chinese)
[18] Zhang L, Xu S Z, Zhao H T. Adaptive Subspace Predictive Control with Time-Varying Forgetting Factor[J]. International Journal of Automation and Computing, 2014, 11(2): 205-209.
[19] 余付平, 冯有前, 雷腾, 等. RLS字典学习中遗忘因子的影响[J]. 应用科学学报, 2014, 32(1): 44-50.
Yu Fuping, Feng Youqian, Lei Teng, et al. Effect of Forgetting Factor on RLS Dictionary Learning[J]. Journal of Applied Science-Electronic and Information Engineering, 2014, 32(1): 44-50. (in Chinese)
[20] 丁玉美, 阔永红, 高新波. 数字信号处理——时域离散随机信号处理[M]. 西安: 西安电子科技大学出版社, 2002.
Ding Yumei, Kuo Yonghong, Gao Xinbo.Digital Signal Processing-Temporal Discrete Random Signal Processing[M]. Xi’an: Press of Xi’an Electronic Science and Technology University, 2002. (in Chinese)
