1 引言
随着无线通信技术从LTE-Advanced向第五代(5G)演进，移动数据业务量将会有爆发性的增长，传输天线端的信号处理负担也会越来越重[1]。云接入网络(C-RAN)，作为5G标准的候补技术之一, 能够有效的解决这个难题。在C-RAN中，传统的基站(BS)的射频单元被分离为独立的射频拉远头(RRHs)，而基带处理部分被聚集并且共享在一个虚拟的基带单元池(BBU Pool)，RRHs可以通过前程链路(fronthaul link)与BBU池相连[2]。文献[3]针对超密集网络(UDN)中的C-RAN场景下的无线传输的新问题设计了一种凸优化方法。文献[4]从软定义的角度，在C-RAN中提出了一种软定义的超蜂窝结构。在文献[5]中，C-RAN将蜂窝系统解耦为控制层面与数据层面，分别针对移动终端与移动服务端,设计了一种聚集边缘结构，并在超级基站建立一种资源管理的架构。在文献[6]的C-RAN系统中，RRHs仅负责通过前程链路传输信号，而BBU池端进行基带信号处理，此时RRHs端的负担能够被有效减轻。在与[6]中相同的结构下，C-RAN同样支持通过用户聚合模式优化提高异构网络性能[7],协作基站蜂窝网络中的多媒体绿色传输[8]，大规模MIMO中的最优传输机制设计[9],多跳网络中的协作中继传输[10]。必须特别指出的是，C-RAN与大规模分布式天线系统[11]虽然在架构上有所相似，但C-RAN特别强调RRHs与云中心之间前程链路容量限制，这也是C-RAN区别于传统网络的核心特征之一。不同于传统网络[12]，C-RAN架构通过将大多数或者全部的信号处理任务转移至BBU池端，能给许多无线网络带来增益。
关于C-RAN的无线传输方案，已经有了一些相关研究。例如，文献[13]在理论上分析了C-RAN系统的复杂度，得出的结论是，比起传统的LTE-Advanced系统，C-RAN减少了10%的复杂度。在文献[14]中，作者针对C-RAN场景下宏基站与RRH之间的干扰消除设计了一个干扰协调的方案。为了降低RRHs与BBU池端的数据通信量，文献[15]针对C-RAN中上行通信过程，在RRHs与BBU池分别设计了一种压缩与解压缩的方法，而文献[16]则在每个RRH端的空间域设计了一种压缩转发的机制。在配置大量RRHs的C-RAN场景下，文献[17]研究了一种低复杂度的预编码方法，并基于ADMM(Alternating Direction Method of Multiplier)设计了一种可行算法。针对包含宏基站的异构C-RAN(heterogeneous C-RAN)，文献[18]应用排队论设计了一种随机梯度算法，用于解决该场景下的资源分配问题。
C-RAN在提供出诸多益处时，其固有问题也不容忽视，即每个RRH与BBU池之间的前程容量是受限的[19]。商业光纤的容量可以达到数十个吉比特(Gigabit)，每个RRH的信息负载一般有兆比特每秒(Mbps)。此外，在密集网络[20]中, RRH通常布置十分密集，这就会导致前程链路的容量很容易超出。在以往的分布式天线系统(DAS)[21]与Massive MIMO[22],前程链路的容量理论上是不受限制的, 但随着通信技术的发展，原本充足的容量很快达到瓶颈。因此，C-RAN中一个重要问题即为如何处理前程链路的容量约束，而常用的处理方法多为在RRH端进行量化/压缩[23-24]，而利用RRHs选择所带来的分集增益来提高系统性能，这一点很少有文献考虑过。
本文的目标是在前程容量的约束下，考虑优化RRHs选择最大化系统总吞吐量。当活动RRHs的数目从零开始增长时，由于越来越多的RRHs被激活进行数据传输，系统总吞吐量不断增长；但由于前程容量的限制，当活动RRHs数目达到一定数目时，吞吐量停止增长，因此如何选择活动RRHs的最优数目是需要考虑的。
在本文中，作者首先推导出不同信道下，已给定RRHs数目时的吞吐量表达式。为了最大化吞吐量，本文设计了一个选择最优RRHs数目的算法，在不同低SNRs与高SNRs的实际环境下推导了选择RRHs数目的闭合表达式。最后，仿真结果表明：比起其他方法，本文方法可以有效提高系统总吞吐量。需要特别指出的是，本文仅考虑单用户场景，主要因为在多用户场景中，优化模型会极其复杂，无法得到最优RRHs的闭合表达式。至于多个RRHs同时服务多个用户，作者将在另外的工作考虑，本文暂不赘述。
符号注释：本文分别使用(·)*，(·)T和(·)H来表示共轭，转置和共轭转置。对于集合Z，本文定义|Z|为其元素个数(Cardinality)。本文采用X～CN (μ,σ2)表示X为一个均值为μ，方差为σ2的复高斯随机变量。
2 系统模型
图1 基于前程容量限制的C-RAN系统架构
Fig.1 C-RAN system architecture based on fronthaul constraints
如图1所示，在C-RAN系统中，BBU池通过回程链路与核心网相连，通过前程链路与RRHs相连，前程链路存在容量约束。RRHs总数为K(K≥1)，通过分布式波束成型协作发送数据给移动用户MU(Mobile User)。本文定义x为经过归一化能量的传输信号，
{|x|2}=1，每个RRH下行传输功率为p0。假定第k个RRH到MU的信道系数建模为hk～CN (m,σ2)，其中m代表变量的均值，σ2代表变量的方差，k=1,...,K，加性高斯白噪声建模型为n～CN (0,1)，则移动用户MS接收到的下行信号为：
(1)
其中，
为分布式波束成型矢量，‖w‖=1。由于前程链路容量是受限的，因此定义BBU池到所有RRHs总容量为C。假设前程容量在RRHs之间是平均分配(即每个RRH特性相同)，因此BBU池与每个RRH之间容量上界为：
(2)
本文中的波束成型采用文献[25]中的最优传输波束成型设计w=h*/‖h‖2。因此，所有RRHs与MS之间无线信号的可达速率表示为：
(3)
R2为MS端接收到的瞬时速率，定义为随不同信道衰落系数的变化而变化的信道容量。在本文中，为了增加分集增益，我们设定，在单位时间内每条前程链路传输相同的数据包data1，因此单个数据包的大小R不仅要小于BBU池与每个RRH之间容量上界(单个RRH到BBU池间前程容量门限)，且必须小于RRHs与MS之间无线信号的可达速率(RRHs到MS的无线信道容量)，即R≤R1与R≤R2同时成立。
基于以上R1，R2表达式，可以得出系统有效吞吐量R的表达式：
R=min{R1,R2}
(4)
在上式中，系统下行有效速率由R1与R2共同决定，在实际中取两者较小值。
从式(3)可以看出，随着RRHs数目的增长，通过无线信道传输的吞吐量R2单调递增，但(2)中的前程链路容量限制R1单调递减。在下一章节中，我们将设计一种算法，寻找最优解K，以实现前程链路与无线信号之间的权衡，并实现有效吞吐量R的最大化。
3 C-RAN中最优RRH选择
在本文中，我们的目标是在前程容量约束下，通过优化RRH选择最大化整个系统的吞吐量。为了简单起见，一般来说，信道系数以降序排列|h1|≥|h2|≥...≥|hK|，则本文考虑的优化问题可以表示为：
(5)
(6)
由式(5)可知，本文的优化问题不仅涉及整数规划，还与max-min优化相关，这是很难解决的。为了处理这个问题，我们首先推导了不同信道条件下不同RRH选择方法的可达速率。
3.1 可达速率
3.1.1 强信道条件下的单RRH选择
此场景下，考虑选择最强信道强度|h1|下的最优RRH，假设信道强度|h1|足够强，使得被选择RRH至MS间的可达速率超过了前程容量限制，即满足：
log2(1+p0|h1|2)≥C
(7)
此时，根据前程链路的限制，单RRH选择下的总系统速率为：
R*=C
(8)
3.1.2 弱信道条件下的单RRH选择
此场景下，同样考虑选择最强信道强度|h1|下的最优RRH，假设信道强度|h1|相对较弱，使得被选择RRH至MS间的可达速率小于前程容量限制，即满足：
log2(1+p0|h1|2)<C
(9)
此时，基于无线信道容量的瓶颈为：
R*=log2(1+p0|h1|2)
(10)
3.1.3 强信道条件下的多RRHs选择
此场景下，RRHs总数目为K，K≥2，此时无线信道质量足够强，并满足以下条件：
(11)
此时可达到的系统吞吐量为：
R*=C/K
(12)
从公式(12)可知，被选择RRH的数目应当在尽可能小，使得吞吐量最大；但在公式(11)中，被选择RRH的数目不能过于小，否则不等式关系无法满足；因此定义Ko为被选择RRH的最优数目,是满足条件(11)的最小整数，并可以通过下文的数值搜索或者公式推导获得，这里暂不赘述。在获得Ko后，对应信号系数{h1,h2,...,hKo}的RRHs被选择调用，从而使公式(12)中的R*最大化。
3.1.4 弱信道条件下的多RRHs选择
此场景中，进行传输的RRHs总数K≥2。在弱信道条件下，K个RRHs所支持的无线信道容量无法支持前程链路的限制容量，即：
(13)
因此，此时整个系统的吞吐量表示为：
(14)
在此场景中，被选择的RRHs应该尽可能的多，使得(14)中的R*取更大值，但取值必须满足公式(13)成立。与强信道场景不同，公式(13)中不能取到等号，因此被选择RRH的最优数目应为Ko+1,是满足条件(11)的最小整数，对应信号系数{h1,h2,...,hKo+1}的RRHs被选择调用。
3.2 渐近最优RRH选择闭合表达式
从(11)与(12)可知，最优Ko应当使(11)取到等式。然而，欲直接得到Ko分析表达式是不可能的。因此，我们使用Jensen不等式方法得到方程式的近似结果：
(15)
在这里，目标转化为得到等式(a)的Ko解析表达式。但是，对于一般SNR表达式，寻求解析表达式仍非常困难。幸运的是，我们已经成功得到等式(a)闭环形式，分别在低SNR与高SNR的渐近最优解，具体如下所示。
在低SNR场景下，等式(a)的左边变化为：
(16)
将(16)代入(a)中，得Kop0(m2+σ2)=C/Ko。因此，我们可得低SNR下的Ko最终解：
(17)
在高SNR场景下，等式(a)的左边变化为：
(18)
此时，在高SNR的最优Ko可以表示为：
log2(Kop0(m2+σ2))=C/Ko
(19)
为了描述方便，令t
log2(Kop0(m2+σ2))，则公式(19)可以表示为：
t2t=Cp0(m2+σ2)
(20)
进一步推导(20),可得：
(t ln 2)et ln 2=Cp0(m2+σ2)ln 2
(21)
通过应用Lambert函数的属性，将反函数
( f )e( f )=f应用到(21),可以得到最终结果如下：
t ln 2={Cp0(m2+σ2)ln 2}
(22)
因此，我们可得高SNR下的Ko：
{Cp0(m2+σ2)ln 2}=log2(Kop0(m2+σ2))
(23)
解方程，可得：
(24)
至此，本章节推导并得出了低SNR与高SNR条件下渐近最优RRH选择闭合表达式。在下面章节中将针对不同信道条件环境，设计相应的RRHs选择优化算法。
3.3 最优RRH选择算法设计
基于以上章节中所描写的四种场景，我们提出以下算法，用于优化RRHs选择：
算法1 基于容量最大化的最优RRHs选择。
步骤1 将所有瞬时信道系数按照降序排序|h1|≥|h2|≥...≥|hK|。
步骤2 检验公式(7)是否成立；如果(7)成立，则信道系数为|h1|的RRH为最优的，并且最大可达速率R*=C，并停止；如果(7)不成立，跳至步骤3。
步骤3 通过(17)与(24)中所提的穷举搜索方法或者推导解析方法决定RRH选择数目Ko，同时满足(11)。如果被选择RRHs为Ko时，公式(11)不能得到满足，则被选择RRHs数目应为Ko+1，并满足公式(13)。
步骤4 已知Ko时，按照公式(12)计算φ=C/Ko，按照公式(14)计算
并得出此时对应的速率为：
Ro=max{(10),(12),(14)}
(25)
步骤5 如果Ro=log2(1+po|h1|2)，在无线传输中选择第一个RRH，对应信道系数为|h1|；如果Ro=φ，选择前KoRRHs，对应信道系数为{|h1|,|h2|,...,|hKo|}；如果Ro=φ，选择前(Ko+1)RRHs,对应信道系数为{|h1|,|h2|,...,|hKo+1|}。
算法1的最优性讨论。当前程容量给定与RRHs传输功率给定时，针对吞吐量的最大化，本文所提出的算法1是最优的。
证明过程如下文两个实例中所述。
证明：
实例1 假设存在另一个算法2胜过本文的算法1。在算法2中，|Ζ|为RRH的数目，实例1中，|Ζ|=1。因此，比起算法1，算法2所实现的可达速率增益ΔR必须是正的。
场景1-A：在此场景中，根据算法1，对应于单RRH选择，最终速率如(8)所示为R*=C。为了使ΔR>0，算法2的可达速率必须大于C，而这明显地与受限前程容量的设定相违背。此时，算法2在此场景中不存在。
场景1-B：根据算法1，单RRH选择的其他场景如同(9)(10)所示。此场景下，算法2的速率为
其中k≠1∈{1,2,...,K}。如果算法2优于算法1，必须存在k使得|hk|>|h1|成立。但根据上文的表述，|h1|是所有信道系数的最大值，因此在此场景中的算法2也不存在。
实例2 |Ζ|为RRH的数目，在实例2中，|Z|≥2。此时算法2所实现的速率为
场景2-A：如果以下关系成立：
此场景中，实际传输速率由前程链路的限制决定，因为无线信道的容量超出最大前程限制。本文所提出的算法1所实现的C-RAN速率为R*=C，而算法2的最大速率为C/|Z|，此时算法2不可能优于算法1。
场景2-B：如果在场景2-B-1存在以下等式
此时，比起前程链路，无线信道的容量为新的瓶颈，即
如果在算法1中总速率如(8)表示，并定义为场景2-B-2。如果若存在算法2优于算法1，则必须存在
而这对于|Z|≥2是不存在的；如果算法1的速率如(25)所示，如果若存在算法2优于算法1，则必须存在以下不等式：
(26)
正如上文所述，{|h1|,|h2|,...,|hKo+1|}已经按照降序排列。从(26)中可知|Z|>Ko+1，即|Z|>Ko，即算法2中选择的RRHs大于算法1中的RRHs。但从(26)中同样可知：
(27)
而(27)中的结论明显与场景2-B-2的设定相矛盾。因此，更优的算法2在场景2-B也不存在。
以上证明可以说明在C-RAN中RRHs选择是最优的，下一章的仿真可以进一步证明该结论。
说明1 在我们提出的方法中，仅有一部分RRHs被选中进行信息传输，而其余的RRHs进行休眠而节能。在这种休眠模式[25-26]中，部分RRHs未被选择可以减少前程链路(通常是光纤)的负担。
说明2 除此以外，被选择的RRHs所发送的功率是可以优化的。在涉及多用户C-RAN网络中，基于一些新的目标(例如速率最大化或者误比特率最小化)，进行这种功率优化是更为必要的，但由于篇幅的原因，本文暂不考虑这种优化。
说明3 我们提出的RRHs选择方法以动态方式工作，其中RRHs选择结果是适应于瞬时信道衰落系数。例如，当瞬时信道系数变得非常小时，越来越多的RRHs被选择用于信息传输,直到达到前程链路的容量瓶颈；与此相反，当瞬时信道系数变大，被选择RRHs数目变小，以尽可能降低前程链路容量负担。
至此，本章节针对不同信道条件下C-RAN中，设计了一种RRH选择优化算法，并且证明了算法的最优性。在下面章节中，这些理论结果会通过仿真进行相关验证。
4 仿真结果
本章节采用蒙特卡洛仿真，所有无线信道随机产生10000次，并服从分布CN ～(0,1),假定噪声的协方差为1，因此信噪比SNR的表达式可以写作p0/1=p0。待选RRH总数为20，即K=20。BBU池与RRHs之间前程链路容量C分别设为{5,15,25,35,45}b/s/Hz。 与本文提出的最优RRHs选择方案对比是另外两种机制，分别是选择单个RRH与选择所有RRHs。因为据作者所知，在C-RAN中还未有其他RRHs选择方案。
图2 前程容量约束下系统吞吐量，此时RRH功率变化
Fig.2 Throughput under fronthaul capacity constraint versus p0
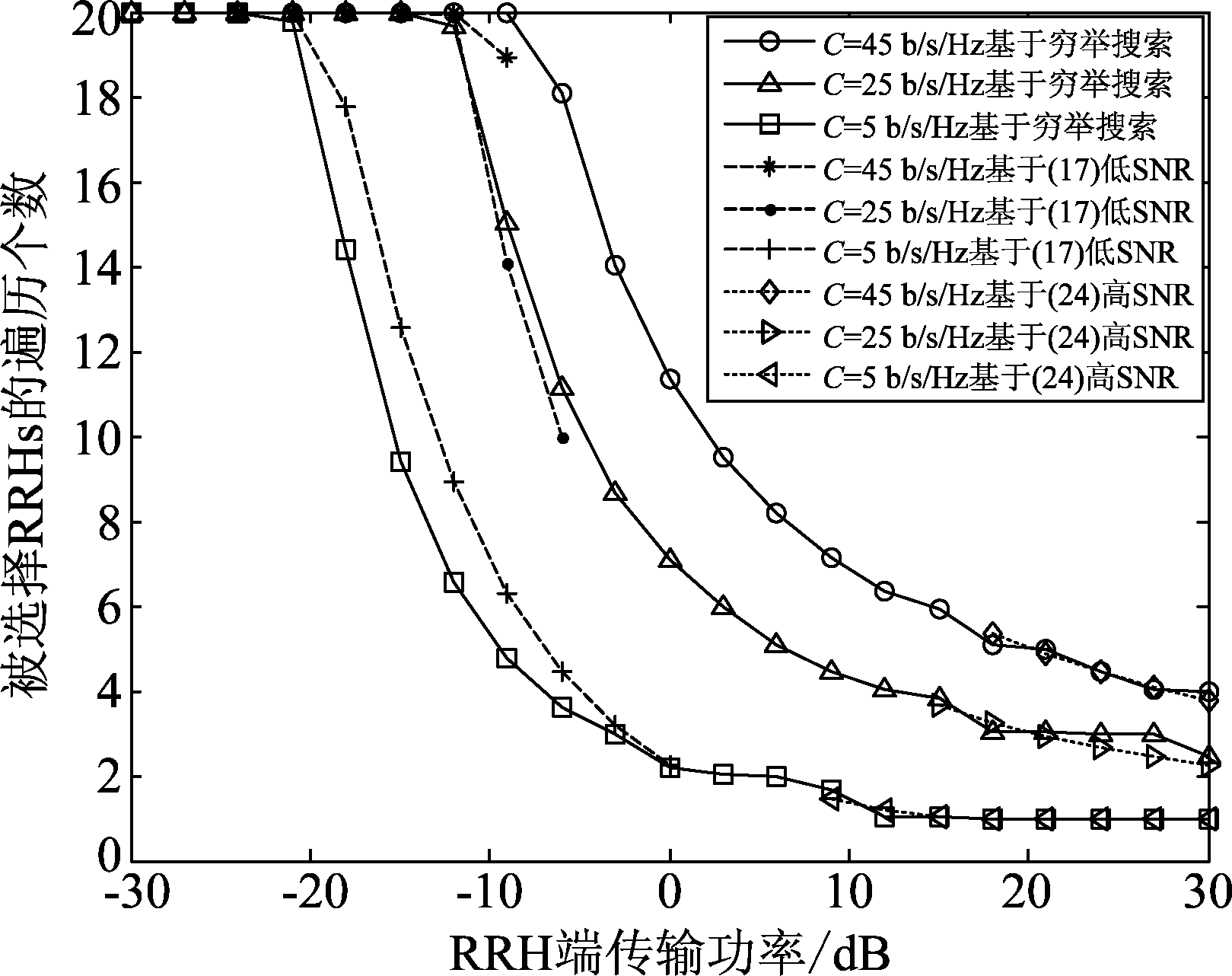
图3 被选择RRHs的遍历数目，此时RRH功率变化
Fig.3 Ergodic number of selected RRHs as a function of p0
图2展示了不同前程容量下，随着传输功率的增长，C-RAN传输速率的变化。对于本文所提出的算法1，当-30 dB≤p0≤-5 dB，图2中的四条容量曲线先保持恒定，具体大小由前程容量决定C/K=1/20=[5,15,25,45]b/s/Hz，然后明显递增，变化转折点在p0=-5 dB：对于算法1中的C=5 b/s/Hz容量曲线在-5 dB<p0<10 dB区间保持持续增长，但在p0>10 dB区间几乎保持不变，这是因为在此区间前程容量成为瓶颈；算法1中其他三条C=15,25,45 b/s/Hz容量曲线在-5 dB<p0<10 dB时单调递增，并不存在C=5 b/s/Hz曲线的瓶颈，但在p0>10 dB时，三条容量曲线均分别达到最大瓶颈。由于文章的篇幅限制，这里仿真图只截取了部分的X轴图，并没有全部体现吞吐量的全部变化范围。当C=5 b/s/Hz时，算法1的容量曲线与单RRH选择容量曲线在高SNR区间p0>10 dB，相互重合，低SNR区间p0<-10 dB有所偏差，这证明了本文提出的算法1比其他选择方案性能更佳。其中原因是C-RAN中传输速率是由前程链路容量与无线信道容量联合决定，并等于两者较小的一个。假设在场景A中，RRHs调用较少，前程链路容量明显大于无线信道容量；场景B中，RRHs调用较多，无限信道容量突破前程容量限制，而本文所提出的算法1，能在场景1中增加RRHs选择，在场景2中减少RRHs选择，比起其他方案，实现系统容量的最大化。值得指出的是，以上提到的信道衰落系数均为瞬时的。
图3揭示了本文提出算法1与另外两种对比方案所选择RRHs的数目Ko，其中本文提出方案Ko数值解对应公式(11)，低SNR场景下Ko拟合解对应公式(20)，高SNR场景下Ko拟合解对应公式(27)。从图3中可知，当p0增长时，被选择的RRHs数目在区域p0∈[-10,10]dB递减，这符合公式(20)验证结果；当在高SNR场景中，当p0>10 dB时，被选择的RRHs数目为1，2，3，4，这与公式(27)结果相同。
图4和图5分别对应在不同K=[50,100,200,400,600,800]条件下的系统吞吐量与选择RRHs的数目。从图4中，可以得知随着备选RRHs增长，系统容量单调递增，但趋向一个恒定值；从图5可以得知，在任何给定的发射功率值下，优化选择的活动RRHs的数量随着所有RRHs候选的数量的减少而增加。这是因为随着RRH分集增益的增长，无线信道容量也随之增长。待选的RRHs数目从50增长到800时，单个RRH对应前程容量变小，优化选择的活动RRHs的数量也变小，并与变小的无线信道容量相对应。在图5，随着无线信道容量达到最大时，此时被选择的RRHs数目降至最小值4。
图4 RRH选择优化后的系统吞吐量，此时RRH功率变化，前程容量C固定
Fig.4 Throughput achieved by the proposed RRH selection approach versus p0 under the fixed C
图5 不同待选RRHs数目下，被选择RRHs的遍历数目，此时RRH功率变化，前程容量C固定
Fig.5 Throughput ergodic number of the selected RRHs at difference values of the RRH candidates versus p0 under the fixed C
5 结论
本文针对新兴C-RAN系统的RRHs选择方案进行优化，以提高系统吞吐量。具体来说，作者设计了一种最佳RRHs选择算法，用于在前程容量约束下最大化C-RAN吞吐量。此外，本文推导了低信噪比与高信噪比下选择RRHs数目的渐进最优的闭合表达式。仿真结果表明，比起现有其他方案，本文所提出的RRHs选择方案能够有效提高系统吞吐量。
[1] Li N, Fei Z, Xing C, et al. Robust low-complexity MMSE precoding algorithm for cloud radio access networks[J]. IEEE Communications Letters, 2014, 18(5): 773-776.
[2] Peng M, Yang S, Poor H V. Ergodic capacity analysis of remote radio head associations in cloud radio access networks[J]. IEEE Wireless Communications Letters, 2014, 3(4): 365-368.
[3] Shi Y, Zhang J, Letaief K B, et al. Large-scale convex optimization for ultra-dense cloud-RAN[J]. IEEE Wireless Communications, 2015, 22(3): 84-91.
[4] Zhou S, Zhao T, Niu Z, et al. Software-defined hyper-cellular architecture for green and elastic wireless access[J]. IEEE Communications Magazine, 2016, 54(1): 12-19.
[5] Liu J, Zhao T, Zhou S, et al. CONCERT: a cloud-based architecture for next generation cellular systems[J]. IEEE Wireless Communications, 2014, 21(6): 14-22.
[6] Dai B B, Yu W. Sparse beamforming and user-centric clustering for downlink cloud radio access network[J]. IEEE Access, 2014, 2: 1326-1339.
[7] Zhang X, Zhang Y, Yu R, et al. Enhancing spectral-energy efficiency for LTE-advanced heterogeneous networks: a user social pattern perspective[J]. IEEE Wireless Communications, 2012, 21(2): 10-17.
[8] Zhang X, Yu R, Zhang Y, et al. Energy-efficient multimedia transmissions through base station cooperation over heterogeneous cellular networks exploiting user behavior[J]. IEEE Wireless Communications, 2014, 21(4): 54- 61.
[9] Xing C, Ma S, Zhou Y. Matrix-monotonic optimization for MIMO systems[J]. IEEE Transactions on Signal Processing, 2015, 63(2):334-348.
[10] Dai M, Kwan H Y, Sung C W. Linear network coding strategies for the multiple-access relay channel with packet erasures[J]. IEEE Transactions on Wireless Communications, 2013, 12(1): 218-227.
[11] Liu A, Lau V K N. Joint Power and Antenna Selection Optimization in Large Cloud Radio Access Networks[J]. IEEE Transactions on Signal Processing, 2014, 62(5):1319-1328.
[12] Li C G, Song K, Li Y S, et al. Energy efficient design for multiuser downlink energy and uplink information transfer in 5G[J]. Science China Information Sciences, 2016, 59(2):74- 81.
[13] Suryaprakash V, Rost P, Fettweis G. Are heterogeneous cloud-based radio access networks cost effective?[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(10): 2239-2240.
[14] Peng M, Xie X, Hu Q, et al. Contract-based interference coordination in heterogeneous cloud radio access networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(6): 1140-1153.
[15] Vu T X, Nguyen H D, Quek T Q S. Adaptive compression and joint detection for fronthaul uplinks in cloud radio access networks[J]. IEEE Transactions on Wireless Communications, 2015, 63(11): 4565- 4575.
[16] Liu L, Zhang R. Optimized uplink transmission in multi-antenna C-RAN with spatial compression and forward[J]. IEEE Transactions on Signal Processing, 2015, 63(19): 5083-5095.
[17] Li N, Fei Z, Xing C, et al. Robust low-complexity MMSE precoding algorithm for cloud radio access networks[J]. IEEE Communication Letters, 2014, 18(5): 773-776.
[18] Li J, Peng M, Cheng A,et al. Resource allocation optimization for delay-sensitive traffic in fronthaul constrained cloud radio-access networks[J]. IEEE Systems Journal, 2014, 99(PP): 1-12.
[19] Liu L, Bi S, Zhang R. Joint power control and fronthaul rate allocation for throughput maximization in OFDMA-based cloud radio access network[J]. IEEE Transactions on Communications, 2015, 63(11): 4097- 4110.
[20] Garcia V, Zhou Y, Shi J. Coordinated multipoint transmission in dense cellular networks with user-centric adaptive clustering[J]. IEEE Transactions on Wireless Communications, 2014, 13(8): 4297- 4308.
[21] Kim T M, Sun F, Paulraj A J. Low-complexity MMSE precoding for coordinated multipoint with per-antenna power constraint[J]. IEEE Signal Process Letters, 2013, 20(4): 395-398.
[22] Hu D, He L, Wang X. Semi-Blind Pilot Decontamination for Massive MIMO Systems[J]. IEEE Transactions on Wireless Communications, 2016,15(1):525-536.
[23] Rao X, Lau V K N. Distributed fronthaul compression and joint signal recovery in cloud-RAN[J]. IEEE Transactions on Signal Processing, 2015, 63(4): 1056-1065.
[24] Zhou Y, Yu W. Optimized backhaul compression for uplink cloud radio access network[J]. IEEE Journal on Selected Areas in Communications, 2014, 32(6): 1295-1307.
[25] Chen W, Wassell I J. Optimized node selection for compressive sleeping wireless sensor networks[J]. IEEE Transactions on Vehicular Technology, 2016, 65(2): 827- 836.
[26] Wu J, Bao Y, Miao G, et al. Base-station sleeping control and power matching for energy-delay tradeoffs with bursty traffic[J]. IEEE Transactions on Vehicular Technology, 2016, 65(5): 3657-3675.
