1 引言
静息态功能磁共振成像(Resting State-funcational Magnetic Resonance Imaging, rs-fMRI)是一种有效研究人脑功能和结构的非介入检测技术。该技术通过对血氧平衡依赖(blood oxygen level-dependent, BOLD)信号的分析来研究人脑的功能机制和神经活动。研究人员一般可以通过对不同脑区之间BOLD信号相关性的分析来度量脑区之间的功能连接,从而构建人脑功能网络[1-3]。
目前大多数研究采用线性相关分析方法来构建人脑功能网络。Geerligs等人[4]用线性Pearson相关分析方法构建脑区之间的功能连接,用于研究功能网络特性随年龄的变化。Ye等人[5]利用Pearson相关分析方法构建人脑功能网络,发现重度抑郁症患者相对于正常人有更高的局部效率和模块化结构。Khan等人[6]用偏相关分析方法构建青少年自闭症患者的脑功能连接关系,发现在大脑感觉运动区域有着更强的功能连接。
但是由于大脑是一个复杂的系统,仅仅采用线性分析方法难以观测其内在特性,尤其是不同脑区之间相互关系随时间变化的动态特性。已有研究表明人脑有着非常明显的非线性特征,而血液动力学响应函数也具有非线性特点[7-9],仅通过线性相关分析方法来构建大脑功能网络并无法捕获两个脑区之间的非线性关系。所以在构建动态功能脑网络时,应该更充分的考虑其非线性属性。
很多研究人员已经开始尝试利用非线性的分析方法来构建人脑功能网络并展开相关研究。Han等人[10]通过非线性斯皮尔曼(Spearman)等级相关分析方法研究不同年龄与不同性别人群间脑功能网络差异。董泽芹等人[11]用肯德尔(Kendall)相关分析方法来探究癫痫患者与正常人的脑功能网络差异。牛宝东等人[12]基于希尔伯特黄变换(Hilbert Huang Transform,HHT)处理非线性脑信号,提高癫痫病的识别率。Salvador等人[13]采用基于相干分析的互信息方法研究发现功能连接主要存在于低频上。蒋进航[14]通过实验发现最大信息系数(Maximal Information Coefficient, MIC)适合应用于脑网络的相关性度量分析。苏龙飞[15]利用MIC从rs-fMRI数据中提取非线性功能连接特征用于精神分裂症的诊断。但是上述研究是将在数据采集期间内的BOLD信号视为静态,通过计算其平均值来分析和构建一个脑区网络,并没有考虑BOLD信号随时间变化的影响,因此不足以全面理解和描述人脑网络的动态特性。也有一些人员开始针对大脑网络的动态特性展开研究,以BOLD时间序列为对象来进行脑区之间的相关性分析,从而确定脑区之间的功能连接网络,但是一般都是采用Pearson线性相关系数的分析方法构建功能连接网络。Yu等人[16]利用时变人脑功能连接的动态图论理论去识别精神分裂症的拓扑异常。Wee等人[17]利用功能动态网络的稀疏特性用于轻度认知障碍的早期诊断。马洒洒等人[18]将滑动窗口应用于功能脑网络的BOLD信号时间序列分析,从多维数据分析的角度研究人脑网络的动态特征。
综上所述,由于人脑的复杂性、实时变化特性以及BOLD信号的非线性特点,无论是采用线性分析方法展开的动态特性研究,还是用非线性分析方法展开的平均时间的分析方法都不足以表现脑区之间的真实动态属性。因此本文以rs-fMRI原始数据提取到的BLOD信号时间序列为对象,讨论了构建全脑脑区功能网络过程中的非线性相关分析方法及阈值确定等关键技术,采用基于滑动窗口的动态数据分析技术,构建得到动态特征矩阵并进行特征降维,将其映射到二维空间内可视化,在此基础上对脑功能网络的状态及系统的动态特性展开进一步研究。将基于3种非线性相关分析方法斯皮尔曼相关分析(Spearman)、肯德尔相关分析(Kendall)和最大信息系数(Maximal Information Coefficient, MIC)的脑网络动态特性的实验对比结果显示:在阈值参数选择合理的前提下,无论对BOLD信号展开哪种非线性分析方法,所得到的脑网络状态及分类结果均显现出相似的规律性,从而为基于非线性相关分析方法的动态脑网络构建方法提供了一种可行的解决方案,为下一步展开脑网络的动态特性分析和演化过程研究奠定了基础。
2 基于非线性相关分析方法的人脑动态特征矩阵构建
2.1 数据来源及数据预处理方法说明
静息态fMRI数据的采集使用美国通用电气(GE)公司制造的3.0Tesla磁共振成像仪,使用头部正交线圈,数据采集过程中要求被试者平躺、闭眼,保持清醒,全身禁止不动,尽量不进行特别的思维活动。采用梯度回波-回波平面成像序列,重复时间TR为1500 ms,回波时间TE为30 ms,采集矩阵为64×64,视野为FOV=256 mm×265 mm,扫描层后4 mm,层间距0 mm,翻转角Filp angle为60°,共采集200个时间点。
本文使用Python/FSL Resting State Pipeline平台[19]对rs-fMRI原始数据进行预处理,采用自动解剖图集(Automated Anatomical Labeling,AAL)[20]将全脑分为90个脑区。对数据进行预处理的过程主要由以下7个步骤:(1)去除前4个时间点;(2)时间层校正;(3)头动校正;(4)颅骨去除;(5)空间标准化;(6)带通滤波;(7)提取脑区的平均BOLD 信号时间序列[18]。预处理后得到90个脑区在196采样点上的BOLD信号时间序列。
2.2 基于非线性相关分析的全脑动态特征矩阵的构建
在文献[18]的研究基础之上,以90个脑区BOLD信号的采样时间轴作为基准,采用滑动窗口技术依次遍历整个时间序列,每一个小窗口内的BOLD信号时间序列形成当前采样点的状态观测窗口[18]。本文滑动窗口的大小设置为n,窗口以步长l从左向右依次移动,即可将整体的BOLD信号时间序列划分为g(g=196-n+l)个状态观测窗口。
以上述步骤得到的g个状态观测窗口为基础,针对脑网络在时间上的同步性和相关性展开分析和研究。本文分别选择Spearman、Kendall和MIC 3种非线性相关分析方法构建每个滑动窗口内脑区之间的动态功能连接,每个观测窗口内均可以得到一个90×90的状态观测矩阵,该状态观测矩阵是沿对角线对称的矩阵,在不考虑自相关的情况下,将脑区之间相关系数作为脑网络的实时特征提取出来,一共有4005个特征。将相关系数矩阵对角线以上的特征依次取出首尾连接可得到1×4005维的脑网络状态观测向量。通过以上方法每一个静息态fMRI样本在采样区间内将得到g个向量,即得到g×4005矩阵G。如果用矩阵G的行向量代表某一扫描时间区间内脑区的功能连接特征,那么该矩阵能够反映全脑网络在全部数据采集时间上的动态变化过程,下文将该矩阵称为动态特征矩阵。构建滑动窗口和人脑动态特征矩阵的原理如下图1所示。
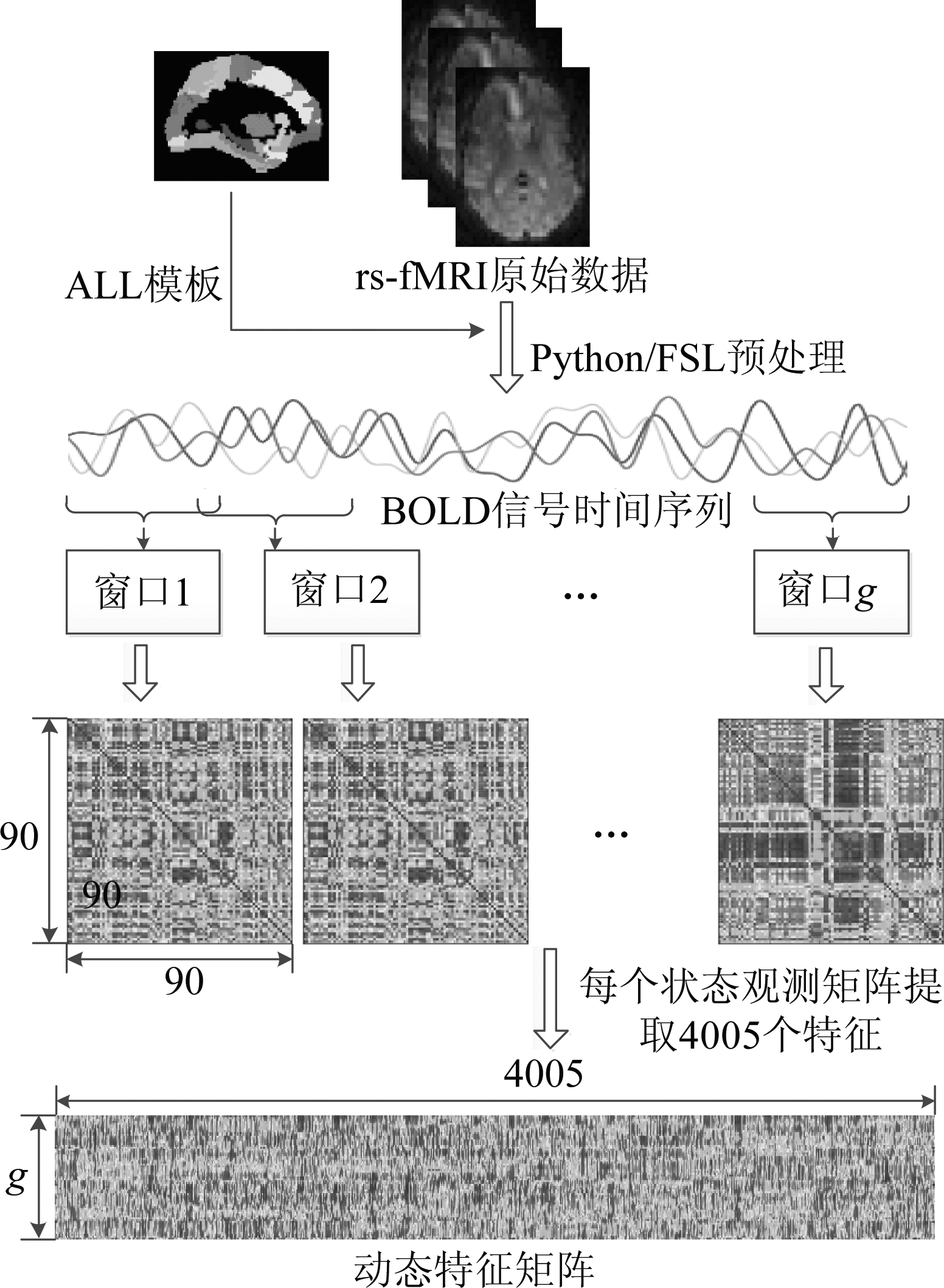
图1 滑动窗口和动态特征矩阵G的构建原理图
Fig.1 The schematic diagram of constructing sliding window and dynamic feature matrix G
2.3 基于非线性相关分析的状态矩阵构建方法
在2.2中所构建的观测窗口的基础上,本文分别采用三种相关分析方法Kendall、Spearman、MIC确定脑区i和脑区j之间的功能连接,从而构建状态矩阵,这三种非线性相关分析方法的原理及算法如下。
2.3.1 斯皮尔曼相关分析(Spearman)
Spearman相关系数与变量的分布和样本容量都无关,只要两个变量的观测都是成对的等级评定资料,就可以用Spearman相关分析法进行研究[21]。在一个窗口内两个脑区的BOLD信号是成对的等级评定资料,所以可用Spearman来测定脑区之间的相关强度。
定义1 对于一个滑动窗口内的n个采样点,脑区i和脑区j的BOLD信号向量分别为X=(X1,X2,…,Xn)和Y=(Y1,Y2,…,Yn),首先分别求取脑区i 和脑区j BOLD信号的秩ri、si以及它们的平均秩![]() 则脑区i和脑区j之间的Spearman相关强度SRij可以定义为:
则脑区i和脑区j之间的Spearman相关强度SRij可以定义为:
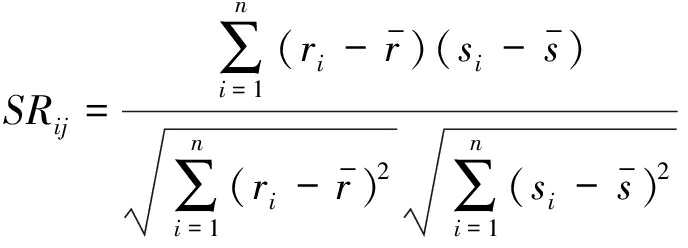
(1)
其中SRij∈[-1,1]。当一个脑区的BOLD信号随着另一个脑区单调递增的时候SRij=1,反之SRij=-1。
2.3.2 Kendall相关分析
Kendall相关分析法(Kendall coefficient concordance)是衡量等级变量相关程度的一个统计量[21]。在脑网络研究中根据两个脑区之间BOLD信号序对的一致性来判断其相关性。
定义2 对于两个时间序列长度为n的脑区,它们之间的Kendall系数KRij定义为:
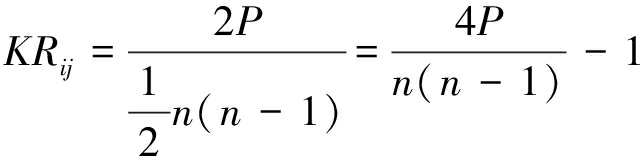
(2)
其中,P表示一致的序对个数。而且KRij∈[-1,1]。
2.3.3 最大信息系数(MIC)
Reshef等人[22]发表在《Science》上提出的最大信息系数MIC属于最大化的基于信息的非参数性探索,可用于衡量两个脑区之间非线性的强度。
定义3 令脑区i和脑区j的n个BOLD信号时间序列为数据集D,将数据集划分为x行y列,则两个脑区之间的最大信息系数MRij定义为:
MRij=max{M(D)x,y}
(3)
其中M(D)为D的特征矩阵,MRij∈[0,1]。具体公式定义可参考文献[22]。
相对于前两种非线性相关系数,最大信息系数能检测出两个脑区之间更复杂的非线性关系[22]。
对于基于滑动窗口技术而展开的脑区非线性相关性分析原理如图 2 所示,在每一个观测窗口内构建状态矩阵的具体步骤如下:
(1)从观测窗口![]() 中选取脑区i和脑区j的n个BOLD时间序列。其中
中选取脑区i和脑区j的n个BOLD时间序列。其中![]()
(2)分别求取脑区i和脑区j的Kendall相关系数(KRij)、Spearman相关系数(SRij)、MIC相关系数(MRij)得到该时刻90×90的脑网络状态观测矩阵;
(3)滑动窗口沿采样时间方向变化,逐一按(1)、(2)中的步骤求取不同时刻的状态观测矩阵;
(4)得到全部采样时刻的状态观测矩阵。
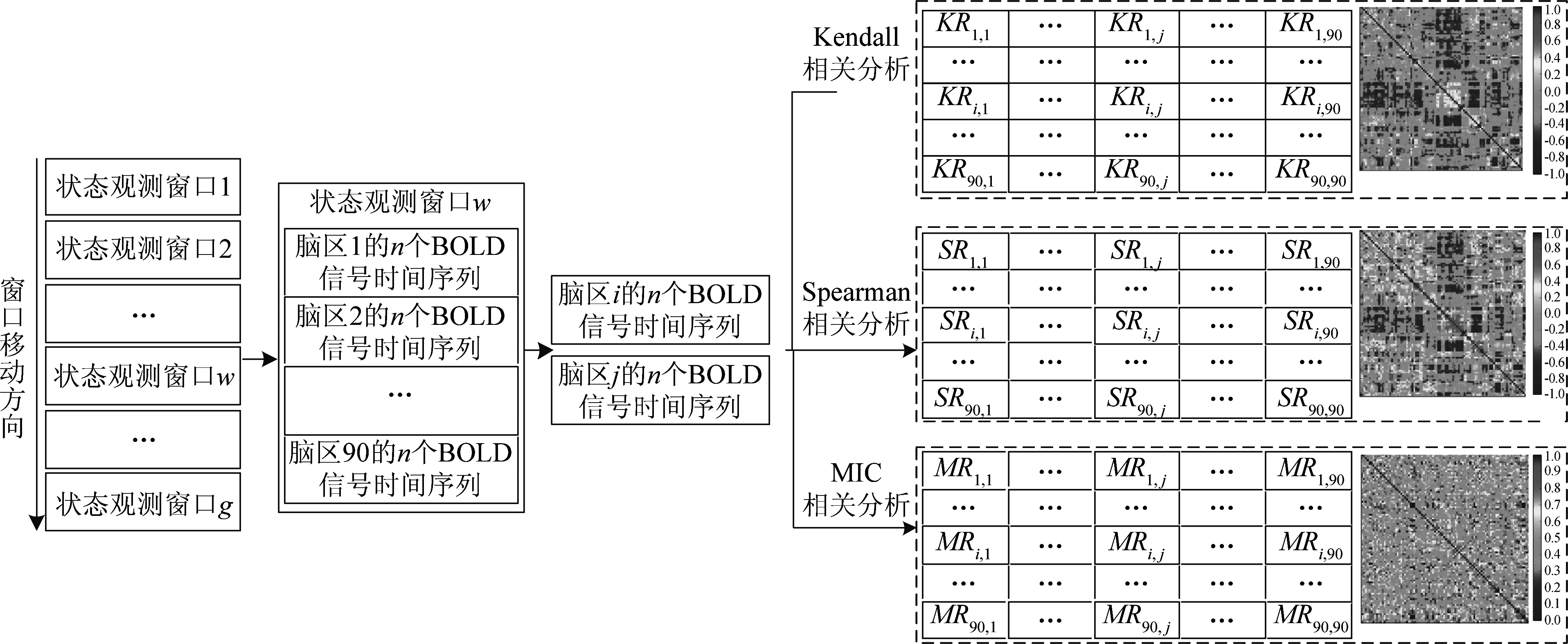
图2 脑区相关性分析原理图
Fig.2 Schematic diagram of correlation analysis of brain regions
3 脑功能网络的构建及阈值确定方法
3.1 脑功能网络的构建准则和阈值范围确定
利用相关分析方法构建脑功能网络时主要有两方面因素需要考虑:确定脑网络的节点及确定节点之间连接的边[23]。本文通过ALL先验模板已经将整个大脑分为90个脑区,即脑网络有90个节点。而节点之间的边即脑区之间的功能连接则可以通过脑区之间196个BOLD信号时间序列的相关系数来确定。但无论采用上述哪种非线性相关分析算法构建得到的动态特征矩阵G,在构建网络的过程中都需要进行阈值处理,其目的是使其符合网络特性,只有当相关强度大小达到某一阈值时,才认为两个脑区之间存在功能连接。但是目前对于确定脑功能网络的阈值并没有统一的标准,大多数研究者都是根据经验或参考其他文献进行阈值选取。同时已有研究发现,在使用相关分析构建人脑功能网络时,不同的阈值会对所构建的脑网络拓扑性质产生较大的影响[23]。所以合理选取阈值是根据动态特征矩阵G进行脑网络构建的关键。
研究发现脑功能网络具有小世界性[24-25]和高效性[26]的特点,所以本节将根据大脑功能网络完整性、小世界性和高效性的要求来讨论不同相关分析方法所对应的合理阈值范围确定方法,上述要求分别可以做如下表述:
(1)大脑功能网络应该是一个完整的网络,90个脑区中的每一个脑区应该与其他脑区存在功能连接,所有网络中节点的度应该大于0。即ki>0,其中i=1,2,…,90。
(2)大脑的平均度值应该大于网络中节点个数的自然对数,即![]()
(3)对大脑功能相关系数矩阵二值化后,矩阵的稀疏度S应该小于![]() 即
即![]()
为了符合脑功能网络的完整性,当阈值设定得太高,会出现于其他脑区不存在功能连接的孤立脑区。而且在高阈值的情况下,脑网络的平均度也会降低,导致构建的网络将失去小世界性。条件3为了满足大脑的高效性,脑功能网络所对应的相关系数矩阵的稀疏度一般要小于![]() 如果阈值减小,二值化后相关系数矩阵的稀疏度将增大而超过
如果阈值减小,二值化后相关系数矩阵的稀疏度将增大而超过![]() 所以通过以上3个条件,可以确定脑网络的阈值范围。其中条件1和条件2可以确定阈值范围的上界,条件3可以确定阈值范围的下界。
所以通过以上3个条件,可以确定脑网络的阈值范围。其中条件1和条件2可以确定阈值范围的上界,条件3可以确定阈值范围的下界。
为了观测不同样本之间的差别,本文采用6个健康人的rs-fMRI数据作为实验样本(S1,S2,S3,S4,S5,S6),拟分别使用以上3种不同的非线性相关分析法计算出长度为196时间序列的相关系数矩阵,并用该阈值将相关系数矩阵二值化从而构建人脑功能网络。为了进行对比分析,除了使用以上3种非线性相关分析之外,还同时采用Pearson进行线性相关性分析。由于MIC相关分析方法对较长的数据对敏感,而且实验结果也显示,在对本文实验数据中的196个时间序列BOLD信号进行MIC相关分析时,所得到的相关系数矩阵中的所有元素值普遍较小,因此不采用与其他三种相关分析相同的方法确定阈值范围,具体方法见下文。如果构建的人脑网络全部满足以上3个条件,则表明构建该功能网络时所用的阈值合理;反之,构建脑功能网络不符合其中的任意一个条件,则该阈值不合理。
对Pearson、Spearman和Kendall算法来说,相关系数值都在-1到1的范围内,在确定阈值范围时具体步骤如下:
(1)以0为起始点,0.01为步长,依次提高阈值大小。并将阈值用于全时间序列相关系数矩阵进行二值化,即矩阵中元素绝对值大于阈值的元素置为1,小于阈值的元素置为0。
(2)将二值化后的矩阵构建为人脑功能网络,1代表脑区之间存在功能连接,0代表脑区之间没有功能连接。若构建的网络满足3.1节中的三个条件,则步骤(1)中的阈值为合理阈值。
(3)将阈值从0遍历至1,最终确定阈值范围。
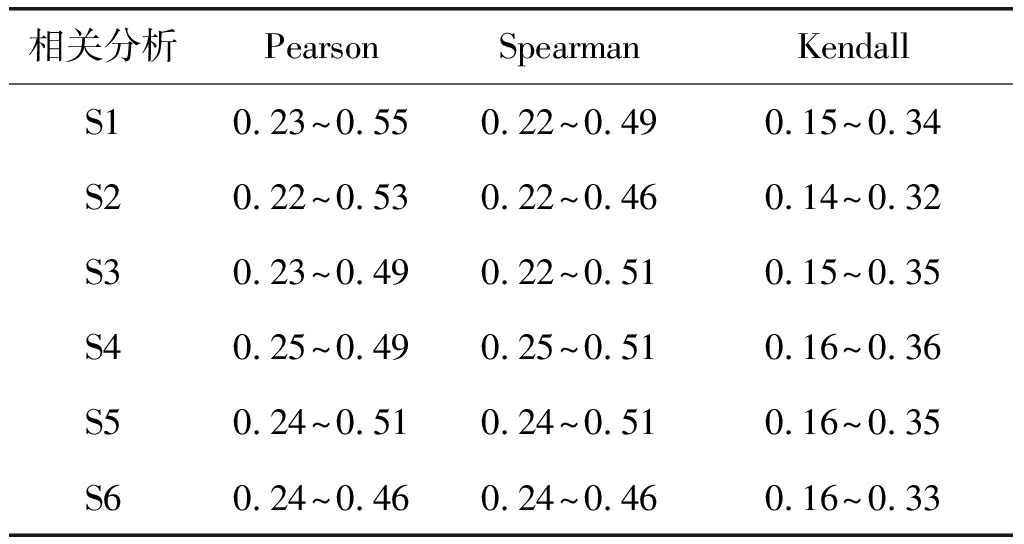
通过以上3个步骤能够得到6个样本的合理阈值范围如表1所示。
表1 三种相关分析方法的阈值范围
Tab.1 Threshold range of three Correlation analysis methods
相关分析PearsonSpearmanKendallS10.23~0.550.22~0.490.15~0.34S20.22~0.530.22~0.460.14~0.32S30.23~0.490.22~0.510.15~0.35S40.25~0.490.25~0.510.16~0.36S50.24~0.510.24~0.510.16~0.35S60.24~0.460.24~0.460.16~0.33
由于人脑样本的个体差异性,每一个样本得到阈值范围有所不同,但是通过表1中的实验结果可以看到,在使用同种相关分析方法时,所有样本的阈值范围均有一定程度的重合。
3.2 小世界性验证实验及最优阈值确定方法
大脑功能网络是典型的小世界网络,为了验证脑功能网络经过阈值处理二值化后,脑功能网络是否具有小世界性,本文选用σ指标进行判定。
σ是由Humphries等人[28]为衡量小世界性而提出的指标。σ指标的计算公式(4)如下:
σ=λ /γ
(4)
其中,λ是小世界网络与随机网络的聚类系数比值,γ是小世界网络与随机网络的平均最短路径系长度的比值。相对于随机网络,小世界网络有着较短的平均最短路径长度和较高的聚类系数,所以同等规模(相同的节点数,边数和度分布)的小世界网络和随机网络,λ大于1,γ约等于1,即当σ大于1时脑功能网络具有小世界性,而且σ越大,则脑网络的小世界性越强。
以Spearman算法为例,本实验中的六个样本采用Spearman相关分析后,按照表1中的阈值范围内不同阈值处理所构建得到的脑功能网络的σ指标值如下图3所示。
从图3可以看出,合理阈值范围内不同阈值处理所构建得到的脑功能网络的σ值基本都大于1,并且随着阈值的增大,脑网络的小世界性越强。为了在这个范围内确定最优的阈值,我们给出了一种将脑功能网络的拓扑特性与小世界性相结合的综合阈值确定方法。
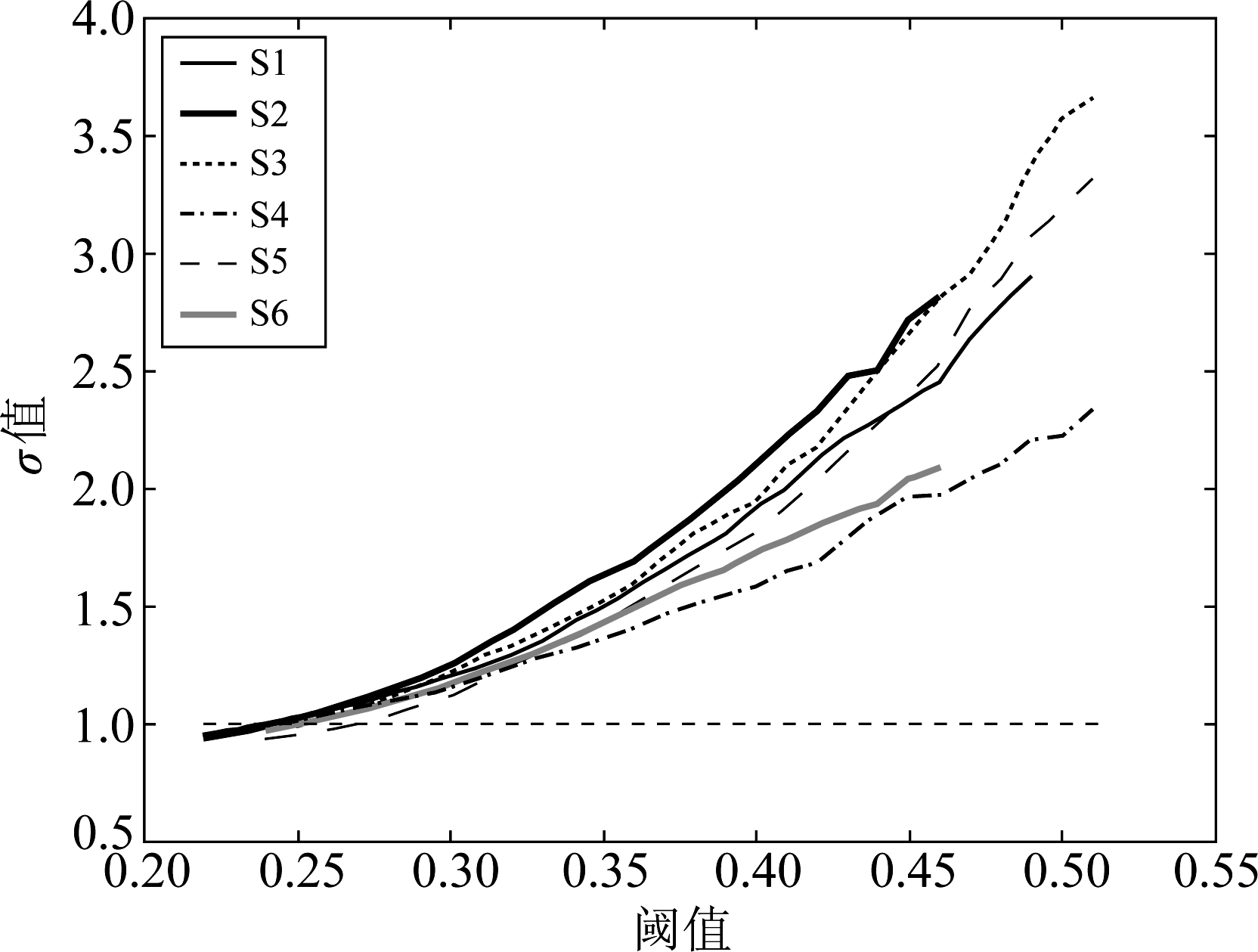
图3 合理阈值范围内的σ指标变化曲线
Fig.3 The variation curve of σ value corresponding to different threshold value
已有研究表明,脑功能网络信息传递效率与网络聚类系数C和网络平均最短路径长度L密切相关,并且与C成正比,与L成反比[24]。本文中脑功能网络聚类系数C和平均最短路径长度L定义如下:
(5)
(6)
其中公式(5)中的ki为脑功能网络中节点i的邻居节点个数,Ei为节点i邻居节点实际连接边数,公式(6)中d(νi,νj)为节点i与节点j的最短路径长度,且i≠j。而脑功能网络的聚类系数C会随着阈值增大而降低,同时脑功能网络平均最短路径长度L会随着阈值增大而增大。所以综合σ、C和L参数的影响,给出一个基于小世界性的网络信息传递效率指标![]() 如公式(7)所示:
如公式(7)所示:
(7)
针对具有小世界性的脑网络信息传递效率而言,σ、C和1/L越大越好,即![]() 值越大越好。图4为上述6个样本使用Spearman相关分析方法在不同阈值下的
值越大越好。图4为上述6个样本使用Spearman相关分析方法在不同阈值下的![]() 指标曲线。
指标曲线。
由图4可以看出,在一定阈值范围内随着阈值增大,![]() 值越来越大,在当阈值增大到一定程度,
值越来越大,在当阈值增大到一定程度,![]() 值会随着阈值变化而出现波动。由于人脑样本的个体差异性,每一个样本在
值会随着阈值变化而出现波动。由于人脑样本的个体差异性,每一个样本在![]() 值最大时所对应的阈值是不可能完全一样的,因此本文选取6个样本
值最大时所对应的阈值是不可能完全一样的,因此本文选取6个样本![]() 值最大时所对应的阈值的平均值作为最终阈值。
值最大时所对应的阈值的平均值作为最终阈值。
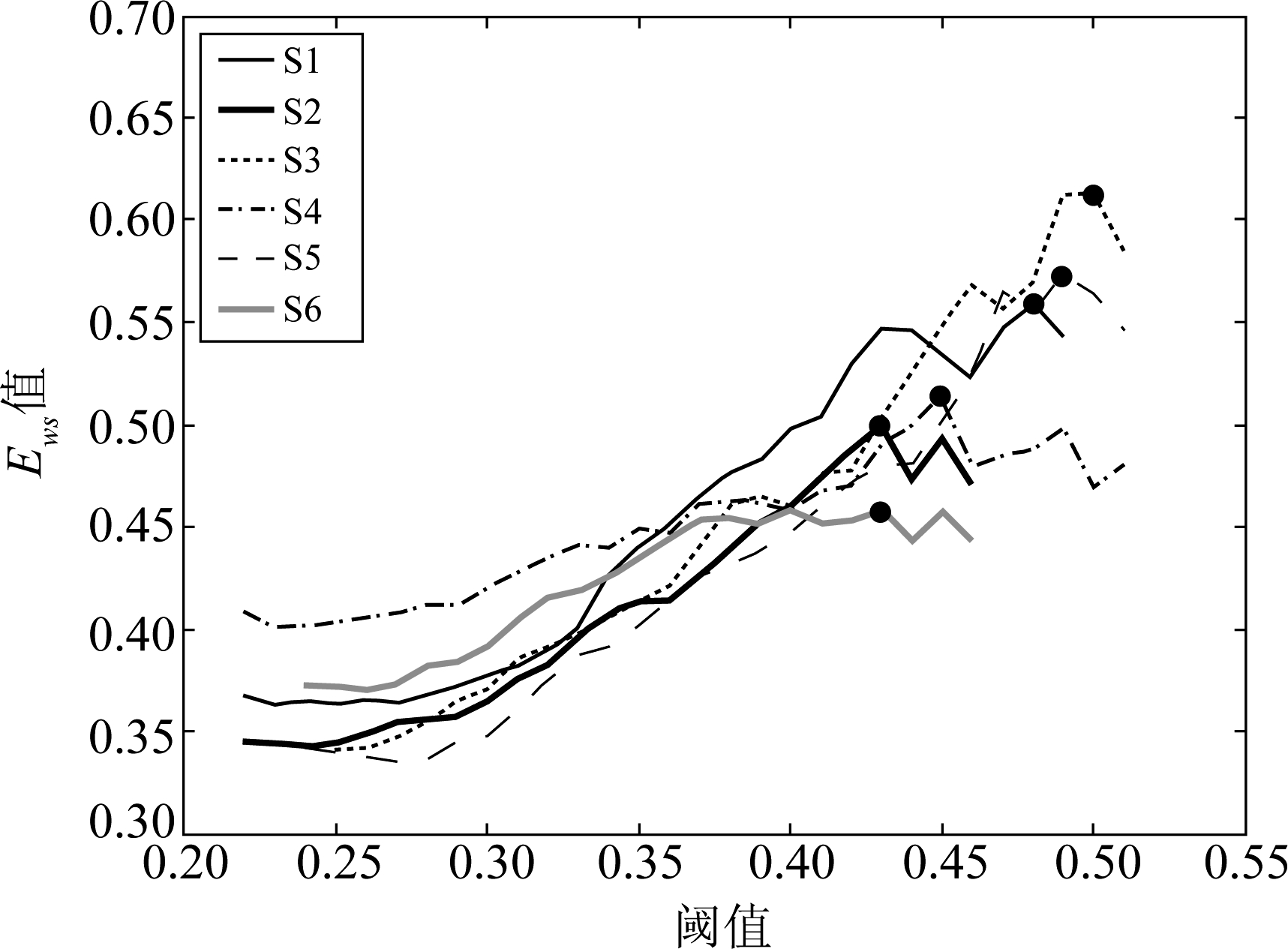
图![]() 值变化曲线
值变化曲线
Fig.4 The variation curve of ![]() value
value
按照本文方法,最后得到的Spearman相关分析方法的最优阈值为0.46,Kendall相关分析方法的最优阈值为0.32,Pearson相关分析方法的最优阈值为0.48。下文将使用这些最优阈值展开动态特征矩阵的稀疏度实验。
3.3 稀疏度实验结果及对比分析
以上述6个样本为对象,将滑动窗口大小设置为n=20,步长l=1,使用四种不同的相关分析方法分别构建人脑动态特征矩阵G。在使用滑动窗口技术来研究脑网络动态特性时,最重要的两个参数就是窗口的大小和步长。但是目前研究者们对于这两个参数的设定并没有达成统一的共识。Shirer等人[29]研究发现人脑认知状态的改变至少需要30~60 s;Li等人[30]研究发现窗口时间长度设定为20~40 s时,能够较好的捕捉脑连接的动态变化。为了减小窗口大小对实验的影响,本实验选择将窗口的时间长度设定为40 s,即窗口大小n为20。而且大部分研究者根据经验将窗口步长设定为1[16,18,31],所以本实验窗口的移动步长设定为1。
并针对动态特征矩阵G设定九种阈值,从0.1到0.9,步长为0.1。然后根据阈值将2.2节构建的动态特征矩阵G二值化,计算每种阈值处理后人脑动态特征矩阵G的稀疏度,即计算矩阵G中元素1与元素0的比值。随着阈值增大,人脑动态特征矩阵G的稀疏度的变化趋势如下图5所示:
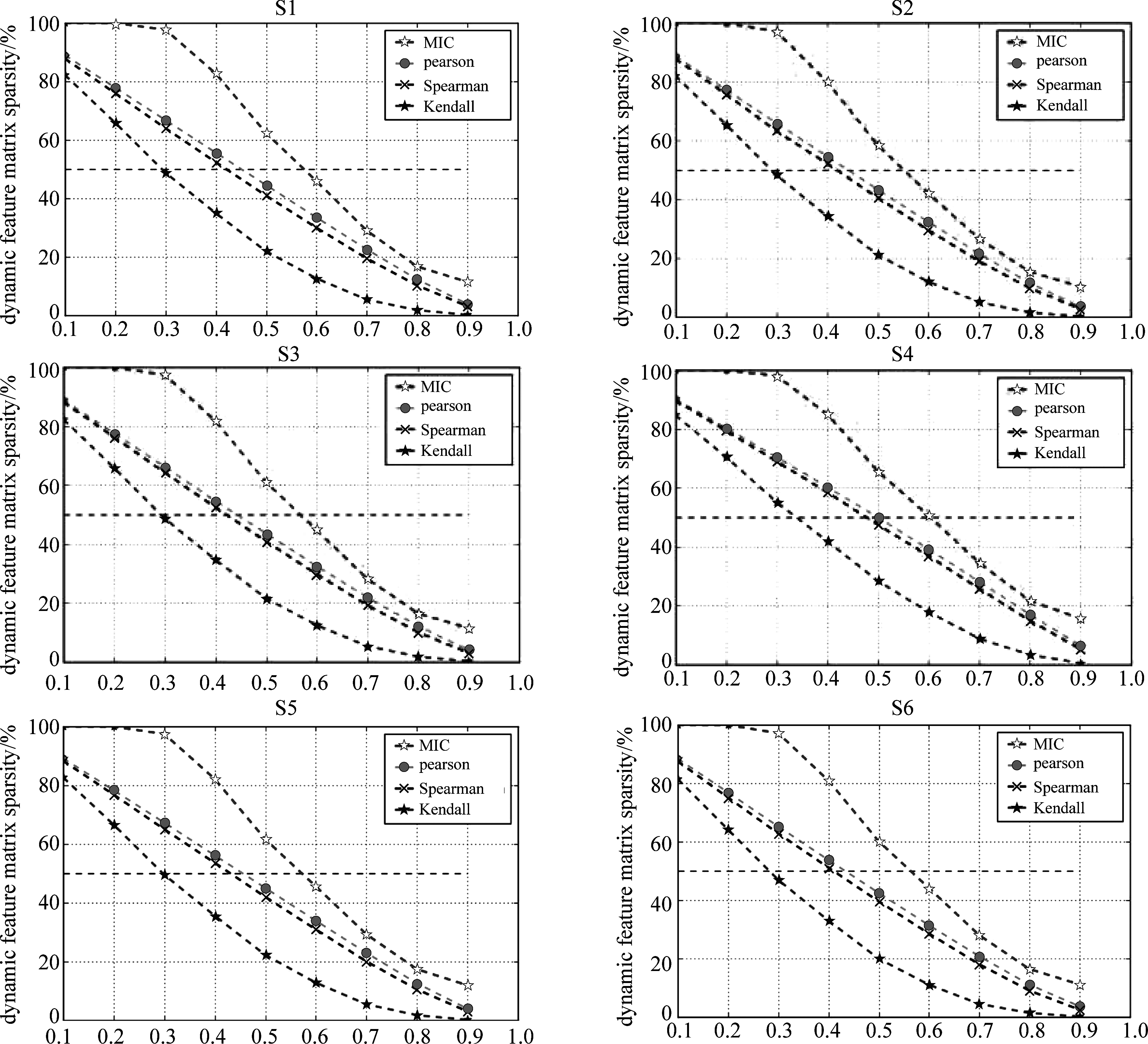
图5 动态特征矩阵稀疏度变化曲线
Fig.5 The sparsity variation curve of the dynamic feature matrix
由图5可知,四种相关分析方法构建的人脑动态特征矩阵随着阈值增大,二值化后矩阵的稀疏度越来越小。相比Pearson,Spearman和Kendall,MIC能检测出更为复杂的非线性相关系数,所以此种方法计算出的脑区相关度很明显大于其他3种相关方法。在同一阈值下,矩阵的稀疏度由大到小依次为MIC、Pearson、Spearman、Kendall,而且不同的相关分析方法对应的稀疏度曲线没有交叉。所以如果使用单一固定阈值同时处理4种相关分析方法得到的相关系数矩阵,会造成MIC构建的脑功能网络相对稠密,而Kendall构建的网络相对稀疏。此外通过图5可知,不同样本在稀疏度为![]() 时,每一种相关分析方法所对应的阈值在一定范围内。几种不同相关分析所构建的6个样本人脑动态特征矩阵二值化后,稀疏度为
时,每一种相关分析方法所对应的阈值在一定范围内。几种不同相关分析所构建的6个样本人脑动态特征矩阵二值化后,稀疏度为![]() 时的阈值如下表2所示。
时的阈值如下表2所示。
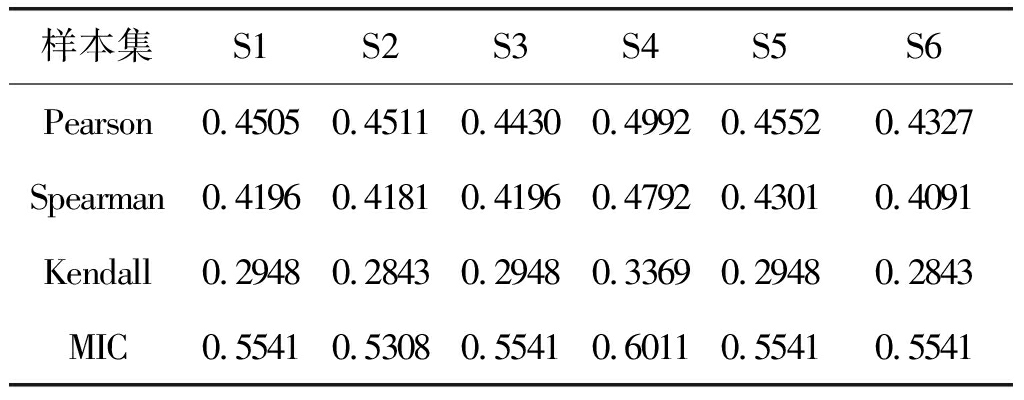
表2 稀疏度为![]() 时的阈值
时的阈值
Tab.2 The threshold of ![]() sparsity
sparsity
样本集S1S2S3S4S5S6Pearson0.45050.45110.44300.49920.45520.4327Spearman0.41960.41810.41960.47920.43010.4091Kendall0.29480.28430.29480.33690.29480.2843MIC0.55410.53080.55410.60110.55410.5541
由图5以及表2可以看出,阈值设定为0.32时,Kendall相关分析构建的人脑动态特征矩阵的稀疏度在50%左右,阈值分别设定为0.46和0.48时,对应的Spearman相关分析和Pearson相关分析构建的人脑动态特征矩阵的稀疏度也在50%左右。所以将MIC的阈值确定为0.55。此时脑网络的稀疏度要求可以得到满足。
由表2可以看出人脑动态特征矩阵G的稀疏度在50%时,Kendall相关分析方法对应的阈值较为接近0.32,Spearman和Pearson相关分析方法对应的阈值分别较为接近0.46和0.48,而当MIC构建的人脑动态特征矩阵二值化后稀疏度为50%时,阈值在0.55左右,为了得到与其他3种相关分析方法大致相同的脑功能网络规模,本文将MIC的阈值确定为0.55。
4 脑网络状态聚类方法及结果分析
根据上文方法所得到的脑网络在每个时刻的状态是一个4005维的矩阵,由于其维数过高,无法直接观测其特征,这使得深入展开人脑网络动态特征的识别、分析和研究变得极其困难。针对这一现状,需要对动态特征矩阵进行降维处理。文献[32]的研究表明,通过利用多种降维算法对脑网络人脑动态特征矩阵进行降维,发现相对于其他降维算法,t分布随机领域嵌入算法(t-Distributed Stochastic Neighbor Embedding, t-SNE)降维效果较为合理,在2维空间上能够观测到状态随时间的变化特征。所以本论文使用t-SNE降维算法对人脑动态特征矩阵从4005维降至2维,并进一步研究和分析不同的相关分析方法对状态识别的影响。
由上文研究可知,在对人脑动态特征矩阵G进行降维之前,还需要对该矩阵进行阈值处理。为了研究静息态脑网络状态的动态变化,在对含有动态信息的人脑动态特征矩阵G进行阈值处理时,并不是简单地对人脑动态特征矩阵进行二值化。上节主要从静态的角度构建人脑功能网络,不需要考虑rs-fMRI数据的动态变化,所以将相关系数矩阵进行阈值二值化时,只需考虑脑区之间是否存在功能连接,即相关系数矩阵二值化后矩阵中元素1表示在某两个脑区之间有功能连接,元素0表示两个脑区之间不存在功能连接。为了观测静息态脑功能网络的动态变化,本文将人脑动态特征矩阵G中正值元素大于阈值T的置为1,负值元素绝对值大于阈值T的置为-1,将元素绝对值小于阈值T的元素置为0。因为元素-1可以表示在一个窗口时间内,两个脑区之间存在功能连接并有着反向响应趋势,所以应该将动态特征矩阵G中相关系数值的正负考虑进去。
动态特征矩阵G阈值处理的方法如式(8):
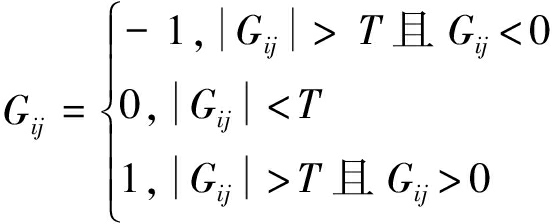
(8)
其中i=1,2,…,177, j=1,2,…,4005。由上文分析可知,Spearman相关分析的阈值为0.46,Kendall相关分析的阈值为0.32,Pearson相关分析的阈值为0.48,MIC相关分析的阈值为0.55。6个样本用2.2节的方法以窗口大小n=20,步长l=1构建人脑动态特征矩阵并进行以上阈值分析后,使用t-SNE降维后的可视化结果图如下图6所示。
通过图6可以看出,4种相关系数构建的人脑动态特征矩阵经过降维后都能表达静息态人脑的状态变化过程。上图中每一个点表示的是人脑动态特征矩阵G通过降维投影到二维空间内后形成的数据点,所以每个图中共有177个数据点,数据点的颜色代表着窗口次序,如颜色条所示,从蓝色到红色依次显示的是窗口状态从1到177随时间的状态表达。由于t-SNE降维方法是高维空间内样本对和低维空间内样本对相似概率的度量和映射,所以映射到2维空间中表现的并不是脑网络状态的实际分布,而是样本间的距离关系,从图中可以看到,尽管每次降维实验高维状态投映到二维坐标上的绝对位置可能不一样,但点之间的相对位置反映的才是状态之间的实际关系。
本文研究主要观测不同状态随时间的变化趋势,以及状态在哪些点发生了跳变,降维后,无论哪种分析方法均能将不同时间点的状态分为4到6类,这表明了人脑在静息态时脑区之间的交互随时间是有状态变化的,并且从断点分析可知,多数图像中断点的位置是在相近范围内的,如果考虑人脑样本在动态脑网络构建中的个体差异性,那么虽然同一种样本使用不同相关分析方法构建的人脑动态特征矩阵经过降维后结果有差异,但基本的聚簇和断点范围是相似的。这可以说明在fMRI数据采集过程中,人脑状态的变化是具有一定的规律性的。

图6 t-SNE降维可视化结果
Fig.6 t-SNE reduced dimensional visualization results
5 结论
本文以辨别和描述人脑网络的状态特征为目标,针对静息态脑功能磁共振的血氧依赖水平信号中的非线性特征,提出使用非线性相关分析的方法来构建动态特征功能连接矩阵,重点对构建脑区构建全脑状态矩阵过程中的不同非线性相关分析方法及关键技术展开了研究,并且讨论了如何通过阈值控制来排除动态特征矩阵中相关程度不够强的连接,从而确保所构建脑网络的合理性。
研究发现,无论采用Spearman、Kendall和MIC三种非线性分析方法中的哪一种,在确保阈值选择合理的条件下,采用基于滑动窗口的动态数据分析技术均可完成对网络属性相似的全脑动态功能网络构建。本文还实现了对所构建的全脑功能网络的降维和可视化聚类分析,实验结果发现人脑在静息态的情况下,脑网络存在自发的状态变化,对于不同的相关分析方法,动态特征矩阵经过降维后,可视化结果显示出的人脑在静息态时人脑功能网络状态的变化具有一定的规律性,从而验证了该方法的有效性。
尽管由于在脑网络构建过程中存在个体差异性,但在不同样本下相同分析方法在聚类和类簇边界上相似,而对于相同样本,不同的相关分析方法构建的动态特征矩阵可视化降维聚类结果也只存在很小的差异,上述实验结果证明了本文方法的普适性和适用性。
下一步将使用本文方法对脑疾病样本展开研究,以进一步验证其有效性,同时对窗口参数对实验结果的影响和状态演变规律展开深入研究。
[1] Mp V D H, Hulshoff Pol H E. Exploring the brain network: a review on resting-state fMRI functional connectivity[J]. European Neuropsychopharmacol, 2010, 20(8):519-534.
[2] Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations[J]. NeuroImage, 2010, 52(3):1059-1069.
[3] Sporns O. Graph-theoretical analysis of brain networks[J]. Brain Mapping, 2015: 629- 633.
[4] Geerligs L, Renken R J, Saliasi E, et al. A brain-wide study of age-related changes in functional connectivity[J]. Cerebral Cortex, 2015, 25(7):1987-1999.
[5] Ye M, Yang T, Qing P, et al. Changes of functional brain networks in major depressive disorder: a graph theoretical analysis of resting-state fMRI[J]. Plos One, 2015, 10(9):e0133775.
[6] Khan A J, Nair A, Keown C L, et al. Cerebro-cerebellar resting-state functional connectivity in children and adolescents with autism spectrum disorder[J]. Biological Psychiatry, 2015, 78(9):625- 634.
[7] Daunizeau J, Stephan K E, Friston K J. Stochastic dynamic causal modelling of fMRI data: should we care about neural noise[J]. NeuroImage, 2012, 62(2):464- 481.
[8] Zwart J A D, Gelderen P V, Jansma J M, et al. Hemodynamic nonlinearities affect BOLD fMRI response timing and amplitude[J]. NeuroImage, 2009, 47(4):1649-1658.
[9] Xie X, Cao Z, Weng X. Detecting spatiotemporal nonlinear dynamics in resting state of human brain based on fMRI datasets[J]. Applied Mathematics and Computation, 2008, 205(1):19-25.
[10] Han C E, Yoo S W, Seo S W, et al. Cluster-based statistics for brain connectivity in correlation with behavioral measures[J]. Plos One, 2013, 8(8):e72332.
[11] 董泽芹, 侯凤贞, 戴加飞, 等. 基于Kendall改进的同步算法癫痫脑网络分析[J]. 物理学报, 2014, 63(20):392-397.
Dong Zeqin, Hou Fengzhen, Dai Jiafei, et al. An improved synchronous algorithm based on Kendall for analyzing epileptic brain network[J]. Acta Physica Sinica, 2014, 63(20):392-397. (in Chinese)
[12] 牛宝东, 马尽文. 基于希尔伯特黄变换的癫痫自动检测[J]. 信号处理, 2016, 32(7):764-770.
Niu Baodong,Ma Jinwen. Automatic detection of epileptic seizure through Hilbert-Huang Transform[J]. Journal of Signal Processing, 2016, 32(7):764-770.(in Chinese)
[13] Salvador R,Suckling J,Schwarzbauer C,et al. Undirected graphs of frequency-dependent functional connectivity in whole brain networks[J]. Philosophical Transactions of the Royal Societ of London, 2005, 360(1457):937-946.
[14] 蒋杭进.最大信息系数及其在脑网络分析中的应用[D].武汉:中国科学院武汉物理与数学研究所,2013.
Jiang Hangjin. Maximal Information coefficient and its application to brain network analysis[D]. Wuhan: University of Chinese Academy of Sciences, 2013. (in Chinese)
[15] 苏龙飞. 人脑核磁共振数据的特征提取与特征选择[D]. 长沙:国防科学技术大学,2014.
Su Longfei. Feature extraction and selection in human brain MRI data[D]. Changsha: National University of Defense Technology, 2014. (in Chinese)
[16] Yu Q B, Erhardt E B, Jing S,et al. Assessing dynamic brain graphs of time-varying connectivity in fMRI data:Application to healthy controls and patients with schizophrenia[J]. NeuroImage, 2015, 107:345-355.
[17] Wee C Y, Yang S, Yap P T. Sparse temporally dynamic resting-state functional connectivity networks forearly MCI identification[J]. Brain Imaging and Behavior,2016, 10(2):342-356.
[18] 马洒洒, 王彬, 薛洁,等. 基于同步多维数据流的脑网络动态特征辨识方法研究[J]. 计算机应用研究, 2017, 34(11):3272-3276.
Ma Sasa, Wang Bin, Xue Jie, et al. Research of dynamic characteristic identification method for human brain network based on multidimensional Synchronization dataflow[J]. Application Research of Computers, 2017,34(11): 3272-3276.(in Chinese)
[19] Brain Imaging and Analysis Center. Python/ FSL Resting State Pipeline[DB/OL]. https:∥wiki.biac.duke.edu/biac:analysis:resting_pipeline.
[20] Tzouriomazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain[J]. NeuroImage,2002,15(1):273-289.
[21] 樊嵘, 孟大志, 徐大舜.统计相关性分析方法研究进展[J]. 数学建模及其应用, 2014, 3(1):1-12.
Fan rong, Meng dazhi, Xu dashun. Research progress of statistical correlation analysis[J]. Mathematical Modeling and Its Applications, 2014,3(1):1-12. (in Chinese)
[22] Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011,334(6062):1518-1524.
[23] Bullmore E T, Bassett D S. Brain graphs: graphical models of the Human Brain Connectome[J].Annual Review of Clinical Psychology,2011,7(7):113-140.
[24] Bassett D S, Bullmore E. Small-world brain networks[J]. Neuroscientist A Review Journal Bringing Neurobiology Neurology and Psychiatry,2006,12(6):512-523.
[25] Salvador R, Suckling J,Coleman M R, et al. Neurophysiological architecture of functional magnetic resonance images of human brain[J]. Cerebral Cortex,2005,15(9):1332-1342.
[26] Achard S,Bullmore E. Efficiency and cost of economical brain functional networks[J]. Plos Computational Biology, 2007, 3(2):174-183.
[27] 胡云奉.基于图论的脑连接关系构建与分析[D]. 上海:华东理工大学,2013.
Hu Yunfeng. Construction and analysis of brain connectivity based on graph theory[D]. Shanghai: East China University of Science and Technology, 2013. (in Chinese)
[28] Humphries M D, Gurney K, Prescott T J. The brainstem reticular formation is a small world, not scale free, network[J]. Proceedings of the Royal Society B Biological Sciences,2006,273(1585):503-511.
[29] Shirer W R, Ryali S, Rykhlevskaia E, et al. Decoding subject-driven cognitive states with whole-brain connectivity patterns[J]. Cerebral Cortex, 2012, 22(1):158-165.
[30] Li X, Zhu D, Jiang X, et al. Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients[J]. Human Brain Mapping, 2014, 35(4):1761-1778.
[31] Li W, Wang M, Li Y, et al. A novel brain network construction method for exploring age-related functional reorganization[J]. Computational Intelligence and Neuroscience, 2016, 2016(2):5.
[32] 董迎朝, 王彬, 马洒洒,等. 基于t-SNE的脑网络状态观测矩阵降维方法研究[J]. 计算机工程与应用, 2018,54(1):42- 47.
Dong Yingzhao, Wang Bin, Ma Sasa, et al. Dimension reduction method research of brain network status observation matrix based on t-SNE[J]. Computer Engineering and Applications, 2018, 54(1):42- 47. (in Chinese)
[33] 王干, 王华力. 基于精细化频带的脑磁信号跨频耦合特性分析[J]. 信号处理, 2016, 32(11):1328-1338.
Wang Gan, Wang Huali. Statistical analysis of the cross frequency coupling characteristic of MEG signals with the refined Frequency Bands[J]. Journal of Signal Processing, 2016, 32(11):1328-1338.


