1 引言
主旋律提取(简称“旋律提取”),是音乐信息检索领域中一项重要研究课题,旨在从音乐片段中提取出被听者识别的作为音乐“本质”的单音高序列[1-2]。当音乐中存在歌声时,则将歌声作为主旋律,否则将最显著乐音成分作为主旋律。尽管音高和基频分别是两个不同的感知量和物理量,但在主旋律提取中,常把两者等同对待,故主旋律音高估计也常被称为“主旋律基频估计”[3]。主旋律提取在哼唱检索、翻唱识别、风格分类、歌手识别等方面具有广泛应用[4-7]。
文献[4]将现有的主旋律提取方法分为三类:基于显著度的方法、基于源分离的方法和其他方法。多数方法都属于基于显著度的方法,该方法先根据某种显著度策略得到每帧信号的多个音高估计,然后从显著度谱峰直接跟踪得到旋律轮廓,或者先把显著度谱峰聚类形成连续音高轮廓并从中选取旋律轨迹,该类方法中最具代表性的方法包括Salamon等提出的旋律轮廓特征法[3]、Dressler等提出的幅度谱加权与谐波谱峰对评估法[8]以及声学-语音模型法[9]。基于源分离的方法先增强混合音频中的主旋律成分或者从音乐中分离出主旋律分量,然后再采用音高估计和轨迹跟踪的方法提取主旋律,典型的该类方法包括:Tachibana等提出的基于乐音/打击乐器音源分离(Harmonic/Percussion Source Separation,HPSS)模型的谱分解法[10]、Durrieu等提出的基于非负矩阵分解的谱分解方法[11]、Arora和Behera提出的两级谐波聚类法[12]以及基于这三种方法的改进方法[13-18]。基于显著度和基于源分离以外的方法都被归类为其他方法,包括:基于数据驱动的分类方法[19]、基于深度神经网络的方法[20]、基于序列贝叶斯模型的方法[21]以及基于认知原理的方法[22]等。
在前期研究中,我们提出了基于改进欧几里得算法的主旋律提取方法[23]。该方法将欧几里得算法扩展到浮点数域,根据各谱峰对频率值,利用改进欧几里得算法,估计出旋律候选音高;然后,采用基于规则的策略,将时间和频率均足够接近的候选音高聚集到一起得到音高轮廓,根据音高轮廓的显著度函数得到最终的主旋律音高序列。该方法在基频丢失或有强低音伴奏的情况下具有较好的效果,但是由于音乐固有的非平稳性,以及候选音高的数量有限,很难精确地描述音高轮廓的显著度,导致旋律轮廓选择不准,且偶有同一音符范围内的估计值在不同音符之间切换的情况发生。
为了解决上述问题,本文提出了基于改进欧几里得算法和动态规划相结合的旋律提取方法,先采用改进欧几里得算法估计出候选音高,然后利用动态规划算法跟踪主旋律轮廓。由于动态规划中引入惩罚因子,减少了同一音符范围内估计值在不同音符间切换的情况,且动态规划中基于每帧音高定义显著度函数,克服了音高轮廓显著度难以精确描述的弊端。
本文章节安排如下:第2部分详细阐述提出的主旋律提取方法;第3部分提供实验结果与分析;第4部分对本文提出的方法进行总结。
2 主旋律提取方法
一般来说,每个音符都包括基频和谐波分量。然而,由于强低音伴奏影响或某些特殊的歌唱技巧,会出现基频丢失,在这种情况,直接跟踪基频的方法无法准确地提取出主旋律。然而,音乐信号中还有丰富的谐波分量,且心理声学研究表明,在基频丢失的情况下,人耳仍能准确地感知音高[24]。根据这一结论,本文方法先完成音乐音频信号的正弦估计,然后采用改进欧几里得算法估计出每帧的候选音高,最后利用动态规划算法跟踪旋律轨迹,其框图如图1所示。
2.1 正弦估计
正弦估计的作用是估计出每帧信号中的正弦分量的幅度和频率,这两个参数估计的准确率直接影响到后续处理结果,由于常Q变换(Constant-Q Transform,CQT)在较低频率范围内具有较高的频率分辨率能保证对低频成分具有较高的区分度,而在较高频率范围内具有较低的频率分辨率,可减少高频范围内伪峰的数量,故本文采用CQT完成音乐信号的谱分析。CQT的第k个分量定义为[25]:
(1)

图1 主旋律提取方法框图
Fig.1 Block diagram of the proposed method for melody extraction
其中Q为常数,x(n)是对连续时间信号x(t)离散化所得的序列,![]() 是长度为N[k]的窗函数。
是长度为N[k]的窗函数。
CQT进行谱分析时,对于不同频率段都具有相同的Q值,实现了频谱多分辨率分析。然后,搜索CQT幅度谱的谱峰,并采用Abe等提出的瞬时频率法[26]对谱峰频率进行校正。
假设信号x(t)的短时傅里叶变换表示为:X(ω,t)=a(ω,t)+jb(ω,t),其中a(ω,t)和b(ω,t)分别是X(ω,t)的实部和虚部。则(ω,t)处的瞬时频率可以表示为:
(2)
其中arg[·]表示取复函数的辐角。
则λ(ω,t)可以通过下式计算:
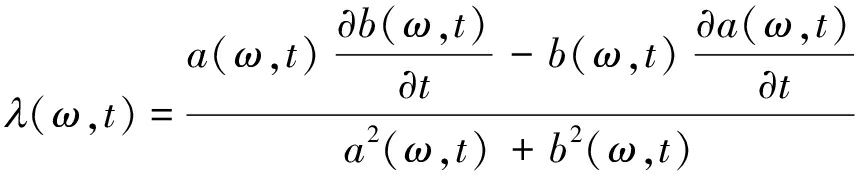
(3)
且瞬时频率(λ0,t)处的幅度可通过下式计算:
(4)
2.2 候选音高估计
欧几里得算法被广泛用于计算两个自然数的最大公约数,而感知音高可看作各次谐波的“最大公约数”(本文也称其为“类最大公约数”)。为了根据谐波求感知音高,我们用改进欧几里得算法估计每帧的候选音高[23]。假设x和y是两个浮点数,且0<x<y,则x和y的商余函数r(x,y)定义为:
(5)
其中[·]代表向最近的整数取整,|·|代表取绝对值运算。
r(x,y)是![]() 和
和![]() 之间的欧几里得距离。如果x接近类最大公约数,则
之间的欧几里得距离。如果x接近类最大公约数,则![]() 和
和![]() 比较接近,进而r(x,y)接近0,否则r(x,y)距离0较远,故r(x,y)是两个频率值谐波性的量度。若r(x,y)<ς(其中ς是某给定的较小阈值),则类最大公约数gcd(x,y)为
比较接近,进而r(x,y)接近0,否则r(x,y)距离0较远,故r(x,y)是两个频率值谐波性的量度。若r(x,y)<ς(其中ς是某给定的较小阈值),则类最大公约数gcd(x,y)为
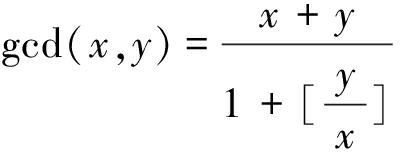
(6)
若r(x,y)≥ς,则令z=y-![]()
![]()
![]() x,其中⎣·」代表向负无穷方向取整,然后取
x,其中⎣·」代表向负无穷方向取整,然后取![]() 再重复计算r(x,y),直至r(x,y)<ς。
再重复计算r(x,y),直至r(x,y)<ς。
如图2所示,每个谱峰可以用两个参数,即频率pl,t和幅度ml,t,l=1,...,np,其中np是谱峰的数量。pi,t和pj,t(pi,t<pj,t)分别赋值给式(5)中的x和y,然后可通过上述的改进欧几里得算法求出候选音高fk,t=gcd(pi,t,pj,t)。除了真值附近的估计值之外,还会得到来自于伴奏音的伪候选值、高次谐波频率或子谐波频率等。因此,需要按照某种策略对估计值进行排序,考虑到旋律的显著性,本论文将两谱峰幅度值的乘积作为由该对谱峰得到的估计值的权重,即
(7)
其中mi,t和mj,t分别为第i和j个谱峰的幅度。
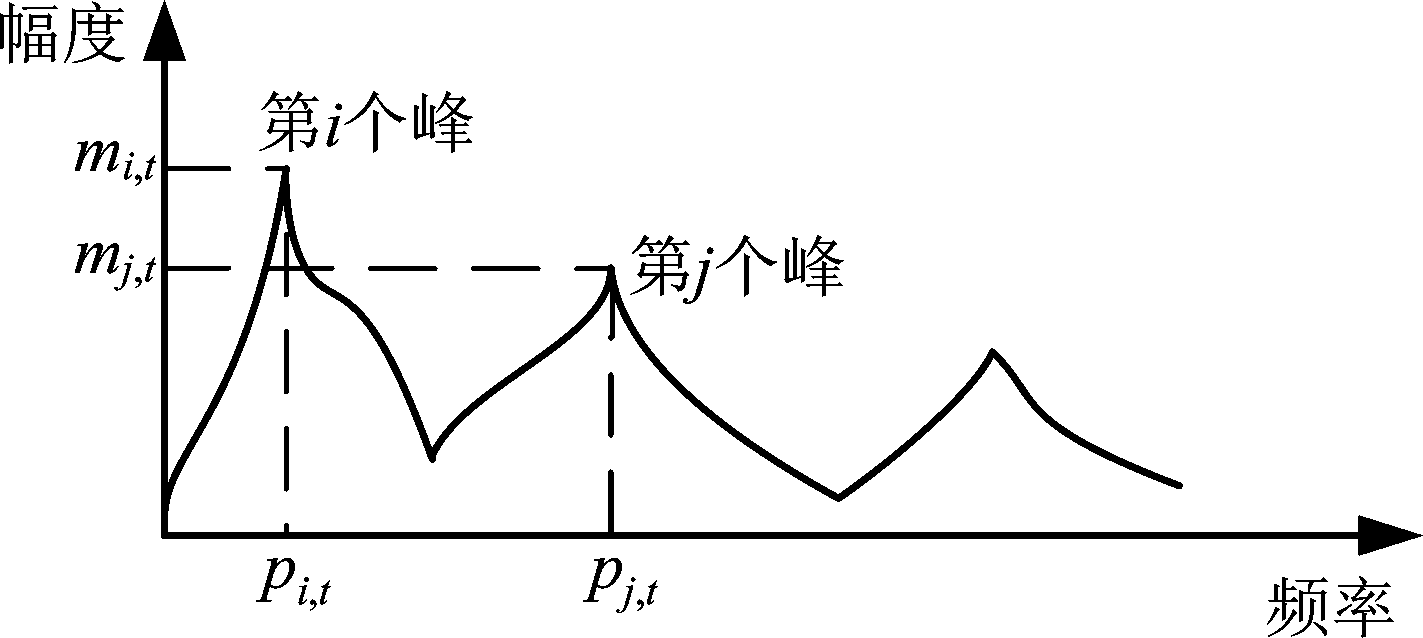
图2 第t帧信号幅度谱
Fig.2 Amplitude spectrum of the t-th frame
2.3 旋律轨迹跟踪
在多音高估计阶段,得到了每帧信号的多个音高候选值,按照音高的权重对音高候选进行初步筛选,仍没有考虑到相邻帧的时序连续性。动态规划能在代价函数中结合显著性和连续性约束,并通过递归求解子问题的方法找到最佳路径,故本文采用动态规划算法实现旋律轨迹跟踪,得到最终的主旋律音高序列估计。
选取权值最大的M个候选参与旋律轨迹跟踪,由于并不能保证每个音高候选估计都来自于某音源幅度最大的两个谱峰,故重新计算每个音高候选的显著度值,本文采用如下的谐波幅度加权求和函数作为音高的显著度值:
(8)
求出每帧各候选音高的显著度值后对这些候选的显著度值进行归一化运算:
(9)
旋律轨迹跟踪中需要同时考虑到旋律的显著性和连续性,故代价函数被定义为:
(10)
其中Nfrm是整个音频的帧数,λ为音高转移惩罚因子,d(ft, ft+1)是第t和t+1帧的音高差,单位是半音。式(10)中的第一项代表显著性约束,而第二项代表时序连续性约束。
动态规划的递归函数表示为:
λd( ft-1,k, ft, j)}
(11)
其中ft, j是第t帧的音高, ft-1,k是第t-1帧音高,d(ft-1,k, ft, j)是ft-1,k和ft, j之间的半音差,且t∈(1,Nfrm]。
D(t, ft, j)的初始条件为:
(12)
3 实验结果与分析
为了评估提出方法的性能,我们采用三个主旋律提取测评数据库进行实验,本节将详细阐述测试数据库、测试性能指标、参数设置及实验结果与分析。
3.1 测试数据库与性能指标
提出的方法采用ISMIR2004(文献[23]中也称其为ADC2004)、MIREX05 train和MIR-1K三个数据库进行性能测试。ISMIR2004由庞培法布拉大学的音乐技术组(Music Technology Group,MTG)提供,共20个音乐片段,包括MIDI、爵士、节奏布鲁斯(R&B)、流行乐和歌剧五种类型,这些片段持续时间大约20 s,采样率为44.1 kHz,标记的旋律音高间隔为5.8 μs。
MIREX05 train由Graham Poliner和Dan Ellis收集,包含13个持续时间在24 s至39 s长的片段,采样率为44.1 kHz,标记的旋律音高间隔为10 μs。
MIR-1K包含1000个歌曲片段,这些片段从110首录制的卡拉OK歌曲中截取,由19个业余歌手演唱,每个片段的持续时间在4 s至13 s范围内。整个数据库中音乐的持续时间为133 min,旋律音高的标记间隔也为10 μs。
各方法性能采用原始音高准确率(Raw Pitch Accuracy,RPA)和原始音度准确率(Raw Chroma Accuracy,RCA)两项指标进行评估,这两项指标定义为[27]:
(13)
(14)
其中#TP是正确估计旋律音高的帧数,#TPC是忽略八度误差后正确估计旋律音高的帧数,#VF是旋律总帧数,当估计值落在标注值半个半音范围内则认为旋律音高被正确估计,否则认为估计错误。由式(13)和(14)可见,RPA和RCA的定义类似,只是RCA忽略了八度错误。
3.2 参数设置
根据经验,主旋律音高的频率范围设为[100,1200]Hz,旋律音高序列的估计值间隔与各数据库相同,即ISMIR2004的旋律音高间隔为5.8 μs,而MIREX05 train和MIR-1K的间隔均为10 μs。CQT借用Schörkhuber等提供的CQT工具箱实现[28],CQT谱分析中每八度频率点数量B和每帧的候选音高数量M的设置及其对性能的影响在MIREX05 train数据库上进行测试,并根据在该数据库的性能结果设定,同样的参数用于ISMIR2004和MIR-1K两个数据库的主旋律提取。
提出的方法中有一些重要的参数需要设置,且参数设置对系统性能起到重要的作用,下面阐述这些参数的选择。改进欧几里得算法中阈值ς的取值在参考文献[23]中有详细讨论,即取之为ς=0.15。还需设定每帧音频中候选音高数量M,每八度频点数量B,式(8)中的Nh和α,以及动态规划中惩罚因子λ。通常,每帧的候选音高数量M在3~10范围内,每八度频点数量B取值在36~84范围内且为12的整数倍,式(8)中的Nh取值范围在5~10之间,α取值在0.80~1之间,λ在0.01~0.20范围内。
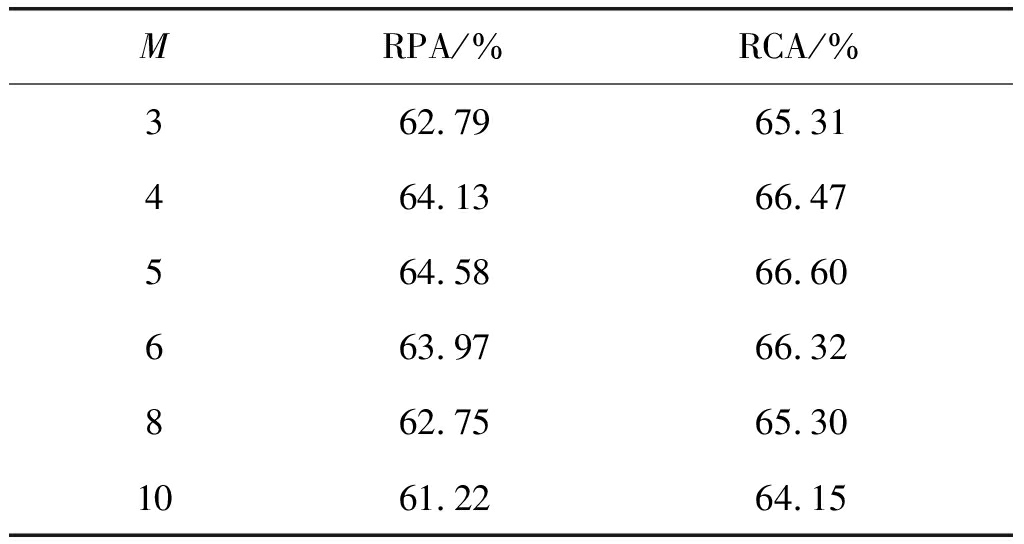
我们采用逐个参数优化的方法得到合理的参数设置,首先设定B=36,Nh=5,α=0.85,λ=0.05,测试每帧候选音高数量M对MIREX05 train数据库上主旋律提取性能RPA和RCA的影响,结果如表1所示。由该表可见,候选音高数量M=5时,取得最高的RPA和RCA。当M过大的时候,会引入较多的错误估计,给滤除错误估计造成困难,而如果M过小,部分准确值又不在跟踪范围内,故后续实验中均将M设为5。
表1 每帧候选音高数量(M)对性能的影响
Tab.1 Influence of candidate number (M) on performances
MRPA/%RCA/%362.7965.31464.1366.47564.5866.60663.9766.32862.7565.301061.2264.15
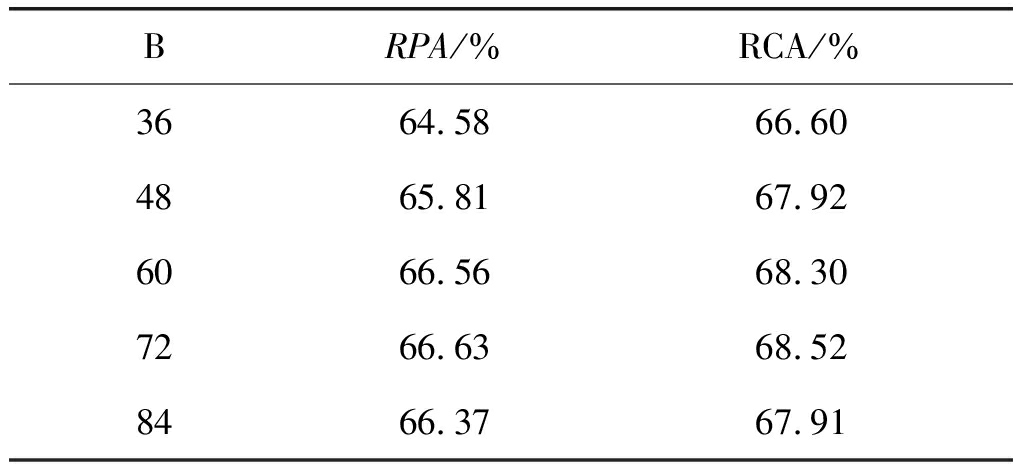
确定了每帧候选音高数量后,测试了CQT谱分析中每八度频率点数量B对MIREX05 train数据库上主旋律提取性能RPA和RCA的影响,实验结果如表2所示。由表2可见,随着B的逐渐增大,RPA与RCA均先增大后减小。由于CQT计算量正比于频率点数量[28],且B=60和B=72时性能差异较小,故在后续实验中均设定B=60。
表2 CQT谱分析中每八度频点数量(B)对性能的影响
Tab.2 Influence of bin number per octave (B) on performances
BRPA/%RCA/%3664.5866.604865.8167.926066.5668.307266.6368.528466.3767.91
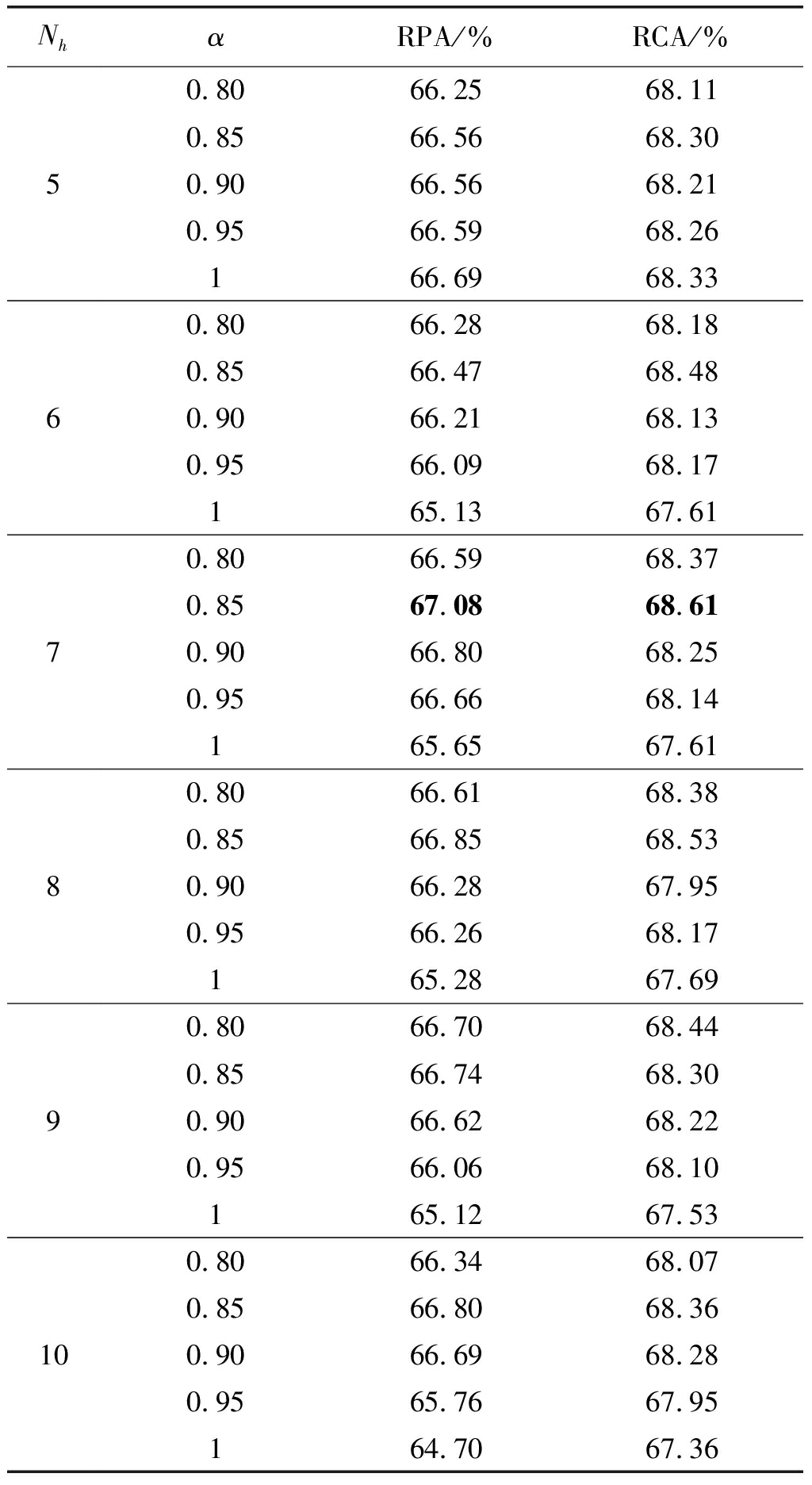
由于Nh和α都在式(8)中,故两者可同时优化,得到结果如表3所示。由该表可见,RPA和RCA均随着Nh和α的取值不同而变化,且变化范围较小,说明该方法性能对这两个参数不敏感。鉴于在Nh=7,α=0.85时,两者均取得了最大值,后续实验中均设定Nh=7,α=0.85。
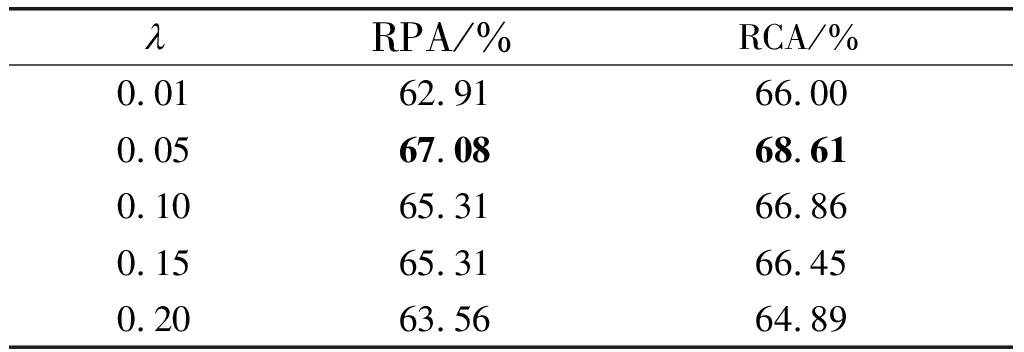
利用以上实验取得最佳性能的参数,在λ不同取值情况下,我们测试了提出方法的性能,得到结果如表4所示。由该表可见,λ=0.05时取得了最好的效果,故后续实验中仍保留此设置。
表3 Nh和α对性能的影响
Tab.3 Influences of Nh and α on performances
NhαRPA/%RCA/%50.8066.2568.110.8566.5668.300.9066.5668.210.9566.5968.26166.6968.3360.8066.2868.180.8566.4768.480.9066.2168.130.9566.0968.17165.1367.6170.8066.5968.370.8567.0868.610.9066.8068.250.9566.6668.14165.6567.6180.8066.6168.380.8566.8568.530.9066.2867.950.9566.2668.17165.2867.6990.8066.7068.440.8566.7468.300.9066.6268.220.9566.0668.10165.1267.53100.8066.3468.070.8566.8068.360.9066.6968.280.9565.7667.95164.7067.36
表4 λ对性能的影响
Tab.4 Influences of λ on performances
3.3 各数据库上的评估结果
根据3.2节中的参数设置,借助前述的数据库对该方法的性能进行了测试,图3给出该方法在ISMIR2004数据库中“daisy3.wav”片段上的处理效果。图3(a)是该段音乐的CQT谱图;该段音乐按照式(7)作为音高权重,每帧取权重排序前5的候选音高构成该帧的候选音高集,整个曲目候选音高集的显著度谱图如图3(b)所示;图3(c)是动态规划后输出的主旋律音高序列,由该图可见,该方法在这段音频上的总体效果较好,仅在1 s附近出现了八度错误。
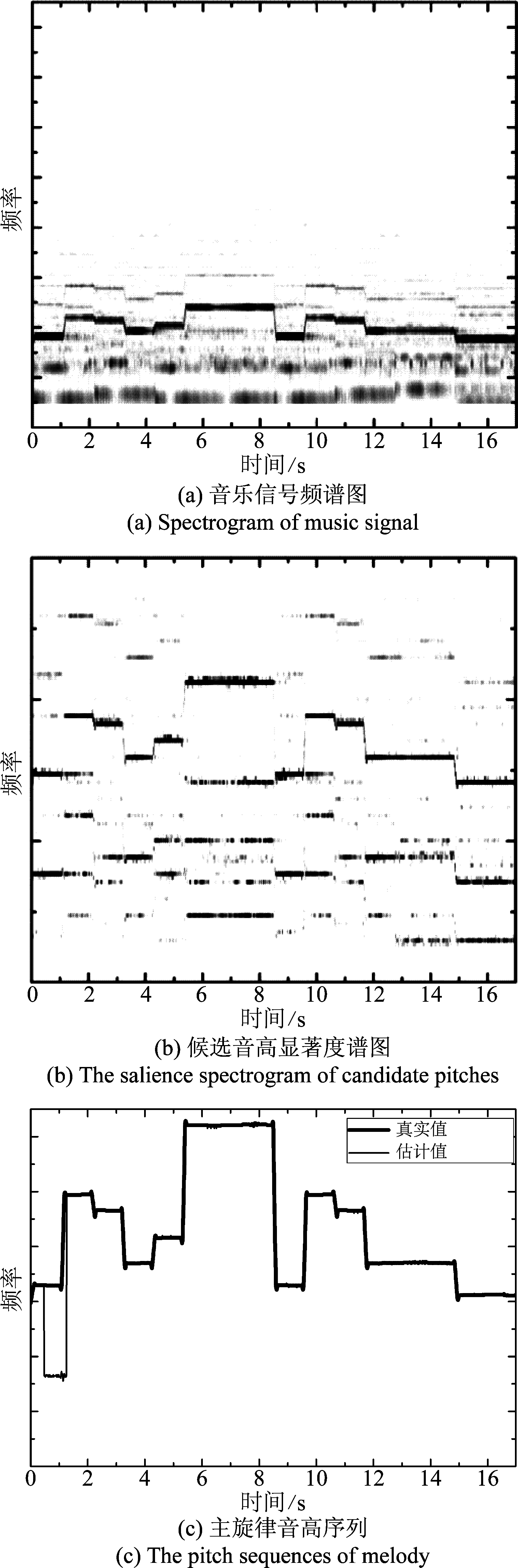
图3 某段音乐的主旋律提取结果
Fig.3 The main melody extraction result for one excerpt
3.4 各数据库上的评估结果
根据3.2节中的参数设置,借助前述的数据库对该方法的性能进行了测试,图3给出该方法在ISMIR2004数据库中“daisy3.wav”片段上的处理效果。图3(a)是该段音乐的CQT谱图;该段音乐按照式(7)作为音高权重,每帧取权重排序前5的候选音高构成该帧的候选音高集,整个曲目候选音高集的显著度谱图如图3(b)所示;图3(c)是动态规划后输出的主旋律音高序列,由该图可见,该方法在这段音频上的总体效果较好,仅在1 s附近出现了八度错误。
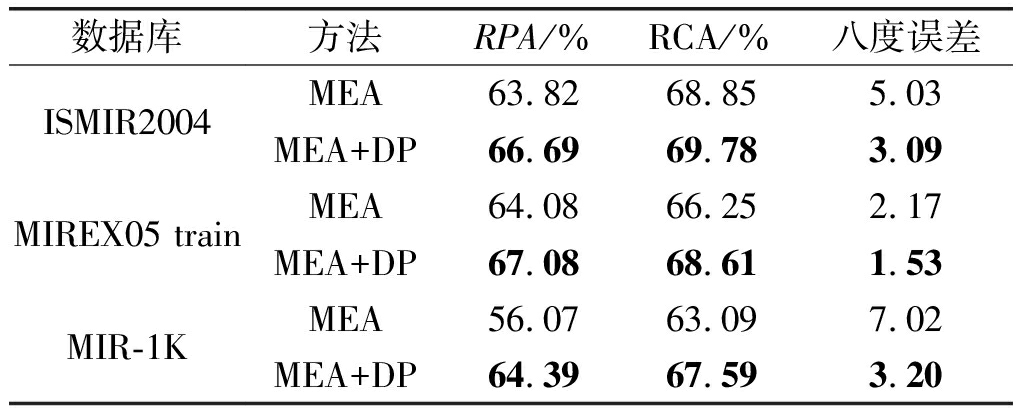
本文提出的方法(MEA+DP)和前期研究提出的改进欧几里得方法(MEA)[23]在三个数据库上的性能比较如表5所示。由表5可见,在三个数据库上,MEA+DP均取得了较MEA更高的RPA和RCA,以及更小的八度误差。
表5 三个数据库上的性能比较
Tab.5 Comparison of performances on three datasets
数据库方法RPA/%RCA/%八度误差ISMIR2004MEA63.8268.855.03MEA+DP66.6969.783.09MIREX05 trainMEA64.0866.252.17MEA+DP67.0868.611.53MIR-1KMEA56.0763.097.02MEA+DP64.3967.593.20
此外,实验中还比较了本方法、Hsu等[17]提出的归一化子谐波求和(NSHS)、乐器分量删除与动态规划相结合(IPD+DP)、乐器分量删除与归一化子谐波求和(IPD+NSHS)以及MEA等方法在ISMIR2004和MIR-1K两个数据库上的原始音高准确率(RPA),除了MEA和MEA+DP外,其他方法的RPA均由相关文献[17]提供,各方法在这两个数据库的结果详见图4。由图4可见,本文提出的方法在这两个数据库上均取得了最高的原始音高准确率。

图4 MIR-1K和ISMIR2004上的性能比较
Fig.4 Performance comparison on MIR-1K and ISMIR2004
4 结论
本文提出了基于改进欧几里得算法和动态规划的主旋律提取方法。该方法先利用改进欧几里得算法估计音乐中的帧级候选音高,再用动态规划算法建模主旋律的显著性和时序连续性,以跟踪主旋律音高序列。实验结果表明,本文提出的方法在三个测试数据库上的性能均优于前期研究提出的基于改进欧几里得算法的主旋律提取方法,与其他的参考方法相比,本方法也取得了较高的原始音高准确率。
[1] 张维维, 陈喆, 殷福亮, 等.复调音乐主旋律提取方法综述[J].电子学报, 2017, 45(4):1000-1011.
Zhang Weiwei, Chen Zhe, Yin Fuliang, et al. Review on melody extraction from polyphonic music[J]. Acta Electronica Sinica, 2017, 45(4):1000-1011. (in Chinese)
[2] Poliner G, Ellis D, Ehmann A, et al. Melody transcription from music audio: Approaches and evaluation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(4):1247-1256.
[3] Salamon J, Gómez E. Melody extraction from polyphonic music signals using pitch contour characteristics[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2012, 20(6):1759-1770.
[4] Salamon J, Gómez E, Ellis D, et al. Melody extraction from polyphonic music signals: Approaches, applications, and challenges[J]. IEEE Signal Processing Magazine, 2014, 31(2):118-134.
[5] Foucard R, Durrieu J, Lagrange M, et al. Multimodal similarity between musical streams for cover version detection[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Dallas: IEEE, 2010: 5514-5517.
[6] 王蒙蒙, 关欣,李锵.基于鲁棒音阶特征和测度学习SVM的音乐和弦识别[J].信号处理, 2017,33(7):943-952.
Wang Mengmeng, Guan Xin, Li Qiang. Musical chord recognition based on robust pitch class profile and metric learning support vector manchine[J]. Journal of Signal Processing, 2017,33(7):943-952. (in Chinese)
[7] Salamon J, Serra J, Gómez E. Tonal representations for music retrieval: from version identification to query-by-humming[J]. International Journal of Multimedia Information Retrieval, 2013, 2(1):45-58.
[8] Dressler K. Pitch estimation by the pair-wise evaluation of spectral peaks[C]∥42nd AES International Conference, Ilmenau: AES, 2011:1-10.
[9] Chien Y-R, Wang H-M, Jeng S-K. An acoustic-phonetic model of F0 likelihood for vocal melody extraction[J]. IEEE/ACM Transactions on Audio, Speech and Language Processing, 2015, 23(9):1457-1468.
[10] Tachibana H, Ono T, Ono N, et al. Melody line estimation in homophonic music audio signals based on temporal-variability of melodic source[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas: IEEE, 2010:425- 428.
[11] Durrieu J-L, Richard G, David B, et al. Source/filter model for unsupervised main melody extraction from polyphonic audio signals[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(3):564-575.
[12] Arora V, Behera L. On-line melody extraction from polyphonic audio using harmonic cluster tracking[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(3):520-530.
[13] Hsu C-L, Wang D, Jang J-S. A trend estimation algorithm for singing pitch detection in musical recordings[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague: IEEE, 2011: 393-396.
[14] Yeh T-C, Wu M-J, Jang J, et al. A hybrid approach to singing pitch extraction based on trend estimation and hidden Markov models[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Kyoto: IEEE, 2012: 457- 460.
[15] 龚君才,刘刚. 一种基于隐马尔科夫模型的波形文件主旋律基频提取算法[J]. 软件, 2013, 34(12):152-155.
Gong Juncai, Liu Gang. A melody pitch extraction algorithm for waveform file based on hidden Markov mode[J]. Software, 2013, 34(12):152-155. (in Chinese)
[16] Wang Y, Ou Z. Combining HMM-based melody extraction and NMF-based soft masking for separating voice and accompaniment from monaural audio[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague: IEEE, 2011:1- 4.
[17] Hsu C-L, Chen L-Y, Jang J, et al. Singing pitch extraction from monaural polyphonic songs by contextual audio modeling and singing harmonic enhancement[C]∥10th International Society for Music Information Retrieval Conference, Kobe: ISMIR, 2009:201-206.
[18] 宋岳阳. 基于单源欠定语音分离的音乐主旋律提取方法研究[D]. 北京:北京邮电大学, 2012.
Song Yueyang. An approach for music melody extraction based on underdetermined single-source speech separation[D]. Beijing:Beijing University of Posts and Telecommunications, 2012. (in Chinese)
[19] Ellis D, Poliner G. Classification-based melody transcription[J]. Machine Learning, 2006, 65(2-3):439- 456.
[20] Fan Z, Jang J, Lu C. Singing voice separation and pitch extraction from monaural polyphonic audio music via DNN and adaptive pitch tracking[C]∥IEEE International Conference on Multimedia Big Data, Taipei: IEEE, 2016:178-185.
[21] Jo S, Yoo C, A. Doucet. Melody tracking based on sequential Bayesian model[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(6):1216-1227.
[22] 李海峰, 孙佳音, 张田, 等. 基于音乐认知原理的音乐旋律发现技术[J].信号处理,2010, 26(10):1456-1465.
Li Haifeng, Sun Jiayin, Zhang Tian, et al. A music cognition based music melody detection approach[J]. Signal Processing, 2010, 26(10):1456-1465. (in Chinese)
[23] Zhang Weiwei, Chen Zhe, Yin Fuliang. Main melody extraction from polyphonic music based on modified Euclidean algorithm[J]. Applied Acoustics, 2016, 112(11):70-78.
[24] 霍华德. 音乐声学与心理声学[M]. 陈小平, 译. 北京:人民邮电出版社, 2014.
Howard D. Acoustics and Psychoacoustics[M]. Chen Xiaoping, translate. Beijing: Posts & Telecom Press, 2014. (in Chinese)
[25] Cancela P, Rocamora M, López E. An efficient multi-resolution spectral transform for music analysis[C]∥10th International Society for Music Information Retrieval, Kobe: ISMIR, 2009:309-314.
[26] Abe T, Kobayashi T, Imai S. The IF spectrogram: A new spectral representation[C]∥International Symposium on Simulation, Visualization and Auralization for Acoustic Research and Education, Tokyo: ASJ, 1997:423- 430.
[27] http:∥www.music-ir.org/mirex/wiki/MIREX_HOME.
[28] Schörkhuber C, Klapuri A, Holighaus N, et al. A MATLAB toolbox for efficient perfect reconstruction time-frequency transforms with log-frequency resolution[C]∥53rd AES International Conference, London: AES, 2014:1- 8.


