1 引言
语音身份识别也称为说话人识别,是通过对说话人的一段语音中所提取出的个性特征进行分析和识别,达到对说话人身份辨认和确认的技术。语音身份识别有着广泛的应用前景,可用于需要进行身份认证的安全领域,也可在智能家居、车载系统等小容量嵌入式系统中运用。目前说话人识别技术已经有了很大突破,在安静环境下表现出了较高的识别率。但是,现有的语音身份识别系统仍存在一些困难,最突出的便是噪声环境下系统的鲁棒性问题。实际应用中,由于现实环境下难免出现的背景噪音的影响,语音识别相关系统的应用环境往往不能很好的和纯净训练模型的环境相匹配,从而出现了由于环境失配所导致的系统识别性能下降的问题[1]。目前针对减小环境失配问题提出的方法主要分为两类[2]。一类是特征域方法,主要是寻求稳健的声学特性来提取鲁棒性语音特征。近年来,许多鲁棒性的语音特征被提出,在噪声环境下能够提升一定的识别率,但仅仅通过鲁棒特征来提升语音识别的效率还是无法满足实际应用的需要;另一类称为模型域方法,通过调整声学模型参数,将噪声信息融合到纯净训练模型的语音状态中,使之能够匹配当前测试中的噪声环境,克服环境失配所带来的影响。模型域中较为经典的方法是并行模型组合(Parallel Model Combination,PMC)算法[3-5]。传统PMC算法需要噪声信息已知,即通过已知的噪声信息对原始语音进行相应变换和调整后提高模型的抗噪能力,这样的做法虽然能够更充分的利用噪声信息改善原有模型,但缺乏一定的自适应性。本文结合PMC算法的原理和高斯混合模型-通用背景模型(Gaussian Mixture Model-Universal Background Model,GMM-UBM)[6-7]特点,提出了自适应并行模型组合APMC(Adaptive Parallel Model Combination)算法。通过从环境中估计出噪声信息来调整训练GMM各高斯单元的均值向量和协方差矩阵,估计出符合当前环境的GMM参数,减少因环境差异而导致的识别率不理想的问题。实验表明,结合了APMC补偿算法的说话人识别系统的抗噪性能较未补偿的系统有明显提升。
2 PMC简介
PMC是一种有效的噪声补偿技术,其核心思想是通过已有的纯净语音声学模型和噪声模型,经相应的变换后估计出含噪语音的模型,从而达到对声学模型的参数调整。该算法的原理是分别对处于时域的纯净语音信号和单纯的噪声信号进行模型训练,得出相对应的纯净语音模型和噪声模型,接着将两个模型变换到能够进行加性计算的对数谱域进行合并,得到含噪语音模型,再经过一系列的反变换后便得出处于时域的含噪语音信号。
为了更有针对性地解决噪声鲁棒性问题,PMC算法假设语音信号和噪声信号之间是相互独立的,在时域中是可加的关系[1],且噪声相对平稳。对于加噪语音y(n)表现为纯净语音x(t)和加性噪声n(t)在对数谱域特征矢量的非线性函数[4,8]:
yln(t)=ln(exp(xln(t))+exp(nln(t)))
(1)
PMC算法原理如图1所示。
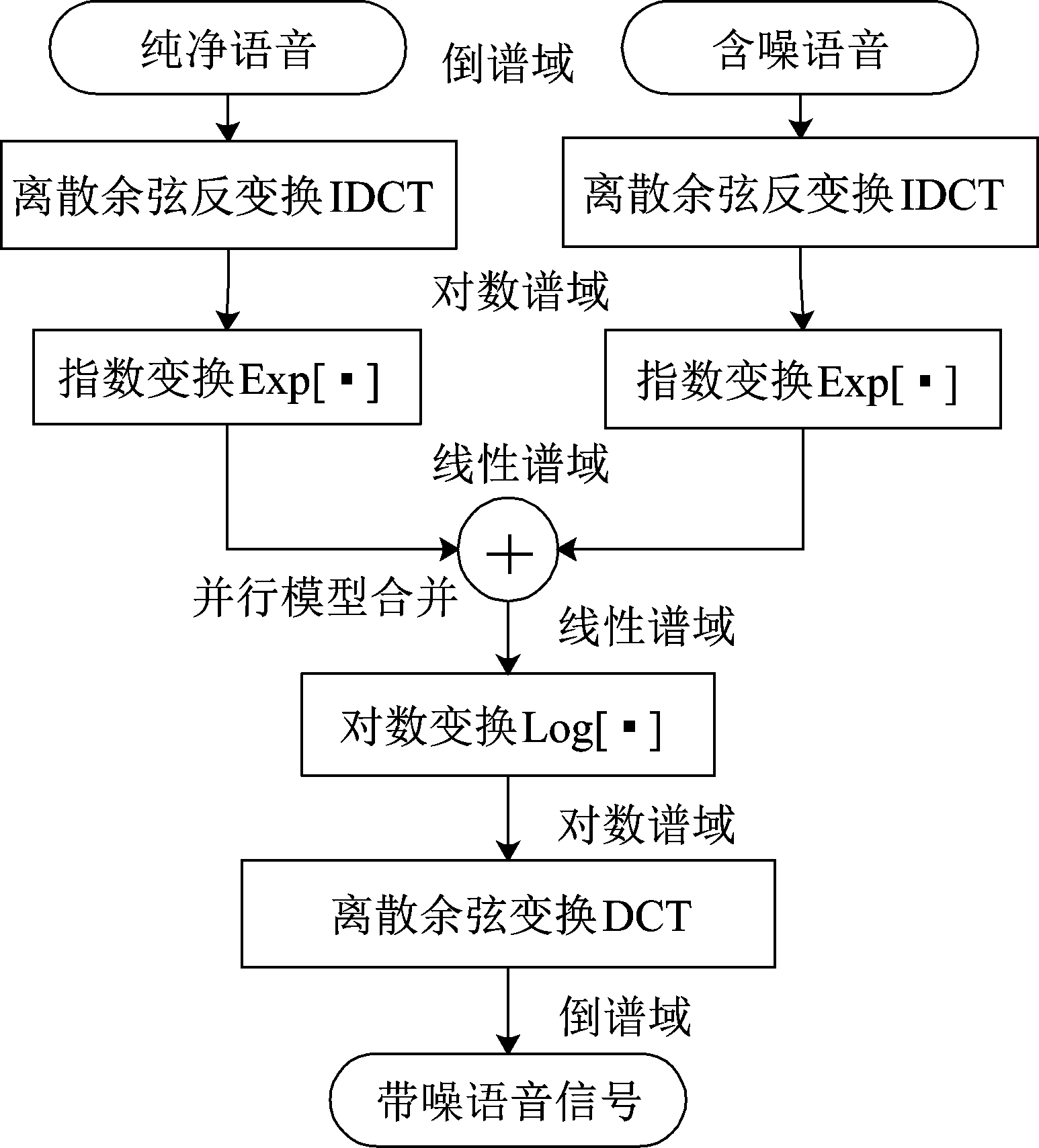
图1 PMC算法原理
Fig.1 Principle of PMC algorithm
3 自适应并行模型组合算法
3.1 APMC算法思想
为了提高模型的自适应性,相较于原始PMC算法而言,本算法不需要当前噪声模型已知,而是在含噪语音中估计出一小段噪声信息,通过该噪声信息得到噪声参数。由于噪声只影响纯净语音GMM中高斯单元的均值与方差[8],用APMC方法对每个说话人GMM各高斯成分的均值与方差进行相应调整,使之与测试中的噪声环境相匹配,来提高模型的抗噪性能以及自适应能力。
算法首先经过自适应的噪声估计得出倒谱域噪声参数,包括均值向量和协方差矩阵,然后利用PMC算法原理,对纯净语音倒谱系数训练成的GMM参数同噪声参数经倒谱提升逆变换和离散余弦反变换一同变换到对数谱域,接着通过指数变换变换到线性谱域,在线性谱域,对原始GMM模型参数和噪声参数进行非线性相加,再经过对数变换将参数变换到对数谱域,进而再通过离散余弦变换和倒谱系数提升变换到倒谱域,便得到了补偿后的GMM模型参数。
APMC算法流程如图2所示。

图2 APMC算法流程
Fig.2 Process of APMC algorithm
3.2 自适应噪声估计
对于短时语音数据而言,背景噪声一般认为是平稳的,因此,可以通过自适应噪声估计算法对当前语音数据提取噪声信息并获取噪声特征,通过利用该噪声特征对纯净语音训练模型GMM参数进行特征补偿,可以提高系统自适应的抗噪能力。具体过程如下:
Step 1 对于输入的语音信号X,先进行分帧处理,并对每一帧求取帧能量[6]E(i):
(2)
其中i表示帧序号,dim表示特征矢量维度。
Step 2 通过多次实验验证,取前五帧能量平均值的1.2倍作为基准门限值H可以有较好的效果:
(3)
Step 3 对帧能量进行平滑处理,利用宽度为5的移动平均滤波器对帧能量序列进行平滑处理,得到平滑后的帧能量E′(i),然后从第一帧开始,对每一帧平滑后的帧能量与门限值H进行比较,若E′(i)≤H,则认为该帧为噪声帧,若E′(i)>H,则认为语音帧开始,进而对该帧的前一帧进行位置标记,记为T′,取该帧及之前的帧作为噪声段进行参数估计。
Step 4 对提取的含噪语音倒谱特征矢量,取前T′帧语音特征矢量作为噪声的特征矢量N,用一个单高斯模型对该特征矢量进行拟合[8],得到噪声特征均值μn和方差![]() n。
n。
Step 5 通过得到的噪声段来估计噪声能量信息![]() ,并作为噪声补偿阶段的阈值。此阈值的作用是在噪声补偿阶段判断是否进行相应补偿。根据多次实验测试得出,在信噪比较小时,噪声对语音破坏影响较大,适当进行补偿有利于提升识别率,但当信噪比较大,也就是噪声对语音污染较小时,补偿的结果一定程度上会破坏原有参数,导致识别效率的下降。因此在噪声估计时通过噪声能量判断该噪声的信噪比大小,以此作为是否进行补偿的阈值和依据。一般认为
,并作为噪声补偿阶段的阈值。此阈值的作用是在噪声补偿阶段判断是否进行相应补偿。根据多次实验测试得出,在信噪比较小时,噪声对语音破坏影响较大,适当进行补偿有利于提升识别率,但当信噪比较大,也就是噪声对语音污染较小时,补偿的结果一定程度上会破坏原有参数,导致识别效率的下降。因此在噪声估计时通过噪声能量判断该噪声的信噪比大小,以此作为是否进行补偿的阈值和依据。一般认为![]() ≥0.01,噪声能量较大,信噪比较低,噪声对语音污染较大,应进行相应补偿。否则,认为噪声影响较小,不再进行特征补偿。其中,
≥0.01,噪声能量较大,信噪比较低,噪声对语音污染较大,应进行相应补偿。否则,认为噪声影响较小,不再进行特征补偿。其中,![]() 为:
为:
(4)
3.3 特征补偿
特征补偿是根据测试环境下提取的信息,通过非线性失配函数对模型参数进行调整,提高模型的鲁棒性。由于语音特征系数各个分量对识别率的影响有所不同,相对于低阶特征分量来说,高阶特征分量具有较好的鲁棒性,不易受到噪声的干扰。针对这种状况,在补偿的过程中采用了一种半升正弦函数(Half Raise-Sine Function,HRSF)[9-10]的系数提升策略对倒谱系数进行非线性的提升。倒谱提升相当于对倒谱系数{Xi}赋予权值{Wi},用正弦波来分配权重,可以降低易受噪声干扰的低阶分量值,同时又提高了数值相对较小的中高阶分量值[9]。由于突出了语音鲁棒性较好的高阶系数值,可以在抗噪能力方面提供更好的性能。
引入了倒谱系数提升的特征补偿过程如下:
Step 1 将纯净语音GMM均值μx、方差![]() x和在倒谱域估计得到的噪声均值μn和方差
x和在倒谱域估计得到的噪声均值μn和方差![]() n变换到对数谱域:
n变换到对数谱域:
(5)
(6)
Step 2 将对数谱域均值和方差通过指数变换的方式将其参数变换到线性谱域,此时变量服从对数正态分布[8,11]:
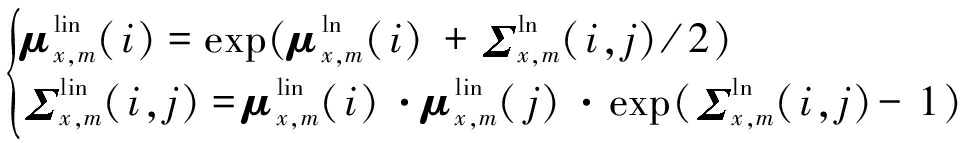
(7)
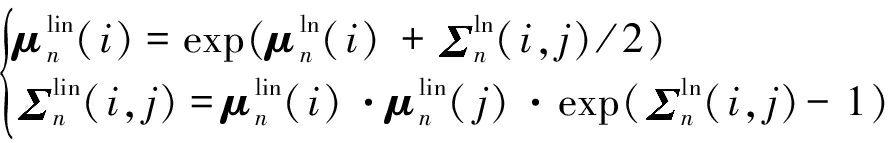
(8)
Step 3 将纯净语音和噪声的线性谱域参数非线性相加,得到处于线性谱域的含噪语音GMM的均值及方差:
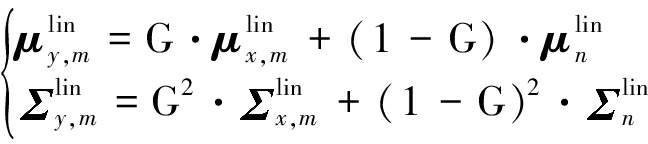
(9)
Step 4 将含噪语音线性谱域均值和方差变换到对数谱域,得到对数谱域参数[11]:
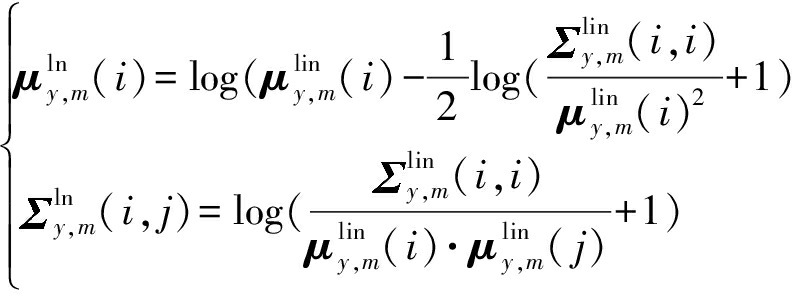
(10)
Step 5 将得到的对数谱域均值与方差通过离散余弦变换和倒谱系数提升变换到倒谱域:

(11)
Step 6 为了提高运算效率,去掉冗余元素,对得到的倒谱域协方差矩阵只保留对角元素:
(12)
其中, μx,m(i)、 μy,m(i)分别表示纯净语音和估计出的含噪语音GMM第m个高斯单元均值向量的第i个元素, μn(i)表示噪声均值向量的第i个元素;![]() x,m(i, j)、
x,m(i, j)、![]() y,m(i, j)分别表示纯净语音和估计出的含噪语音GMM第m个高斯单元协方差矩阵的第i行j列元素,
y,m(i, j)分别表示纯净语音和估计出的含噪语音GMM第m个高斯单元协方差矩阵的第i行j列元素,![]() n(i, j)表示噪声协方差矩阵的第i行j列元素。为了区分不同的声学特征域,上标lin表示线性谱域, 上标ln表示对数谱域。G为常数,表示补偿增益因子;C和C-1分别是离散余弦变换矩阵及其反变换矩阵;L和L-1分别是倒谱系数提升矩阵及其逆矩阵[10]。
n(i, j)表示噪声协方差矩阵的第i行j列元素。为了区分不同的声学特征域,上标lin表示线性谱域, 上标ln表示对数谱域。G为常数,表示补偿增益因子;C和C-1分别是离散余弦变换矩阵及其反变换矩阵;L和L-1分别是倒谱系数提升矩阵及其逆矩阵[10]。
N维离散余弦变换矩阵第m行n列的定义是:
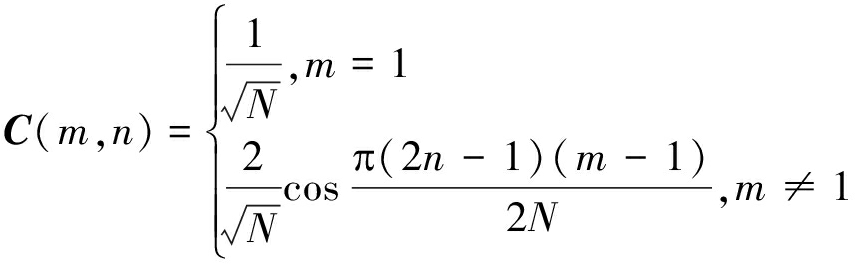
(13)
N维离散余弦反变换矩阵为:
C-1=CT
(14)
N维倒谱系数提升矩阵定义为:
(15)
N维倒谱系数提升逆矩阵定义为:
(16)
4 APMC语音身份识别过程
语音身份识别模型较为常用的模型是高斯混合模型-通用背景模型,将本文提出的自适应特征补偿方法应用于GMM-UBM,通过对原始训练GMM参数进行适当调整,以提高整个模型的抗噪能力和鲁棒性。APMC语音身份识别的过程如下:
1)对所有的纯净训练语音数据提取倒谱特征,训练通用背景模型UBM,利用提取的语音特征通过自适应得到每个说话人的GMM[6,12],其中第q个说话人模型对应的高斯混合模型参数
其中wm、 μm、![]() m分别表示GMM中第m个高斯单元的混合权重、均值向量及协方差矩阵。
m分别表示GMM中第m个高斯单元的混合权重、均值向量及协方差矩阵。
2)对于输入的测试语音,提取特征矢量,对该语音矢量和训练好的GMM模型通过自适应并行模型组合算法,首先估计出噪声特征均值、方差,接着对每个说话人GMM高斯单元中的均值和方差进行补偿,得到调整后的GMM参数![]()
3)最后进入识别阶段,对输入的测试语音提取特征,通过最大似然估计与所有说话人的GMM参数![]() 进行相应计算,得出具有最大概率的说话人模型所对应的身份作为识别结果进行输出[12]。
进行相应计算,得出具有最大概率的说话人模型所对应的身份作为识别结果进行输出[12]。
自适应并行模型组APMC语音身份识别过程如图3所示。
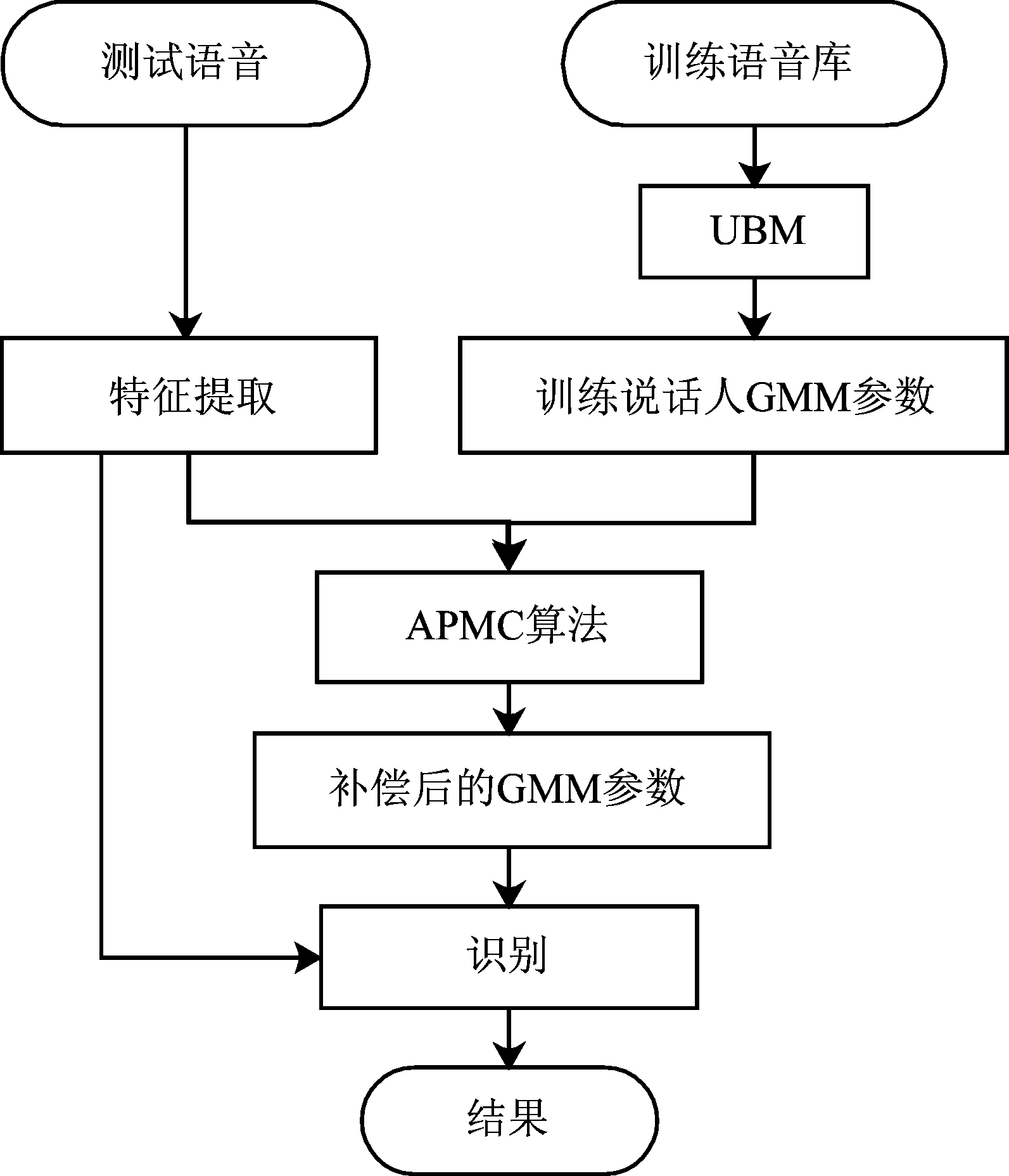
图3 APMC语音身份识别流程
Fig.3 APMC speaker recognition process
5 实验与分析
5.1 APMC算法对GMM高斯单元均值分布的重构
影响识别误差的问题与含噪语音模型均值与估计含噪语音模型均值之间的距离有关,距离越小,说明相似度越高,拟合效果越好,相应的识别率也会随之提高[10]。本实验通过对同一段纯净语音加噪前和加噪后,以及对原始纯净语音补偿后的GMM高斯单元均值分布进行了比较,以此来突出本方法对声学模型的重构是有效的。
实验选取12维的MFCC倒谱系数作为语音特征,在TIMIT语音库中选取了一段语音,结合NoiseX-92数据库中的Babble噪声和Mixed噪声。其中Mixed噪声是利用NoiseX-92数据库中较具代表性的Babble噪声、Factory噪声以及Cafe噪声三种加性混合产生的噪声。对原始语音进行加噪处理,信噪比SNR=0 dB。用32分量的高斯混合模型进行训练,得出不同状态下的GMM高斯单元均值分布。
图4、图5分别给出了在Babble噪声和Mixed噪声环境下不同状态语音GMM各高斯单元均值的分布情况。其中,图4(a)显示的是原始纯净语音12维MFCC特征的GMM均值分布情况,图4(b)是纯净语音混入信噪比为0 dB加性Babble噪声后得到的含噪语音的GMM均值分布,图4(c)是通过对含噪语音估计出的噪声参数,经APMC算法对原始纯净语音的GMM均值分布的重构结果。
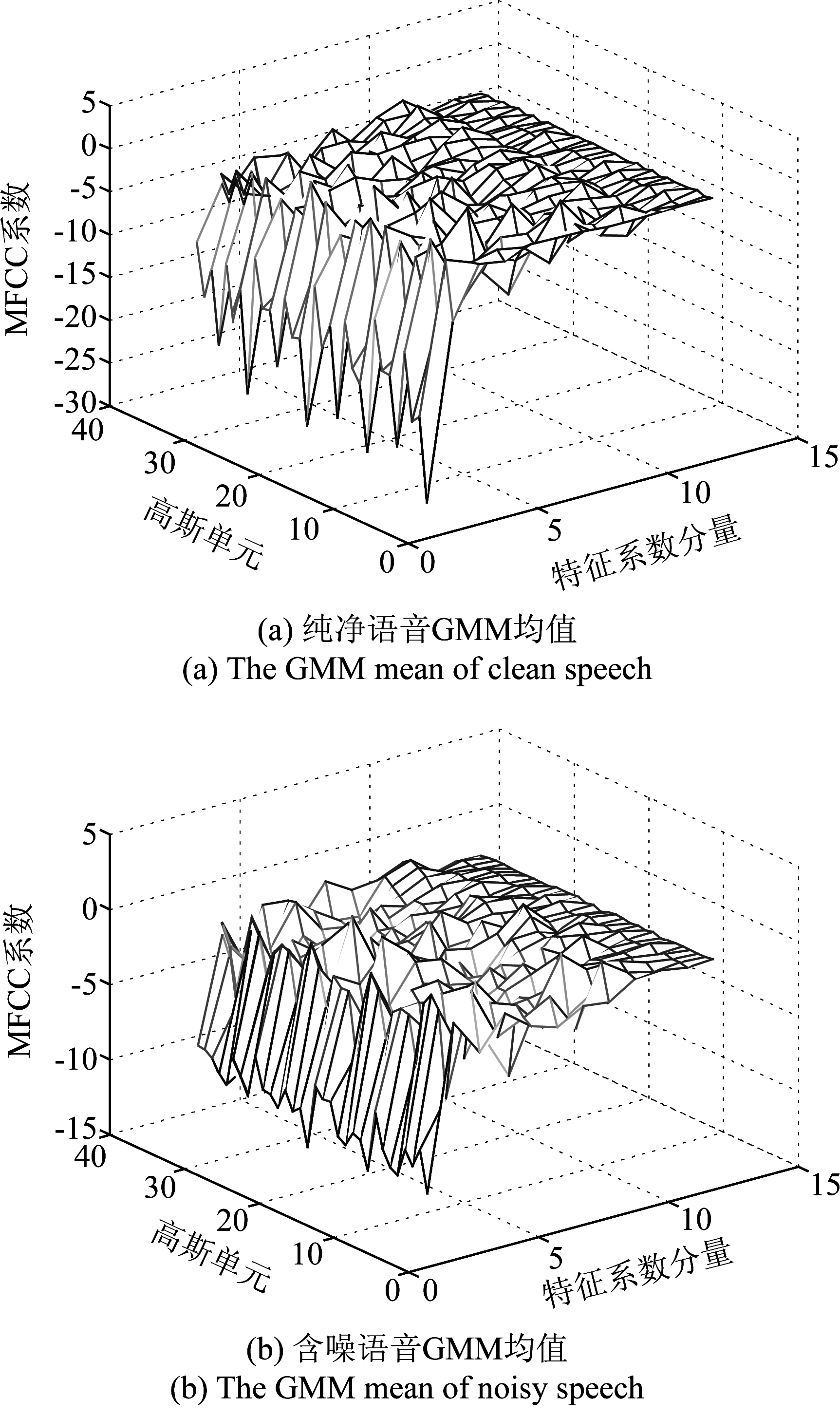
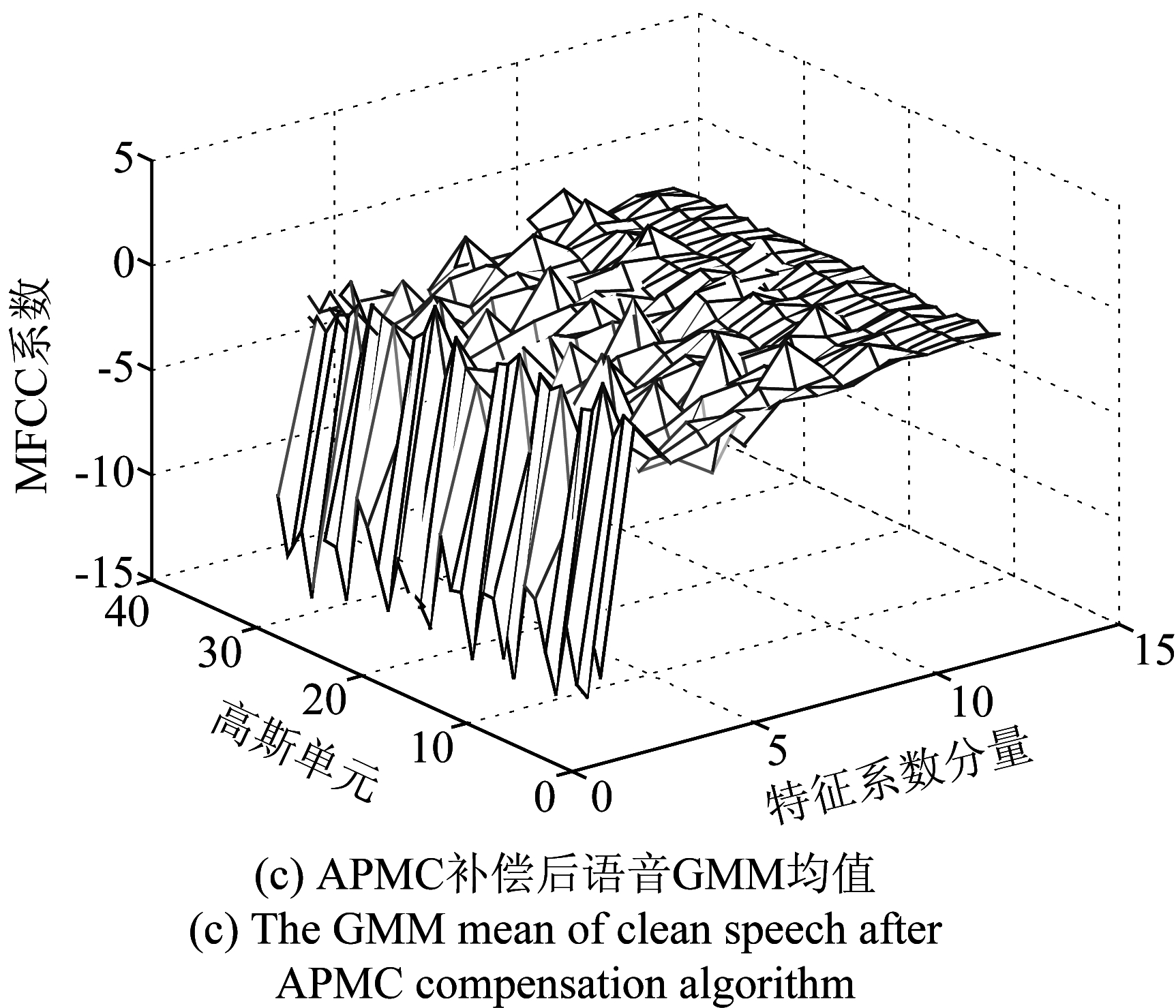
图4 Babble噪声下语音GMM均值分布
Fig.4 The GMM mean distribution of speech in Babble noise
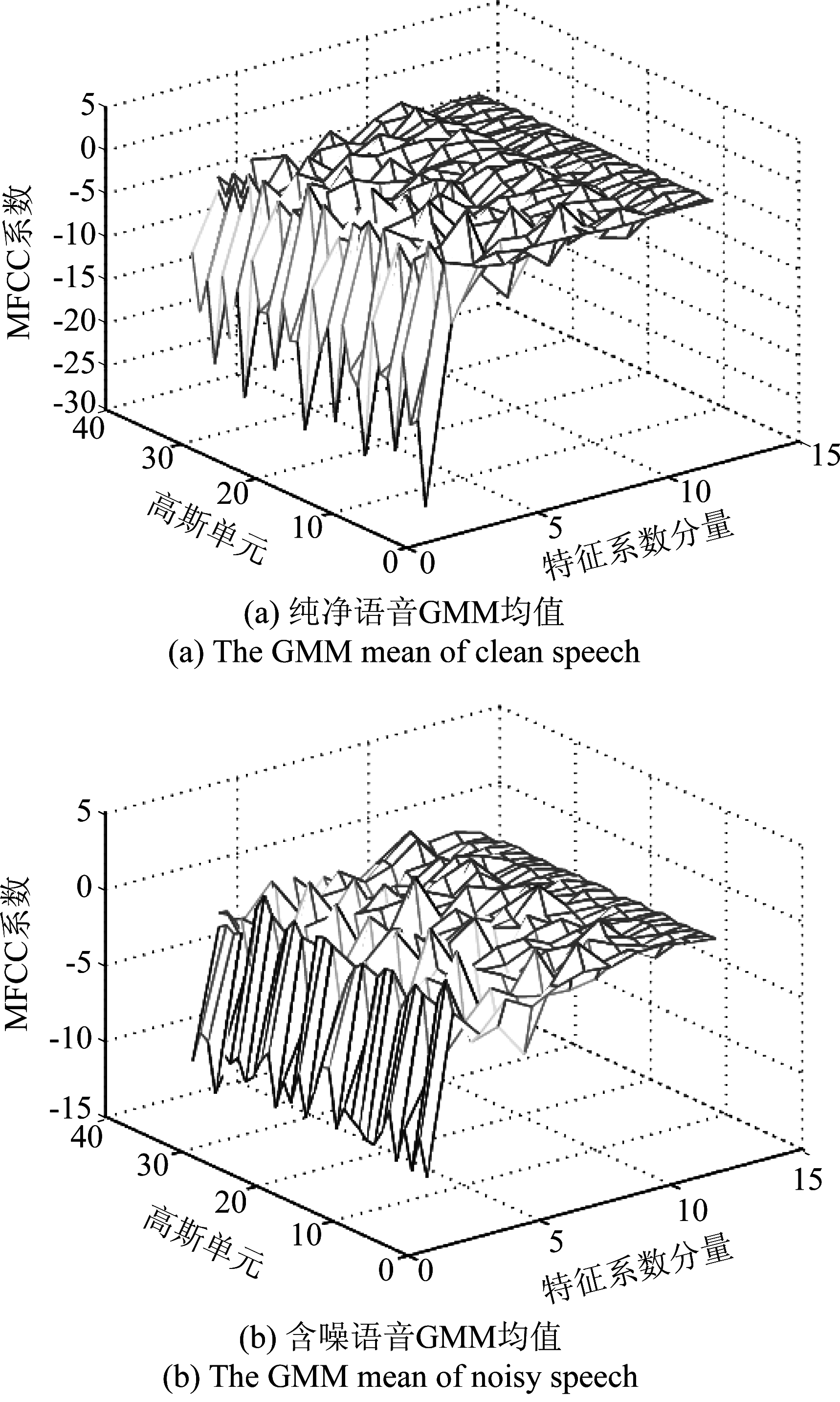
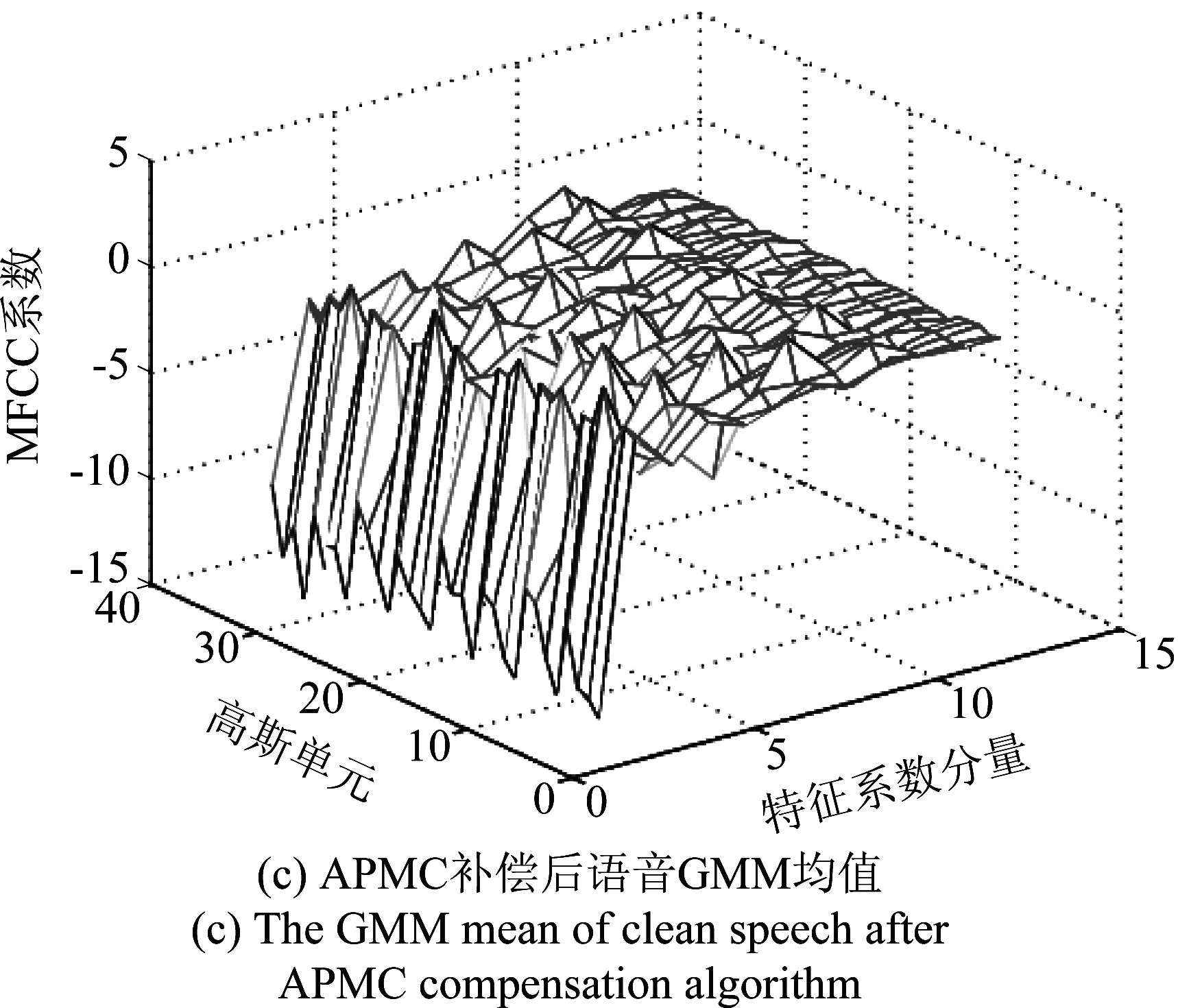
图5 Mixed噪声下不同状态语音GMM均值分布
Fig.5 The GMM mean distribution of speech in Mixed noise
通过对GMM均值的补偿可以看出,补偿前未调整的参数与含噪语音均值参数差距较大,通过自适应的并行模型组合算法补偿后,两者之间的距离差距有明显的降低,也就是相较于图4(a),图4(c)的均值分布更加接近图4(b)的均值分布,图5的均值分布亦是如此。这说明补偿后的纯净语音能够更加接近含噪语音的GMM均值分布,从而可以减少噪声污染所带来的误差问题,提供更好的识别性能。
本文采取的加噪方法是根据信噪比的大小,通过噪声能量与信号能量的比值来确定比例因子调整噪声信号的幅值,进而将噪声与语音信号加性混合作为含噪语音。如图6所示,上部分显示的是一段纯净语音的时间波形图,下半部分是同一语音混入信噪比SNR=0 dB的Mixed噪声后的信号波形图。
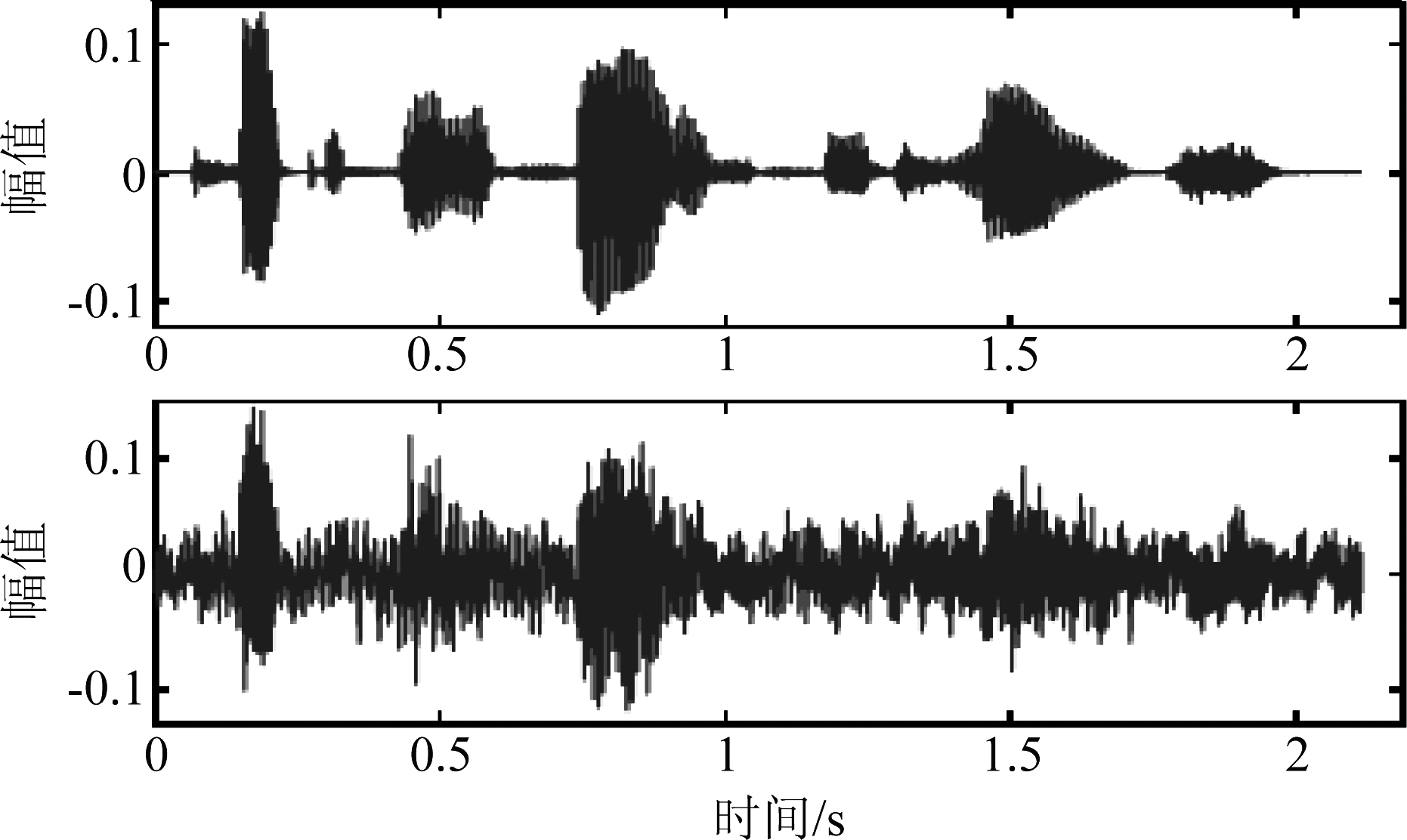
图6 纯净语音和含噪语音
Fig.6 Clean speech and noisy speech
5.2 噪声环境下的说话人身份识别
本实验数据来自TIMIT语音库,选取其中50人的发音数据进行文本无关说话人识别实验。语音采样频率为16 kHz,其中男性和女性各25人,每人10段语音数据,每段语音长度约为3~5 s,用每个说话人发音数据中的5段语音作为训练数据,另外5段语音单独在不同信噪比下混合噪声后作为测试数据,共250组测试样本。噪声语音数据来自NoiseX-92数据库,选用了其中生活中常出现的几种噪声,包括工厂噪声Factory噪声、嘈杂话语噪声Babble噪声、咖啡厅噪声Cafe噪声和混合Mixed噪声。噪声混合信噪比SNR分别取-5 dB、0 dB、5 dB、10 dB、15 dB、20 dB进行实验。实验中设定GMM的混合度为32,语音分帧长度为20 ms,帧移为帧长的一半。特征补偿的增益因子初始值G设为0.5。当无噪声或噪声较小时,为了防止补偿造成的失配问题,算法会根据噪声能量的阈值判断自动调整G的值为1,G=1意味着不再进行特征补偿。
为了突出本算法的有效性,在同样条件下,分别选取较为经典的12维静态MFCC特征和近几年提出的抗噪性能较好基于Gammatone滤波器组[13]的26维GFCC[14]特征进行对比实验,并且将基于ivector+PLDA系统的39维差分MFCC和26维GFCC特征的识别正确率作为基线对比数据。通过与结合APMC算法的两种特征进行实验对比,得出了不同噪声环境下算法识别率的对比结果。
其中ivector+DMFCC和ivector+GFCC分别表示在ivector+PLDA架构下采用差分MFCC特征和GFCC特征算法的实验结果,MFCC、GFCC分别代表在GMM-UBM框架下使用两种特征的实验结果,MFCC+APMC和GFCC+APMC则分别表示结合了APMC补偿算法的实验结果。
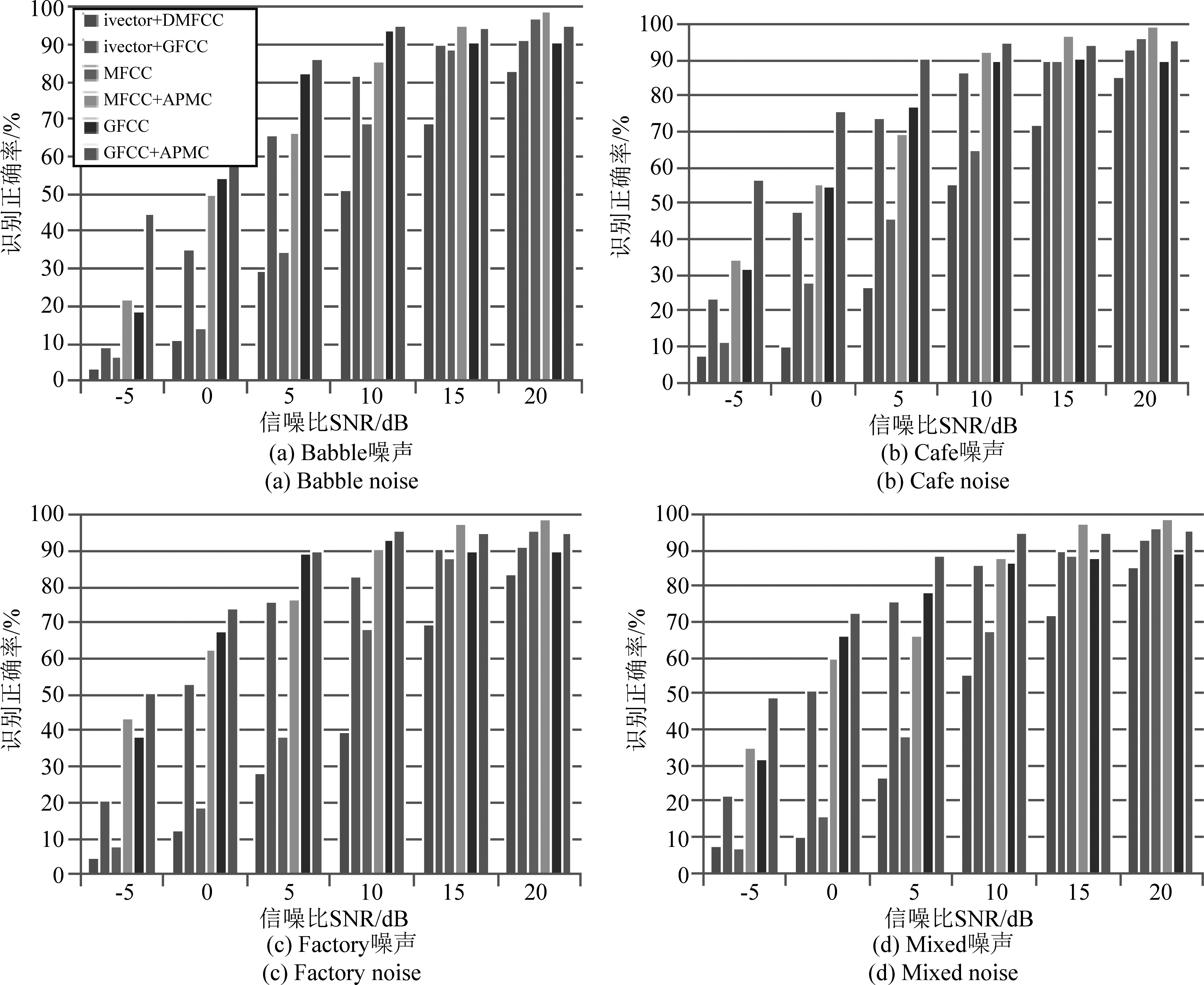
图7 不同加性噪声环境下的识别率
Fig.7 Recognition accuracy in various types of additive noise
如图7的实验结果表明,在信噪比较大,也就是噪声污染较小时,所有算法都能给出较好的识别结果,在信噪比较小的情况下,MFCC和差分MFCC特征都对噪声较为敏感,识别性能会随着信噪比的降低而迅速下降, GFCC特征的鲁棒性较MFCC有一定改善,但在信噪比较低时,识别效果仍然不理想。在结合了自适应特征补偿APMC算法后,这两种特征说话人身份识别系统在抗噪能力上较未补偿的MFCC和GFCC特征有较为明显的改善,尤其是在信噪比较低时,该算法的优势就比较明显,与ivector+PLDA算法的基线系统相比,对噪声的鲁棒性同样有较大的提升。并且APMC算法在各种噪声和不同强度下都展现出了较好的鲁棒性和稳定性,证明了该算法在抗噪方面的有效性。
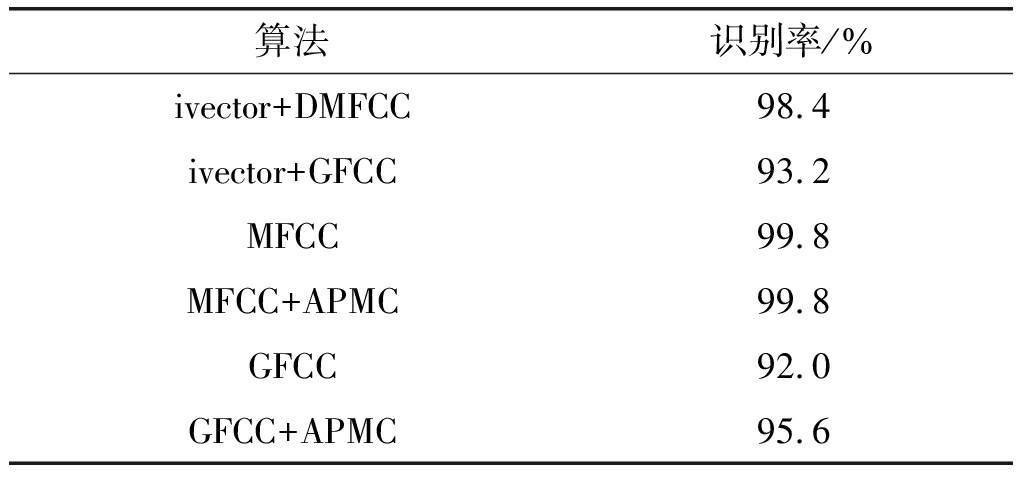
表1 无噪声环境下不同算法的识别正确率
Tab.1 Recognition accuracy of different algorithms in noise-free environment
算法识别率/%ivector+DMFCC98.4ivector+GFCC93.2MFCC99.8MFCC+APMC99.8GFCC92.0GFCC+APMC95.6
表1给出了几种算法在未添加噪声的纯净环境下的平均识别率,从结果来看,几种算法的整体识别率都达到了较高的水平,尤其是在UBM下结合MFCC特征,几乎达到了全部识别正确的识别率。本文算法为了防止低噪或无噪环境下的由于补偿所导致的失配现象,特在噪声估计时根据阈值对补偿因子进行一定的调整,所以识别率并没有因为补偿的缘故而下降,算法的有效性在无噪声环境下也得到了充分的体现。
6 结论
现实环境中背景噪声对语音信号的影响是制约语音识别相关系统发展的一大难题。本文深入研究了针对噪声环境下的鲁棒性语音身份识别方法,提出了基于高斯混合模型下的自适应并行模型组合特征补偿算法。该算法通过利用含噪测试语音估计得到噪声参数,将该参数结合到原始GMM训练模型参数中,既降低了实际测试环境与训练环境之间的失配现象,同时又提高了模型的抗噪性和自适应能力,使整个语音身份识别系统在噪声环境下具有较好的识别率和鲁棒性。
[1] 胡郁. 语音识别中基于模型补偿的噪声鲁棒性问题研究[D]. 合肥:中国科学技术大学, 2009.
Hu Y. A Study on Noisy Robust Problems in Automatic Speech Recognition by Using Model Compensation[D]. Hefei: University of Science and Technology of China,2009. (in Chinese)
[2] Zhong Y, Xie W, Xiao D, et al. Speech Recognition Algorithm in Complex Noisy Environments Based on Multi-Space Compensation[J]. International Journal of Smart Home, 2016, 10(9):197-206.
[3] Veisi H, Sameti H. The integration of principal component analysis and cepstral mean subtraction in parallel model combination for robust speech recognition[J]. Digital Signal Processing, 2011, 21(1):36-53.
[4] Kim W, Hansen J H L. Advanced parallel combined Gaussian mixture model based feature compensation integrated with iterative channel estimation[J]. Speech Communication, 2015, 73: 81-93.
[5] 李海静. 语音识别系统中的VTS特征补偿算法优化[D]. 南京:东南大学, 2016.
Li H J. Optimization on VTS Feature Compensation for Speech Recognition[D]. Nanjing: Southeast University, 2016. (in Chinese)
[6] Arias-Vergara T, Vasquez-Correa J C, Orozco-Arroyave J R, et al. Parkinson’s Disease Progression Assessment from Speech Using GMM-UBM[C]∥INTERSPEECH, International Speech and Communication Association, Baixas, France, 2016:1933-1937.
[7] Zhou L, Li H, Chen Y, et al. VTS feature compensation based on two-layer GMM structure for robust speech recognition[C]∥International Conference on Wireless Communications & Signal Processing. IEEE, 2016:1-5.
[8] 吕勇, 吴镇扬. 基于隐马尔可夫模型与并行模型组合的特征补偿算法[J]. 东南大学学报:自然科学版, 2009, 39(5):889- 893.
Lu Y, Wu Z Y. Feature compensation algorithm based on hidden Markov model and parallel model combination[J]. Journal of Southeast University: Natural Science, 2009, 39(5):889- 893. (in Chinese)
[9] 魏艳, 张雪英. 噪声条件下的语音特征PLP参数的提取[J]. 太原理工大学学报, 2009, 40(3):222-224.
Wei Y, Zhang X Y. A PLP Speech Feature Extraction Method in Noisy Environmen[J]. Journal of Taiyuan University of Technology, 2009, 40(3):222-224. (in Chinese)
[10] Hu X, Zhang H, Zhan L, et al. Isolated Word Speech Recognition System Based On FPGA[J]. Journal of Computers, 2013, 8(12):270-273.
[11] Khe Chai SIM. Approximated parallel model combination for efficient noise-robust speech recognition[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2013:7383-7387.
[12] McClanahan R, De Leon P L. Reducing computation in an i-vector speaker recognition system using a tree-structured universal background model[J]. Speech Communication, 2015, 66: 36- 46.
[13] 赵红, 李双田. Gammatone滤波器修正的多级线性预测去混响[J]. 信号处理, 2014,30(9):1019-1024.
Zhao H,Li S T. Dereverberation Using Multiple-step Linear Prediction Modified with Gammatone Filter Bank[J]. Journal of Signal Processing, 2014,30(9):1019-1024. (in Chinese)
[14] Shi X, Yang H, Zhou P. Robust speaker recognition based on improved GFCC[C]∥IEEE International Conference on Computer and Communications. IEEE, 2017:1927-1931.

