1 引言
通信信号的调制样式识别是频谱管理、智能调制解调、信号确认、无线电侦听、电子对抗和威胁分析等领域[1]的关键技术。国内外大量学者对此做了深入研究,传统的调制样式识别方法包括特征参数提取和分类器两部分。文献[1- 8]通过提取信号包络统计特征、时域瞬时特征、谱特征以及高阶累积量特征等作为特征参数,分类器采用基于决策树算法,完成了多种调制信号经过高斯或者多径衰落信道的调制识别。文献[9]提出一种利用局部密度和距离特征对MFSK信号调制样式识别的方法,识别性能较好。但是这些算法的缺点是识别性能受判决门限影响,尤其对于特征参数区分度较小的信号,门限值的微小偏差对算法识别性能影响非常大。为了解决决策树分类识别方法受判决门限影响问题,文献[10]提取高阶累积量、功率谱峰值、能量密度、瞬时频率包络系数作为特征参数,利用支持矢量机作为分类器完成8种信号的调制样式识别。文献[11]提取信号的11种特征参数,并采用高斯过程方法进行拟合和识别,实现了对11种模拟和数字调制信号的识别。文献[12]提出一种基于记忆因子的CPM信号的最大似然调制识别新方法,通过计算映射符号后验概率构造记忆因子,进一步结合CPM分解和EM算法,推导了CPM信号似然函数,在低信噪比下完成8种CPM信号的识别。
深度学习(Deep Learning)模型从底层级特征提取抽象不变的高层属性特征,实现复杂的非线性函数逼近,比浅层模型泛化能力强、刻画数据本质信息更丰富。鉴于深度学习模型优良的特征提取和学习能力,近年来一些研究人员将深度学习方法应用到数字调制样式识别中。 Zhao Z J等采用受限玻尔兹曼机模型和信号两个高阶累积量特征参数,完成了6种数字调制样式识别[13]。赵雄文等利用高阶累积量和循环谱构造三种信号特征参数,BP神经网络作为分类器,实现了9种信号的调制样式识别[14]。Khan F N等对信号进行变换得到其异步时延图,利用深度神经网络(Deep Neural Network,DNN)提取异步时延图特征,完成了信号调制样式识别和码元估计[15]。Khan F N对接收信号进行变换得到其幅度分布直方图,利用深度自编码(Deep AutoEncoder,DAE)神经网络完成幅度分布直方图的特征提取和信号调制样式识别[16]。Byeoungdo Kim等将MPSK和MQAM信号的21种统计特征参数输入DNN网络,完成了6种信号的调制样式识别[17]。Gihan J提取信号谱相关特征,利用深度信念神经网络(Deep Belief Network,DBN)处理谱相关特征实现了5种数字信号的调制样式识别[18]。以上这些算法虽然取得了较好的识别效果,但是针对较为复杂MAPSK、MQAM等信号没有相应的深度学习算法实现其调制样式识别,同时已有的基于深度学习实现调制样式识别算法需要较为复杂的预处理工作,或者需要较多的特征参数。
为解决上述问题,本文利用稀疏自编码器(Sparse Auto-Encoder,SAE)网络和Softmax分类器,提出一种基于特征参数和SAE的BPSK、QPSK、8PSK、16QAM、32QAM、16APSK和32APSK调制样式识别算法(简记为FSAE算法)。首先给出复杂MAPSK信号的高阶矩理论推导,然后采用两个高阶累积量特征参数的格雷编码值作为SAE网络的输入样本,利用SAE级联Softmax分类器构造调制样式识别系统。为了减小网络训练时间,本文对原训练算法增加整体优化过程;通过逐层训练和整体优化,缓解多层神经网络在训练过程中容易陷入局部最优的问题。仿真结果表明:相比于其他调制样式识别算法,本文算法在低信噪比条件下识别率高,识别相同种类调制样式所需特征参数少,同时对于较复杂的幅相信号MAPSK和MQAM信号具有较好的识别性能。
2 信号高阶累积量特征参数
2.1 高阶矩和高阶累积量
对于连续平稳复随机过程{X(t)},其p阶混合矩表示为
Mpq=E[X(t)p-qX*(t)q]
(1)
其中,X*(t)为X(t)的复数共轭,q为其取共轭的序列个数。其k阶累积量定义为:
Ckx(t1,t2,...,tk-1)=Cum{X(t),X(t+τ1),...,X(t+τk-1)}
(2)
文献[2]给出了具有零均值的平稳复随机过程X(t)的各阶累积量与混合矩的关系式。
2.2 调制信号模型
假设在接收端对接收到信号进行下变频后的复基带信号为:
(3)
其中,N为发送端码元的序列长度,ak为码元序列,p(t)为基带码元的波形,Ts为码元周期,A为信号能量,本文假设初始相位θc=0。u(t)为零均值的复高斯白噪声,与发送信号s(t)相互独立。
MPSK信号的ak∈{ej2π(m-1)/M,m=1,2,...,M},其中M为进制数,本文M的取值分别为2,4和8。
MQAM信号的![]() φk=arctan(qk/pk)。本文M分别为16和32。
φk=arctan(qk/pk)。本文M分别为16和32。
16APSK和32APSK信号模型比较复杂,信号的每个点都有自己的半径和相位,第k个圆周上第i个基带信号表示为:
(4)
其中,A为信号能量,ik为星座图中第k个圆周的第i个,nk和Rk分别为第k个圆上信号点个数和圆周半径,θk为第k个圆上信号点的初始相位,本文假设信号的初始相位为零。信号模型为:
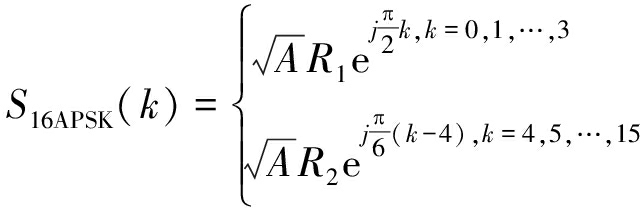
(5)
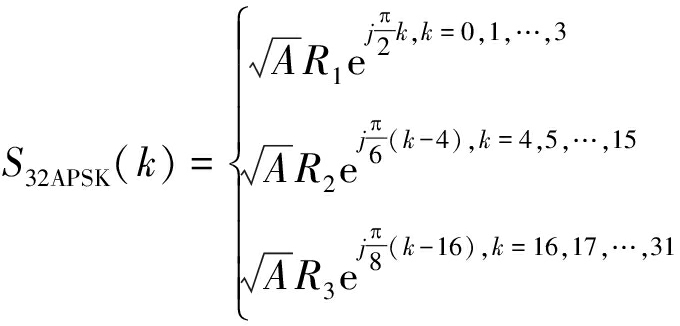
(6)
16APSK半径分别为R1=1.00,R2=2.70,32APSK半径分别为R1=1.00,R2=2.70,R3=5.71。
2.3 特征参数选取
对于任何零均值高斯随机过程,理论上其高阶(高于二阶)累积量恒为零[3]。利用文献[3]中公式(5)~(12)可计算得到的MPSK信号(M=2,4,8)和MQAM(M=16,32)信号各阶累积量理论值如表1所示。
本文对MAPSK信号的累积量详细推导如下:对16APSK信号,根据式(1)和式(5)可得:
Mmn=E[Sm-n(k)(S*(k))n]=
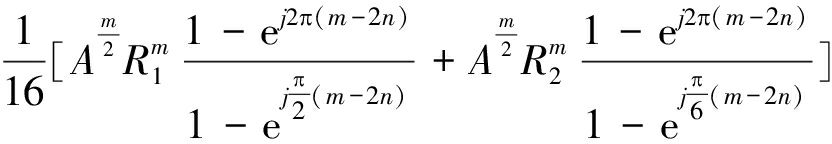
(7)
对于32APSK信号,根据式(1)和式(6)可得:
Mmn=E[Sm-n(k)(S*(k))n]=
(8)
将16APSK和32APSK计算得到的高阶矩分别代入文献[2]给出的累积量计算公式中,可以计算得到这两种信号各阶累积量理论值如表1所示。
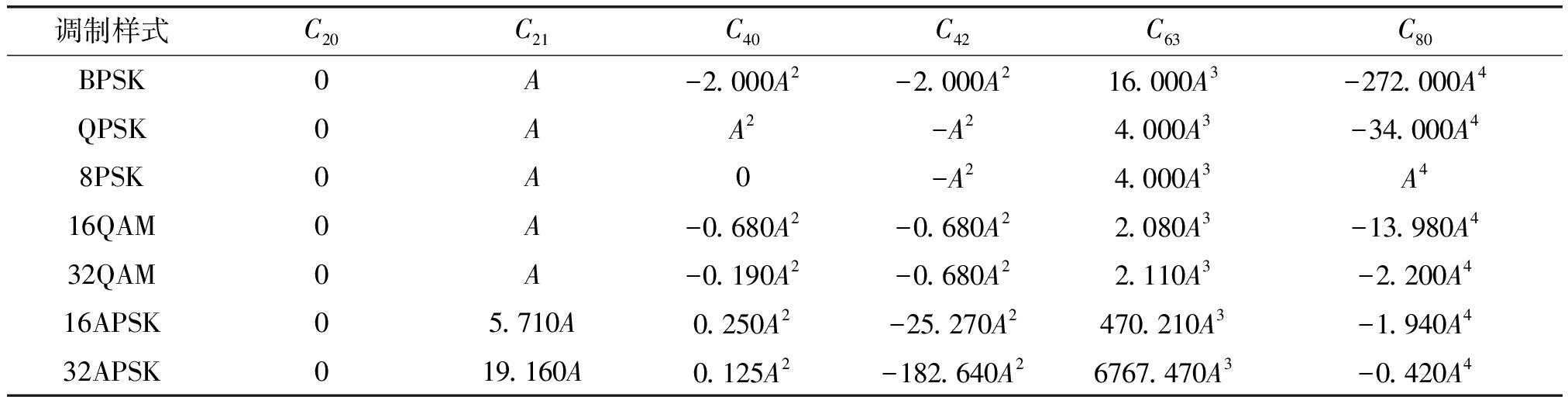
由表1可以看出:本文待识别的7种信号的八阶累积量值都不同,所以利用八阶和四阶累积量构造高阶累积量特征参数F1=|C80|/|C42|2,特征参数F1的理论值如表2所示。
从表2可以看出: 8PSK,16APSK和32APSK这3种信号的特征参数F1理论值区分度较小。为了有效识别这3种信号,本文给出高阶累积量特征参数F2=|C63|/|C21|3,计算得到特征参数F2理论值如表3所示。
表1 7种信号各阶累积量理论值
Tab.1 Theoretical values of each order cumulant of seven kinds of signals
调制样式C20C21C40C42C63C80BPSK0A-2.000A2-2.000A216.000A3-272.000A4QPSK0AA2-A24.000A3-34.000A48PSK0A0-A24.000A3A416QAM0A-0.680A2-0.680A22.080A3-13.980A432QAM0A-0.190A2-0.680A22.110A3-2.200A416APSK05.710A0.250A2-25.270A2470.210A3-1.940A432APSK019.160A0.125A2-182.640A26767.470A3-0.420A4
表2 高阶累积量特征参数F1理论值
Tab.2 Theoretical values of character parameters F1of high-order cumulant

调制样式BPSKQPSK8PSK16QAM32QAM16APSK32APSKF16834130.234.760.000.00
表3 高阶累积量特征参数F2理论值
Tab.3 Theoretical values of character parameters F2of high-order cumulant

调制样式BPSKQPSK8PSK16QAM32QAM16APSK32APSKF216442.082.112.530.96
3 基于稀疏自编码器的调制样式识别算法
3.1 稀疏自编码模型
针对应用背景和神经网络基本理论[20],本文采用稀疏自编码器(SAE)提取信号特征。SAE是由自编码器(Auto-Encoder,AE)进行改进得到。AE是一个三层神经网络[21],包括一个编码器和一个解码器。输出输入关系为Zw,b(x)≅x,即使得输出的重构逼近输入数据。通过最小化重构误差对网络进行训练。如果隐藏层的节点个数比输入层节点个数少,AE通过学习得到输入数据的压缩表示,即反映输入数据的特征信息,通过数据特征能够在解码层重构输入数据。自编码器的平均重构误差函数为:
(9)
其中,W表示自编码器权重矢量,b是节点偏置矢量,Nm是训练集样本的数目,Zw,b(x(i))表示第i个样本的重构输出数据,x(i)表示第i个样本。通常为了防止出现过拟合问题,自编码器增加了权重惩罚项Jweight(W)如式(10)所示:
(10)
其中,λ1是权重衰减系数,W1和W2分别表示输入层到隐藏层、隐藏层到输出层的权值矢量。为了用尽可能少的节点来表示输入数据,通过对隐藏层节点加入稀疏约束构造稀疏自编码器[22],即只有当输出接近1时隐藏层节点才被激活,其他情况下被抑制。稀疏自编码器在损失函数上增加稀疏惩罚项如式(11)所示。
(11)
其中![]() 表示第i个隐藏层节点的平均激活概率,ai(x( j))表示第i个隐藏层节点的输出概率,L是隐藏层的节点数目,ρ为稀疏系数。SAE的总体损失函数如式(12)所示, μ为稀疏惩罚项权重系数。
表示第i个隐藏层节点的平均激活概率,ai(x( j))表示第i个隐藏层节点的输出概率,L是隐藏层的节点数目,ρ为稀疏系数。SAE的总体损失函数如式(12)所示, μ为稀疏惩罚项权重系数。
Jloss(W,b)=Jrec(W,b)+Jweight(W)+μJsparse(ρ)
(12)
在神经网络训练阶段,首先通过最小化式(12)训练得到SAE网络的各层参数,然后利用样本对Softmax分类层做有监督训练,最后通过整体优化再次微调网络参数。在进行信号调制样式识别时对完成训练的网络去掉SAE的重构层,将自编码器的隐藏层连接输出层。 SAE网络完成信号特征提取,Softmax分类层完成信号的调制样式识别。
3.2 基于稀疏自编码器的调制样式识别算法
由于SAE输入是一维矢量,本节选取第2节给出的两个高阶累计量特征参数F1、F2来识别7种调制样式信号,对两种特征参数进行编码后联合构造输入向量如式(13)所示。
x=[F1 F2]
(13)
其中F1和F2分别是第2节特征参数进行格雷编码后的格雷码数值,x为经过合并处理后的序列值,x∈Rn1′,n1为SAE网络的输入信号维度。
编码和解码的非线性映射函数均采用sigmoid函数,即f(x)=1/(1+e-x)。得到的隐藏层编码结果X∈Rn2(n2为隐藏层神经元个数)和利用隐藏层数据进行重构的解码输出Z∈Rn1分别如式(14)和式(15)所示。
(14)
(15)
其中,x为SAE的输入信号矢量,W1、W2、b1、b2分别代表输入层到隐藏层、隐藏层到重构输出层的权重矢量和偏置矢量。根据式(12)所示的网络损失函数,利用梯度法对参数W1、W2、b1、b2进行更新的公式如下:
(16)
(17)
其中,W和b分别表示SAE的权重矢量和偏置矢量, Z,x分别为SAE的重构输出数据和原始输入数据,α为迭代步长系数,也叫学习率。通过训练得到稀疏自编码器网络的权重矢量和偏置矢量。
训练完成的SAE网络实现对输入数据的深层特征提取,分类部分采用Softmax回归模型进行分类识别。对g类m个样本构成回归模型训练集{(v(1),y(1)),(v(2),y(2)),…,(v(m),y(m))},假设模型参数为θ,在Softmax回归模型中将测试目标v归为类别k的概率为

(18)
其中![]() 进行归一化处理,保证所有测试目标属于g类的概率之和为1。采用有监督训练算法训练,最小化损失函数如式(19)所示,训练得到最优模型参数θ。
进行归一化处理,保证所有测试目标属于g类的概率之和为1。采用有监督训练算法训练,最小化损失函数如式(19)所示,训练得到最优模型参数θ。
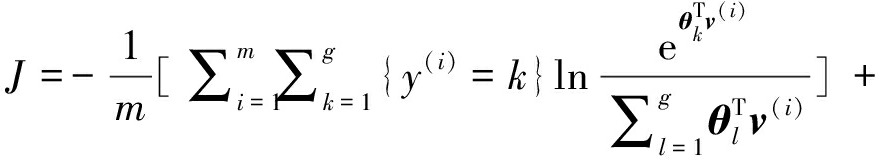
(19)
其中,λ2表示权重衰减项。如果输出结果k等于标签y(i)则{y(i)=k}取值为1,否则为0。n1表示输入Softmax模型的数据维度,采用梯度下降法训练保证结果收敛到全局最优。
最后,采用BP算法进行有监督的整体优化。假设当网络的层数为nL时,输入每一个样本为(X,Y),定义代价函数为:
(20)
其中, h(X)为对应输入X的网络输出标签。对于给定pL个样本集{(X(1),Y(1)),...,(X(pl),Y(pL))},定义总体代价函数为:
(21)
在式(21)中,第一项是均方误差项,第二项为防止过拟合的正则化项,W(i,i+1)表示第i层和第i+1层之间的权重矩阵。整体优化的过程就是对整体损失函数进行优化的过程,通过BP算法的正向处理信号,反向处理误差的思想进行实现。经过整体优化后能够避免神经网络训练过程陷入局部最优的问题。由于这一阶段输入数据不变,因此不需要对输入层偏置矢量进行优化。
综上可得本文提出的基于特征参数,利用SAE实现调制样式识别算法(简记为FSAE算法)具体流程如图1所示。网络训练部分采用逐层无监督预训练、分类层有监督训练和整体优化结合。信号识别部分采用训练完毕的SAE网络对输入信号进行处理完成信号调制样式识别。
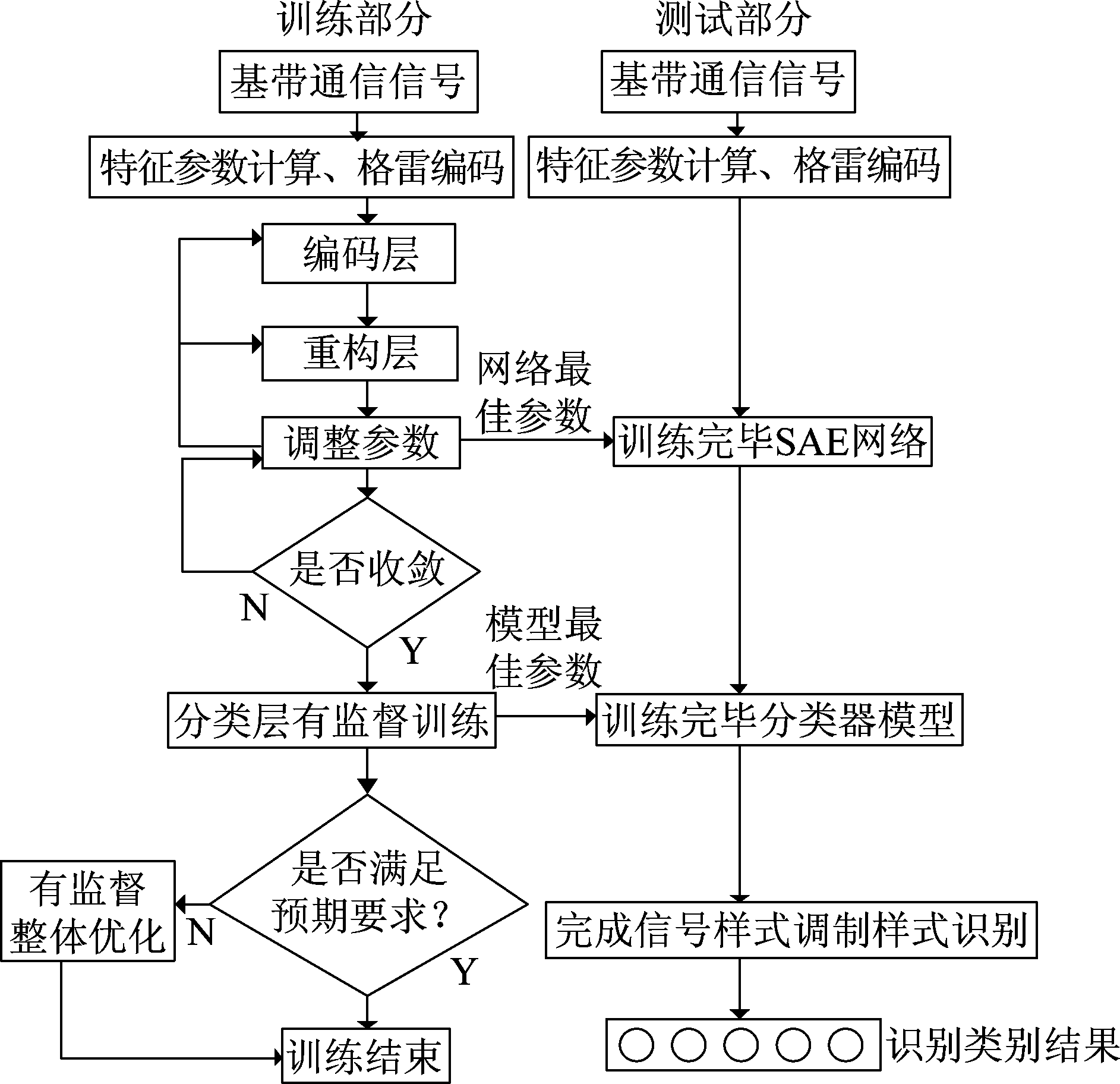
图1 利用稀疏自编码器实现调制样式识别模型图
Fig.1 Model of modulation recognition based on sparse auto-encoder
4 算法仿真与性能分析
为了验证FSAE算法的有效性,利用Matlab软件对算法进行仿真。待识别信号集合包括BPSK、QPSK、8PSK、16QAM、32QAM、16APSK和32APSK。信号参数设置为:载波速率为24 kHz,采样速率为60 kHz,初始相位设置为θc=0,每个码元采样个数为5;16APSK信号半径为R1=1、R2=2.70,32APSK信号半径为R1=1、R2=2.70、R3=5.71。加性噪声为零均值高斯白噪声,仿真信号信噪比从0 dB至20 dB。两个特征参数的格雷码编码位数均为20。
每种信号计算其特征参数F1和F2,进行格雷编码构造训练集和测试集。训练集包括8400个样本,每种信号的每种信噪比数据样本在训练样本集中随机出现。测试集包括4200个样本,按照信号的信噪比进行分组,每组中每种信号在测试集中随机出现。隐藏层节点个数为20,稀疏系数ρ为0.1,权重衰减系数λ1和λ2均为0.03,稀疏惩罚项权重μ为3,学习率α初始设置为0.05。这些参数的设置是在文献[23]基础上通过格点搜索得到。
实验1 特征参数随信噪比变化情况
仿真信噪比为0 dB到20 dB。计算得到7种信号的特征参数F1和F2和随信噪比的变化曲线如图2和图3所示,其中每条曲线是100次仿真结果的平均值。
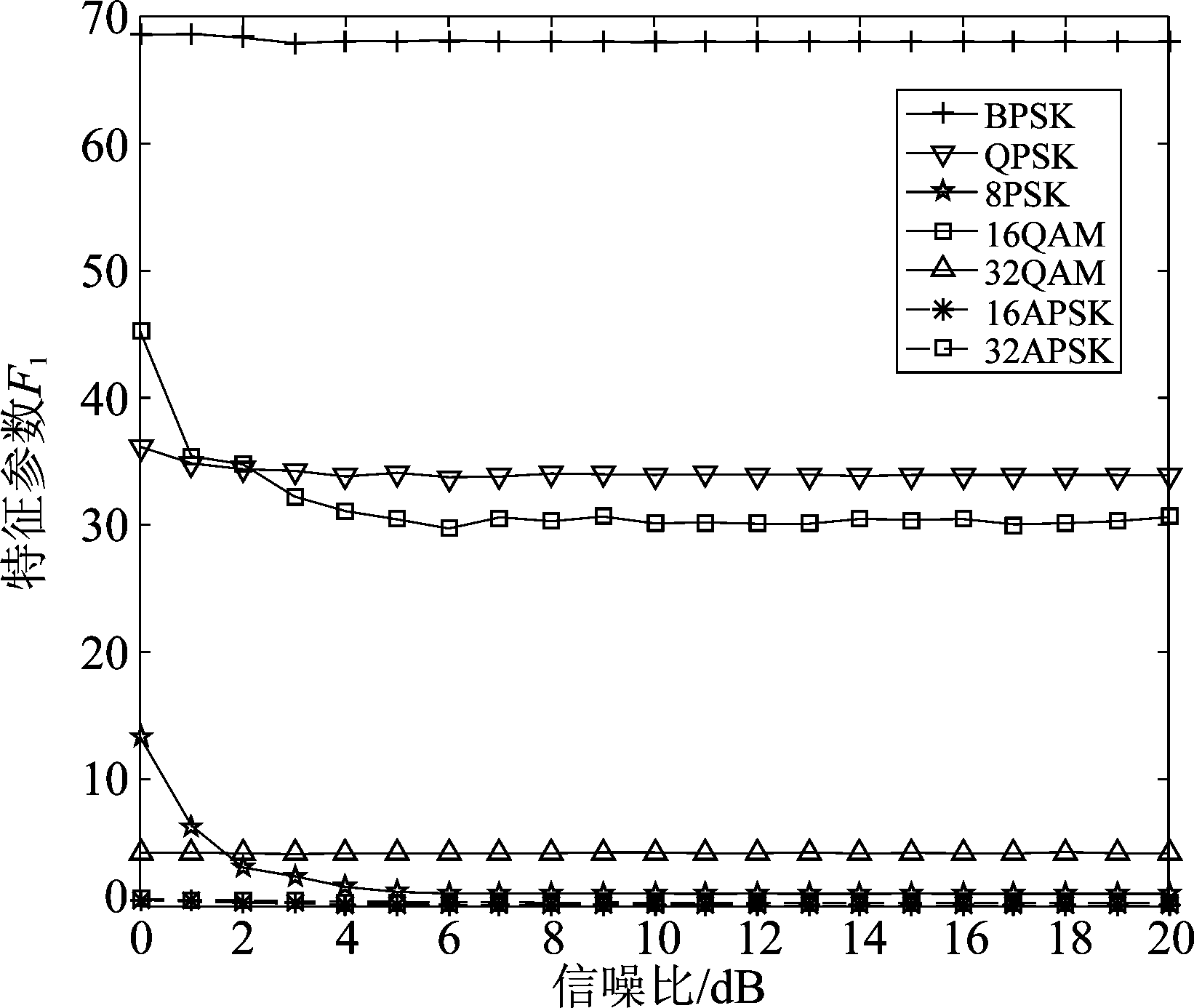
图2 特征参数F1随信噪比的变化曲线
Fig.2 Curve of character parameters F1 with SNR
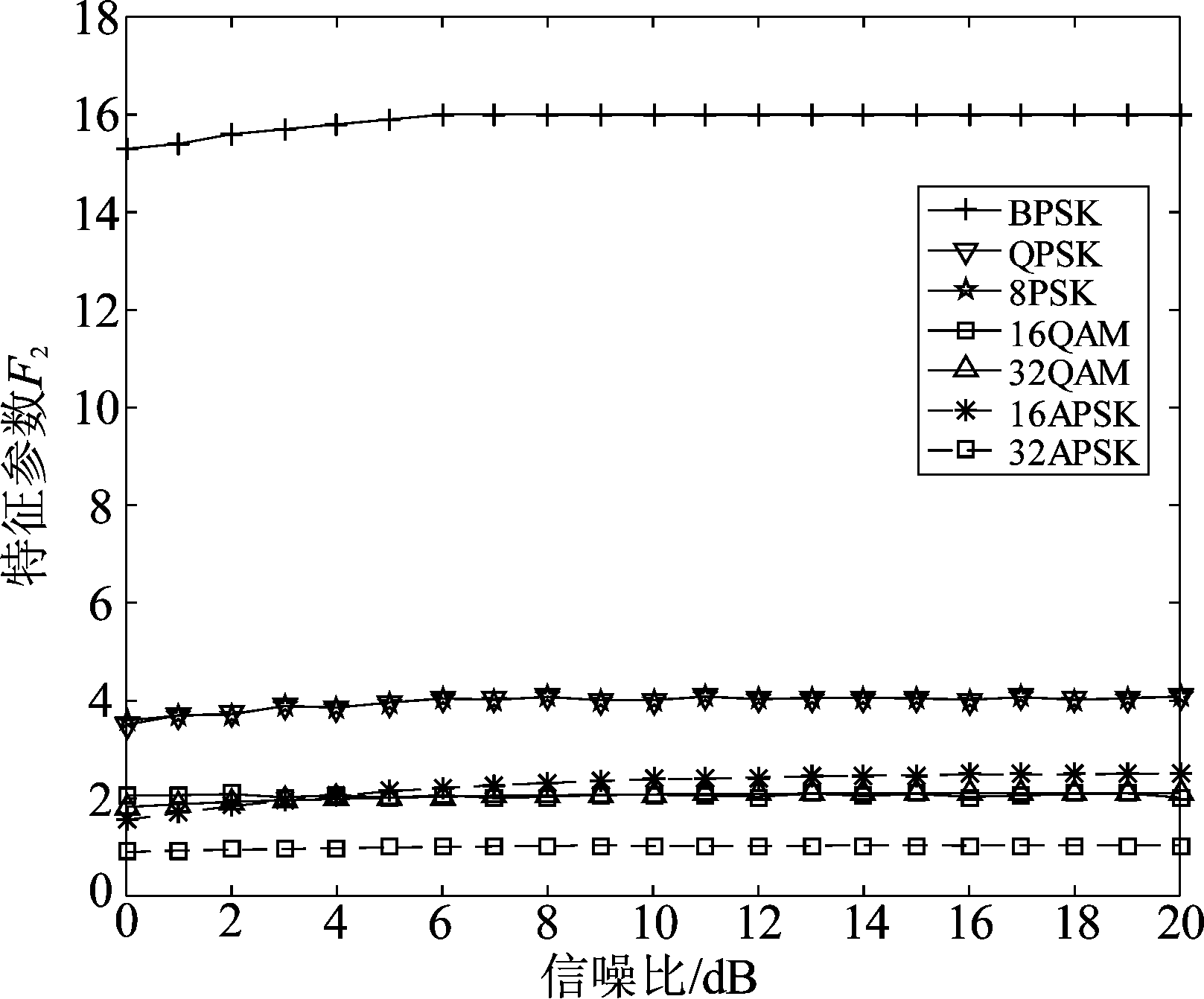
图3 特征参数F2随信噪比的变化曲线
Fig.3 Curve of character parameters F2 with SNR
从图2可以看出:当信噪比为0 dB至5 dB时,由于估计误差和噪声对信号的影响,7种信号的特征参数值F1值偏离理论值较大;当信噪比大于5 dB时,7种信号的特征参数F1值都稳定在理论值,说明特征参数F1的稳定性和抗噪声性能较好,也说明了特征参数F1选取的合理性。
从图3可以看出:当信噪比为0 dB至2 dB时,由于估计误差和噪声的影响,7种信号的特征参数F2值略偏离理论值;当信噪比大于2 dB时,7种信号的特征参数F2值都稳定在理论值,信号8PSK、16APSK和32APSK的特征参数F2区分度大。同时可以看到每条曲线的方差很小,说明特征参数F2抗噪声性能较好,也说明了参数F2的有效性。
实验2 不同编码方式对识别性能影响
为了说明编码方式对算法的识别性能影响,本文分别选取二进制码和格雷码对特征参数进行编码,然后得到不同信噪比下7种信号的平均正确识别率曲线如图4所示。

图4 不同编码方式下7种信号平均正确识别率曲线图
Fig.4 The average correct recognition rate curve of 7 kinds of signals under different coding methods
从图4可以看出,当特征参数选用二进制码编码时,7种信号的平均正确识别率最高只有90%,平均正确识别率为75.3%;当特征参数采用格雷码编码时,在信噪比高于2 dB时7种信号的平均正确识别率高于95%。同一种信号采用格雷码编码时,算法识别率要高于采用二进制编码。基于此下文仿真均选用格雷码进行特征参数编码。
实验3 SAE网络提取特征有效性分析
为了说明采用SAE提取特征有效性,本文选取信噪比分别为0 dB、2 dB、4 dB、6 dB、8 dB和10 dB数据集,分别采用FSAE和经典降维主成分分析算法(Principal Component Analysis,PCA算法)对数据集进行同样维度降维,然后利用重构误差衡量提取特征性能好坏。两种方法分别进行100次实验得到平均重构误差如图5所示。
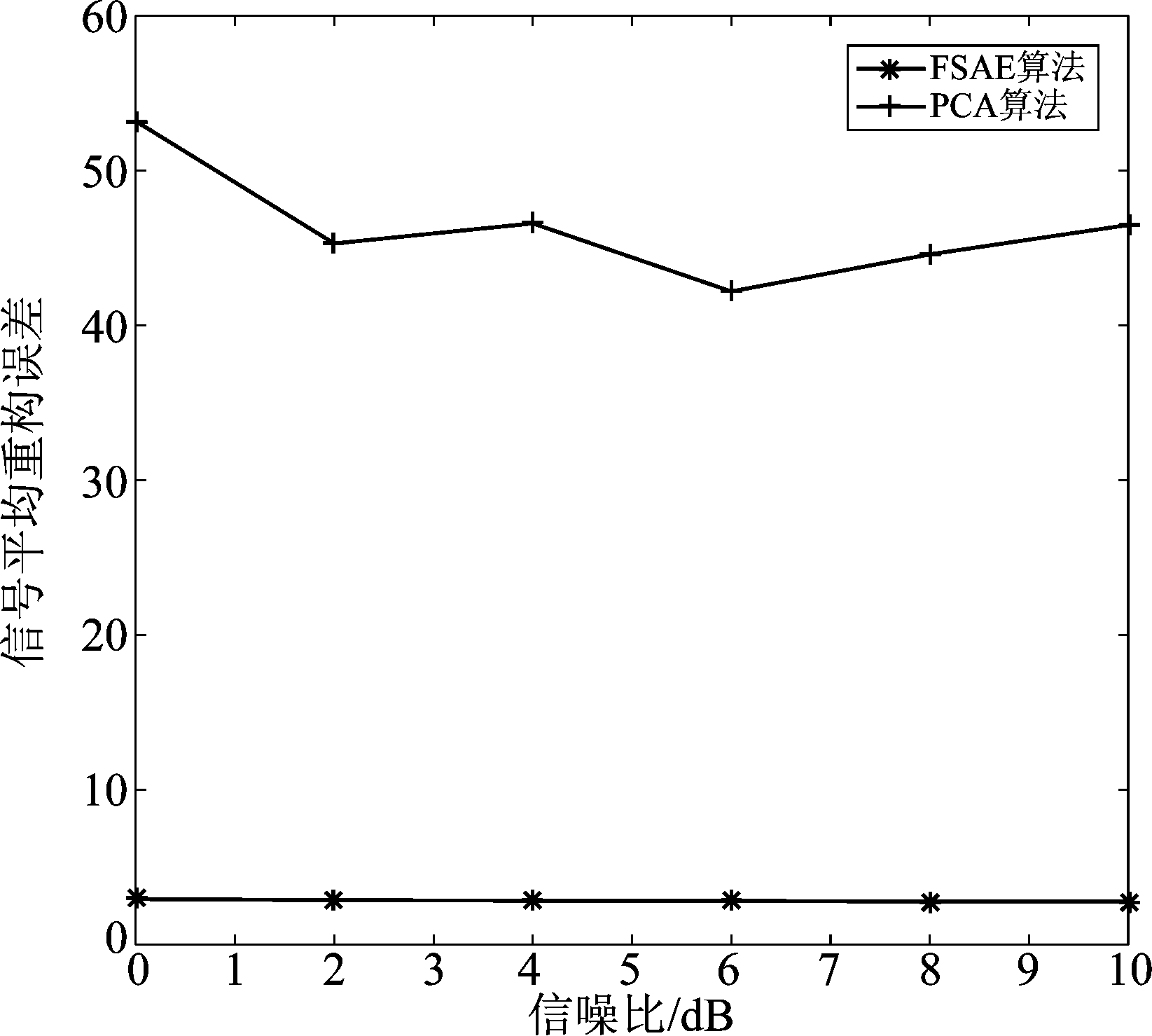
图5 SAE与PCA算法的信号平均重构误差
Fig.5 Signal average reconstruction error of SAE and PCA algorithms
由图5可知:在选取的信号数据集上,SAE的平均重构误差在2.85附近,而PCA算法的平均重构误差在45.6附近。SAE的重构误差要远小于PCA算法,说明对于本文待识别信号数据集,SAE在数据降维后进行数据重构的准确性较高,提取信号有效特征能力较强;这也是本文下面采取SAE进行特征提取主要原因之一。
实验4 神经网络隐藏层单元节点个数选取
SAE网络输入层(第一层)节点个数为特征参数编码后的长度,设置为40,Softmax节点个数为信号的调制样式类别数目,设置为7。重构层的节点个数与输入层相同设置为40。根据文献[23]对自编码器介绍可知,隐藏层节点个数对于提取特征具有重要影响,节点个数太多会导致提取特征过拟合,太少会导致提取特征不完整、不准确。为了分析得到本文SAE网络最佳节点个数,在网络其他参数固定,测试集选取信号信噪比为4 dB情况下,给定不同隐藏层节点个数时,得到FSAE算法平均正确识别率和模型训练时间如表4所示。
表4 隐藏层节点个数与平均正确识别率和模型训练时间关系
Tab.4 The relationship between average correct recognition rate,model training time and the number of hidden layer nodes
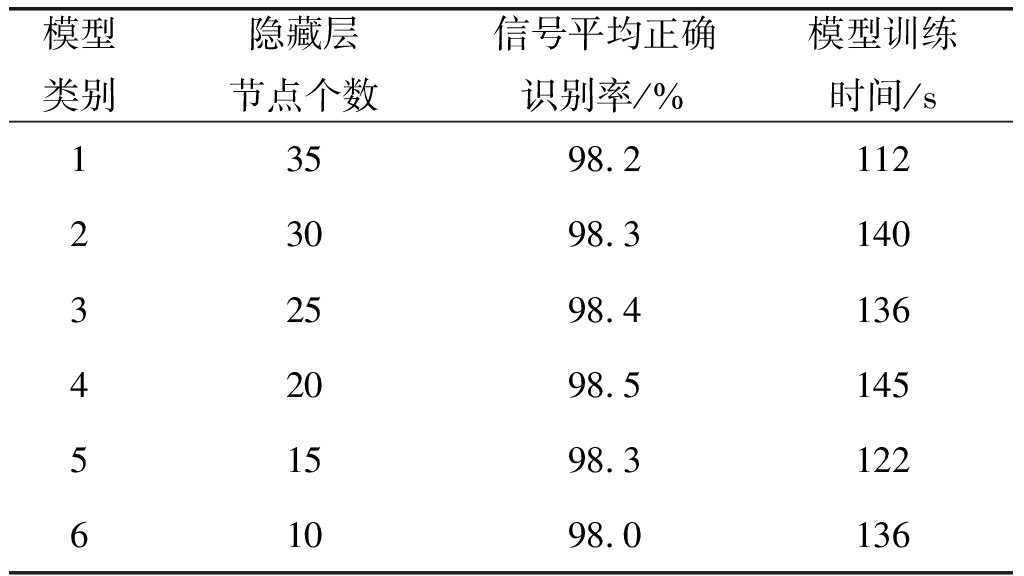
模型类别隐藏层节点个数信号平均正确识别率/%模型训练时间/s13598.211223098.314032598.413642098.514551598.312261098.0136
从表4可以看出:算法平均正确识别率随着节点个数增加呈现先增加后减小的趋势,在隐藏层节点个数取20时,算法的平均正确识别率最大;同时模型训练时间与隐藏层节点个数之间没有较强的关系。综合考虑选取隐藏层节点个数为20。所以,下文仿真中神经网络的每层单元节点个数设置为[40 20 7]。
实验5 网络训练迭代次数设置
网络的训练迭代次数是算法快慢的一个重要参量,本文通过实验验证得到最佳迭代次数。在网络其他参数固定,对网络采用不同的训练迭代次数进行训练,选取信噪比为4 dB的测试集信号进行识别,得到算法的平均正确识别率和模型训练时间如表5所示。
表5 不同训练迭代次数下信号平均正确识别率和模型训练时间
Tab.5 Average correct recognition rate and model training time under different training iterations
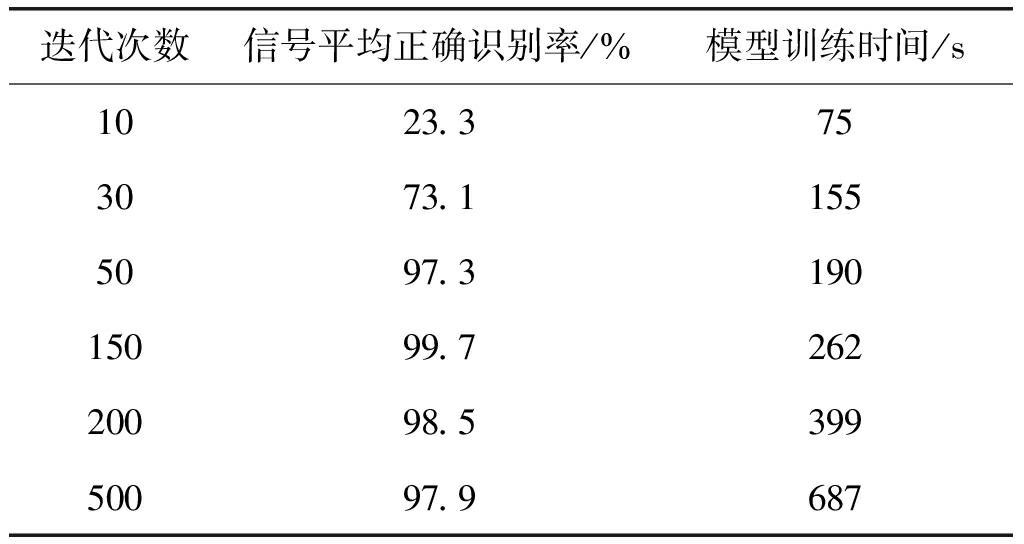
迭代次数信号平均正确识别率/%模型训练时间/s1023.3753073.11555097.319015099.726220098.539950097.9687
由表5可以看到:在迭代次数低于150时,随着训练迭代次数的增加,信号平均正确识别率呈现快速增长,但是当迭代次数大于150以后,信号平均正确识别率降低,而模型训练时间却是随着迭代次数增加而增加。综合考虑信号正确识别率和模型训练时间,下文仿真均选取迭代次数为150。
实验6 信号样本数对算法性能影响
神经网络的输入样本数据量对网络的特征学习有着至关重要影响。网络输入样本数据太少会导致网络无法学习到数据样本隐含信息,网络输入样本数据太多又会导致网络训练时间过长。为了测试本文数据的最佳样本数目,在网络其他参数固定时,训练样本数目中每类信号的个数设置为不同数目构造不同的训练集,以此训练集对网络进行训练,然后采用训练好网络对信噪比为4 dB的样本进行测试,得到不同信号样本数下的算法的平均正确识别率如表6所示。
表6 平均正确识别率和模型训练时间随样本个数变化
Tab.6 The average correct recognition rate and the training time of model vary with the number of samples

样本每类信号个数信号平均正确识别率/%模型训练时间/s10065.36830077.45650081.212170090.6139100099.5178150099.7201200099.8414
由表6可见:当每类样本个数低于1000时,信号平均正确识别率随着样本数目增加而增加,说明此时网络的学习特征随着样本个数的增加变得越来越健壮;当每类样本个数高于1000时,信号的平均正确识别率提升很小,说明此时输入数据个数已经使得网络学习到足够完整特征;而模型训练时间随着样本数目的增加而增加。综合考虑识别性能和模型训练时间,下文仿真中选取训练样本中每类信号的个数为1000。
实验7 调制样式识别算法性能对比分析
本实验分析比较本文的FSAE算法和文献[24]中基于特征参数和HRBM的调制样式识别算法(简记为FHRBM算法)的识别性能。待识别7种信号在不同信噪比下两个高阶累积量特征参数的格雷码编码分别构成FHRBM和FSAE算法的训练样本和测试样本,信噪比在-4 dB至18 dB范围内,得到FSAE算法对单个信号正确识别率如图6所示,FSAE算法和FHRBM算法的平均识别率曲线如图7所示。
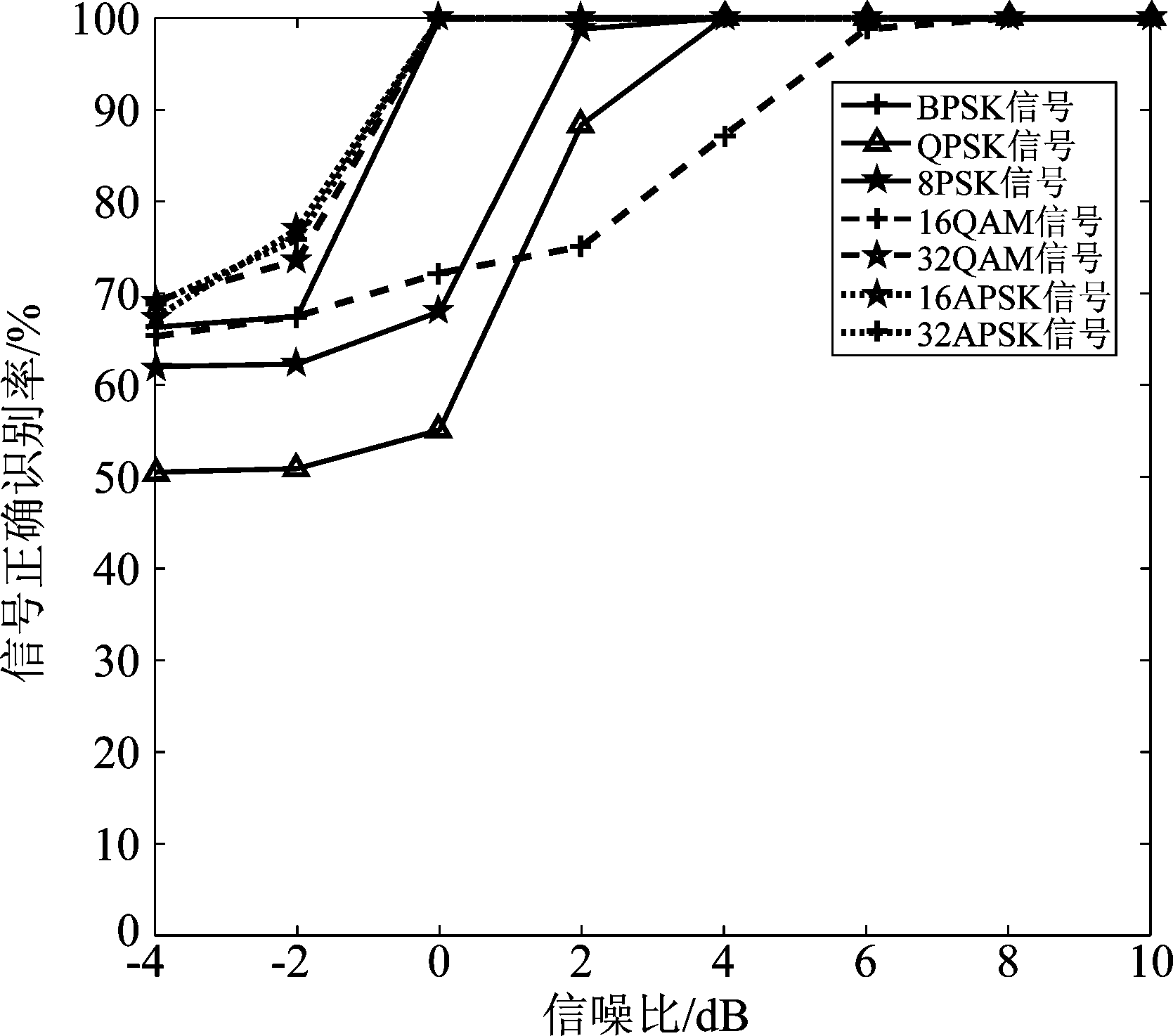
图6 FSAE算法单个信号识别率曲线
Fig.6 FSAE algorithm signal recognition rate curve
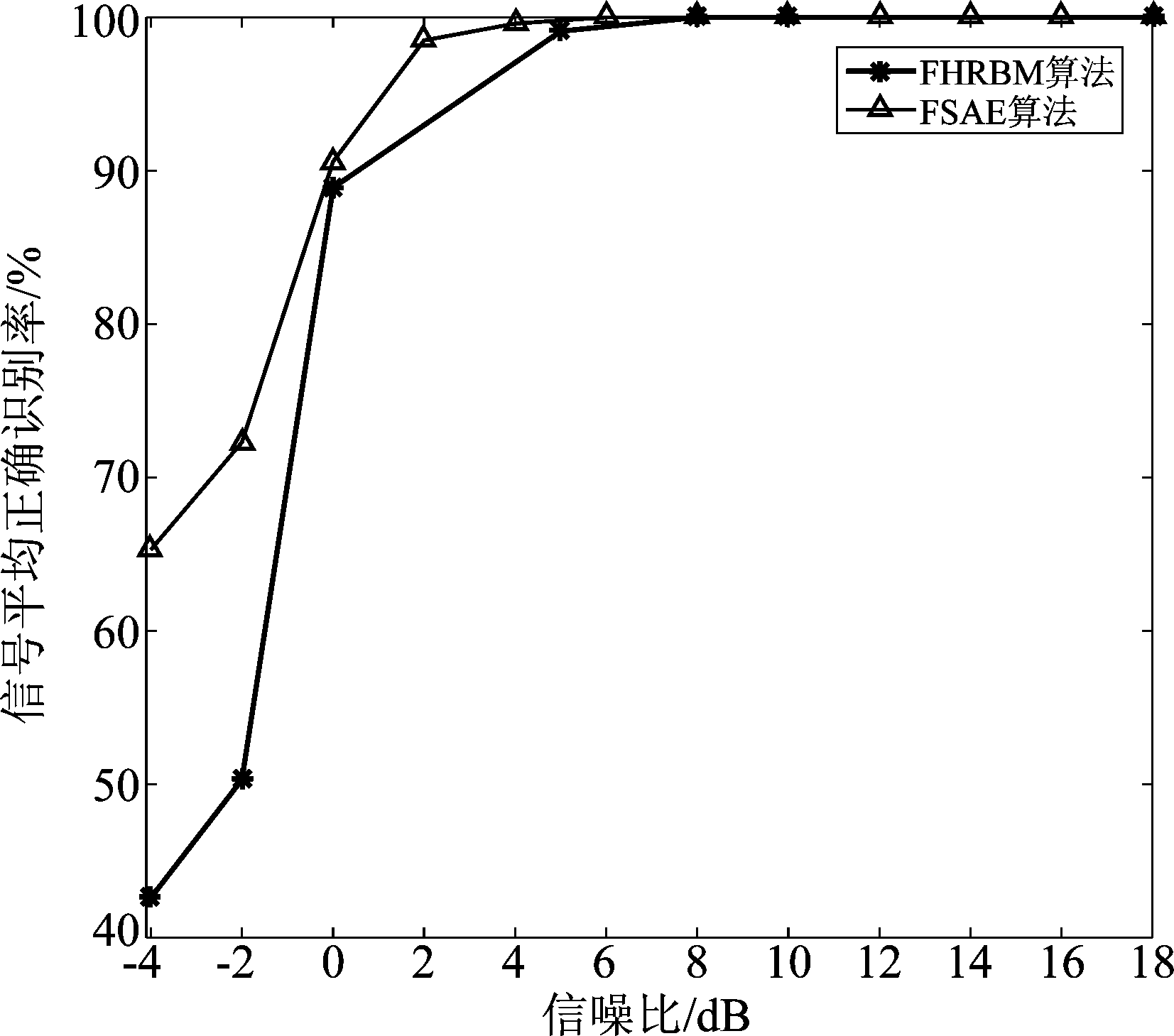
图7 两种调制样式识别算法性能对比曲线
Fig.7 Two algorithm performance comparison curves
从图6可以看出:FSAE算法的单个信号识别率达到90%以上时,BPSK、QPSK、8PSK、16QAM、32QAM、16APSK和32APSK信号所需信噪比分别为0 dB、3 dB、2 dB、8 dB、0 dB、0 dB、0 dB和0 dB;其中16APSK和32APSK信号在信噪比高于0 dB时正确识别率均达到了91%,说明了FSAE算法对于复杂幅相信号的识别能力强。但对QPSK和16QAM信号的识别性能比其他5种信号差。
从图7可以看出:当测试信号信噪比低于8 dB时,FSAE算法的识别性能优于FHRBM算法;信号平均正确识别率随测试信号信噪比增加而增大;FSAE算法在信噪比大于6 dB以后平均正确识别率达到100%,FHRBM算法平均正确识别率达到100%需要信噪比大于8 dB;因为FHRBM算法的训练集采用的是0 dB训练集样本,根据文献[24]实验结果可知,当测试数据集信噪比低于0 dB时,FHRBM算法的识别性能迅速恶化。
5 结论
针对BPSK、QPSK、8PSK、16QAM、32QAM、16APSK和32APSK等7种信号调制样式识别问题,本文提出利用特征参数和稀疏自编码器的调制样式识别算法。对信号两个特征参数进行格雷编码作为SAE的输入样本,网络训练方法采用预训练和整体优化相结合,利用深度神经网络自动完成信号特征提取和调制样式识别,计算机仿真结果验证了算法的有效性。
[1] 裴立业, 江桦. 卫星常用调相信号自动调制识别算法[J]. 太赫兹科学与电子信息学报, 2013, 11(6):964-969.
Pei L Y, Jiang H. Automatic Recognition for the Satellite Phase Modulated Signals[J]. Journal of Terahertz Science & Electronic Information Technology, 2013,11(6):964-969. (in Chinese)
[2] 甘新泰, 程伟, 胡登鹏,等. 数字卫星通信信号调制方式识别方法研究[J]. 空军预警学院学报, 2014,28(2):111-115.
Gan X T, Cheng W, Hu D P, et al. Recognition of Modulation Modes in Digital Satellite Communication[J]. Journal of Air Force Early Warning Academy, 2014,28(2):111-115. (in Chinese)
[3] 赵知劲, 强芳芳, 陈颖. 利用高阶累积量的数字调相信号识别[J]. 杭州电子科技大学学报, 2016, 36(3):1-5.
Zhao Z J, Qiang F F, Chen Y. Modulation Recognition of MPSK Signals Using Higher Order Cumulant[J]. Journal of Hangzhou Dianzi University, 2016, 36(3):1-5. (in Chinese)
[4] 孔豫京, 黄焱, 马金全. Alpha稳定分布噪声背景下衰落信号的调制识别方法[J]. 信号处理, 2015,31(8):975-985.
Kong Y J,Huang Y,Ma J Q. Modulation Recognition Method of Fading Signals under Alpha Stable Distribution Noise Background[J]. Journal of Signal Processing, 2015,31(8):975-985. (in Chinese)
[5] 王辉, 王斌. 多径衰落信道下基于循环累积量的调制分类算法[J]. 信号处理, 2016, 32(10):1194-1201.
Wang H, Wang B. The Identification Classification Algorithm Based on Cyclic Statistics in Multipath Fading Channel[J]. Journal of Signal Processing, 2016, 32(10):1194-1201. (in Chinese)
[6] 党月芳, 徐启建, 张杰,等. 高阶累积量和分形理论在信号调制识别中的应用研究[J]. 信号处理, 2013, 29(6):761-765.
Dang Y F, Xu Q J, Zhang J, et al. Research on Modulation Classification Based on High-order Cumulants and Fractal Theory[J]. Journal of Signal Processing, 2013, 29(6):761-765. (in Chinese)
[7] 元洪波, 王珂. 航空信道下MPSK类信号的调制识别[J]. 信号处理, 2013, 29(2):249-255.
Yuan H B, Wang K. Modulation Identification of MPSK Signals in the Aeronautical Channel[J]. Journal of Signal Processing, 2013, 29(2):249-255. (in Chinese)
[8] 王宁, 彭华. 基于环形统计量和支持矢量机的CPM信号调制识别[J]. 信号处理, 2012, 28(1):47-53.
Wang N, Peng H. Modulation Recognition of CPM Signals based on Circular Statistics and SVM[J]. Signal Processing, 2012,28(1):47-53. (in Chinese)
[9] 沈连腾, 巩克现, 范磊,等. 利用局部密度与距离特征的MFSK识别方法[J]. 信号处理, 2016, 32(12):1478-1488.
Shen L T,Gong K X. Fan L,et al. MFSK Signal Recognition Method based on the Feature of Local Density and Distance[J]. Journal of Signal Processing,2016,32(12):1478-1488. (in Chinese)
[10] 史文娟, 冯全源. 一种改进的基于支持矢量机的OFDM识别算法[J]. 微电子学与计算机, 2014,31(10):98-102.
Shi W J, Feng Q Y. Improved Automatic Modulation Recognition Algorithm for OFDM based on SVM[J]. Microelectronics & Computer, 2014,31(10):98-102. (in Chinese)
[11] 吴明, 宋博, 王锋,等. 基于高斯过程分类的调制识别方法[J]. 计算机仿真, 2015, 32(10):14-18.
Wu M, Song B, Wang F, et al. A Method of Modulation Recognition based on Gaussian Process for Classification[J]. Computer Simulation, 2015, 32(10):14-18. (in Chinese)
[12] 吴斌, 袁亚博, 汪勃. 基于记忆因子的连续相位调制信号最大似然调制识别[J]. 电子与信息学报, 2016, 38(10):2546-2552.
Wu B, Yuan Y B, Wang B. Maximum Likelihood Modulation Recognition for Continuous Phase Modulation Signals Using Memory Factor[J]. Journal of Electronics & Information Technology, 2016, 38(10):2546-2552. (in Chinese)
[13] Zhao Z J, Gu J W. Recognition of Digital Modulation Signals based on Hybrid Three-order Restricted Boltzmann Machine[C]∥IEEE, International Conference on Communication Technology. IEEE, 2015:166-169.
[14] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法[J]. 电子与信息学报, 2016, 38(3):674- 680.
Zhao X W, Guo C X, Li J C. Mixed Recognition Algorithm for Signal Modulation Schemes by High-order Cumulants and Cyclic Spectrum[J]. Journal of Electronics & Information Technology, 2016, 38(3):674- 680. (in Chinese)
[15] Khan F N, Lu C, Lau A P T. Joint Modulation Format/bit-rate Classification and Signal-to-noise Ratio Estimation in Multipath Fading Channels Using Deep Machine Learning[J]. Electronics Letters, 2016, 52(14):1272-1274.
[16] Khan F N, Zhong K, Al-Arashi W H, et al. Modulation Format Identification in Coherent Receivers Using Deep Machine Learning[J]. IEEE Photonics Technology Letters, 2016, 28(17):1-1.
[17] Byeoungdo Kim, Jaekyum Kim, Hyunmin Chae, et al. Deep Neural Network-based Automatic Modulation Classification Technique[C]∥2016 International Conference on Information and Communication Technology Convergence (ICTC), 2016.
[18] Gihan J,Mendis,Jin Wei,Arjuna Madanayake. Deep Learning-based Automated Modulation Classification for Cognitive Radio[C]∥2016 IEEE International Conference on Communication Systems(ICCS), 2016.
[19] O'Shea T J, Corgan J, Clancy T C. Unsupervised Representation Learning of Structured Radio Communication Signals[C]∥International Workshop on Sensing, Processing and Learning for Intelligent Machines. IEEE, 2016:1-5.
[20] Lecun Y, Bengio Y, Hinton G. Deep Learning[J]. Nature, 2015, 521(7553):436- 444.
[21] Vincent P, Larochelle H, Lajoie I, et al. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion[J]. Journal of Machine Learning Research, 2010, 11(12):3371-3408.
[22] Tsinalis O, Matthews P M, Guo Y. Automatic Sleep Stage Scoring Using Time-Frequency Analysis and Stacked Sparse Autoencoders[J]. Annals of Biomedical Engineering, 2016, 44(5):1-11.
[23] 鲁亚平. 面向深度网络的自编码器研究[D]. 苏州:苏州大学, 2016.
Lu Y P. Research on Deep Networks-Oriented Auto-Encoders[D]. Soochow: Soochow University,2016.(in Chinese)
[24] 杨安锋, 赵知劲, 陈颖. 基于混合受限波尔兹曼机的调制样式识别[J]. 杭州电子科技大学学报:自然科学版, 2017, 37(6):18-23.
Yang A F, Zhao Z J, Chen Y. Modulation Type Recognition Based on Hybrid Restricted Boltzmann Machine[J]. Journal of Hangzhou Dianzi University: Natural Sciences, 2017, 37(6):18-23. (in Chinese)


