1 引言
跟踪干扰是指干扰信号能跟踪信号频率跳变的一种干扰方式，按典型实现途径，跟踪干扰可分为波形跟踪干扰、转发跟踪干扰和引导跟踪干扰三种[1]。波形跟踪干扰指干扰机在破译用户跳频图案的基础上，同步施放与跳频通信每一跳信号的时间和频率都一致的干扰信号，干扰效率高。但由于在战场复杂电磁环境下，进行实时网台分选并破译跳频图案的难度大，目前还未见实用化波形跟踪机的报导。转发跟踪干扰是将接收到的跳频通信信号直接或处理后转发出去，从而对当前跳的跳频通信频率形成干扰。转发跟踪干扰需要接收和转发整个跳频带宽内的信号，若跳频带宽足够宽，干扰机功放的大部分功率会被无效消耗，实际干扰效果不佳。引导跟踪干扰指干扰机对跳频通信信号快速检测和识别，并立即引导干扰机在该频率上施加干扰。由于该干扰方式的实现途径简单且干扰效果较好，从而被广泛使用。本文主要研究抗引导跟踪干扰方法。面对跟踪干扰，一种直接的方式是通过提高跳频速率来实现抗干扰[1]。然而，由于射频器件及自动增益控制器等的限制，用户切换频率后存在器件状态不稳定的换频时间，换频时间内用户无法进行通信[2]。在时间一定的条件下，若跳速过快，则由于换频时间的存在导致实际通信时间减少；若跳速较慢，则被敌方有效感知并实施跟踪干扰的概率增加。因此，跳频通信的最优跳速选择是一个需要解决的重要问题。
在已有的通信抗干扰实践中，主要有两种确定抗跟踪干扰跳速的方法：一是当跳频通信的跳频速率高于跟踪干扰机的最高跳速，即安全跳速，则可有效抵抗跟踪干扰[1]。但在实际应用中，通信方的跳频速率往往难以达到安全跳速。二是由跳频通信的收、发信机位置以及干扰机位置确定的干扰椭圆来决定抗跟踪干扰跳速[1]，即跳频周期满足：T<(d1+d2-L)/V+Tj，其中d1、d2和L分别为发信机与干扰机、干扰机与收信机以及发信机与收信机之间的距离，V为电波传播速率，Tj为干扰机反应时间。然而，干扰机的位置和反应时间等信息在实际中往往是未知的，上式中的相关参数难以确定。近年来，学者将博弈论应用于不同的通信抗干扰场景，提出了多种基于博弈论的通信抗干扰方法。文献[3- 4]针对反应式扫频干扰，采用随机博弈的方法研究了数据通信信道、控制信道的最佳频率分配策略和跳频策略；文献[5]采用马尔可夫博弈方法研究了反应式扫频干扰条件下跳频频率和传输速率的联合优化问题；文献[6-7]采用Stackelberg博弈方法研究了多载波通信条件下的最佳干扰功率和最佳通信功率分配问题。但是以上文献假设通信博弈双方无需付出任何代价即可完全准确已知对方的决策信息，该假设在实际中往往难以成立。文献[8-9]通过引入相对观测误差
推导了存在检测误差条件下的最优发射功率，结果表明：随着干扰方观测误差的增加，通信方在均衡条件下获得的效用函数和抗干扰效果增加。然而，以上文献假设决策者获取对方决策信息时没有开销，且没有考虑获取对方决策信息所付出的开销与回报之间的关系：例如，反应式干扰由信号检测、干扰决策和干扰实施三个步骤构成[10]，检测时间越长，检测概率往往越高；反之，检测时间越短，检测概率往往越低。因此，为了获得最优抗干扰效果，通信方需要在考虑干扰方检测开销和检测误差的条件下选择合适的跳速，使得干扰造成的误码和跳频损伤[2]之间折中。
本文针对引导跟踪干扰，将跳频通信信号检测与抗干扰博弈结合起来，采用Stackelberg博弈模型[13]研究通信干扰方与抗干扰方在时域的博弈问题。在该模型中，存在一个先行者(leader)和一个跟随者(follower)，通信方作为先行者首先以一定跳速进行通信，干扰方作为跟随者在已知跳速的基础上分配合适的信号检测时间和干扰时间；然后，通信方在检测到干扰方的检测时间与干扰时间后，重新调整跳频速率，博弈过程依次持续进行。本文首先建立了基于Stackelberg博弈的通信干扰与抗干扰模型，然后推导了相应的Stackelberg均衡解，并将所提方法的抗干扰性能与盲跳频和变速跳频[12]的抗跟踪干扰性能进行比较，证明了所提方法的抗跟踪干扰性能显著优于已有方法。
2 系统模型与问题描述
2.1 系统模型
典型的跳频信号结构示意图如图1所示。令跳频用户的跳频频率集为F，满足|F|=M，即跳频信号在M个相邻但不相交的子频带内伪随机跳变。假设跳频周期为T，且T∈[0,Tmax]，Tmax为最大跳频周期，即跳频用户能够根据引导式跟踪干扰的参数，在0到Tmax的范围内自适应调整跳频周期。受器件和工艺水平等的限制，跳频信号的频率切换不可避免地存在不稳定的暂态过程，在该过程期间跳频通信系统既不发射也不接收信号[2]。令该暂态过程的持续时间为Tc，在跳频通信系统工作期间可以将其看成是固定值。
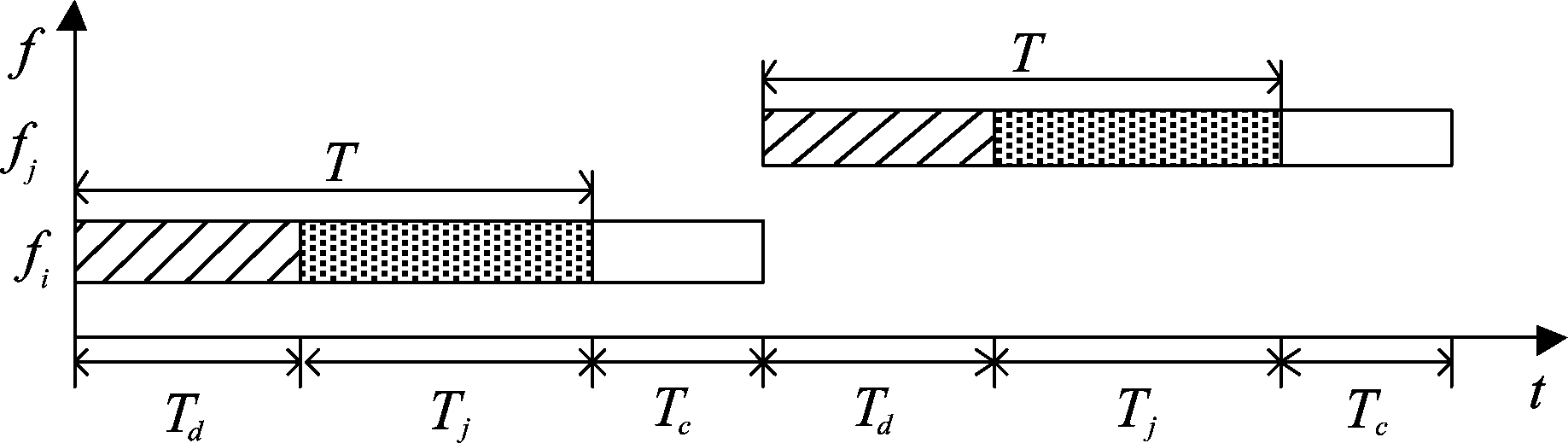
图1 跳频信号结构示意图
Fig.1 The framework of frequency-hopping signal
引导式跟踪干扰的干扰策略是[10]：在每个跳频周期内，干扰方首先检测跳频信号，若检测到跳频通信信号，则立即引导干扰机进行干扰；否则，干扰机不发射干扰信号。因此，可以将每个跳周期T分成两部分：信号检测时间Td和干扰时间Tj，且T=Td+Tj。由于信号检测概率往往与检测时间或检测信号长度有关：检测时间越长，检测概率越高；反之，则越低，因此，为跳频通信信号的检测概率可以表示为p(Td)，那么，一个跳周期内通信方的平均接收信噪比可以表示为：
(1)
其中，γ1和γ2分别为无干扰和有干扰条件下的信噪比。考虑到军事无线通信对抗的特点，假设干扰方一旦检测到跳频通信信号，则以足够高的功率对跳频通信信号实施压制干扰，即使得干扰下的信噪比趋近于零：γ2→0(需要指出，若同时考虑双方在时间域和功率域的博弈[6-9]，则可以直接采用公式(1)，但分析更加复杂)。因此，
可以简化为：
(2)
2.2 问题描述
在通信抗干扰博弈过程中，通信方首先以一定的跳周期T进行通信，然后干扰方将根据通信方的跳周期T以合适的信号检测时间Td和干扰时间Tj进行信号检测和施放干扰，其目标是使得通信方的平均接收信噪比最小；之后，通信方将根据干扰方的信号检测时间Td和干扰时间Tj调整跳频周期T，以使得己方的平均接收信噪比最大。因此，通信方和干扰方的效用函数UC(T)和UJ(Td,Tj)可以分别表示为：
(3)
在博弈过程中，干扰方作为跟随者根据跳频通信信号的检测结果，由如下优化问题确定最优检测时间：
(4)
进一步地，干扰时间为：
其中，
为干扰方对跳频周期的估计结果。同样地，通信方作为先行者由如下优化问题确定最优跳频周期：
(5)
其中，
为通信方对干扰方检测时间的估计结果。由此，我们建立了存在检测误差和检测时间条件下的通信抗干扰博弈模型，其中，通信方为先行者，干扰方为跟随者；双方的行动集分别满足0≤T≤Tmax和
双方的效用函数分别为式(4)、(5)。与已有的通信抗干扰博弈模型不同，该模型考虑了检测时间和检测误差对博弈的影响。
3 基于Stackelberg博弈的最优跳速设计
将式(2)带入式(4)、(5)，并通过简要分析可知通信博弈双方的目标函数可以分别等效为：
(6)
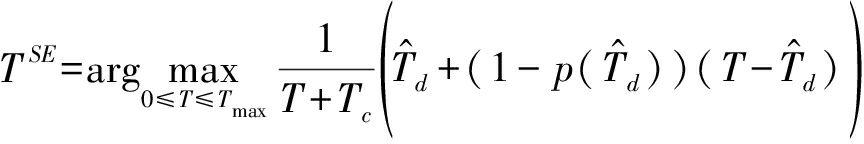
(7)
可以看出，博弈双方的最优策略与信号检测性能p(Td)有关，下面结合具体的信号检测方法进行分析。常用的信号检测方法包括能量检测、匹配滤波检测和循环平稳特征检测等[14]。本文不以信号检测研究为重点，因此假设干扰方采用能量检测作为跳频通信信号的检测方法：对M个正交子频带的接收信号进行能量检测，取能量最大者作为跳频通信信号所在频率的估计结果。附录1给出了该检测方法的近似检测概率表达式：
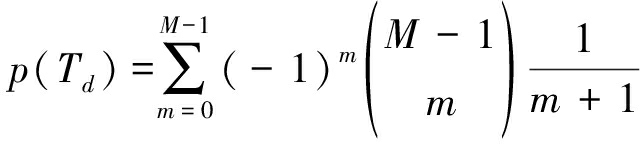
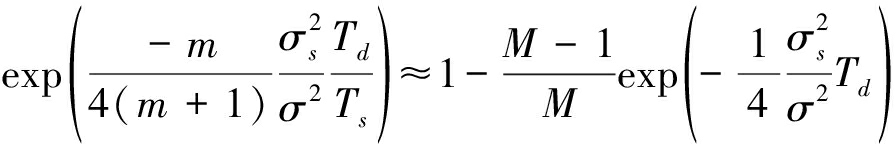
(8)
其中，为便于分析，在上式中令Ts=1，即Td为归一化检测时间或采样信号个数，另外，上式中的近似处理是取m/(m+1)≈1得到的。下面，结合式(8)给出的检测概率p(Td)，求解式(6)、(7)的目标函数，确定通信博弈双方的最优策略。
3.1 干扰方的最优干扰策略
将式(6)的目标函数写成
其中，检测概率p(Td)是关于检测时间Td的单调增函数，且p(0)=1/M，p(+
)
是关于Td的单调减函数，因此，
存在两种情况：
1. 当
时，在
内随Td单调递减，此时，等效目标函数的最大值为
2. 当
时，随Td先单调递增，后单调递减，等效目标函数的最大值由下式等于0时对应的函数值给出：
(9)
因此，
对应的信噪比给出了干扰方采取不同最优干扰策略的门限。附录2对该信噪比门限进行了求解，结果为：
(10)
干扰方的最优解由下式给出：
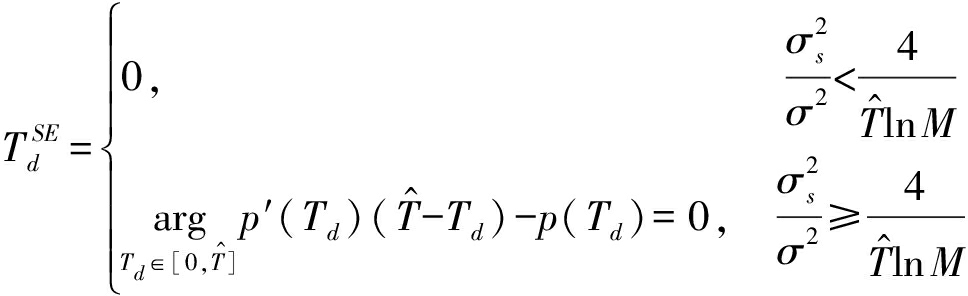
(11)
对式(11)的物理解释：当信噪比较低时，干扰方对通信信号的检测概率也较低，对于干扰方来说，检测通信信号付出的代价大于由此获得的收益，采用随机干扰策略更为合适，即信号检测时间为0；当信噪比较高时，干扰方付出一定检测代价可以有效检测到通信信号，并实施有效干扰，此时，干扰方的最优策略是先检测后干扰。为得到
的显式解，将式(8)代入式(11)，并进行化简，可将
条件下满足的方程写成：
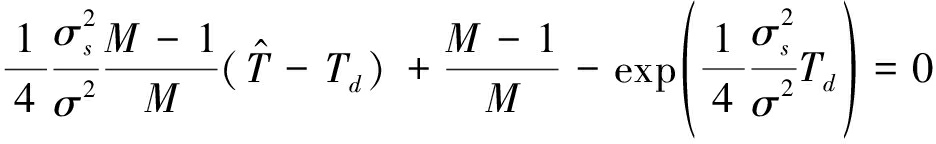
(12)
进一步地，将上式中的指数函数用二阶泰勒展开近似：ex≈1+x+x2/ 2，可求解得到
的近似解：
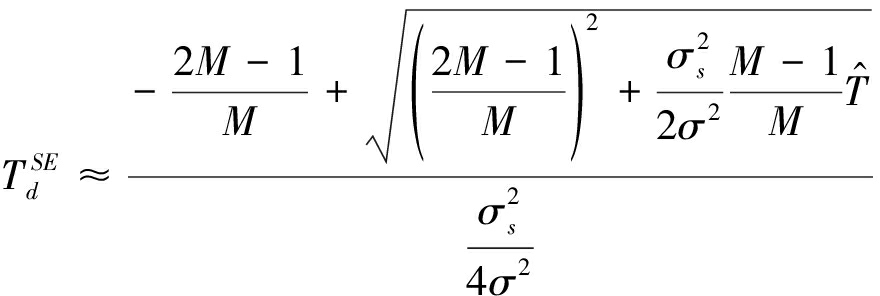
(13)
由此，得到干扰方最优干扰策略的近似解析解：
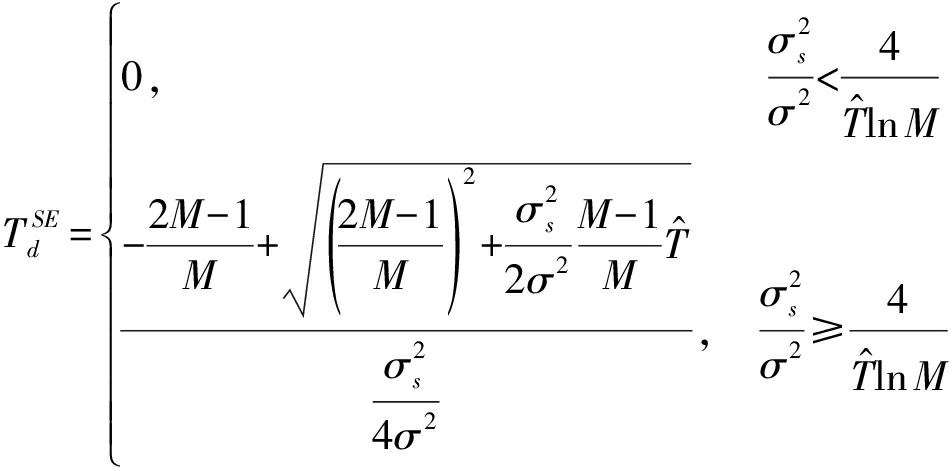
(14)
本文将在第4部分对近似解式(14)和精确解式(11)的近似程度进行比较和分析。
3.2 抗干扰方的最优抗干扰策略
为了求解通信方的最优抗干扰策略，将式(11)代入式(7)，并求解可得：
1. 当
时，有：
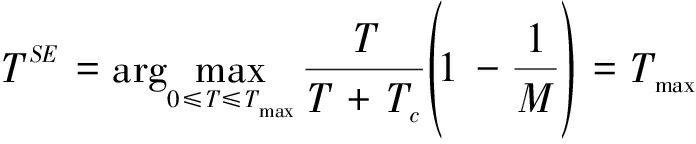
(15)
2. 当
时，有如下定理成立：
定理1 在
的条件下，当T较小时，式(7)中的目标函数
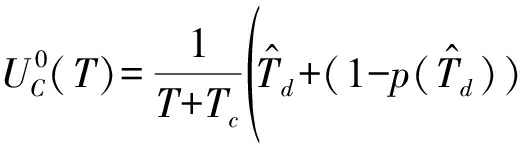
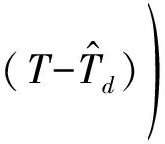单调递增；当T较大时，单调递减，因此，式(7)存在唯一的最大值。
附录3给出了定理1的详细证明。由式(11)以及定理1可知：干扰方和通信方的目标函数都为单峰函数，因此，存在唯一的Stackelberg均衡解。但是，通信方的目标函数都较为复杂，难以得到其导数的解析表达式，因此，采用黄金分割法寻找双方的最优解[15]。
第1步：将最大跳周期设为搜索区间，即设a1=0，b1=Tmax，k=1，搜索精度为t0>0，计算试探点λ1、 μ1及对应的函数值UC(λ1)、UC(μ1)，其中：λ1=a1+0.382(b1-a1)，μ1=a1+0.618(b1-a1)；UC(λ1)、UC(μ1)的计算可以首先将λ1、 μ1分别代入式(14)计算Td(λ1)、Td(μ1)的近似解，也可以将λ1、 μ1代入式(11)采用黄金分割法的方法求解Td(λ1)、Td(μ1)的精确解。
第2步：若bk-ak<t0，停止搜索；否则，若UC(λ1)>UC(μ1)，转入第3步；若UC(λ1)≤UC(μ1)，转入第4步；
第3步：ak+1=λk，bk+1=bk，λk+1=μk，μk+1=ak+1+0.618(bk+1-ak+1)，计算UC(μk+1)，转入第5步；
第4步：ak+1=ak，bk+1=μk，μk+1=λk，λk+1=ak+1+0.382(bk+1-ak+1)，计算UC(λk+1)，转入第5步；
第5步：k=k+1，转入第2步。
4 仿真与分析
本节主要通过计算机仿真验证理论分析的有效性，同时，将本文所提算法与盲跳频和变速跳频[12]进行比较，验证所提算法在抗跟踪干扰能力的优越性。首先验证当
时，干扰方和通信方的目标函数都具有先增加后减小的特性，因此，存在唯一的最优解。图2给出了M=32，Ts=1 ms，T=50 ms时，干扰方的目标函数随信号检测时间的变化曲线，图中还给出了式(14)的最优检测时间近似解。可以看出，当信噪比高于式(10)给出的信噪比门限0.023时，干扰方的目标函数先增加后减小，且随着信噪比的增加，目标函数随检测时间的变化更加陡峭。图3给出了Tmax=40 ms时，通信方的目标函数随跳周期的变化曲线。可以看出，当信噪比高于式(10)给出的信噪比门限时，通信方的目标函数也具有先增后减的特性。
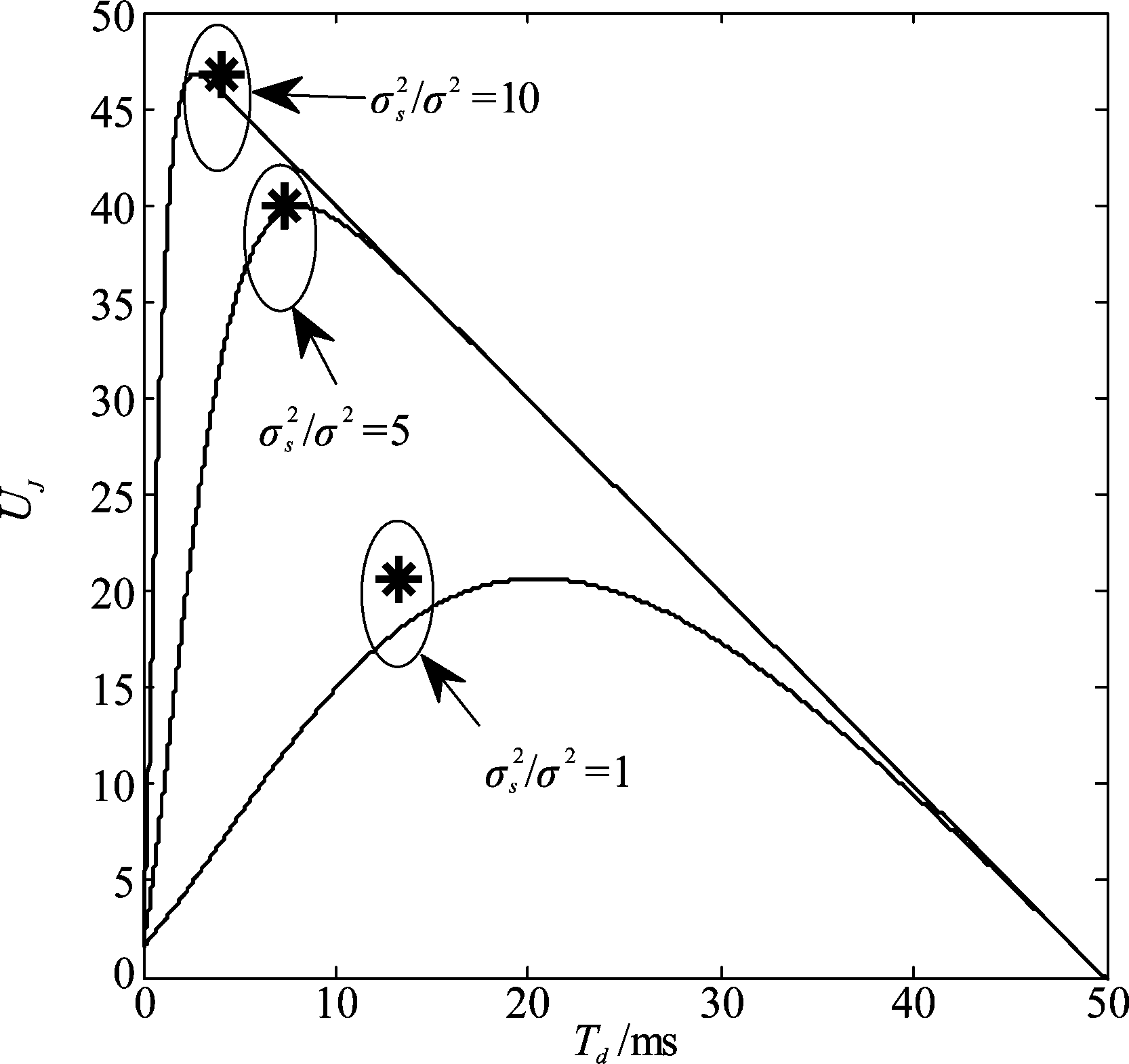
图2 干扰方的目标函数曲线
Fig.2 The objective curve of jammer
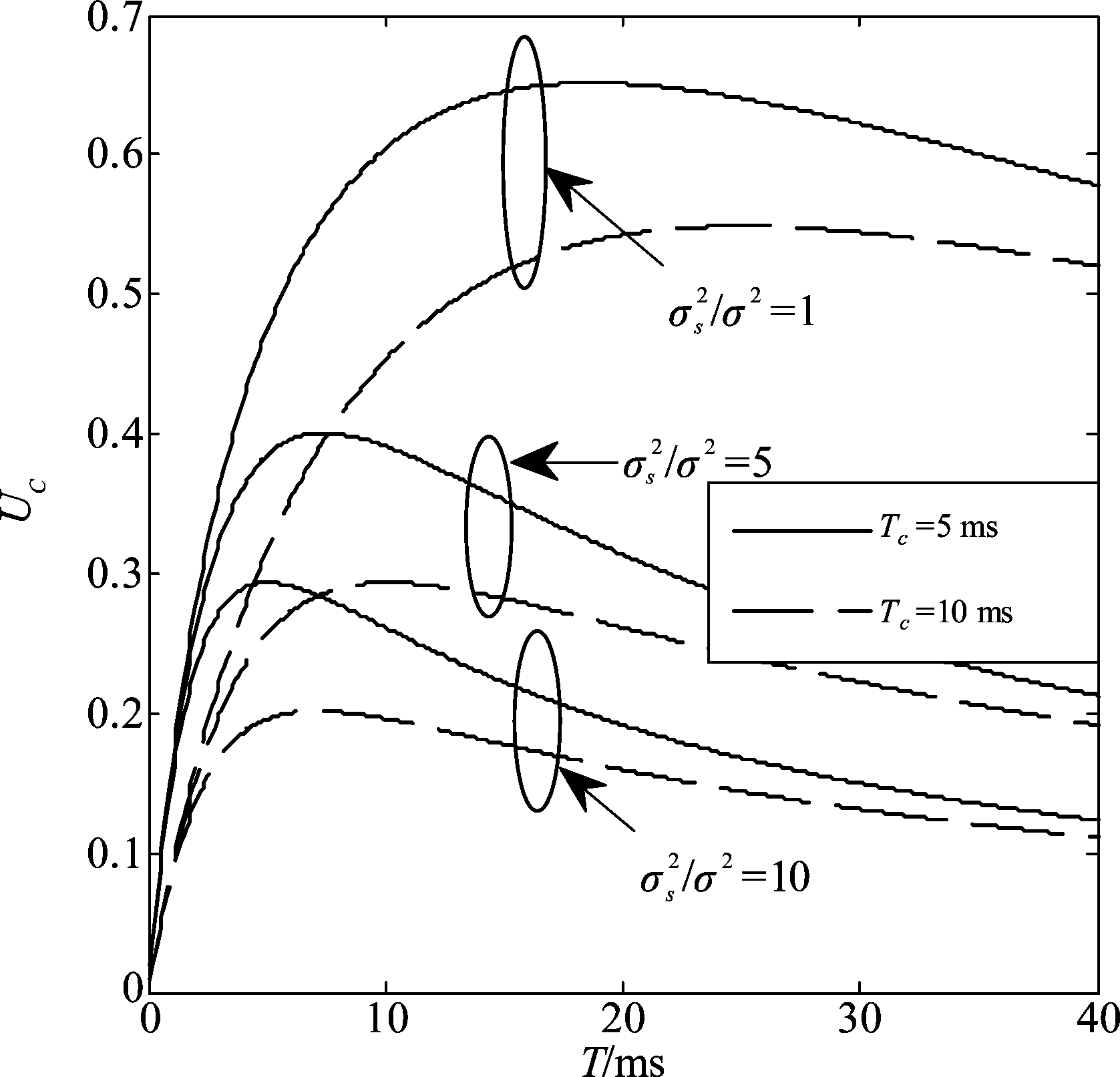
图3 通信方的目标函数曲线
Fig.3 The objective curve of communicator
图4给出了最优检测时间的精确解和近似解(式(14))随信噪比的变化曲线。仿真中，取M=8。可以看出，随着信噪比、跳周期的变化，近似解与精确解具有相同的变化趋势，且当信噪比适中时，近似解对精确解的近似程度最好。另外，随着信噪比的增加，干扰方的最优检测时间减小。这是因为当信噪比较高时，只需较少的检测时间即可以较高的概率有效检测跳频信号，干扰方可以减小检测时间，增加干扰时间，从而获得最优干扰效果。
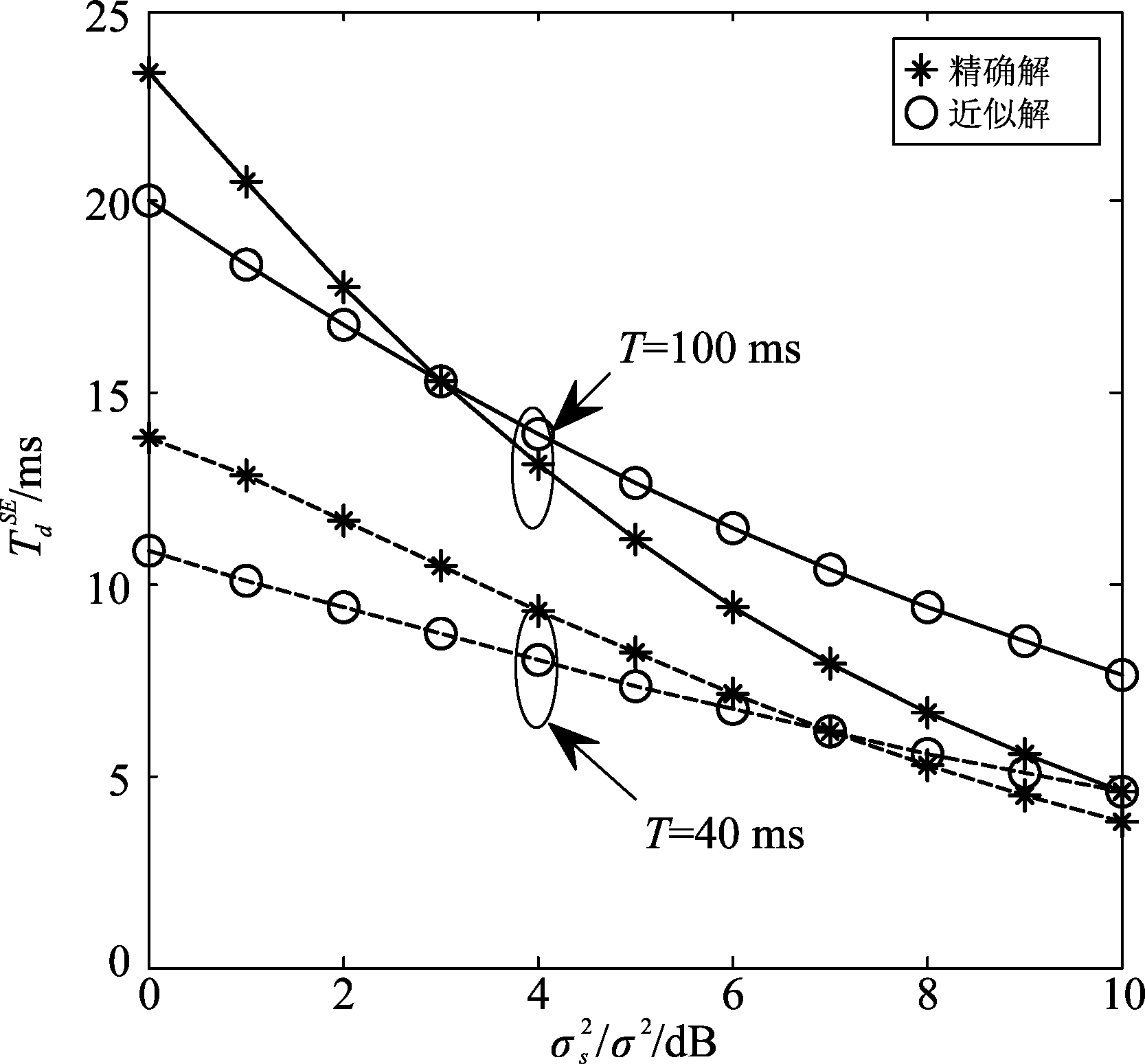
图4 最优检测时间随信噪比的变化曲线
Fig.4 The optimal detection time vs. SNR
图5给出了取Tmax=50 ms时，最优跳周期随信噪比的变化曲线。可以看出，当信噪比较小时，通信方的最优跳周期较大，即采用慢跳频；当信噪比增加时，通信方的最优跳周期减小，即提高跳速。这是因为当信噪比较低时，干扰方需要较多时间用于检测跳频信号，因此通信方采用尽可能慢的跳频速率，以减小跳频损伤的影响；当信噪比较高时，干扰方能够快速检测到跳频信号，因此通信方需要提高跳速，尽可能减小干扰的影响。同时，从图5可以看出，随着信道数的增加，通信方的最优跳频周期将有所增加。
图5 最优跳周期随信噪比的变化曲线
Fig.5 The optimal frequency-hopping cycle vs. SNR
最后，将所提算法与盲跳频和变速跳频的抗跟踪干扰性能进行比较，其中，盲跳频是指通信双方的载波频率始终以固定跳速在频率集内伪随机跳变；变速跳频是指通信双方的跳频速率以约定的规律伪随机跳变。仿真中，令跳频通信系统的跳频频率集有M=32个频点，换频时间为Tc=0.5 ms，最大跳频周期为Tmax=10 ms，最小跳频周期为Tmin=1 ms，假定盲跳频的固定跳周期为Tblind=5 ms，变速跳频以等概率选择[Tmin,Tmax]之间所有可能跳频周期。图6给出了三种跳频模式下的平均接收信噪比仿真结果。从图6可以得出以下三点结论：一是本文所提方法的抗跟踪干扰性能显著优于盲跳频和变速跳频；二是针对跟踪干扰，变速跳频模式相对于盲跳频模式获得的抗干扰性能增益并不明显；三是跟踪干扰对跳频通信系统构成严重威胁，例如，当信道信噪比
dB时，盲跳频、变速跳频和本文所提方法的平均信噪比分别约为0.2 dB、0.6 dB和4.2 dB。这是因为随着信道信噪比的增加，干扰方检测通信信号付出的时间代价减小，检测的准确性增加，从而在很大程度上抵消了信道信噪比增加带来的性能改善程度。因此，如何有效降低干扰方的检测概率或增加其检测时间是提高通信系统抗干扰性能的重要途径之一。
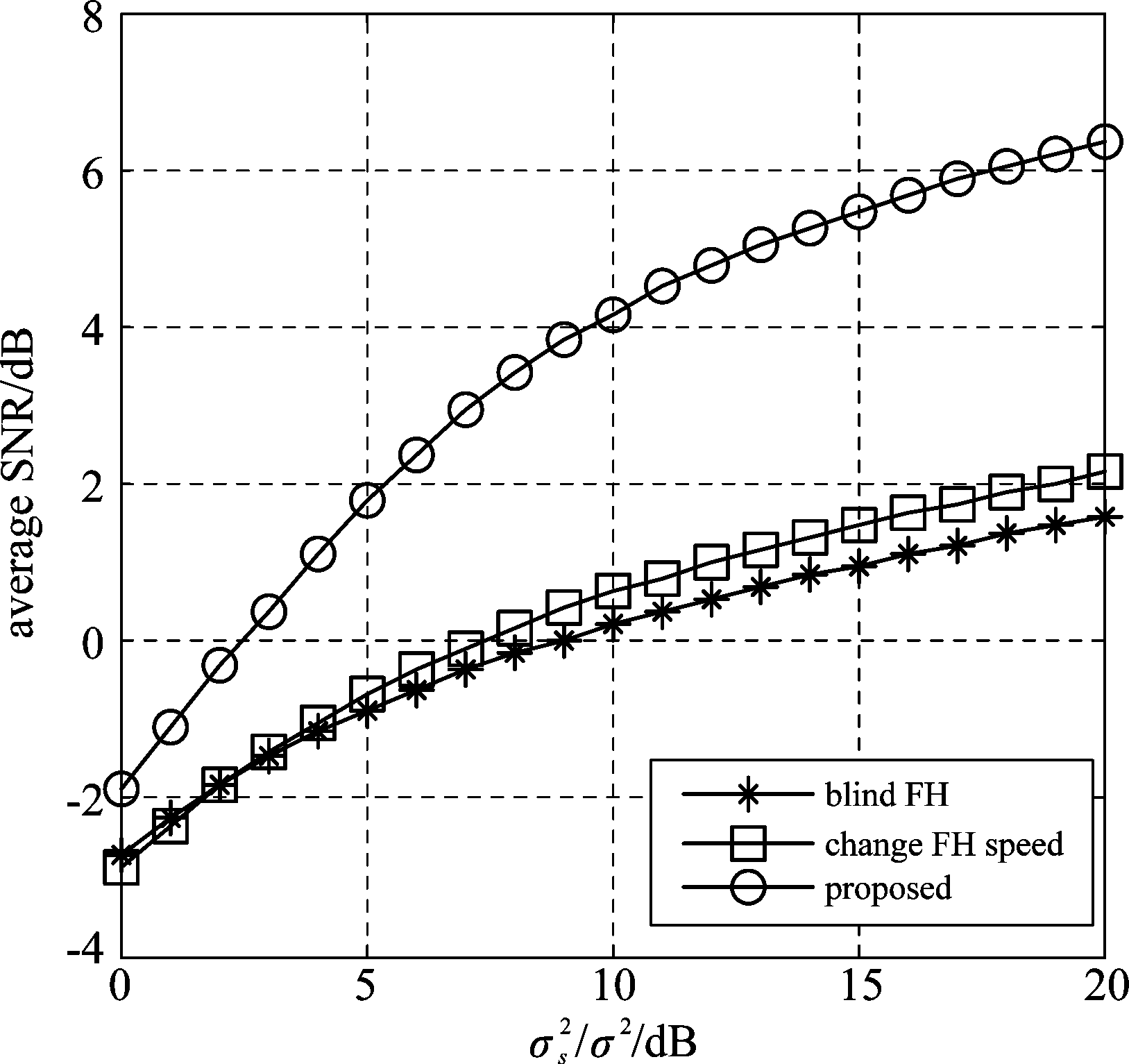
图6 多种跳频模式的抗跟踪干扰性能
Fig.6 The anti-following jamming performance
for different hopping model
5 结论
基于博弈论的通信干扰与抗干扰是目前的研究热点之一，本文将已有的功率域、频率域的博弈框架扩展到时间域，结合干扰方检测通信信号需要付出时间开销和存在检测误差的特点，提出了存在检测误差条件下的最优跳速设计问题，并采用Stackelberg博弈模型对该问题进行了求解。理论分析与仿真结果表明，当信噪比小于4/T ln M时，干扰方的最优干扰策略是盲干扰，通信方的最优抗干扰策略是慢速跳频；反之，干扰方的最优干扰策略是先检测后干扰，通信方将相应地调整跳频周期已获得最优抗干扰性能。需要指出，尽管本文所提方法在一定程度上克服了已有研究难以考虑检测开销与检测性能的关系对最优跳速设计的不足，但该方法需要通信对抗双方准确获取对方的决策信息。下一步将结合强化学习技术研究干扰方决策信息的在线学习方法[17]。另外，本文所提方法可以与功率域、频率域博弈相结合，构造多域博弈抗干扰，以进一步提高抗干扰性能。
附录1 跳频通信信号检测概率
采用能量检测方法对M个子频带上的接收信号进行检测时，跳频通信信号的检测概率可以表示为：
p(Td)=p(R2(Td)<R1(Td),...,RM(Td)<R1(Td))=
(p(R2(Td)<R1(Td)|R1(Td)=x))M-1fR1(Td)(x)dx
(A1)
其中，Ri(Td)为第i个子信道的接收信号能量，i=1,2,...,M；由于跳频信号在M个子频带出现的概率是相同的，因此式(A1)假设跳频信号处于第1个子信道， fR1(Td)(x)表示第1个子信道内接收信号能量概率密度函数。为便于分析，假设各子频带的噪声是方差为σ2的高斯信号，跳频通信信号是方差为
的高斯信号。通过将该跳频信号检测方法与文献[16]中MFSK信号的非相干解调方法进行对比可知两者具有类似的检测或解调结构。因此，跳频信号检测概率可以由文献[16]中的式(5.4- 45)表示：
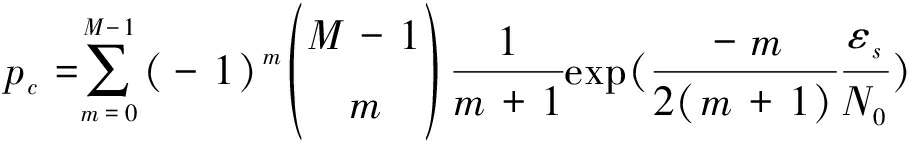
(A2)
其中，εs为符号能量，N0为噪声功率谱密度。分别作如下变量代换：
和N0=2σ2，则能量检测概率为：
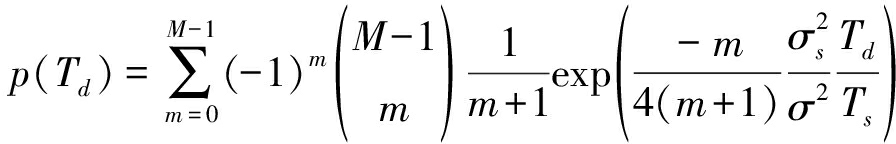
(A3)
其中，Ts为采样周期。
附录2 信噪比门限的求解
对式(8)求导可知：
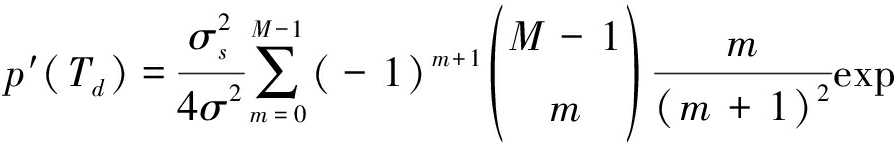
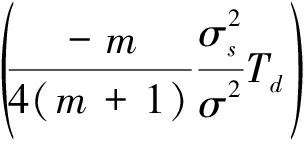
(A4)
将Td=0代入上式并化简可得：
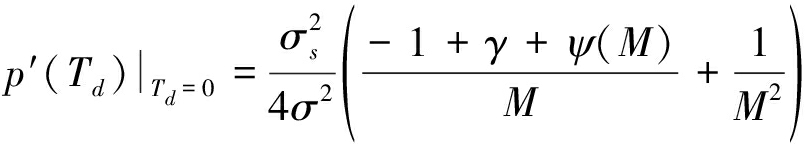
(A5)
其中，γ为欧拉常数：γ≈0.577216；ψ(M)为双Γ函数：
由于有ψ(x)∈(ln(x-1/ 2),ln(x))成立，因此：
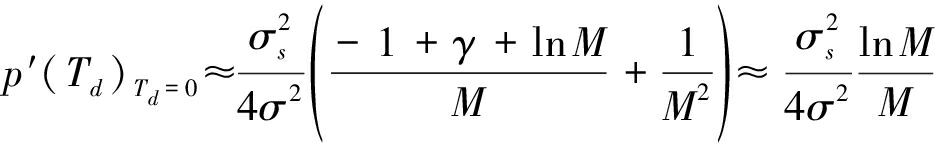
(A6)
将式(A6)和p(0)=1/M代入式(9)得：
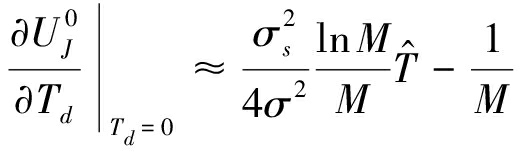
(A7)
由此可以得到
对应的信噪比门限为
附录3 定理1的证明
证明：证明的主要思路是分别针对T→0和T→的情况，分析
的单调性。首先，当M较大时，式(13)给出的
可以近似为
进一步地，当T→0时，对根号函数进行一阶泰勒展开：(1+x)1/ 2≈1+x/ 2，因此，可以近似为下式：
(A8)
同样地，对式(8)中的指数函数进行一阶泰勒展开，并将式(A8)代入其中，可得：
(A9)
将式(A8)、(A9)代入式(7)，得到T→0条件下通信方等效目标函数的近似表达式：
(A10)
通过对式(A10)求导可知，当
时，目标函数单调递增。
其次，当T→时，由式(13)可知
其中α是与T无关的大于0的常数，同时，当T→时，p(Td)趋近于1，因此，令p(Td)=1-β，其中，β→0，将以上近似结果代入式(7)，得到T→条件下通信方等效目标函数的近似表达式：
(A11)
通过对式(A11)求导可知，当
时，目标函数单调递减。综上可知，由式(7)所示的目标函数存在唯一的最大值，证毕。
[1] 姚富强. 通信抗干扰工程与实践[M]. 第2版.北京：电子工业出版社，2012.
Yao F Q. Communication anti-jamming engineering and practice[M].Second edition. Beijing: Publishing House of Electronics Industry, 2012. (in Chinese)
[2] 张毅，姚富强. 跳频通信损伤研究[J]. 西安电子科技大学学报:自然科学版，2005，32(6): 472- 476.
Zhang Y,Yao F Q. The research on impairment of frequency hopping communication systems[J]. Journal of Xi’dian University, 2005, 32(6): 472- 476.(in Chinese)
[3] Wang B, Wu Y, Liu K J R, et al. An anti-jamming stochastic game for cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(4): 877- 889.
[4] Wu Y, Wang B, Liu K J R, et al. Anti-jamming games in multi-channel cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(1): 4-15.
[5] Hanawal M K, A-rahman M J, Krunz M. Joint adaptation of frequency hopping and transmission rate for anti-jamming wireless systems[J]. IEEE Transactions on Mobile Computing, 2016, 15(9): 2247-2259.
[6] Yang D, Xue G, Zhang J, et al. Coping with a smart jammer in wireless networks: a stackelberg game approach[J]. IEEE Transactions on Wireless Communications, 2013, 12(8): 4038- 4047.
[7] Slimeni F, Nir V L, Scheers B, et al. Optimal power allocation over parallel Gaussian channels in cognitive radio and jammer games[J]. IET Communications, 2016, 10(8): 980-986.
[8] Xiao L, Chen T, Liu J, et al. Anti-Jamming transmission Stackelberg game with observation errors[J]. IEEE Communications Letter, 2015, 19(6): 949-952.
[9] Jia L, Yao F, Sun Y, et al. Bayesian Stackelberg game for antijamming transmission with incomplete information[J]. IEEE Communications Letters, 2016, 20(10): 1991-1994.
[10] Poisel R A.现代通信干扰原理与技术[M]. 第2版. 楼才义,等,译，杨小牛,审校. 北京：电子工业出版社，2014.
Poisel R A. Modern communications jamming principles and techniques[M]. Second edition. Lou C Y, et al, translate, Yang X N, checkup. Beijing: Publishing House of Electronics Industry, 2014. (in Chinese)
[11] 岳文静，沈冬冬，陈志. 噪声不确定下基于进化博弈论的协作频谱检测[J]. 信号处理，2017，33(10): 1385-1392.
Yue W J, Shen D D, Chen Z. Research on cooperative spectrum detection based on evolutionary game theory under noise uncertainty[J]. Journal of Signal Processing, 2017, 33(10): 1385-1392. (in Chinese)
[12] 柳永祥,姚富强. 变参数跳频通信反侦察机理及若干工程问题探讨[C]∥2009军事通信抗干扰会议论文集，南京: 2009: 174-177.
Liu Y X, Yao F Q.Counterreconnaissance mechanism of frequency-hopping communication with time-varying parameters and some engineering problems[C]∥2009 Conference of Military Communication Anti-jamming, Nanjing: 2009:174-177. (in Chinese)
[13] Han Z, Niyato D, Saad W, et al. Game theory in wireless and communication networks[M]. Cambridge: Cambridge University Press, 2012.
[14] Sun H, Nallanathan A, Wang C, et al. Wideband spectrum sensing for cognitive radio networks: a survey[J]. IEEE Wireless Communications, 2013(4): 74- 81.
[15] 陈宝林. 最优化理论与算法[M]. 第2版. 北京：清华大学出版社，2005.
Chen B L. Optimization theory and algorithm[M]. Second edition. Beijing: Publishing House of Qinghua University, 2005. (in Chinese)
[16] Proakis J G. Digital Communications[M]. Fourth edition. New York: McGraw-Hill Companies, 2001.
[17] Yu L, Wu Q, Xu Y, et al. Power control games for multi-user anti-jamming communications[J]. Wireless Networks, Published online，DIO:10.1007/S11276- 018-1664-9.
