1 引言
第五代移动通信(5G)[1]被提出以满足更高的业务要求，非正交多址技术(Non-orthogonal Multiple Access，NOMA)[2]频谱效率较高，因此成为5G的一个备选方案。作为NOMA技术的一种，从低密度信号(Low Density Signature，LDS)[3]发展来的稀疏码多址接入(Sparse Code Multiple Access，SCMA)[4]技术，可利用码字的稀疏性得到较高的接入量。因为接收的是各用户码的叠加信号，所以要进行多用户检测。由于码字是稀疏的，因此可用消息传递算法(Message Passing Algorithm，MPA)[5]进行检测。
但MPA的高计算复杂度限制了SCMA技术的实际应用。影响复杂度的因素有算法的迭代次数、码本大小、系统因子图中的分支数等。文献[6]通过简化星座图来减小码本大小。文献[7- 8]在每次迭代中将节点消息的更新顺序重新编排，越靠后更新的节点消息越有效，因此减少了迭代次数。文献[9-10]根据信道条件差异，将信道条件差的分支近似为高斯噪声，同时添加反馈机制来弥补性能的下降，通过减少分支来降低复杂度。文献[11]提出了一种基于动态因子图的MPA检测器，因子图中置信度较高的分支从当前迭代开始将不参与消息传递。文献[12]提出了一种部分边缘化的MPA(Partial Marginalization-Message Passing Algorithm，PM-MPA)，迭代结束前将部分用户数据先解出来，在后续迭代中再解出剩余用户数据，牺牲了一部分性能的同时带来了复杂度下降的收益。
以上文献中算法的节点更新方法基本一致，各节点将其概率分布状态传递给相邻节点，从而改变相邻节点的概率分布状态。所有节点消息更新后，进入下一轮节点消息更新。当所有节点的码字消息概率收敛后迭代结束，接着进行软解码。因为每次迭代要更新所有码字消息，所以复杂度较高。基于实验的研究发现，一些节点比其他节点收敛快[8]，意味着各码字消息的收敛速度不同。针对这一特点，为降低算法复杂度，本文提出了一种动态选择消息更新的检测算法DSM-MPA(Dynamically Select Message-Message Passing Algorithm，DSM-MPA)。不同于文献[8]，本文算法在单次迭代中，不再更新因子图中的所有节点消息，只选择更新收敛较慢的节点消息，通过减少消息更新次数来降低算法复杂度。消息若收敛快，则其概率变化量小而接近收敛值，可直接用于软解码。仿真结果表明，选择合适的比重因子，相比较于原始MPA，本文算法的复杂度明显下降，同时误比特率(Bit Error Rate，BER)性能基本不变。在实际应用中可降低上行链路接收机设计复杂度，同时保证性能。
本文其余部分安排如下：第2节简述SCMA系统模型及MPA算法；第3节给出本文的改进算法；第4节对仿真结果进行性能比较分析；最后第5节给出结论。
2 系统模型
2.1 SCMA系统模型
假定有J个用户共享K个资源块(J>K)，则该系统的过载系数定义为λ=J/K。对于每个用户j，其比特数据与此用户码本χj中的SCMA码一一对应，χ的维度是K。码本中的SCMA码表示为xj。K维SCMA码中非零元素个数为N，N<K。系统模型如图1所示，这里J=6，K=4。其中，F是系统因子图矩阵，行表示资源块，列表示用户，值为1的位置表示此位置所在行的资源块被所在列的用户所使用。
接收信号可写为：
(1)
其中，xj=[x1j x2j...xKj]T为用户j的SCMA码，hj=[h1j h2j...hKj]T为用户j的信道条件向量，n是高斯白噪声，n～CN(0,σ2I)，y=[y1 y2...yK]T是接收端从K个资源块中检测到的信号。
由接收信号y和信道条件H=[h1h2...hJ]T，就可通过最大后验概率估计算法(Maximum A Posteriori, MAP)来检测用户数据X=[x1x2...xJ]，如式(2)：
(2)
式中，
2.2 原始MPA
假定系统中6个用户共用4个资源块。MPA的消息传递如图2所示，uj是用户j在因子图中的节点，ck为资源块k在因子图中的节点。单个uj和单个ck的连接称为一个边缘，码字消息在边缘上传递。MPA主要有两步：步骤1如式
表示ck到uj的码字消息更新；步骤2如式
表示uj到ck的码字消息更新：
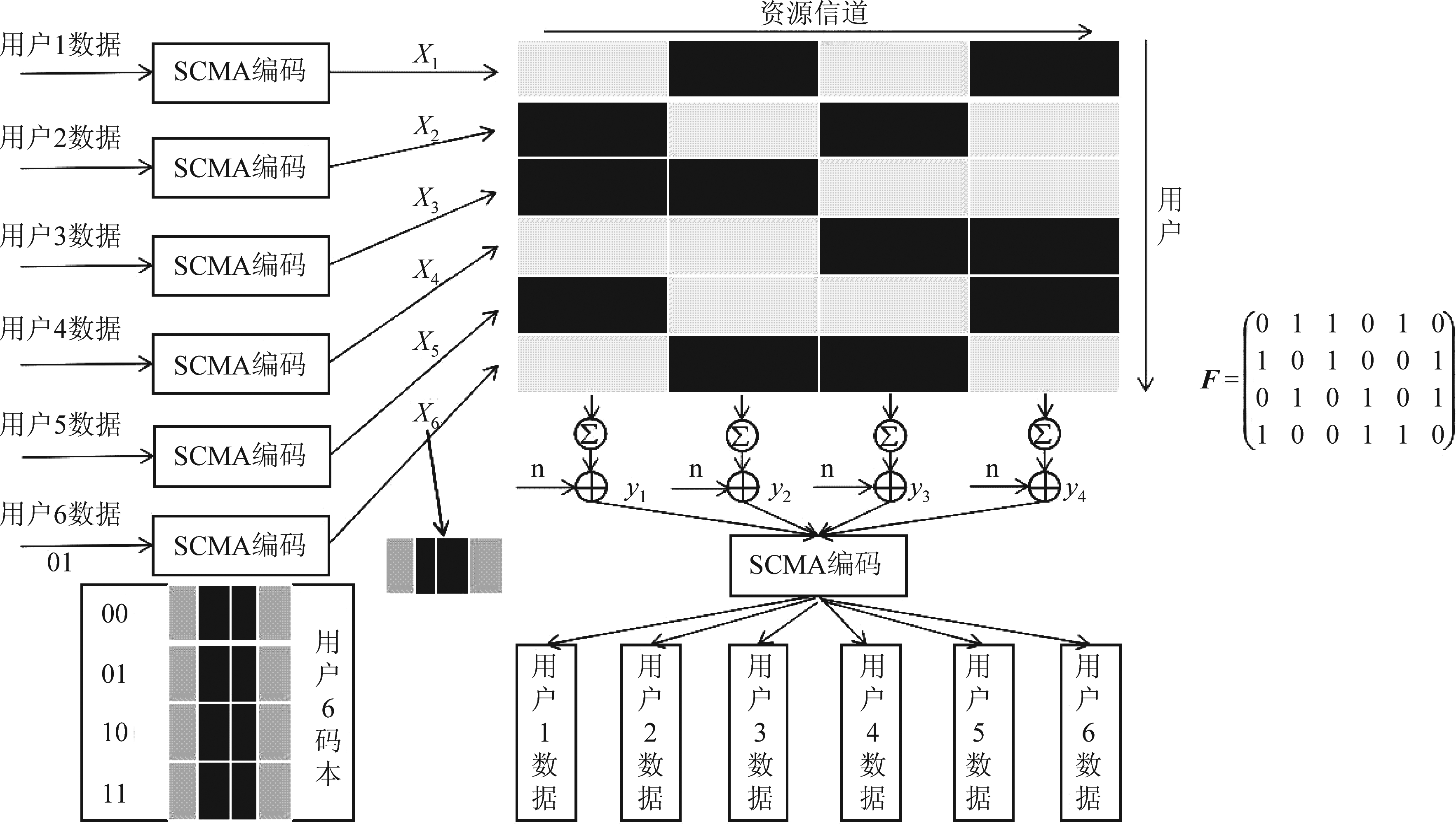
图1 SCMA系统模型
Fig.1 Model of SCMA system
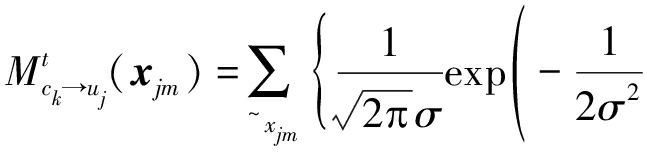
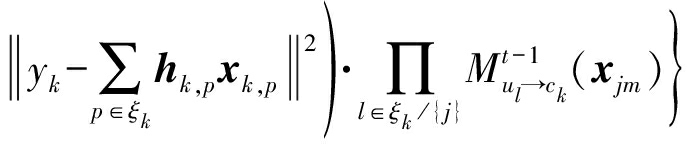
(3)
(4)
其中，t表示第t次迭代，ξk是与资源块k连接的用户序号集合，ζj是用户j所占用的资源块序号集合，xjm∈[xj1 xj2...xjM]T为用户j码本中第m个码字。yk为资源块k上检测的信号，σ是噪声的标准差，hk,p和xk,p分别是资源块k与用户间的信道条件向量和用户码。
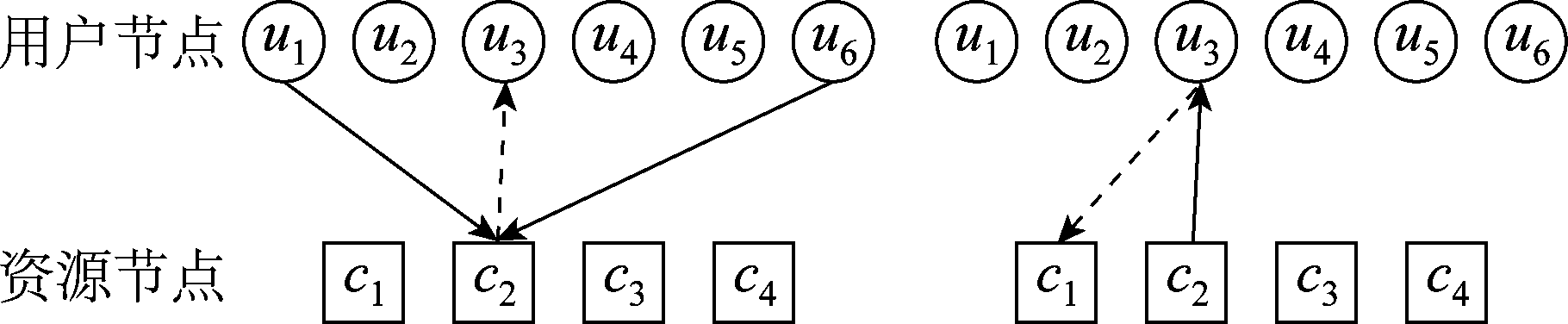
图2 MPA算法示意图，实线表示来自其他边缘的先验概率，虚线表示边缘上消息的更新
Fig.2 Scheme diagram of MPA. The solid line indicates the prior probability from other edges. The dashed line indicates the update of the message at the edge
MPA达到最大迭代次数T后，各用户码字xjm出现的概率Q(xjm)用式(5)来计算：
(5)
3 本文提出的算法
原始MPA迭代更新所有码字消息，直到每个码字消息收敛。所以，MPA算法复杂度较高。实际上，有些码字消息可以更快地接近收敛值，对这些消息继续更新，所得的概率值变化量小。因此，可以有选择地更新收敛较慢的消息，提前结束更新收敛快的消息。因为退出更新的消息已接近收敛，所以可直接用于软解码。在保持性能的同时，通过减少消息更新次数来降低计算复杂度。
3.1 动态选择消息更新的MPA
针对以上问题，本文提出了一种动态选择消息更新的MPA。在保持BER性能与原始MPA基本相同的情况下，可明显降低算法复杂度。
算法基本思想是：第一次迭代更新所有码字消息；从第二次迭代开始，对参与此次迭代的消息，用式(6)来计算迭代前后消息的差值Dt(xjm)：
(6)
若差值小，则表明此消息的变化量较小，收敛速度较快。将所有Dt(xjm)值按大小排序，选出差值最小的Nit个码字消息。这Nit个码字消息将被判为收敛最快，在后续迭代中将不更新。定义R为比重因子，被判为差值最小的消息数Nit，用式(7)来计算：
Nit=R·Nat
(7)
Nat是参与第t次迭代的消息数。定义nit-1=[Dt-1(xjm)1 Dt-1(xjm)2...Dt-1(xjm)Nit-1]为前次迭代中选出的收敛最快消息集合。
为前次迭代中未被判为收敛最快的码字消息，
为前次迭代中被判为收敛最快的码字消息。式(8)中，改写为
表示此消息将不再更新：
(8)
所以，只需更新消息
式(3)和式(4)分别改写为式(9)和式(10)：
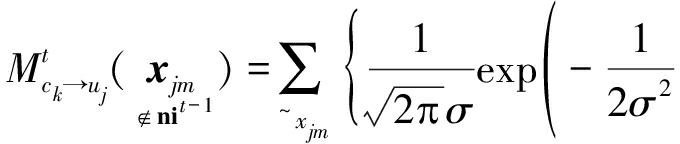
(9)
(10)
比重因子R取值合适，对于判为收敛快的消息
其概率分布可达到或接近稳态。因此，这些消息可不再更新，将这些消息传递到用户节点的更新，各用户节点仍能和MPA算法一样最终收敛于一个稳态。最后，通过软解码检测出各用户数据。
算法过程如表1。
表1 动态选择消息更新的MPA算法
Tab.1 MPA based on dynamically selecting message to update
续表1
6. Use formula (3) to update all Mtck→uj(xjm)7. Use formula (4) to update all Mtuj→ck(xjm)8. else do四、选择消息更新:9. Mtck→uj(xjm∉nit-1)=∑～xjm{Φn·∏l∈ξk/{j}Mt-1ul→ck(xjm)}10. M∗ck→uj(xjm)=Mtck→uj(xjm∈nit-1)=Mt-1ck→uj(xjm∈nit-1)11. Mtuj→ck(xjm)=∏q∈ζj/{k}Mtcq→uj(xjm∉nit-1)M∗cq→uj(xjm)12. end if13. do Dt(xjm)=Mtck→uj(xjm∉nit-1)-Mt-1ck→uj(xjm∉nit-1)14. createaggregatenit15. t=t+116. end while五、消息输出17. Q(xjm)=∏k∈ζjMTck→uj(xjm∉nit-1)M∗ck→uj(xjm)
3.2 复杂度分析
当用户码本大小为M，资源节点数为K，每个ck上所连接的边缘数为ds。MPA的算法复杂度可表示为O(MdsKdsT)[9]，主要计算量来自
的MKdsT次消息更新。本文通过减少消息更新次数来降低复杂度。du是单个uj上连接的ck数，有Kds=Jdu。在消息更新中，第t次迭代有Nat=(1-R)t-1·MKds个码字消息要更新。若总迭代次数为T，则本文算法所需更新的码字消息次数为MKds·
因此，DSM-MPA的算法复杂度可表示为
本文算法与原始MPA[9]以及PM-MPA[12](m和Rs是算法中的参数)可用表2来比较复杂度，以算法执行的加法和乘法次数为衡量标准。
4 仿真结果与分析
为了验证本文算法在上行SCMA无线通信系统中的性能，将本文算法与原始MPA以及PM-MPA进行了仿真比较实验。仿真参数如表3所示。
表2 复杂度比较
Tab.2 Comparison of complexity
算法MPADSM-MPAPM-MPA加法((ds+1)Mds-M)·KdsT((ds+1)Mds-M)Kds·∑Tt=1(1-R)t-1mKds[(ds+1)Mds-M]+Rsds[(ds+1)Mds-Rsdu-M](T-m)+(K-Rs)ds[(ds+1)Mds-M](T-m)乘法(2ds+1)MdsKdsT+MJduT(du-2)(2ds+1)MdsKds·∑Tt=1(1-R)t-1+MJduT(du-2)(ds-2)TJduM+(2ds+1)mKdsMds+RsdsMds-Rsdu(2ds+1)(T-m)+(K-Rs)dsMds(2ds+1)(T-m)
表3 仿真参数
Tab.3 Parameters of simulation
参数取值用户数J6码本大小M4资源块数K4信道类型高斯白噪声信道ds3du2
4.1 性能分析
在图3中，最上面的五条曲线是原始MPA，PM-MPA(m=3，Rs=2)以及本文算法(前两者算法曲线用实线表示，本文算法用虚线表示)在Eb/N0取8 dB时的收敛情况；最下面五条曲线是各算法在Eb/N0取10 dB时的收敛情况。本文算法取R=0.2和0.3时，收敛性与原始MPA和PM-MPA一致，迭代6次后收敛。本文算法R取0.4时，3次迭代后大多消息已不再更新，因此相比于原始MPA会提前收敛。但R取值比较大时，判为收敛快的消息中有很多未达到收敛条件。提前停止更新这些消息，会使后面软解码误差较大，造成BER性能大幅下降。由图3、图4可知，当信道条件较差(Eb/N0≤8 dB)，噪声对消息传递的干扰较大，为保证BER性能，R取值应该小(R<=0.2)；当信道条件较好(Eb/N0≥8 dB)时噪声小，对消息传递的干扰小，少数迭代后趋于收敛的消息多，所以R可取较大值(R>=0.2)。但为保障BER性能，R取值应小于0.3。
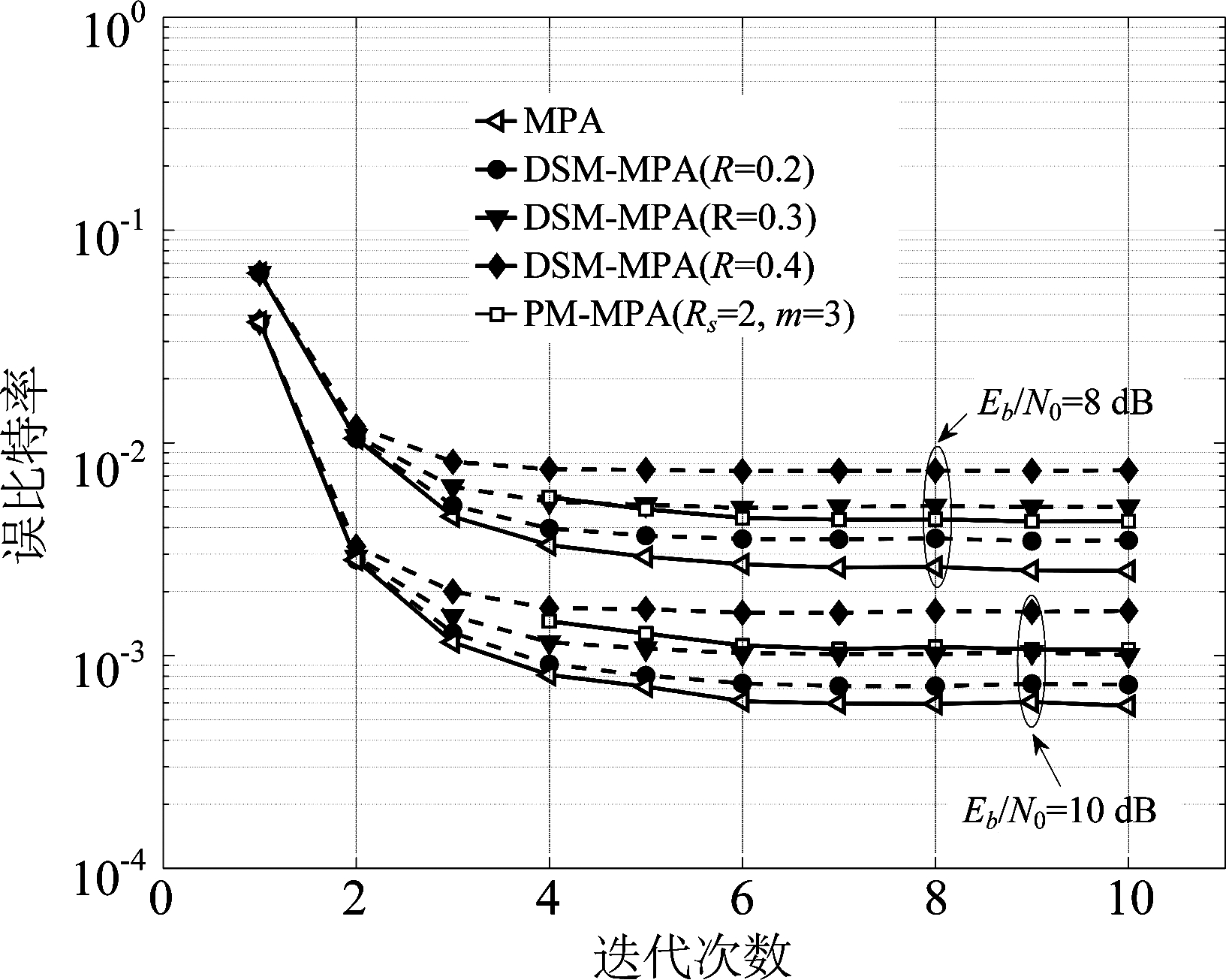
图3 各算法收敛速度
Fig.3 Convergence rate of various algorithm
比重因子R取值若越小(R<=0.2)，对于迭代中被判为收敛快的消息，其前后迭代的差值就越小。因此，这些消息的概率分布也更容易趋于稳态。这些不更新的消息越接近收敛，其他消息更新得到的收敛值与原始MPA的就更接近。因此，图4中本文算法BER性能会与原始MPA更接近。反之，R取值越大(R>=0.2)，收敛快的消息中不满足收敛条件的就越多。停止更新这些消息会使其他消息难以收敛到原始MPA的值，消息可靠性就越低，BER性能将越差。
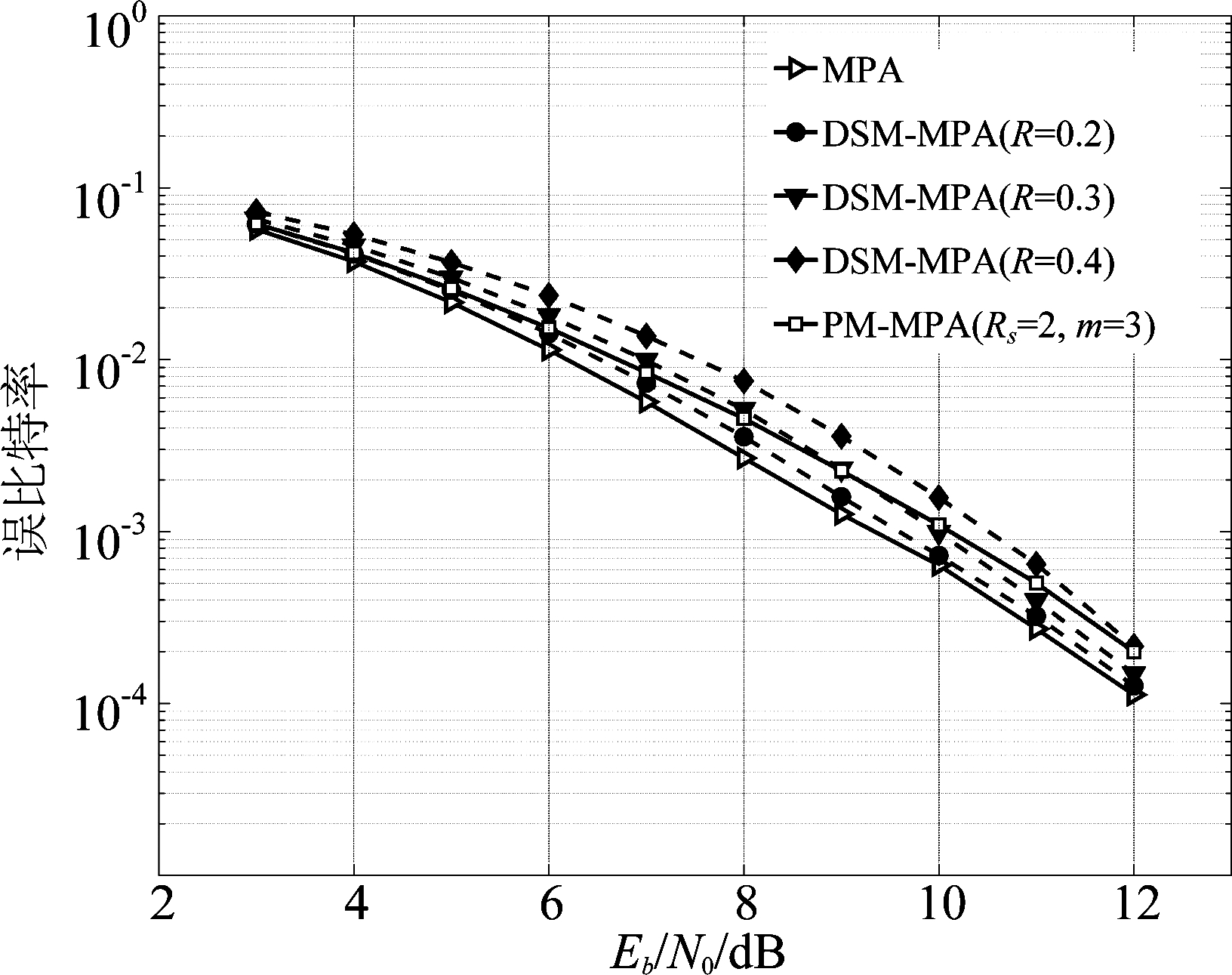
图4 各算法性能
Fig.4 Performance of various algorithm
图4中各算法迭代次数都为T=6。在BER=1.0×10-3时，取R=0.2，每次迭代中被判为收敛快的消息数较少。前面提到，R取值越小(R<=0.2)，这些消息的概率分布更接近稳态，可直接传递给其他消息的后续更新，对其他消息收敛到原稳定值影响小。因此，所有消息的最终概率分布接近于原始MPA。所以，此时本文算法BER性能基本和原始MPA一致；和PM-MPA算法相比，本文算法有0.5 dB左右的增益。因为PM-MPA是直接提前解特定用户的数据，此用户消息可能依然与稳定值相差较远，已收敛消息的准确性不如本文算法。因此，选择合适的R，本文算法的BER性能要优于PM-MPA算法。R取0.3和0.4时，由于R取值较大，本文算法的性能损失较多，相比原始MPA分别下降了0.7 dB和1.2 dB。
4.2 复杂度对比
由表2中各算法复杂度可知，比重因子R取值越大，本文算法相比于其他两种，复杂度就越低。由图3、图4可知，为有效地降低算法复杂度，同时保障BER性能，取比重因子R=0.2，迭代次数T=6。结合表2，如表4所示，原始MPA、PM-MPA(m=3，Rs=2)及本文(R=0.2)算法所执行的加法次数分别为18144次、14688次和11156次；执行的乘法次数分别为32256次、26496次和19834次。本文算法相比于原始MPA，加法次数减少了约38.5%，乘法次数减少了约38.5%。PM-MPA为保障解码性能，提前解出的用户节点数是很有限的，相比于本文算法可以降低的复杂度有限。与PM-MPA相比，本文算法的加法次数减少了约24.0%，乘法次数减少了约25.1%。综上所述，参数R取0.2比较合理。此时，BER性能基本与原始MPA一致，优于PM-MPA，同时复杂度都明显低于这两种算法。
表4 各算法复杂度比较
Tab.4 Comparison of complexity
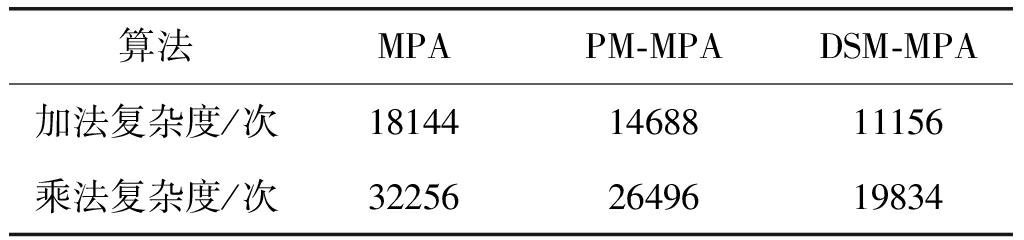
算法MPAPM-MPADSM-MPA加法复杂度/次181441468811156乘法复杂度/次322562649619834
5 结论
原始MPA每次迭代会更新所有码字消息，直到所有码字消息概率收敛后迭代结束，因此复杂度较高。为降低复杂度，针对不同码字消息概率的收敛速度不同，本文提出了一种动态选择消息更新的DSM-MPA算法。在当次迭代中找出收敛最快的码字消息，这些消息将不再更新，通过减少消息更新次数来降低复杂度。选择合适的比重因子，可使BER性能基本与原始MPA一致，并且复杂度更低；和PM-MPA相比，不仅复杂度较低，且性能也有优势。所以，本文算法在SCMA系统的应用中优势明显，可降低接收机设计复杂度，同时可以保持性能。但该算法仍存在一些不足，如比重因子R的选择固定。当信道条件变化时，每次迭代中选出的不更新的消息，就带有随机和波动性。有些消息实际并未收敛或接近收敛，这将给解码带来较大误差。因此，可设定硬性的收敛判定条件，以更有效地选择已收敛的消息不更新。可弥补由随机和波动性带来的性能损失，并可适应信道变化。
[1] Pirinen P. A brief overview of 5G research activities[C]∥1st International Conference on 5G for Ubiquitous Connectivity, Akaslompolo, Finland, 2014: 17-22.
[2] Benjebbour A, Saito Y, Kishiyama Y, et al. Concept and practical considerations of Non-orthogonal Multiple Access (NOMA) for future radio access[C]∥2013 International Symposium on Intelligent Signal Processing and Communication Systems, Naha, Japan, 2013: 770-774.
[3] Hoshyar R, P.Wathan F R, Tafazolli R. Novel Low-density Signature for synchronous CDMA systems over AWGN channel[J]. IEEE Transaction on Signal Processing, 2008, 56(4): 1616-1626.
[4] Nikopour H, Baligh H. Sparse code multiple access[C]∥2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 2013: 332-336.
[5] 雷菁, 文磊, 高永强. 基于联合判决消息传递机制的LDPC码译码算法研究[J]. 信号处理, 2009, 25(12): 1917-1921.
Lei J, Wen L, Gao Y Q. A decoding algorithm based on joint judging message passing schedule for Low-Density Parity Check Codes[J]. Signal Processing, 2009, 25(12): 1917-1921. (in Chinese)
[6] Bayesteh A, Nikopour H, Taherzadeh M, et al. Low complexity techniques for SCMA detection[C]∥2015 IEEE Globecom Workshops(GC Wkshps). San Diego, CA, USA, 2015: 1- 6.
[7] 杜洋, 董彬虹, 王显俊, 等. 基于串行策略的SCMA多用户检测算法[J]. 电子与信息学报, 2016, 38(8): 1888-1893.
Du Y, Dong B H, Wang X J, et al. Multiuser detection scheme for SCMA systems based on serial strategy[J]. Journal of Electronics & Information Technology, 2016, 38(8): 1888-1893. (in Chinese)
[8] Du Y, Dong B H, Chen Z, et al. A fast convergence multiuser detection scheme for uplink SCMA systems[J]. IEEE Wireless Communications Letters, 2016, 5(4): 388-391.
[9] Du Y, Dong B H, Chen Z, et al. Low complexity detector in sparse code multiple access systems[J]. IEEE Communications Letters, 2016,20(9): 1812-1815.
[10] Wang Y D, Qiu L. Edge selection-based low complexity detection scheme for SCMA system[C]∥2016 IEEE 84th Vehicular Technology Conference(VTC-Fall). Montreal, QC, Canada,2016: 1-5.
[11] Ma X Y, Yang L, Chen Z, et al. Low complexity detection based on dynamic factor graph for SCMA systems[J]. IEEE Communications Letters, 2017, 21(12): 2666-2669.
[12] Mu H, Ma Z, Alhaji M, et al. A fixed low complexity message pass algorithm detector for up-link SCMA system[J]. IEEE Wireless Communications Letters, 2015, 4(6): 585-588.
