1 引言
安全性有两方面的要求，一是确保合法用户通信的可靠性，二是确保传输信息的安全性。无线信道由于其固有的开放性和广播性，很容易受到窃听、篡改等威胁，无线通信中的安全性尤为重要。
目前，物理层安全是无线通信安全的热点。在物理层密钥技术中，合法用户Alice和Bob通过对无线信道的信道特征进行提取获得共享比特串。基于通信双方信道互异原理[1-2]，合法用户间可以提取基本一致的上、下行信道特征，得到实时独立的密钥，从而避免密钥的传输，实现“一次一密”，达到通信安全的目的。
但是，在无线通信中，由于实际信道中噪声的干扰，Alice和Bob得到的密钥序列X和Y在有些位置会存在一定的误差，并且信道中的窃听者Eve还有可能窃听到部分密钥序列[1-2](Z)，因此要得到安全的密钥序列，还需要经过密钥协商和保密增强两个过程，其中密钥协商是纠正密钥序列X和Y间不一致位，而保密增强则是保证Eve不能从Z中获取有关安全密钥的信息。
由于合法通信双方信道估计的强相干性，双方生成的初始密钥只有极小部分密钥比特不匹配，利用纠错码技术可以使得通信双方获得一致的密钥序列。例如，文献[3]利用二分法分组算法来提高密钥序列的一致性。由于二分法每轮只能纠正奇数个错误，所以二分法协商需要进行多次通信，纠错效率低。文献[4]提出了基于散列函数的检错方案，利用散列函数校验通信双方信道特征的一致性。文献[5]在Winnow算法的基础上利用卷积码进行密钥协商。文献[6]把低密度奇偶校验码(Low Density Parity Check Code，LDPC码)应用到密钥协商算法中，获得了比散列函数和卷积码更高的一致性和纠错成功率。但是基于LDPC码的协商协议是通过校验信息进行纠错的，在初始密钥序列不一致比特较多时，会达不到协商纠错的要求。
Polar码是Arikan在2007年提出的一种新型编码方式，对于二进制对称信道，Polar码理论上可以达到信道容量[7]。S.Korada，R.Urbanke和E.Sasoglu等人证明了对于任意的二进制输入离散信道(Discret memoryless channel，DMC)，Polar码同样可以达到信道容量[8]；同时，Polar码的编译码复杂度都较低，利用Polar码的这些优势，Jouguet等人将Polar码应用到量子密钥分发(Quantum key distribution，QKD)协商协议中[9]。我们小组对高斯信道中的Polar码进行了设计研究，并将Polar码应用于经典物理层密钥协商协议和量子密钥分发协商协议中[10-11]。
本文将Polar码应用到无线信道密钥协商中，针对由无线信道特征提取的密钥存在不完全一致的问题，提出了一种基于Polar码的密钥协商方法。在这个协商方法中，合法用户(发送端Alice和接收端Bob)分别进行信道估计生成各自的原始密钥，然后Bob对自己的原始密钥进行Polar码逆编码，并将冻结位信息传输给Alice。Alice在获得冻结位及其位置信息的基础上，进行Polar码的译码，对自已的原始密钥进行纠错，最后，再通过Polar的编码，获得与Bob一致的密钥序列。分析了基于Polar码的无线信道密钥协商协议的性能，并与相同条件下采用LDPC码的协商协议结果进行了比较。
2 基于Polar码的无线信道密钥协商协议
假设通信双方为Alice和Bob，基于Polar码的密钥协商协议可以描述为图1，主要有3个部分，即信道估计部分、原始密钥生成部分和Polar码协商部分。
2.1 信道估计
信道模型建立时要考虑到无线信道的互异性和有噪声干扰的传输特性，现考虑信道中是加性噪声且满足正态分布。
信道估计过程如图1中第一部分所示，图中xa、xb分别表示Alice和Bob的探测信息，hab、hba分别表示上行信道、下行信道的信道特征，ya和yb表示Alice和Bob端接收到的响应信号。首先Alice和Bob分别向对方发送探测信息xa、xb，由信道噪声的加性特性可知他们分别接受到的响应信号ya和yb可表示为：
ya(t)=xb·hba+n(t)
(1)
yb(t)=xa·hab+n(t)
(2)
对通信双方而言，已知对方的探测信号，所以根据自己接收到的相应信号，Bob端得到对上行信道特征的估计为：
同理可得Alice端得到对下行信道的估计为：
在这一过程中，由于Alice和Bob是在相干时间内完成探测任务，所以它们对于信道的特征估计具有极大的相似性，可以认为
在通信双方进行探测和通信时，无线信道都可能有窃听者(Eve)存在，如图所示，窃听者通过窃听信道对Alice和Bob的通信进行窃听。而无线信道的短时互异性[2-3]表明每次信道探测得到的信道特性都是不同的，即保证通信双方可以同时、异地、独立地生成实时更新的密钥，实现安全加密通信。
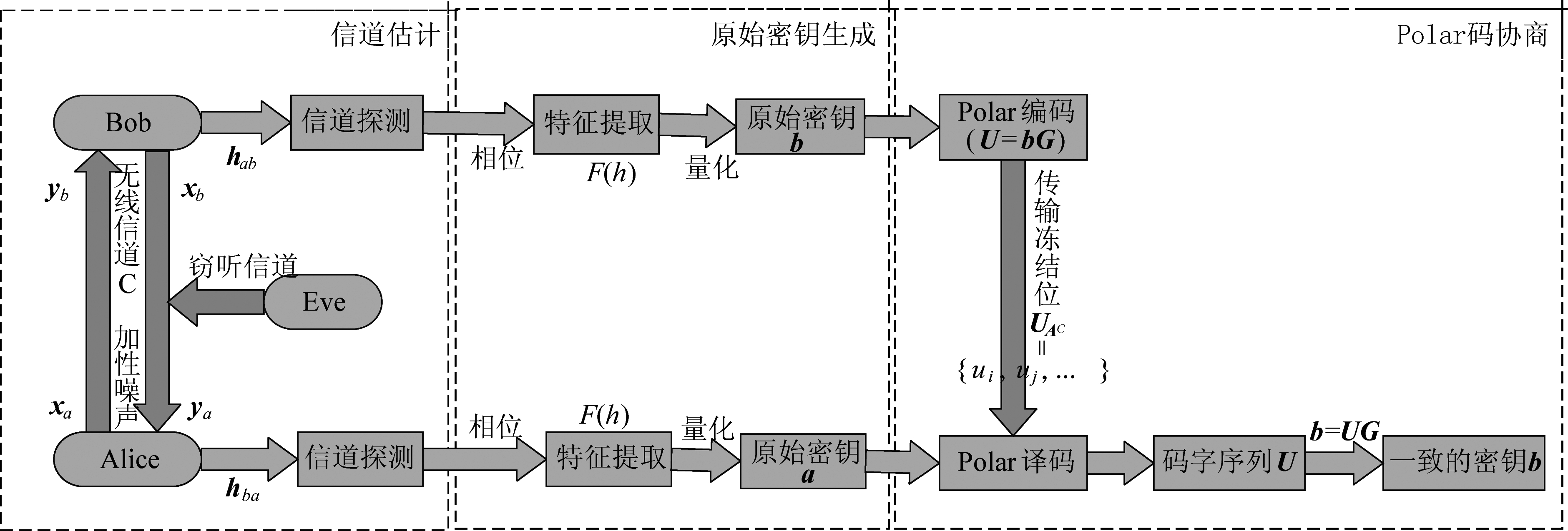
图1 密钥协商流程图
Fig.1 The process diagram of key reconciliation
2.2 原始密钥生成
上一节介绍了Alice和Bob对信道特征的估计过程，下面介绍从信道特征提取原始密钥的过程。
根据公式(1)或(2)，设无线传输的探测信号为x，由于无线信道多径效应和噪声干扰，所以接收到的信号可以表示为：
(3)
上式中ξ(t)表示加性噪声n(t)在经过信道调制后的窄带随机噪声信号。对于窄带随机信号ξ(t)，它的波形可表示为包络和相位都是随机缓变的正弦波，所以噪声信号ξ(t)可以表示为：
ξ(t)=aξ(t)cos[ωct+φξ(t)]
(4)
式中，aξ(t)和φξ(t)分别是噪声的随机包络和随机相位，而且ξ(t)是一个均值为零，方差为
的平稳高斯窄带过程，因此，其随机相位的统计特性为：
φξ∈[0,2π]
(5)
由上式可知，相位φξ服从均匀分布。而Alice和Bob对无线信道特征的估计反应的是信道噪声的统计特性，所以特征信息的相位也服从均匀分布。
原始密钥获取如图1第二部分所示，Alice和Bob分别从各自的信道估计信息中提取相位信息，目前主要是用信道估计算法[2]对估计信号进行特征提取，常用的信道估计算法主要有互相关法和代价函数法，图中用F表示信道估计算法，则得到的信道特征(相位)可以用F(h)表示。
Alice对得到的信道相位信息F(h)均匀量化后就可以得到密钥比特序列，Alice端得到的原始密钥序列为a(a1,a2,…,an)；同理Bob提取
的相位信息，量化后进行得到的原始密钥序列为b(b1,b2,…,bn)。
2.3 Polar码协商
在协商过程前，合法用户Alice和Bob需根据传输信道特征，设计并构造Polar码。根据Polar码构造特点，Alice和Bob共享将共享信息位集合、冻结位集合。
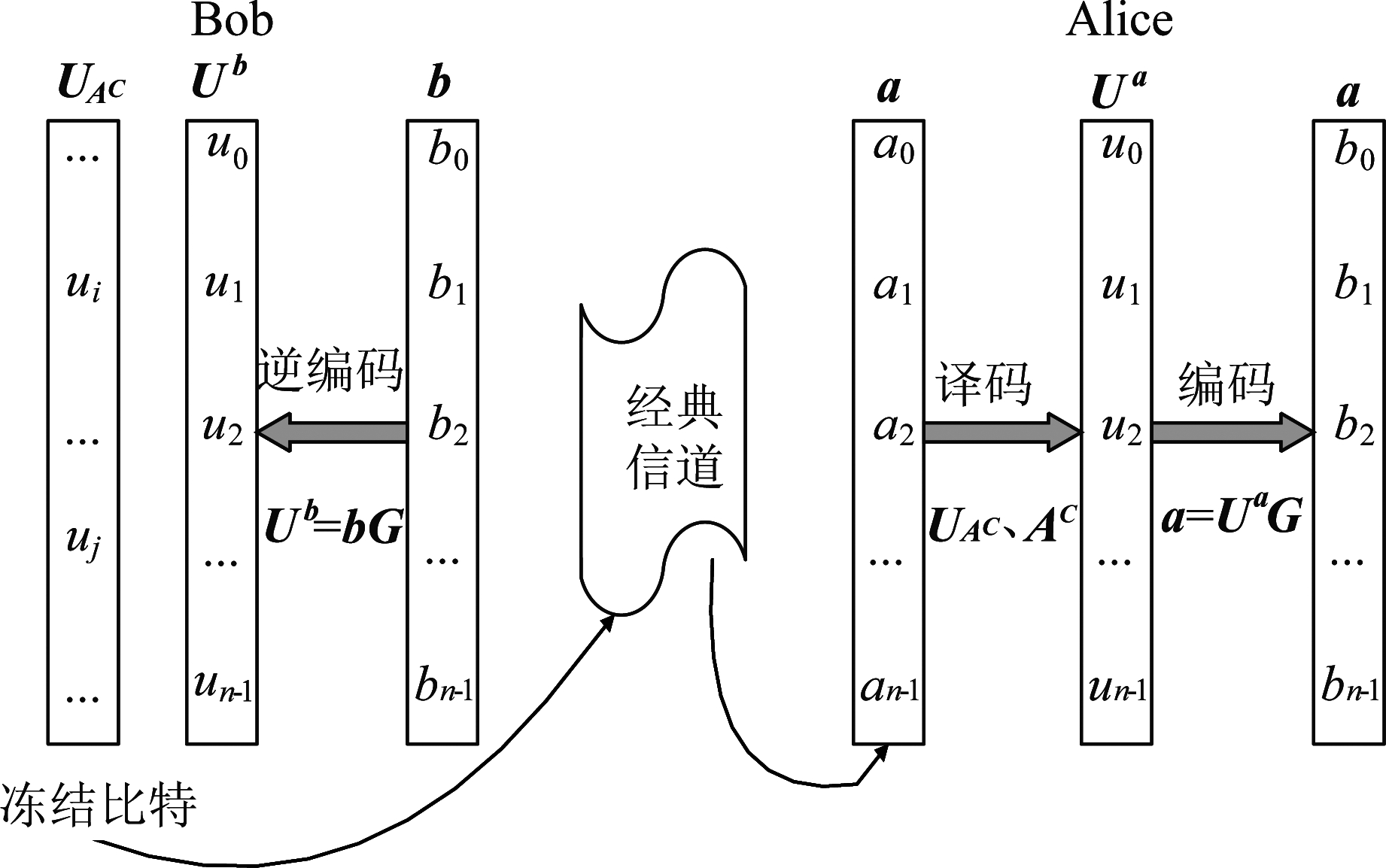
图2 Polar码纠错过程流程图
Fig.2 The flow diagram of Polar code reconciliation
如图1中Polar码协商部分所示，现用N表示码长，K表示信息位集合A中元素的个数，AC表示冻结位位置集合。
Polar码协商部分设计如图2所示，Bob端首先对原始密钥b进行Polar码逆编码：
Ub=bG-1
(6)
式中Ub表示逆编码得到的序列，且序列Ub由K位信息比特UA和N-K位冻结比特UAC构成。G-1表示Polar码生成矩阵的逆矩阵。根据Polar码生成矩阵的构造特性，G的逆矩阵等于它自身[7- 8]，所以此时有Ub=bG。生成矩阵G由信息位集合A中索引对应的行向量组成的矩阵GN(A)和冻结位集合AC中索引对应的行向量组成的矩阵GN(AC)组成。
然后，Bob通过无线信道把N-K个冻结比特UAC={ui,uj,...}传送给Alice。Alice根据接收到的冻结比特UAC和共享的冻结位位置信息对原始密钥a对应位置上的比特进行替换，并对替换后得到的密钥序列进行译码，得到序列Ua。
本文采用的Polar码译码算法是连续消除(successive cancellation，SC)算法。在SC算法中，根据码字序列给定的参数(N，K,A，UAC)，对每位ui根据如下判决函数进行判断：
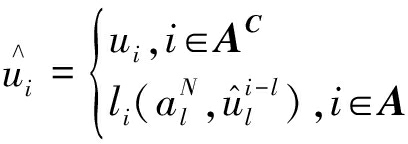
(7)
式(7)表明：如果是冻结位(i∈AC)，直接将冻结位信息赋给译码值，
如果不是冻结位(i∈A)，将根据前面译出的码字的估计值
计算判决函数[9]li，确定当前符号的译码值。其中，计算判决函数li的定义如下:
(8)
式中
表示当前比特的似然比：
(9)
式中
表示在已知
的条件下，发送比特0，收到比特
的条件概率；
表示在已知
的条件下，发送比特1，收到比特
的条件概率。
Alice译码得到比特序列Ua后，通过a=UaG即可得到与序列b一致的密钥序列a，这样Alice和Bob就可以利用一致的密钥序列b进行加密通信。
在Polar码协商方案中如果记一次模二加的复杂度为1、翻转一次长度为N的序列的复杂度为N，则Polar码编码和译码的复杂度为：
(10)
χD(N)=Nlog N
(11)
其中χE(N)和χD(N)[11]分别表示Polar码编码复杂度和SC译码复杂度。
如图2所示，Polar协商过程包括两次编码过程(Alice端的逆编码过程和Bob获得最终密钥的编码过程)和一次译码过程，所以Polar协商方案的复杂度χ(N)为：
χ(N)=2χE(N)+χD(N)≤4Nlog N=O(Nlog N)
(12)
3 数值仿真及分析
现通过数值仿真验证该协商协议对密钥一致性的影响。数值仿真中基本参数设置如下：最大帧数设为2000，纠错码分别采用码长为2048码率为0.75和0.5的Polar码、码长为4096码率为0.5的Polar码；码长为2048码率为0.5的Polar码和LDPC码，LDPC码中BP译码最大迭代次数设置为100次。
图3是通过对比不同参数Polar码的纠错情况，得到的译码成功率与信噪比的关系图。由图3可以看出：当码率相同时，随着信噪比的增大，译码成功率越来越高，即成功完成纠错的概率越来越高，且在相同信噪比条件下，码长为4096的Polar码的译码成功率一直高于码长为2048的Polar码；另一方面，当码长相同时，在相同信噪比条件下，码率为0.5的Polar码的译码成功率一直高于码率为0.75的Polar码。
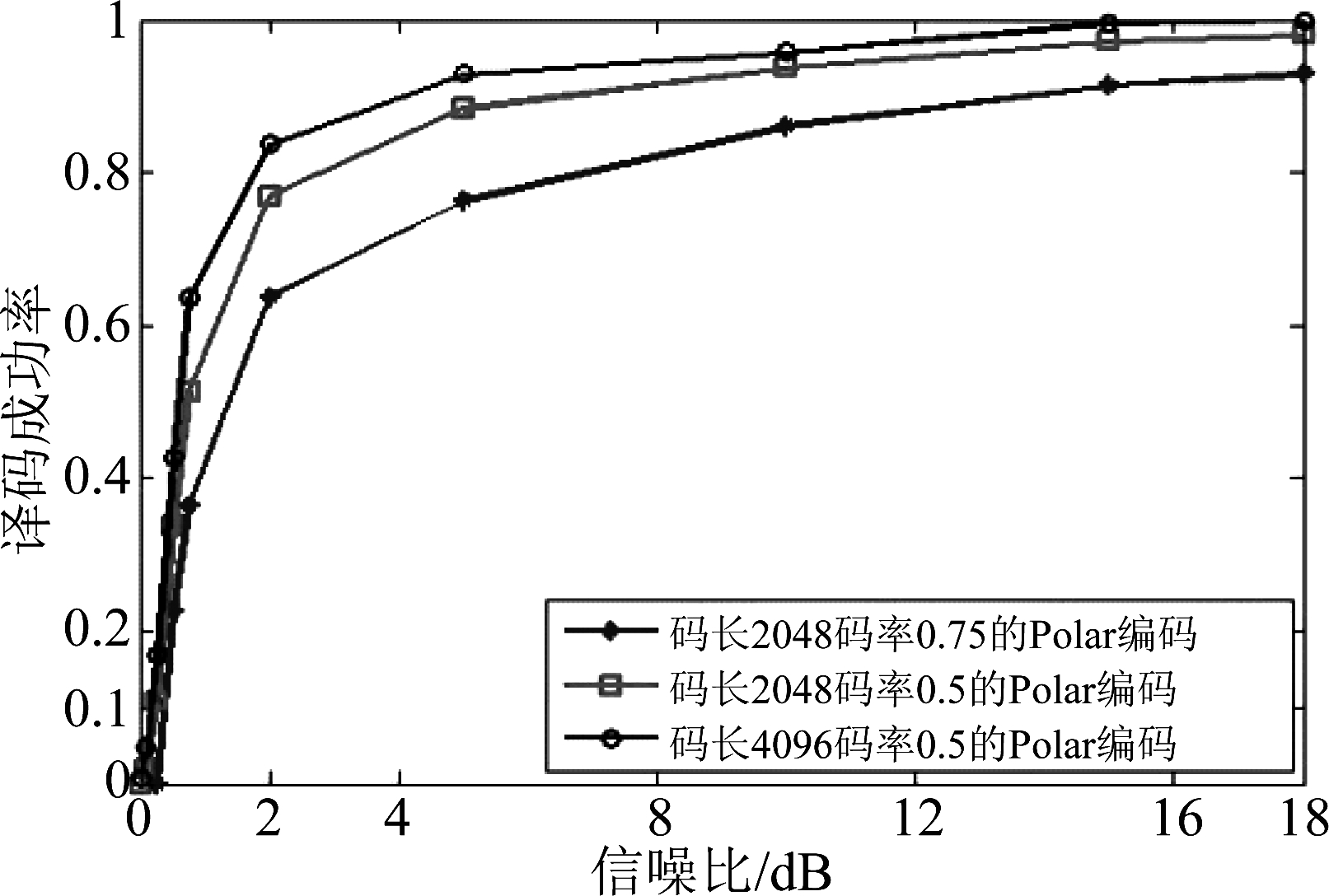
图3 Polar码译码成功率与信噪比关系图
Fig.3 The figure of the success rate of Polar decoding with different SNRs
图4是根据通信双方原始密钥的初始不一致率，对比码率为0.5，码长为2048的Polar码和LDPC码的译码成功率，得到译码成功率与初始不一致率关系图。由图3的对比图可以看出，在初始错误率很低时，LDPC码的译码成功率略高于Polar码，但是，随着初始错误率的增大即信道噪声干扰的增加，LDPC码的译码成功率下降明显而Polar码相对下降平缓并在初始错误率大于0.15后获得优于LDPC码的译码效果。总的来说，当初始错误率处于大于0.2的一段区间内，Polar码仍可获得较好的译码纠错效果，而LDPC码基本很难实现成功译码。
图4 LDPC码和Polar码初始错误率与译码成功率对比图
Fig.4 The figure of the success rate of Polar decoding with established key inconsistent rate
4 结论
本文针对无线信道特征的密钥提取技术中获得的信道特征不完全一致的问题，把Polar运用到密钥协商协议中，提出了一种基于Polar码的密钥协商方案。通过信道估计、原始密钥生成和Polar码协商，Alice和Bob可获得一致的密钥。仿真实验结果表明：码率一定时，随着信噪比的增大，基于Polar码的密钥协商协议的译码成功率越来越高；相同码率时，Polar码的码长越长其译码成功率越高；与基于LDPC码的协商协议相比，当初始错误率处于大于0.15时，基于Polar码协商协议可获得较好的纠错性能。
[1] 李古月, 胡爱群, 石乐. 无线信道的密钥生成方法[J]. 密码学报,2014, 1(3): 211-224.
Li Guyue, Hu Aiqun, Shi Le. A key generation method for a wireless channel[J]. Journal of Cryptography,2014,1(3):211-224.(in Chinese)
[2] 尚昭辉. 无线物理层密钥生成方法的研究[D]. 西安: 西安电子科技大学, 2013.
Shang Zhaohui. Research on Wireless Physical Layer Key Generation Method[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2013. (in Chinese)
[3] 马文峰, 曾贵华.量子密钥分发中Cascade协议的一种改进方案[J].量子光学学报，2010,16(4):271-275.
Ma Wenfeng, Zeng Guihua. An improvement on “Cascade” protocol in quantum key distribution[J]. Acta Sinica Quantum Optica,2010,16(4):271-275.(in Chinese)
[4] 戴峤, 金梁, 黄开枝. 基于信道特征量化的自适应密钥生成方案设计[J]. 通信学报, 2014, 35(1):191-197.
Dai Jiao, Jin Liang, Huang Kaizhi.Design of Adaptive Key Generation Scheme Based on Channel Feature Quantization[J]. Journal of Communications, 2014, 35(1):191-197. (in Chinese)
[5] Treeviriyanupab P, Sangwongngam P. Performance of 1/2 rate convolutional code on winnow protocol for quantum key reconciliation[C]∥International Symposium on Communications and Information Technologies, IEEE, 2010: 550-553.
[6] 林毅，何广强，曾贵华. LDPC码在量子密钥分配多维协商算法中的应用[J]. 量子光学学报, 2013, 19(2): 116-121.
Lin Yi, He Guangqiang, Zeng Guihua. Application of LDPC Code in Multidimensional Negotiation Algorithm of Quantum Key Distribution[J]. Journal of Quantum Optics, 2013, 19(2): 116-121.(in Chinese)
[7] Ar
kan E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transaction on Information Theory, 2009, 55: 3051-3073.
[8] Korada S,Urbanke R, Sasoglu E. Polar codes: characterization of exponent, bounds, and constructions[J]. IEEE Transaction on Information Theory, 2010, 56(12): 6253- 6264.
[9] Jouguet P, Kunz-Jacques S. High performance error correction for quantum key distribution using polar codes[J]. Quantum Information & Computation, 2012,14(3):329-338.
[10] 钱凯，赵生妹. 高斯窃听信道中删余Polar码的设计方法研究[J]. 信号处理，2014,30(11):1345-1348.
Qian Kai, Zhao Shengmei. Research on the Design Method of Puning Polar Codes in Gaussian Eavesdropping Channel[J]. Journal of Signal Processing, 2014,30(11):1345-1348. (in Chinese)
[11] 肖红，施鹏，赵生妹. 基于Polar码的纠错延后量子协商协议[J]. 中国科学：科学技术, 2015, 45(8):843- 848.
Xiao Hong, Shi Peng, Zhao Shengmei. Polar Codes Based Error Correction Delayed Quantum Negotiation Protocol[J]. Chinese Science: Science and Technology, 2015,45(8):843- 848.(in Chinese)
[12] Arikan E. Channel Polarization: A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels[J]. IEEE Transactions on Information Theory, 2008, 55(7):3051-3073.
[13] Afser H, Delic H. On the channel-specific construction of Polarcodes[J].IEEE Communications Letters, 2015, 19(9): 1480-1483.
[14] Nakassis A, Mink A. Polar codes in a QKD environment[C]∥Quantum Information and Computation XII, 2014:912305.
[15] Guo Jianfeng, Shi Zhiping, Liu Zilong. Multi-CRC Polar codes and their applications[J]. IEEE Communications Letters, 2015:211-215.
[16] Fang Yi,Bi Guoan, Guan Yongliang, et al.A Survey on Protograph LDPC Codes and Their Applications[J]. IEEE Communications Surveys & Tutorials, 2015, 17(4): 1989-2016.
[17] 王春丽, 吴晓富, 朱卫平. 利用LDPC编译码构建无线密钥协商协议的研究[J]. 信号处理, 2017,33(8):1115-1121.
Wang Chunli, Wu Xiaofu, Zhu Weiping.The Research of Using LDPC Encoding and Decoding to Structure Wireless Key Reconciliation Protocol[J]. Journal of Signal Processing, 2017,33(8):1115-1121. (in Chinese)
[18] Zhang Zhaoyang, Zhang Liang, Wang Xianbin, et al. A split-reduced Successive Cancellation List Decoder for Polar Codes[J]. IEEE Communication Letters, 2016,34(2): 292-302．
