1 引言
人对房间混响效应的感受效果与声源信号本身密切相关。众所周知，在报告厅、教室等场所，混响效应使声音听起来有一种遥远感，降低了语音可懂度，是影响语音感知质量的重要因素之一。如何有效地消除或抑制语音信号中的混响效应，对提高语音信号感知质量或语音识别率均有着重要意义，去混响也是高性能免提电话、电视电话会议系统、助听器、人机对话系统、音频监听监录系统、立体声影院、立体声汽车音响系统、多媒体等应用中的关键技术，具有广泛的应用前景[1-3]。
在房间内，混响效应由房间内声音反射面对说话人语音的多次反复反射引起。麦克风或人耳接收到的信号是声源(说话人)信号与房间内各个方向反射回来的信号的叠加，数学上表现为声源信号与房间内冲激响应的卷积。因此，语音信号去混响过程本质上是信号的解卷积过程。由于语音信号功率谱的非白性，适用于通信信道自适应均衡的一些传统方法如Bussgang算法等并不适用于语音信号的去混响[4]。
最早用于语音信号去混响的方法是基于单麦克风系统(Single input single output, SISO)的复倒谱解卷积[5]。在复倒谱域内，上述卷积关系转化为线性叠加关系，并且声源信号集中于复倒谱的低时部分，而冲激响应则集中于高时部分，故可以用低时窗滤波来消除混响。但是，由于声源信号和房间冲激响应在复倒谱域内有一定重叠，因此这种方法去混响效果并不理想。
通常情况下，为了提高去混响性能，常采用麦克风阵列，即所谓单输入多输出(Single Input Multiple Output, SIMO)系统。一方面可借助于波束形成技术实现部分语音去混响，如延时-叠加技术。这种方法可部分地消除混响，同时抑制白噪声，从而使语音信号得到增强；另一方面，可以借助于信道间的交叉关联(Cross Relation, CR)关系[7]实现房间冲激响应(Room Impulse Response, RIR)的盲辨识，在盲辨识基础上对混响信号实施逆滤波处理，从而实现声源信号恢复，即去混响目的。
如果已知房间冲激响应，则可以直接对混响信号进行逆滤波以便实现去混响[9]。但在很多情况下，房间冲激响应是未知的，且不可独立测量，那么只能根据麦克风输出信号在某种准则下对它们去混响，这类算法称之为盲去混响算法。语音获取过程的去混响算法(或称之为后补偿)基本上都属于盲去混响算法。
盲去混响算法还可以细分为倒谱分析去混响算法[5- 6]、多级线性预测分析去混响算法(Multi-Step Linear Prediction, MSLP)[10]、最大似然估计去混响算法等[12]、谱减去混响算法(Spectral Subtraction, SS)[13]等, 这些算法均为建立在SISO系统上的去混响算法，它们通过消除或抑制晚期混响以实现听觉去混响，达到语音增强的目的。而基于房间冲激响应盲辨识的逆滤波算法[15-17]、自适应逆滤波算法(不需辨识RIR，直接估计去混响系统)[18]、波束形成去混响算法(Beamforming, BF)[19]等则是建立在SIMO (或MIMO)系统上的盲去混响算法，它们通过完全恢复声源信号以实现去混响的目的。除此之外，尚有很多出于不同应用目标、利用混响语音信号不同特性的去混响方法，如在[21]中提出的语音特征参数域去混响方法可直接应用在自动语音识别(Automatic Speech Recognition, ASR)中；利用混响语音相对于声源语音在时间、频率域内的稀疏性改变，通过时频域内稀疏性最大化实现去混响[22]。已有的这些去混响方法抗噪声性能弱，在有噪声环境中很难达到理想效果。此外，目前流行的深度神经网络方法也广泛应用于语音去混响，并获得不错的去混响效果，其缺点是需要较长的训练学习过程[25]。
在短时傅里叶变换(STFT)域内，文献[29]提出卡尔曼滤波和EM算法相结合的去混响算法，即在E步用卡尔曼滤波进行声源信号估计，而在M步对噪声强度和房间冲激响应进行最大似然估计；而文献[30]提出对混响信号采用自回归模型并建立卡尔曼滤波问题，在该模型中声源信号看成是过程噪声，并且需要对其自相关矩阵进行最大似然估计。在[31]中不仅考虑混响信号的自回归模型，同时考虑声源信号的隐马尔可夫模型。文献[29]所提方法给出不错的结果，但美中不足的是它未充分利用SIMO系统输出信号之间的交叉关联关系进一步提高去混响效果。
2 混响效应数学模型与去混响系统
对于SIMO系统，设房间中有N个麦克风，第i个麦克风接收到的数字化混响语音信号(即观测信号)为xi(n) (i=1, 2, …, N; n为时间)，则观测信号与声源信号s(n)之间的关系为:
(1)
其中,hi(k)是第i个麦克风与声源之间的房间冲激响应,长度为L；νi(n)为第i个观测信号的观测噪声，为零均值、方差为
的高斯白噪声。同时假设各路观测噪声之间互不相关，且与声源信号也不相关。
去混响过程就是从观测信号xi(n)(i=1,2,…,N)恢复声源信号s(n)的过程。当然，也可以从听觉感知角度去混响，即不完全解卷积过程[10]。Miyoshi等人证明[7]，如果N个观测信号所对应的N个房间冲激响应不存在公共零点，则可以由这N个观测信号准确重建声源信号
(在忽略噪声影响的情况下)，即
(2)
其中gi(n)(i=1,2,…,N)为去混响滤波器组，其长度为Lg。令去混响滤波器组矢量
(NLg×1维矢量，其中gi=[gi(0),gi(1),…,gi(Lg-1)]T)，及房间冲激响应矩阵
其中
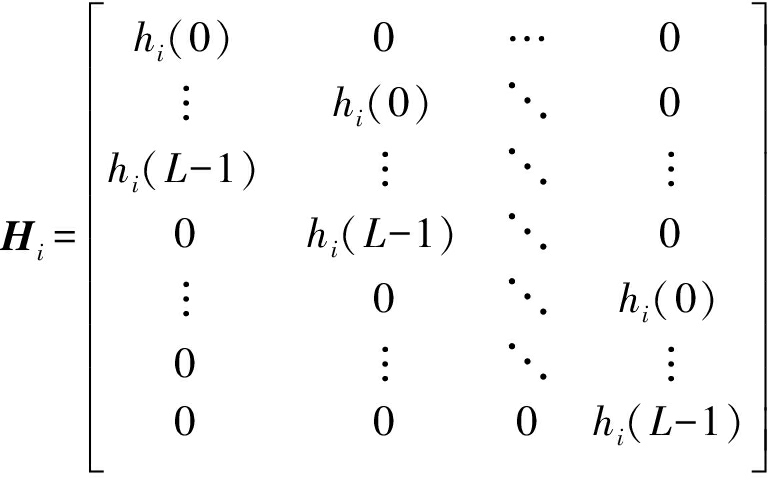
为(L+Lg-1)×Lg的卷积矩阵，则去混响滤波器组矢量g满足如下方程：
(3)
其中ui是(L+Lg-1)维矢量空间的第i个标准正交基底矢量。这时去混响滤波器的长度需满足条件：Lg≥
(·表示向上舍入取整)，说明麦克风越多，所需的去混响滤波器的长度越短。式(3)是熟知的MINT定理。该式说明，对于SIMO系统，可以通过增加麦克风数来降低去混响滤波器的阶数。
MINT定理说明了去混响滤波器与造成混响效应的房间冲激响应之间的关系。只要能把房间冲激响应估计出来，就可以根据MINT定理来确定去混响滤波器。但是实践表明，MINT定理给出的去混响滤波器对房间冲激响应的估计误差很敏感，这种方法实践中并不可行。
3 基于交叉关联关系的反幂法SIMO系统盲辨识
在本节中将给出基于信道间交叉关联关系和反幂法的房间冲激响应估计新算法。基于二阶统计量的多信道盲辨识是建立在如下的信道间交叉关联关系基础上的[7]，即，
[xi(n)-νi(n)]*hj(n)=[xj(n)-νj(n)]*hi(n)
(4)
其中,i, j=1,2,…,N;i≠j;“*”为卷积算符。
令
其中hi=[hi(0),hi(1),…,hi(L-1)]T)表示由N路房间冲激响应构成的(NL×1)维列矢量；C(n)和V(n)分别表示由观测信号和观测噪声构成的
维矩阵：
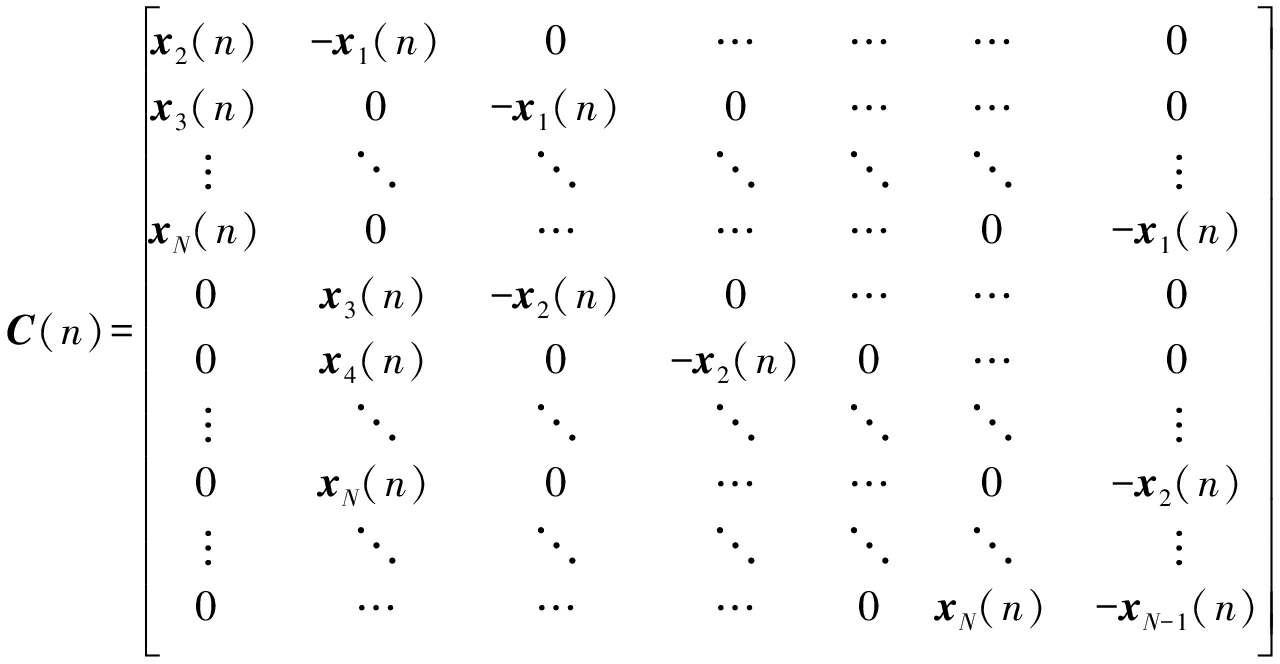
(5)
和
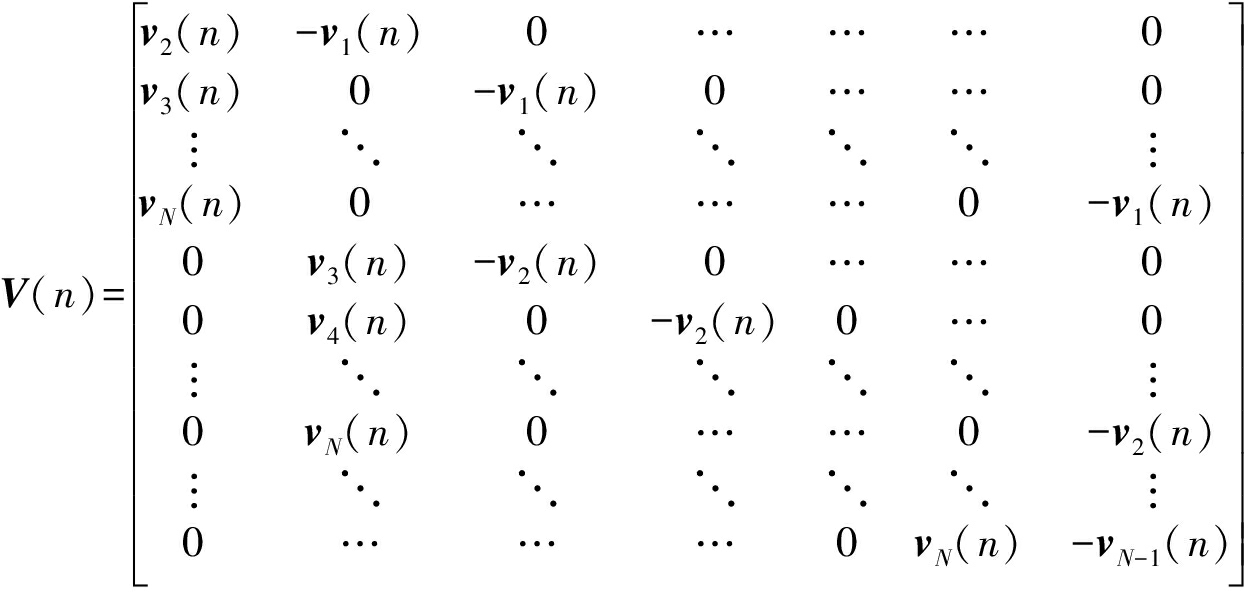
(6)
其中，在式(5)和式(6)中，(1×L)维行矢量xi(n)=[xi(n),xi(n-1),…,xi(n-L+1)]和vi(n)=[νi(n),νi(n-1),…,νi(n-L+1)]，则式(4)中的交叉关联关系公式可以写成如下的矩阵形式：
[C(n)-V(n)]h=0
(7)
对式(7)两边同时左乘[C(n)-V(n)]T并取统计平均，同时令R(n)=E[CT(n)C(n)](其中, E[·]表示进行统计平均操作)，则有：
(8)
其中I为NL×NL的单位矩阵。由于矩阵
为非负定矩阵，因此式(8)意味着非零矢量h是矩阵最小特征值(为零)对应的特征矢量(简称之为最小特征矢量)。
定义矩阵R(n)的特征值为λi(i=1,2,…,NL)，则易证矩阵
的特征值为
因此有
这说明
是R(n)的最小特征值，这也说明在有噪声情况下，R(n)是正定矩阵。由式(8)得，
(9)
这说明非零矢量h也是矩阵R(n)的最小特征值
对应的特征矢量。因此只要求得矩阵R(n)的最小特征矢量，就实现了SIMO系统盲辨识。
对于(NL×NL)维矩阵R(n)，其最小特征矢量可以采用反幂法(Inverse Power Method)迭代求解以便降低计算复杂度。令h0为h的初值，则反幂法最小特征矢量的迭代过程为在hk已知的前提下求解hk+1(迭代次数k=0,1,2,…)：
(10)
式(10)即为建立在交叉关联关系基础上的反幂法SIMO系统盲辨识算法。如果考虑到房间冲激响应的时变性，那么n时刻房间冲激响应矢量由反幂法给出的迭代过程可以表示如下：
(11)
其中，式(11)中的n代表时间，而上标k代表n时刻h(n)的迭代次数。在上式中，每一时刻的反幂法迭代初值是前一时刻的迭代结果。无论是时变系统还是非时变系统，相邻时刻的房间冲激响应总是高度相关的，因此在每一时刻对反幂法甚至可以只做一次迭代，从而得到如下的基于反幂法的系统自适应盲辨识算法(在前一时刻h(n-1)已知的前提下求解h(n))：
(12)
4 基于卡尔曼滤波的多路信号解卷积算法
在已知房间冲激响应的情况下，利用卡尔曼滤波进行解卷积(去混响)不需要利用MINT定理进行逆系统估计，而是直接估计出解卷积信号，有利于提高系统的噪声稳定性。
利用卡尔曼滤波进行解卷积的关键是建立卡尔曼滤波模型，包括过程方程和测量方程。
令X(n)=[x1(n),x2(n),…,xN(n)]T 为n时刻观测信号矢量；n时刻状态矢量为声源信号s(n)构成的矢量S(n)=[s(n),s(n-1),…,s(n-L+1)]T；n时刻测量矩阵H(n)=[h1,h2,…,hN]T由反幂法估计得到的房间冲激响应构成(反幂法(11)或(12)中得到的h(n)矢量重新排列得到！)，则多路信号解卷积的卡尔曼滤波问题描述如下：
过程方程:
S(n+1)=W(n+1,n)S(n)+u1(n)
(13)
测量方程：
X(n)=H(n)S(n)+u2(n)
(14)
其中，u1(n)和u2(n)分别为均值为零的过程白噪声和测量白噪声，它们各自的协方差矩阵分别为
和
状态转移矩阵定义为：
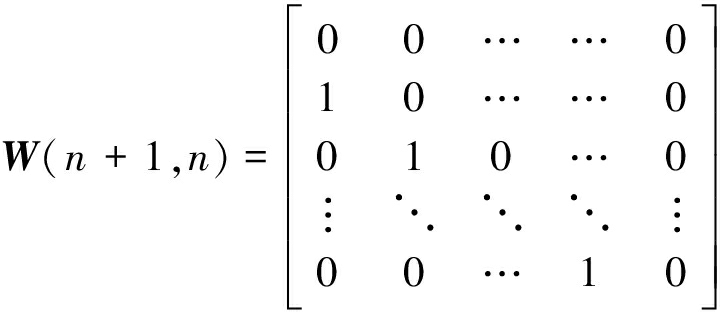
(15)
此外，W(n,n+1)=WT(n+1,n)。
状态矢量的实际更迭过程应该是S(n+1)=W(n+1,n)S(n)+[1,0,…,0]Ts(n+1)+噪声项，而在过程方程中，直接把[1,0,…,0]Ts(n+1)和噪声项看成是过程噪声u1(n)(但其第一个分量的方差要远大于其他分量的方差，见表1)，实践表明，这样做是可行的。
由卡尔曼滤波器输出的n时刻声源信号：
s(n)=S(n+1)的第L个分量
(16)
5 SIMO系统自适应去混响新算法
当把式(12)中给出的自适应盲辨识算法与基于卡尔曼滤波的多路信号解卷积算法相结合后，就得到了一种SIMO系统自适应去混响新算法。新算法的迭代步骤列于表1中，对应的系统框图如图1所示。
在新算法的系统辨识阶段，反幂法需要进行线性方程组的求解：R(n)h(n)=h(n-1)。由于R(n)是对称正定矩阵，因此可以采用乔莱斯基分解法求解，可以显著减少计算量。当然也可以采用LU分解或QR分解来求解。
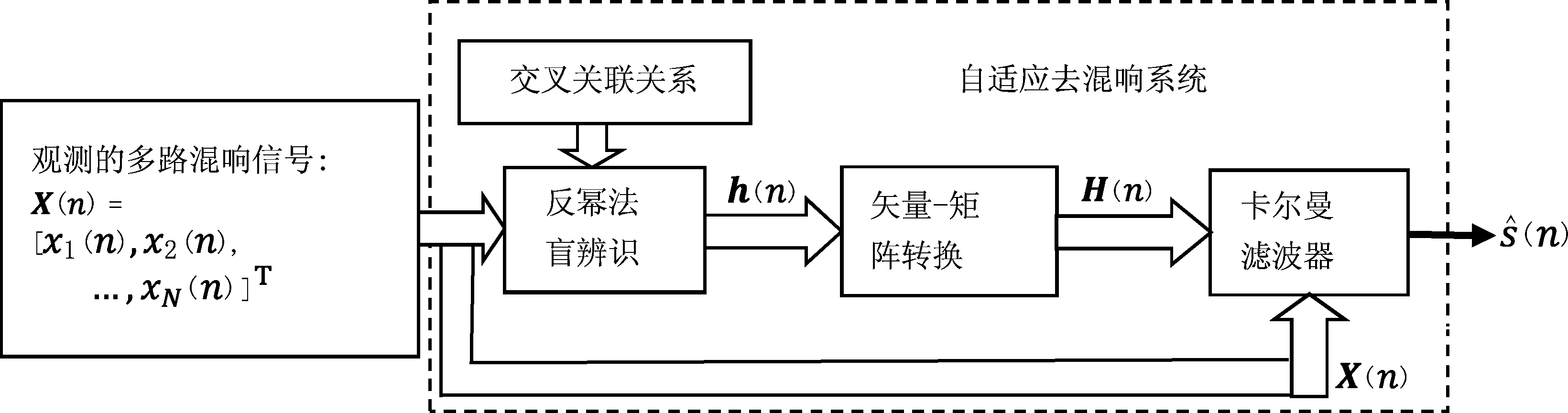
图1 基于反幂法和卡尔曼滤波的SIMO系统自适应去混响算法的系统框图
Fig.1 The system diagram of the adaptive dereverberation algorithm based on inverse power method and Kalman filter
表1 SIMO系统自适应去混响新算法
Tab.1 The proposed dereverberation algorithm for SIMO system
6 实验与讨论
为了评估新算法的性能，进行了仿真实验和真实实验。在仿真实验中，采用实测房间冲激响应与无噪声语音进行卷积而得到仿真的混响信号，并且在混响信号中增加不同强度的噪声来模拟不同信噪比下的实测混响语音信号。仿真实验中所需的房间冲激响应与真实实验中所用到的实测混响信号是在同一个实验过程中获得的。具体实施过程如下。
在一个相对封闭且安静的会议室(约10 m×6 m×3 m)中用扬声器播放一段语音(该语音已知，这里称之为声源信号，声源信号时长3.98 s，连续重复播放8次)，用四个与扬声器距离分别为1 m、2 m、3 m、4 m的麦克风进行录音，得到四路实测的混响语音信号(分别对应声道1～4)，录音时间长度31.9 s，初始采样率为64 kHz。由于房间冲激响应持续时间比较长，为了降低数据量和计算量，对获得的数据通过降采样算法降低采样率，在房间冲激响应辨识和去混响阶段所用采样率为8 kHz。
大量的计算表明，无论是用仿真数据对新算法进行性能测试，还是利用新算法对实测信号进行处理时，下面两种数据预处理措施和后滤波处理是必要的，可以显著改善新算法的去混响性能。
预处理措施：首先，通过时延估计对四路混响信号进行时延补偿处理，使得时延补偿后的四路麦克风信号(或仿真信号)中的直达信号分量对齐。这样估计得到的房间冲激响应的主脉冲是对齐的。其次，对混响语音信号进行预白化处理。其过程如下：先计算其中一路混响信号的50阶线性预测系数，然后利用该线性预测系数对四路混响语音信号分别进行预白化滤波，得到预白化混响信号。预白化信号仍然满足交叉关联关系。
后滤波处理：仿真实验发现，卡尔曼滤波会使去混响信号的极低频和极高频分量过份放大，对卡尔曼滤波器输出的解卷积信号的后带通滤波处理可以很好地解决这个问题。
6.1 仿真实验
首先，利用LMS算法由四路实测混响信号和已知的声源信号得到四路实测房间冲激响应，用hLMS表示，用于本文所提出算法的仿真实验。
在利用LMS算法进行房间冲激响应辨识时，只追求辨识精度而不要求收敛速度，因此尽量降低LMS算法中的学习步长参数。最后采用声源信号平均功率与LMS算法输出的误差信号的平均功率之比(暂称之为信号干扰比)来衡量算法是否收敛。在算法收敛后该值也大体上反映了实测信号的噪声水平，用分贝数表示，即
SIR=-10log10(P声源功率/P误差功率)(dB)
(17)
在本实验中，房间冲激响应的长度为L=1300点(采样率为8 kHz)，公式(17)给出的四路实测信号相应的信号干扰比分别为(29.24 dB，26.23 dB，24.98 dB，24.08 dB)。说明麦克风离声源越近，信号干扰比越高，房间冲激响应估计的越准。
用声源信号与hLMS进行卷积，并对其增加给定强度的高斯白噪声，用于模拟实测混响语音信号。利用本文所提基于反幂法的盲辨识算法所得房间冲激响应辨识结果用hNEW表示。用四路房间冲激响应的平均NPM(Normalized Projection Misalignment)来表示hNEW 与hLMS之间的差距：
NPM=10log10(1-r2)(dB)
(18)
其中，
仿真时，在矩阵R(n)的估计公式中(见表1)，设定λ=0.99999；为了加速收敛，反幂法的迭代次数设定为111。
在混响信号的信噪比SNR=30 dB时，算法收敛后hNEW 与hLMS的比较见图2。当SNR=30 dB，40 dB，50 dB，60 dB，70 dB时，代表反幂法盲辨识算法收敛特性的NPM曲线如图3所示，说明建立在反幂法基础上的新辨识算法对噪声很不敏感，即具有噪声鲁棒性。当信噪比进一步提高到大于100 dB时，NPM迅速下降，几乎可以准确辨识系统。
在研究去混响效果时发现，由卡尔曼滤波器输出的去混响信号的低频与高频部分均被不合理地放大了，因此必须对其进行带通滤波，消除低频畸变和高频噪声。在本实验中，所用的201点FIR带通滤波器的通带范围为[100,3000]Hz，可以显著改善去混响信号的波形。在图4中给出的是声源信号(1)、混响信号(2)、去混响信号(3, 4)(分别用hLMS 和hNEW去混响)波形比较。在图5中给出的是图4中方框区域的放大图。从图4、图5可以看出，在波形上，去混响信号(3, 4)要比混响信号(2)更接近声源信号(1)。当然，去混响信号(3)比(4)更好些。在图6中给出的是去混响信号(3, 4)相对声源信号的全局响应，与房间冲激响应hLMS相比能量更集中，衰减更快，说明混响效应得到有效抑制。从听觉感知角度来评价的话，去混响信号(3, 4)几乎听不到混响效应，但会听见较弱的背景噪音。总体效果还是比较令人满意的。
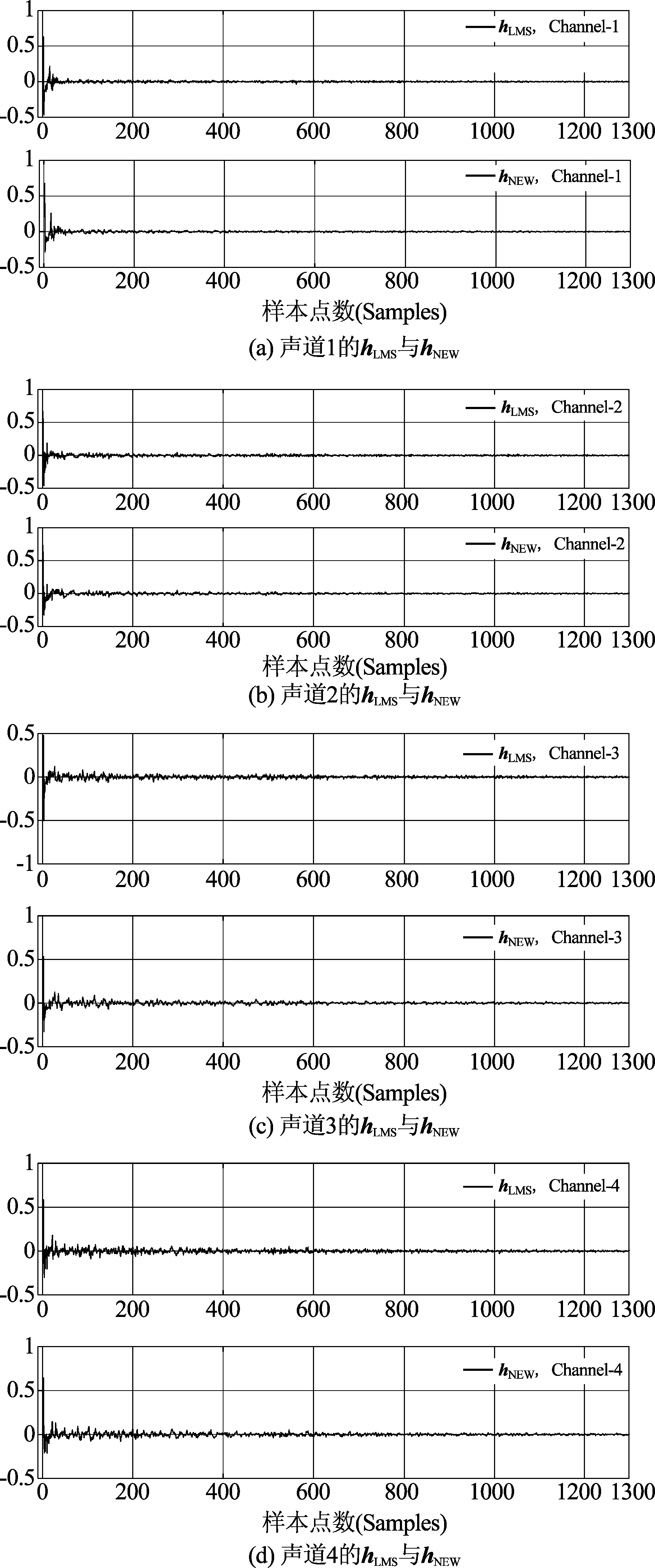
图2 仿真实验：由四路仿真含噪混响信号经新盲辨识方法辨识的房间冲激响应hNEW与hLMS的比较(SNR=30 dB)
Fig.2 Simulations: comparison between the blindly identified room impulse responses hNEW and hLMS(SNR=30 dB)
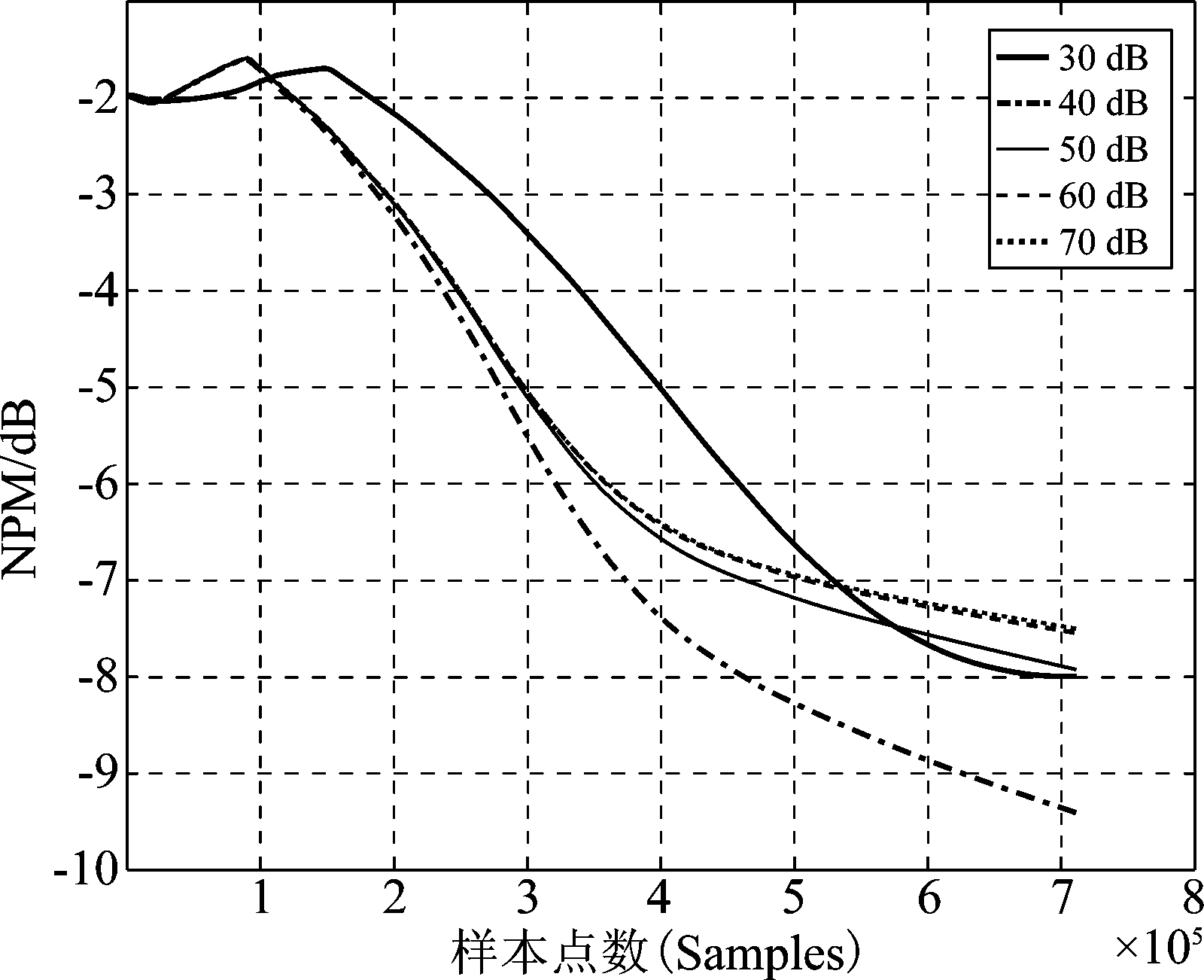
图3 仿真实验：仿真信号在不同信噪比下进行RIR辨识时的NPM曲线
Fig.3 Simulations: the NPM of the identified RIR under different SNR of the simulated reverberant signals
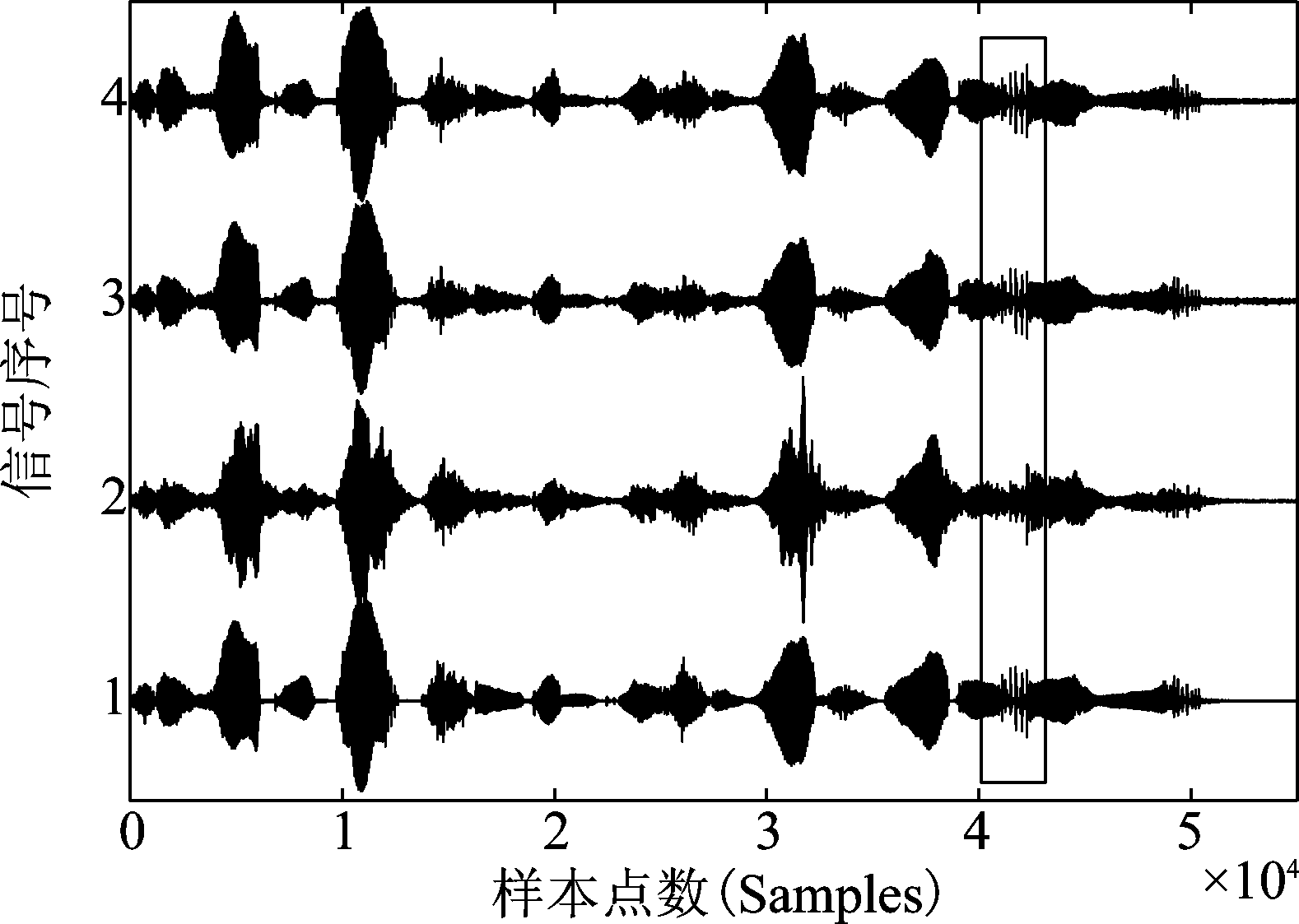
图4 仿真实验：声源信号(1)、仿真混响信号(2)、去混响信号 (3:用hLMS去混响；4: 用hNEW去混响)波形比较
Fig.4 Simulations: the source speech signal (1), the simulated reverberant signal (2) and the dereverberated signals (3: dereverberation with hLMS; 4: dereverberation with hNEW)
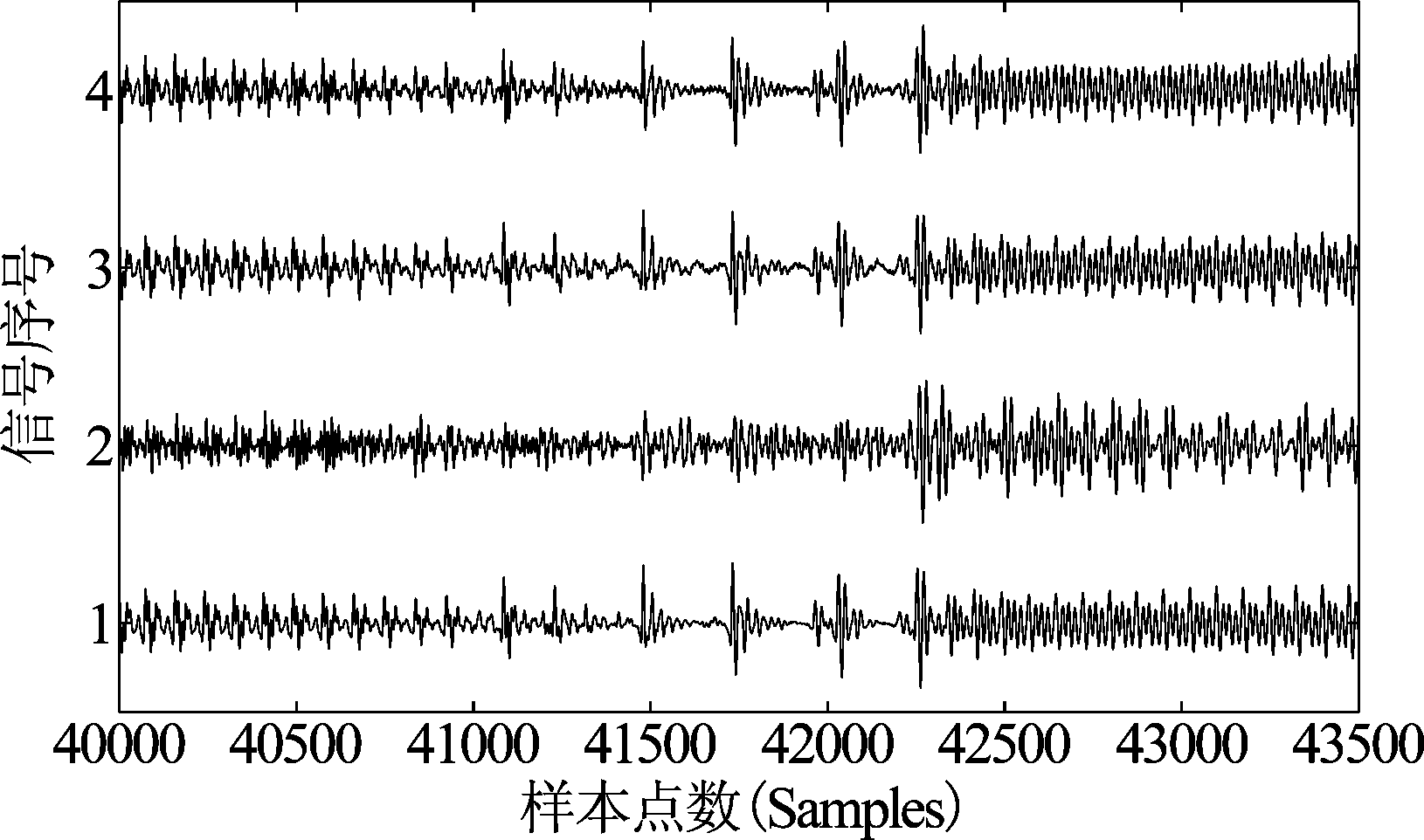
图5 图4中方框区域波形的放大图
Fig.5 The zoomed-in graph of the part in rectangle in Figure 4
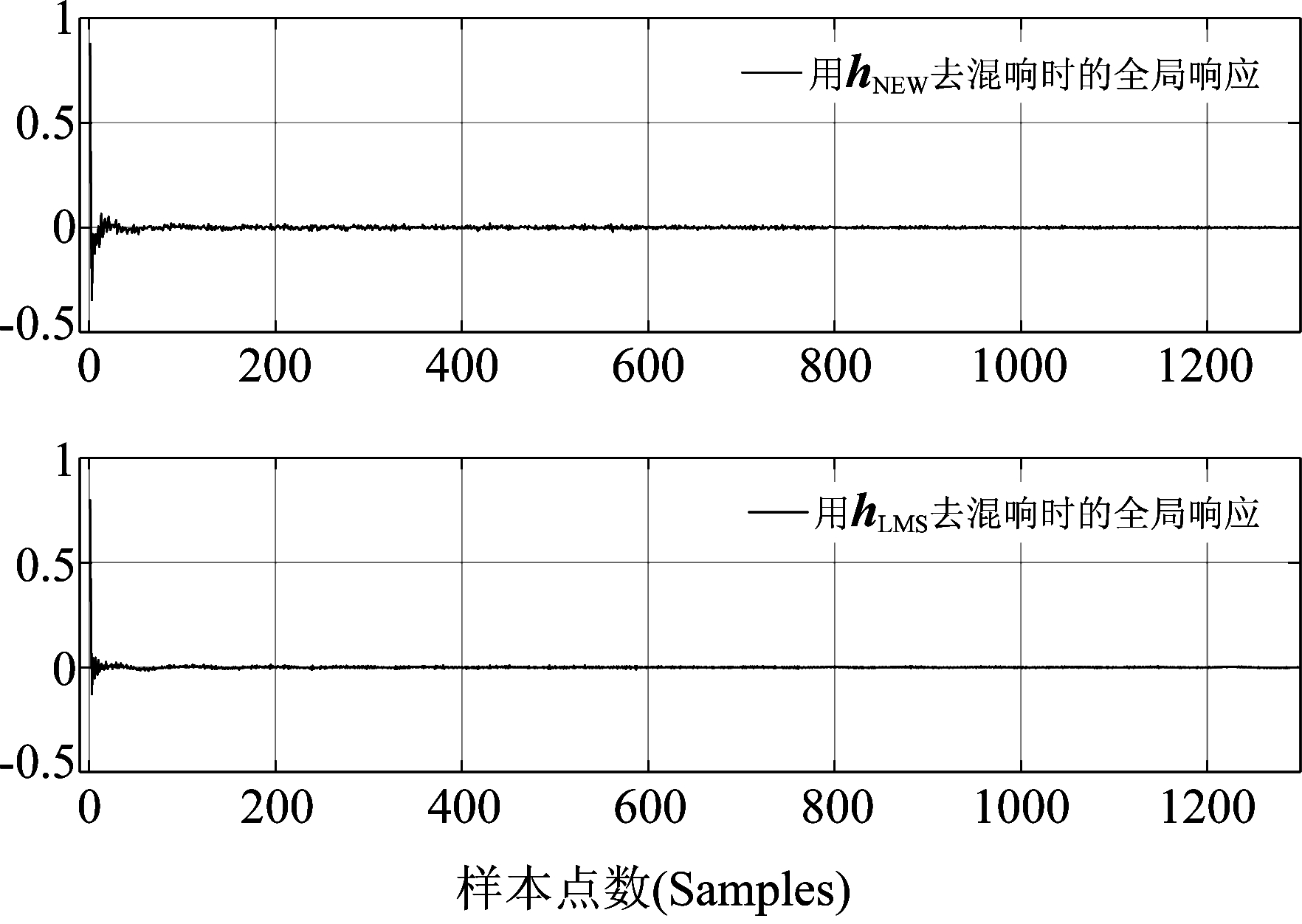
图6 仿真实验：去混响信号(图4中信号3、4)相对于声源信号的全局响应
Fig.6 Simulations: the global impulse response between the dereverberated signals (the 3rd and 4th signals in Figure 4) and source speech signal
6.2 真实实验
在本实验中，不需要声源信号的任何信息，直接由实测的4路麦克风输出信号利用本文所给出的盲辨识算法来辨识房间冲激响应，用
表示，并同时用对4路麦克风输出信号进行卡尔曼滤波解卷积。算法收敛后，盲估计房间冲激响应如图7所示。在辨识的过程中，把hLMS(见图2)作为是否收敛的判断标准。相对hLMS的动态NPM曲线如图8所示，图中NPM曲线上的折点是由于数据重用造成的。
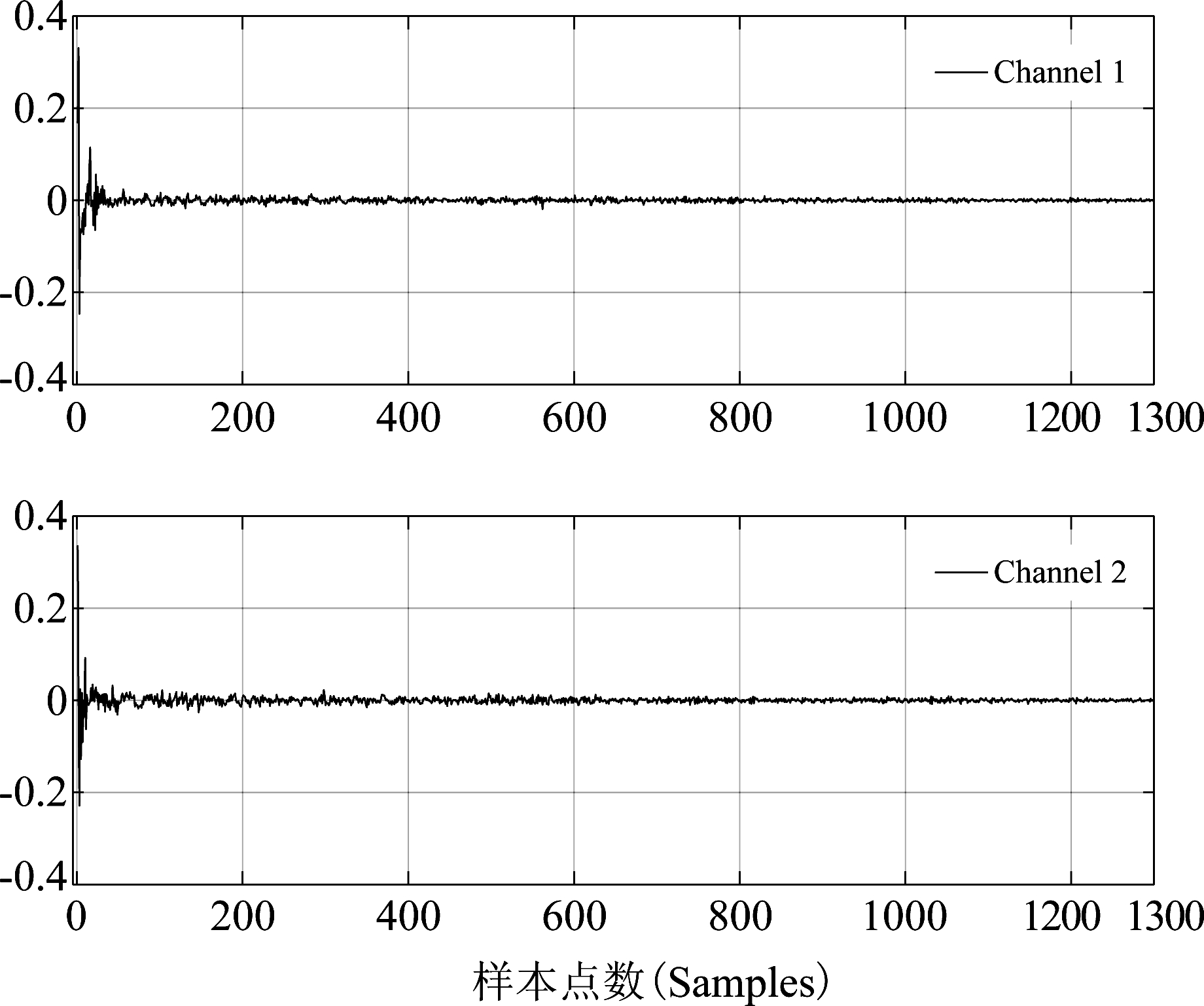
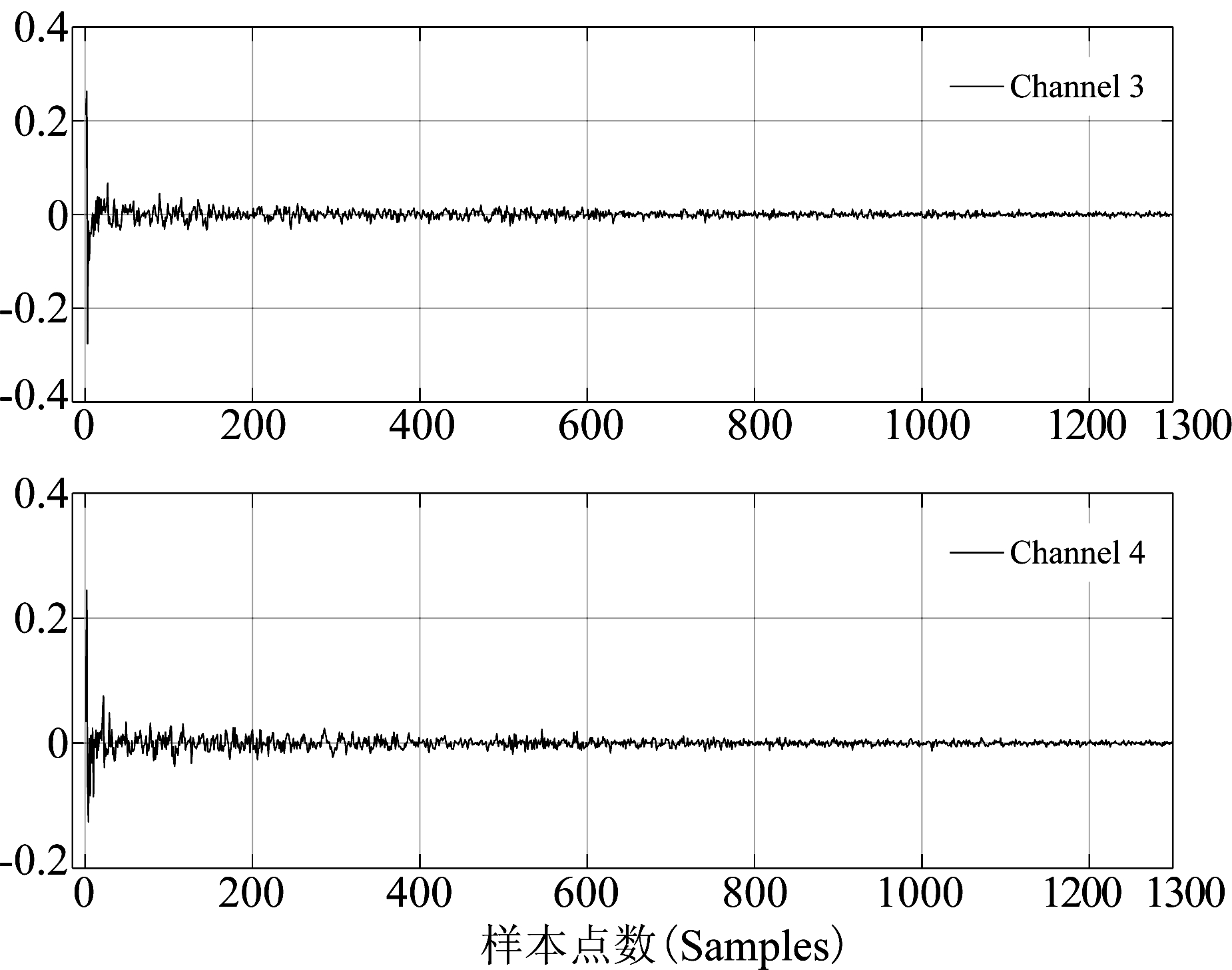
图7 真实实验：由实测数据用新盲辨识算法得到的4路房间冲激响应
Fig.7 Experiments: the four channel impulse responses identified with the proposed algorithm (from top to bottom: channel 1- 4)
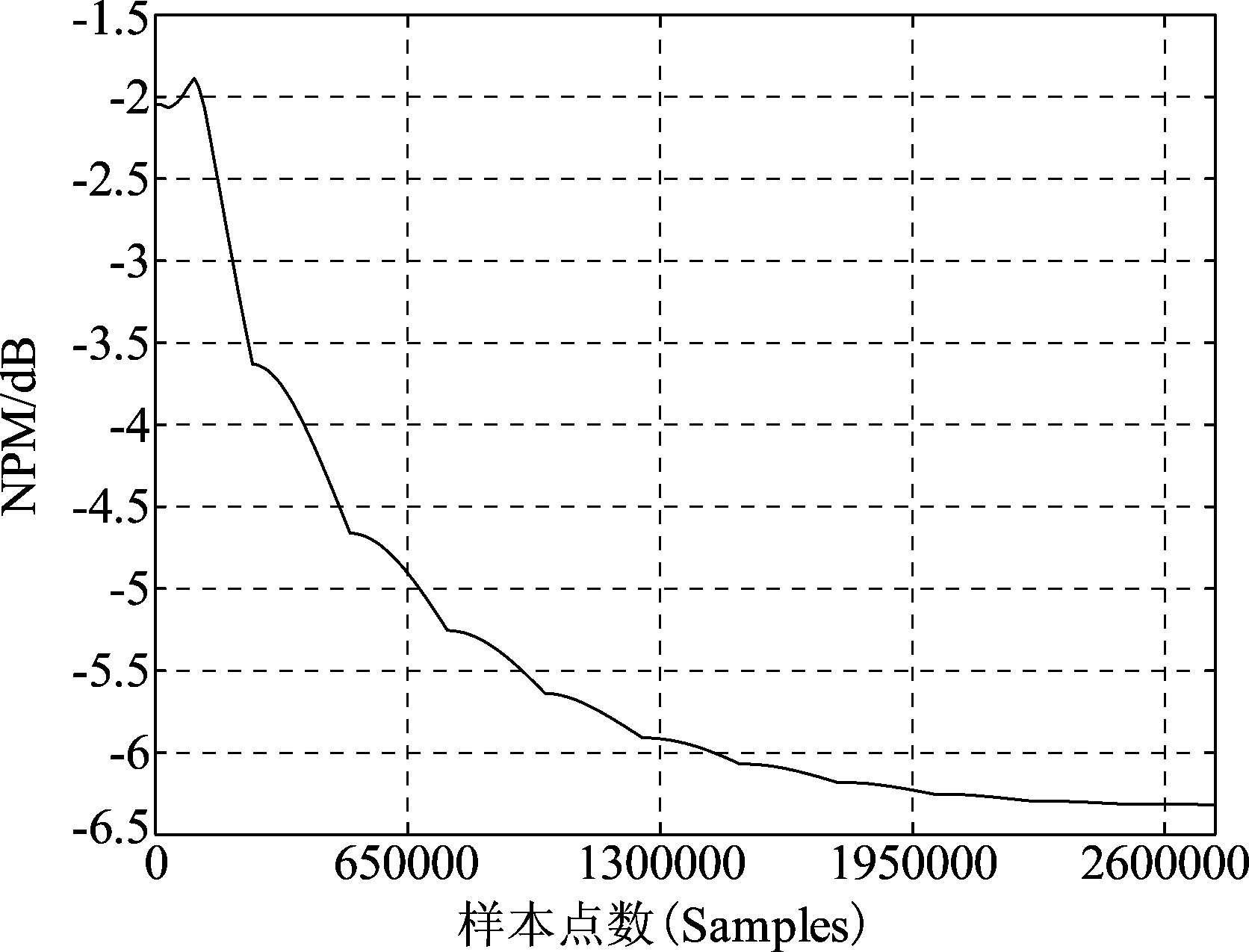
图8 真实实验：实测数据盲冲激响应辨识时相对hLMS的动态NPM曲线
Fig.8 Experiments: the dynamic NPM of the blind identification of (comparing with hLMS) from the real recorded signals
在图9中给出了声源信号、实测混响信号及去混响信号波形比较。无论是从波形比较，还是听觉测试，实测信号的混响效应经去混响处理后得到明显削弱。
图10 给出的是由盲辨识算法得到的各声道房间冲激响应
去混响信号(图9中信号3)相对于声源信号(图9中信号1)的全局响应(主脉冲归一化后的结果)。由图可见，去混响信号的全局响应比实际房间冲激响应能量更集中于主脉冲，说明经过去混响处理后，混响效应得到明显削弱。
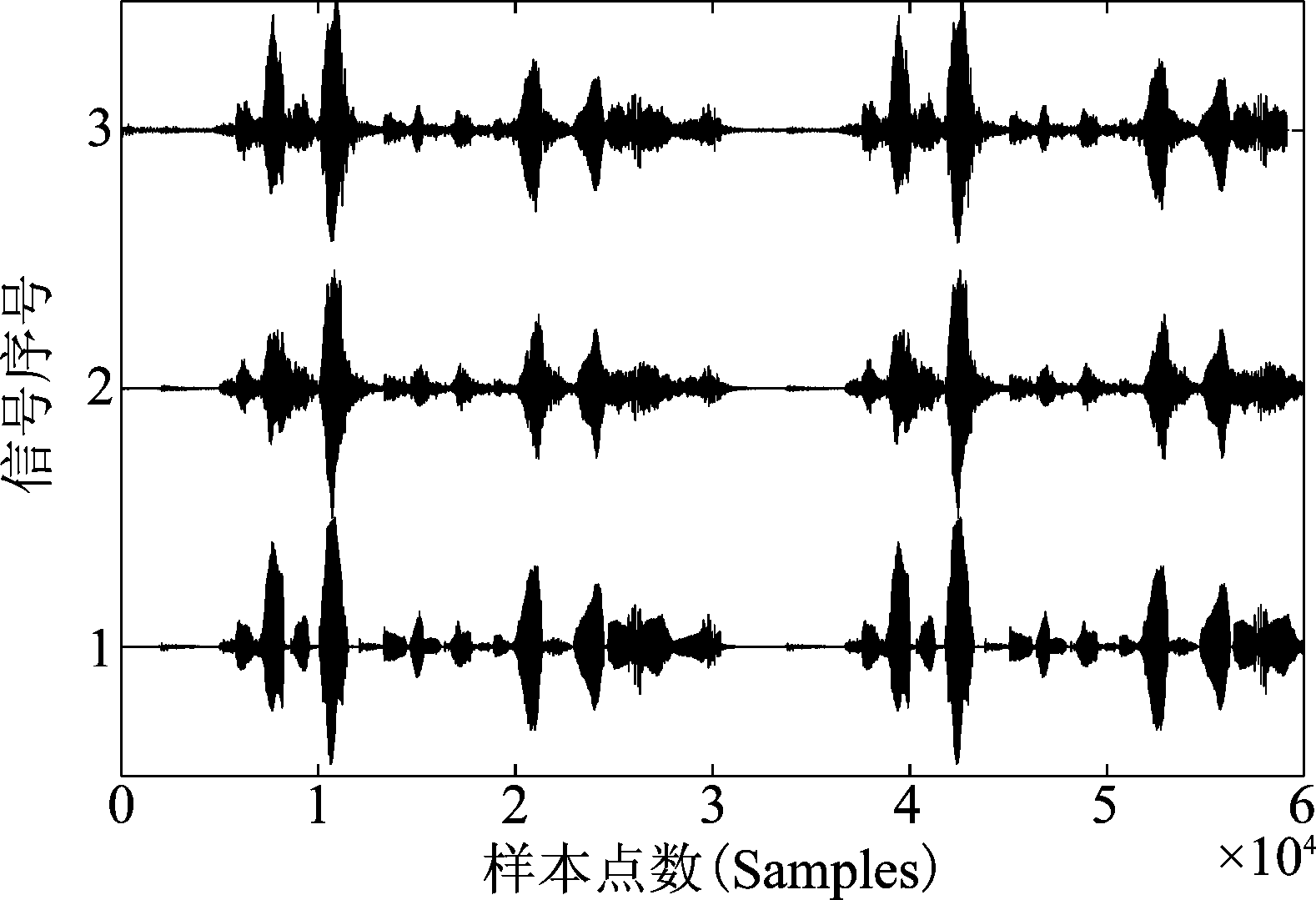
图9 真实实验：声源信号(1)、实测混响信号(2: 声道4)、去混响信号(3)波形比较
Fig.9 Experiments: the source speech signal (1), real recorded signal (2: channel 4) and the dereverberated signal (3)
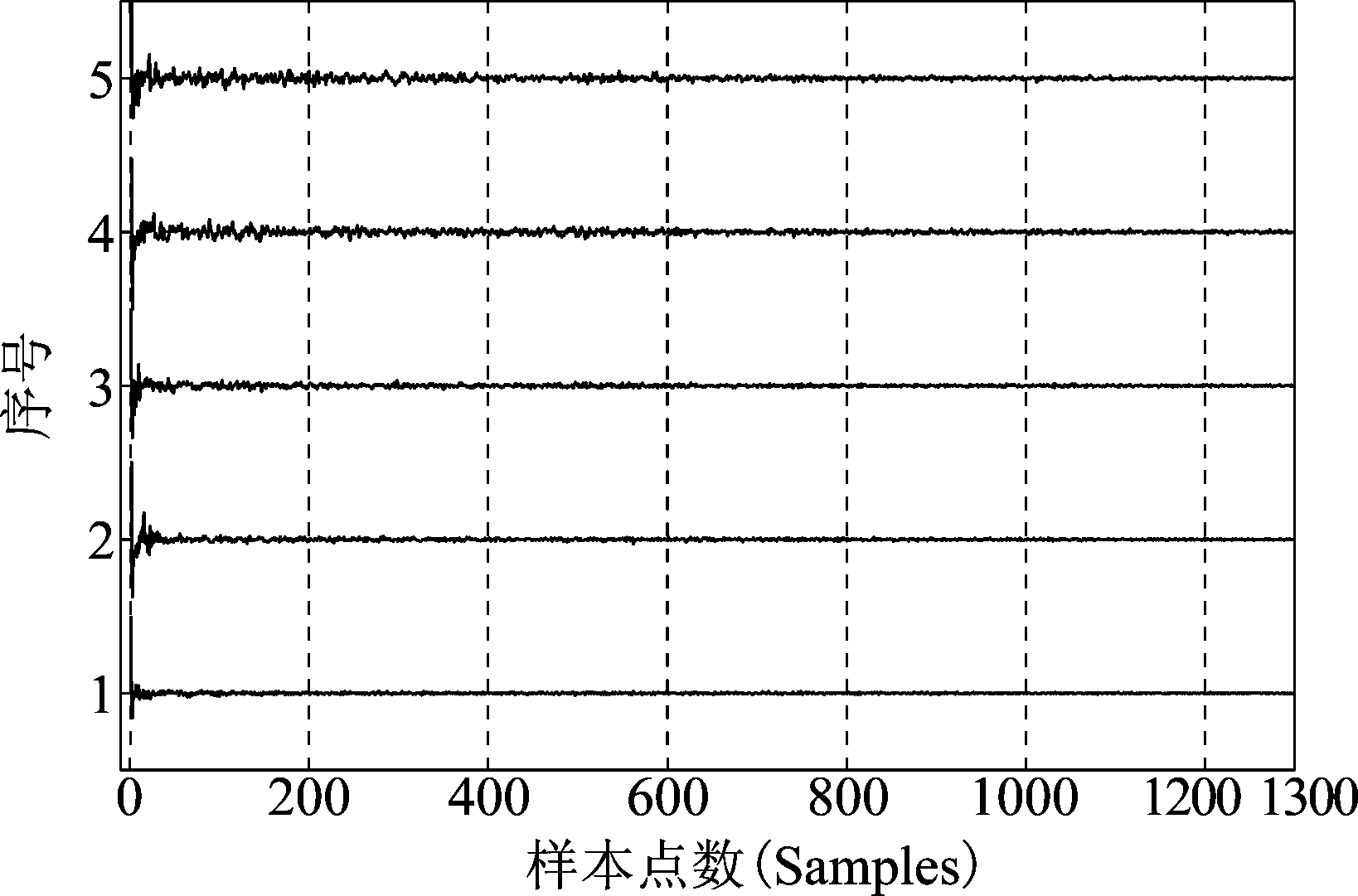
图10 真实实验：实测信号去混响后的全局响应与各路房间冲激响应比较(各路响应的主脉冲归一化)。(1)去混响信号的全局响应；(2～5)由四路实测信号盲辨识得到的房间冲激响应
Fig.10 Experiments: the global impulse response of the dereverberated signal and the four blindly identified room impulse responses from the real recorded signals (from bottom to top, the main pulse is normalized for each channel
6.3 与其他算法的比较
在语音去混响中，由于房间冲激响应的超长性，语音信号的非白性等因素的影响，去混响算法的噪声鲁棒性都比较差。通常来说，晚期混响抑制算法的噪声鲁棒性更好些，但是去混响性能有限；而逆滤波去混响算法鲁棒性会相对较差，但是在信噪比较高的情况下，其去混响性能要更好些。新算法对于安静环境下实测语音信号的去混响效果可以与文献[30]所给的结果相媲美，但新算法的计算复杂度要低于后者[注]参见https:∥www.audiolabs-erlangen.de/resources/ 2016-SPL-MAR-KALMAN。
7 结论
本文所提出的基于SIMO系统输出信号交叉关联关系和反幂法最小特征向量求解的SIMO系统盲辨识方法是可行的，并具有较好的抗噪声性能；盲辨识算法与卡尔曼滤波解卷积方法的有机结合为我们提供了实时SIMO系统解卷积的可能性。对观测信号的预处理(时延对齐、预白化)和对解卷积信号的后处理(带通滤波)是必要的。仿真与实验研究表明，本文所提出的方法可以实时地有效削弱房间的混响效应，并具有较好的噪声鲁棒性。
[1] Kellermann W, Buchner H, Herbordt W, et al. Multichannel acoustic signal processing for human/machine interfaces-fundamental problems and recent advances[C]∥ International Commission for Acoustics (ICA) Proceedings of International Congress on Acoustics, Kyoto, Japan, 2004,1: 243-250.
[2] Kinoshita K, Nakatani T, Miyoshi M. Efficient blind dereverberation framework for automatic speech recognition[C]∥Proceedings of INTERSPEECH 2005-Eurospeech, European Conference on Speech Communication and Technology, Lisbon, Portugal, 2005: 3145-3148.
[3] Kinoshita K, Delcroix M, Gannot S, et al. A summary of the REVERB challenge: state-of-the-art and remaining challenges in reverberant speech processing research[J]. EURASIP Journal on Advances in Signal Processing (2016), 2016:7. https:∥doi.org/10.1186/s13634- 016- 0306- 6.
[4] Haykin S. Adaptive filter theory[M]. Third edition. Original Edition Published by Prentice-Hall, 1996: 302-321, 323-324.
[5] Bees D, Blostein M, Kabal P. Reverberant speech enhancement using cepstral processing[C]∥Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Toronto, Ontario, Canada,1991, II: 977-980.
[6] 沈希忠, 孟光. 单通道的语音盲去混响[J]. 上海交通大学学报, 2010, 44(2): 229-233.
Shen Xizhong, Meng Guang. Speech dereverberation of single channel[J]. Journal of Shanghai Jiaotong University, 2010, 44(2): 229-233. (in Chinese)
[7] Xu G, Liu H, Tong L, et al. A least-square approach to blind channel identification[J]. IEEE Transactions on Signal Processing, 1995, 43(12): 2982-2993.
[8] Avendano C, Benesty J, Morgan D R. A least squares component normalization approach to blind channel identification[C]∥Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Phoenix, USA, 1999, 4: 1797-1800.
[9] Miyoshi M, Kaneda Y. Inverse filtering of room acoustics[J]∥IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(2): 145-152.
[10] Kinoshita K, Delcroix M, Nakatani T, et al. Suppression of Late Reverberation Effect on Speech Signal Using Long-Term Multiple-step Linear Prediction[J]. IEEE Transactions on Audio Speech and Language Processing, 2009, 17(4):534-545.
[11] 赵红，李双田. 改进的多级线性预测晚期混响抑制算法[J]. 信号处理，2014, 30(6): 674- 682.
Zhao Hong, Li Shuangtian.Improved late reverberation suppression algorithm using multiple step linear prediction[J]. Journal of Signal Processing, 2014, 30(6): 674- 682. (in Chinese)
[12] Yoshioka T, Nakatani T, Hikichi T, et al. Maximum likelihood approach to speech enhancement for noisy reverberant signals[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, Nevada, USA, 2008: 4585- 4588.
[13] Chen Zhe, Wang Rui, Yin Fuliang, et al. Speech dereverberation method based on spectral subtraction and spectral line enhancement[J]. Applied Acoustics, 2016, 112: 201-210.
[14] Kinoshita K, Nakatani T, Miyoshi M. Spectral subtraction steered by multi-step forward linear prediction for single channel speech dereverberation[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Toulouse, France, 2006, I: 817- 820.
[15] Mei Tiemin, Hang Pengcheng, Mertins A. Adaptive estimation and reshaping of room impulse response[J]. International Journal of Speech Technology, 2014, 18(1): 91-95.
[16] Huang Yiteng, Benesty J, Chen J. Speech acquisition and enhancement in a reverberant, cocktail-party-like environment[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Toulouse, France, 2006, v: 25-28.
[17] Gannot S. Multi-microphone speech dereverberation based on eigen-decomposition: A study[C]∥Signals, Systems and Computers, 2008, Asilomar Conference on. IEEE, 2009: 801- 805.
[18] Ken’ichi Furuya, Sumitaka Sakauchi, Akitoshi Kataoka. Speech dereverberation by combining MINT-based blind deconvolution and modified spectral subtraction[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Toulouse, France, 2006, I: 813- 816.
[19] Chen J, Benesty J, Huang Y. An acoustic MIMO framework for analyzing microphone-array beamforming[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Honolulu, Hawaii, USA, 2007, I: 25-28.
[20] Habets E A P, Gannot S. Dual-microphone speech dereverberation using a reference signal[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Honolulu, Hawaii, USA, 2007, IV: 901-904.
[21] Sehr A, Kellermann W. A new concept for feature-domain dereverberation for robust distant-talking ASR[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Honolulu, Hawaii, USA, 2007, IV: 369-372.
[22] Jukic A，Waterschoot T V, Gerkmann T, et al. A General Framework for Incorporating Time-Frequency Domain Sparsity in Multichannel Speech Dereverberation[J]. Journal of the Audio Engineering Society, 2017,65(1/2): 17-30.
[23] Zhang Long, Xu Xu, Chen Huang, et al. Supervised single-channel speech dereverberation and denoising using a two-stage model based sparse representation[J]. Speech Communication, 2018, 97: 1- 8.
[24] Kodrasi I, 
A, Doclo S. Robust sparsity-promoting acoustic multi-channel equalization for speech dereverberation[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Shanghai, China, 2016: 166-170.
[25] Yoshioka T, Chen X, Gales M J F. Impact of single-microphone dereverberation on DNN-based meeting transcription systems[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,Florence, Italy, 2014: 5527-5531.
[26] Xiao Xiong, Zhao Shengkui, Nguyen D H H, et al. Speech dereverberation for enhancement and recognition using dynamic features constrained deep neural networks and feature adaptation[J]. EURASIP Journal on Advances in Signal Processing, 2016, 2016(1):1-18.
[27] Williamson D S, Wang D L. Speech dereverberation and denoising using complex ratio masks[C]∥Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing,New Orleans, LA, USA, 2017: 5590-5594.
[28] Williamson D S, Wang D. Time-Frequency Masking in the Complex Domain for Speech Dereverberation and Denoising[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2017, 25(7): 1492-1501.
[29] Schwartz B, Gannot S, Habets E A P. Online speech dereverberation using Kalman filter and EM algorithm[J]. IEEE Transactions on Audio Speech and Language Processing, 2015, 23(2):394- 406.
[30] Braun S, Habets E A P. Online Dereverberation for Dynamic Scenarios Using a Kalman Filter With an Autoregressive Model[J].IEEE Signal Processing Letters, 2016, 23(12):1741-1745.
[31] Doire C S J, Brookes M, Naylor P A, et al. Single-Channel Online Enhancement of Speech Corrupted by Reverberation and Noise[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2017, 25(3): 572-587.
