1 引言
多站雷达中一般能够获取到的量测信息有：到达时间(Time of Arrival, TOA)[1-3]、接收信号强度、到达时间差(Time Difference of Arrival, TDOA)[4- 6]、到达频率差(Frequency Difference of Arrival, FDOA)[7- 8]等。它们可以单独或联合起来用于目标定位及跟踪。本文着眼于仅使用TOA信息完成目标跟踪。在之前的研究中，文献[9]使用基于区间分析的算法对唯距离信息进行处理从而完成单目标跟踪，文献[10]考虑了杂波情况下的唯距离多目标跟踪问题，其跟踪算法建立在卡尔曼滤波之上，对非线性量测方程跟踪性能较差，文献[11]使用TOA以及多普勒信息联合完成多目标跟踪，取得了较好的效果。
当前的某雷达发射器采用了多普勒容错波形，如线性调频(LFM)信号，以提高目标检测的鲁棒性，但是利用这类波形获取TOA信息时会引入了一些额外的偏差，即距离-多普勒耦合(Range-Doppler Coupling， RDC-TOA)[12]。在这种情况下，使用基于卡尔曼滤波器的跟踪算法性能下降十分严重。文献[13]研究了距离-多普勒耦合情况下的单目标跟踪问题，但作者仅将目标建模至一维情况下(即目标状态为距离，距离变化率)。此外，文献[14]给出了距离-多普勒耦合情况下目标跟踪的概率克拉美-罗界(PCRLB)，文献[15]研究了距离-多普勒耦合情况下单目标起始及跟踪算法。以上算法均建立在理想跟踪环境下，即单目标，无杂波。而对于存在杂波的多目标环境下的多普勒耦合TOA跟踪则未见报道。此外，由于监测环境内随时可能有目标进入或者消亡，目标数量在各量测时刻间可能发生变化[16]。因此，多目标跟踪问题应同时考虑动态估计目标数量以及各目标状态。
经典的杂波情况下多目标跟踪方法有联合概率数据关联算法(JPDA)[17]以及概率假设密度(MHT)[18]等，其中，JPDA算法要求已知目标数量，在做状态估计之前通过关联的方式将目标状态与量测信息对应起来，耗费较多时间。MHT算法可起始和删除航迹，但它需要在每一时刻列举量测的所有来源，计算量很大。最近，Mahler提出基于随机有限集(RFS)[16]进行贝叶斯框架下目标跟踪，可动态估计目标数量，受到广泛关注。但是，最优的RFS目标跟踪算法没有解析解，需要进行矩近似。成功的近似方法包括概率假设密度(PHD)[16]、势概率假设密度(CPHD)[19]算法，将随机有限集的状态空间从高维度降至单目标空间，大大降低了计算量，但PHD、CPHD算法本身也不具备解析解。它们的近似方法一般有高斯混合[20]以及粒子滤波[21]。其中，由于粒子滤波近似法能够更好的处理非线性问题，因而其成为最近使用最为广泛的跟踪算法。但它有两个较为严重的问题，一个由于粒子滤波自身引入，即粒子贫瘠问题[22]；另一个则是在算法进行目标状态估计时需要进行聚类，当目标数量估计有误时，提取出的状态与真实状态相距甚远。RFS跟踪方法的另一种近似算法为多伯努利滤波器(MeMBer)[23]跟踪，它通过维持多个伯努利项，在状态估计时无需使用聚类算法，提取精度较高。
本文主要为解决只使用RDC-TOA信息做多目标跟踪时面临的问题。首先，本文将文献[13,15]中的场景扩展至更符合实际的含杂波环境的被动声呐系统多目标跟踪场景。此外，本文引入最近提出的基于RFS的多传感器多伯努利算法解决本文建立的场景，介绍了三种基于RFS的多传感器多目标跟踪框架。在此基础之上，本文分析了RDC-TOA信息的可观性，理论上得出了仅使用RDC-TOA信息做目标跟踪时需要的最少传感器数量。最后，基于仿真结果进一步验证了本文所提结论。
2 问题描述
2.1 理想条件下的跟踪模型
令多站被动声呐系统使用一个发射站，位于u=[xt,yt]，接收站数量为N，位于
目标m的状态向量为：
(1)
令θm=(xm,ym)表示二维笛卡尔坐标下的目标位置，
表示对应方向的速度。目标m的运动方程为：
xm(k+1)=Fxm(k)+Γν(k)
(2)
其中F表示目标的运动模型，常见的有匀速运动、转弯运动及匀加速运动等。ν(k)表示高斯白噪声，Γ表示噪声功率。
假定所有雷达所有接收站能够被精确同步，第i个传感器中源于目标m的量测为：
(3)
式中，ωi(k)是独立同分布的高斯白噪声，其方差为
表示信号由发射站经过目标反射回接收站的时延，式中c代表信号的传播速度，‖·‖表示欧几里得范数。
表示由于目标运动造成的多普勒耦合。τi[θm(k)]与的计算式为：
(4)
(5)
式中，κ代表距离-多普勒耦合因子。若发射站使用LFM信号，其脉宽为Tp，信号起始频率为f1，终止频率为f2，则：
(6)
2.2 本文使用的跟踪模型
实际环境中，由于目标可随时进入或运动出监测区域，第k+1次采样时的目标数量相对于k次采样时可能发生变化，则目标状态应被建模为：
Xk+1=C(Xk)∪B(Xk)∪B
(7)
其中，C(Xk)表示由k时刻存活下来的目标按式(2)转移后得到的状态；B(Xk)表示k时刻目标衍生出来的目标，如潜艇发射的鱼雷等；B表示完全自然新生的目标，一般由先验知识或直接从量测中采样得到。由于衍生目标在建模上一般直接赋予另外一个运动模型，本质上与存活目标相似，因此本文仅考虑存活目标与新生目标。
对于量测模型，从实际角度出发，雷达并非总能够检测到目标。此外，由于监测区域内可能存在其他信号反射点，如凸起的海床、暗礁等，造成对应分辨单元内信号强度较大，因此可能被声呐当作目标检测出来，这样的点称为杂波。设接收站i在第k次采样时对目标m的检测概率为
杂波数量在其监测范围内呈强度为λi的泊松分布，每个杂波在监测区域内呈均匀分布。则k时刻的量测应被建模为：
(8)
其中，|·|表示集合的势，
表示杂波，获得
的概率表示为：
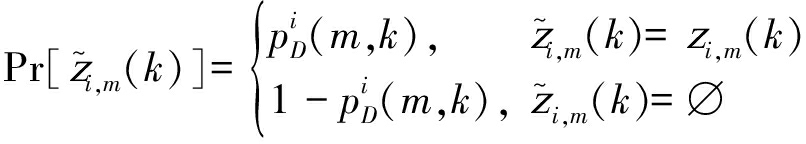
(9)
3 多传感器多模型多伯努利滤波器(MS-MM-MeMBer)
3.1 势平衡多伯努利滤波器
令k时刻监测区域内共有M个目标，按照RFS理论，目标m可建模为伯努利RFS，其分布πm(Xk)表示为：
(10)
其中，
代表目标m的存在概率，p(·)表示目标的空间分布。将所有目标的伯努利表示为一个集合，记为πk，则有：
(11)
其具体表示为：
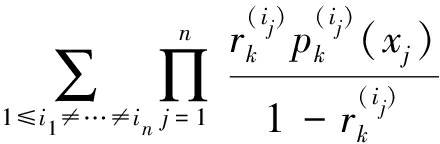
(12)
按贝叶斯理论，多伯努利滤波器可分为预测，更新两步。如下式所示：
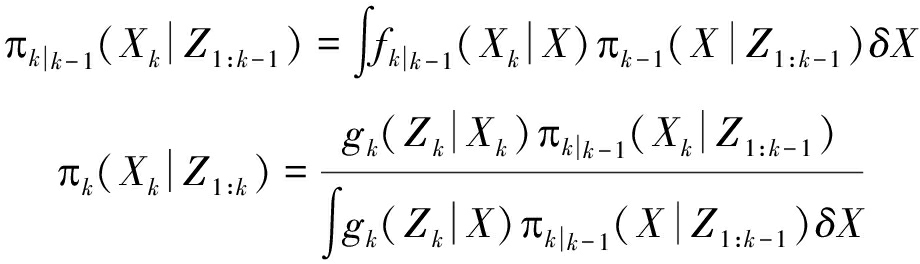
(13)
式中， fk|k-1(·),gk(·)分别表示目标的多目标状态转移及多目标似然方程。式中的积分为随机有限集积分[24]，直接计算上两式无法获得解析解。在将目标按式(11)进行伯努利表示后，预测后的伯努利项由两部分组成：存活目标与新生目标，如下式所示：
(14)
在式(14)中，Mk-1表示k-1时刻遗留下来的目标数，MBk表示k时刻新生的目标数，Mk|k-1表示预测完成后的总目标数。式中几个参数项的计算可由下式完成：
(15)
(16)
在式(15)、(16)中，
表示状态为x的目标在k时刻的存活概率，〈·,·〉表示内积，由下式定义：
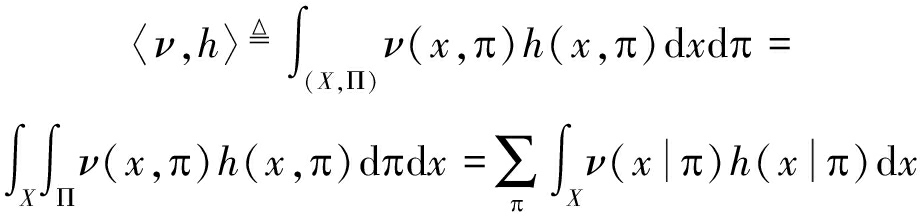
(17)
更新后的伯努利项由两部分组成：未被量测更新的漏检目标以及被量测更新的目标，如下所示：
(18)
在式(18)中的变量定义如下：
(19)
(20)
其中，
表示k时刻状态为x的目标被第i个传感器检测到的概率。量测更新目标由下式完成：
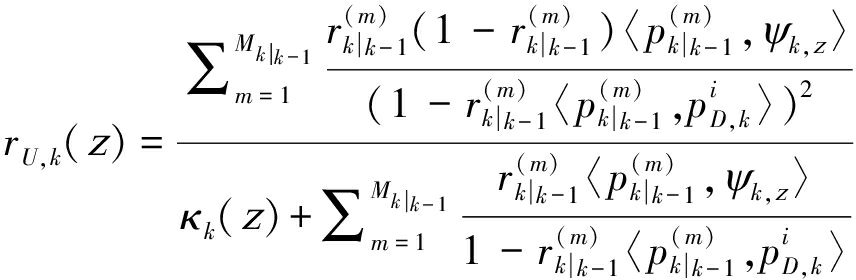
(21)
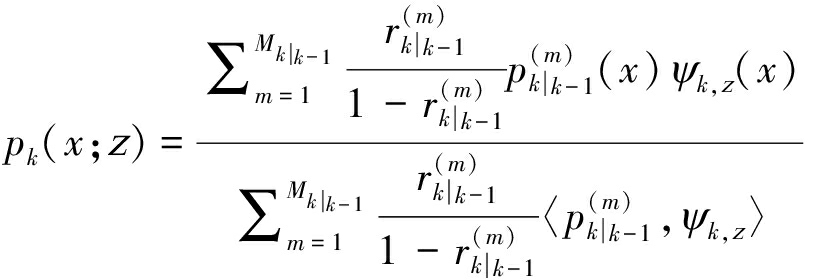
(22)
(23)
在式(23)中，
表示目标似然函数。以上为MeMBer滤波器的迭代步骤，由于迭代中出现了积分项，它们无法得到解析解。因此， MeMBer滤波器发展出了多种近似方法，其中，SMC方法能够处理目标模型与量测模型中的高度非线性问题，受到广泛关注与使用。
3.2 SMC-MeMBer滤波器
令多伯努利项可由多簇粒子表征，如下所示：
πk=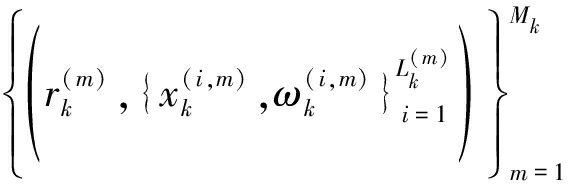
(24)
其中，
表示描述第m个目标伯努利项使用的粒子数量，
与
分别表示第i个粒子的状态及权重。这样表示的一个好处即将式中的积分项用求和式代替，使其能够被近似计算。
预测：
对于存活目标：
(25)
(26)
上式中的参数表示如下：
(27)
(28)
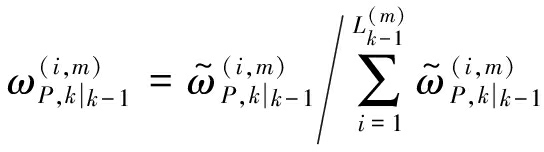
(29)
其中，
为目标状态的重要性采样分布。新生目标RFS的强度
由先验知识给出，且其空间分布用粒子表示为：
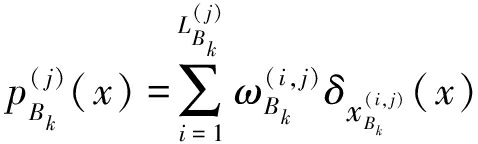
(30)
在式(30)中变量定义如下：
(31)
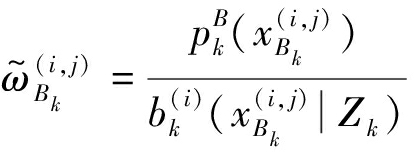
(32)
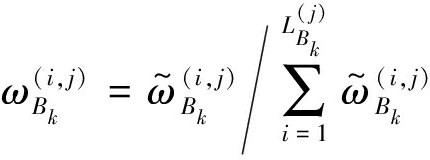
(33)
其中，
分别代表新生目标的状态分布。
更新：
对于漏检目标：
(34)
(35)
上式中的参数表示如下：
(36)
(37)
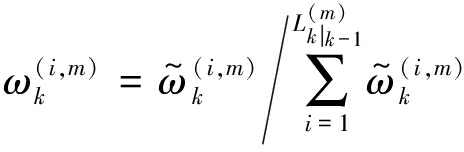
(38)
对于量测更新目标：
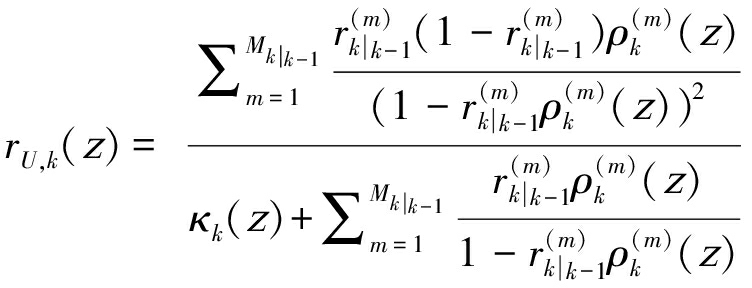
(39)
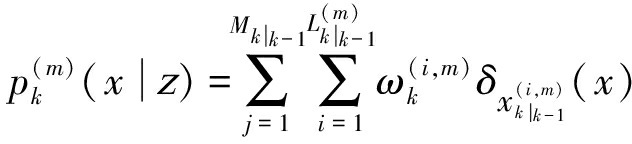
(40)
上式中的参数表示如下：
(41)
(42)
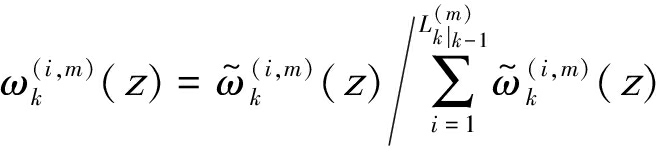
(43)
重采样：
为解决粒子贫瘠问题，需要在更新完成后引入重采样步骤[25]。令描述单个伯努利项的粒子数量介于Lmin与Lmax之间，则更新完成后的伯努利项粒子数量为：
因此需要从
粒子中采样出
个，到目前为止，已有很多种重采样方法能够完成这一步骤，由于重采样并非本文重点关注的内容，因此不详细展示其技术细节，可具体参阅文献[21,23]。
此外，由于每次迭代将额外产生|Zk|个伯努利项，随着迭代次数增加，算法计算负担加重。因此，在更新完成后将对当次迭代得到的伯努利项进行修枝与合并，即去除掉强度小于某阈值的伯努利项，同时合并代表相同目标的伯努利项，具体可以两个伯努利项之间的距离，若已知伯努利项之间的互协方差矩阵时，可以马氏距离作为判断标准[23]。
3.3 序贯更新多传感器多伯努利滤波(MS-MeMBer)
在应对多传感器多目标跟踪问题时，Mahler提出了RFS框架下序贯更新后验概率的方法，在多伯努利情况下，算法更新流程为：
4 RDC-TOA量测观测性分析
在没有多普勒耦合时，单运动站唯距离跟踪的观测性分析在之前的文章中已有详尽的分析。借鉴文献[26]中的方法，此处给出多普勒耦合下的唯距离跟踪观测性分析。
本质上，可观测性问题是纯数学的概念。观测性可通过分析雅可比矩阵(Jacobian Matrix)进行推导。而雅可比矩阵的行列式实际上就提供了关于目标状态信息的一组不确定定位曲线的定位下边界值。由观测性可以得出无模糊跟踪目标需要的最少传感器数量。不失一般性，此处仅考虑单目标时的观测性。令
表示由N个传感器接收到的时延信号，那么k时刻的观测量
其为非线性的方程组，现将非线性的观测量近似为线性的方程：
z(k)≈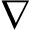
F·x(k)
(44)
x(k)为第k时刻的目标状态变量，由于只对k时刻的观测性进行分析，所以为了简化表示，省略k时刻的表示，则线性观测矩阵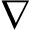F有如下表示形式：
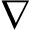
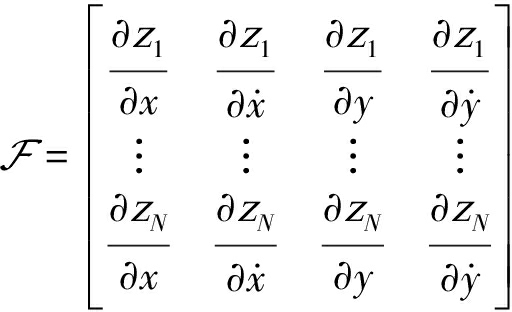
(45)
在上式中，
分别表示第i个观测量对目标的二维位置和速度求得的偏导数。x，y表示目标在二维平面的位置，
表示目标在二维平面的速度，根据定义，它们有如下表达形式：
(46)
(47)
(48)
(49)
在式(46)至(49)中，
有如下表示形式：
(50)
(51)
(52)
(53)
(54)
(55)
对目标进行无模糊跟踪的前提使用是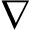F中的元素联立关于目标状态向量的多元方程时只有单一解。由于目标状态向量中有4个待估计的元素，根据矩阵理论相关知识，F的秩必须大于等于4，不难验证其必要条件是N≥4。
5 仿真实验
5.1 算法参数设置
假定机动目标一共通过两个模型来描述，分别是匀速直线运动(CV)以及匀速转弯运动(CT)，其状态转移矩阵及其方程噪声功率如式(56)所示，其中转弯速率θ=90°，其轨迹图如图1所示。
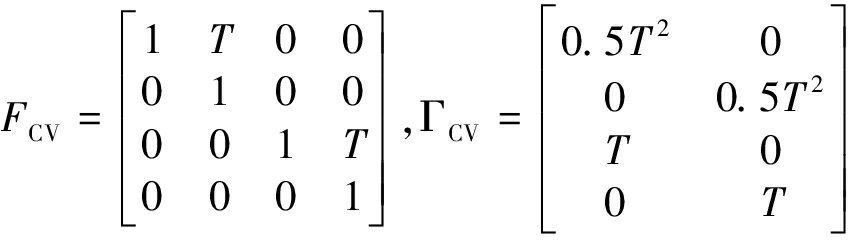
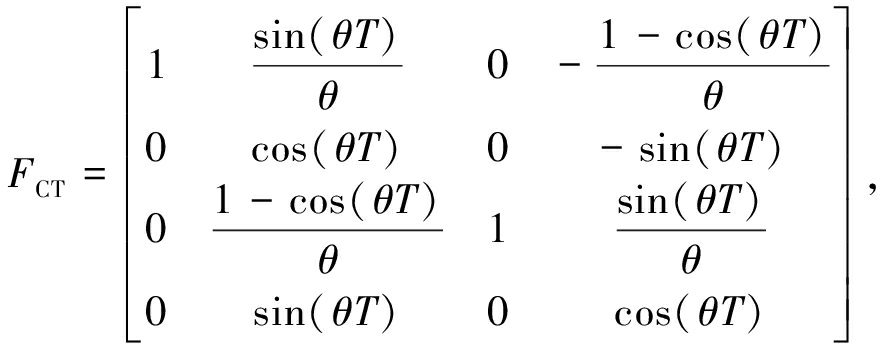
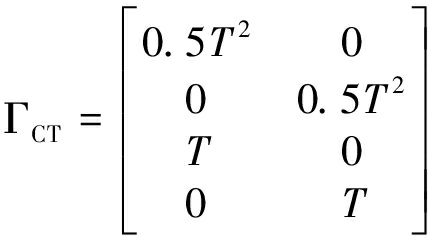
(56)
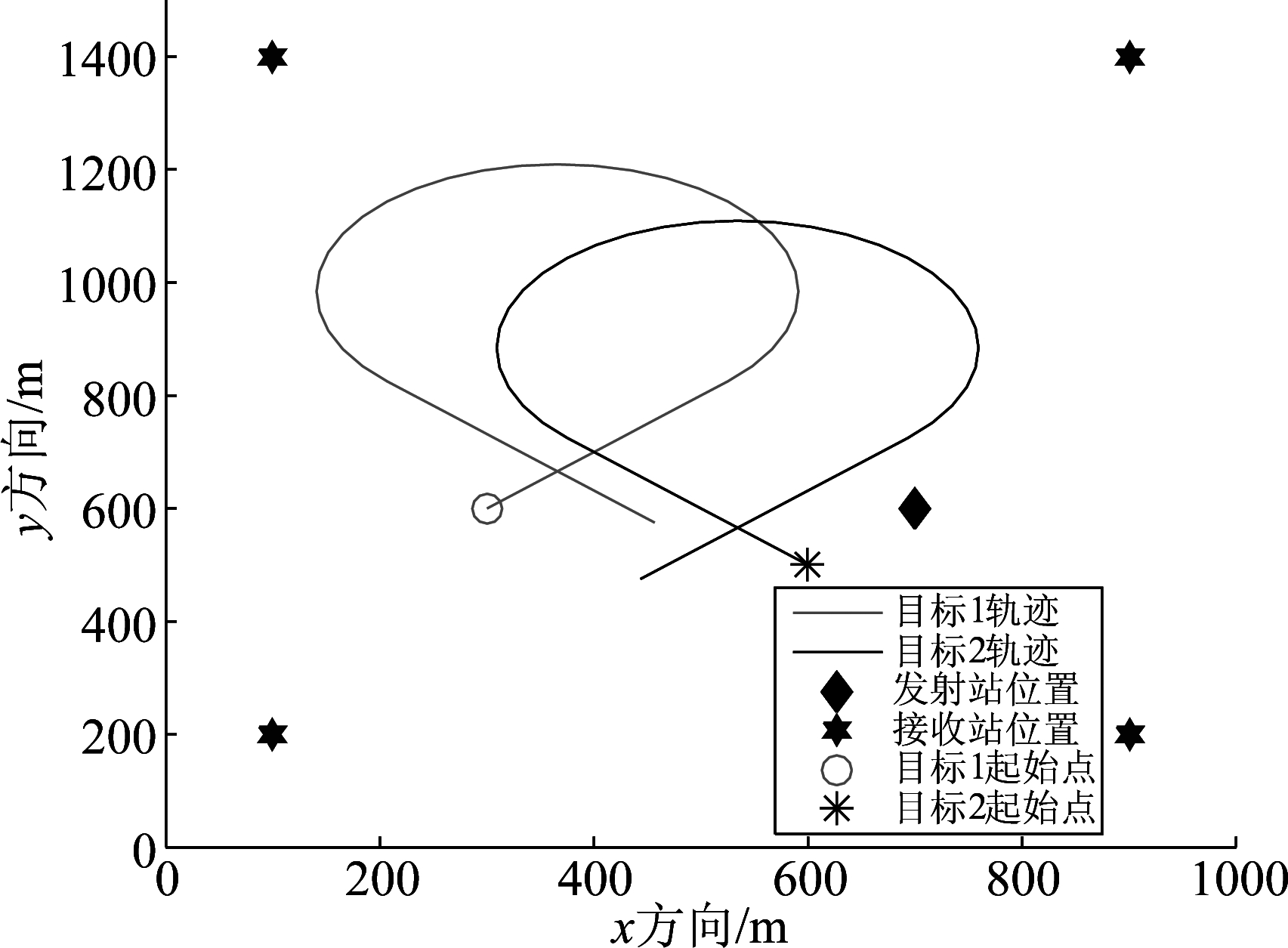
图1 目标轨迹及发射站、接收站示意图
Fig.1 The sketch map of target trajectory, transmitter and receivers
令监测区域内有1个发射站及4个被动接收声呐(N=4)，它们的位置分别为：
(57)
为了验证所提算法的有效性和对比不同参数对算法性能的影响，我们将仿真条件设定为三种情况，令所有被动接收声呐量测的标准偏差στ=0.001，监测区域内杂波呈均匀分布，为计算方便，不失一般性，令信号的传播速度c=1500[15]。新生目标强度为0.2，由Lmin个粒子表征。
第一种对比情况：
杂波数量服从期望值为1的泊松分布。算法对于单个伯努利项粒子数量设置为：Lmin=200,Lmax=5000。
第二种对比情况：
杂波数量服从期望值为1的泊松分布。算法对于单个伯努利项粒子数量设置为：Lmin=500,Lmax=8000。
第三种对比情况：
杂波数量服从期望值为1.5的泊松分布。算法对于单个伯努利项粒子数量设置为：Lmin=200,Lmax=5000。
由于基于RFS的滤波器同时估计监测区域内的目标数量及各目标状态，传统的评价方法无法正确评估它们的性能。本文采用计算OSPA距离进行评估，其截断参数设置为1，p参数设置为300。所有实验数据均由200次Monte Carlo仿真平均后得来。其中，基于Monte Carlo仿真的平均OSPA距离估计对比如图2所示，平均目标数估计对比如图3所示。可以看出，在考虑了多普勒耦合这一观测现象之后，目标跟踪和目标数的估计效果得到了显著提高，从图2中的对比情况可以看出，在杂波的期望值一定时，把粒子数提高会使跟踪性能提高，当粒子数一定时，增大杂波的期望值时，会使目标的跟踪性能降低。但是这三种对比情况对目标数的估计性能均无影响。
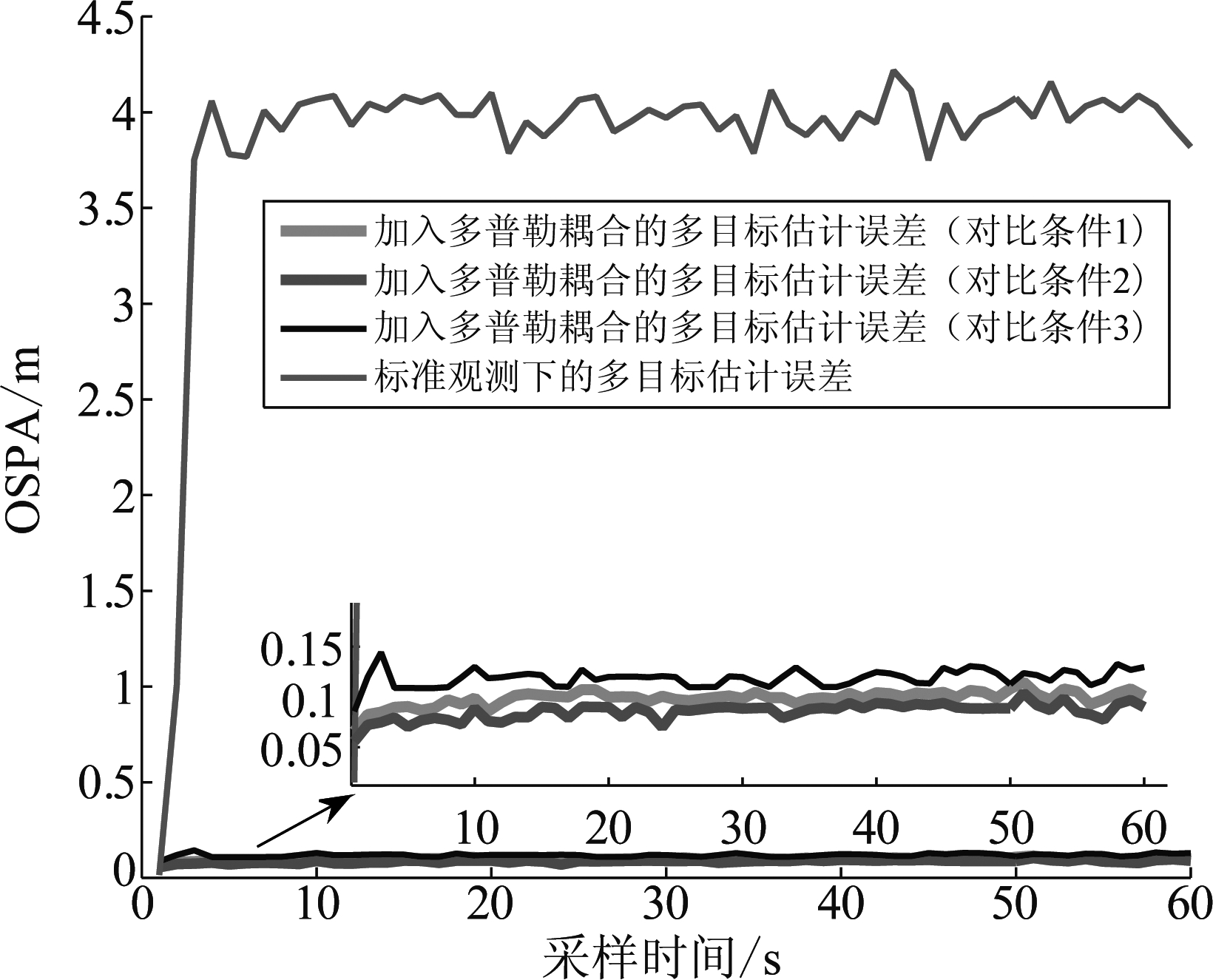
图2 OPSA估计对比
Fig.2 The comparison of the estimation of OPSA
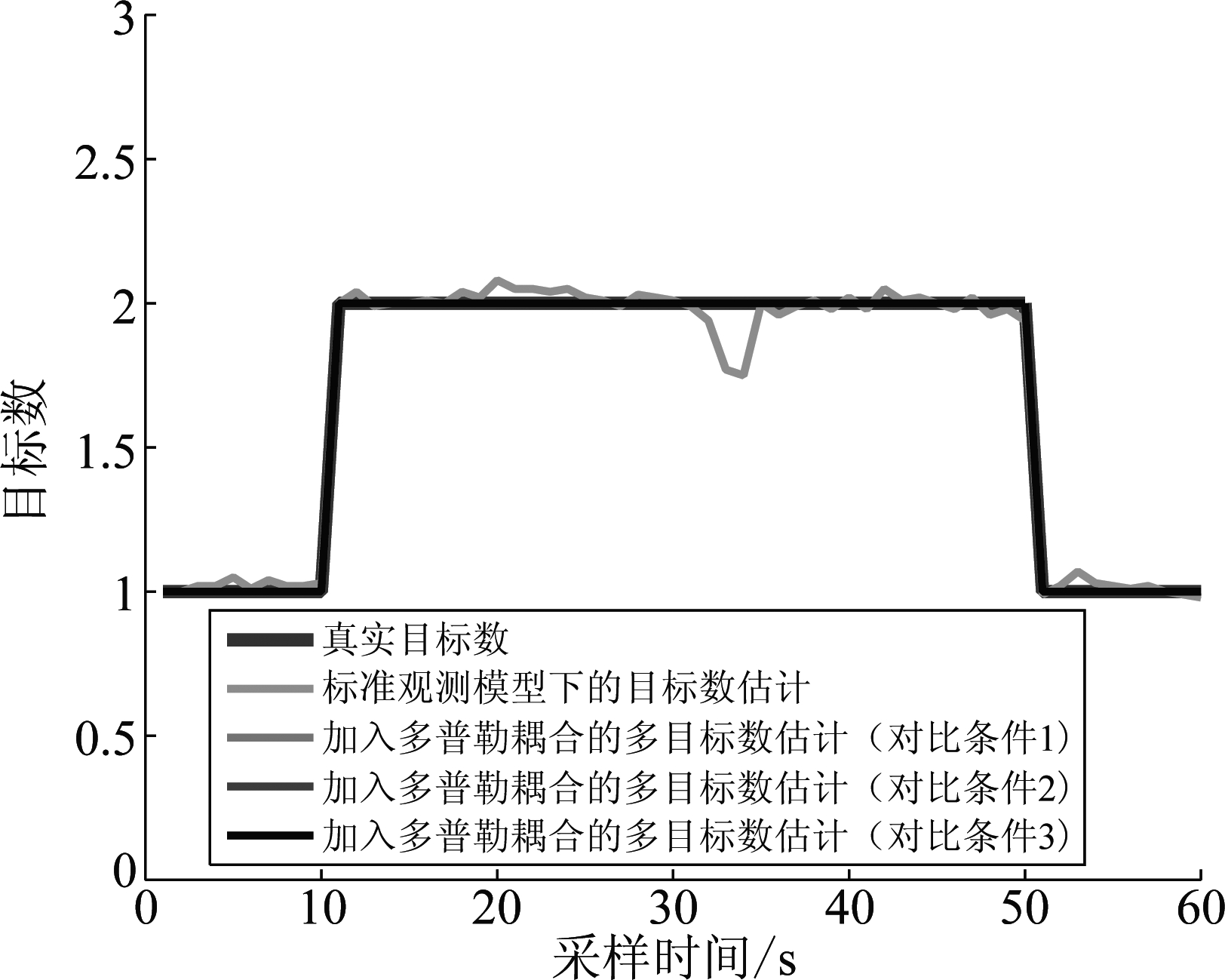
图3 目标数估计对比
Fig.3 The comparison of the estimation of target number
6 结论
本文主要研究了分布式场景下唯距离多目标跟踪问题。近来，随着多站(被动)雷达重新受到重视以及MIMO雷达成为研究热点，多传感器多目标跟踪必将吸引研究目光。至目前为止，共有多种传感器融合框架被用于多传感器多目标跟踪，但其技术手段远未达到成熟。若要达到精确的信息融合，必然带来无法企及的计算量，而低计算量算法往往又会引入量测信息的损失。作为研究多传感器多目标跟踪的“潜力股”，RFS必将在分布式目标跟踪下受到广泛重视。本文使用了最近提出的多伯努利滤波器解决了在多站被动声呐系统下的多目标跟踪问题，本文只使用了TOA做为量测信息，并且假定量测受到多普勒耦合干扰。在引入多模型后，MS-MM-MeMBer成功跟踪了目标数量变化下的多机动目标跟踪。然而该算法尚有很多不足之处：序贯性更新方法的跟踪效果受传感器排序的影响较大，并且MS-MM-MeMBer无法获得多目标的连续航迹，这将是接下来工作的重点内容。
[1] Chen L, Thevenon P, Seco-Granados G, et al. Analysis on the TOA tracking with DVB-T signals for positioning[J]. IEEE Transactions on Broadcasting, 2016, 62(4): 957-961.
[2] Manickchand K, Strydom J J, Mishra A K. Comparative study of TOA based emitter deinterleaving and tracking algorithms[C]∥AFRICON, 2017 IEEE. IEEE, 2017: 221-226.
[3] 刘泽龙, 刘文彦, 丁宏,等. UWB密集多径下基于检测概率差值最大的TOA估计方法[J]. 信号处理, 2012, 28(8):1120-1126.
Liu Zelong, Liu Wenyan, Ding Hong, et al. A Novel Probability of Detection Difference Maximum-Based TOA Estimation Method in UWB Dense[J]. Signal Processing, 2012, 28(8):1120-1126. (in Chinese)
[4] 李宁, 曹祯, 邓中亮,等. 干扰源定位中到达时间差参数估计方法[J]. 系统工程与电子技术, 2016, 38(5):994-997.
Li Ning, Cao Zhen, Deng Zhongliang, et al. TDOA estimation algorithm for interference source positioning[J]. Journal of Systems Engineering and Electronics, 2016, 38(5): 994-997. (in Chinese)
[5] 叶诚, 杨淑莹. 基于到达时间差的声源定位算法与实现[J]. 天津理工大学学报, 2015(2):50-54.
Ye Cheng, Yang Shuying. Sound source localization algorithm and its implementation based on time difference of arrival[J]. Journal of Tianjin University of Technology, 2015(2): 50-54. (in Chinese)
[6] 梁加洋, 赵拥军, 赵闯,等. 利用约束加权最小二乘的单站外辐射源时差定位算法[J]. 信号处理, 2017, 33(6):880- 886.
Liang Jiayang, Zhao Yongjun, Zhao Chuang, et al. Constrained weighted least squares algorithm for single-observer TDOA location estimation using illuminators of opportunity[J]. Journal of Signal Processing, 2017, 33(6):880- 886. (in Chinese)
[7] 赵勇胜, 赵闯, 赵拥军. 利用外辐射源的TDOA和FDOA目标定位算法[J]. 计算机工程与应用, 2017, 53(8):50-56.
Zhao Yongsheng, Zhao Chuang, Zhao Yongjun. TDOA and FDOA location algorithm using illuminators of opportunity[J]. Computer Engineering and Applications, 2017, 53(8): 50-56. (in Chinese)
[8] 曹景敏, 万群, 欧阳鑫信,等. 观测站有位置误差的多维标度时频差定位算法[J]. 信号处理, 2017, 33(1):1-9.
Cao Jingmin, Wan Qun, Ouyang Xinxin, et al. Multidimensional scaling-based passive emitter localization from time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties[J]. Journal of Signal Processing, 2017, 33(1):1-9. (in Chinese)
[9] Soares G L, Arnold-Bos A, Jaulin L, et al. An Interval-Based Target Tracking Approach for Range-Only Multistatic Radar[J]. IEEE Transactions on Magnetics, 2008, 44(6):1350-1353.
[10] Song T L, Mušicki D. Range only multistatic tracking[C]∥Information Fusion. IEEE, 2010:1- 8.
[11] Deming R, Schindler J, Perlovsky L. Multi-Target/Multi-Sensor Tracking using Only Range and Doppler Measurements[J]. IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(2):593- 611.
[12] Bar-Shalom Y. Negative correlation and optimal tracking with Doppler measurements[J]. IEEE Transactions on Aerospace & Electronic Systems, 2001, 37(3):1117-1120.
[13] Jain V, Blair W D. Filter Design for Steady-State Tracking of Maneuvering Targets with LFM Waveforms[J]. IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(2):765-773.
[14] Song X, Willett P, Zhou S. Posterior Cramér-Rao bounds for Doppler biased multistatic range-only tracking[C]∥Proceedings of the, International Conference on Information Fusion. IEEE, 2011:1- 8.
[15] Dou W, Bar-Shalom Y, Willett P, et al. Initialization and tracking using Doppler-biased multistatic time-of-arrival measurements with linear frequency modulated waveforms[C]∥International Conference on Information Fusion. IEEE, 2014:1-7.
[16] Mahler R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 39(4):1152-1178.
[17] Fortmann T, Bar-Shalom Y, Scheffe M. Sonar tracking of multiple targets using joint probabilistic data association[J]. IEEE Journal of Oceanic Engineering, 2003, 8(3):173-184.
[18] Reid D. An algorithm for tracking multiple targets[J]. IEEE Trans. Autom. Control, 1979, 24(6):843- 854.
[19] Mahler R. PHD filters of higher order in target number[J]. IEEE Transactions on Aerospace & Electronic Systems, 2007, 43(4):1523-1543.
[20] Vo B N, Ma W K. The Gaussian Mixture Probability Hypothesis Density Filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11):4091- 4104.
[21] Vo B N, Singh S, Doucet A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace & Electronic Systems, 2005, 41(4):1224-1245.
[22] Li T, Bolic M, Djuric P M. Resampling Methods for Particle Filtering: Classification, implementation, and strategies[J]. Signal Processing Magazine IEEE, 2015, 32(3):70- 86.
[23] Vo B T, Vo B N, Cantoni A. The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2):409- 423.
[24] Mahler R P S. Statistical multisource-multitarget information fusion[M]. Norwood: Artech House, Inc., 2007：655- 682.
[25] Ristic B, Arulampalam S, Gordon N. Beyond the Kalman Filter-Particle Filters for Tracking Applications[J]. IEEE Transactions on Aerospace & Electronic Systems, 2003, 19(7):37-38.
[26] Liang M, Du Y K, Kai X. Multi-Bernoulli filter for target tracking with multi-static Doppler only measurement[J]. Signal Processing, 2015, 108:102-110.
