1 引言
无线信道的分析与研究对于移动网络规划,移动通信技术的升级与改进等具有重要意义[1]。随着5G通信技术的发展,对无线信道特有的高速移动、分类广泛、快速时变特征缺乏有效的研究方法。传统的基于单一时域或者单一频域角度来表示信道的脉冲响应(CIR,channel impulse response)方法或者基于频域功率谱密度的方法不能建立信道的全局特性表示。已有研究成果表明,如果同时从频域和时域角度出发建立无线信道的特性分析函数,则能够避免以往仅在单一域(时域或者频域)内进行信道时频特性分析的缺陷。尤其是5G无线通信中,大多数终端处于快速移动状态,信道状态信息随时间快速变化,导致信道非平稳,呈现快衰落。研究如何准确同时在时频域表征非平稳时变信道的表示方法已成为近年来的学术热点。
目前针对非平稳快衰落时变信道的时频表示算法主要通过短时傅里叶变换(STFT,short time Fourier transform)、小波变换(WT,wavelet transform)、魏格纳-威尔分布(WVD,Wegener-Ville distribution)构建信道的时频二维分布,再实现对瞬时频率(IF,instantaneous frequency)等特征参量的求解以实现信道的时频表示。文献[2]利用STFT算法实现了对小尺度衰落信道的时频表示,通过窗函数在时间轴上的移动,将信道分割为若干离散片段,利用局部拟平稳原理,采用傅里叶变换对每个离散片段进行处理,从而获得了信道CIR的一系列平稳离散片段频谱,从而实现无线信道的非平稳时变特性的观察与提取。在小波域对无线信道进行特征分析是文献[3]的核心内容,该文献得出了小波信号在经历快时变信道传播环境后的时频谱图,并探讨了时频表示性能与小波基函数间的关系。然而,在STFT时频分析方法中,窗函数的类型和大小都会影响信道的时频表示效果,窗长过长,则频域特性会失真;而在小波域时频分析方法中,首先面临的是选择何种基函数问题,其次是当前所选基函数的适用性问题,导致该方法不具备信道时频分析的自适应性,并且基函数的不断修正过程使算法的实时性较差,无法满足高速移动和快速时变场景下信道分析的需求。
为此,本文利用自适应傅里叶分解提出一种基于信道自适应傅里叶分解的Clarke无线信道的时频表示,该方法无需借助窗函数,也不依赖于信道分解基函数,可克服STFT,小波变换等在时频二维表示方面的缺陷。我们推导了信道的等效瞬时频率表示、时频二维分布模型,并在信道自适应傅里叶分解的基础上,利用能量误差最小原则,重构了信道函数。实验结果验证了本文所提出的表示方法对高速时变信道时频表示的有效性和鲁棒性。
2 Clarke信道的时频表示问题
考虑非平稳时变信道中的Clarke模型。文献[4]推导了Clarke非平稳时变信道下模型信道参数基于最小均方误差准则(MMSE,Minimum mean square error)的Jakes功率谱密度函数以及时频表示模型,以模型信道参数为中间变量建立了与Clarke非平稳时变信道的变换域表示式,由此得出Clarke非平稳时变信道的时变特征。
在Clarke非平稳时变信道中,CIR可表示为[4]:
(1)
其中L为信号传播时的可视传播路径数目,Cl是第l条路径信号的幅度,ωc=2πfc是载波频率,ωm=2πfm是最大多普勒频偏,Al是第l条路径信号的到达方位角,φl是初始相角,Cl、Al均服从[0,2π]的独立均匀分布。据文献[4],数据信号在Clarke信道中传播时,由第i个符号在第l路径上传播生成的离散多普勒频移按式(2)计算:
(2)
Ni是叠加的正弦波个数,i表示发送信号的序数(i=1、2、3…),l表示当前路径, fmax表示最大多普勒频移。由式(3)可得第i个符号在第l路径上传播生成的离散多普勒系数ci,l:
(3)
式中,J0(·)表示第一类零阶贝塞尔函数,τmax是信道的最大时延扩展,m表示积分变量。
选择多径接收信号![]() 用于仿真Clarke信道模型[4]:
用于仿真Clarke信道模型[4]:
(4)
式(4)中θi,l表示随机相位,服从(0,2π]之间的均匀分布,此时![]() 符合确定性随机过程[5]。由式(4)可得信道参数在Clarke非平稳时变衰落信道下的自相关函数为[2]:
符合确定性随机过程[5]。由式(4)可得信道参数在Clarke非平稳时变衰落信道下的自相关函数为[2]:
(5)
τ表示接收信号的时延,T表示信道传输周期。据文献[2],Clarke信道模型基于Jakes功率谱密度的频域结果可表示为:
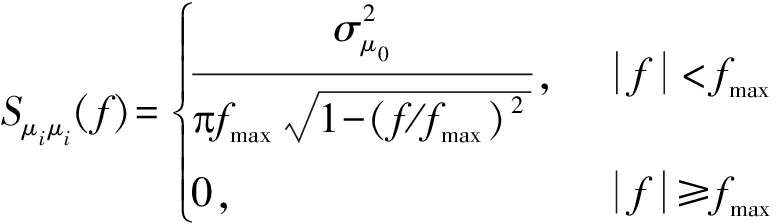
(6)
这里,![]() 表示高斯随机过程
表示高斯随机过程![]() 的方差。根据维纳-辛钦定理,对Sμiμi(f)进行逆傅里叶变换,得到Clarke非平稳时变信道模型下基于Jakes功率谱密度的自相关函数[2]:
的方差。根据维纳-辛钦定理,对Sμiμi(f)进行逆傅里叶变换,得到Clarke非平稳时变信道模型下基于Jakes功率谱密度的自相关函数[2]:
(7)
式(4)中![]() 的确定需要根据MMSE准则得到:
的确定需要根据MMSE准则得到:
(8)
然而根据所得Jakes功率谱的仿真结果以及式(6)发现,基于MMSE准则产生的Clarke频率非选择性衰落信道的功率谱密度符合典型的U型谱,但是这种单一频域的功率谱密度只能反映信道能量在频域的分布特征,且并未建立信道的时域同信道能量或者频率的直接或间接联系,因此不能整体的观察到信道在时-频域的联合变化特征。此外,Clarke频率非选择性衰落信道的STFT为:
STFT(t,ω)=![]() h(t)γ*(τ-t)e-jωτdτ
h(t)γ*(τ-t)e-jωτdτ
(9)
其中,γ(t)为实偶的窗函数。由于时间窗函数γ(t)的存在,信道CIR h(t)在每个局部离散平稳区间内都是时间域以及频率域的二维表示。但另一方面,窗函数γ(t)的大小和类型都会制约STFT的分析性能。而且根据Heisenberg测不准原理的限制,时间分辨率以及频率分辨率之间互相制约,同时获得理想的时间和频率分辨效果是不切实际的。因此,尽管STFT利用时间窗函数得到了信道的“局部性”频谱,但是针对不同的信道频段,合适的窗长也随之改变,很难找到统一的时间窗长[6-9]。
本文根据自适应傅里叶分解(AFD, adaptive Fourier decomposition)理论,在不借助窗函数或者特定基函数的情况下,对信道函数进行自适应分解后依然能够以较低的能量误差恢复出原始信道函数,并进行信道的时频域表示,下面将对利用AFD方法实现Clarke非平稳衰落信道的时频表示方法予以推导,并进一步将模型信道的时频域特征同时表征出来,提高表示精度。
3 基于AFD的信道时频表示方法
与FT、小波变换不同,AFD对信号进行分解时,其表示基函数都由能量极大选择原则进行自适应的选取,具有收敛速度快的特点,可实现对原始函数的最优稀疏表示。本文将其引入,对无线信道进行分解,利用分解表示结果对信道进行时频表示[10-16]。
本文根据[10]的方法对信道进行分解,分解的过程与匹配追踪(MP,matching tracking)算法相似。
3.1 信道的AFD表示
首先对Clarke频率非选择性衰落信道的CIR h(t)按照式(10)转换到Hardy空间,得到只含正频率的信号h+(t):
h+(t)=[h(t)+iHh(t)]/2+c0/2
(10)
其中Hh(t)是h(t)的环希尔伯特变换,i表示复数,c0c0是对h(t)进行傅里叶分解的第一项系数。
(11)
接着,我们对得到的h+(t)按照式(12)进行分解:
(12)
这里,〈•〉表示内积运算,单分量hk(eit)由式(13)计算得到:
(13)
eak(eit)定义为单位模化的Szegö核:
(14)
点ak根据MSP逐次选出[10],如![]() 是ak的共轭,一般取a1=0。
是ak的共轭,一般取a1=0。
(15)
Bk(eit)是有理正交基,如式(16):
(16)
在实际中,当分解过程满足如(17)的误差约束关系[8]时,分解结束,此时h+(t)取前N项作为近似:
(17)
式(17)中ε是最小化的分解误差,N为分解项数。
最后按照式(18)从Hardy空间[10]转换到时域,实现原始信道的重构:
(18)
其中, ρk(t)是信号的幅值,θk(t)是极化相位[10],且:
ρk(t)eiθk(t)=2〈hk(eit),eak(eit)〉Bk(eit)
(19)
进一步:
ρk(t)=|〈hk(eit),eak(eit)〉Bk(eit)|
(20)
3.2 基于AFD的信道时间-频率分布
式(18)中,令gk(t)=ρk(t)cos θk(t),由于基能量受限,因此满足[10]中对单分量的定义,进一步的,可对gk(t) 建立如下的时频二维分布:
(21)
其中,![]() 是θk(t)的一阶导数。
是θk(t)的一阶导数。
可求得h(t)整体上的时间-频率分布为:
(22)
此处H(t,ω)是Clarke信道函数的整体时间-频率分布;又由于θ′(t)的取值是连续的,因此H(t,ω)是时频二维分布的连续谱。
时频分析的常用方法是傅里叶变换及其逆变换。傅里叶变换中,需要对h(t)在整个时间域求积分:
H(ω)=![]() h(t)e-jωtdt
h(t)e-jωtdt
(23)
式(23)中,由于h(t)的变换是全局性的,导致建立的时频分布仅是单一频域的,并且不是连续谱。
3.3 基于AFD的信道能量谱密度
根据富比尼定理[10],对时频二维分布H(t,ω)在时间域上求积分可得Clarke信道在AFD变换域下的能量谱密度:
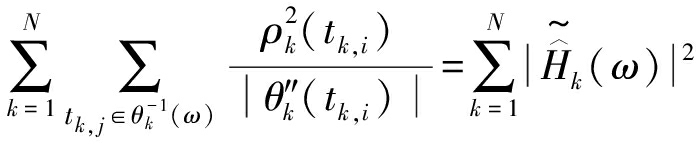
(24)
![]() 即为Clarke信道CIR基于AFD的能量谱密度。
即为Clarke信道CIR基于AFD的能量谱密度。
在傅里叶功率谱密度中,需要先对h(t)求自相关:
(25)
式(26)中,Hp是h(t)的傅里叶级数的系数,因此信道响应的傅里叶功率谱密度是:
(26)
根据式(26)可得,傅里叶功率谱密度是一系列的冲激,幅值是其傅里叶级数系数的平方,即其傅里叶变换系数的平方,而基于AFD的功率谱密度是连续谱,可以更直观连续地表示出信道的功率变化。
此时,将式(18) 带入公式(26),类比于傅里叶的级数分解,则P(ω) 可重新表示为:
(27)
4 AFD仿真模拟与性能分析
无线信道的时频表示侧重于信道的变换域分析,并给出信道的时频表示谱图。假设Clarke信道为双径传输,设置本文所用仿真参数及其数值如表1所示。
表1 Clarke信道仿真参数
Tab.1 The parameters of Clarke channel simulation

参数名参数值参数名参数值E01ωm1/Hz0C11ωm2/Hz222C22An130°ωc/Hz4000An245°ϕ10ϕ230°
本文对Clarke信道模型在AFD、FT以及STFT域下的时频表示进行了Matlab仿真并进行了性能对比。针对AFD,设定自适应傅里叶分解阶数为50;针对FT,设置分解级数为110;针对STFT,设定抽样窗口为汉宁窗,窗长为51。考虑到载波信号的载频为4000 Hz,所以抽样频率为8000 Hz。
图1、图2表明了信道幅度随时间的变化情况,同时显示了原始信道的重构结果。相较与原始信号,AFD的重构误差为0.0024,而FT的重构误差为0.027。根据仿真图像进一步表明AFD能够表示Clarke非平稳信道的时频变特性。图3给出了信道AFD以及FT重构的能量误差随分解步长的变化关系,AFD方法对原始信道的逼近效果优于传统傅里叶变换方法,且收敛性较好。在信道重构实现复杂度方面,FT和STFT两种算法均需大量的先验参数,如各次谐波系数、分段时长等,这将极大的增加系统执行复杂度;并且STFT重构信道时,只是分段进行,对于时延要求较高的场景,不能较好的适用。而AFD凭借MSP能够精简信道表示系数,降低系统负载,从而提升系统对于信道特征的快速判断能力。根据图4、图5的信道谱图,频率轴的8000 Hz和200 Hz处出现了频率峰值。图6和图7是分别基于AFD和STFT的时频分布,结果表明在约4000 Hz和200 Hz频点处存在较强的数值强度。显而易见的是,AFD的频点集中度要优于STFT,而STFT表示中,窗长越长,频率定位越模糊,频率分辨率性能较差。另外,在快时变非平稳信道中,信道特性随着相对移动速度、地理环境、天气等快速改变,则STFT方法将更不适用,而基于AFD方法没有上述缺点。
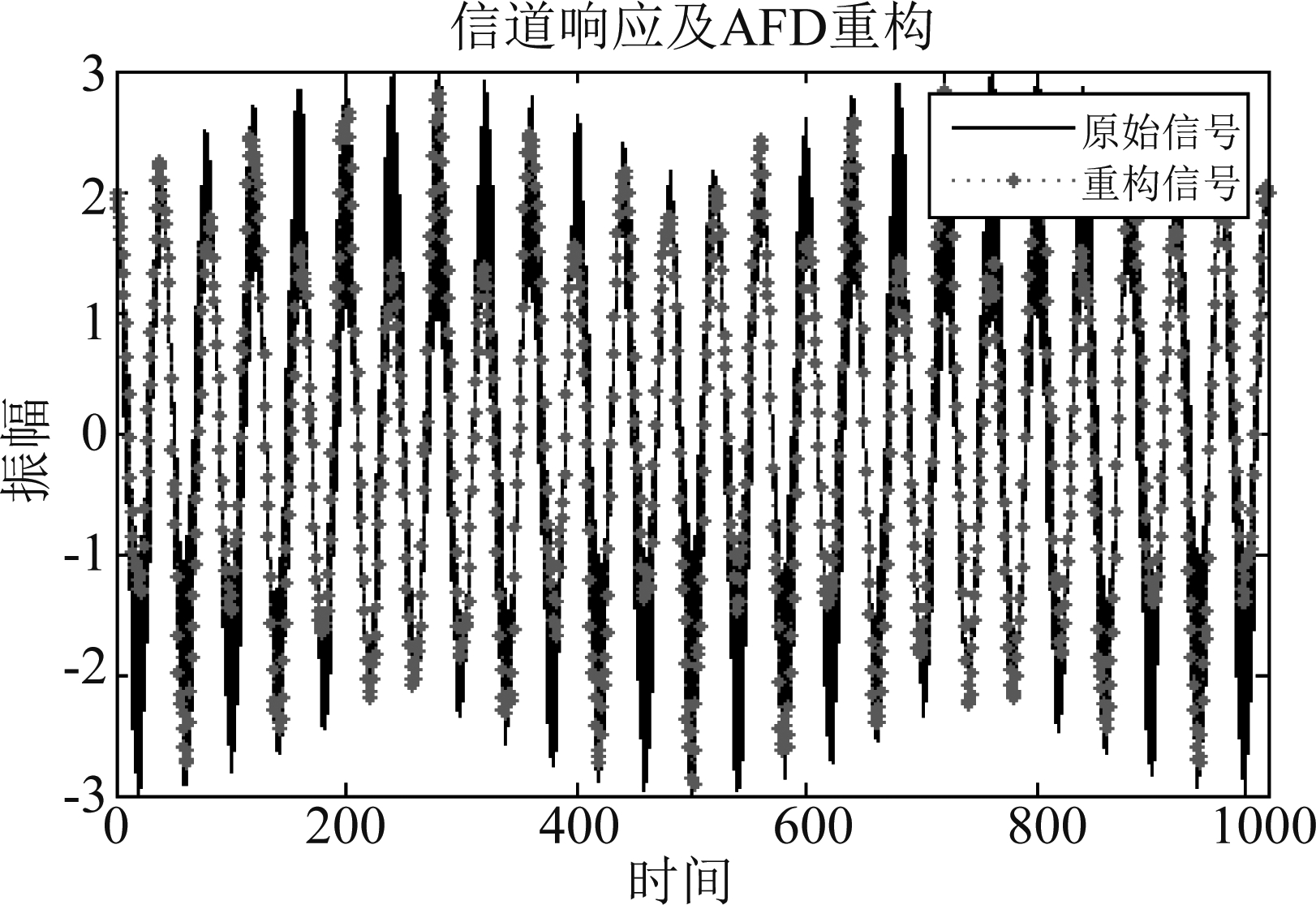
图1 基于AFD的信道重构
Fig.1 Channel reconstruction based on AFD
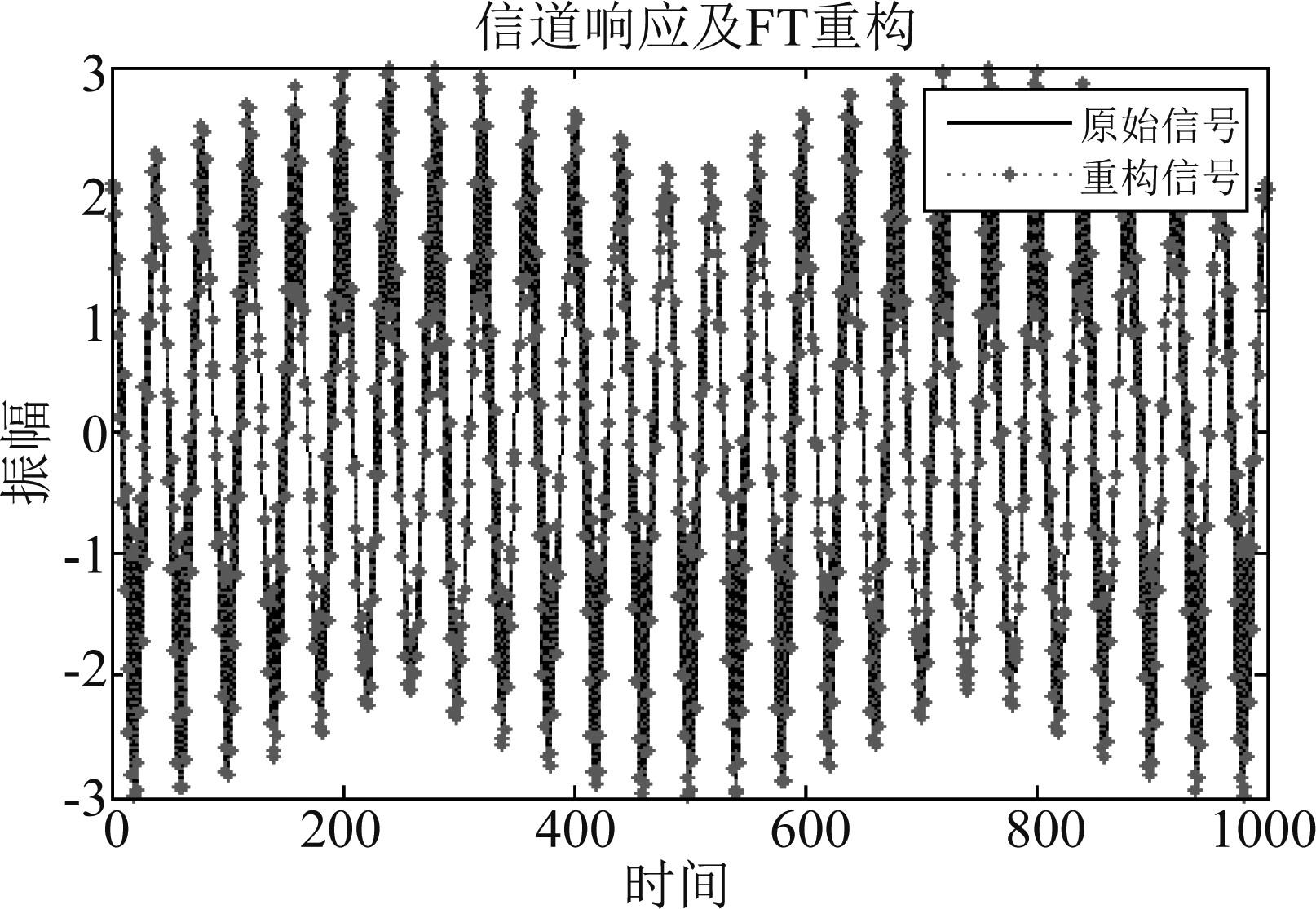
图2 基于FT的信道重构
Fig.2 Channel reconstruction based on FT

图3 重构误差随分解步长的改变
Fig.3 The change of reconstruction error with the step length of decomposition
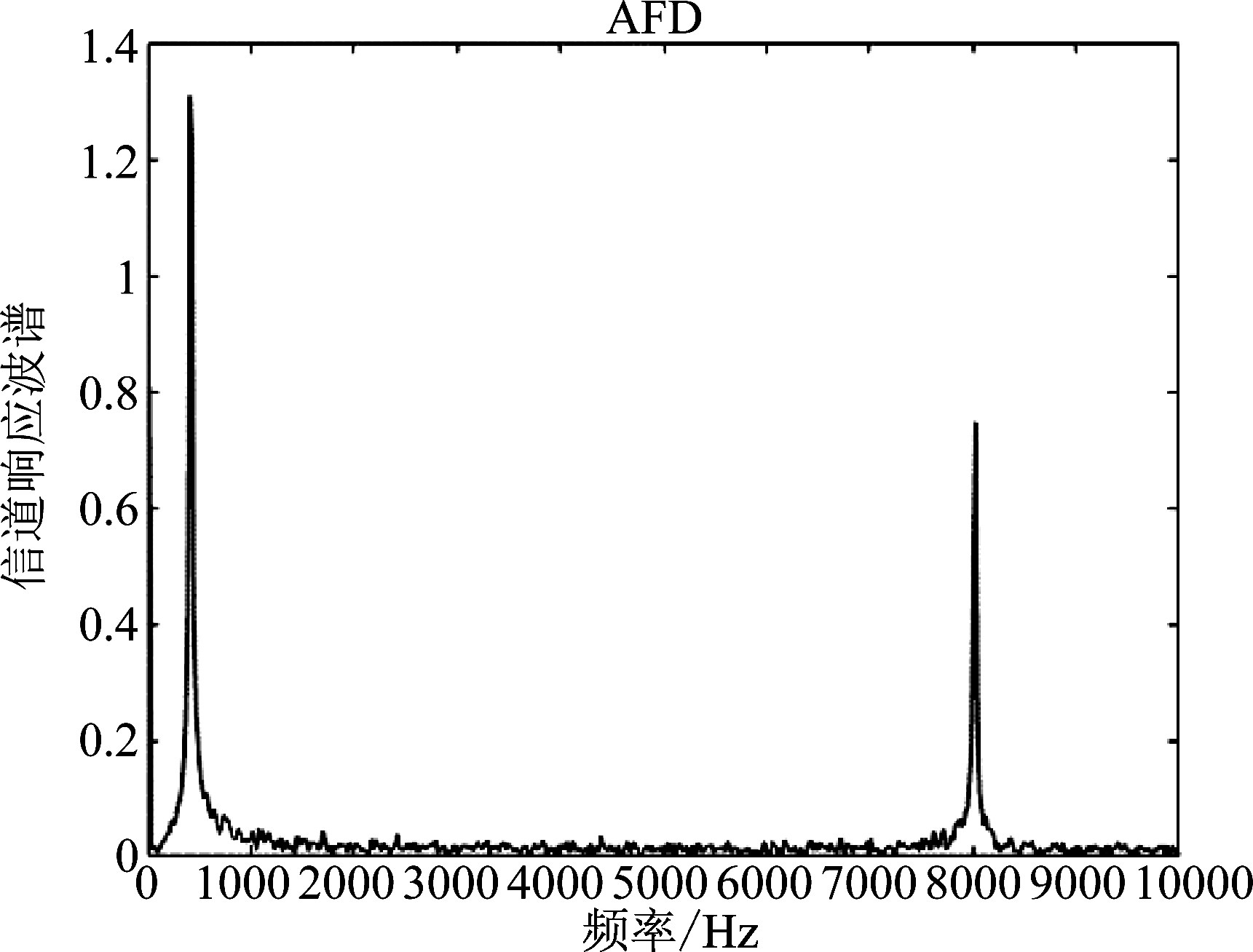
图4 基于AFD的信道谱图
Fig.4 Channel spectrum based on AFD
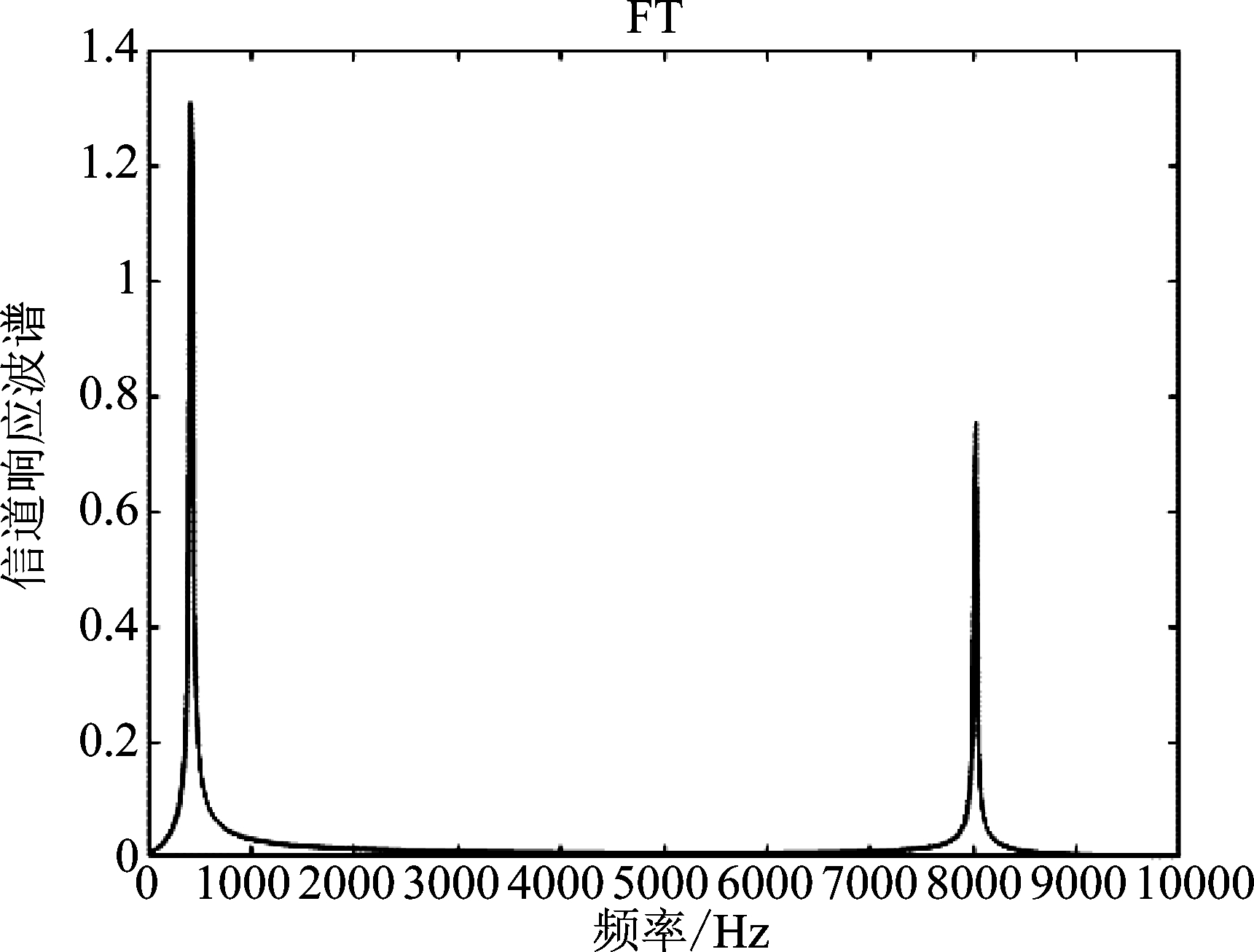
图5 基于FT的信道谱图
Fig.5 Channel spectrum based on FT
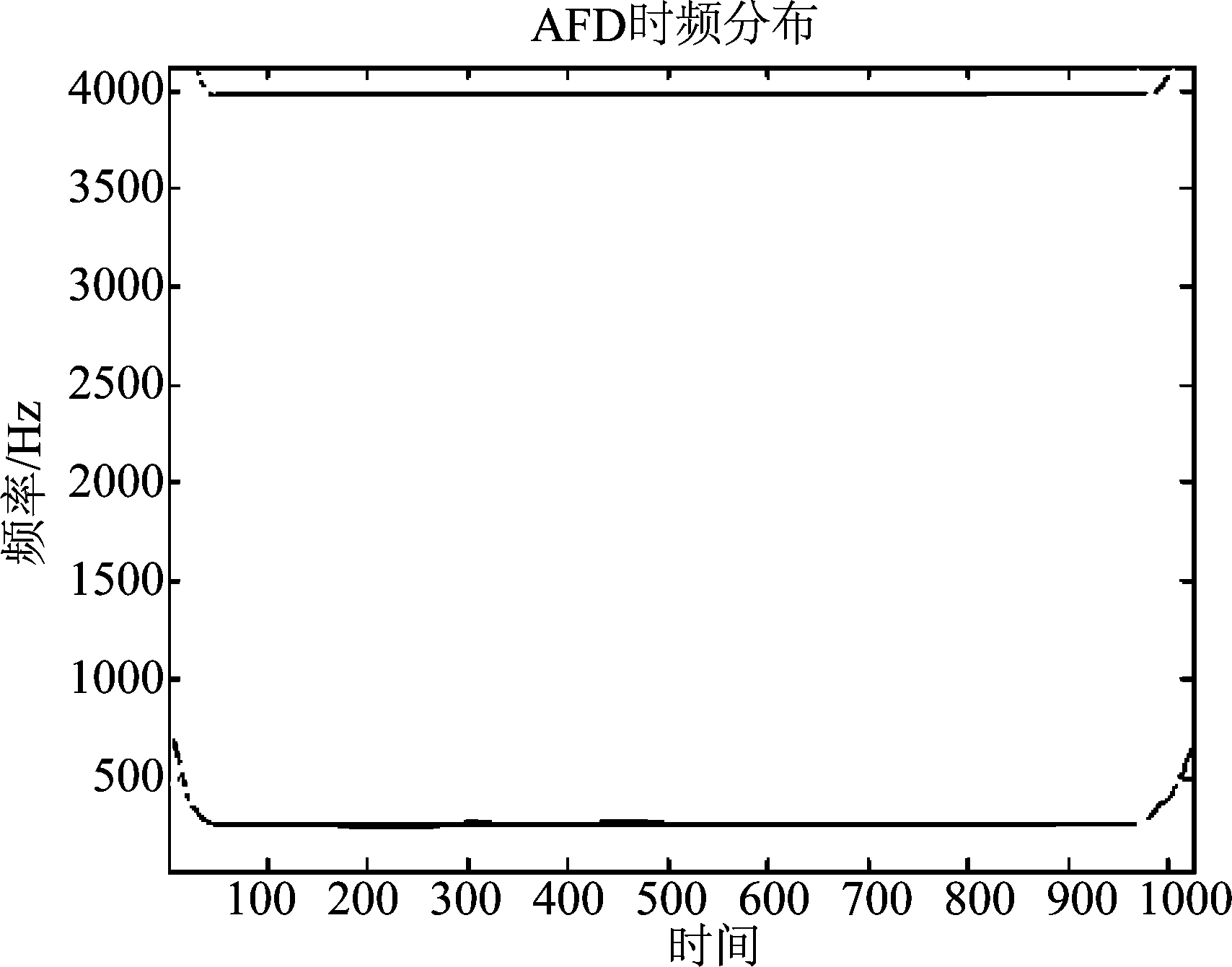
图6 基于AFD的信道时频分布
Fig.6 Time frequency distribution of the channel based on AFD
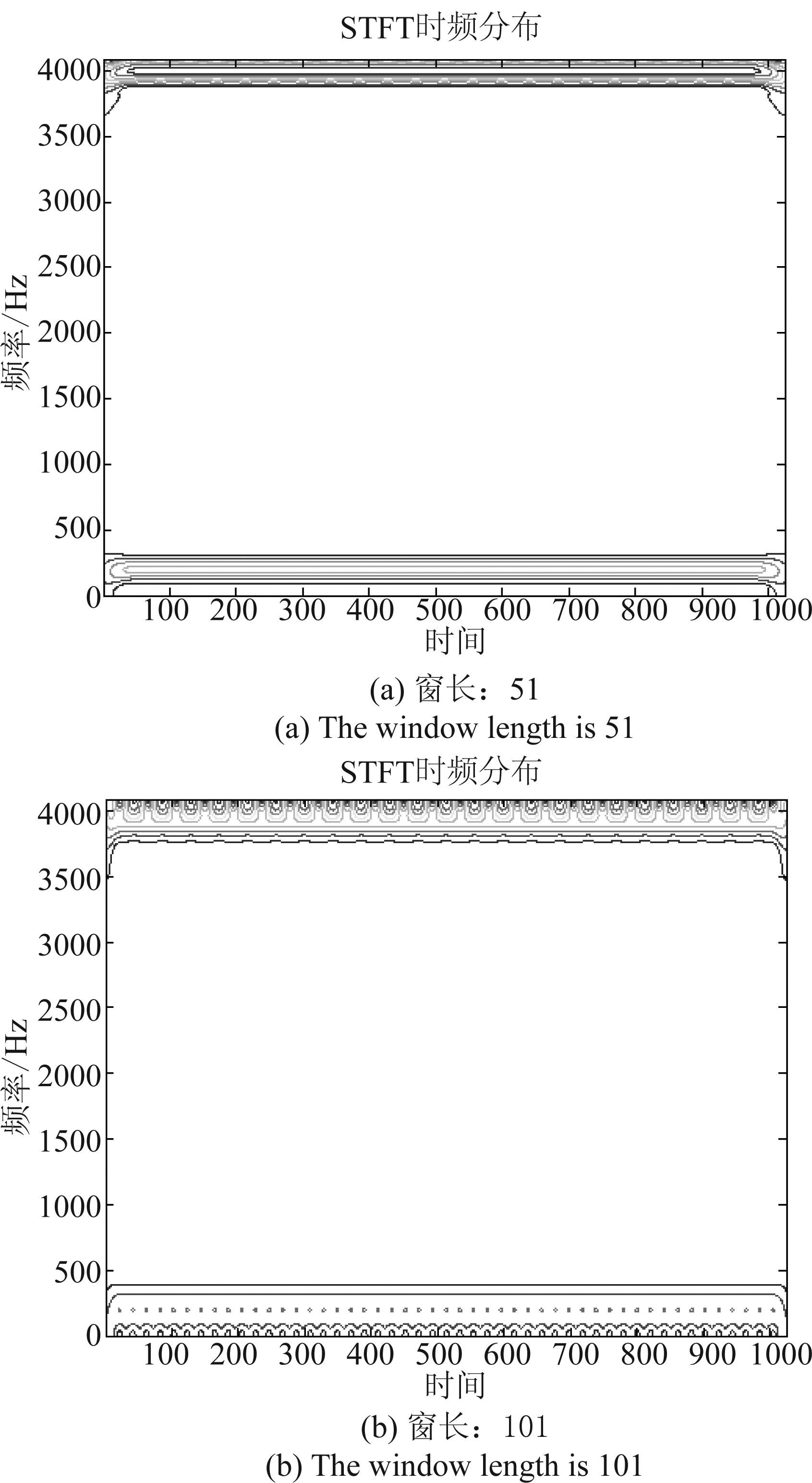
图7 基于STFT的信道时频分布
Fig.7 Time frequency distribution of the channel based on STFT
5 结论
本文研究了无线信道的时频二维表示方法,引入了一种基于AFD的非平稳无线信道时频表示方法。该方法克服了窗函数参数选择,小波基函数的选择判决准则问题,突破了信道时频表示中现有方法的制约,并吸收了AFD的以最大选择原理为基础的自适应傅里叶基的表示特性,通过对双径Clarke信道时域冲激响应的AFD表示与仿真,得到了信道的单分量分解表示式、等效瞬时频率表示式、时频二维分布模型,证明了AFD相较于传统傅里叶相关分析方法的优越性,同时揭示了AFD的低误差可重构特性,适用于非平稳高速无线信道。
[1] 孙舒鹏.移动通信系统近距离覆盖传播模型研究[D].北京:北京邮电大学, 2014.
Sun Shupeng. Research and application of wave propagation model in mobile communication system[D]. Beijing: Beijing University of Posts and Telecommunications, 2012. (in Chinese)
[2] 岳瑞.基于时-频域的无线信道分析及其在LTE下行链路的研究[D].成都:西南交通大学, 2013.
Yue Rui. Wireless channel analysis based on time domain and its research on LTE downlink[D]. Chengdu:Southwest Jiaotong University, 2013. (in Chinese)
[3] Okonkwo U A K,Ngah R, Rahman T A. Wavelet-domain channel characterization for mobile broad-band communication systems[C]∥RF and Microwave Conference, 2008. RFM 2008. IEEE International. IEEE, 2009:283-288.
[4] Jakes W C. Microwave Mobile Communications[M]. Finite Element Method Electromagnetics: Antennas, Microwave Circuits, and Scattering Applications, 1998.
[5] 陆大淦,张颢.随机过程及其应用[M].北京:清华大学出版社, 2012.
Lu Dagan, Zhang Hao. The stochastic process and its application[M].Beijing: Tsinghua University Press,2012.(in Chinese)
[6] Cho S H, Jang G, Kwon S H. Time-Frequency Analysis of Power-Quality Disturbances via the Gabor-Wigner Transform[J]. IEEE Transactions on Power Delivery, 2010, 25(1):494- 499.
[7] Skima M A, Ghariani H, Lahiani M. A multi-criteria comparative analysis of different Rayleigh fading channel simulators[J]. AEU-International Journal of Electronics and Communications, 2014, 68(6):550-560.
[8] Qian T, Wang Y B. Adaptive Fourier series-a variation of greedy algorithm[J]. Advances in Computational Mathematics, 2011, 34(3):279-293.
[9] Ohshima S, Kobayashi S, Yamamoto S, et al. Highly time-resolved evaluation technique of instantaneous amplitude and phase difference using analytic signals for multi-channel diagnostics[J]. Review of Scientific Instruments, 2014, 85(11):11E814.
[10] Zhang L, Qian T, Mai W, et al. Adaptive Fourier decomposition-based Dirac type time-frequency distribution[J]. Mathematical Methods in the Applied Sciences, 2017, 40:2815-2833.
[11] York S N. Mathematical Theory of Communication[M]. Springer New York, 2013.
[12] Orovic I, Orlandic M, Stankovic S, et al. A Virtual Instrument for Time-Frequency Analysis of Signals With Highly Nonstationary Instantaneous Frequency[J]. IEEE Transactions on Instrumentation & Measurement, 2011, 60(3):791- 803.
[13] Tao Q. Intrinsic mono-component decomposition of functions: An advance of Fourier theory[J]. Mathematical Methods in the Applied Sciences, 2010, 33(7):880- 891.
[14] 任喜顺,沈越泓,高猛, 等. 基于时频分析的混合矩阵估计方法[J]. 信号处理, 2012, 28(4):545-553.
Ren Xishun, Shen Yuehong, Gao Meng, et al. Hybrid matrix estimation method based on time frequency analysis[J]. Signal Processing, 2012, 28(4): 545-553. (in Chinese)
[15] 李雷,郭英,张坤峰, 等. 块稀疏贝叶斯模型下的跳频信号时频分析[J]. 信号处理, 2018, 34(1): 107-113.
Li Lei,Guo Ying, Zhang Kunfeng, et al. The time-frequency analysis of frequency hopping signal under the block sparse Bayesian model[J]. Journal of Signal Processing, 2018, 34(1): 107-113. (in Chinese)
[16] Lin R, Du C, Luo S,et al. Performance on a combined representation for time-frequency analysis is[C]∥International Conference on Image, Vision and Computing. IEEE, 2017:858- 862.
 methods such as short time Fourier transform (STFT) and wavelet transform (WT). It can also represent the time-frequency representation and reduce the reconstruction error of the wireless channel accurately.
methods such as short time Fourier transform (STFT) and wavelet transform (WT). It can also represent the time-frequency representation and reduce the reconstruction error of the wireless channel accurately.

