1 引言
近年来,随着手机、平板、便携式电脑和大量物联网设备的接入,无线网络的数据流量呈现指数级增长,这要求未来的无线网络不仅具有更高的容量,以保证更多的用户接入网络,而且应具有更高的频谱效率,以保证每个用户对更高传输速率的需求。考虑到目前的3G/4G网络并不能满足用户更高容量和高速率的需求,对第五代移动通信(fifth generation,5G)的研究已刻不容缓。事实上,5G网络早已经成为国内外研究的热点[1]。其中异构网络(heterogeneous networks,HetNets)因其在有较高系统吞吐量的同时能保证网络高稳定和高服务质量的特性,得到业界及学术界的高度重视,其被视为5G网络的一个关键技术。HetNets的基本思想是在传统的宏小区上高度密集地部署大量小小区网络[2],小小区网络主要包括微蜂窝、微微蜂窝、家庭蜂窝等各类低功率节点网络。宏小区主要负责高速移动用户的接入和网络资源管理,而小小区则负责室内等小范围用户和低速移动用户的接入,将多种不同类型基站(base station,BS)同时存在的HetNets称为多层HetNets,例如在传统的宏蜂窝上部署微蜂窝、微微蜂窝构成三层HetNets。然而,规模如此庞大的异构部署必然会引发新问题,如运营费用的负担及资本支出等[3]。此外,另一个问题也随之出现:当用户接入网络时,怎样从各层BS或中继中为其找到一个最佳的接入点以最高效地挖掘HetNets的潜能,即HetNets用户级联(user association,UA)问题。
目前,已有大量文献提出有关UA的方案。其中讨论最为广泛的是基于最大接收信号功率(maximum received signal power,MRSP)和信号与干扰加噪声比 (signal-to-interference-noise ratio,SINR)的UA方案,这两种方案均使用户级联至能提供最大MRSP/SINR的接入点[4]。然而,这两种方案都是面向传统蜂窝网的,并不适用于本文的HetNets。如果在HetNets中,继续使用这两种级联方案,小小区BS将只会有少量的用户级联从而引起BS间负载的不均衡[5]。为此,相关文献提出了基于偏置的UA方案,通过在网络中增加偏置因子来提高UA概率。然而这些方案只适用于以往的单跳网络,都仅单一的研究了网络的上行或者下行链路,并未联合考虑上下行链路进行研究。为此,本文提出了中继协作HetNets。众所周知,中继协作是未来5G网络的另一个关键技术[6-9]。例如,在文献[10]中作者提出了同时部署宏小区,小小区,D2D和中继网络的一种新颖HetNets。在单跳网络中,用户与宏BS和小BS的连接使用了基于偏置的UA方案[5- 6],但该方案并不适用于中继协作双跳HetNets。这是因为在两跳中继网络中,信号传输由信源-中继和中继-信宿两跳组成[11]。考虑两跳中继系统的传输特性,在此类中继协作多层HetNets中,服务中继的选择必须联合考虑两跳链路性能,即单跳最佳并不能保证双跳最佳。此外,在中继协作HetNets中,上下行链路应当级联到同一中继。虽然文献[12]和[13]中提出的解耦上行-下行链路用户级联方案考虑了上行链路和下行链路,但该方案也是基于单跳传输方案,其并不适合于中继网络。此外,除UA问题外,由于开放的网络架构和无线传输的广播特性,超密集HetNets的物理层安全也是一个重要问题[14]。传统网络的安全通过在应用层实施加密得以保证。这种方法是基于一定的假设,如计算复杂性等[15];但是,随着基于量子等技术的高速设备的出现和发展,这种基于计算复杂度的加密技术将受到极大的挑战。实际上,从信息理论的角度出发,可以通过利用衰落、噪声、干扰等信道物理特性实现可靠的通信,即物理层安全。如果合法用户比窃听者(eavesdroppers, Eves)具有更好的信道条件,收发器以一定速率进行可靠通信,物理层则视为安全。基于此考虑,文章[16]在安全吞吐量和安全中断概率方面做了HetNets物理层安全分析。然而,在基于中继的HetNets中,物理层安全分析尚未有文献公开发表。
同时,近来研究结果表明,对于用户和网络接入点随机分布的异构网,随机几何是一个有效的分析方法[17-18]。在该随机几何方法中,将网络终端元素建模为泊松点过程(Poisson point process, PPP),文献[19]的研究结果表明,利用PPP方法可以很好地界定蜂窝网的性能界,并且文献[20]采用蒙特卡洛仿真的方法进一步证明了用随机几何方法分析大规模随机网络的有效性,得出利用随机几何方法可以获得可靠的网络性能数学模型的结论,从而避免了复杂的蒙特卡洛仿真。由此,对于基于物理层安全的大规模中继协作HetNets,不仅网络中的基站、中继和用户对分布具有泊松随机性,而且Eves的分布也具有泊松随机性。为了避免复杂的蒙特卡洛仿真,需借助随机几何和PPP过程方法一方面来研究网络级联概率及其距离等的统计特性,另一个方面需要研究网络的安全性,所有网络中的元素借助随机几何方法即可获得清晰的数学模型。
基于上述文献和考虑,本文研究了中继协作多层HetNets的用户对级联(user-pair association,UPA)准则及物理层安全性能。首先,基于HetNets和中继协作技术,构建了一种中继协作多层HetNets模型,其由宏蜂窝、微蜂窝和微微蜂窝等不同功率节点的网络构成。同时,为了增强UPA概率,系统引入了偏置因子。特别地,根据参考文献[21]中的方法,在充分考虑中继信道特征的基础上提出了两种新颖的UPA准则,称其为最大-最小用户对级联(maximum-minimum UPA,MM-UPA)和最大和谐均值用户对级联(maximum harmonic mean,MHM-UPA)准则。随后,基于随机几何和概率统计工具,给出了相应的UPA概率。此外,为证明两种UPA准则的现实可行性,研究了网络总的平均安全概率。在仿真部分,给出了MM-UPA和MHM-UPA准则之间用户级联概率和总平均安全概率的比较分析。同时,为验证数学推导,本文还与传统单跳HetNets的UA概率进行了比较[5]。
2 系统模型及假设
本文考虑了一个多层中继协作两跳HetNets模型。在该HetNets中,不同类型的中继用于协助用户对之间的通信。每层网络间的中继类型、无线电传播环境、覆盖范围和发射功率以及空间位置强度均不相同,且各层之间相互独立。在任意给定的第k层网络中,中继的空间物理位置分布服从强度为λk的齐次PPP,记作Φk,其中k=1,2,…,K。同时,每层网络中的一组移动用户对均由一个信源和一个信宿两个节点构成,相应地将其空间物理位置建模为强度是λu的两个独立齐次PPPs,分别记作ΦS和ΦD。为了方便研究,在同一层网络中,假设信源的发送功率和中继发送功率均相同,分别设置为![]() 和
和![]() 其中k=1,2,…,K。此外,所有的中继通信链路均受到恶意Eve窃听,且所有的Eve只对信号进行被动地窃听和拦截,并不对其进行篡改。这里进一步假定所有的Eve空间物理位置满足强度为λe 的独立PPP,记作Φe。考虑到中继链路的特征,这些Eve不仅窃听源到中继链路,同时还窃听中继到信宿链路。如图1所示,以K=3为例,考虑了由宏小区、微小区、微微小区和被动Eves组成的中继协作三层HetNets。由于较强的信道衰落,假定位置随机的信源和信宿不能直接通信而使用其服务中继进行通信。
其中k=1,2,…,K。此外,所有的中继通信链路均受到恶意Eve窃听,且所有的Eve只对信号进行被动地窃听和拦截,并不对其进行篡改。这里进一步假定所有的Eve空间物理位置满足强度为λe 的独立PPP,记作Φe。考虑到中继链路的特征,这些Eve不仅窃听源到中继链路,同时还窃听中继到信宿链路。如图1所示,以K=3为例,考虑了由宏小区、微小区、微微小区和被动Eves组成的中继协作三层HetNets。由于较强的信道衰落,假定位置随机的信源和信宿不能直接通信而使用其服务中继进行通信。
在此中继协作K层HetNets中,每个中继节点均采用解码转发(decode and forward, DF)中继协议来协助完成通信。因此,当某一个移动用户对需要与第k层的中继级联时,该用户对之间的通信将由两个阶段组成。其中,第一阶段,该移动用户对中的信源以功率为![]() 将信号发送至服务中继,在第二个阶段中,级联中继以功率
将信号发送至服务中继,在第二个阶段中,级联中继以功率![]() 根据DF协议将接收到的信号转发至移动用户对信宿。当考虑无线传播时,无线信道衰落由大规模衰落和小规模衰落两部分组成,假设第k层路径损耗指数为αk,两个随机用户节点i和j间小规模衰落无线信道增益
根据DF协议将接收到的信号转发至移动用户对信宿。当考虑无线传播时,无线信道衰落由大规模衰落和小规模衰落两部分组成,假设第k层路径损耗指数为αk,两个随机用户节点i和j间小规模衰落无线信道增益![]() 建模为功率归一化的Rayleigh衰落即
建模为功率归一化的Rayleigh衰落即![]() 每个接收端的接收信号均受均值为0、方差为w的加性高斯噪声CN(0,w)的影响。
每个接收端的接收信号均受均值为0、方差为w的加性高斯噪声CN(0,w)的影响。
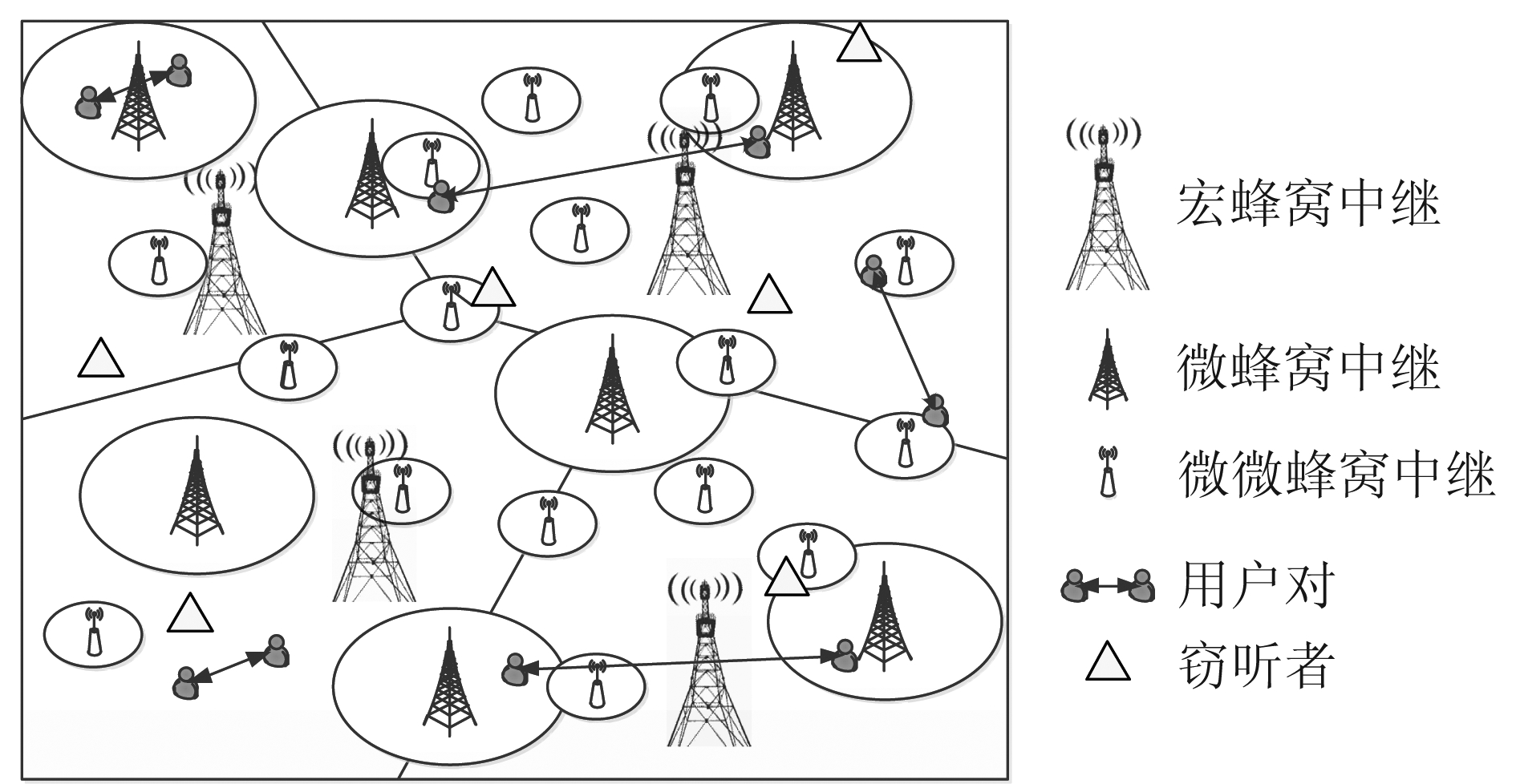
图1 中继协作3层异构网络模型
Fig.1 Relay-assisted 3-tier HetNets
在此网络模型中,选择的服务中继表示为:
(1)
其中βj是第j层网络的偏置因子。![]() 表示中继链路的端到端偏置接收功率(Biased Receive Power,BRP)均值。
表示中继链路的端到端偏置接收功率(Biased Receive Power,BRP)均值。
3 用户对级联准则
3.1 MM-UPA准则
传统的单跳网络中,用户级联仅单一地考虑下行链路(或上行链路)的平均偏置接收功率(average biased received power, ABRP)[5],而在本文提及的双跳中继协作HetNets中,考虑任意给定一组用户对的级联问题时,级联的中继必须兼顾信源-中继和中继-信宿两跳传输性能。所以,文献[5]中将每层中最近中继作为级联中继的UA方案是不可取的,为此提出了MM-UPA准则。该准则建立在开放接入机制下,即一个用户对可被分配至任意层的中继。不失一般性,根据DF中继协议的思想,对于任一给定的用户组,当其通过第j层网络的第i个中继通信时,其等效的信源到信宿ABRP由该端到端的瓶颈链路功率决定,表示为:
(2)
其中,L0表示在参考距离r0处的路径损耗,![]() 和
和![]() 分别表示该第j层的第i个中继到信源和信宿的距离,βj表示第j层网络的偏置因子。一般考虑的级联基站是每层的最近基站[5],但是该方法对于文章所讨论的双跳中继通信系统并不有效,主要原因是双跳的任一链路最近并不能保证另一条链路也是最近或最短。因此,定义每层最佳中继使得对于所有i有最小的
分别表示该第j层的第i个中继到信源和信宿的距离,βj表示第j层网络的偏置因子。一般考虑的级联基站是每层的最近基站[5],但是该方法对于文章所讨论的双跳中继通信系统并不有效,主要原因是双跳的任一链路最近并不能保证另一条链路也是最近或最短。因此,定义每层最佳中继使得对于所有i有最小的![]() 表示为
表示为![]() 即:
即:
(3)
其中,![]() 和
和![]() 分别表示该最佳中继到信源和信宿的距离。因为在PPP中,任一给定端点与其服务端点间的距离可用Rayleigh分布来近似,所以,距离
分别表示该最佳中继到信源和信宿的距离。因为在PPP中,任一给定端点与其服务端点间的距离可用Rayleigh分布来近似,所以,距离![]() 和
和![]() 的概率密度函数可分别近似写为:
的概率密度函数可分别近似写为:
(4)
为了便于后续处理,采用MM-UPA准则时,可将式(3)进一步写为:
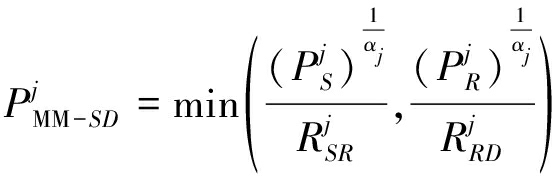
(5)
据此,根据DF协议准则,可得用户对级联准则:
服务中继:![]()
(6)
根据该准则,可以为任一给定用户选择服务中继。可以发现,该准则是最大化所有两跳链路ABRP的最小值,故将其称为MM-UPA准则。
3.2 MHM-UPA准则
基于DF中继协议的思想,在上一部分中文章提出了MM-UPA准则。但是,当系统采用DF中继协议时,系统性能将受到瓶颈项的制约,系统的性能仅由瓶颈链路所决定,并没有考虑信源-中继和中继-信宿两跳链路的综合影响。为克服此困难,面向该系统本文又提出了另一种用户对级联准则,即MHM-UPA准则。顾名思义,该准则利用两个随机变量的和谐均值代替相应的统计最小值,这时能使两个中继链路ABRPs的和谐均值最大化的中继即为最佳服务中继。为此,在MM-UPA准则中,可令![]() 式(5)中两随机变量Xj和Yj的和谐均值为:
式(5)中两随机变量Xj和Yj的和谐均值为:
(7)
利用该和谐均值定义![]() 可得基于和谐均值的用户对级联准则:
可得基于和谐均值的用户对级联准则:
服务中继:![]()
(8)
显然地,最大和谐均值准则同时兼顾了两条链路的影响,因此,该准则具有鲁棒性。
4 用户对级联概率
4.1 基于MM-UPA准则的UPA概率
本小节先研究基于MM-UPA准则的用户对级联概率。在此,用![]() 表示在该中继协作双跳HetNets中任意给定的一组用户对连接至层第k网络最佳中继的用户对级联概率。为得到
表示在该中继协作双跳HetNets中任意给定的一组用户对连接至层第k网络最佳中继的用户对级联概率。为得到![]() 这里用n表示级联层的系数。根据MM-UPA准则的基本思想,当一组给定用户对级联至第k层最佳中继时,对于所有的j∈{1,2,...,K}, j≠k,都有
这里用n表示级联层的系数。根据MM-UPA准则的基本思想,当一组给定用户对级联至第k层最佳中继时,对于所有的j∈{1,2,...,K}, j≠k,都有![]() 当该用户对与第k层的最佳中继级联时,有n=k。由此,可得用户对级联概率
当该用户对与第k层的最佳中继级联时,有n=k。由此,可得用户对级联概率![]()
(9)
其中![]() 表示关于
表示关于![]() 的期望运算,使用顺序统计思想和双跳链路的独立性假设,以及式(4)中概率密度函数,对其做进一步推导得:
的期望运算,使用顺序统计思想和双跳链路的独立性假设,以及式(4)中概率密度函数,对其做进一步推导得:

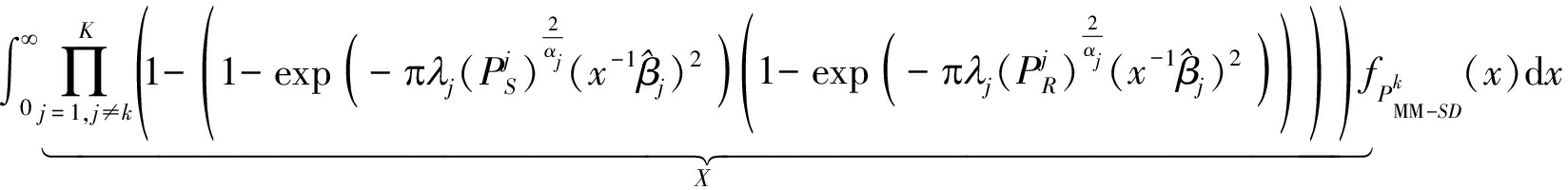
(10)
其中定义![]() 为随机变量
为随机变量![]() 的概率密度函数,根据定义式(5),该概率密度函数可表示为:
的概率密度函数,根据定义式(5),该概率密度函数可表示为:
(11)
此外。式(10)以多项连乘的形式给出,为了获得易于处理的形式,根据以下公式:
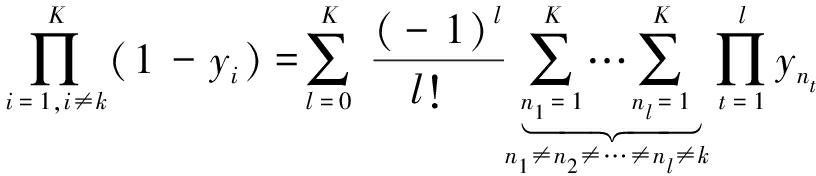
(12)
式(10)中X可以化简为:
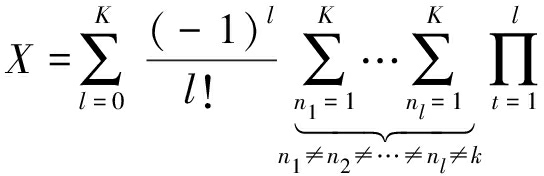
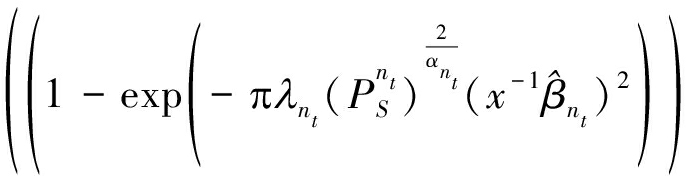
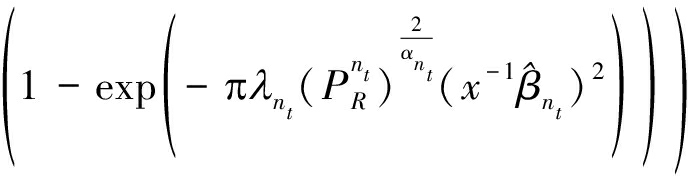
(13)
类似的,可对式(13)中的连乘项做进一步的分解,可得:
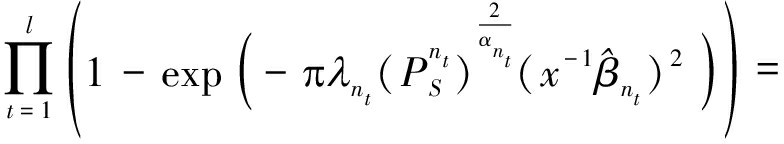
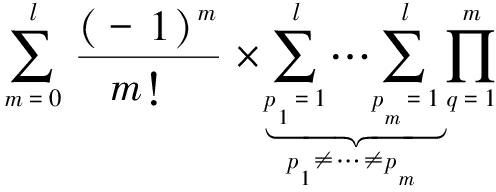
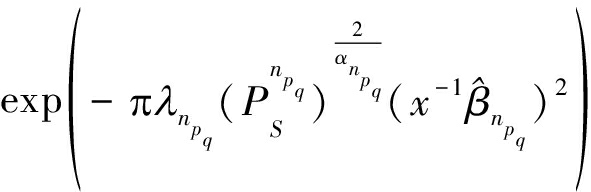
(14)
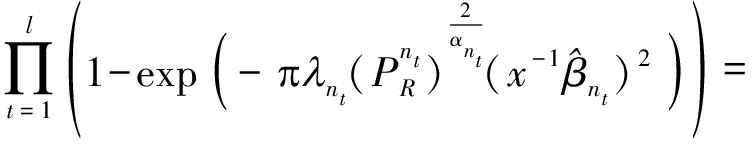
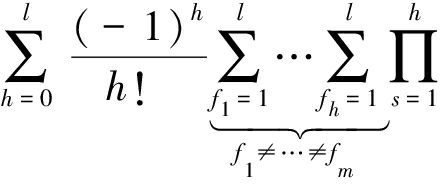
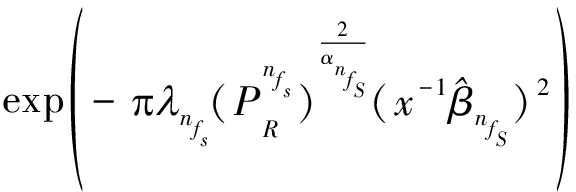
(15)
结合式(15)、(14)、(13)和(10),可得出定理1,其给出了中继协作多层HetNets中基于MM-UPA准则的用户对级联概率。
定理1 对于文章所考虑的中继协作多层HetNets,当系统采用MM-UPA方案时,任意给定的一组用户对级联至第k层最佳中继的概率为:
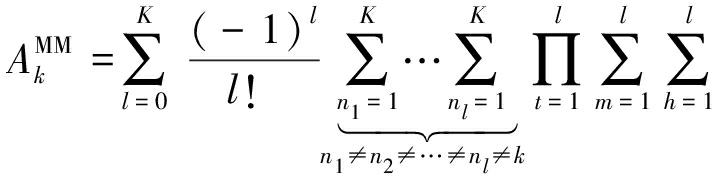
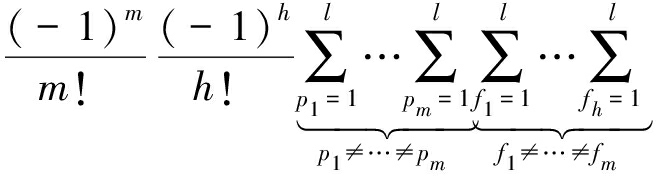
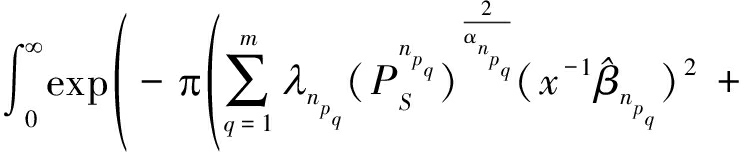

(16)
其中,随机变量![]() 的概率密度函数
的概率密度函数![]() 由式(11)给出。
由式(11)给出。
4.2 基于MHM-UPA准则的UPA概率
与上文类似,用![]() 表示在中继协作双跳HetNets中任意给定的一组用户对连接至层k的最佳中继的UPA概率。参考
表示在中继协作双跳HetNets中任意给定的一组用户对连接至层k的最佳中继的UPA概率。参考![]() 可得
可得![]()
(17)
其中![]() 在式(7)中已经给出。根据式(7)中随机变量
在式(7)中已经给出。根据式(7)中随机变量![]() 的定义,将
的定义,将![]() 作进一步计算可得:
作进一步计算可得:
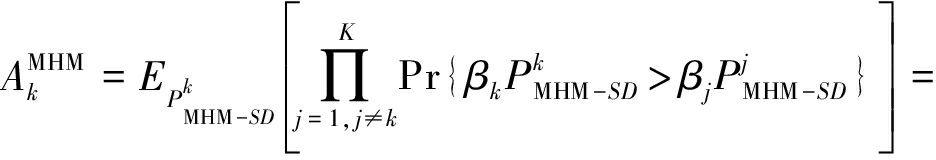
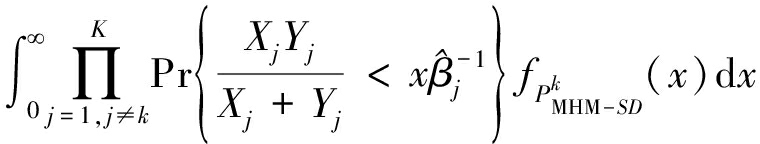
(18)
其中![]() 为随机变量
为随机变量![]() 的概率密度函数。由此,可得出定理2。
的概率密度函数。由此,可得出定理2。
定理2 在中继协作多层HetNets中,当系统采用MHM-UPA方案时,任意给定的一组用户对级联至第k层最佳中继的概率为:
(19)
其中,随机变量![]() 的分布函数
的分布函数![]() 为:
为:
(20)
(21)
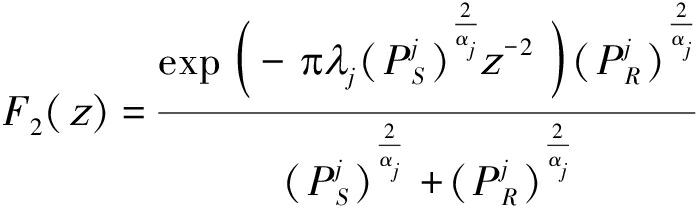
(22)
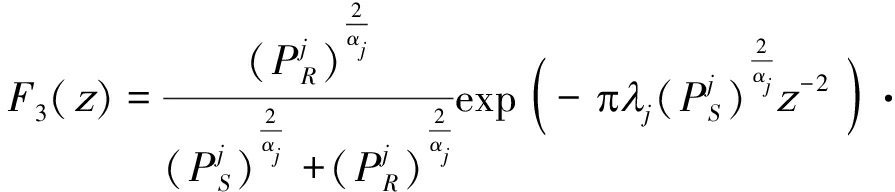
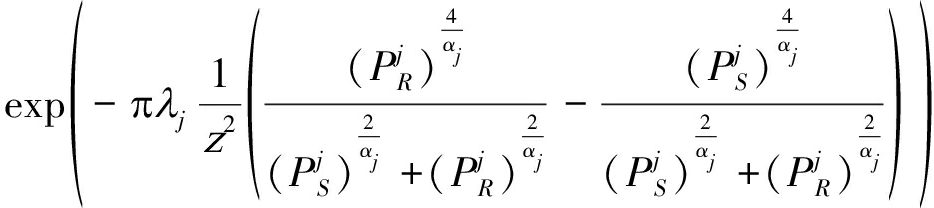
(23)
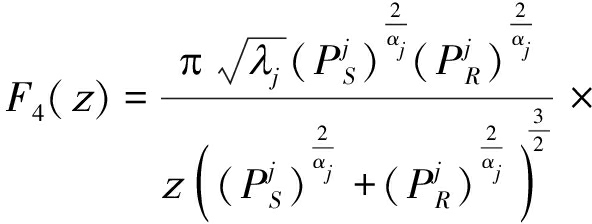
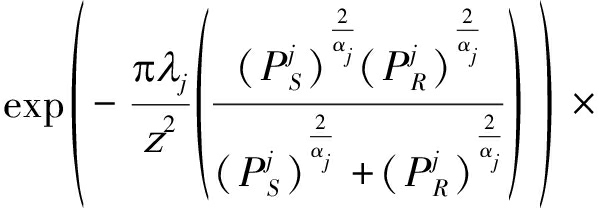
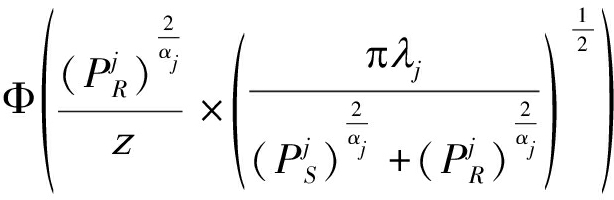
(24)

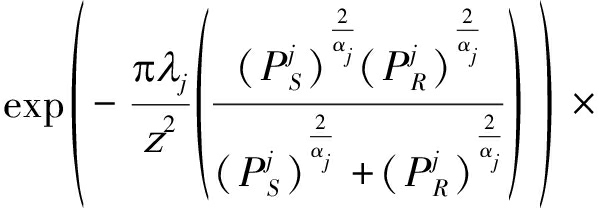
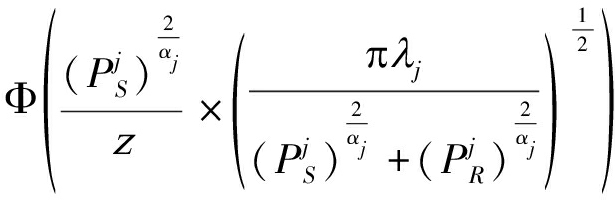
(25)
其中,随机变量![]() 的概率密度函数
的概率密度函数![]() 为
为![]() 用k替换式(20)中的j,可得分布函数
用k替换式(20)中的j,可得分布函数![]()
5 安全概率分析
利用PPP,前面对文章提出的MM-UPA和MHM-UPA方案的用户对级联到网络中任意一层最佳中继的概率做了研究,获得了基于两种用户对级联准则的用户对级联概率;基于获得的用户对级联概率,可以分析网络的统计性能,比如:覆盖概率、吞吐量和安全性能等。作为一个重要的应用,本节利用随机几何和PPP方法,比较研究基于MM-UPA和MHM-UPA方案的网络安全性能。
不失一般性,首先考虑任意给定一组用户对的通信链路的安全性能。由于中继系统的特殊性,在考虑网络的安全性能时,需同时考虑信源-中继和中继-信宿两条通信链路,这也是本文与已有成果的区别。因此,对于位于![]() 处的Eve,其接收到来自于级联至层k的移动用户对信源的SINR可以写为:
处的Eve,其接收到来自于级联至层k的移动用户对信源的SINR可以写为:

(26)
类似的,基于DF中继协议的思想,Eve从该移动用户对在第k层服务中继处的接收SINR可写为:
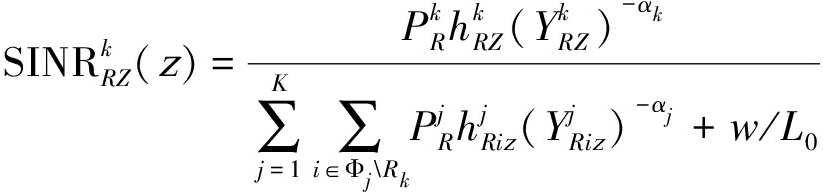
(27)
其中,式(26)和式(27)中![]() 和
和![]() 分别表示位于
分别表示位于![]() 处的Eve到信源和服务中继的距离,
处的Eve到信源和服务中继的距离,![]() 是相应的Rayleigh衰落信道增益;
是相应的Rayleigh衰落信道增益;![]() 和
和![]() 分别表示位于
分别表示位于![]() 处的窃听者到其他信源和中继的距离,
处的窃听者到其他信源和中继的距离,![]() 和
和![]() 是相应的Rayleigh信道增益。在此,\R(S)k表示除去给定用户对的服务中继(信源)。
是相应的Rayleigh信道增益。在此,\R(S)k表示除去给定用户对的服务中继(信源)。
由于文章考虑了更加一般的情形,假设每条链路都暴露给所有的恶意Eve,每个非共谋和被动Eve独立地截取信号而没有任何攻击。在这种情况下,根据保密传输要求,有:当这两条通信链路信源-中继链路和中继-信宿链路中的任意一条不安全时,该给定用户对的通信是不安全的。此外,由于该用户对的中继链路暴露给多个被动窃听者,所以仅需要分析最恶意的Eve,即具有最大接收SINR的Eve假定传输的安全门限值为TSec,考虑双跳中继链路的瓶颈属性,即可得到当用户对级联至层k的中继时相应的安全概率:
(28)
该式表明,当且仅当来自信源和中继的两个最大SINR都低于给定安全门限时,用户对的中继通信即为安全的。因此,通过使用顺序统计和独立性假设,式(28)可以进一步写成:
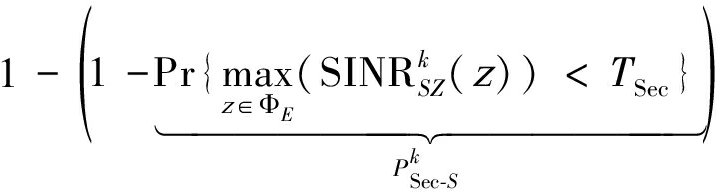
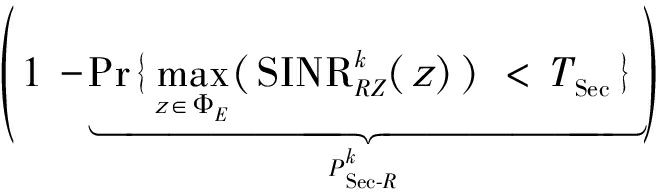
(29)
由于用户对最多只能与某一层BS级联,因此根据全概定理,有定理3。
定理3 在中继协作多层HetNets中,当所有中继链路暴露给非共谋和被动窃听者时,基于MM-UPA或MHM-UPA准则,该HetNets在给定的安全门限TSec下,总的平均安全概率为:
(30)
其中![]() 定义为:
定义为:
(31)
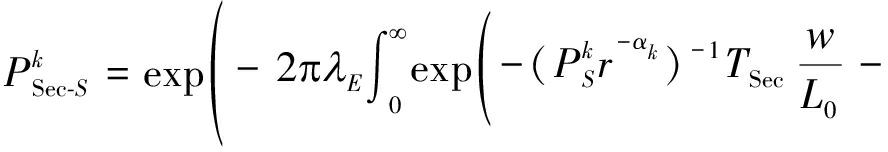
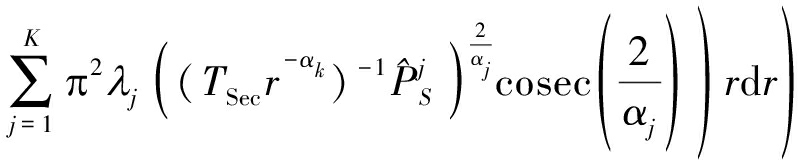
(32)
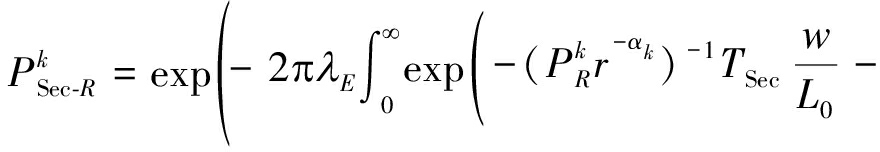
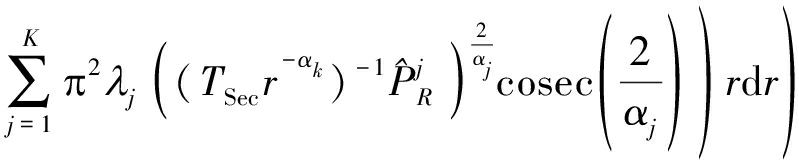
(33)
证明 这里,利用PPP和随机几何方法,给出定理3简单的证明。
根据式(29),首先计算![]() 其可以表示为:
其可以表示为:
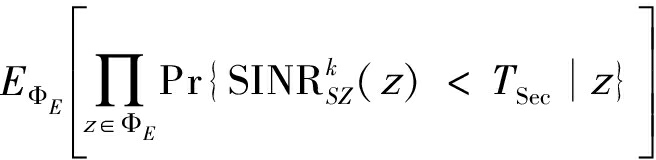
(34)
将式(26)代入上式可得:
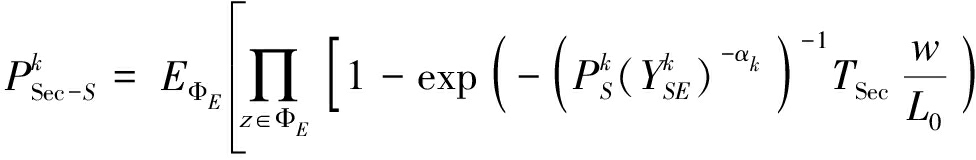
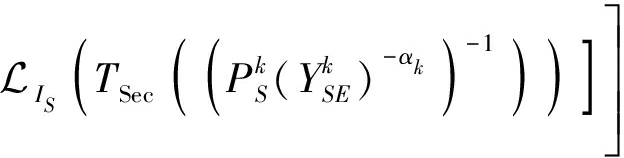
(35)
其中,![]() 表示IS的拉普拉斯变换。利用文献[22]中随机几何方法,拉普拉斯变换
表示IS的拉普拉斯变换。利用文献[22]中随机几何方法,拉普拉斯变换![]() 可写为:
可写为:
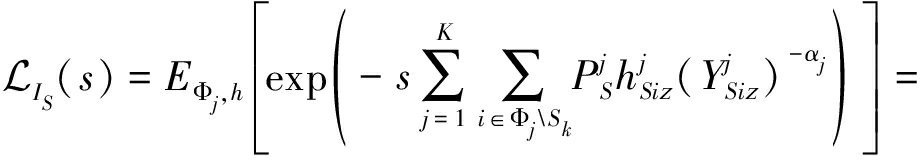
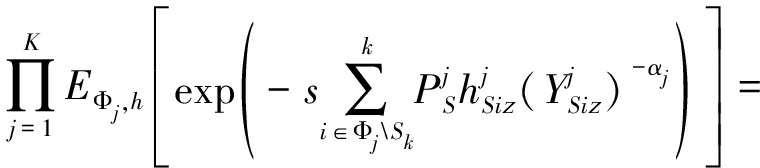
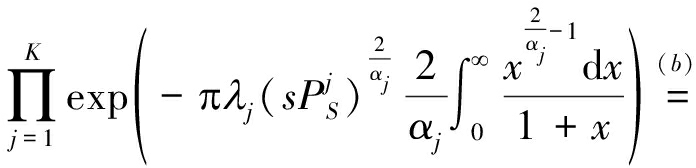
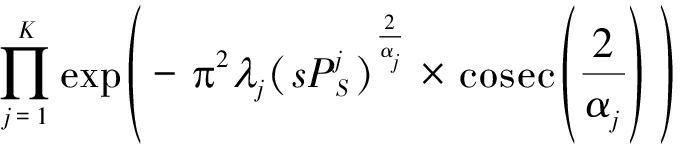
(36)
同时,式(35)可以写为:
(37)
类似地,可得![]()
6 仿真及数值分析
基于先前的数学推导,本节给出了中继协作多层HetNets用户对级联和安全概率的仿真及数值结果。除非另有说明,在整个性能分析中,考虑在一个宏小区、微小区和微微小区构成的3层HetNets,其中每米的路径损耗假设为L0=38.5 dB,接收机加性高斯噪声功率为w=-104 dBm,三个小区路径损耗指数分别为α1=3.8,α2=3.8和α3=4.0。与此同时,为验证上文的推导和与已有的结论比较,这里还给出了传统单跳网络的用户级联概率,用![]() 和
和![]() 分别表示信源-中继和中继-信宿两条链路的UA概率。
分别表示信源-中继和中继-信宿两条链路的UA概率。
在图2中,取![]() 给出了用户级联概率
给出了用户级联概率![]() 和
和![]() 与传输功率
与传输功率![]() 的关系,其中X∈{MM,MHM,T-UA-SR,T-UA-RD}。由于概率
的关系,其中X∈{MM,MHM,T-UA-SR,T-UA-RD}。由于概率![]() 类似于
类似于![]() 两者有同样的变化规律,故在图2(b)中只给出了
两者有同样的变化规律,故在图2(b)中只给出了![]() 图2(a)和图2(b)分别表示不同层的UPA概率。其中图2(a)表示第1层网络的级联概率,而图2(b)则表示第3层网络的用户对级联概率,故而两者曲线趋势不同。
图2(a)和图2(b)分别表示不同层的UPA概率。其中图2(a)表示第1层网络的级联概率,而图2(b)则表示第3层网络的用户对级联概率,故而两者曲线趋势不同。
在图2(a)中,观察可以发现,当k=1时,单跳网络用户级联概率![]() 与
与![]() 和双跳用户对级联概率
和双跳用户对级联概率![]() 与
与![]() 均随着信源发射功率
均随着信源发射功率![]() 的增大而增大,其原因是随着
的增大而增大,其原因是随着![]() 的增大,第1层网络中继接收到的ABRP增大,故用户对级联概率增大。再观察
的增大,第1层网络中继接收到的ABRP增大,故用户对级联概率增大。再观察![]() 发现在该参数下,单跳网络UA概率
发现在该参数下,单跳网络UA概率![]() 大于本文提出的双跳UPA概率
大于本文提出的双跳UPA概率![]() 和
和![]() 但是概率
但是概率![]() 却小于
却小于![]() 和
和![]() 这是由于在图2(b)中,参数
这是由于在图2(b)中,参数![]() 即中继的发功率远远大于信源的发功率。图2(b)表明文章提出的MM-UPA和MHM-UPA准则均适用于中继协作的HetNets。图2(b)中曲线下降是因为总的用户级联概率等于1,第1层网络用户级联概率随
即中继的发功率远远大于信源的发功率。图2(b)表明文章提出的MM-UPA和MHM-UPA准则均适用于中继协作的HetNets。图2(b)中曲线下降是因为总的用户级联概率等于1,第1层网络用户级联概率随![]() 的增大而增大,且第2层与第3层曲线变化趋势一致,故第3层网络曲线整体下降。此外,还可以从图2中发现
的增大而增大,且第2层与第3层曲线变化趋势一致,故第3层网络曲线整体下降。此外,还可以从图2中发现![]() 这是因为MHM-UPA全面地考虑了两条链路的影响,而MM-UPA受瓶颈链路影响,故而MHM-UPA优于MM-UPA。也就是说,和谐均值方案有较好的性能,可以克服MM-UPA方案的缺点。
这是因为MHM-UPA全面地考虑了两条链路的影响,而MM-UPA受瓶颈链路影响,故而MHM-UPA优于MM-UPA。也就是说,和谐均值方案有较好的性能,可以克服MM-UPA方案的缺点。
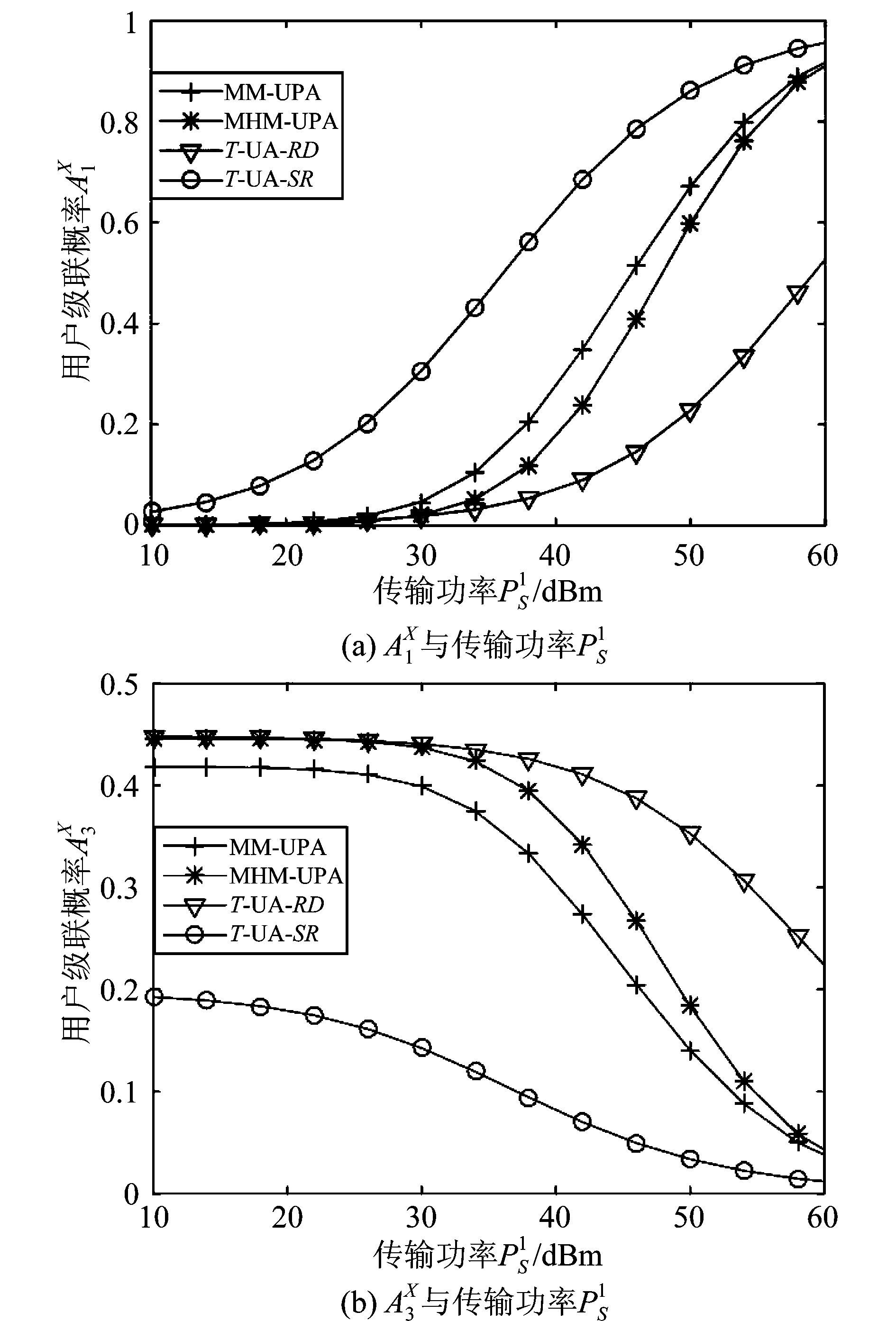
图2 用户级联概率与传输功率![]() 的比较
的比较
Fig.2 Comparison of user association probability versus transmission power ![]()
图3给出了安全概率仿真分析。在图3(a)中,取![]() 可以发现,当
可以发现,当![]() 取值较大时,安全概率曲线重合,表明两种方案有相近的安全概率;但当
取值较大时,安全概率曲线重合,表明两种方案有相近的安全概率;但当![]() 较小时,两种方案的安全概率明显不同,差别显著,也就是说,在
较小时,两种方案的安全概率明显不同,差别显著,也就是说,在![]() 较小时,MHM-UPA的安全概率高于MM-UPA。此外,还可以发现在
较小时,MHM-UPA的安全概率高于MM-UPA。此外,还可以发现在![]() 的整个区间内,基于MHM-UPA准则的用户安全概率随
的整个区间内,基于MHM-UPA准则的用户安全概率随![]() 增大而减小。然而,在MM-UPA方案中,当
增大而减小。然而,在MM-UPA方案中,当![]() 较小时,用户安全概率随
较小时,用户安全概率随![]() 增大而增大,当
增大而增大,当![]() 较大时,用户安全概率会随之减少。此外,还能发现,当
较大时,用户安全概率会随之减少。此外,还能发现,当![]() 和
和![]() 较小时,MHM-UPA方案比MM-UPA方案获得更高的安全概率,并且随着
较小时,MHM-UPA方案比MM-UPA方案获得更高的安全概率,并且随着![]() 的减小MHM-UPA方案比MM-UPA方案获得多的增益越来越高。相反,当
的减小MHM-UPA方案比MM-UPA方案获得多的增益越来越高。相反,当![]() 和
和![]() 较大时,就总平均安全概率而言,MM-UPA比MHM-UPA准则有更好的性能。产生此现象的原因是,MHM-UPA准则较MM-UPA更加兼顾了信号传输两跳的综合影响,在只有一层网络时,性能将会稍稍低于MM-UPA准则。同时,图3(b)还给出了当
较大时,就总平均安全概率而言,MM-UPA比MHM-UPA准则有更好的性能。产生此现象的原因是,MHM-UPA准则较MM-UPA更加兼顾了信号传输两跳的综合影响,在只有一层网络时,性能将会稍稍低于MM-UPA准则。同时,图3(b)还给出了当![]() 时,网络总安全概率与传输功率比
时,网络总安全概率与传输功率比![]() 或
或![]() 的关系对比分析。很容易的发现,总安全概率会随传输功率比
的关系对比分析。很容易的发现,总安全概率会随传输功率比![]() 的增大而增大。这是因为随着
的增大而增大。这是因为随着![]() 增大,对于Eves而言,链路越来不稳定。结合图3(a)、(b)发现,尽管当
增大,对于Eves而言,链路越来不稳定。结合图3(a)、(b)发现,尽管当![]() 和
和![]() 较大时,MM-UPA方案总平均安全概率高于MHM-UPA方案,但也仅仅存在较小的差距。
较大时,MM-UPA方案总平均安全概率高于MHM-UPA方案,但也仅仅存在较小的差距。
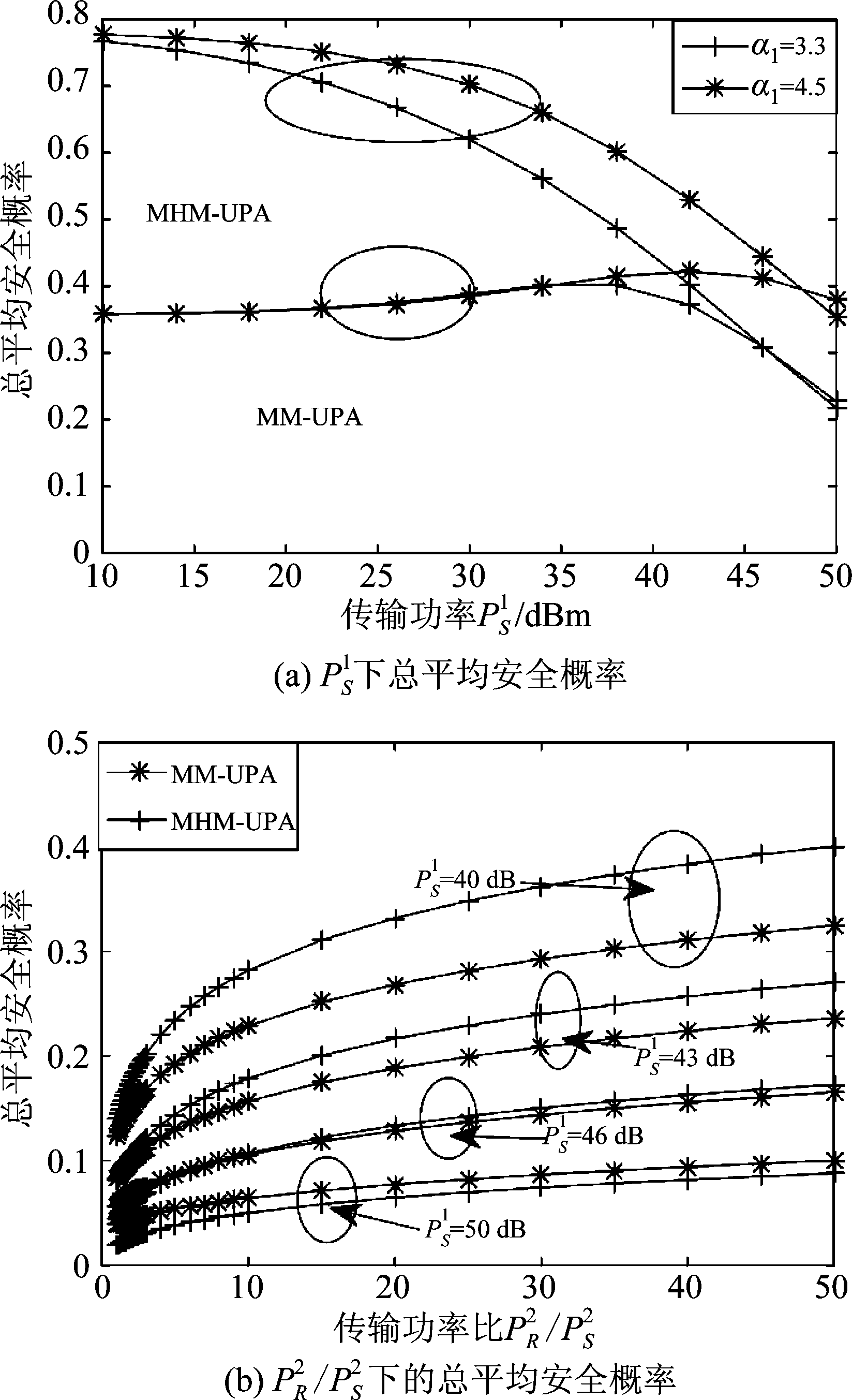
图3 安全概率比较分析
Fig.3 Secrecy probability comparison analysis
7 结论
本文研究了中继协作多层HetNets用户对与中继的级联和网络的物理层安全问题,不同于传统的单跳HetNets,在文章考虑的中继协作多层HetNets中,每层随机分布的中继协助信源-信宿用户对进行通信。为了解决用户对与网络中任意一层中继的级联问题,本文提出了MM-UPA和MHM-UPA准则,并获得了用户对级联概率。在此基础上,作为MM-UPA和MHM-UPA准则的应用,考虑了该中继协作多层HetNets的安全性能,利用PPP和随机几何方法,获得了用户对总的平均安全概率。
[1] 尤肖虎, 潘志文, 高西奇,等. 5G移动通信发展趋势与若干关键技术[J]. 中国科学:信息科学, 2014, 44(5):551-563.
You Xiaohu, Pan Zhiwen, Gao Xiqi, et al. 5G mobile communication development trend and several key technologies[J]. China Science: Information Science, 2014, 44(5):551-563. (in Chinese)
[2] Kamel M, Hamouda W, Youssef A. Physical layer security in ultra-dense networks[J]. IEEE Wireless Communications Letters, 2017, PP(99):1-1.
[3] Wang S, Ran C. Rethinking cellular network planning and optimization[J]. IEEE Wireless Communications, 2016, 23(2):118-125.
[4] 刘杰群, 陈瑾, 任国春,等. 能量收集全双工中继网络中的中继选择策略研究[J]. 信号处理, 2017, 33(1):116-125.
Liu Jiequn, Chen Jin, Ren Guochun, et al. Research on relay selection strategy of energy harvesting full-duplex relay network[J]. Journal of Signal Processing, 2017, 33(1):116-125. (in Chinese)
[5] Jo H S, Sang Y J, Xia P, et al. Heterogeneous cellular networks with flexible cell association: A comprehensive downlink SINR analysis[J]. IEEE Transactions on Wireless Communications, 2011, 11(10):3484-3495.
[6] Jo H S, Sang Y J, Xia P, et al.Outage probability for heterogeneous cellular networks with biased cell association[C]∥Global Telecommunications Conference. IEEE, 2012:1-5.
[7] Jia X, Fu H, Yang L, et al. Superposition coding cooperative relaying communications: Outage performance analysis[J]. International Journal of Communication Systems, 2015, 24(3):384-397.
[8] Jia X, Yang L, Zhu H. Cognitive opportunistic relaying systems with mobile nodes: average outage rates and outage durations[J]. Iet Communications, 2014, 8(6):789-799.
[9] Al-Hourani A, Kandeepan S, Hossain E. Relay-assisted device-to-device communication: A stochastic analysis of energy saving[J]. IEEE Transactions on Mobile Computing, 2016, 15(12):3129-3141.
[10] Agiwal M, Roy A, Saxena N. Next generation 5G wireless networks: A comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2017, 18(3):1617-1655.
[11] 俞菲,胡莹,巴特尔,等. 多中继协作通信系统容量分析及中继选择协作分集策略[J]. 信号处理, 2013, 29(12):1660-1669.
Yu Fei, Hu Ying, Bateer, et al. Capacity scaling of multi-relay channels and cooperative scheme based on relay selection[J]. Journal of Signal Processing, 2013, 29(12):1660-1669. (in Chinese)
[12] Jha S C, Sivanesan K, Vannithamby R, et al. Dual connectivity in LTE small cell networks[C]∥Globecom Workshops, Austin, TX, USA, 2015: 1205-1210.
[13] Semiari O, Saad W, Valentin S, et al. Matching theory for priority-based cell association in the downlink of wireless small cell networks[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2014:444- 448.
[14] Yang N, Wang L, Geraci G, et al. Safeguarding 5G wireless communication networks using physical layer security[J]. Communications Magazine IEEE, 2015, 53(4):20-27.
[15] Mukherjee A, Fakoorian S A A, Huang J, et al. Principles of physical layer security in multiuser wireless networks: A survey[J]. IEEE Communications Surveys & Tutorials, 2014, 16(3):1550-1573.
[16] Wang H M, Zheng T X, Yuan J, et al. Physical layer security in heterogeneous cellular networks[J]. IEEE Transactions on Communications, 2016, 64(3):1204-1219.
[17] Stoyan D, Kendall W S, Mecke J. Stochastic geometry and its applications[J]. Journal of the Royal Statistical Society, 1988, 151(1):239-240.
[18] Andrews J G, Baccelli F, Ganti RK. A tractable approach to coverage and rate in cellular networks[J]. IEEE Transactions on Communications, 2011, 59(11):3122-3134.
[19] Lee C, Haenggi M. Interference and outage in Poisson cognitive networks[J]. IEEE Transactions on Wireless Communications, 2012, 11(4):1392-1401.
[20] Brown T X. Cellular performance bounds via shotgun cellular systems[J]. IEEE Journal on Selected Areas in Communications, 2000, 18(11):2443-2455.
[21] 颉满刚, 贾向东, 周猛, 等. 多层中继协作HetNets用户对关联方案[J]. 计算机工程, 2017, 43(9):133-137.
Xie Mangang, Jia Xiangdong, Zhou Meng, et al. User-pair association scheme for multi-tier relay cooperativeHetNets[J]. Computer Engineering, 2017, 43(9):133-137. (in Chinese)
[22] Haenggi M, Ganti R K. Interference in large wireless networks[J]. Foundations & Trend![]() in Networking, 2008, 3(2):127-248.
in Networking, 2008, 3(2):127-248.



